§3.7本章复习(2)
章末测试(2)声的世界 课件 沪科版(2024)物理八年级全一册

-31-
(3)两位同学的测量结果存在误差,请你说出一条产生误 差的原因。
解:(1)金属管道的长度是:s=vt=340 m/s×2.6 s=884
m;
(2)因为声音在空气和金属中传播的速度不同,根据t=
s v
可知,在传播距离一定时,传播速度不同,所以小强先
(2)小华想选用三根琴弦来验证音调的高低与琴弦横截面 积的关系,应选_A__、__B_、__C__(填写编号)三根琴弦。
-27-
(3)小华认为:若想选用三根琴弦来验证音调的高低与琴 弦的材料的关系,还要添加一根琴弦J,则它的长度应为 __8_0_cm,横截面积应为__1_._0_2__mm2。
(4)本实验采用的探究方法是_控__制__变__量___法。
-20-
丙:吹笛子时,手指按住不同的孔便会发出不同的声音。 丁:放在钟罩内的闹钟正在响铃,把钟罩内的空气抽出 一些后,铃声明显减小。 (1)能说明声音产生条件的两个实验现象是_甲___、__乙__。 (2)__丁__说明了声音传播需要介质。 (3)_丙___说明了发声体振动频率不同,__音__调____不同。
-21-
19.超过50分贝(昼间)或40分贝(夜间)的声都属于噪声。 噪声尤以损害神经系统最为明显,严重影响人的健康, 人们把噪声称为无形杀手。朵朵同学想知道什么样的材 料隔音性能会更好,于是她设计了如下探究:
①先搜集各种材料,如衣服、报纸、平装书、锡箔纸; ②把闹钟放到一个鞋盒里,将衣服盖在鞋盒上方,然后 逐渐远离盒子直到听不见滴答声,记下此时人离盒子的 距离;
其形似于笛,与笛不同的是两端都是封闭的,而且吹孔
与孔指不在同一直线上,无孔膜而“有底”。演奏过程中
本章复习(教案) (3)

第十章数据的收集、整理与描述本章复习【知识与技能】1.了解通过全面调查和抽样调查收集数据的方法;会设计简单的调查问卷与收集数据;能根据问题查找有关资料,获得数据信息.2.通过抽样调查,初步感受抽样的必要性,通过案例了解简单随机抽样,体会用样本估计总体的思想.3.了解频数及频数分布,掌握划记法,会用表格整理数据表示频数分布,体会表格在整理数据中的作用.4.学会用简单频数分布直方图(等距分组)和折线图描述数据,进一步体会统计图表在描述数据中的作用,会根据问题需要选择适当的统计图描述数据.【过程与方法】先复习本章全部知识点,特别要回顾用表格整理数据和用条形图、扇形图、折线图、直方图描述数据的的技能技巧,再通过典题剖析、小结反思、拓展练习等手段培养学生综合地分析问题和解决问题的能力.【情感态度】通过实际参与收集、整理、描述和分析数据的活动,经历统计的一般过程,感受统计在生活和生产中的作用,增强学习统计的兴趣,初步建立统计的观念,培养重视调查研究的良好习惯和科学态度.【教学重点】1.利用图表描述数据.2.综合地运用统计知识分析问题和解决问题.【教学难点】运用统计知识解决有关的综合题、难题,提高学生的变通能力.一、知识框图,整体把握数据处理的一般过程:二、回顾思考,梳理知识1.数据处理一般包括收集数据、整理数据、描述数据和分析数据等过程,数据处理可以帮助我们更好地了解周围世界,对未知的事物作出合理的推断和预测.2.全面调查和抽样调查是收集数据的两种方式,全面调查通过调查总体来收集数据,抽样调查通过调查样本收集数据.全面调查的优点:全面、准确;缺点:(1)费时、费力;(2)对带有破坏性的实验无法采用.抽样调查的优点:(1)省时、省力;(2)适宜于对实验带有破坏性的事物进行调查;缺点:不全面,不准确.3.实际调查中常常采用抽样调查的方法获取数据.简单随机抽样的特点是总体中的每个个体都有相等的机会被抽到,抽取的样本具有代表性.4.利用统计图表描述数据是统计分析的重要环节,对于收集到的数据加以整理,并用统计图表描述出来,可以使我们了解数据的分布特征和规律,帮助我们从数据中获取信息,得出结论.5.条形图能够显示每组中的具体数据;扇形图能够显示部分在总体中所占的百分比;折线图能够显示数据的变化趋势;直方图能够显示数据的分布情况. 三、典例精析,复习新知例1 某校320名学生在电脑培训前后参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,随机抽取32名学生的两次考试考分等级,所绘制的统计图如图所示.试回答下列问题:(1)这32名学生经过培训,考分等级“不合格”的百分比由___下降到____.(2)估计该校,培训后考分等级为“合格”与“优秀”的学生共有____名.(3)你认为上述估计合理吗?理由是什么?答:__________,理由______________________________.解:(1)考前24/32×100%=75%,考后8/32×100%=25%.(2)320×(16/32+8/32)=240(名)(3)不合理,它只是随机抽取,而没有以“不合格”、“合格”、“优秀”的三个等级中按一定的比例分别来随机抽取,即没有分层抽取,故样本缺乏代表性.例2为了解居民使用超薄塑料袋的情况,某中学课外实践小组的同学利用业余时间对本城区居民家庭使用超薄塑料袋的情况进行了抽样调查.统计情况如图所示,其中A为“不再使用”,B为“明显减少了使用量”,C为“没有明显变化”.(1)本次抽样的样本容量是_______;(2)图中a=_______(户),c=_______(户);(3)若被调查的家庭占全城家庭数的10%,请估计该城区不再使用超薄塑料袋的家庭数;(4)针对本次调查结果,请用一句话发表你的感想.解:(1)800÷72°/360°=4000(户),故本次抽样的样本容量为4000;(2)a=4000×(1-10%-20%)=2800;c=4000×10%=400;(3)2800÷10%=28000(户)或4000÷10%×70%=28000(户);(4)“不再使用超薄塑料袋的家庭占绝大多数”、“环保意识增强的家庭是多数”、“少数家庭还应该增强环保意识”等.例3初三某班对最近一次数学测验成绩(得分取整数)进行统计分析,将所有成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题:(1)该班共有____名同学参加这次测验;(2)在该频数分布直方图中画出频数折线图;(3)若这次测验中,成绩80分以上(不含80分)为优秀,那么该班这次数学测验的优秀率是多少?解:(1)2+9+10+14+5=40(名);(2)图略;(3)14540×100%=47.5%.例4(云南楚雄中考)在2009年楚雄州“火把节”房交会期间,某房地产公司对参加本次房交会的消费者进行了随机的问卷调查,共发放1000份调查问卷,并全部收回.根据问卷调查,将消费者年收入的情况整理后,制成表格如下:根据调查问卷,将消费者打算购买住房面积的情况整理后,作出如图所示的部分频数分布直方图和扇形统计图.注:每组包含最小值不包含最大值,且住房面积取整数.(1)根据表格可得a=_____,被调查的1000名消费者的平均年收入为_____万元.(2)补全频数分布直方图和扇形统计图.(3)若楚雄州现有购房打算的约有40000人,请估计购房面积在80至120平方米的大约有多少人?解:(1)200;2.39;(2)图略(3)(36%+24%)×40000=24000(人),所以估计购房面积在80至120平方米的大约有24000人.例5 一个水库养了某种鱼10万条,从中捞了20条,称得的质量如下(单位:kg):2.50 1.50 1.00 2.80 1.601.702.903.00 1.90 2.802.60 2.80 2.70 2.60 2.701.602.00 2.10 2.20 2.30经市场调查,1.00~1.50(不包括1.50)kg的鱼每千克8元,1.50~2.00(不包括2.00)kg的鱼每千克9元,2.00~2.50(不包括2.50)kg的鱼每千克10元,2.50~3.00(不包括3.00)kg的鱼每千克11元,3.00(包括3.00kg)以上每千克12元.请你用本章所学的知识估计该水库中这种鱼的价值.分析:用频数分布表、频数分布直方图或频数折线图分析.解:依题意,取组距为0.5kg,3.00 1.000.5=4,所以应分成5组.列频数分布表.可画频数分布直方图与频数折线图,如图所示:于是可估计在 1.00~1.50kg范围内的鱼有100000×1/20=5000(条),在1.50~2.00kg范围内的鱼有100000×5/20=25000(条),在2.00~2.50kg范围内的鱼有100000×4/20=20000(条),在 2.50~3.00kg范围内的鱼有100000×9/20=45000(条),在3.00kg(包括3.00kg)以上的鱼有5000(条).可估计价值为:8×5000×1.25+9×25000×1.75+10×20000×2.25+11×45000×2.75+12×5000×3.25=2450000(元).可估计该水库中这种鱼的总价值为2450000元.【教学说明】用统计知识估产、估值是现实生活中经常遇到的问题,也是中考命题者非常青睐的问题,同学们一定要加强这方面的训练.四、师生互动,课堂小结中考中对本章知识点的考查主要是用图表描述数据,同学们一定要加强对往届这方面的中考题的训练与研究,以便在今后的考试中得心应手,立于不败之地.1.布置作业:从教材“复习题10”中选取.2.完成练习册中本课时的练习.这节课的内容主要是让学生学会收集数据,感受生活中处处有数学,会把数据分类、收集,掌握整理数据的方法.教学中努力用课标中的新理念指导教学,使学生真正成为学习的主人.在教学中,注重让学生全程参与学习活动——课前参与、课中体会、课后反思,激发学生的学习积极性、主动性,使学生体会数学知识的产生、形成与发展的过程,获得积极的情感体验,感受数学的力量,同时,让学生掌握必要的基础知识与基本技能.。
物理化学03章_热力学第二定律(二)

Ssys = 19.14 J K
Ssur = 0
1
(系统未吸热,也未做功)
Siso = Ssys + Ssur = 19.14 J K 1 > 0
(2)为不可逆过程.
例2:在273 K时,将一个 22.4 dm3 的盒子用隔板一分为二,
0.5 mol 0.5 mol O2 (g) N2 (g)
p1 V1 p2 V2 T2 p2 V2 ∵ = ∴ = T1 T2 T1 p1V1
V2 p2V2 ∴ S = nR ln + nCV ,m ln V1 p1V1
V2 p2 V2 = nR ln + nC V ,m ln + nC V ,m ln V1 p1 V1
p2 V2 ∴ S = nCV ,m ln + nC p ,m ln p1 V1
因为在可逆相变中压力恒定,所以可逆热即为相 因为在可逆相变中压力恒定, 变焓.又由于温度一定,所以, 变焓.又由于温度一定,所以,物质 B 由 α 相态 转化为 β 相态
p ,T B (α ) → B ( β )
的相变熵为: 的相变熵为:
β α H β α S = T
用上式,可计算正常熔点下的熔化熵, 用上式,可计算正常熔点下的熔化熵,正常 沸点下的蒸发熵等等. 沸点下的蒸发熵等等.
= TC S > 0
Q W
热源
R2
TC
1
W2
Q W2
TB热源做功能力低于TA
TB热源做功能力低于TA
其原因是经过了一个不可逆的热传导过程 功变为热是无条件的,而热不能无条件 地全变为功. 热和功即使数量相同,但"质量"不等, 功是"高质量"的能量. 高温热源的热与低温热源的热即使数量相 同,但"质量"也不等,高温热源的热"质量" 较高,做功能力强. 从高"质量"的能贬值为低"质量"的能 是自发过程.
傅里叶变换的证明

1 T nm 2 cos(nw1t ) cos(m w t ) dt 1 0 n m
即有: t
t0 T1
0
t0 T1
t0
1 T nm 2 sin(nw1t ) sin(m w t ) dt 1 0 n m
n
F (nw1)e
jnw1t
n
jnw1t F e n (6)
证明:思路由三角形式→指数形式
f (t ) a0 [an cos(nw1t ) bn sin(nw1t )] ( 7)
n 1
利用欧拉公式:
jnw1t jnw1t 1 cos( nw t ) ( e e ) 1 2 8) jnw1t jnw1t ( 1 e ) sin(nw1t ) 2 j (e
把(10),(11)代入(9)得
f (t ) a0 [ F (nw1 )e jnw1t F (nw1 )e jnw1t ] ( 12 )
n 1
令a0 F (0)
F ቤተ መጻሕፍቲ ባይዱnw )e
n1 1
jnw1t
n
F (nw )e
1
1
jnw1t
(12)式写为f (t )
an
t0 T1 1 T1 t 0
f (t )dt
信号的平均值、直流分量
是nw1的偶函数 是nw1的奇函数
t0 T1 2 T1 t 0
f (t ) cos(nw1t )dt
2 bn T 1
t0 T1
t0
f (t ) sin(nw1t )dt
高中数学 第3章 空间向量与立体几何 3.7 点到平面的距离课件 湘教版选修2-1

d=|AP1|=___||_A_P_|_c_o_s_∠_P_A__N_|__=___|_A_|Pn_·|_n_| __.
1.已知直线 l 过点 A(1,-1,2),和 l 垂直的一个向量为 n=
(-3,0,4),则 P(3,5,0)到 l 的距离为( )
A.5
B.14
C.154
D.45
答案:C
2.已知直线 l 与平面 α 相交于点 O,A∈l,B 为线段 OA 的中
d=
|B→C|2-B→|CA→·′AC→′|C2=
16 4-14
=2
35 7.
用向量法求点到直线的距离的一般步骤 (1)建立空间直角坐标系; (2)求直线的方向向量; (3)计算所求点与直线上某一点所构成的向量在直线的方向向 量上的射影长; (4)利用勾股定理求解.另外,要注意平行直线间的距离与点到 直线的距离之间的转化.
则 A(4,0,0),B(0,3,0),P0,0,95, 所以A→B=(-4,3,0),A→P=-4,0,95, 所以A→P在 AB 上的投影长为|A→P|A·→BA→| B|=156, 所以点 P 到 AB 的距离为 d= |A→P|2-1562= 16+8215-22556=3. 答案:3
点到直线的距离 如图,在空间直角坐标系中有长方体 ABCD-A′B′C′D′, AB=1,BC=2,AA′=3,求点 B 到直线 A′C 的距离.
又 AC∥平面 PEF,
所以
AC
到平面
PEF
的距离为
17 17 .
用向量法求点面距的步骤 (1)建系:建立恰当的空间直角坐标系; (2)求点坐标:写出(求出)相关点的坐标; (3)求向量:求出相关向量的坐标; (4)利用公式即可求得点到平面的距离.
03-7其他固定灭火设施简介
第3章建筑消防系统3.7其他固定灭火设施简介3.7 其他固定灭火设施因建筑物使用功能不同,其内的可燃物质性质各异,因此,仅使用水做为消防手段不能达到扑救火灾的目的,甚至还会带来更大的损失。
应根据可燃物的物理、化学性质,采用不同的灭火方法和手段,才能达到预期的目的。
干粉灭火系统卤代烷灭火系统二氧化碳灭火系统泡沫灭火系统 蒸汽灭火系统 烟雾灭火系统 固定消防水炮灭火系统原理以干粉作为灭火剂的灭火系统称为干粉灭火系统。
干粉灭火剂是一种干燥的、易于流动的细微粉末,平时贮存于干粉灭火器或干粉灭火设备中,灭火时靠加压气体(二氧化碳或氮气)的压力将干粉从喷嘴射出,形成一股携夹着加压气体的雾状粉流射向燃烧物。
历时短、效率高、绝缘好、灭火后损失小、不怕冻、不用水、可采期储存等。
优点:扑救燃烧过程能释放氧气或提供氧源化合物的火灾;燃烧过程中具有阴火的火灾;精密仪器、精密电气设备、电子计算机等场所发生的火灾。
适用范围 易燃、可燃液体燃料或可熔化固体的火灾; 可燃气体或液体因压力喷射而形成的火灾; 室内外变压器、油浸开关等电气设备火灾; 木材、造纸、印刷、棉纺、胶带等明火燃烧的火灾; 钾、钠、镁、铝镁合金、钛、铝钛合金、锆、锂等金属发生的火灾。
不 适 用 于干粉有普通型干粉(BC类)、多用途干粉(ABC类)和金属专用灭火剂(D类火灾专用干粉)。
BC类干粉根据其制造基料的不同有钠盐、钾盐、氨基干粉之分。
这类干粉适用于扑救易燃、可燃液体如汽油、润滑油等火灾,也可用于扑救可燃气体(液化气、乙炔气等)和带电设备的火灾。
ABC类干粉按其组成的基料有磷酸盐、硫酸铵与磷酸铵混合物和聚磷酸铵之分。
这类干粉适用于扑救易燃液体、可燃气体、带电设备和一般固体物质如木材、棉、麻、竹等形成的火灾。
D类火灾专用灭火剂,当其投加到某些燃烧金属时,可与金属表层发生反应而形成熔层;而与周围空气隔绝,使金属燃烧窒熄。
干粉灭火系统按其安装方式有固定式、半固定式之分。
七年级下学期数学各章复习资料
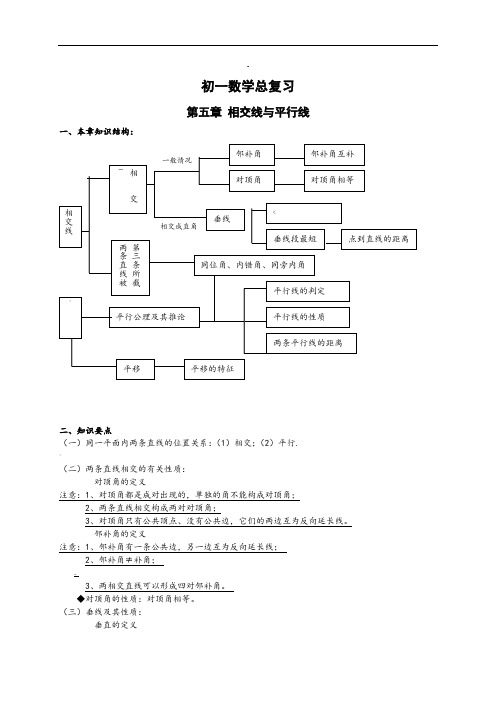
·初一数学总复习第五章 相交线与平行线一、本章知识结构:{-二、知识要点(一)同一平面内两条直线的位置关系:(1)相交;(2)平行. '(二)两条直线相交的有关性质:对顶角的定义注意:1、对顶角都是成对出现的,单独的角不能构成对顶角;2、两条直线相交构成两对对顶角;3、对顶角只有公共顶点、没有公共边,它们的两边互为反向延长线。
邻补角的定义注意:1、邻补角有一条公共边,另一边互为反向延长线;2、邻补角≠补角; 。
3、两相交直线可以形成四对邻补角。
◆对顶角的性质:对顶角相等。
(三)垂线及其性质:垂直的定义一般情况相交成直角相交线相交{两条直线第三条所截两条直线被邻补角 垂线邻补角互补 点到直线的距离同位角、内错角、同旁内角、平行线平行公理及其推论平行线的性质 平行线的判定 平移 对顶角对顶角相等垂线段最短<存在性和唯一性两条平行线的距离平移的特征两条直线相交,夹角为90°时,这两条直线的位置关系称为垂直,这两条线互为对方的“垂线”,它们的交点称为“垂足”;根据定义判断两直线是否垂直时,只需要判断其夹角是不是90°。
垂线的性质1、过一点有且只有一条直线与已知直线垂直;2、连接直线外一点与直线上各点的所有线段中,垂线段最短(其它的线段称为“斜线段”)。
;距离1、点到直线的距离:从直线外一点到这条直线的垂线段的长度,称为点到直线的距离;2、平行线之间的距离:作平行线的垂线,两个垂足之间的线段的长度,称为平行线之间的距离。
(四)两条直线被第三条直线所截,三种位置的角:同位角;内错角;同旁内角。
(五)平行线及平行线的判定、性质:1.在同一平面内,不相交的两条直线叫做平行线;2.平行公理及其推论:◆经过直线外一点,有且只有一条直线与已知直线平行;》◆平行于同一条直线的两条直线互相平行。
平行线的判定平行线的性质1、同位角相等,两直线平行2、内错角相等,两直线平行3、同旁内角互补,两直线平行4、平行于同一条直线的两直线平行5、—6、垂直于同一条直线的两直线平行1、两直线平行,同位角相等2、两直线平行,内错角相等3、两直线平行,同旁内角互补4、经过直线外一点,有且只有一条直线与已知直线平行(六)平移及其性质:平移的条件:(1)平移的方向(2)移动的距离平移的性质:~◆平移变换只改变图形的位置,不改变图形的形状和大小;◆平移变换中,连结各组对应点的线段平行(或共线)且相等。
3.7Python语言基础—本章小结(习题)浙教版(2019)高中信息技术必修第一册教学设计

作用与目的:
-巩固学生在课堂上学到的Python语言基础知识点和技能。
-通过拓展学习,拓宽学生的知识视野和思维方式。
-通过反思总结,帮助学生发现自己的不足并提出改进建议,促进自我提升。
教学资源拓展
1.拓展资源:
- Python编程实战案例:提供一些与Python编程相关的实战案例,如简单的游戏开发、数据分析、网页爬虫等,让学生通过实际操作加深对Python编程的理解。
在课中强化技能环节,我通过讲解知识点、组织课堂活动和解答疑问,帮助学生深入理解Python语言基础知识,掌握编程技能。在讲解知识点时,我注重结合实例,使抽象的概念具体化,以便学生更好地理解和掌握。然而,在课堂活动中,我发现部分学生参与度不高,可能是因为他们对编程实践还存在一定的恐惧心理。因此,在今后的教学中,我需要更多地鼓励和引导这部分学生参与课堂活动,帮助他们克服恐惧,提高编程实践能力。
(1)Python语言的语法和编程技巧:学生可能对一些新的概念和语法规则感到困惑,需要通过讲解示例代码、引导学生讨论和解决问题,帮助他们理解和掌握。
(2)编程实践:学生可能对编写程序解决实际问题感到困难,需要通过示例和练习,引导学生逐步掌握编程方法。
(3)本章小结的编写:学生可能对本章小结的编写方式和内容感到困惑,需要通过指导学生回顾和总结本章所学知识,帮助他们完成小结。
-提问与讨论:针对不懂的问题或新的想法,勇敢提问并参与讨论。
教学方法/手段/资源:
-讲授法:通过详细讲解,帮助学生理解Python语言基础知识。
-实践活动法:设计实践活动,让学生在实践中掌握编程技能。
-合作学习法:通过小组讨论等活动,培养学生的团队合作意识和沟通能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3.7本章复习(2)
【教学目标】
1.梳理本章的基础知识,形成合理的知识体系和网络,进一步认识和理解指数函数、对数函数的概念与基本性质和它们之间的联系;并且能够清晰明辨三类函数模型的增长速度的差异,理解直线增长、指数增长、对数增长的含义;
2.会运用指数函数和对数函数解决一些相关的实际问题以及较简单综合问题,在解决问题的过程中,提高学生提出问题、分析问题和解决问题的能力;
3.会利用方程函数、数形结合、转化等数学思想方法解决与指数函数和对数函数有关的问题;
4.在解题过程中引导学生探究、提问,促使学生形成良好的学习习惯,养成积极向上的学习精神;通过对相关知识的简介,使学生了解数学问题的实际背景,从而增强学生学习数学的兴趣。
【重点难点】
1.重点:指数函数、对数函数基本性质及其初步运用
2.难点:指数函数、对数函数综合问题的解决
【教学过程】
本节主要是关于指数、对数、幂函数的较简单的综合问题的解决. Ⅰ.典型例题
【例1】若()(0,1)x f x a a a =>≠且,则1212()()
(
)22
x x f x f x f ++≤
.
证明:12
12
12122
()()()222
x x x x f x f x x x a a f a
++++-=-0==≥. ∴ 1212()()
(
)22
x x f x f x f ++≤
. (注:此性质为函数的凹凸性)
【例2】已知函数2()(0,0)1
bx
f x b a ax =
≠>+. (1)判断()f x 的奇偶性; (2)若3211(1),log (4)log 42
2
f a b =-=,求a ,b 的值.
解:(1)()f x 定义域为R ,2
()()1
bx
f x f x ax --=
=-+,故()f x 是奇函数. (2)由1
(1)12
b f a =
=+,则210a b -+=.又log 3(4a -b )=1,即4a -b =3. 由{21043
a b a b -+=-=得a =1,b =1.
【例3】设a >0, ()x x e a
f x a e
=+是R 上的偶函数.
(1)求a 的值; (2)证明()f x 在(0,)+∞上是增函数.
解:(1)∵ ()x x e a
f x a e =+是R 上的偶函数,∴ ()()0f x f x --=.
∴ 110()()x x x x x x e a e a a e a e a e a e a a ---+--=⇒-+-10()()0x x a e e a
-=⇒--=.
e x -e -x 不可能恒为“0”, ∴ 当
1
a
-a =0时等式恒成立, ∴a =1. (2)在(0,)+∞上任取x 1<x 2,
12121212
12111()()()()x x x x x x x x e f x f x e e e a e e e e -=+--=-+-12121
()(1)x x x x e e e e =-- ∵ e >1,x 1<x 2, ∴ 1
2
1x x e e >>, ∴12
x x e e >1,121212
()(1)
x x x x x x e e e e e e --<0,
∴ 12()()0f x f x -<, ∴ ()f x 是在(0,)+∞上的增函数.
点评:本题主要考查了函数的奇偶性以及单调性的基础知识.此题中的函数,也可以看成指数函数x y a =与x a y a
x
=+的复合,可以进一步变式探讨x a y a
x
=+的单调性. Ⅱ. 巩固提高练习
1.已知1,1a b ><-,则函数x y a b =+的图象必不过第 象限; 函数2
1(0,x y a
a -=+>且1)a ≠的图像必经过点 ;
2.若01a <<且函数()|l g |a f x o x =,则下列各式中成立的是( )
A.1(2)(3)()4f f f >>
B. 11
()(2)()43f f f >>
C. 11()(2)()34f f f >>
D. 11
()()(2)43
f f f >>
3.已知函数()lg()x x f x a b =-(,a b 为常数,10a b >>>),若(1,)x ∈+∞时,()0f x >恒成立,则( )
A.1a b -≥
B.1a b ->
C. 1a b -≤
D.1a b =+
4.对于函数()f x 定义域中任意的)(,2121x x x x ≠,有如下结论:
①1212()()()f x x f x f x +=⋅;②)()()(2121x f x f x x f +=⋅;③
0)
()(2
121>--x x x f x f ;
④2)
()(22121x f x f x x f +<
⎪⎭
⎫
⎝⎛+. 当()lg f x x =时,上述结论正确结论的序号是 . 当()2x f x -=时,上述结论正确结论的序号是 ;
当1
2
()f x x =时,上述结论正确结论的序号是 .
6.函数()log (1)x a f x a x =++在[0,1]上的最大值与最小值之和为a ,则a 值为 7.求函数4221x x y =+⋅+的值域 .
8.设函数()f x 的定义域为(0)+∞,对任意的0,0x y >>,都有()()x f f x f y y ⎛⎫
=- ⎪⎝⎭恒成
立,且当1x >时,()0f x >.
(1) 求(1)f 的值;
(2) 探究()f x 在区间(0,) 上是否具有单调性;
(3) 你能找出符合本题条件的一个函数吗?请将你找出得函数写出来,并由此发 表看法.
9.一片森林的面积为a ,计划每年砍伐一批木材,每年砍伐面积的百分比相等,则砍伐到原面积的一半时,所用的时间是t 年.为保护生态环境,森林面积至少要保留
原面积的1
4
,已知到今年为止,森林剩余面积为2a . (1) 问到今年为止,该森林已砍伐了多少年? (2) 问今后最多还能砍伐多少年?
Ⅲ. 课时小结
说说本节后有什么收获?
【专家点评】
本节是在上节课梳理基础知识、形成合理的知识体系和网络的基础上,进一步认识和理解指数函数、对数函数的概念与基本性质和它们之间的联系,在解决一些相关的实际问题以及较简单综合问题的过程中能引导学生探究、提问,促使学生形成良好的学习习惯,养成积极向上的学习精神,提高学生提出问题、分析问题和解决问题的能力;且例题选择典型,难易程度适中,为本节课教学任务的完成和教学目标的达到创造了条件.设计具有良好的操作性. (点评人:陕西师范大学附属中学 张文俊)。
