2008年成都外国语学校
成都外国语学校初中英语九年级全册Unit 6经典复习题(含答案)

一、选择题1.We each _____ strong points and each of us on the other hand _____weak points. A.have, have B.has, haveC.has, has D.have, has D解析:D【详解】句意:我们每个人都有的长处,换言之,,我们每个人都有缺点。
考查主谓一致。
“We each”中的each是We的同位语,故谓语动词用复数,第一空用have;“each of us”强调主语为每个人,故谓语动词用单数,第二空用has。
故选D。
【点睛】2.---Would you help me work out the physics problem,Bill?--- .A.Yes,quite right B.Never mind C.That’s right D.With pleasure D解析:D【详解】句意:--你能帮我做出这个物理题吗?--很乐意帮忙。
A. Yes,quite right是的,很正确;B. Never mind没关系;C. That’s right那是正确的;D. With pleasure很乐意;只有D选项符语言习惯。
故选D。
3.----Must I finish my homework now ?----No, you _____. You _____ do it tomorrow.A.mustn’t, can B.needn’t, can C.couldn’t , may D.can’t, must B解析:B【详解】句意:--我现在必须完成我的作业吗?--不,你不必。
你可以明天完成。
根据No,可知下面为否定回答,must的含义是必须一定,其否定形式mustn't表示禁止的含义。
在这里不是禁止的意思。
must的否定回答一般可借助于needn't来构成,根据题意可知,故选B。
四川省成都市外国语学校2023-2024学年高二下学期期末考试数学试题(含解析)

成都外国语学校2023-2024学年度下期期末考试高二数学试卷注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.2.本堂考试120分钟,满分150分.3.答题前,考生务必先将自己姓名、学号填写在答题卡上,并使用2B 铅笔填涂.4.考试结束后,将答题卡交回.第Ⅰ卷(选择题)一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数z 满足,则( )A .BCD2.函数的单调增区间是( )A .B .C .D .3.关于线性回归的描述,有下列命题:①回归直线一定经过样本点的中心;②相关系数r 越大,线性相关程度越强;③决定系数越接近1拟合效果越好;④随机误差平方和越小,拟合效果越好.其中正确的命题个数为( )A .1B .2C .3D .44.设,,)A .B .C .D .5.在空间直角坐标系中,,,,,三角形ABC 重心为G ,则点P 到直线AG 的距离为( )A .BCD6.已知点,抛物线上有一点,则的最小值是( )A .10B .8C .5D .47.有5名大学生到成都市的三所学校去应聘,若每名大学生至多被一个学校录用,每个学校至少录用其中一人,则不同的录用情况种数是( )A .390B .150C .90D .420(1i)3i z +=-z =()(3)e xf x x =-(,2)-∞(0,3)(1,4)(2,)+∞2R 1cos 662a =︒︒2sin13cos13b =︒︒c =a b c>>a b c<<a c b<<b c a<<(0,0,0)P (1,0,0)A (0,2,0)B (0,0,3)C 67(A 2:4C y x =()00,P x y 202||2y PA +8.双曲线的左、右焦点分别为,,,右支上一点P 满足,直线l 平分,过点,作直线l 的垂线,垂足分别为A ,B .设O 为坐标原点,则的面积为()A .B .C .D .10二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有错选的得0分.9.若“,”为假命题,则实数a 的取值可以为( )A .8B .7C .6D .510.我国5G 技术研发试验在2016~2018年进行,分为5G 关键技术试验、5G 技术方案验证和5G 系统验证三个阶段.2020年初以来,5G 技术在我国已经进入高速发展的阶段,5G 手机的销量也逐渐上升.某手机商城统计了2022年5个月5G 手机的实际销量,如下表所示:月份2022年1月2022年2月2022年3月2022年4月2022年5月月份编号x 12345销量y (部)5096a185227若y 与x 线性相关,且求得回归直线方程为,则下列说法正确的是( )A .B .y 与x 的相关系数为负数C .y 与x 正相关D .2022年7月该手机商城的5G 手机销量约为365部11.已知定义在R 上的函数满足为偶函数,为奇函数,当时,,则下列说法正确的是( )A .B .C .函数为R 上的偶函数D .函数为周期函数三、填空题:本题共3小题,每小题5分,共15分.12.若“”是“”的充分不必要条件,则实数m 的取值范围为__________.13.若,则的值为__________.14.若数列满足,(,d 为常数),则称数列为调和数列.已知数列为调和数列,且,则的最大值为__________.222:1(0)5x y C a a -=>1F 2F 12PF PF ⊥12F PF ∠1F 2F OAB △[4,6]x ∃∈210x ax -->ˆ455yx =+142a =()y f x =132f x ⎛⎫-⎪⎝⎭(21)f x +10,2x ⎡⎤∈⎢⎥⎣⎦()0f x '>(0)0f =4133f f ⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭()y f x =()y f x =12x <<|2|1x m -<7270127(2)(1)(1)(1)x a a x a x a x -=+++++++ 0127a a a a ++++ {}n a 111n n d a a +-=*n ∈N {}n a 21n x ⎧⎫⎨⎬⎩⎭222212320222022x x x x ++++= 92014x x +四、解答题:共77分,解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)在中,角A ,B ,C 所对的边分别为a ,b ,c ,设向量,,,.(1)求函数的最小值;(2)若,,求的面积.16.(本小题满分15分)如图,在四棱锥中,,,平面PAB ,,E 、F 分别是棱PB 、PC 的中点.(1)证明:平面ACE ;(2)求平面ACE 与平面PAD 的夹角的正弦值.17.(本小题满分15分)某校为了解本校学生课间进行体育活动的情况,随机抽取了50名男生和50名女生,通过调查得到如下数据:50名女生中有10人课间经常进行体育活动,50名男生中有20人课间经常进行体育活动.(1)请补全列联表,试根据小概率值的独立性检验,判断性别与课间经常进行体育活动是否有关联;体育活动合计性别课间不经常进行体育活动课间经常进行体育活动男女合计(2)以样本的频率作为概率的值,在全校的男生中任取4人,记其中课间经常进行体育活动的人数为X ﹐求X 的分布列、数学期望和方差.附表:0.10.050.010.0050.0012.7063.8416.6357.87910.828附:,其中.ABC △4sin ,m A ⎛= ⎝ 1cos ,2cos 22n A A ⎛⎫= ⎪⎝⎭ ()f A m n =⋅ π5π,46A ⎡⎤∈⎢⎥⎣⎦()f A ()0f A =a =b c +=ABC △P ABCD -//AD BC 224PA BC AD AB ====AD ⊥PA AB ⊥//DF 22⨯0.05α=αx α22()()()()()n ad bc a b c d a c b d χ-=++++n a b c d =+++18.(本小题满分17分)已知椭圆的左、右焦点别为,,过点的动直线l 交E 于A ,B两点,点A 在x 轴上方,且l 不与x 轴垂直,的周长为与E 交于另一点C ,直线与E 交于另一点D ,点P 为椭圆E 的下顶点,如图.(1)求E 的方程;(2)证明:直线CD 过定点.19.(本小题满分17分)定义运算:,已知函数,.(1)若函数的最大值为0,求实数a 的值;(2)若函数存在两个极值点,,证明:;(3)证明:.成都外国语学校2023-2024学年度下期期末考试高二数学试卷 参考答案:1.A【分析】利用复数的运算性质求出共辄复数,再求模即可.【详解】因为,所以,所以,,故C 正确.故选:A .2.D【分析】对函数求导,根据导函数的正负,确定函数的单调递增递减区间即得.【详解】由求导得,,则当时,,即函数在上单调递增;2222:1(0)x y E a b a b +=>>1F 2F 1F 2ABF △2AF 2BF m n mq np p q =-ln 1()1x x f x a -=1()1g x x=-()f x ()()()h x f x g x =+1x 2x ()()121220h x h x a x x --+<-222211111111e 234n ⎛⎫⎛⎫⎛⎫⎛⎫+++⋯+< ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭(1i)3i z +=-23i (3i)(1i)34i i 34i 112i,1i (1i)(1i)22z ----+--=====-++-12i z =+z ==()(3)e xf x x =-()(2)e xf x x '=-2x >()0f x '>()(3)e xf x x =-(2,)+∞当时,,即函数在上单调递减,故函数的单调递增区间为.故选:D .3.C【分析】根据回归直线方程的性质,相关系数、决定系数及随机误差平方和的意义判断各项的正误即可.【详解】对于①,回归直线一定经过样本点的中心,故①正确;对于②,相关系数r 的绝对值越接近于1,线性相关性越强,故②错误;对于③,决定系数R 越接近1拟合效果越好,故③正确;对于④,随机误差平方和越小,拟合效果越好,故④正确.故选:C .4.C【分析】利用二倍角公式及两角差的正弦公式化简,再根据正弦函数的性质判断即可.【详解】,,,因为在上单调递增,所以,故.故选:C .5.B【详解】在空间直角坐标系中,,,,,三角形ABC 重心为G ,所以,,,所以在上的投影为:所以点P 到直线AG.故选:B .6.B【分析】结合坐标运算和焦半径公式,转化,再利用数形结合求最值.【详解】已知抛物线上有一点,则,即.2x <()0f x '<()(3)e xf x x =-(,2)-∞()(3)e xf x x =-(2,)+∞()1cos 66sin 30cos 6cos30sin 6sin 306sin 242a =︒︒=︒︒-︒︒=︒-︒=︒sin26b =︒sin 25c ====︒sin y x =π0,2⎛⎫⎪⎝⎭sin 26sin 25sin 24︒>︒>︒a c b <<(0,0,0)P (1,0,0)A (0,2,0)B (0,0,3)C 12,,133G ⎛⎫ ⎪⎝⎭(1,0,0)PA =22,,133AG ⎛⎫=- ⎪⎝⎭PA AG PA AG AG⋅== =22||2(||||)22y PA PF PA +=+-2:4C y x =()00,P x y 2004y x =2004y x =又,故在抛物线的外部,则,因为抛物线的焦点为,准线方程为,则,故.由于,当A ,P ,F 三点共线(P 在A ,F 之间)时,取到最小值,则的最小值为.故选:B .7.A【分析】根据录用的人数,结合组合和排列的定义分类讨论进行求解即可.【详解】若5人中有且仅有3人被录用,满足条件的录用情况有种,若5人中有且仅有4人被录用,满足条件的录用情况有种,若5人都被录用,满足条件的录用情况有种,由分类加法计数原理可得符合要求的不同的录用情况种数是390.故选:A .8.D【分析】根据给定条件,求出,结合几何图形及双曲线定义可得的面积得解.【详解】由双曲线,解得,243>⨯(A 2:4C y x =()()220002||2||2||21|224y y PA PA x PA x PA ⎛⎫+=+=+=++- ⎪⎝⎭∣2:4C y x =(1,0)F 1x =-0||1PF x =+()2002||21||22(||||)22y PA x PA PF PA +=++-=+-||||||PF PA AF +≥||||PF PA +||5AF ==202||2(||||)22y PA PF PA +=+-2528⨯-=35A 60=1143435322C C C A 180A =1122335453332222C C C C A A 150A A +=2a OAB △212S a =222:1(0)5x y C a a -=>=220a =令直线交的延长线交于Q ,直线交于N ,则,,由PA 平分,且,得,则,,,显然A ,B 分别为线段,的中点,而O 是的中点,于是,,,即,,所以的面积.故选:D .【点睛】关键点点睛:本题求出面积的关键是作出点Q ,借助几何图形的特征,结合双曲线定义求得.9.ABC【分析】根据条件,将问题转化成即在恒成立,令,利用其单调性,求出的最大值,即可求解.【详解】因为“,”为假命题,所以,恒成立,即在恒成立,所以且.令,易知在上是增函数,所以,所以.故选:ABC .10.AC【分析】对A ,根据样本中心在回归直线上即可求解;对B ,从表格数据看,y 随x 的增大而增大,即可判1F A 2PF 2PF 2F B 1PF 1PA FQ ⊥2PB F N ⊥12F PF ∠1290F PF ∠=︒112245PFQ PQF PF N PNF ∠=∠=∠=∠=︒1||PA PF =2||PB PF =||||||2AB PA PB a =-==1FQ 2F N 12F F //OA PQ 1//OB PF 145OAB APQ APF OBA ∠=∠=︒=∠=∠90AOB ∠=︒||||||OA OB AB a ===OAB △2211||1022S OA a ===OAB △||AB =1x a x -≤[]4,61()f x x x=-()f x [4,6]x ∃∈210x ax -->[4,6]x ∀∈210x ax --≤1x a x -≤[]4,6max 1a x x ⎛⎫≥- ⎪⎝⎭[4,6]x ∈1()f x x x =-1()f x x x=-[]4,6max 135()(6)666f x f ==-=356a ≥断;对C ,因为y 与x 正相关,所以y 与x 的相关系数为正数,故可判断;对D ,将月份编号代入到回归直线即可求解判断.【详解】对A ,,,因为点在回归直线上,所以,解得,所以选项A 正确;对C ,从表格数据看,y 随x 的增大而增大,所以y 与x 正相关,所以选项C 正确;对B ,因为y 与x 正相关,所以y 与x 的相关系数为正数,所以选项B 错误;对D ,2022年7月对应的月份编号,当时,,所以2022年7月该手机商城的5G 手机销量约为320部,所以选项D 错误.故选:AC .11.AD【分析】首先利用函数的奇偶性得到函数的对称轴和对称中心,结合关系式的变换得到函数周期判断B ,利用特殊值代入判断A ,根据导函数判断函数单调性结合关系式和偶函数定义判断C ,根据函数的关系式和单调性判断D .【详解】因为为偶函数,,故函数图象关于直线对称,为奇函数,,函数图象关于对称,对于D ,,,故2是函数的周期,函数为周期函数,故D 正确;对于A ,,令,,故,又,故A 正确;对于C ,,当时,,即函数在上递增,函数图象关于对称,故函数在上递减,故函数在上递增,所以,故函数不是偶函数,故C 错误;7x =1234535x ++++==509618522755855a ay +++++==(),x y 55845355a+=⨯+142a =7x =7x =ˆ4575320y=⨯+=132f x ⎛⎫-⎪⎝⎭111133()(1)2222f x f x f x f x f x f x ⎛⎫⎛⎫⎛⎫⎛⎫-=+⇔-=+⇔=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭12x =(21)f x +(21)(21)(1)(1)f x f x f x f x -+=-+⇔-+=-+(1,0)()(1)(1)f x f x f x =-=-+(2)(1)()f x f x f x +=-+=(21)(21)f x f x -+=-+0x =(1)(1)f f =-(1)0f =(0)(11)(1)0f f f =-==131222f f f ⎛⎫⎛⎫⎛⎫-==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭10,2x ⎛⎫∈ ⎪⎝⎭()0f x '>10,2⎛⎫⎪⎝⎭(1,0)13,22⎛⎫ ⎪⎝⎭11,22⎡⎤-⎢⎥⎣⎦1122f f ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭对于B ,,故B 错误,故选:AD .【点睛】抽象函数的判断一般会从函数奇偶性、周期性和对称性的定义推得相关的函数性质;12.【详解】由,得,因为“”是“”的充分不必要条件,所以集合是集合的真子集,所以(不同时取等号),解得,所以实数m 的取值范围为.故答案为:.13.128【详解】令,得.14.2【分析】根据调和数列,可得为等差数列,即可根据等差数列求和公式得,进而利用不等式即可求解.【详解】数列为调和数列,故,所以为等差数列,由,所以,故,所以,故,故,由于.当且仅当时等号成立,故的最大值为2.故答案为:2.15.【详解】(1).因为,所以,124333f f f ⎛⎫⎛⎫⎛⎫=> ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭|2|1x m -<2121m x m -<<+12x <<|2|1x m -<{12}x x <<∣{2121}x m x m -<<+∣211212m m -≤⎧⎨+≥⎩112m ≤≤112m ≤≤112m ≤≤0x =701272128a a a a ++++== {}2n x 22920142x x +=21n x ⎧⎫⎨⎬⎩⎭221n n x x d +-={}2n x 222212320222022x x x x++++= ()2212022202220222xx +⨯=22120222x x +=22920142x x +=22920149201422x x x x +=≥920141x x ≤()222920149201492014920142224x x x x x x x x +=++=+≤92014x x =92014x x +ππ()4sin cos cos sin 2cos 233f A m n A A A ⎛⎫⎛⎫=⋅=⋅-+-⋅ ⎪ ⎪⎝⎭⎝⎭πsin 222sin 23A A A ⎛⎫==- ⎪⎝⎭π5π,46A ⎡⎤∈⎢⎥⎣⎦ππ4π2,363A ⎡⎤-∈⎢⎥⎣⎦所以当,即时,有最小值(2)因为,所以,所以,,因为,所以.由正弦定理,,所以,.又因为,所以,得,由余弦定理有:,所以.所以.16.【详解】(1)如图所示,连接EF .因为E ,F分别是棱PB ,PC 的中点,所以,.因为,,所以,,所以四边形ADFE 是平行四边形,则.因为平面ACE ,平面ACE ,所以平面ACE .(2)因为平面PAB ,PA 、平面PAB ,所以,,又因为,所以AB ,AP ,AD 两两垂直,以A 为坐标原点,,,的方向分别为x ,y ,z 轴的正方向,建立如图所示的空间直角坐标系.π4π233A -=5π6A =()f A ()0f A =π2sin 203A ⎛⎫-= ⎪⎝⎭π2π3A k -=k ∈Z π5π,46A ⎡⎤∈⎢⎥⎣⎦2π3A =2sin sin sin b c a B C A====sin 2b B =sin 2c C =sin sin B C +=22b c +=b c +=2222cos a b c bc A =+-3bc =11sin 322ABC S bc A ==⨯=△//EF BC 2BC EF =//AD BC 2BC AD =//EF AD EF AD =//AE DF AE ⊂DF ⊂///DF AD ⊥AB ⊂AD PA ⊥AD AB ⊥PA AB ⊥AB AP AD由题中数据可得,,,,.设平面ACE 的法向量为,则令,得.因为,,,所以平面PAD .平面PAD 的一个法向量为.设平面ACE 与平面PAD 的夹角为,则.故,即平面ACE 与平面PAD17.【详解】(1)依题意,列出列联表如下:课间不经常进行体育活动课间经常进行体育活动合计男302050女401050合计7030100零假设为:性别与课间经常进行体育活动相互独立,即性别与课间是否经常进行体育活动无关,因为,根据小概率值的独立性检验,我们推断不成立,即认为性别与课间是否经常进行体育活动有关联,此推断犯错误的概率不大于0.05.(2)由题意得,经常进行体育活动者的频率为,所以在本校中随机抽取1人为经常进行体育活动者的概率为,(0,0,0)A (2,0,4)C (1,2,0)E (2,0,4)AC = (1,2,0)AE =(,,)n x y z = 240,20,n AC x z n AE x y ⎧⋅=+=⎪⎨⋅=+=⎪⎩2x =(2,1,1)n =--PA AB ⊥AB AD ⊥PA AD A = AB ⊥(1,0,0)AB m ==θcos cos ,n m n m n m θ⋅==== sin θ==22⨯0H 220.05100(30102040)1004.762 3.8415050703021x χ⨯⨯-⨯==≈>=⨯⨯⨯0.05α=0H 202505=25由题意得,则,,可得,,,,,X 的分布列为:X 01234PX 的数学期望为,X 的方差为.18.【分析】(1)利用椭圆的第一定义和离心率,求解椭圆方程;(2)设点,,,,的方程为,联立直线与椭圆的方程,根据韦达定理求出点的坐标,同理得到点的坐标,进而得到直线的方程,根据对称性,如果直线CD 过定点,则该定点在x 轴上,即可得到定点坐标;【详解】(1)由椭圆定义可知,,所以的周长为,所以,所以,所以,又,所以椭圆的方程:.(2)(ⅰ)设点,,,,则直线的方程为,则,2~4,5X B ⎛⎫⎪⎝⎭4422()C 155kkk P X k -⎛⎫⎛⎫==- ⎪⎪⎝⎭⎝⎭0,1,2,3,4k =04042281(0)C 155625P X ⎛⎫⎛⎫==⨯⨯-= ⎪ ⎪⎝⎭⎝⎭131422216(1)C 155625P X ⎛⎫⎛⎫==⨯⨯-= ⎪ ⎪⎝⎭⎝⎭222422216(2)C 155625P X ⎛⎫⎛⎫==⨯⨯-= ⎪ ⎪⎝⎭⎝⎭31342296(3)C 155625P X ⎛⎫⎛⎫==⨯⨯-= ⎪ ⎪⎝⎭⎝⎭40442216(4)C 155625P X ⎛⎫⎛⎫==⨯⨯-= ⎪ ⎪⎝⎭⎝⎭81625216625216625966251662528()455E X np ==⨯=2224()(1)415525D X np p ⎛⎫=-=⨯⨯-= ⎪⎝⎭()11,A x y ()22,B x y ()33,C x y ()44,D x y 2AF 11(1)1y y x x =--7,05⎛⎫⎪⎝⎭122AF AF a +=122BF BF a +=2ABF △4a =a =c a =1c =2221b a c =-=2212x y +=()11,A x y ()22,B x y ()33,C x y ()44,D x y 2AF 11(1)1y y x x =--1111x x y y -=+由得,,所以,因为,所以,所以,故,又,同理,,,由A ,,B 三点共线,得,所以,直线CD 的方程为,由对称性可知,如果直线CD 过定点,则该定点在x 轴上,令得,,故直线CD 过定点.19.【分析】(1)求导后,分类讨论单调性,进而得到最值,求出a 的值即可;(2)条件等价于有两个不等的正根,结合判别式非负,以及韦达定理求出a 的范围,要证,即证,令求导确定函数的单调性,证明结论.(3)利用(1)结论可得则当时,,进而利用裂项相消求11221112x x y y x y -⎧=+⎪⎪⎨⎪+=⎪⎩221111112210x x y y y y ⎡⎤⎛⎫⎛⎫--⎢⎥++-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦211322211111121212y y y x x y x y --==-++⎛⎫-+ ⎪⎝⎭221112x y +=221122x y +=2113123y y y x =-13123y y x =-111133311111134112323x x y x x y y y y x x ---=+==+=--24223y y x =-2423423x x x -=-1F 121211y yx x =++211221x y x y y y -=-43111431342323y y y x y x x x x x ⎛⎫---=- ⎪---⎝⎭0y =()()()()()1431431433423y x x x y y x x y y --+--=--()()21211121212112134343423232323232323x x y y y x x x x x y y x x x ⎛⎫⎛⎫----+-- ⎪ ⎪----⎝⎭⎝⎭=⎛⎫-- ⎪--⎝⎭()()()()()()()()1221121221211212122134344372323325y x y x y y x y x y y x y x y y x y x y --+--+-===----+-7,05⎛⎫ ⎪⎝⎭()0h x '=()()121220h x h x a x x --+<-22212ln 0x x x -+<1()2ln (1)x x x x x ϕ=-+>()x ϕ1n >22211111ln 1111n n n n n⎛⎫⎛⎫+<+-=<- ⎪ ⎪-⎝⎭⎝⎭和证明结论.【详解】(1)由题意知:,,①当时,,在单调递减,不存在最大值.②当时,由得,当,;,,函数的增区间为,减区间为.,.(2),,“函数存在两个极值点,”等价于“方程有两个不相等的正实数根”;故,解得.,要证,即证,,不妨令,故,由得,令,在恒成立,()ln 1f x a x x =-+()1(0)af x x x∴'=->0a ≤()0f x '<()f x (0,)+∞0a >()0f x '=x a =(0,)x a ∈()0f x '>(,)x a ∈+∞()0f x '<∴()y f x =(0,)a (,)a +∞max ()()ln 10f x f a a a a ∴==-+=1a ∴=1()()()ln h x f x g x a x x x=+=-+ 22211()1a x ax h x x x x -+-'∴=--=()h x 1x 2x 22211()10a x ax h x x x x -+-'=--==212124010a x x x x a ⎧∆=->⎪=⎨⎪+=>⎩2a >()()11221212121211ln ln a x x a x x h x h x x x x x x x -+-+--=--()()()21122112121212ln ln ln ln 2x x a x x x x a x x x x x x x x --+-+-==---()()121220h x h x a x x --+<-1212ln ln 1x x x x -<-121x x = 1201x x <<<1211x x =<1212ln ln 1x x x x -<-22212ln 0x x x -+<1()2ln (1)x x x x xϕ=-+>222222121(1)()10x x x x x x x x ϕ-+---'=--==<(1,)+∞所以函数在上单调递减,故.成立.(3)由(1)知,,即,当时,,,.【点睛】知识点点睛:本题以新定义为载体,考查了利用导数研究函数单调性和最值,考查了不等式的放缩,裂项相消求和知识,属于难题.()x ϕ(1,)+∞()(1)0x ϕϕ<=()()121220h x h x a x x -∴-+<-ln 10x x -+≤ln 1x x ≤-∴1n >22211111ln 1111n n n n n ⎛⎫⎛⎫+<+-=<- ⎪ ⎪-⎝⎭⎝⎭222111111111ln 1ln 1ln 1111232231n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫∴++++⋯++<-+-+⋯+-=-< ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭222211111111e 234n ⎛⎫⎛⎫⎛⎫⎛⎫∴+++⋯+< ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭。
经典课件:四川省近三年高考文理科状元

30
文科状元
姓名: 邱汛
学校:内江六中
语文 134
数学 144
英语 148
文综 251
总分 677
.
31
.
32
.
33
四川省高考理科状元被曝5年前就考入清华
就读于四川省绵阳中学2010级41班,
今年又以676分成为四川省理科状元的杨山
楷,其实是2005年被清华大学录取的杨依
坪。帖中还公布了杨依坪2005年的录取通
知书号和学号,记者根据这组号码查到,这
是2005年清华大学在四川省录取的106名考
生之一,杨依坪的录取通知书号和学号,他
学校:成都外国语学校
语文 131
数学 143
外语 143
文综 219
总分 636
.
13
理科状元
姓名:高蕊馨
学校:成都外国语学校
语文 119 数学 137 英语 136 理综 290 总分 682
.
14
.
15
1999—2012年四川中学高考状元排行榜
名次 1
学校名称 成都实验外国语学校
所在省市 四川
高中励志教育
四川省近三年文理科状元
2013年5月
.
1
四川2010年高考文理科状元
理科 676
文科 654
姓名:杨山楷 学校:绵阳中学
姓名:向昊天 .学校:成都实验外国语学2 校
理科状元
姓名:杨山楷 学校:绵阳中学
(首个拿第一的复读生)
语文 117 数学 141 英语 139 理综 275 . 总分 676 3
数学 134
英语 138
综合 259
总分 649
带你了解成都4、7、9中
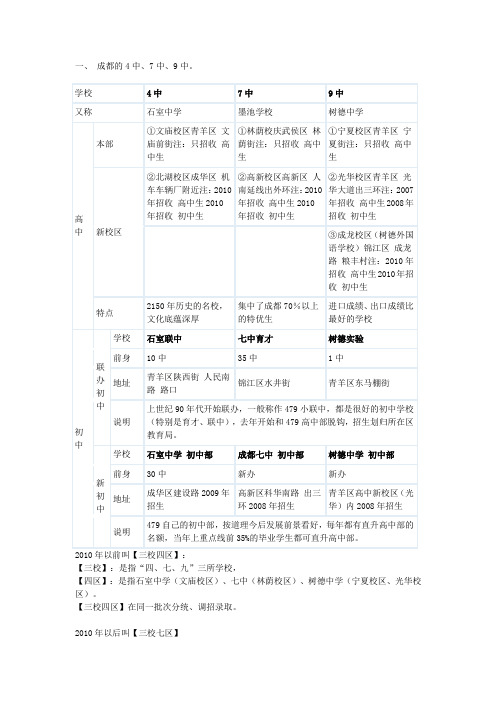
一、成都的4中、7中、9中。
【三校】:是指“四、七、九”三所学校,【四区】:是指石室中学(文庙校区)、七中(林荫校区)、树德中学(宁夏校区、光华校区)。
【三校四区】在同一批次分统、调招录取。
2010年以后叫【三校七区】增加石室中学(北湖校区)、成都七中(高新校区)、树德中学(成龙校区)二、4、7、9中是怎样招生的?先看2009年的招生情况02001 石室中学校址:成都市文庙前街93号班数:16 计划800名(其中含指标到校生、对口保送生共220名,艺体特长生108名) 统招 720名调招 80名备注:另招收2个外地学生班,2个剑桥英语项目班。
注:此处的统招人数720名要扣除:“保送生”、“特长生”,所以实际对成都五城区的统招人数为:720-220-108=392名。
注:1. 4、7、9 在成都五城区实际共招收1215名统招生、225名调招生。
共计:1440人。
2010年4、7、9新校区招生,估计增加400×3=1200名。
(对比光华的人数)2. 保送生指:【指标到校生】、【部分初中 对口保送生】、【直升生】。
a. 【指标到校生】:479向所在服务区学校分配名额。
占学校统一招生计划,比例为479统招计划的15%(07年)、25%(08年)、35%(09年)50%(10年)。
b. 【对口保送生】:根据2007文件:保送生政策执行到2009年截至。
今年有没有 还要看文件。
c. 【直升生】:现阶段指普高。
今后479自己的初中部咋个直升,还不知道。
2009年部分初中学校对口保送国家级示范性高中具体情况注:1. 以上每个分数和实际的分数可能有2-3分的误差,以前记录的。
2. 以上各个分数都包含加分。
3. 2010年中考,取消区优干、区三好加分,体育、科技、艺术等加分大多数都从以前的15分调整为5分,再加上4、7、9新校区招生,如果2010中考难度不变的话,今年各校的录取分数估计会下降12-15分。
NOIP2008全国青少年信息学奥林匹克联赛获奖名单(提高组

171
廖孜
男
成都市大弯中学
高二
李植武朱章惠
190
172
任飞宇
男
成都石室中学
高二
文仲友
190
173
唐钟鸣夫
男
成都石室中学
高二
李显清
190
174
代云
男
成都石室中学
高三
李显清
190
175
李睿捷
女
七中嘉祥外国语学校
初2009级
徐淑君
190
176
潘一桥
女
七中嘉祥外国语学校
初2009级
徐淑君
190
177
黄凯文
四川省绵阳中学
高三
欧阳建昭
300
37
谢青松
男
四川省绵阳中学
高二
曾贵胜
300
38
赵焜钰
男
绵阳南山中学
高二
叶诗富
300
39
缪佳君
男
绵阳南山中学
高二
叶诗富
300
40
陈昊阳
男
绵阳南山中学
高二
叶诗富
290
41
肖月
男
成都石室中学
高三
文仲友
290
42
吴克
男
四川省绵阳中学
高二
曾贵胜
290
43
赵牧云
女
绵阳南山中学
高二
高二
李植武朱章惠
180
185
宋雨坤
男
七中嘉祥外国语学校
高2011级
徐淑君杜明军
180
186
谢留峰
男
成都市10个最著名的初中排行榜_排行榜

成都市10个最著名的初中排行榜_排行榜10、成都第七中学初中学校成都七中初中学校是高新区社事局直属全额拨款正科级公办的初级中学。
由成都七中领办,按照成都七中优秀办学传统精心打造,与成都七中高中教育“无缝衔接”。
成都七中初中学校自2008年办学以来,秉承“启迪有方,治学严谨,爱生育人”的优良传统,以“创造最适宜学生的教育”为己任,努力实践“着眼整体发展,立足个体成才,充分发挥学生主体作用”的教育思想,朝着“学生成才、教师成功、学校领先”的办学目标奋力推进。
取得了令教育同行和社会各界惊叹的办学业绩。
9、成都石室联合中学成都石室联合中学是由原成都市第十中学依托石室中学,进行办学体制改革而创办的一所直属市教育局公办民助收费制学校。
学校从1997年创办以来,将石室中学悠久的历史传统与现代教育思想相融合,注重自身办学特色,走出了一条办学新路子,学校管理,教育教学,基础设施建设一年上一个新台阶。
学校以团结务实,开拓进取,勤政廉洁的领导班子为核心,把实施素质教育和“三个面向”作为学校指导思想,把培养具有创新精神和创造能力,生动活泼、全面发展的“四有”新人作为目标,注重学生的可持续发展,注重培养和提高学生综合素质。
8、成都实验外国语学校成都实验外国语学校,简称成都实外,是成都市教育局直属外语特色民办学校、四川省创办最早的外国语学校之一。
学校前身为1963年创办的成都西乡路中学;1995年更名为成都实验外国语学校;2002年改制为民办公助股份制学校。
据2016年12月学校官网显示,学校占地面积近200亩,建筑面积约70000平方米;有教职工500余人,有101个教学班,在校初高中学生5000多人。
7、成都市树德实验中学成都市树德实验中学是成都市第一所“公办民助”办学体制改革学校,前身系创办于1935年的成都市第一中学。
它是以成都市树德中学为依托,由成都一中和成都市树德中学共同举办的国家所有、实行“公办民助”的全日制学校,为独立建制由教育局直接管理的中学;是一所集树德中学和成都一中两校办学经验和教育资源、融公立和民办两种办学模式优势的新机制学校。
四川省成都初中排名前10排行榜

四川省成都初中排名前10排行榜1,成都七中嘉祥外国语学校2000年,嘉祥教育集团第一所学校成立,这就是成都七中嘉祥外国语学校&成都嘉祥外国语学校。
学校始终以“办百年名校”为长远目标,以“创中华名校育国际英才”为办学目标,坚持“以生为本、以师为根、多元创新、和谐共赢”的办学理念,致力培养“包容坚毅、健康快乐、德佳优先、国际”的嘉祥才子,以良好的校风和优异的业绩2,成都市西川中学简介成都西川中学是一所由四川省教育厅批准,以寄宿制为主的民办普通完全中学,是中学数学教改实验基地,是教育部北师大基础教育课程研究中心的"全国新世纪初中数学实验基地"学校,是成都市体育传统项目学校。
该校被四川省推荐为全国首批表彰的"民办中小学先进集体",荣获"四川省民办教育先进集体"称号、荣获由中国民办教育协会、中小学专业委员会3,四川师范大学附属第一实验中学师大一中凭借严明的校风、严谨的学风和一流的教学质量,多年来一直稳居成都市初中教学水平前三甲。
学校教师队伍阵容强大,本科学历全面覆盖,硕士研究生比例高达35%,中高级职称达85%,特级教师、学科带头人、市级以上优秀教师、优秀班主任,市级以上各类赛课一等奖以上获得者达55%,锦江师大一中,办学至今已逾半个世纪。
学校位于环境优美4,电子科技大学实验中学电子科技大学实验中学(以下简称科大实验)是2009年由电子科技大学与成都高新区联合创办的公立高完中。
2016年6月,成都市教育局批准年轻的科大实验高中招生第二批次录取。
科大实验是成都市六城区实施全封闭、住宿制管理的公立学校,是严格与关爱相融的学校,是弥漫着创新创造力的学校,当然也是大学味道最浓的学校。
学校地处川蜀文化发源地5,成都外国语学校成都外国语学校创办于1989年,是经四川省教育厅批准,四川省第一所具有外语特色的高完中,是教育部批准的具有保送资格的外国语学校(全国仅16所,四川唯1所)、国家拔尖创新人才培养试点学校(全省仅6所)、全国安全教育先进单位、四川省普通高中课程改革样本学校、四川省校风示范学校、四川省民办教育先进集体、四川省阳光体育示范校6,成都七中育才学校成都七中育才学校成立于1997年,依托百年名校成都七中的高位发展,在短短20年的办学历程中,志存高远,追求卓越的七中育才,已经成长为成都市、四川省乃至全国都有影响力的名校,构筑起初中教育新高度,引领着成都市乃至四川省的初中教育发展,成为中国初中教育的一个品牌,并正向着“优质教育示范校”,“素质教育实验校”的办学目标前进成都市树德实验中学7,成都市树德实验中学,是成都市青羊区教育局直属的公办全日制普通初级中学。
四川省近三年高考文理科状元

5
富顺二中
攀枝花七中
屏山中学
什邡中学
蜀光中学
巴中中学
四川
3
四川
3
四川
1
四川
1
四川
1
四川
1
四川
1
四川
1
四川
1
四川
1
四川
1
四川
1
附: 2005-2009年四川高考状元 四川2009年高考文理科状
理科 655 姓名:董伟 学校:巴中中学
.文科 634 姓名:叶思雨 学校:成都市实验外国语学校
姓名:董伟
姓名: 兰雪
学校:内江六中
姓名: 邱汛
学校:内江六中
理科状元
姓名: 兰雪
学校:内江六中
语文 128 数学 148 英语 142 理综 298 总分 716
文科状元
姓名: 邱汛
学校:内江六中
语文 134 数学 144 英语 148 文综 251 总分 677
理科状元
姓名:李沛伦
学校:成都外国语学校
语文 121 数学 144 英语 135 理综 291 总分 691
2012四川高考最高分
文科:636
理科: 682
姓名:周小琪
姓名:高蕊馨
学校:成都外国语学校 学校:成都外国语学校
文科状元
姓名:周小琪
学校:成都外国语学校
语文 131 数学 143 外语 143 文综 219 总分 636
2005年考入清华大学的杨依坪(左)
1、 为啥改名重复考试? 2、替考还是赚取奖励?
泪流满面讲秘密 清华大三时“被退学”
依然填报清华
附:试读学分未达30分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年成都外国语学校"德瑞杯"知识竞赛数学试卷
一、判断(每题2分,共10分)
1、甲、乙两杯水的含糖率为25%和30% ,甲杯水中的糖比乙杯中的少。
( )
2、a -b=3
1b (a 、b 不为0) a 与b 成正比例。
( )
3、体积是1立方厘米的几何体,一定是棱长为1厘米的正方体。
( )
4、把一个不为零的数扩大100倍,只需要在这个数的末尾添上两个零。
( )
5.把三角形的三条边都扩大3倍,它的高也会扩大3倍。
( )
二、填空(每题3分,共33分)
1.从甲地到乙地骑车去,步行返回共用时30分钟,往返都骑车只要18分钟,那么往返都步行要( )分钟。
2、一次竞赛的参赛人数在120-130之间,男女生人数的比如4: 3,参加这次比赛的男生有( )人。
3、底层在同一平面上的两栋大楼各有12层,新楼每层高2.80米,旧楼每层高3.20米。
新楼的第( )层天花板和旧楼的第( )层的天花板齐平。
(楼板厚度不计)
4、数对(2,2) ,(5,2) ,(3,4),(6,4 )是四边形的四个顶点。
这个四边形绕点(6,4)顺时针旋转900后,其他三个顶点用数对表示分别为:
( , ) , ( , ), ( , )。
5、一个六面体的棱长和为36厘米,这个六面体表面积最大为( )平方厘米。
6、用自然数n 去除63,91,129,得到的三个余数之和是25,那么n=
( )。
7、铺路,每天比计划少铺10米,结果时间比计划多用121,计划每天铺路( )米。
8、李明画了许多个长一样、宽不一样的长方形,量出了它们的长、宽,计算出了它们的面积,然后把宽和面积所对应的点描在方格纸上,当他把这些点顺次连接起来后,惊喜地发现了一个"秘密"。
这个"秘密"是
( )。
9、某校有学生465人,其中女生的32比男生的5
4少20人,男生( )人。
10、如图:在长、宽、高分别为2分米、2分米、4分米的长方
体上有一只蚂蚁从顶点A 出发,要爬到顶点D ,这只蚂蚁爬过
的线路正好最短并经过B 点,则BC 长( )分米。
11、用一张斜边为17厘米的红色三角形纸片,一张斜边长为29厘米的黄色三角形纸片,一张蓝色正方形纸片,拼成一个直角三角形,红黄两个三角形的面积和为( )平方厘米。
三、选择(每题3分,共15分)
1、口袋中装着大小相同的2个红球和1个白球,甲乙两人蒙眼任意各摸1个球;甲先摸(不放回去)。
比较两人摸到红球的可能性( )。
A
①甲大②乙大③同样大④无法比较
2、一长方体盒子,从里面量长、宽、高分别为40厘米、12厘米、7厘米。
在盒子里最多可以放()块长、宽、高为5厘米、4厘米、3厘米的小长方体。
①60 ②56 ③100 ④48
3、两个三角形,最多可以把一个正方形分割成()块。
①15 ②13 ③10 ④9
4、把1到2008从左到右依次排列起来,每隔三个数字点一个",",如123,456,789,…那么,第100个逗号前的数字是( )。
①4 ②5 ③ 6 ④7
5、将一个圆柱体削成一个最大的长方体,这个长方体体积与圆柱体体积之比是( )。
①2:π②3: :π③3:4 ④2:3四、计算(每题3分.关12分) 四、计算(每题3分,共12分)
94
:2:0.5 27
x=
59
23 5.2220060.4 1.6 910() 52720080.52008 26 5.22
950
+-⨯
÷+
⨯
-+
20081143
982251020028
42554
-⨯+⨯
1+2-3+4+5-6+7+8-9 -……+601 +602 -603 +604 +605 -606
五、图形问题(6分)
用四个边长为1O厘米的正方形拼成右图的形状。
现有一个半径为2厘米的小圆紧靠此图形内侧滚动一圈后回到出发点。
求圆心经过的路线的长度是多少厘米?
六、解决问题(每题4分,共24分)
1、某校合唱队与舞蹈队的人数之比是3:2,如果将合唱队队员调10人到舞
蹈队,则人数比为7:8。
原合唱队有多少人?
2、一件工作,甲乙合作6天完成;乙丙合作10天完成;甲丙合作3天,乙独
做12天也可以完成。
乙独做多少天可以完成?
3、小华从A到B,先下坡再上坡共用71
6
上小时。
如果两地相距24千米,下
坡每小时行6千米,上坡每小时行3千米,那么原路返回要多少小时?
4、一次考试共有5道题。
考试结果统计如下:做对第一题的占总人数的80% ,做对第二道题的占总人数的95% ,做对第三道题的占总人数的85% ,
做对第四道题的占总人数的 79% ,做对第五道题的占总人数的74%。
如果做
对三道以上(包括三道)题目为及格,那么这次考试的及格率至少是百分之几?
5、如图:将一个圆锥从顶点沿底面直径切成两半的截面是一个等腰三角
形,
如果圆锥的高是6厘米,求此圆锥的体积。
6、甲车以每小时160千米,乙车以每小时20千米的速度在长210千米的环
形公路上同时同向地出发。
每当甲追一次甲速就减少1
3,乙速就提高1
3
,在
两车速度正好相等的时候,甲车行了多少千米?。
