二次函数综合题——等腰三角形
二次函数中等腰三角形专题

二次函数中等腰三角形专题一.解答题(共15小题)1.如图,经过点A(0,-6)的抛物线y= 1/2x2+bx+c与x轴相交于B(-2,0),C两点.(1)求此抛物线的函数关系式和顶点D的坐标;(2)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1,若新抛物线y1的顶点P在△ABC 内,求m的取值范围;(3)在(2)的结论下,新抛物线y1上是否存在点Q,使得△QAB 是以AB为底边的等腰三角形?请分析所有可能出现的情况,并直接写出相对应的m的取值范围.2.如图,二次函数y=4/3 x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.(1)求该二次函数的解析式及点C的坐标;(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.(3)当P,Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请判定此时四边形APDQ 的形状,并求出D点坐标.3.在平面直角坐标系xOy中,二次函数y=-1/2 x2+3/2 x+2的图象与x轴交于点A,B(点B 在点A的左侧),与y轴交于点C.过动点H(0,m)作平行于x轴的直线l,直线l与二次函数y=-1/2 x2+3/2 x+2的图象相交于点D,E.(1)写出点A,点B的坐标;(2)若m>0,以DE为直径作⊙Q,当⊙Q与x轴相切时,求m的值;(3)直线l上是否存在一点F,使得△ACF是等腰直角三角形?若存在,求m的值;若不存在,请说明理由.4.如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.(1)求a,k的值;(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标;(3)在抛物线及其对称轴上分别取点M、N,使以A,C,M,N为顶点的四边形为正方形,求此正方形的边长.5.二次函数图象的顶点在原点O,经过点A(1,1/4);点F(0,1)在y轴上.直线y=-1与y轴交于点H.(1)求二次函数的解析式;(2)点P是(1)中图象上的点,过点P作x 轴的垂线与直线y=-1交于点M,求证:FM平分∠OFP;(3)当△FPM是等边三角形时,求P点的坐标.6.如图,抛物线y=-1/2 x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).(1)求抛物线的表达式;(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.7.如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.(1)求抛物线的解析式;(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.8.已知抛物线经过A(-2,0),B(0,2),C(3/2,0)三点,一动点P从原点出发以1个单位/秒的速度沿x轴正方向运动,连接BP,过点A作直线BP的垂线交y轴于点Q.设点P的运动时间为t秒.(1)求抛物线的解析式;(2)当BQ=1/2 AP时,求t的值;(3)随着点P的运动,抛物线上是否存在一点M,使△MPQ为等边三角形?若存在,请直接写t 的值及相应点M的坐标;若不存在,请说明理由.9.如图,对称轴为直线x=2的抛物线经过A(﹣1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;(2)当a=1时,求四边形MEFP的面积的最大值,并求此时点P的坐标;(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.10.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0) C(8,0) D(8,8)抛物线y=ax2+bx 过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P 作PE⊥AB交AC于点E(1)直接写出点A的坐标,并求出抛物线的解析式。
中考数学各类计算题型专练 二次函数特殊三角形(等腰_直角)存在性问题
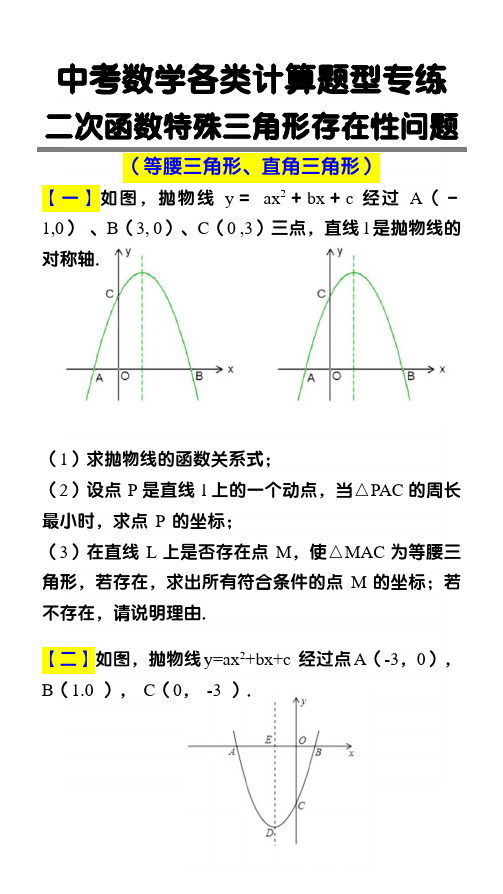
中考数学各类计算题型专练二次函数特殊三角形存在性问题(等腰三角形、直角三角形)【一】如图,抛物线y=ax2+bx+c 经过A(-1,0)、B(3, 0)、C(0 ,3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P 的坐标;(3)在直线L上是否存在点M,使△MAC为等腰三角形,若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.【二】如图,抛物线y=ax2+bx+c 经过点A(-3,0),B(1.0 ),C(0,-3 ).(1)求抛物线的解析式;(2)若点P 为第三象限内抛物线上的一点,设△PAC 的面积为S,求S 的最大值并求出此时点P 的坐标;(3)设抛物线的顶点为D,DE⊥x轴于点E,在y 轴上是否存在点M,使得△ADM是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.【三】在平面直角坐标系中,现将一块等腰直角三角板放在第一象限,斜靠在两坐标轴上,且点A(0,2),点C (1,0),如图所示,抛物线y=ax2−ax−2经过点B.(1)求点B的坐标;(2)求抛物线的解析式;(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
【四】如图,抛物线y=ax 2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x 轴上,点C 在y 轴上,且AC=BC.(1)求抛物线的对称轴;(2)写出A,B,C 三点的坐标并求抛物线的解析式;(3)探究:若点P 是抛物线对称轴上且在x 轴下方的动点,是否存在△PAB是等腰三角形?若存在,求出所有符合条件的点P 坐标;不存在,请说明理由.【五】如图,已知二次函数y=ax2+bx+3的图象交x轴于点A(1,0),B(3,0),交y轴于点C。
(1)求这个二次函数的表达式;(2)点P是直线BC下方抛物线上的一动点,求△BCP面积的最大值;(3)直线x=m分别交直线BC和抛物线于点M,N,当△BMN是等腰三角形时,直接写出m的值【六】如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y= -1/2x ﹣1交于点C.(1)求抛物线解析式及对称轴;(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.【七】如图,已知抛物线于x轴交于A(-1,0)、B (3,0)两点,与y轴交于点C(0,3)。
二次函数中的等腰三角形

专题11 二次函数中的等腰三角形类型一 在坐标轴上找点成等腰1.如图,二次函数2142y x x =--+的图象与x 轴交于A 、B 两点(点A 在点B 的右侧),与y 轴交于点C .(1)求点A 、B 、C 的坐标;(2)若点P 在x 轴上,且△PBC 为等腰三角形,请求出所有符合条件的点P 的坐标.(1) 解:令21402x x --+= 解得12x =,24x =-△A (2,0), B (4,0)-令0x =,得4y =,△C (0,4)△点A 的坐标为(2,0),点B 的坐标为(4,0)-,点C 的坐标为(0,4).(2)解:设P 点的坐标为(,0)m△(4,0)B -,(0,4)C △BC =22(4)BP m =+,2216CP m =+当△PBC 是等腰三角形时,分三种情况求解:①当BP CP =时,由题意可得22(4)16m m +=+解得0m =△P 的坐标为(0,0);②当BP BC =时,由题意可得()(224m +=解得4m =-+4m =--△P 的坐标为()4-+或()4--;③当CP CB =时,由题意可得(2216m +=解得4m =或4m =-(不合题意,舍去)△P 的坐标为(4,0);综上所述,P 点的坐标为(0,0) 或 (4,0) 或()4-+ 或()4--.【点睛】本题考查了二次函数与坐标轴的交点坐标,对称的性质,二次函数与周长的综合,二次函数与特殊三角形的综合等知识.解题的关键在于对知识的熟练掌握与灵活运用.2.如图,已知二次函数23y x bx =-++的图象与x 轴的两个交点为A (4,0)与点C ,与y 轴交于点B .(1)求此二次函数关系式和点C 的坐标;(2)在x 轴上是否存在点P ,使得△PAB 是等腰三角形?若存在,请你直接写出点P 的坐标;若不存在,请说明理由.解:(1)△二次函数23y x bx =-++的图象与x 轴的一个交点为()4,0A ,△20443=-++b ,解得134b =, △此二次函数关系式为:21334y x x =-++,当0y =时,213304-++=x x 解得134x =-,24x = △点C 的坐标为3,04⎛⎫- ⎪⎝⎭. (2)存在,设点P 的坐标为(x ,0),由题意得:AB 2=42+32=25,AP 2=(x -4)2,BP 2=x 2+9,①当AB=AP 时,则25=(x -4)2,解得x=9或-1,△P(9,0)或P (﹣1,0);②当AB=BP 时,同理可得x=4(舍去)或-4,△P (﹣4,0)③当AP=BP 时,如图所示△OP=x ,△AP=BP=4-x在Rt△OBP 中,222OB OP BP +=△()2223+x =4x - △x=78△P (78,0) 综上点P 的坐标为(9,0)或(-1,0)或(-4,0)或(78,0).【点睛】本题考查的是二次函数综合运用,涉及到等腰三角形的性质、面积的计算等,其中(3),要注意分类求解,避免遗漏.3.如图所示,关于x 的二次函数2y x bx c =++的图象与x 轴交于点1,0A 和点B ,与y 轴交于点()0,3C ,抛物线的对称轴与x 轴交于点D .(1)求二次函数的表达式;(2)在y 轴上是否存在一点P ,使PBC 为等腰三角形?若存在,求出点P 的坐标;若不存在,请说明理由;解:(1)把()1,0A 和()0,3C 代入2y x bx c =++,10,3,b c c ++=⎧⎨=⎩解得:4b =-,3c =,∴二次函数的表达式为:243y x x =-+.(2)令0y =,则2430x x -+=,解得:1x =或3x =,()3,0B ∴,BC ∴=点P 在y 轴上,当PBC 为等腰三角形时分三种情况进行讨论:如图1,①当CP CB =时,PC =3OP OC PC ∴=+=+或(10,3P ∴+,(20,3P -; ②当BP BC =时,3OP OB ==,()30,3P ∴-;③当PB PC =时,3OC OB ==,∴此时P 与O 重合,()40,0P ∴;综上所述,点P 的坐标为:(0,3+或(0,3-或()03-,或()0,0.4.如图,已知二次函数21134=-++y x x c 的图像与x 轴的一个交点为A (4,0),与y 轴的交点为B ,过,A B 的直线为2y kx b =+.(1)求二次函数1y 的解析式及点B 的坐标;(2)在两坐标轴上是否存在点P ,使得ABP △是以AB 为底边的等腰三角形?若存在,求出P 的坐标;若不存在,说明理由.【答案】(1)211334y x x =-++,()0,3B (2)存在,点P 的坐标为7,08⎛⎫ ⎪⎝⎭或70,6⎛⎫- ⎪⎝⎭ 【解析】【分析】(1)根据待定系数法,可得函数解析式,根据自变量为零,可得B 点坐标(2)根据线段垂直平分线上的点到线段两点间的距离相等,可得点P 在线段的垂直平分线上,利用两点间距离公式求解即可(1)解:将(4,0)A 代入21134=-++y x x c ,得16130c -++= 解得c =3△二次函数1y 的解析式为211334y x x =-++ △点B 是二次函数与y 轴的交点所以点B 的横坐标为0将x =0带入解析式中,求得y =3所以点B 的坐标为()0,3(2) 存在,满足题意的点P ,使得ABP △是以AB 为底边的等腰三角形.当使得ABP △是以AB 为底边的等腰三角形,点P 在线段AB 的垂直平分线上①当点P 在y 轴上时,P A=PB设()0,P m△(4,0)A ,()0,3B=解得76m =- 此时17(0,)6P - ②当点P 在x 轴上时,P A=PB设(),0P n△(4,0)A ,()0,3B解得78n = 此时27(0)8,P 综上所述:17(0,)6P -,27(0)8,P ,使得ABP △是以AB 为底边的等腰三角形 【点睛】此题考察了二次函数的相关知识点,(1)利用待定系数法求函数解析式;(2)抛物线和坐标轴的交点,勾股定理,等腰三角形的性质,熟练运用相关知识点是解题关键类型二 在对称轴上找点成等腰5.如图,直线y =﹣12x +2与x 轴交于点B ,与y 轴交于点C ,已知二次函数的图象经过点B 、C 和点A (﹣1,0).(1)求B 、C 两点的坐标;(2)求该二次函数的解析式;(3)若抛物线的对称轴与x 轴交于点D ,则在抛物线的对称轴上是否存在一点N ,使NCD 为等腰三角形?若存在,求点N 的坐标;若不存在,请说明理由.【答案】(1)B (4,0),C (0,2);(2)213222y x x =-++;(3)存在,123435353325(,),(,),(,4),(,),22222216N N N N - 【解析】【分析】(1)令直线y =12-x +2的x =0,y =0,求出对应的y 和x 的值,得到点C 、B 的坐标; (2)用待定系数法设二次函数解析式,代入点A 、B 、C 的坐标求出解析式;(3)利用“两圆一中垂”找到对应的等腰三角形,结合勾股定理和等腰三角形的性质求点P 的坐标.【详解】(1)对直线y =12-x +2,当x =0时,y =2;y =0时,x =4, △B (4,0),C (0,2).(2)设二次函数为y =a (x ﹣m )(x ﹣n )(a ≠0),△二次函数图象经过B (4,0),A (﹣1,0),△y =a (x ﹣4)(x +1),把点C (0,2)代入y =a (x ﹣4)(x +1)得:a (0﹣4)(0+1)=2,解得:a =12-, △y =12-(x ﹣4)(x +1)=12-x 2+32x +2. (3)存在,理由如下:△二次函数图象经过B(4,0),A(﹣1,0),△对称轴为直线x=32,△D(32,0),△C(0,2),△CD=52,①如图1,当DC=DN时,DN=52,△N1(32,52),N2(32,﹣52),②如图2,当CD=CN3时,过点C作CH△DN3于点H,△CD=CN3,CH△DN3,△DH=N3H,△C(0,2),△DH=2,△N3H=2,△N3D=4,△N3(32,4),③如图3,当N 4C =DN 4时,过点C 作CE △DN 4于点E ,设DN 4=t ,则EN 4=2﹣t ,CE =32, 由勾股定理可知,(2﹣t )2+(32)2=t 2, 解得t =2516. △N 4(32,2516), 综上所述:存在123435353325(,),(,),(,4),(,),22222216N N N N -,使△NCD 是等腰三角形. 【点睛】本题考查了待定系数法求二次函数的解析式,直线与坐标轴的交点,等腰三角形的性质,用到了分类讨论思想.6.如图,直线122y x =-+与x 轴交于点B ,与y 轴交于点C ,已知二次函数的图象经过点B ,C 和点()1,0A -.(1)求B ,C 两点的坐标.(2)求该二次函数的解析式.(3)若抛物线的对称轴与x 轴的交点为点D ,则在抛物线的对称轴上是否存在点P ,使PCD是以CD 为腰的等腰三角形?如果存在,直接写出点P 的坐标;如果不存在,请说明理由.【答案】(1)()4,0B ,()0,2C (2)213222y x x =-++ (3)存在135,22P ⎛⎫ ⎪⎝⎭,235,22P ⎛⎫- ⎪⎝⎭,33,42P ⎛⎫ ⎪⎝⎭,使PCD 是以CD 为腰的等腰三角形 【解析】【分析】(1)令直线122y x =-+的x =0,y =0,求出对应的y 和x 的值,得到点C 、B 的坐标; (2)用待定系数法设二次函数解析式,代入点A 、B 、C 的坐标求出解析式;(3)利用“两圆一中垂”找到对应的等腰三角形,结合勾股定理和等腰三角形的性质求点P 的坐标.(1) 解:对直线122y x =-+,当0x =时,2y =,0y =时,4x =, ()4,0B ∴,()0,2C .(2)解:设二次函数为()()()0y a x m x n a =--≠,二次函数图象经过()4,0B ,()1,0A -,()()41y a x x ∴=-+,把点()0,2C 代入()()41y a x x =-+得:()()04012a -+=, 解得:12a =-, ()()2113412222y x x x x ∴=--+=-++. (3) 解:二次函数图象经过()4,0B ,()1,0A -,∴对称轴为41322x -==, 3,02D ⎛⎫∴ ⎪⎝⎭, ()0,2C ,52CD ∴=, ①如图1,当CD PD =时,52PD =, 135,22P ⎛⎫∴ ⎪⎝⎭,235,22P ⎛⎫- ⎪⎝⎭, ②如图2,当3CD CP =时,过点C 作3CH DP ⊥于点H ,3CD CP =,3CH DP ⊥,3DH P H ∴=,()0,2C ,2DH ∴=,32P H ∴=,34P D ∴=,33,42P ⎛⎫∴ ⎪⎝⎭, 综上所述:存在135,22P ⎛⎫ ⎪⎝⎭,235,22P ⎛⎫- ⎪⎝⎭,33,42P ⎛⎫ ⎪⎝⎭,使PCD 是以CD 为腰的等腰三角形. 【点睛】本题考查了一次函数与坐标轴的交点、二次函数的解析式、等腰三角形的性质、勾股定理,解题的关键是用一般式或者两点式结合待定系数法求解,求点P 的坐标的时候要学会用“两圆一中垂”找到P 点,注意这里只要用“两圆”即可.7.如图,抛物线y =ax 2-bx -3与x 轴交于点A 、C ,交y 轴于点B ,OB =OC =3OA .(1)求抛物线的解析式及对称轴方程;(2)如图1,连接AB ,点M 是对称轴上一点且在第四象限,若△AMB 是以△MBA 为底角的等腰三角形,求点M 的坐标;(1)解:在y =ax 2-bx -3中,令x =0得y =-3,△B (0,-3),△OB =3,△OB =OC =3OA ,△OA =1,OC =3,△A (-1,0)、C (3,0),把A (-1,0)、C (3,0)代入y =ax 2-bx -3得:309330a b a b +-=⎧⎨--=⎩,解得12a b =⎧⎨=⎩, △抛物线的解析式为y =x 2-2x -3,而y =x 2-2x -3=(x -1)2-4,△对称轴方程为x =1;(2)解:设M (1,m ),而A (-1,0)、B (0,-3),△MA 2=4+m 2,MB 2=1+(m +3)2,AB 2=10,△AMB 是以△MBA 为底角的等腰三角形,分两种情况:①若MA =AB ,则MA 2=AB 2,如图:△4+m2=10,解得m m=,△M是对称轴上一点且在第四象限,△M(1,,②若MB=MA,则MA2=MB2,如图:△4+m2=1+(m+3)2,解得m=-1,△M(1,-1),综上所述,M坐标为(1,)或(1,-1);类型三在抛物线上或已知直线上找点成等腰8.如图,已知二次函数y=ax2+bx+3的图象交x轴于点A(1,0),B(3,0),交y轴于点C.(1)求这个二次函数的表达式;(2)直线x=m分别交直线BC和抛物线于点M,N,当△BMN是等腰三角形时,直接写出m 的值.(1)将(1,0)A ,(3,0)B 代入函数解析式,得309330a b a b ++=⎧⎨++=⎩, 解得14a b =⎧⎨=-⎩, 这个二次函数的表达式是243y xx =-+;(2)(,3)M m m -+,2(,43)N m m m -+ 23MN m m =-,3|BM m =-,当MN BM =时,①233)m m m -=-,解得m②233)m m m -=-,解得m =当BN MN =时,45NBM BMN ∠=∠=︒,2430m m -+=,解得1m =或3m =(舍)当BM BN =时,45BMN BNM ∠=∠=︒,2(43)3m m m --+=-+,解得2m =或3m =(舍),当BMN ∆是等腰三角形时,m ,1,2.【点睛】本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是利用面积的和差得出二次函数,又利用了二次函数的性质,解(3)的关键是利用等腰三角形的定义得出关于m 的方程,要分类讨论,以防遗漏.9.如图,已知二次函数()20y x bx c c =-++>的图象与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,且OB =OC =3,顶点为M .(1)求该二次函数的解析式;(2)探索:线段BM 上是否存在点P ,使PMC 为等腰三角形?如果存在,求出点P 的坐标;如果不存在,请说明理由.解:(1)△3OB OC ==,△()3,0B ,()0,3C ,代入2y x bx c =-++中,得930,3.b c c -++=⎧⎨=⎩, 解得2,3.b c =⎧⎨=⎩, △该二次函数的解析式为2y x 2x 3=-++;(2)线段BM 上存在点716,55P ⎛⎫ ⎪⎝⎭,14⎛ ⎝⎭,()2,2,使PMC △为等腰三角形.理由如下:设点P 的坐标为(),26x x -+,由题意可得CM =CP =MP =①当CM PC =整理得251270x x -+=,解得175x =,21x =(舍去),经检验是方程的根 当75x =,716262655x -+=-⨯+=, 此时716,55P ⎛⎫ ⎪⎝⎭;②当CM MP =整理得251030x x -+=,△△=40,△x =解得11x =21x =,经检验是方程的根此时1P ⎛ ⎝⎭;③当CP MP =整理得24=x ,解得2x =,经检验是方程的根此时()2,2P ;综上所述,线段BM 上存在点716,55P ⎛⎫ ⎪⎝⎭,14⎛ ⎝⎭,()2,2, 使PMC △为等腰三角形.【点睛】本题考查二次函数与几何综合题型,利用待定系数法求函数解析式;求坐标系中四边形的面积,需分割三角形与梯形来解,注意动点所在的位置决定了自变量的取值范围;等腰三角形分类考虑,可以用勾股定理,构造方程是解题关键.10.如图,已知二次函数y =ax 2+bx +3的图象与x 轴交于点A (﹣1,0)、B (4,0),与y轴交于点C .(1)二次函数的表达式为 ;(2)点M 在直线BC 上,当△ABM 为等腰三角形时,求点M 的坐标;解:(1)将A (﹣1,0),B (4,0)代入y =ax 2+bx +3得: 3016430a b a b -+=⎧⎨++=⎩, △a =34-,b =94, △239344y x x =-++, 故二次函数表达式为:239344y x x =-++; (2)当x =0时,y =3,△点C 的坐标是(0,3),设直线BC 的表达式为:y =kx +c (k ≠0),将B (4,0),C (0,3)代入y =kx +c 得:4303k c +=⎧⎨=⎩, △343k c ⎧=-⎪⎨⎪=⎩,△直线BC 的解析式为:334y x =-+,使得△ABM 为等腰三角形,存在如图所示的三种情况:过点M 1作M 1D △AB ,△A (﹣1,0),B (4,0),△AD =12AB =52, △OD =32, 设M 1(x ,﹣34x +3), △M 1(32,158), △△ABM 为等腰三角形,△AB =BM 2=5或AB =BM 3=5,设M 2(x 1,﹣34x 1+3),△BM 25, 解得x 1=8或0,当x 1=0时,y =3,当x 1=8时,y =﹣3,△点M 为(0,3)或(8,﹣3)或(32,158); 11.如图,已知二次函数213442y x x =--的图象与y 轴交于点C ,与x 轴交于A 、B 两点,其对称轴与x 轴交于点D .(1)点C 的坐标为___________,点B 的坐标为___________; (2)连接BC ,在线段BC 上是否存在点E ,使得EDB △为等腰三角形?若存在,求出所有符合条件的点E 的坐标;若不存在,请说明理由; 解(1)213442y x x =--, 当x=0时,y=-4,C (0,-4),当y=0时,2134=042x x --, 整理得:2616=0x x --,变形得:()()820x x -+=,解得122,8x x =-=,△B 点坐标为(8,0);(2)C(0,-4),B(8,0),设BC 解析式为y kx b =+,把C 、B 坐标代入得, 480b k b =-⎧⎨+=⎩, 解得412b k =-⎧⎪⎨=⎪⎩, BC 解析式为1-42y x =, EDB △为等腰三角形,点E 在线段BC 上,设E (x, 1-42x )D(3,0), 以DB 为底边,作BD 中垂线与BC 交点为E ,x=()13+8=5.52,115-4= 5.5-4224x ⨯=-, E 11524⎛⎫ ⎪⎝⎭,-,以BD为腰,当BD=EB=5时5,()2820x-=,x=-(舍去,81x2E(8-,当ED=BD=5时点E与点C重合,E(0,-4),EDB △为等腰三角形符合条件的点E 的坐标为:E (0,-4),(8-,11524⎛⎫ ⎪⎝⎭,-; 类型四 综合探究12.如图,二次函数2y ax bx c(a 0)=++>图象的顶点为D ,其图象与x 轴的交点A 、B 的横坐标分别为1-,3.与y 轴负半轴交于点C .()1若ABD 是等腰直角三角形,求a 的值.()2探究:是否存在a ,使得ACB 是等腰三角形?若存在,求出符合条件的a 的值;不存在,说明理由.【答案】(1)1a 2=;(2)存在,a =. 【解析】【分析】 ()1作DE AB ⊥于点E ,根据ABD 是等腰直角三角形,即可求得D 的坐标,利用待定系数法求得函数的解析式,从而求得a 的值.()2根据三边分别相等可以分三种情况:①当AB BC =时,根据勾股定理列方程:222OC BC OB 1697=-=-=,可得a 的值; ②当AB AC =时,根据勾股定理列方程:2OC 16115=-=,可得a 的值;③当AC BC =时,由于OA 1=,OB 3=,不成立.【详解】()1如图,作DE AB ⊥于点E ,()AB 314=--=, ABD 是等腰直角三角形,1DE AB 22∴==, 则D 的坐标是()1,2-.设二次函数的解析式是2y a(x 1)2=--,把()1,0-代入得4a 20-=, 解得:1a 2=. ()2存在,分三种情况:①当AB BC =时,CB AB 4∴==,在Rt OBC 中,222OB OC BC +=,222OC BC OB 1697∴=-=-=,OC ∴=(C 0,∴, 设二次函数的解析式为:()()y a x 1x 3=+-,将(C 0,代入,a ∴= ②当AB AC =时,AC AB 4∴==,在Rt AOC 中,222AO OC AC +=,2OC 16115∴=-=,OC ∴=(C 0,, ()()y a x 1x 3=+-,a ∴= ③当AC BC =时,CO AB ⊥,O ∴是AB 的中点,而AO 1=,BO 3=,AO BO ∴≠,AC BC ∴=不成立,a ∴= 【点睛】本题是二次函数的综合题,考查了待定系数法求函数的解析式,第1问正确根据等腰直角三角形的性质求得D 的坐标是关键,第二问根据等腰三角形的判定正确分类讨论是关键. 13.综合与探究 如图,抛物线2315344y x x =-+与x 轴交于A ,B 两点,且点A 在点B 的左侧,与y 轴交于点C .(1)求点A ,B 和C 的坐标;(2)点P 从点B 出发沿BC 以1个单位长度/秒的速度向终点C 运动,同时,点Q 从点O 出发以相同的速度沿x 轴的正半轴向终点B 运动,一点到达,两点同时停止运动.连接PQ ,当BPQ 是等腰三角形时,请直接写出运动的时间.(1)解:把0x =代入2315344y x x =-+中,得3y =.△点C 的坐标是(0,3).把0y =代入2315344y x x =-+中,得23153044-+=x x . 解得11x =,24x =.△点A 的坐标是(1,0),点B 的坐标是(4,0).△点A 的坐标是(1,0),点B 的坐标是(4,0),点C 的坐标是(0,3).(2)2秒,2013秒和3213秒 解:设运动时间为t ,根据题意,若要构成BPQ ,则P 、Q 不与点B 重合,t 的取值范围为04t <<,△PB OQ t ==,4BQ t =-,如图,过点P 作PD x ⊥轴于点D ,设点P 的坐标为3,34a a ⎛⎫-+ ⎪⎝⎭,则4BD a =-,334PD a =-+,根据勾股定理,在Rt PDB △中,222PD DB PB +=,()2223344a a t ⎛⎫-++-= ⎪⎝⎭, 解得1445a t =-,2445a t =+(不符合题意,舍去), △点P 的坐标为434,55t t ⎛⎫- ⎪⎝⎭, △点Q 的坐标为(),0t △222243907241655255t t t PQ t t ⎛⎫⎛⎫=--+=-+ ⎪ ⎪⎝⎭⎝⎭, △PB OQ t ==,4BQ t =-,222243907241655255t t t PQ t t ⎛⎫⎛⎫=--+=-+ ⎪ ⎪⎝⎭⎝⎭,①当BP BQ =时,即4t t =-,解得:2t =;②当BP PQ =时,22907216255t t t =-+, 解得:12013t =,24t =(不符合题意,舍去), ③当BQ PQ =时,()229072416255t t t -=-+, 解得:13213t =,20t =(不符合题意,舍去),综上所述:当BPQ 是等腰三角形时,时间为2秒,2013秒,3213秒. 【点睛】本题考查二次函数综合运用,包括求抛物线与x 轴的坐标,一次函数的解析式,利用坐标求线段长度,等腰三角形的性质,熟悉掌握求抛物线与x 轴的交点坐标、顶点坐标以及等腰三角形的性质本题的解题关系.。
二次函数特殊三角形存在性问题(等腰三角形、直角三角形)

特殊图形存在性问题一、等腰三角形1、情景:平面内有点A、B,要找到点P使得△ABP为等腰三角形。
2、思想:分类讨论(1)A为顶点:AB=AP(以A为圆心、AB长为半径画圆)(2)B为顶点:AB=BP(以B为圆心、AB长为半径画圆)(3)P为顶点:PA=PB(AB中垂线)【注】:1.利用两圆一线,找到符合要求的点,如P在抛物线对称轴上,在x轴上等;然后将问题转化为,求线段等长。
2.求线段等长:两点间距离(最笨的方法);向坐标轴做垂线,构造一线三等角例1.如图,抛物线y=−x2+2x+3y=−x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为______.练习1.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B 两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,−3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式;(2)在直线BC找一点Q,使得△QOC为等腰三角形,写出Q点坐标.练习2、已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.练习3.如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣x+1与y轴交于点D.(1)求抛物线的解析式;(2)证明:△DBO∽△EBC;(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.练习4.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c(a≠0)与x轴交A(−1,0),B(−3,0)两点,与y轴交于点C(0,−3),其顶点为D.(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x−h)2+k的形式;(2)动点M从点D出发,沿抛物线对称轴方向向上以每秒1个单位的速度运动,运动时间为t,连接OM,BM,当t为何值时,△OMB为等腰三角形?练习5.如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n (m<n)分别是方程x2﹣2x﹣3=0的两根.(1)求抛物线的解析式;(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E 两点(点D在y轴右侧),连接OD、BD.①当△OPC为等腰三角形时,求点P的坐标;②求△BOD 面积的最大值,并写出此时点D的坐标.25.(10分)如图,在平面直角坐标系中,抛物线y=x2+bx+c经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).(Ⅰ)求抛物线的解析式及它的对称轴;(Ⅱ)点P(0,n)在线段OB上,点Q在线段BC上,若OP=2BQ,且P A=QA.求n 的值;(Ⅲ)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.19-红桥一模25.(10分)如图,抛物线y=x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).(1)求该抛物线的解析式.(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.(17河北一模)25(10分)如图,己知抛物线y=x2+bx+c图象经过点A(﹣1,0),B(0,﹣3),抛物线与x轴的另一个交点为C.(1)求这个抛物线的解析式:(2)若抛物线的对称轴上有一动点D,且△BCD为等腰三角形(CB≠CD),试求点D的坐标;二、直角三角形1.情景:平面内有点A、B,要找到点P使得△ABP为直角三角形2.思想:分类讨论(1)A为顶点:∠A(过A做垂线)(2)B为顶点:∠B(过B做垂线)(3)P为顶点:∠C(AB为直径的圆)【注】1.等腰直角三角形,只需在两直线上上下找与AB等长以及过O做AB垂线与圆交点即可例1.如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过矩形OABC的顶点A,B与x 轴交于点E,F且B,E两点的坐标分别为B(2,32)E(−1,0)(1)求二次函数的解析式;(2)在抛物线上是否存在点Q,使△QBF为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.练习1.如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=13(1)求抛物线的对称轴和PP的坐标.(2)在抛物线的对称轴上是否存在这样的点D,使△ABD为直角三角形?如果存在,求点D 的坐标;如果不存在,请说明理由.例2.如图,抛物线y=−x2+bx+c与x轴相交于AB两点,与y 轴相交与点C,且点B与点CC 的坐标分别为(3,0),C(0,3),点M是抛物线的顶点.(1)求二次函数的关系式(2)在MB上是否存在点P,过点P作PD⊥x轴于点D,OD=m,使△PCD为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由练习2.如图,在平面直角坐标系中,直线y=−13x+2交x轴点P,交y轴于点A.抛物线y=x2+bx+c的图象过点E(−1,0),并与直线相交于A、B两点.(1)求抛物线的解析式(关系式);(2)过点A作AC⊥AB交x轴于点C,求点C的坐标;(3)除点C外,在坐标轴上是否存在点M,使得△MAB是直角三角形?若存在,请求出点M 的坐标;若不存在,请说明理由.练习3.如图,抛物线y=x2+bx+c与直线y=x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.(1)求抛物线的解析式;(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标.(18东丽-一模)25.如图,在平面直角坐标系中,点A、B的坐标分别为(1,1)、(1,2),过点A、B分别作y轴的垂线,垂足为D、C,得到正方形ABCD,抛物线y=x2+bx+c经过A、C两点,点P为第一象限内抛物线上一点(不与点A重合),过点P分别作x轴y轴的垂线,垂足为E、F,设点P的横坐标为m,矩形PFOE与正方形ABCD重叠部分图形的周长为l.(1)直接写出抛物线所对应的函数表达式.(2)当矩形PFOE的面积被抛物线的对称轴平分时,求m的值.(3)当m<2时,求L与m之间的函数关系式.(4)设线段BD与矩形PFOE的边交于点Q,当△FDQ为等腰直角三角形时,直接写出m的取值范围.三、平行四边形存在性问题类型一:1.情景:一直平面内三点A、B、C,求一点P使四边形ABCP为平行四边形2.思想:分类讨论(1)以AC为对角线:ABCP1(2)以AB为对角线:ACBP3(3)以BC为对角线:ACP2B【注】找到P点后,用平行四边形的判定定理,求等长线段,或利用等角度、平行线求坐标即可。
二次函数中等腰直角三角形 -回复

二次函数中等腰直角三角形 -回复
您好,关于二次函数中等腰直角三角形,我们可以通过以下步骤来解决:
1. 二次函数一般式:$y=ax^2+bx+c$。
2. 因为中位线长度为右腰,所以这个中位线对应的$x$可以用平移的方法求出:设中位线长度为$t$,则该中位线对应的$x$值为$-\frac{b}{2a}+t$。
3. 由直角三角形性质可知,斜边的平方等于直角腰的平方和,即$(\frac{t}{2})^2+(at^2+c)^2=(\frac{t}{2}+b)^2$。
4. 将第3步中的方程式化简后解出$t$,再带回第2步中的式子,求出该中位线对应的$x$值。
5. 根据对称性,可以得出第二条中位线的长度与第一条中位线相等,且对应的$x$值也相等。
6. 根据中位线长度与底边长度相等的定义,可以得出三角形的底边长度为$2\times(\frac{t}{2}+b)$。
7. 最终,我们就可以得出该等腰直角三角形的底边长、两条直角边长及其顶点的坐标。
希望以上解释能够解决您的问题,任何疑问,请随时追问。
二次函数与几何综合专题 等腰直角三角形存在性问题

III、若 是等腰直角三角形,当DM为斜边时,则: ,
即: ,解得 ,
此时: ,
故不存在M坐使 是以DM为斜边的等腰直角三角形;
综上所述:点M坐标为(0,-1).
(3)解:∵ ,
∴ ,
以点P、C、Q为顶点的三角形是等腰直角三角形,有3种情况,
I.当 时,则 ,
∵四边形OHGQ是矩形,
∴ ,
∴ ,
设 ,其中 ,则P点坐标为(x,-x)
∵P在抛物线 上,即 ,解得: (不合题意舍去), ,
故此时P坐标为 ,
综上所述:点P在x轴上方的抛物线上,点Q在y轴正半轴上,当 是以AQ为斜边的等腰直角三角形时,符合条件的点P的坐标 或 .
易得: (AAS)
∴ , ,
∵四边形OHGQ是矩形,
∴ ,
∴ ,
设 ,则P点坐标为(x,x)
∵P在抛物线 上,即 ,解得: , (不合题意舍去),
此时点P坐标为
II、点P在y轴左侧的抛物线上时,如图:
以等腰 构造K字形,过P点作PH⊥x轴,垂足为H,过Q点作QG⊥PH,垂足为G,
易得: (AAS)
∴ , ,
(2)在y轴上是否存在点M,使得 是等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
(3)直线AC下方的抛物线上有一动点P,直线AC上有一动点Q,若以点P、C、Q为顶点的三角形是等腰直角三角形,求出点Q的坐标.
(4)点P在x轴上方的抛物线上,点Q在y轴正半轴上,当 是以AQ为斜边的等腰直角三角形时,求出符合条件的点P的坐标.
(2)解:如图,设M点坐标为(0,y)
∵点A坐标为(-3,0),点D坐标为(-1,-4),
2023年重庆中考数学第二轮专题复习第24题二次函数综合题等腰三角形类

重庆中考数学第二轮专题复习第24题二次函数综合题等腰三角形类(2022-2023学年版)1.二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使得△PBC为等腰三角形?若存在,请求出点P的坐标;(3)有一个点M从点A出发,以每秒1个单位长度的速度在AB上向点B运动,另一个点N从点D同时出发,以每秒2个单位长度的速度在抛物线的对称轴上运动,设运动时间是t且0≤t≤5,当点M,N运动到何处时,△MNB的面积最大,试求出最大面积.2.如图,已知点A的坐标为(−2,0).直线y=−3x+3与x轴,y轴分别交于点B和点C,连接AC,4顶点为D的抛物线y=ax2+bx+c过A,B,C三点.(1)求拋物线的解析式及顶点D的坐标;(2)设抛物线的对称轴DE交线段BC于点E,P为第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标;(3)设点M是线段BC上的一动点,过点M作MN//AB,交AC于点N,Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒).当以MN为直角边的▵QMN是等腰直角三角形时,直接写出此时t的值.3.在平面直角坐标系中,抛物线y=−x2+bx+c经过点A、B、C,已知A(−1,0),C(0,3).(1)求抛物线的解析式;(2)如图1,P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△CDP为等腰三角形时,求点P的坐标;(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是直线EF上一动点,M(m,0)是x轴一个动MB的最小值以及此时点M、N的坐标.点,请直接写出CN+MN+124.抛物线y=ax2+bx+4交x轴于A(−3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.M为线段OB上的一个动点,过点M作PM⊥x轴,交抛物线于点P,交BC于点Q.(1)求抛物线的解析式;(2)过点P作PN⊥BC,垂足为点N,设M点的坐标为M(m,0),请用含m的代数式表示线段PN 的长,并求出当m为何值时PN有最大值,最大值是多少?(3)试探究点M在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.5.已知:如图,抛物线y=ax2+bx+c(a≠0)与坐标轴分别交于点A(0,6),B(6,0),C(−2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P运动到什么位置时,△PAB的面积有最大值?(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE//x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.6.如图,在平面直角坐标系中,抛物线y=−23x2−23x+4与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.点D是抛物线的顶点,对称轴与x轴交于点E,过点E作BC的平行线交AC于点F.(1)如图1,求点D的坐标和直线BC的解析式;(2)如图1,在对称轴右侧的抛物线上找一点P,使得∠PDE=45°,点M是直线BC上一点,点N是直线EF上一点,MN//AC,求PM+MN+NB的最小值;(3)如图2,将△BOC绕点O逆时针旋转至△B′O′C′的位置,点B,C的对应点分别为点B′,C′,点B′恰好落在BC上,点T为B′C′的中点,过点T作y轴的平行线交抛物线于点H,将点T沿y轴负方向平移3个单位长度得到点K.点Q是y轴上一动点,将△QHK沿直线QH折叠为△QHK′,△BKK′是否能为等腰三角形?若能,请直接写出所有符合条件的点Q的坐标;若不能,请说明理由.7.如图,直线y=−3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x−2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.(1)求a,k的值;(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标;(3)在抛物线及其对称轴上分别取点M、N,使以A,C,M,N为顶点的四边形为正方形,求此正方形的边长.8.如图,抛物线y=ax2+bx−3经过点A(2,−3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)若抛物线上有一点N,且S△OCN=6,求点N的坐标;(3)点P是对称轴上的一个动点,若存在P使△ABP是等腰三角形,请求出此时P点的坐标.9.如图,已知二次函数y=−x2+bx+3的图象与x轴的两个交点为A(4,0)与点C,与y轴交于点B.(1)求此二次函数关系式和点C的坐标;(2)请你直接写出△ABC的面积;(3)在x轴上是否存在点P,使得△PAB是等腰三角形?若存在,请你直接写出点P的坐标;若不存在,请说明理由.10.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(−2,0)、B(6,0)两点,与y轴交于点C(0,6),D为抛物线的顶点.(1)求此二次函数的表达式;(2)求△CDB的面积.(3)在其对称轴右侧的抛物线上是否存在一点P,使△PDC是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.11.在平面直角坐标系中,抛物线y=−x2+bx+c经过点A,B,C,已知A(−1,0),C(0,3).(1)求抛物线的表达式.(2)如图①,P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△CDP为等腰三角形时,求点P的坐标.(3)如图②,抛物线的顶点为点E,EF⊥x轴于点F.若N是直线EF上一动点,M(m,0)是x轴上MB的最小值以及此时点M,N的坐标.一个动点,请直接写出CN+MN+1212.如图,抛物线y=ax2+bx+2交x轴于点A(−3,0)和点B(1,0),交y轴于点C.(1)求这个抛物线的函数表达式.(2)点D的坐标为(−1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.(3)点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠MNO为直角?若存在,求出点N的坐标;若不存在,请说明理由.13.如图,抛物线y=−35x2+125x+3与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C,连接BC.(1)直接写出A、B、C三点坐标及直线BC的函数表达式;(2)如图1,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.点P是直线AB上的动点.当△NBC面积取得最大值时,求出点N的坐标及△NBC面积的最大值,并求此时PN+CP 的最小值;(3)如图2,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.14.抛物线y=ax2+bx+c(a、b、c为参数)与x轴交于A、B两点,与y轴交于点C,其中A(−2,0).已知M(−1+n,m)和N(5−n,m)是抛物线上两点.图1图2(1)求抛物线的解析式(结果用含a的式子表示);(2)如图1,对称轴与x轴的交点为D,若△AOC绕原点顺时针旋转90°得到△COD,点E为x轴正半轴上一点,且满足∠CDO=∠CEO+∠CBO,求点E的坐标;(3)如图2,若△OBC为等腰三角形,点F为OC中点,连接BF;若点P在B点左侧的抛物线上,过点P作PQ⊥BF,垂足为Q,直线PQ与x轴交于点R,且S△PQB=2S△QRB,求点P的坐标.15.如图,抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C(0,3),顶点F的坐标为(1,4),x+1交x轴于点D,交y轴于点E,交抛物线的对称轴于点G.对称轴交x轴于点H,直线y=12备用图(1)求抛物线的解析式.(2)点M为抛物线对称轴上一个动点,若△DGM是以DG为腰的等腰三角形时,请求出点M的坐标.(3)点P为抛物线上一个动点,当点P关于直线y=1x+1的对称点恰好落在x轴上时,请直接2写出此时点P的坐标.16.如图,抛物线y=ax2+bx+4交x轴于A(−3,0),B(4,0)两点,与y轴交于点C,连结AC,BC.M为线段OB上的一个动点,过点M作PM⊥x轴,交抛物线于点P,交BC于点Q.(1)求抛物线的表达式;(2)过点P作ON⊥BC,垂足为点N.设点M的坐标为M(m,0),请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?(3)试探究点M在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点且以AC为腰长的三角形是等腰三角形.若存在,求出此时点Q的坐标;若不存在,请说明理由.17.已知抛物线y=ax2+34x+c经过点A(−2,0)和C(0,94),与x轴交于另一点B,顶点为D.(1)求抛物线的解析式;(2)如图,点E,F分别在线段AB,BD上(E点不与A,B重合),且∠DEF=∠DAB,设AE=x,BF=y,求y与x的函数关系式;(3)在(2)问的条件下,△DEF能否为等腰三角形?若能,求出DF的长;若不能,请说明理由;18.如图,抛物线y=1x2+bx+c与x轴交于A(−3,0),B(4,0)两点,与y轴交于点C,连接AC,3BC,点M是抛物线在第四象限内的一个动点,过点M作MN⊥BC于点N,点M的横坐标为m.(1)求抛物线的表达式;(2)请用含m的代数式表示线段MN的长;(3)试探究在点M运动的过程中,是否存在点N,使得△ACN是等腰三角形?若存在,直接写出点N的坐标;若不存在,请说明理由.第11页,共1页。
二次函数中的等腰三角形问题

教学过程一、复习预习1.二次函数的基础知识2.等腰三角形的性质3.相似三角形的性质二、知识讲解考点1 二次函数的基础知识1.一般地,如果y=ax 2+bx+c (a ,b ,c 是常数且a ≠0),那么y 叫做x 的二次函数,它是关于自变量的二次式,二次项系数必须是非零实数时才是二次函数,这也是判断函数是不是二次函数的重要依据.当b=c=0时,二次函数y=ax 2是最简单的二次函数.2.二次函数y=ax 2+bx+c (a ,b ,c 是常数,a ≠0)的三种表达形式分别为:一般式:y=ax 2+bx+c ,通常要知道图像上的三个点的坐标才能得出此解析式;顶点式:y=a (x -h )2+k ,通常要知道顶点坐标或对称轴才能求出此解析式;交点式:y=a (x -x 1)(x -x 2),通常要知道图像与x 轴的两个交点坐标x 1,x 2才能求出此解析式;对于y=ax 2+bx+c 而言,其顶点坐标为(-2ba,244ac b a).对于y=a (x -h )2+k 而言其顶点坐标为(h ,k ),•由于二次函数的图像为抛物线,因此关键要抓住抛物线的三要素:开口方向,对称轴,顶点. 考点2 等腰三角形的性质1.等腰三角形的两个底角度数相等(简写成“等边对等角”)。
2.等腰三角形的顶角的平分线,底边上的中线,底边上的高重合(简写成“等腰三角形的三线合一性质”)。
3.等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。
7.等腰三角形是轴对称图形,(不是等边三角形的情况下)只有一条对称轴,顶角平分线所在的直线是它的对称轴,等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方9.等腰三角形的腰与它的高的关系直接的关系是:腰大于高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数综合题——等腰三角形一.解答题(共30小题)1.(2014?新余模拟)如图,已知二次函数图象的顶点为(1,﹣3),并经过点C(2,0).(1)求该二次函数的解析式;(2)直线y=3x与该二次函数的图象交于点B(非原点),求点B的坐标和△AOB的面积;(3)点Q在x轴上运动,求出所有△AOQ是等腰三角形的点Q的坐标.2.(2014秋?怀宁县校级月考)如图,二次函数y=﹣x2+mx+3的图象与y轴交于点A,与x 轴的负半轴交于点B,且△AOB的面积为6.(1)求该二次函数的表达式;(2)如果点P在x轴上,且△ABP是等腰三角形,请直接写出点P的坐标.3.(2011?淮安)如图.已知二次函数y=﹣x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.(1)求此二次函数关系式和点B的坐标;(2)在x轴的正半轴上是否存在点P.使得△PAB是以AB为底边的等腰三角形若存在,求出点P的坐标;若不存在,请说明理由.4.(2014?曲靖模拟)如图,已知二次函数y=ax2﹣4x+c的图象与坐标轴交于点A(﹣1,0)和点C(0,﹣5).(1)求该二次函数的解析式和它与x轴的另一个交点B的坐标.(2)在上面所求二次函数的对称轴上存在一点P(2,﹣2),连接OP,找出x轴上所有点M 的坐标,使得△OPM是等腰三角形.5.(2008秋?密云县期末)已知二次函数y=ax2+bx+c的图象分别经过点(0,3)(3,0)(﹣2,﹣5),(1)求这个二次函数的解析式;(2)若这个二次函数的图象与x轴交于点C、D(C点在点D的左侧),且点A是该图象的顶点,请在这个二次函数的对称轴上确定一点B,使△ABC是等腰三角形,求出点B的坐标.6.(2008?海淀区二模)已知二次函数y=ax2+bx+c的图象分别经过点(0,3),(3,0),(﹣2,﹣5).求:(1)求这个二次函数的解析式;(2)求这个二次函数的最值;(3)若设这个二次函数图象与x轴交于点C,D(点C在点D的左侧),且点A是该图象的顶点,请在这个二次函数的对称轴上确定一点B,使△ACB是等腰三角形,求出点B的坐标.7.(2006?松江区二模)如图,已知二次函数y=x2+bx+c(c≠0)的图象经过点A(﹣2,m)(m<0),与y轴交于点B,AB∥x轴,且3AB=2OB.(1)求m的值;(2)求二次函数的解析式;(3)如果二次函数的图象与x轴交于C、D两点(点C在左恻).问线段BC上是否存在点P,使△POC为等腰三角形如果存在,求出点P的坐标;如果不存在,请说明理由.8.(2010秋?永新县校级月考)已知二次函数y=(x﹣1)(x﹣4)的图象与x轴交于A、B 两点(A在B的左边),与y轴交于点C.(1)求出A、B、C三点的坐标;(2)求△ABC的面积;(3)在y轴上是否存在点P,使P、A、C能组成以AC为腰的等腰三角形若存在,求出点P 的坐标;若不存在,说明理由.9.(2013?德宏州)如图,已知直线y=x与抛物线交于A、B两点.(1)求交点A、B的坐标;(2)记一次函数y=x的函数值为y1,二次函数的函数值为y2.若y1>y2,求x的取值范围;(3)在该抛物线上存在几个点,使得每个点与AB构成的三角形为等腰三角形并求出不少于3个满足条件的点P的坐标.10.(2014?曲阜市模拟)设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.(1)当△ABC为等腰直角三角形时,求b2﹣4ac的值;(2)当△ABC为等边三角形时,求b2﹣4ac的值.11.(2015?赤峰)已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.(1)求此二次函数解析式;(2)连接DC、BC、DB,求证:△BCD是直角三角形;(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形若存在,求出符合条件的点P的坐标;若不存在,请说明理由.12.(2013秋?本溪期末)如图,在平面直角坐标系xOy中,二次函数y=﹣x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E.(1)求二次函数的解析式;(2)连接OE交AB于F点,连接AE,在动点C的运动过程中,若△AOF的面积是△AEF面积的2倍,求点C的坐标(3)在动点C的运动过程中,△DEF能否为等腰三角形若能,请直接写出点F的坐标;若不能,请说明理由.13.(2011?临川区模拟)如图,已知二次函数y=ax2+bx+c的图象经过三点A(﹣1,0),B (3,0),C(0,﹣3),它的顶点为M,且正比例函数y=kx的图象与二次函数的图象相交于D、E两点.(1)求该二次函数的解析式和顶点M的坐标;(2)若点E的坐标是(2,﹣3),且二次函数的值小于正比例函数的值时,试根据函数图象求出符合条件的自变量x的取值范围;(3)试探究:抛物线的对称轴上是否存在点P,使△PAC为等腰三角形如果存在,请直接写出点P的坐标;如果不存在,请说明理由.14.(2006?孝感)如图,已知二次函数y=x2+bx+c的图象与x轴只有一个公共点M,与y轴的交点为A,过点A的直线y=x+c与x轴交于点N,与这个二次函数的图象交于点B.(1)求点A、B的坐标(用含b、c的式子表示);(2)当S△BMN=4S△AMN时,求二次函数的解析式;(3)在(2)的条件下,设点P为x轴上的一个动点,那么是否存在这样的点P,使得以P、A、M为顶点的三角形为等腰三角形若存在,请写出符合条件的所有点P的坐标;若不存在,请说明理由.15.(2011?东营模拟)如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.(1)求二次函数的解析式;(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形如果存在,求出点N的坐标;如果不存在,请说明理由.16.(2010?徐州)如图,已知二次函数y=的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.(1)点A的坐标为,点C的坐标为;(2)线段AC上是否存在点E,使得△EDC为等腰三角形若存在,求出所有符合条件的点E 的坐标;若不存在,请说明理由;(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S 取何值时,相应的点P有且只有2个17.(2011?呼伦贝尔)如图,已知二次函数y=ax2+bx+3的图象与x轴相交于点A、C,与y轴相交于点B,A(),且△AOB∽△BOC.(1)求C点坐标、∠ABC的度数及二次函数y=ax2+bx+3的关系式;(2)在线段AC上是否存在点M(m,0).使得以线段BM为直径的圆与边BC交于P点(与点B不同),且以点P、C、O为顶点的三角形是等腰三角形若存在,求出m的值;若不存在,请说明理由.18.(2013?廊坊一模)如图,二次函数y=ax2+x+c的图象与x轴交于点A、B两点,且A点坐标为(﹣2,0),与y轴交于点C(0,3).(1)求出这个二次函数的解析式;(2)直接写出点B的坐标为;(3)在x轴是否存在一点P,使△ACP是等腰三角形若存在,求出满足条件的P点坐标;若不存在,请说明理由;(4)在第一象限中的抛物线上是否存在一点Q,使得四边形ABQC的面积最大若存在,请求出Q点坐标及面积的最大值;若不存在,请说明理由.19.(2012?景宁县模拟)已知二次函数y=﹣x2+4x+5图象交x轴于点A、B,交y轴于点C,点D是该函数图象上一点,且点D的横坐标为4,连BD,点P是AB上一动点(不与点A重合),过P作PQ⊥AB交射线AD于点Q,以PQ为一边在PQ的右侧作正方形PQMN.设点P的坐标为(t,0).(1)求点B,C,D的坐标及射线AD的解析式;(2)在AB上是否存在点P,使△OCM为等腰三角形若存在,求正方形PQMN 的边长;若不存在,请说明理由;(3)设正方形PQMN与△ABD重叠部分面积为s,求s与t的函数关系式.20.(2013?徐州)如图,二次函数y=x2+bx﹣的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.(1)请直接写出点D的坐标:;(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;(3)是否存在这样的点P,使△PED是等腰三角形若存在,请求出点P的坐标及此时△PED 与正方形ABCD重叠部分的面积;若不存在,请说明理由.21.(2013?鞍山一模)如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交与A,B两点,与y轴交与点C,已知点A的坐标为(﹣2,0),sin∠ABC=,点D是抛物线的顶点,直线DC交x轴于点E.(1)求抛物线的解析式及其顶点D的坐标;(2)在直线CD上是否存在一点Q,使以B,C,Q为顶点的三角形是等腰三角形若存在,请直接写出点Q的坐标;若不存在,请说明理由;(3)点P是直线y=2x﹣4上一点,过点P作直线PM垂直于直线CD,垂足为M,若∠MPO=75°,求出点P的坐标.22.(2013?菏泽)如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=﹣x+3的图象与y轴、x轴的交点,点B在二次函数的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.(1)试求b,c的值,并写出该二次函数表达式;(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:①当P运动到何处时,有PQ⊥AC②当P运动到何处时,四边形PDCQ的面积最小此时四边形PDCQ的面积是多少23.(2014?北塘区二模)已知二次函数y=mx2﹣5mx+1(m为常数,m>0),设该函数图象与y 轴交于点A,图象上一点B与点A关于该函数图象的对称轴对称.(1)求点A、B的坐标;(2)点O为坐标原点,点M为函数图象的对称轴上一动点,求当M运动到何处时△MAO的周长最小;(3)若该函数图象上存在点P与点A、B构成一个等腰三角形,且△PAB的面积为10,求m 的值.24.(2015?黔东南州)如图,已知二次函数y1=﹣x2+x+c的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为y2=kx+b.(1)求二次函数y1的解析式及点B的坐标;(2)由图象写出满足y1<y2的自变量x的取值范围;(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形若存在,求出P 的坐标;若不存在,说明理由.25.(2015?曲靖一模)如图,直线y=﹣x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B、C和点A(﹣1,0).(1)求B、C两点坐标;(2)求该二次函数的关系式;(3)若抛物线的对称轴与x轴的交点为点D,则在抛物线的对称轴上是否存在点P,使△PCD 是以CD为腰的等腰三角形如果存在,直接写出P点的坐标;如果不存在,请说明理由;(4)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大求出四边形CDBF的最大面积及此时E点的坐标.26.(2014?怀集县二模)如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=﹣x+3的图象与y轴、x轴的交点,点B在二次函数y=x2+bx+c的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.(1)试求点B、D的坐标,并求出该二次函数的解析式;(2)P、Q分别是线段AD、CA上的动点,点P从A开始向D运动,同时点Q从C开始向A 运动,它们运动的速度都是每秒1个单位,求:①当P运动到何处时,△APQ是直角三角形②当P运动到何处时,四边形PDCQ的面积最小此时四边形PDCQ的面积是多少27.(2015?铜仁市)如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形若存在.请求出点P的坐标);(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.28.(2015?丹东)如图,已知二次函数y=ax2+x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.(1)请直接写出二次函数y=ax2+x+c的表达式;(2)判断△ABC的形状,并说明理由;(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN 面积最大时,求此时点N的坐标.29.(2013?无锡)如图,直线x=﹣4与x轴交于点E,一开口向上的抛物线过原点交线段OE 于点A,交直线x=﹣4于点B,过B且平行于x轴的直线与抛物线交于点C,直线OC交直线AB于D,且AD:BD=1:3.(1)求点A的坐标;(2)若△OBC是等腰三角形,求此抛物线的函数关系式.30.(2014?遵义)如图,二次函数y=x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC 边运动,其中一点到达端点时,另一点也随之停止运动.(1)求该二次函数的解析式及点C的坐标;(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q 为顶点的三角形为等腰三角形若存在,请求出E点坐标;若不存在,请说明理由.(3)当P,Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请判定此时四边形APDQ的形状,并求出D点坐标.二次函数综合题——等腰三角形参考答案一.解答题(共30小题)1.; 2.; 3.; 4.; 5.; 6.;7.; 8.; 9.; 10.;11.;12.;13.;14.;15.;16.(0,4);(8,0);17.;18.(6,0);19.;20.(-3,4);21.;22.;23.;24.;25.;26.;27.;28.;29.;30.;。
