高三总复习讲义三角函数的图像与性质
高考数学总复习 基础知识名师讲义 第三章 第五节三角函数的图象与性质 文
第五节 三角函数的 图象与性质1.能画出y =sin x ,y =cos x ,y =tan x 的图象.2.理解正弦函数、余弦函数在区间[0,2π]上的性质(如值域、单调性、奇偶性、最大值和最小值以及与x 轴交点等),理解正切函数在区间⎝⎛⎭⎫-π2,π2上的性质.了解三角函数的周期性.知识梳理一、正弦函数、余弦函数、正切函数的性质(续上表)二、研究函数y =A sin(ωx +φ)性质的方法类比于研究y =sin x 的性质,只需将y =A sin(ωx +φ)中的ωx +φ看成y =sin x 中的x ,但在求y =A sin(ωx +φ)的单调区间时,要特别注意A 和ω的符号,通过诱导公式先将ω化为正数.研究函数y =A cos(ωx +φ),y =A tan(ωx +φ)的性质的方法与其类似,也是类比、转化.三、求三角函数的周期的常用方法经过恒等变形化成“y =A sin(ωx +φ),y =A cos(ωx +φ),y =A tan(ωx +φ)”的形式,再利用周期公式.如:函数y =A sin(ωx +φ),y =A cos(ωx +φ)的最小正周期都是2π|ω|;函数y =A tan(ωx +φ)的最小正周期是π|ω|.另外还有图象法和定义法.基础自测1.(2013·揭阳二模)设函数f (x )=cos(2π-x )+3cos ⎝⎛⎭⎫π2-x ,则函数的最小正周期为( ) A.π2B .πC .2πD .4π解析:函数f (x )=cos x +3sin x =2⎝⎛⎭⎫32sin x +12cos x =2sin ⎝⎛⎭⎫x +π6, 故其最小正周期为2π1=2π,故选C.答案:C2.(2013·天津卷)函数f (x )=sin ⎝⎛⎭⎫2x -π4在区间⎣⎡⎦⎤0,π2上的最小值为( ) A .-1B .-22C.22D .0解析:因为x ∈⎣⎡⎦⎤0,π2,所以-π4≤2x -π4≤3π4,令n =2x -π4,则sin ⎝⎛⎭⎫2x -π4=sin n 在n ∈⎣⎡⎦⎤-π4,3π4上的最小值为sin ⎝⎛⎭⎫-π4=-22.故选B. 答案:B3.(2012·浙江名校新高考联盟二联) 若函数f (x )=sin (x +α)-2cos(x -α)是奇函数,则sin αcos α=________.解析:因为函数f (x )=sin(x +α)-2cos(x -α)是奇函数,所以f (0)=sin α-2cos α=0,即tan α=2.所以sin αcos α>0,不妨设α为锐角,可得sin α=25,cos α=15.所以sin αcos α=25.答案:254.(2012·合肥模拟)已知函数f (x )=sin ⎝⎛⎭⎫ωx -π6(ω>0)在⎝⎛⎭⎫0,4π3上单调递增,在⎝⎛⎭⎫4π3,2π上单调递减,则ω=___________.1.(2013·山东卷)函数y =x cos x +sin x 的图象大致为( )解析:函数y =x cos x +sin x 为奇函数,排除B.取x =π2,排除C ;取x =π,排除A ,故选D.答案:D2.已知函数f (x )=4cos x sin ⎝⎛⎭⎫x +π6-1. (1)求f (x )的最小正周期;(2)求f (x )在区间⎣⎡⎦⎤-π6,π4上的最大值和最小值. 解析:(1)∵f (x )=4cos x ⎝⎛⎭⎫sin x cos π6+cos x sin π6-1 =23sin x cos x +2cos 2x -1 =3sin 2x +cos 2x =2sin ⎝⎛⎭⎫2x +π6, ∴函数f (x )的最小正周期为π.(2)∵-π6≤x ≤π4,∴-π6≤2x +π6≤2π3.∴当2x +π6=π2,即x =π6时,函数f (x )取得最大值2;当2x +π6=-π6,即x =-π6时,函数f (x )取得最小值-1.1. (2013·佛山一模)函数y =sin x +sin ⎝⎛⎭⎫x -π3 的最小正周期为________,最大值是________.解析:因为函数y =sin x +sin ⎝⎛⎭⎫x -π3=sin x +12sin x -32cos x =3sin ⎝⎛⎭⎫x -π6. 所以函数的周期为T =2π1=2π;函数的最大值为: 3. 答案:2π32.已知函数f (x )=2sin x cos x +cos 2x (x ∈R ).(1)当x 取什么值时,函数f (x )取得最大值?并求其最大值. (2)若θ为锐角,且f ⎝⎛⎭⎫θ+π8=23,求tan θ的值. 解析:(1)f (x )=2sin x cos x +cos 2x =sin 2x +cos 2x =2⎝⎛⎭⎫22sin 2x +22cos 2x =2sin ⎝⎛⎭⎫2x +π4. ∴当2x +π4=2k π+π2,即x =k π+π8(k ∈Z )时,函数f (x )取得最大值,其最大值为 2.(2)∵f ⎝⎛⎭⎫θ+π8=23, ∴2sin ⎝⎛⎭⎫2θ+π2=23. ∴cos 2θ=13.∵θ为锐角,即0<θ<π2,∴0<2θ<π.∴sin 2θ=1-cos 22θ=223.∴tan θ=sin θcos θ=2sin θcos θ2cos 2θ=sin 2θ1+cos 2θ=22. 中国书法艺术说课教案今天我要说课的题目是中国书法艺术,下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。
高考数学总复习 第三章 第3讲 三角函数的图象与性质课件 理

考点2 三角函数的对称性
例2:(1)函数y=cos2x+π3图象的对称轴方程可能是(
)
A.x=-π6
B.x=-1π2
C.x=6π
D.x=1π2
解析:(1)令2x+
π 3
=kπ(k∈Z),得x=
kπ 2
-
π 6
(k∈Z),令k=
0,得该函数的一条对称轴为x=-6π.
答案:A
(2)函数y=sin3x-4π的图象的一ห้องสมุดไป่ตู้对称中心是(
(0,0),π2,1,(π,0),32π,-1,(2π,0). (2)y=cosx的图象在[0,2π]上的五个关键点的坐标为 (0,1),π2,0,(π,-1),32π,0,(2π,1).
2.三角函数的图象和性质
函数
y=sinx
y=cosx
定义域
R
R
y=tanx
x|
xk2,kZ
图象
值域
[-1,1]
2.使 cosx=1-m 有意义的 m 值为( C )
A.m≥0
B.m≤0
C.0≤m≤2
D.-2≤m≤0
3.(2013 年上海)既是偶函数又在区间(0,π)上单调递减的
函数是( B )
A.y=sinx
B.y=cosx
C.y=sin2x
D.y=cos2x
4.函数 y=5tan(2x+1)的最小正周期为( B )
【规律方法】本题主要考查函数 y=Asin(wx+φ)的图象特 征,正弦函数的值域与最值.解题关键在于将已知的函数表达式 化为三角函数模型,再根据此三角函数模型的图象与性质进行 解题即可.
【互动探究】 3.已知函数 f(x)=2cos2x+sin2x-4cosx.
三角函数的图像和性质讲解(定义域,值域,周期,单调性等)

三角函数的图象与性质教学目标:1、掌握正、余弦函数的定义域和值域;2、进一步理解三角函数的周期性和奇偶性的概念,会求它们的周期,会判断它们的奇偶性;3、能正确求出正、余弦函数的单调区间教学重点:正、余弦函数的性质教学难点:正、余弦函数的单调性知识要点:1、定义域:函数sin y x =及cos y x =的定义域都是(),-∞+∞,即实数集R2、值域:函数sin y x =,x R ∈及cos y x =,x R ∈的值域都是[]1,1-理解:(1)在单位圆中,正弦线、余弦线的长都是等于或小于半径的长1的,所以sin 1x ≤,cos 1x ≤,即1sin 1x -≤≤,1cos 1-≤≤。
(2)函数sin y x =在2,()2x k k Z ππ=+∈时,y 取最大值1,当22x k ππ=-,()k Z ∈时,y 取最小值-1;函数cos y x =在2x k π=,()k Z ∈时,y 取最大值1,当2x k ππ=+,()k Z ∈时,y 取最小值-1。
正弦函数s i n y x =,x R ∈和余弦函数cos y x =,x R ∈是周期函数,2k π(0)k Z k ∈≠且都是它们的周期,最小正周期是2π。
4、奇偶性正弦函数sin y x =,x R ∈是奇函数,余弦函数cos y x =,x R ∈是偶函数。
理解:(1)由诱导公式()sin sin x x -=-,cos()cos x x -=可知以上结论成立;(2)反映在图象上,正弦曲线关于原点O 对称,余弦曲线关于y 轴对称。
5、单调性(1)由正弦曲线可以看出:当x 由2π-增大到2π时,曲线逐渐上升,sin x 由-1增大到1;当x 由2π增大到32π时,曲线逐渐下降,sin x 由1减至-1,由正弦函数的周期性知道:①正弦函数sin y x =在每一个闭区间2,222k k ππππ⎡⎤-++⎢⎥⎣⎦()k Z ∈上,都从-1增大到1,是增函数; ②在每一个闭区间32,222k k ππππ⎡⎤++⎢⎥⎣⎦()k Z ∈上,都从1减小到-1,是减函数。
高考数学必修4总复习《三角函数:三角函数的图像与性质》

∴y=sin2x+52π为偶函数.
答案:B
4. (教材改编题)函数 f(x)=tanx+π4的单调递增区间为(
)
A. kπ-2π,kπ+π2(k∈Z)
B. (kπ,(k+1)π)(k∈Z)
C. kπ-34π,kπ+4π(k∈Z)
D. kπ-π4,kπ+34π(k∈Z)
(2)求满足 f(x)=0 的 x 的取值;
(3)求函数 f(x)的单调递减区间.
解 (1) 2sin2x-3π>0⇒
sin2x-π3>0⇒2kπ<2x-π3<2kπ+π,
k
∈
Z
⇒
kπ
+
π 6
<x<kπ
+
2 3
π
,
k
∈
Z.
故
函
数
的
定
义
域
为
kπ+π6,kπ+23π,k∈Z.
(2)∵f(x)=0,∴sin 2x-3π =
第五节 三角函数的图像与性质
1. 理解正弦函数、余弦函数、正切函数的图像和性质,会用 “五点法”画正弦函数、余弦函数的简图. 2. 了解周期函数与最小正周期的意义.
1. 周期函数
(1)周期函数的定义
对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值
时,都有 f(x+T)=f(x,) 那么函数f(x)就叫做周期函数. 非零常数T 叫做这个函数
2 2
⇒2x-
π 3
=2kπ+
π 4
或2kπ+
3 4
π,k∈Z⇒x=kπ+
7 24
π或x=kπ+
13 24
π,k∈Z,故x的取值是
x|x=kπ+274π或x=kπ+1234π,k∈Z. (3)令2kπ+π2≤2x-π3<2kπ+π,k∈Z⇒2kπ+56π≤2x<2kπ+43π,
高考数学总复习 基础知识 第三章 第五节三角函数的图象与性质 理
第五节 三角函数的图象与性质知识梳理1m in 2偶函数1.能画出y =sin x ,y =cos x ,y =tan x 的图象.2.理解正弦函数、余弦函数在区间[0,2π]上的性质(如值域、单调性、奇偶性、最大值和最小值以及与x 轴交点等),理解正切函数在区间⎝ ⎛⎭⎪⎫-π2,π2上的性质.了解三角函数的周期性.类比于研究y =sin x 的性质,只需将y =A sin(ωx +φ)中的ωx +φ看成y =sin x 中的x ,但在求y =A sin(ωx +φ)的单调区间时,要特别注意A 和ω的符号,通过诱导公式先将ω化为正数.研究函数y =A cos(ωx +φ),y =A tan(ωx +φ)的性质的方法与其类似,也是类比、转化.三、求三角函数的周期的常用方法经过恒等变形化成“y =A sin(ωx +φ),y =A cos(ωx +φ),y =A tan(ωx +φ)”的形式,再利用周期公式.如:函数y =A sin(ωx +φ),y =A cos(ωx +φ)的最小正周期都是2π|ω|;函数y =A tan(ωx +φ)的最小正周期是π|ω|.另外还有图象法和定义法.基础自测1.(2013·广州一测)如果函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π6(ω>0)的两个相邻零点之间的距离为π12,则ω的值为( ) A .3 B .6 C .12 D .24解析:T =π6,ω=2πT=12,故选C.答案:C2.若函数f (x )=sin x +φ3(φ∈[0,2π]) 是偶函数,则φ=( )A.π2B.2π3C.3π2D.5π3解析:∵f (x )为偶函数,关于y 轴对称,x =0为其对称轴. ∴x +φ3=π2+k π,令x =0,φ=3k π+32π,当k =0时,φ=32π,选C 项.答案:C3. 若函数f (x )=sin(x +α)-2cos(x -α)是奇函数,则sin αcos α=________.解析:因为函数f (x )=sin(x +α)-2cos(x -α)是奇函数,所以f (0)=sin α-2cosα=0,即tan α=2.所以sin αcos α>0,不妨设α为锐角,可得sin α=25,cos α=15. 所以sin αcos α=25.答案:254.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx -π6(ω>0)在⎝ ⎛⎭⎪⎫0,4π3上单调递增,在⎝ ⎛⎭⎪⎫4π3,2π上单调递减,则ω=________.解析:由题意f ⎝ ⎛⎭⎪⎫4π3=sin ⎝ ⎛⎭⎪⎫4πω3-π6=1⇒4πω3-π6=2k π+π2⇒ω=32k +12,k ∈Z .又ω>0,令k =0,得ω=12(如k >0,则ω≥2,T ≤π与已知矛盾).答案:121.(2013·山东卷)函数y =x cos x +sin x 的图象大致为( )解析:函数y =x cos x +sin x 为奇函数,排除B.取x =π2,排除C ;取x =π,排除A ,故选D.答案:D2.已知函数f (x )=4cos x sin ⎝⎛⎭⎪⎫x +π6-1.(1)求f (x )的最小正周期;(2)求f (x )在区间⎣⎢⎡⎦⎥⎤-π6,π4上的最大值和最小值.解析:(1)∵f (x )=4cos x ⎝⎛⎭⎪⎫sin x cos π6+cos x sin π6-1 =23sin x cos x +2cos 2x -1=3sin 2x +cos 2x=2sin ⎝ ⎛⎭⎪⎫2x +π6, ∴函数f (x )的最小正周期为π.(2)∵-π6≤x ≤π4,∴-π6≤2x +π6≤2π3.∴当2x +π6=π2,即x =π6时,函数f (x )取得最大值2;当2x +π6=-π6,即x =-π6时,函数f (x )取得最小值-1.1. (2013·佛山一模)函数y =sin x +sin ⎝⎛⎭⎪⎫x -π3 的最小正周期为________,最大值是________.解析:因为函数y =sin x +sin ⎝ ⎛⎭⎪⎫x -π3=sin x +12sin x -32cos x =3sin ⎝⎛⎭⎪⎫x -π6.所以函数的周期为T =2π1=2π;函数的最大值为 3. 答案:2π 32.已知函数f ()x =2sin x cos x +cos 2x (x ∈R ).(1)当x 取什么值时,函数f ()x 取得最大值?并求其最大值.(2)若θ为锐角,且f ⎝⎛⎭⎪⎫θ+π8=23,求tan θ的值.解析:(1)f ()x =2sin x cos x +cos 2x =sin 2x +cos 2x=2⎝ ⎛⎭⎪⎫22sin 2x +22cos 2x=2sin ⎝ ⎛⎭⎪⎫2x +π4. ∴当2x +π4=2k π+π2,即x =k π+π8(k ∈Z )时,函数f ()x 取得最大值,其最大值为2.(2)∵f ⎝⎛⎭⎪⎫θ+π8=23, ∴2sin ⎝ ⎛⎭⎪⎫2θ+π2=23. ∴cos 2θ=13.∵θ为锐角,即0<θ<π2,∴0<2θ<π.∴sin 2θ=1-cos 22θ=223. ∴tan θ=sin θcos θ=2sin θcos θ2cos 2θ=sin 2θ1+cos 2θ=22.。
三角函数图像与性质-知识点总结及题型归纳讲义
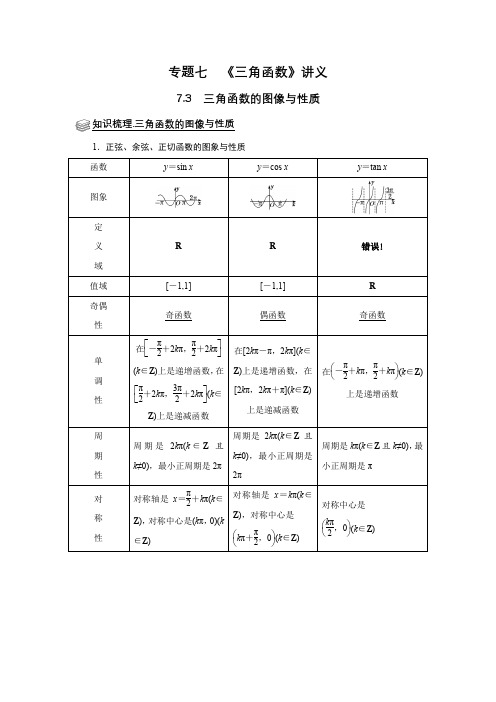
专题七《三角函数》讲义7.3 三角函数的图像与性质知识梳理.三角函数的图像与性质1.正弦、余弦、正切函数的图象与性质函数y=sin x y=cos x y=tan x 图象定义域R R错误!值域[-1,1][-1,1]R奇偶性奇函数偶函数奇函数单调性在⎣⎡⎦⎤-π2+2kπ,π2+2kπ(k∈Z)上是递增函数,在⎣⎡⎦⎤π2+2kπ,3π2+2kπ(k∈Z)上是递减函数在[2kπ-π,2kπ](k∈Z)上是递增函数,在[2kπ,2kπ+π](k∈Z)上是递减函数在⎝⎛⎭⎫-π2+kπ,π2+kπ(k∈Z)上是递增函数周期性周期是2kπ(k∈Z且k≠0),最小正周期是2π周期是2kπ(k∈Z且k≠0),最小正周期是2π周期是kπ(k∈Z且k≠0),最小正周期是π对称性对称轴是x=π2+kπ(k∈Z),对称中心是(kπ,0)(k∈Z)对称轴是x=kπ(k∈Z),对称中心是⎝⎛⎭⎫kπ+π2,0(k∈Z)对称中心是⎝⎛⎭⎫kπ2,0(k∈Z)题型一. 三角函数图像的伸缩变换1.要得到函数y =3sin (2x +π3)的图象,只需要将函数y =3cos2x 的图象( ) A .向右平行移动π12个单位 B .向左平行移动π12个单位C .向右平行移动π6个单位D .向左平行移动π6个单位2.(2017•新课标Ⅰ)已知曲线C 1:y =cos x ,C 2:y =sin (2x +2π3),则下面结论正确的是( )A .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2B .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2C .把C 1上各点的横坐标缩短到原来的12,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2D .把C 1上各点的横坐标缩短到原来的12,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 23.(2021春•闵行区校级期中)函数y =cos (2x +φ)的图象向右平移π2个单位长度后与函数y =sin (2x +2π3)的图象重合,则|φ|的最小值为 .4.(2016春•南通期末)将函数f(x)=sin(ωx +φ),(ω>0,−π2<φ<π2)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移π4个单位长度得到y =sin x 的图象,则f(π6)= .5.(2015•湖南)将函数f (x )=sin2x 的图象向右平移φ(0<φ<π2)个单位后得到函数g (x )的图象.若对满足|f (x 1)﹣g (x 2)|=2的x 1、x 2,有|x 1﹣x 2|min =π3,则φ=( ) A .5π12B .π3C .π4D .π6题型二. 已知图像求解析式1.图是函数y =A sin (ωx +φ)(x ∈R )在区间[−π6,5π6]上的图象,为了得到这个函数的图象,只要将y =sin x (x ∈R )的图象上所有的点( )A .向左平移π3个单位长度,再把所得各点的横坐标缩短到原来的12,纵坐标不变B .向左平移π3个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C .向左平移π6个单位长度,再把所得各点的横坐标缩短到原来的12,纵坐标不变D .向左平移π6个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变2.已知函数y =sin(ωx +φ)(ω>0,|φ|<π2)的部分图象如图所示,则( )A .ω=π2,φ=−π4 B .ω=π2,φ=π4C .ω=π,φ=−π4D .ω=π,φ=π43.已知函数f (x )=A cos (ωx +φ)的图象如图所示,f (π2)=−23,则f (0)=( )A .−23B .−12C .23D .124.已知函数f (x )=A tan (ωx +φ)(ω>0,|φ|<π2)的部分图象如图所示,下列关于函数g (x )=A cos (ωx +φ)(x ∈R )的表述正确的是( )A .函数g (x )的图象关于点(π4,0)对称B .函数g (x )在[−π8,3π8]递减 C .函数g (x )的图象关于直线x =π8对称D .函数h (x )=cos2x 的图象上所有点向左平移π4个单位得到函数g (x )的图象题型三. 三角函数的性质 考点1.单调性1.函数y =sin (﹣2x +π3)的单调递减区间是( ) A .[k π−π12,k π+5π12],k ∈Z B .[2k π−π12,2k π+5π12],k ∈ZC .[k π−π6,k π+5π6],k ∈ZD .[2k π−π6,2k π+5π6],k ∈Z2.已知函数f(x)=Asin(x +φ)(A >0,−π2<φ<0)在x =5π6时取得最大值,则f (x )在[﹣π,0]上的单调增区间是( ) A .[−π,−5π6] B .[−5π6,−π6] C .[−π3,0]D .[−π6,0]3.已知函数f (x )=sin (2x +π3)在区间[0,a ](其中a >0)上单调递增,则实数a 的取值范围是( ) A .{a |0<a ≤π12} B .{a |0<a ≤π2} C .{a |a =k π+π12,k ∈N *} D .{a |2k π<a ≤2k π+π12,k ∈N *} 4.已知ω>0,函数f (x )=sin (ωx +π4)在区间(π2,π)上单调递减,则实数ω的取值范围是( ) A .[12,54] B .[12,34]C .(0,12]D .(0,2]考点2.周期性、奇偶性、对称性1.已知函数f (x )=cos 2x +sin 2(x +π6),则( )A .f (x )的最小正周期为π,最小值为12B .f (x )的最小正周期为π,最小值为−12C .f (x )的最小正周期为2π,最小值为12D .f (x )的最小正周期为2π,最小值为−122.已知f (x )=sin2x +|sin2x |(x ∈R ),则下列判断正确的是( ) A .f (x )是周期为2π的奇函数 B .f (x )是值域为[0,2]周期为π的函数 C .f (x )是周期为2π的偶函数 D .f (x )是值域为[0,1]周期为π的函数3.将函数y =sin2x −√3cos2x 的图象沿x 轴向右平移a 个单位(a >0)所得图象关于y 轴对称,则a 的最小值是( ) A .712π B .π4C .π12D .π64.已知函数f (x )=a sin x ﹣b cos x (ab ≠0,x ∈R )在x =π4处取得最大值,则函数y =f (π4−x )是( )A .偶函数且它的图象关于点(π,0)对称B .偶函数且它的图象关于点(3π2,0)对称 C .奇函数且它的图象关于点(3π2,0)对称 D .奇函数且它的图象关于点 (π,0)对称考点3.三角函数性质综合1.(2019•天津)已知函数f (x )=A sin (ωx +φ)(A >0,ω>0,|φ|<π)是奇函数,将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ).若g (x )的最小正周期为2π,且g (π4)=√2,则f (3π8)=( )A .﹣2B .−√2C .√2D .22.(2015•天津)已知函数f (x )=sin ωx +cos ωx (ω>0),x ∈R ,若函数f (x )在区间(﹣ω,ω)内单调递增,且函数y =f (x )的图象关于直线x =ω对称,则ω的值为 .3.(2014•大纲版)若函数f (x )=cos2x +a sin x 在区间(π6,π2)是减函数,则a 的取值范围是 .4.(2016•新课标Ⅰ)若函数f (x )=x −13sin2x +a sin x 在(﹣∞,+∞)单调递增,则a 的取值范围是( ) A .[﹣1,1]B .[﹣1,13]C .[−13,13]D .[﹣1,−13]5.(2013•安庆二模)已知函数f (x )=sin (ωx +π6),其中ω>0,若f (π6)=f (π3),且f (x )在区间(π6,π3)上有最小值、无最大值,则ω等于( )A .403B .283C .163D .436.(2014•北京)设函数f (x )=A sin (ωx +φ)(A ,ω,φ是常数,A >0,ω>0)若f (x )在区间[π6,π2]上具有单调性,且f (π2)=f(2π3)=﹣f (π6),则f (x )的最小正周期为 .题型四. 三角函数最值1.函数f (x )=15sin (x +π3)+cos (x −π6)的最大值为( ) A .65B .1C .35D .152.函数f (x )=cos (ωx +π3)(ω>0)在[0,π]内的值域为[﹣1,12],则ω的取值范围为( ) A .[32,53]B .[23,43]C .[23,+∞)D .[23,32]3.已知函数f (x )=cos2x +sin x ,则下列说法中正确的是( ) A .f (x )的一条对称轴为x =π4 B .f (x )在(π6,π2)上是单调递减函数C .f (x )的对称中心为(π2,0)D .f (x )的最大值为14.若0<x ≤π3,则函数y =sin x +cos x +sin x cos x 的值域为 .5.已知函数f(x)=2sinωx ⋅cos 2(ωx 2−π4)−sin 2ωx(ω>0)在区间[−2π5,5π6]上是增函数,且在区间[0,π]上恰好取得一次最大值1,则ω的取值范围是( ) A .(0,35]B .[12,35]C .[12,34]D .[12,52)6.已知函数f (x )=cos x •sin (x +π3)−√3cos 2x +√34,x ∈R (1)求f (x )的最小正周期;(2)求f (x )在闭区间[0,π2]上的最大值和最小值及相应的x 值;(3)若不等式|f (x )﹣m |<2在x ∈[0,π2]上恒成立,求实数m 的取值范围.题型五.三角函数零点1.已知函数f (x )=sin ωx −√3cos ωx (ω>0),若方程f (x )=﹣1在(0,π)上有且只有四个实数根,则实数ω的取值范围为 .2.已知函数f (x )=√3sin ωx cos ωx +cos 2ωx −12,(ω>0,x ∈R ),若函数f (x )在区间(π2,π)内没有零点,则ω的取值范围( ) A .(0,512] B .(0,512]∪[56,1112]C .(0,58]D .(0,56]∪[1112,1)3.函数f(x)=2sin(2ωx +π6)(ω>0)图象上有两点A (s ,t ),B (s +2π,t )(﹣2<t <2),若对任意s ∈R ,线段AB 与函数图象都有五个不同交点,若f (x )在[x 1,x 2]和[x 3,x 4]上单调递增,在[x 2,x 3]上单调递减,且x 4−x 3=x 2−x 1=23(x 3−x 2),则x 1的所有可能值是课后作业. 三角函数的图像与性质1.函数f (x )=A sin (ωx +φ)(A >0,ω>0,﹣π<φ<0)的部分图象如图所示,为了得到g (x )=A sin ωx 的图象,只需将函数y =f (x )的图象( )A .向左平移π3个单位长度B .向左平移π12个单位长度 C .向右平移π3个单位长度D .向右平移π12个单位长度2.关于函数y =2sin (3x +π4)+1,下列叙述正确的是( ) A .其图象关于直线x =−π4对称 B .其图象关于点(π12,1)对称 C .其值域是[﹣1,3]D .其图象可由y =2sin (x +π4)+1图象上所有点的横坐标变为原来的13得到 3.已知函数f (x )=(12a −√3)sin x +(√32a +1)cos x ,将f (x )的图象向右平移π3个单位长度得到函数g (x )的图象,若对任意x ∈R ,都有g (x )≤g (π4),则a 的值为 . 4.已知函数f (x )=sin (ωx +φ)(ω>1,0≤φ≤π)是R 上的偶函数,其图象关于点M (3π4,0)对称,且在区间[0,π2]上是单调函数,则ω和φ的值分别为( )A .23,π4B .2,π3C .2,π2D .103,π25.已知函数f (x )=sin (ωx +φ),其中ω>0,|φ|≤π2,−π4为f (x )的零点:且f (x )≤|f (π4)|恒成立,f (x )在区间(−π12,π24)上有最小值无最大值,则ω的最大值是( )A .11B .13C .15D .176.已知函数f (x )=2sin (ωx −π6)sin (ωx +π3)(ω>0),若函数g (x )=f (x )+√32在[0,π2]上有且只有三个零点,则ω的取值范围为( )A .[2,113) B .(2,113) C .[73,103) D .(73,103)。
高三数学一轮复习讲义三角函数图像与性质
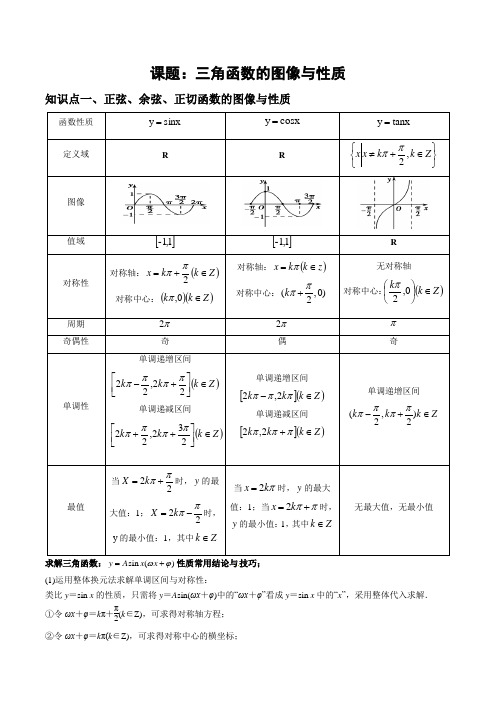
课题:三角函数的图像与性质知识点一、正弦、余弦、正切函数的图像与性质函数性质sinx y =cosx y =tanx y =定义域RR⎭⎬⎫⎩⎨⎧∈+≠Z k k x x ,2ππ图像值域[]1,1-[]1,1-R 对称性对称轴:()Z k k x ∈+=2ππ对称中心:()()Z k k ∈0,π对称轴:()z k k x ∈=π 对称中心:(,0)2k ππ+无对称轴对称中心:()Z k k ∈⎪⎭⎫⎝⎛0,2π 周期 π2π2π奇偶性奇 偶奇单调性单调递增区间()Z k k k ∈⎥⎦⎤⎢⎣⎡+-22,22ππππ 单调递减区间()Z k k k ∈⎥⎦⎤⎢⎣⎡++232,22ππππ单调递增区间[]()Z k k k ∈-πππ2,2单调递减区间[]()Z k k k ∈+πππ2,2单调递增区间Z k k k ∈+-)2,2(ππππ最值当22ππ+=k X 时,y 的最大值:1;22ππ-=k X 时,y 的最小值:1,其中Z k ∈当πk x 2=时,y 的最大值:1;当ππ+=k x 2时,y 的最小值:1,其中Z k ∈无最大值,无最小值求解三角函数:sin ()y A x x ωϕ=+性质常用结论与技巧; (1)运用整体换元法求解单调区间与对称性:类比y =sin x 的性质,只需将y =A sin(ωx +φ)中的“ωx +φ”看成y =sin x 中的“x ”,采用整体代入求解.①令ωx +φ=k π+π2(k ∈Z),可求得对称轴方程;②令ωx +φ=k π(k ∈Z),可求得对称中心的横坐标;(2)周期性:函数y =A sin(ωx +φ)(或y =A cos(ωx +φ))的最小正周期T =2π|ω|,注意y =Atan (ωx +φ)的周期T =π|ω|.(3)最值(或值域):求最值(或值域)时,一般要确定u =ωx +φ的范围,然后结合函数y =sin u 或y =cos u 的性质可得函数的最值(值域).【典型例题】【例1】函数cos()3y x π=-的单调增区间是( )A .42,2()33k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ B .22,2()33k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦C .32,2()88k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦ D .52,2()66k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦【例2】函数[]1sin ,2,223y x x πππ⎛⎫=+∈-⎪⎝⎭的单调递增区间是( )A .52,3ππ⎡⎤--⎢⎥⎣⎦ B .52,,233ππππ⎡⎤⎡⎤--⎢⎥⎢⎥⎣⎦⎣⎦和 C .5,33ππ⎡⎤-⎢⎥⎣⎦ D .,23ππ⎡⎤⎢⎥⎣⎦ 【例3】函数)62cos()(π+=x x f 的一条对称轴为( )A .6πB .125πC .32πD .32π-【例4】函数2()cos cos f x x x x =+([0,]x π∈)的单调递减区间为( )A .[0,]3πB .2[,]63ππC .5[,]36ππD .5[,]6ππ 【例5】函数()sin 24f x x π⎛⎫=- ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值是( )A. 1-B.C.D. 0 【例6】已知函数2()sin 2+sin 22cos 1.33=+-+-∈f x x x x x R ππ()(),(Ⅰ)求函数)(x f 的最小正周期; (Ⅱ)求函数)(x f 在区间[,]44ππ-上的最大值和最小值.【举一反三】1.余弦函数cos()4y x π=+在下列哪个区间为减函数( )A .3,44ππ⎡⎤-⎢⎥⎣⎦B .[],0π-C .3,44ππ⎡⎤-⎢⎥⎣⎦ D .,22ππ⎡⎤-⎢⎥⎣⎦2.函数的最小正周期为( )A. B. C. D.3.下列函数中,周期为π,且在⎥⎦⎤⎢⎣⎡2,4ππ上为减函数的是( )A.)2sin(π+=x y B.)2cos(π+=x y C.)22cos(π+=x y D.)22sin(π+=x y4.已知函数2()3cos sin f x x x x =-,则()f x 的最小正周期为 ;单调减区间为 .5.若函数()()13cos ,36f x x x x ππ=+-≤≤,则()f x 的最大值为( )A.1B.2 3 31 6.已知函数()sin sin()6f x x x π=+.(1)求()f x 的最小正周期;(2)当[0,]2x π∈时,求()f x 的取值范围.【课堂巩固】1.已知函数))(32cos(3)(R x x x f ∈-=π,下列结论错误的是( )A .函数)(x f 的最小正周期为πB .函数)(x f 图象关于点)0,125(π对称 C. 函数)(x f 在区间]2,0[π上是减函数 D .函数)(x f 的图象关于直线6π=x 对称2.设函数()sin()3)f x x x ωϕωϕ=++(0ω>,||2πϕ<)的最小正周期为π,且()()f x f x -=,则( )A .()f x 在(0,)2π单调递减 B .()f x 在3(,)44ππ单调递减 C .()f x 在(0,)2π单调递增 D .()f x 在3(,)44ππ单调递增 3.函数3sin 6y x π⎛⎫=+⎪⎝⎭的单调递增区间为_________.4.函数x x y 2cos 32sin -=的图象的一条对称轴方程为( ) A .12π=x B .12π-=x C. 6π=x D .6π-=x5.函数的最小正周期是__________ .6.函数2sin 2y x ππ⎛⎫=+⎪⎝⎭的最小正周期是 . 7.已知函数3()2sin cos()32f x x x π=++. (Ⅰ)求函数()f x 的单调递减区间;(Ⅱ)求函数()f x 在区间[0,]2π上的最大值及最小值.【课后练习】正确率:________1.当函数()取得最大值时,( )A. B. C. D.2.设函数()()()sin 30,2f x x x πωϕωϕωϕ⎛⎫=++>< ⎪⎝⎭的最小正周期为π,且()()f x f x -=,则( ) A .()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减 B .()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 C .()f x 在0,2π⎛⎫ ⎪⎝⎭单调递增 D .()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 3.已知函数()()()2sin 20f x x θθπ=-+<<,14f π⎛⎫=-⎪⎝⎭则()f x 的一个单调递减区间是( ) A .5,1212ππ⎛⎫-⎪⎝⎭ B .7,1212ππ⎛⎫ ⎪⎝⎭ C .,63ππ⎛⎫- ⎪⎝⎭ D .5,1212ππ⎛⎫- ⎪⎝⎭4.函数()sin cos()6f x x x π=--的值域为( )A .33⎡⎢⎣⎦B .3,3⎡-⎣C .[]2,2-D .[]1,1-5.函数)2sin()(ϕ-=x A x f 的图象关于点)0,34(π成中心对称,则ϕ最小的ϕ的值为( ) A .3π B .6πC .3π-D .6π- 6.已知角ϕ的终边经过点(3,4)P -,函数()sin()(0)f x x ωϕω=+>图像的相邻两条对称轴之间的距离等于2π,则()4f π=( ) A .35- B .35C .45-D .457.设函数()sin(2)cos(2)44f x x x ππ=+++,则( )A 、()y f x =在(0,)2π单调递增,其图象关于直线4x π=对称B 、()y f x =在(0,)2π单调递增,其图象关于直线2x π=对称C 、()y f x =在(0,)2π单调递减,其图象关于直线4x π=对称D 、()y f x =在(0,)2π单调递减,其图象关于直线2x π=对称8.函数sin 22y x x =的图象的一条对称轴方程为( ) A. π12x =B.π12x =-C.π6x =D.π6x =-9.已知函数2()cos cos f x x x x =+,x R ∈.(1)求4()3f π;(2)求函数()f x 的最小正周期与单调减区间.。
高考数学复习讲义:三角函数的图象与性质

2
突破点二 三角函数的性质
3
课时跟踪检测
返回
突破点一 三角函数的定义域和值域
返回
抓牢双基·自学回扣
[基本知识]
三角
余弦函数 y=
正弦函数 y=sin x
正切函数 y=tan x
函数
cos x
图象
定义 R
域
{ x| x∈R ,且 x
R
≠
kπ+π2
,k∈Z
返回
三角 函数 值域
正弦函数 y=sin x
()
返回
二、填空题
1.y= 2sin x- 2的定义域为________________________.
解析:要使函数式有意义,需2sin
x-
2≥0,即sin
x≥
2 ,借 2
助正弦函数的图象(图略),可得 π4 +2kπ≤x≤34π +2kπ,k∈Z,所
以该函数的定义域是π4+2kπ,34π+2kπ(k∈Z).
换元法 asin xcos x+b(sin x±cos x)+c的三角函数,可先设t =sin x±cos x,化为关于t的二次函数求值域(最值)
返回
[集训冲关]
1.[考法一]函数y=log2(sin x)的定义域为________.
解析:根据题意知sin x>0,得x∈(2kπ,2kπ+π)(k∈Z).
(2)依题意,f(x)=sin2x+ 3cos x-34=-cos2x+ 3cos x
+14=-cos x- 232+1, 因为 x∈0,π2,所以 cos x∈[0,1],
因此当 cos x= 23时,f(x)max=1.
返回
(3)设t=sin x-cos x, 则t2=sin2x+cos2x-2sin xcos x, 即sin xcos x=1-2 t2,且-1≤t≤ 2. ∴y=-t22+t+12=-12(t-1)2+1. 当t=1时,ymax=1;当t=-1时,ymin=-1. ∴函数的值域为[-1,1]. [答案] (1)B (2)1 (3)[-1,1]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⑶求f(x)图象的对称轴,对称中心。
10.求函数f (x)=的单调递增区间
典型例题
EG1、三角函数图像变换
将函数的图像作怎样的变换可以得到函数的图像?
变式1:将函数的图像作怎样的变换可以得到函数的图像?
变式2:将函数的图像作怎样的变换可以得到函数的图像?
变式3:将函数的图像作怎样的变换可以得到函数的图像?
4. 函数的最小正周期是_____
5.函数的最大值等于
6.(07年浙江卷理2)若函数,(其中,)的最小正周期是,且,则(
)
A. B. C. D.
7.(2007年辽宁卷7).若函数的图象按向量平移后,得到函数的图
象,则向量( )
A. B. C. D.
8.(2007年江西卷文2).函数的最小正周期为( )
心对称,则向量的坐标可能为( )
A.
B.
C.
D.
8.(湖北卷5)将函数的图象F按向量平移得到图象,若的一条对称轴是
直线,则的一个可能取值是
A.
B.
C.
D.
9.(湖南卷6)函数在区间上的最大值是(
)
A.1
B.
C.
D.1+
10.(重庆卷10)函数f(x)=() 的值域是
A[-]
B[-1,0] C[-]
D[-]
(3)若(),求证:方程在内没有实数解. (参考数据:,)
实战训练B
1.(全国一8)为得到函数的图像,只需将函数的图像( )
A.向左平移个长度单位
B.向右平移个长度单位
C.向左平移个长度单位
D.向右平移个长度单位
2.(全国二8)若动直线与函数和的图像分别交于两点,则的最大值为
()
A.1
B.
C.
D.2
A.关于点对称 B.关于直线对称
C.关于点对称 D.关于直线对称
15.(2007年江苏卷1).下列函数中,周期为的是( )
A. B. C. D.
16.(2007年江苏卷5).函数的单调递增区间是( )
A. B. C. D.
17.(2007年天津卷文9)设函数,则( )
A.在区间上是增函数
B.在区间上是减函数
A. B. C. D.
21.(2007年安徽卷理6)函数的图象为
①图象关于直线对称;
②函灶在区间内是增函数;
③由的图象向右平移个单位长度可以得到图象.
其中正确的个数有( )个
(A)0
(B)1
(C)
2
(D)3
22.(2007年北京卷文3).函数的最小正周期是( )
A.
B.
C.
D.
23.(2007年四川)下面有五个命题:
的对称轴方程是(),对称中心; 的对称中心().
写出满足条件的x的集合 sinx>cosx ________________________________ sinx<cosx _________________________________ |sinx|>|cosx| __________________________________ |sinx|<|cosx| __________________________________
EG5、三角恒等变换
化简:.
变式1:函数y=的最大值是( ).
A.-1
B. +1
C.1-
变式2:已知,求的值.
D.-1-
变式3:已知函数,.求的最大值和最小值.
实战训练
1.方程(为常数,)的所有根的和为 .
2.函数的最小正周期为 3.若函数的图象(部分)如图所示,则的取值是( ) (A) (B) (C) (D)
4.(四川卷5)若,则的取值范围是:( )
A B C D
5.(天津卷6)把函数()的图象上所有点向左平行移动个单位长度,
再把所得图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到
的图象所表示的函数是
A,
B,
C,
D,
6.(天津卷9)设,,,则
ABC D
7.(安徽卷5)将函数的图象按向量平移后所得的图象关于点中
如下:那么ω=( )
A. 1
B. 2
C. 1/2
D. 1/3
14.(上海卷6)函数f(x)=sin x +sin(+x)的最大值是
15.(江苏卷1)的最小正周期为,其中,则=
.
16.(广东卷12)已知函数,,则的最小正周期是
.
17.(辽宁卷16)已知,且在区间有最小值,无最大值,则=
__________.
(D)向左平移个单位长度
7.将函数的图象上各点的横坐标扩大为原来的2倍,纵坐标不变,再把
所得图象上所有点向左平移个单位,所得图象的解析式是
__________________.
8. 函数在区间[]的最小值为______.
9.已知f(x)=5sinxcosx-cos2x+(x∈R)
⑴求f(x)的最小正周期; ⑵求f(x)单调区间;
①函数的最小正周期是.
②终边在y轴上的角的集合是
③在同一坐标系中,函数的图象和函数y=x的图象有三个公共点.
④把函数
⑤函数
其中真命题的序号是 (写出所有真命题的编号)
24.(07年重庆卷理)设f (x) =
(1)求f(x)的最大值及最小正周期;
(2)若锐角满足,求tan的值。
24.(2007年重庆卷文)(18)已知函数。
EG2、三角函数图像
函数一个周期的图像如图所示,试确定A,的值.
变式1:已知简谐运动的图象经过点,则该简谐运动的最
小正周期和初相分别为( )
A., B., C., D., 变式2:函数在区间的简图是( )
变式3:如图,函数 的图象与轴交于点,且在该点处切线的斜率为.
求和的值. EG3、三角函数性质 求下列函数的最大、最小值以及达到最大(小)值时的值的集合.
A.
B.
C.
D.
9.(2007年江西卷文8).若,则下列命题正确的是( )
A. B. C. D.
10.(2007年湖北卷理2).将的图象按向量平移,则平移后所得图象
的解析式为( )
A. B.C.D.
11.(2007年海南宁夏卷理3).函数在区间的简图是( )
A. B. C. D.
12.(2007年广东卷理3).若函数,则f(x)是
课前预习
1.函数的最小正周期是
.
2. 函数的最小正周期T= .
3.函数的最小正周期是( )
(A)
(B)
(C) (D)
4.函数为增函数的区间是( )
(A) (B)
(C) (D)
5.函数的最小值是( )
6.为了得到函数的图象,可以将函数的图象( )
(A)向右平移个单位长度
(B)向右平移个单位长度
(C)向左平移个单位长度
定义域 R
R
值域
周期性
奇偶性 奇函数
偶函数
单调性
上为增函数; 上为减函数. ()
上为增函数;
上为减函数. ()
(A、>0) R
当非奇非偶, 当奇函数 上增函数; 上减函数()
定义域
值域 R
R
周期性
奇偶性 奇函数
奇函数
单调性 上为增函数()
上为减函数()
高三数学总复习讲义——三角函数性质与图像 知识清单: 反三角函数符号的运用: 、、 注意:反三角数符号只表示这个范围的角,其他范围的角需要用诱导公 式变到这个范围.备注: 以上性质的理解记忆关键是能想象或画出函数图象. 函数的图像和性质以函数为基础,通过图像变换来把握.如①②(A>0,>0) 相应地, ①的单调增区间 的解集是②的增区间. 注: ⑴或()的周期; ⑵的对称轴方程是(),对称中心;
③存在,使f(x)是奇函数;
④对任意的,f(x)都不是偶函数。 其中一个假命题的序号是_____.因为当=_____时,该命题的结论不 成立。
变式4、函数的最小正周期是
.
变式5、下列函数中,既是(0,)上的增函数,又是以π为周期的偶函
数是( ) (A)y=lgx2
(B)y=|sinx|
(C)y=cosx (D)y=
C.在区间上是增函数
D.在区间上是减函数
18.(07年山东卷文4).要得到函数的图象,只需将函数的图象( )
A.向右平移个单位
B.向右平移个单位
C.向左平移个单位
D.向左平移个单位
19.(07年全国卷二理2).函数的一个单调增区间是( )
A. B. C. D.
20.(2007年全国卷一理12)函数的一个单调增区间是( )
(1) ; (2) 变式1:已知函数在区间上的最小值是,则的最小值等 于
() (A) (B) (C)2 (D)3 变式2:函数y=2sinx的单调增区间是( )
A.[2kπ-,2kπ+](k∈Z)B.[2kπ+,2kπ+](k∈Z) C.[2kπ-π,2kπ](k∈Z)D.[2kπ,2kπ+π](k∈Z) 变式3:关于x的函数f(x)=sin(x+)有以下命题: ①对任意的,f(x)都是非奇非偶函数; ②不存在,使f(x)既是奇函数,又是偶函数;
满足函数y=Asin(ωx+)+b. (Ⅰ)求这段时间的最大温差; (Ⅱ)写出这段曲线的函数解析式. 变式3:如图,单摆从某点给一个作用力后开始来回摆动,离开平 衡位置O的距离s厘米和时间t秒的函数关系为. (1)单摆摆动5秒时,离开平衡位置多少厘米? (2)单摆摆动时,从最右边到最左边的距离为多少厘米? (3)单摆来回摆动10次所需的时间为多少秒?
23.(湖北卷16).已知函数
