第二章 第十三节 定积分与微积分基本定理
高考数学第一轮复习 第二篇 第13讲 定积分与微积分基本定理课件 理 新人教A版
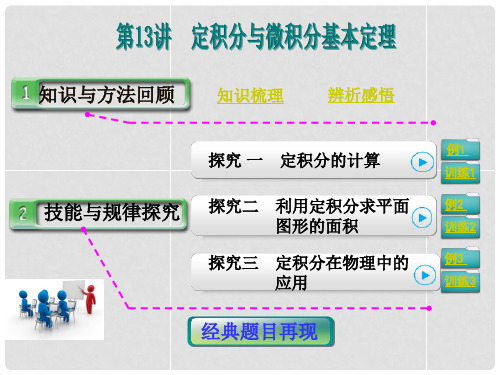
面积的代数和,即bf(x)dx= A1+A3-A2
.
a
2.定积分的性质
((12))abbk[ff1((xx))d±x=f2(x)]dkx=abf(x)abdfx1(x)dx±(k为baf常2(数x)d).x . a
ቤተ መጻሕፍቲ ባይዱ
(3)bf(x)dx=cf(x)dx+bf(x)dx(其中 a<c<b).
在每个小区间上任取一点 ξi(i=1,2,…,n),作和式i=n1f(ξi)Δx=i=n1b-n af(ξi),
当 n→∞时,上述和式无限接近于某个常数,这个常数叫做函数 f(x)在区
间[a,b]上的定积分,记作 abf(x)dx ,即abf(x)dx=nl→im∞i=n1b-n af(ξi).
定积分的计算
【例 1】 (1)若π2 (sinx+acosx)dx=2,则实数 a 等于(
).
0
A.-1 B.1 D. 3 D.- 3
(2)定积分3 9-x2dx 的值为________. 0
(3)已知函数 f(x)=sin5x+1,则-π2π2f(x)dx 的值为________.
n→+∞
时
,和式
n
f(ξi)·Δx
i=1
=
n
i=1
b-a
n f(ξi)
无
限趋近
于
某一
确
定的
常
数.( )
(3)设函数 y=f(x)在区间[a,b]上连续,则abf(x)dx=abf(t)dt.( )
2.定积分的几何意义与物理意义
(4)在区间[a,b]上的连续的曲线 y=f(x)和直线 x=a,x=b(a≠b),y=0 所围
成的曲边梯形的面积 S=ab|f(x)|dx.( ) (5)若abf(x)dx<0,那么由 y=f(x),x=a,x=b 以及 x 轴所围成的图形一定
定积分与微积分基本定理 课件

【解析】 (2)由定积分的几何意义知,
3
1
和 x=1,x=3,y=0 围成的图形的面积,∴
3
1
3 1 2
dx=2·
= .
3 0 3
2
x
3 + 2- 2 dx 表示半圆(x-1)2+y2=4(y≥0)
1
4
3 + 2- 2 dx= ×π×4=π.
点拨:运用微积分基本定理求定积分时要注意以下几点:
为了方便,常把 F(b)-F(a)记作
即
曲边梯 F(x)
,
f(x)dx=F(x) =F(b)-F(a).
四、定积分与曲边梯形面积的关系
设阴影部分的面积为 S.
(1)S= f(x)dx;
(2)S=-
(3)S=
(4)S=
f(x)dx-
f(x)dx;
f(x)dx;
f(x)dx-
[f1(x)±f2(x)]dx=
f(x)dx=
1
f(x)dx+
f (x)dx± f2(x)dx.
f(x)dx(其中 a<c<b).
答案
三、微积分基本定理
一般地,如果 f(x)是区间[a,b]上的连续函数,且 F'(x)=f(x),那么
f(x)dx= F(b)-F(a) ,
这个结论叫作微积分基本定理,又叫作牛顿-莱布尼茨公式.
−π
π
+ 2)dx=(-cos x+2x)
定积分与微积分基本定理

定积分与微积分基本定理1.定积分的概念如果函数f (x )在区间[a ,b ]上连续,用分点a =x 0<x 1<…<x i -1<x i <…<x n =b 将区间[a ,b ]等分成n 个小区间,在每个小区间[x i -1,x i ]上任取一点ξi (i =1,2,…,n ),作和式∑ni =1f (ξi )Δx =∑ni =1b -a nf (ξi ),当n →∞时,上述和式无限接近某个□01常数,这个常数叫做函数f (x )在区间[a ,b ]上的定积分,记作⎠⎛a b f (x )d x ,即⎠⎛a b f (x )dx =limn →∞∑n i =1b -an f (ξi ).其中f (x )称为□02被积函数,a 称为积分□03下限,b 称为积分□04上限.2.定积分的几何意义3.定积分的性质性质1:⎠⎛a b kf (x )d x =□01k ⎠⎛ab f (x )d x (k 为常数).性质2:⎠⎛a b [f (x )±g (x )]d x =□02⎠⎛a b f (x )d x ±⎠⎛abg (x )d x .性质3:⎠⎛a b f (x )d x =⎠⎛a c f (x )d x +□03⎠⎛c b f (x )d x . 4.微积分基本定理一般地,如果f (x )是在区间[a ,b ]上的连续函数,且F ′(x )=f (x ),那么⎠⎛a b f (x )d x=□01F (b )-F (a ).这个结论叫做微积分基本定理,又叫做牛顿—莱布尼茨公式.可以把F (b )-F (a )记为F (x )|b a ,即⎠⎛ab f (x )dx =F (x )|b a =□02F (b )-F (a ). 5.定积分与曲边梯形面积的关系设阴影部分的面积为S. (1)S =⎠⎛ab f (x )d x ;(2)S =□01-⎠⎛ab f (x )d x ;(3)S =□02⎠⎛a c f (x )d x -⎠⎛cb f (x )d x ;(4)S =⎠⎛a b f (x )d x -⎠⎛a b g (x )d x =⎠⎛a b [f (x )-g (x )]d x . 6.函数f (x )在闭区间[-a ,a ]上连续,则有: (1)若f (x )为偶函数,则⎠⎜⎛-aaf (x )d x =2⎠⎛0a f (x )d x .(2)设f (x )为奇函数,则⎠⎜⎛-aaf (x )d x =0.1.概念辨析(1)在区间[a ,b ]上连续的曲线y =f (x )和直线x =a ,x =b (a ≠b ),y =0所围成的曲边梯形的面积S =⎠⎛ab |f (x )|d x .( )(2)若⎠⎛a b f (x )d x <0,那么由y =f (x ),x =a ,x =b 以及x 轴所围成的图形一定在x轴下方.( )(3)已知质点的速度v =mt (m >0),则从t =0到t =t 0质点所经过的路程是⎠⎛0to mt d t=mt 202.( )答案 (1)√ (2)× (3)√2.小题热身(1)如图,指数函数的图象过点E (2,9),则图中阴影部分的面积等于()A.8ln 3 B .8 C.9ln 3 D .9答案A答案B(3) ⎠⎛-12|x |d x =________.答案 52解析 ⎠⎛-12|x |d x 的几何意义是函数y =|x |的图象与x 轴围成的图形(如图阴影所示)的面积,所以⎠⎛-12|x |d x =12×1×1+12×2×2=52.(4)若⎠⎛0t x 2d x =9,则常数t 的值为________.答案 3解析 ⎠⎛0t x 2d x =x 33|t 0=t 33=9,解得t =3.题型 一 定积分的计算答案 C 解析。
高中数学课件第二章第13节《定积分与微积分基本定理

利用定积分计算球体的体积,利用球 体体积公式V=4/3πr³,对r在区间 [a,b]上积分。
定积分在物理中的应用
变速直线运动的路程
定积分可以用来计算变速直线运动的路 程,将速度函数在时间区间[a,b]上积分 。
VS
静力矩
在力学中,定积分可用于计算平面图形对 某点的静力矩,将力矩函数在区间[a,b]上 积分。
高中数学课件第二章第13节《定积 分与微积分基本定理》
目 录
• 定积分的概念与性质 • 微积分基本定理 • 定积分的计算方法 • 定积分的应用 • 习题与解析
01
定积分的概念与性质
定积分的定义
定积分定义
牛顿-莱布尼茨公式
定积分是积分的一种,是函数在闭区 间上某个函数的代数和的极限,也可 以理解为求函数在闭区间上的整体效 果。
04
定积分的应用
平面图形的面积
矩形面积
定积分可以用来计算矩形区域的面积 ,只需将矩形的长度在区间[a,b]上 积分即可。
圆面积
定积分也可用于计算圆面积,利用圆 的面积公式A=πr²,其中r为半径,对r 在区间[a,b]上积分即可。
体积的计算
圆柱体体积
定积分可用于计算圆柱体的体积,将 圆柱体的底面积在高度方向上进行积 分。
详细描述:这道题目综合了定积分和微积分基本定理的知识点,需要学生灵活运用所学知识来解决复 杂问题,能够提高学生的综合运用能力。
THANKS
感谢观看
下限常数性质
∫(a→b)f(x)dx=∫(a→b)f(x+c)dx,其中c为常数。
02
微积分基本定理
微积分基本定理的表述
01 02
微积分基本定理
如果函数$f(x)$在区间$[a, b]$上连续,那么该函数在区间$[a, b]$上的 定积分$int_{a}^{b}f(x)dx$等于$F(b) - F(a)$,其中$F(x)$是$f(x)$的一 个原函数。
2-13 定积分与微积分基本定理
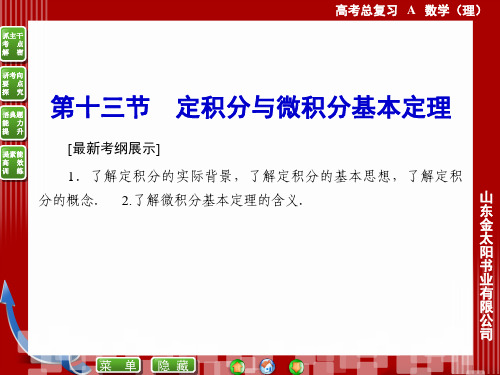
1 D 4
山 东 金 太 阳 书 业 有 限 公 司
菜 单
隐 藏
高考总复习 A 数学(理)
抓主干 考 点 解 密
研考向 要 点 探 究 悟典题 能 力 提 升 提素能 高 效 训 练
1 y=4, 1 1 [解析] 由 ⇒x= 或x=- (舍 ), 2 2 2 y=x 所以阴影部分面积
定积分在物理中的应用 (1)变速直线运动问题 如果作变速直线运动的物体的速率v关于时间t的函数是v= v(t)(v(t)≥0),那么物体从时刻t=a到t=b(a<b)所经过的路程为s= v(t)dt. (2)变力做功问题 物体在变力 F(x)的作用下作直线运动,并且物体沿着与力F(x)相同 的方向从x=a移动到x=b(a<b),则变力F(x)所做的功为 W= F(x)dx.
研考向 要 点 探 究 悟典题 能 力 提 升 提素能 高 效 训 练
π π 2.(2014年青岛模拟)由直线x=- ,x= ,y=0与曲线y=cos x所 3 3 围成的封闭图形的面积为( 1 A. 2 3 C. 2 ) B.1 D. 3
山 东 金 太 阳 书 业 有 限 公 司
菜 单
隐 藏
高考总复习 A 数学(理)
高考总复习 A 数学(理)
抓主干 考 点 解 密
研考向 要 点 探 究 悟典题 能 力 提 升 提素能 高 效 训 练
定积分在物理中的应用
【例3】 (2014年长沙模拟)一物体在变力F(x)=5-x2(x的单位: m,F的单位:N)的作用下,沿着与F(x)成30° 角的方向做直线运动,则 从x=1处运动到x=2处时变力F(x)所做的功为( 2 3 A. J 3 4 3 C. J 3 B. 3 J D.2 3 J )
第十三节定积分与微积分基本定理

a
图1
(2)由三条直线 x=a、x=b(a<b)、x 轴、一条曲线 y=
f(x)[f(x)≤0]围成的曲边梯形的面积(如图 2):
S=|bf(x)dx|=-bf(x)dx.
a
a
图2
(3)由两条直线 x=a、x=b(a<b)、两条曲线 y=f(x)、y= g(x)[f(x)≥g(x)]围成的平面图形的面积(如图 3);
题型一 计算积分 例 1 计算以下定积分:
解析:(1)函数 y=2x2-1x的一个原函数是 y=23x3-lnx,所
以12(2x2-1x)dx=(23x3-lnx)
2 1
21=136-ln2-23=134-ln2.
(2)3( 2
x+ 1x)2dx=23(x+1x+2)dx
∴在 t=4s 时的路程为
s=1(t2-4t+3)dt+|3(t2-4t+3)dt|+4(t2-4t+3)dt=4m.
0
1
3
点评:用定积分解决变速运动的位置与路程问题时,将物 理问题转化为数学问题是关键,另外,路程是位移的绝对值之 和,一定要判断在不同区间上位移的符号,否则会出现计算错 误.
第十三节 定积分与微积分基本定理
【知识梳理】
1.定积分的概念
(1)设f(x)是在区间[a,b]上有定义的函数,在a,b之间取若干分点
a=Δx0<xxk中1<x最2<大…<xn=b.记小区间[xk-1,xk]为Δ k,其长度x_k-__x_k-_1_记作Δ xk, __的__________记作d.再在每个小区间Δ k上任取一点代表点zk,作和式
f(x)在[a,b] 表示位于x轴上方的曲边梯形的面积减去位于x轴 上有正有负 下方的曲边梯形的面积
第二章 第十三节 定积分与微积分基本定理

的部分,
∴ 13 3+2x是-x圆2 d面x 积的
1, 4
∴
13
3+2x-x2 dx=1gg22=. 4
答案:π
【互动探究】在本例题(3)中条件不变,求 31 f(x)dx的值.
【解析】由本例题(3)的解答过程知,
3 1
f
x表d示x 以
(1,0)为圆心,2为半径的圆在x轴上方的部分的面积,故
|02
(4x
x2 2
22 3
3
x 2 ) |82
16 38 18. 33
方法二:S=
2[4
4-y
-
y2 2
]dy
=(4y
1 2
y2
1 6
y3
)
|24
=18.
答案:18
(3)由
y
x得3 ,
y x
所求xy 旋11,,转体的体积等于由
y x,xx 轴1所,围成的图形绕x轴旋转一周形成的旋转体
判断出 f x= 3+表2x-示x的2 几何意义,再利用定积分的
几何意义求解.
【规范解答】(1)
11
x2 sin x
dx
(1 3
x3
cos
x)|11
2. 3
答案:2
3
(2)
2 0
1 sin
2xdx
2 0
sin
x cos
x
dx
04
(cosx
sin
_________________.
(2)(2013·芜湖模拟)
定积分、微积分基本定理-高中数学知识点讲解

定积分、微积分基本定理1.定积分、微积分基本定理【定积分】定积分就是求函数在区间中图线下包围的面积.即由所围成图(f X)[a,b] y=0,x=a,x=b,y=(f X)形的面积.这个图形称为曲边梯形,特例是曲边三角形,表示的是一个面积,是一个数.定积分的求法:求定积分首先要确定定义域的范围,其次确定积分函数,最后找出积分的原函数然后求解,这里以例题为例.【微积分基本定理】在高等数学中对函数的微分、积分的研究和对相关概念及用途的数学称作微积分.积分学、极限、微分学及其应用是微积分的主要内容.微积分也称为数学分析,用以研究事物运动时的变化和规律.在高等数学学科中,微积分是一个基础学科.其中,微积分的核心(基本)定理是푏푎F(x)=(f x)(f x)푓(푥)푑푥= 퐹(푏)―퐹(푎),其中,而必须在区间(a,b)内连续.2例 1:定积分|3 ―2푥|푑푥=1解:1 | 3﹣2x | dx2=321(3 ―2푥)푑푥+232(2푥―3)푑푥3=(﹣2)1 +(x2﹣3x)|233x x |221/ 2=12通过这个习题我们发现,第一的,定积分的表示方法,后面一定要有;第二,每一段对应的被积分函数的表dx达式要与定义域相对应;第三,求出原函数代入求解.例 2:用定积分的几何意义,则39 ―푥2푑푥.―3解:根据定积分的几何意义,则39 ―푥2푑푥表示圆心在原点,半径为3的圆的上半圆的面积,―3故3―39 ―푥2푑푥=12 × 휋× 32 =9휋.2这里面用到的就是定积分表示的一个面积,通过对被积分函数的分析,我们发现它是个半圆,所以可以直接求他的面积.【考查】定积分相对来说比较容易,一般以选择、填空题的形式出现,这里要熟悉定积分的求法,知道定积分的含义,上面两个题代表了两种解题思路,也是一般思路,希望同学们掌握.2/ 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答案:C
2.设变力F(x)作用在质点M上,使M沿x轴正向从x=1运动
到x=10,已知F(x)=x2+1且和x轴正向相同,求变力
F(x)对质点M所做的功.
解:变力 F(x)=x2+1 使质点 M 沿 x 轴正向从 x=1 运动 到 x=10 所做的功为 1 ∫10F(x)dx=∫10(x2+1)dx=( x3+x)|10=342. W= 1 1 1 3
;
2. [f(x)± g(x)]dx=
b
f(x)dx± g(x)dx
b c
;
3. f(x)dx=
a
c a
f(x)dx+
f(x)dx
(其中 a<c<b).
二、定积分的几何意义 1.当函数 f(x)在区间[a,b]上恒为正时,定积分
b a
f(x)dx
的几何意义是由直线 x=a,x=b(a≠b),y=0 和曲线 y =f(x)所围成的曲边梯形的面积(图(1)中阴影部分).
提示:相等.
2.一个函数的导数是唯一的,反过来导函数的原函 数唯一吗? 提示:一个函数的导数是唯一的,而导函数的原函数 则有无穷多个,这些原函数之间都相差一个常数,在 利用微积分基本定理求定积分时,只要找到被积函数 的一个原函数即可,并且一般使用不含常数的原函数,
这样有利于计算.
[题组自测]
1 ∫4 dx 等于 1.(2010· 湖南高考) 2x A.-2ln2 C.-ln2 B.2ln2 D.ln2 ( )
(3)根据图形的形状用积分面积公式计算所求区域的面积.
[题组自测] 1.已知自由落体的速度为 v=gt,则落体从 t=0 到 t=t0 所 走过的路程为 1 2 A. gt0 3 1 2 C. gt0 2
解析:
t0 0
( B.gt2 0 1 2 D. gt0 4
)
1 2 t0 1 2 gtdt= gt | 0 = gt0. 2 2
3.列车以72 km/h的速度行驶,当制动时列车获得加速度
a=-0.4 m/s2,问列车应在进站前多长时间,以及离
车站多远处开始制动?
解:因列车停在车站时,速度为 0,故应先求出速度 的表达式,之后令 v=0,求出 t,再根据 v 和 t 应用 定积分求出路程. 已知列车速度 v0=72 km/h=20 m/s,列车制动时获 得的加速度为 a=-0.4 m/s2, 设列车开始制动到经过 t 秒后的速度为 v, 则 v=v0+∫t0adt=20-∫t00.4dt=20-0.4t, 令 v=0,得 t=50(s).
以客观题的形式出现的,难度较小,着重于基础知识、基
本方法的考查.
二、考题诊断 1.(2010· 山东高考)由曲线 y=x2,y=x3 围成的封闭图形 面积为 1 A. 12 1 C. 3 1 B. 4 7 D. 12 ( )
解析:由题可知 y=x2,y=x3 围成的封闭图形的面积 1 1 1 1 1 ∫1(x2-x3)dx=( x3- x4) |1= - = . 为 0 3 4 0 3 4 12
1 1 2 2 5 3 =3x -2x |1= . 6
答案:A
3.计算下列定积分: (1)∫3 1(3x2-2x+1)dx; - 1 1 e (2)∫1(x+ + 2)dx; x x (3)∫π(2sinx-3ex+2)dx; 0 (4)∫2|3-2x|dx. 1
解:(1)∫3 1(3x2-2x+1)dx=(x3-x2+x) |3 1=24. - - 1 1 1 1 ∫e (x+ + 2)dx=∫e xdx+∫e dx+∫e 2dx (2) 1 1 1 1 x x x x 1 2e 1e e = x |1+lnx |1-x |1 2 1 2 1 1 = (e -1)+(ln e-ln1)-( - ) 2 e 1 1 2 1 3 = e- + . 2 e 2
因此,所求图形的面积为
1 S=∫0(3x-x)dx+∫3(3x-x2)dx 1 3 =∫12xdx+∫1(3x-x2)dx 0
3 2 1 3 3 21 =x |0+( x - x )|1 2 3 3 2 1 3 3 2 1 3 13 =1+( · - · )-( · - · )= . 3 3 1 1 2 3 2 3 3
(4)利用牛顿——莱布尼兹公式求出各个定积分的值;
(5)计算所求定积分的值.
[题组自测] 3π 1.曲线 y=cosx(0≤x≤ )与两坐标轴所围成图形的面积 2 为____________.
解析:S= =3. 答案:3
cosxdx-
cosxdx=sinx
-sinx
2 2.抛物线 y=x 与直线 y= x 所围成的图形的面积是 3
2
__________.
y=x2 2 4 2 可得两曲线交点为(0,0)与( , ),且当 解析:由 3 3 y=3x 2 2 x∈(0, )时 x>x2, 3 3 则它们所围成的图形的面积是 S=
2 3 0
2 1 2 1 3 2 ( x-x )dx=( x - x ) 3 3 3
4 = . 81
4 答案: 81
3.求曲线y=x2,直线y=x,y=3x围成的图形的面积.
解:作出曲线 y=x2,直线 y=x,y=3x 的图象,所求面 积为图中阴影部分的面积.
y=x2, 解方程组 y=x, y=x2, 解方程组 y=3x,
得交点(1,1),
得交点(3,9),
(3)∫π(2sinx-3ex+2)dx 0
π =2∫πsinxdx-3∫πexdx+2∫0 dx 0 0
=2(-cosx) |π-3ex |π+2x |π 0 0 0 =2[(-cosπ)-(-cos0)]-3(eπ-e0)+2(π-0) =7-3eπ+2π.
(4) |3-2x|dx=
1
2
b a
f(x)dx= F(b)-F(a) .这个结论叫做微积分基
本定理,又叫做牛顿—莱布尼兹公式. 其中 F(x)叫做 f(x)的一个原函数.
b F(x)|a ,即 为了方便,常把 F(b)-F(a)记作
b a
b f(x)dx=F(x)|a=F(b)-F(a).
[究 疑 点] 1. 若积分变量为 t, ∫b f(x)dx 与∫b f(t)dt 是否相等? 则 a a
b 2.一般情况下,定积分∫a f(x)dx 的几何意义是介于 x 轴、曲
线 f(x)以及直线 x=a、x=b 之间的曲边梯形面积的代数和 (图(2)中阴影所示),其中在 x 轴上方的面积等于该区间上 的积分值,、微积分基本定理 一般地, 如果 f(x)是在区间[a, b]上的连续函数, F′(x) 且 =f(x).那么
[归纳领悟] 利用定积分求平面图形面积的关键是画出几何图形,
结合图形位置,确定积分区间以及被积函数,从而得到面
积的积分表达式,再利用微积分基本定理求出积分值. 求平面图形面积的步骤: (1)根据条件作出所求面积的区域草图; (2)通过图形直接判定(或联立方程组求出交点的横坐标),
确定积分上、下限;
b 速度函数 a=a(t)在时间区间[a,b]上的定积分∫aa(t)dt.
2.如果力 F(x)使得物体沿力的方向由 x=a 运动到 x=
b b(a<b),则力 F(x)对物体所作的功 W=∫aF(x)dx.
一、把脉考情 微积分基本定理是高中数学的新增内容.通过分析近 三年的高考试题,可以看到对它考查的频率较低,且均是
3 2 1
|3-2x|dx+ 3 |3-2x|dx
2 2
2
=
3 2 1
(3-2x)dx+ 3
2
(2x-3)dx
3 2 1 2 2 =(3x-x ) 2 +(x -3x) 3 = . 2 1 2
[归纳领悟] 计算简单定积分的步骤:
(1)把被积函数变为幂函数、正弦函数、余弦函数、指数函
数与常数的和或差; (2)利用定积分的性质把所求的定积分化为若干个定积分的 和或差; (3)分别用求导公式找到F(x),使得F′(x)=f(x);
设该列车由开始制动到停止时所走的路程是 s,则 s=∫50vdt=∫50(20-0.4t)dt=500(m), 0 0 所以列车应在进站前 50 s,以及离车站 500 m 处开 始制动.
[归纳领悟] 1.作变速运动的物体在一段时间间隔内所经过的路程,可以 利用该物体运动的速度关于时间的函数在该时间段上的 积分来求解.因此要求一个物体在一段时间内的位移,只 要求出其运动的速度函数,再利用微积分基本定理求出该 时间段上的定积分即可, 即物体作变速直线运动的路程 s, 等于其速度函数 v=v(t)(v(t)≥0)在时间区间[a,b]上的定 积分∫bv(t)dt.另外物体作变速直线运动的速度 v,等于加 a
41 4 ∫2 dx=lnx |2=ln4-ln2=ln2. 解析: x
答案:D
2.(2010· 浙江丽水模拟)设函数 f(x)=xm+ax 的导函数 f′(x) =2x+1,则∫2 f(-x)dx 的值等于 1 5 A. 6 2 C. 3 1 B. 2 1 D. 6 ( )
解析:由于 f(x)=xm+ax 的导函数为 f′(x)=2x+1, 所以 f(x)=x2+x, 于是∫2f(-x)dx=∫2(x2-x)dx 1 1
定积分与微积分基本定理 1. 了解定积分的实际背景,了解定积分的基本思 想,了解定积分的概念.
2.了解微积分基本定理的含义.
[理 要 点] 一、定积分的性质 1. kf(x)dx=
b a
b a
k
b a
f(x)dx(k 为常数)
b a b a
答案:A
2.(2010· 陕西高考)从如图所示的长方形区域内任取一 个点M(x,y),则点M取自阴影部分的概率为_____.
