论台球碰撞中的运动问题
台球受力分析.doc

台球受力浅析运动中的球与桌面:相对滑动速度:球心速度为c V ,角速度为),,(z y x ωωω=Ω。
球面上任意一点的位置为),,(z y x R ,则球面上该点的速度为R ΩV ⨯+c 。
如图所示,球引起桌面形变,球如果纯滚动,则球与桌面之间没有滑动。
而球面上某点与形变接触面的相对滑动速度是该点速度在球面上的投影(记为r V ),即: R ΩR R V V R R R ΩV R ΩV V ⨯+•-=•⨯+-⨯+=2/)(/)/)((R R R c c c c r 滑动动摩擦力:1.摩擦力的作用点都在接触面内2.每一点的摩擦力的方向与该点的相对滑动速度r V 方向相反3.假设接触面内的压力分布为),,(z y x p 因此摩擦力的合力为PdS S r r ⎰-=V V f μ,其中S 表示接触面的面积区域。
滑动动摩擦力矩: 由摩擦力计算公式可知力矩PdS S rr ⎰⨯-=V V R M μ r V 的展开式:记j i Ωy x ωω+=//,k Ωz ω=⊥因为R k R ∆+-=R ,所以:)()(/)))(((//2R k ΩΩR k R k V V V ∆+-⨯++∆+-∆+-•-=⊥R R R R c c r 展开并忽略二阶小量得:R ΩR Ωk R V k ΩV V ∆⨯+∆⨯+∆•+⨯-≈⊥////)/(R R c c r 受力分析:接触面很小,R ∆的量级远小于R ,若c V 和//Ω不是很小,可认为k ΩV V R c r ⨯-≈//,即可以用球最低点的速度来计算摩擦力的方向。
因此可以认为整个接触面以k ΩV R c ⨯-//的速度整体相对于桌面滑动。
我们可以注意到⊥Ω对球在桌面的滚动不起作用,实际上暗示着⊥Ω将在球撞击桌边时起重要作用。
碰撞过程:碰撞瞬间,只有两球接触面的正压力以及摩擦力较大,其他方向的冲量可忽略不计。
为了方便起见,假设两球接触面很光滑,摩擦因数很小,则两球碰撞,两球接触面的摩擦力就可以忽略。
台球中碰撞分析
A
v
v0
v
A
球B的运动与正碰中相似。
v
f1
f2
v
2.角速度w不为零,且方向为从外向里。
v
W
A
B
a. 若两球发生正碰
碰撞后的瞬间,球B获得了速度v,而球A相对于台面,只有转动的角速度w。
由前面的计算,球A将加速向前运动,并且最终速度将略小于
v=2/7 w r
所以 , 若Va=2/5w r 比V1大了较多 ( 即2wr>>5v0 ),那么若球B没有受阻碍,或没有进洞,球A追上球B并与之再次碰撞。
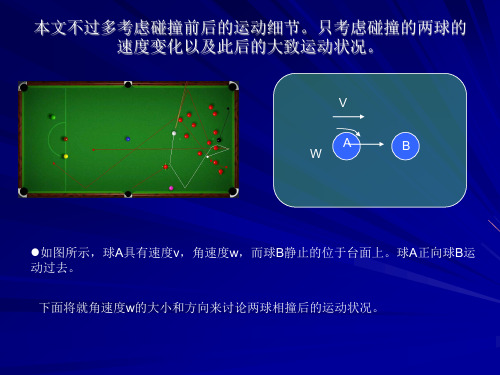
本文不过多考虑碰撞前后的运动细节。只考虑碰撞的两球的速度变化以及此后的大致运动状况。 NhomakorabeaA
B
V
如图所示,球A具有速度v,角速度w,而球B静止的位于台面上。球A正向球B运动过去。
下面将就角速度w的大小和方向来讨论两球相撞后的运动状况。
W
1.角速度w=0
此时,两个台球碰撞时可分为正碰和斜碰两种,如图1和图2所示:
A
v
v0
v
A
v
v
v
V
2.角速度w不为零,且方向为从里向外。
v
W
A
B
a. 先来看两球发生正碰时的情况
碰撞后的瞬间,球B获得了速度v,而球A相对于台面,已没有了初速度v, 只剩下转动的角速度w。
此后,对于球A,由于受到球与台面间的摩擦力的作用,将向后加速, 并且由牛顿定律,和角动量定理,可列出如下方程:
v
W
A
B
V1=5/7v
A
B
v=2/7w r
b. 当两球发生斜碰时,情况基本与正碰相仿,只是此时球A还具有一个初速度v。 这时球受到两个摩擦分力的作用f1和f2 在f1作用下,球A将具有一个向后的速度 在f2的作用下,球A的角速度w将改变一个方向 所以球A的运动轨迹将向后偏离,如下图所示:
台球瞄左打右的物理原理

台球瞄左打右的物理原理台球是一项深受人们喜爱的运动,而瞄左打右的技巧则是台球技巧中的重要组成部分。
本文将从物理原理的角度,探讨瞄左打右的技巧及其应用。
一、物理原理在台球中的应用台球是一项基于物理原理的运动,通过球的碰撞和运动,产生一系列的力学和运动学效应。
瞄左打右的技巧,就是在这种情况下,根据球的碰撞和运动规律,合理调整击球方向和力度,以达到最佳的进球效果。
在物理学中,物体的运动和受力是相互关联的。
当球被击出后,它会受到重力和空气阻力的影响,同时也会受到击球方向和力度的影响。
因此,在台球运动中,我们需要根据球的受力情况,合理调整击球方向和力度,以达到最佳的进球效果。
二、瞄左打右的技巧及其原理瞄左打右的技巧,是指在台球比赛中,当需要将球打入左侧的袋口时,却瞄准了右侧的位置。
这是因为,在击球时,球杆的方向会影响球的飞行轨迹。
如果我们直接瞄准左侧的位置,由于球杆的方向与球的实际飞行方向存在偏差,往往会导致进球失败。
而通过瞄左打右的技巧,我们可以通过调整球杆的方向,使球杆的出杆方向与球的飞行方向保持一致,从而更容易地将球打入左侧的袋口。
这种技巧的实现,主要是基于物理学中的惯性原理和空气动力学原理。
惯性原理认为,物体在受到外力作用时,会保持原有的运动状态继续运动一段时间。
因此,当球被击出后,它会按照原来的运动方向飞行一段时间。
而空气动力学原理则指出,空气阻力会随着速度的增加而增大。
因此,当球杆的方向与球的飞行方向不一致时,球的飞行速度会受到影响,导致进球难度增加。
而通过瞄左打右的技巧,我们可以使球杆的方向与球的飞行方向保持一致,从而减少了空气阻力的影响,提高了进球的成功率。
三、实际应用与注意事项在实际应用中,瞄左打右的技巧不仅适用于台球比赛,也适用于其他需要精确控制击球方向的体育运动。
例如,在棒球、高尔夫等运动中,也需要根据球的受力情况,合理调整击球方向和力度。
然而,在使用瞄左打右的技巧时,也需要注意一些注意事项。
台球运动中的力学问题

质心运动速台球运动中的力学问题台球运动中的力学问题—T0P147网友爱球人关于台球力学的认识台球运动在国外已有200多年的历史,清代末期传到中国,到现在这种运动已经在 我国城乡广为普及。
我本人就是一个台球迷,自从六岁接触台球以来,对他的兴趣 始终是有增无减。
随着年龄,技术的增长,逐渐发现在台球运动中涉及到很多物理 方面的知识。
下面就把我个人的一点心得写下来作为一个物理小论文。
对于两个球的碰撞问题,在这里我只定量讨论理想状态下的两球碰撞问题。
平面上 两相同的球做非对心完全弹性碰撞,其中一球开始时处于静止状态,另一球速度为 v.当它们两个做非弹性碰撞时,碰撞后两球速度总互相垂直母球的质量=子球的 质量,将两球视为刚体。
忽略如下图所示:设碰撞后門球的速度为vl,v2・有动量守恒mv=mvl+mv2两边平方山机械能守恒(势能无变化)质心运动速度不变非对v 1=0或v2二0ed 〃vl 二0对心碰撞 vl*v2=0 {vl 丄v2非对心碰撞恨 对于完全弹性碰撞则很容易判断两球的运动轨迹,0度或者180度。
球速的传送公式,是指母球在撞击子球时,两球接触的瞬间,母球的动量会一分为 二,一部分将分配给变慢的母球,另一部分会传送给子球。
我们可以观察到的:两 球速度的改变,此速度与滚动的距离成正比。
球速传送公式是推导岀来的。
我认 为,球的力量传递必定存在着公式的关系,若此公式为一简单的数学关系,对于出 杆力道控制的知识推断,必定会有很大的帮助。
以下所推导的公式为平面碰撞,只 单纯计算母球的动量传递。
不考虑声波消耗的能量、球台布摩擦力消耗的能量与球 旋转的转矩等移动中的母球撞击静止的子球(动量为零),撞击前母球的动 量P,在撞击子球后,会将一部分动量传给子球P2,而母球保有部分动量P1。
按 照力与向量的计算,合力二两分力,P 二Pl + P2,且两分力垂直。
按照动量的公 式P 二mv 条件:母球的质量二子球的质量,将两球视为刚体。
探索台球运动背后的物理学原理

探索台球运动背后的物理学原理探索台球运动背后的物理学原理引言台球是一项受到广大人们喜爱的运动,主要以使用球杆推动球体在球桌上进行击球、碰撞等动作。
背后的运动规则和技术动作看似简单,但实际上涉及到丰富的物理学原理。
本文将探索台球运动背后的物理学原理,力求揭示台球运动的本质。
1. 动量守恒定律在台球运动中,动量守恒定律是最基本的物理学原理之一。
动量守恒定律表明,在系统内部没有外力作用的情况下,系统的总动量始终保持不变。
具体到台球运动中,当球体碰撞时,碰撞前后球体的总动量保持不变。
以两个球相撞为例,当一个球以一定的速度撞向另一个球时,由于没有其他外力的作用,球体之间的碰撞只会改变它们的运动状态。
根据动量守恒定律,撞球前后两球的总动量不变。
这意味着,如果一个球向另一个球传递了动量,那么另一个球将以相同的动量继续运动,而原来的球则会减少相同的动量。
2. 动能守恒定律除了动量守恒定律外,动能守恒定律也是台球运动中的重要物理学原理。
动能守恒定律指出,在系统内部没有外力作用的情况下,系统的总动能保持不变。
对于台球运动来说,当球体相撞时,碰撞前后球体的总动能保持不变。
动能是一个物体运动时所具有的能量,它与物体的速度和质量有关。
在台球运动中,当球体彼此碰撞时,部分动能会转化为其他形式的能量,比如热能和声能等。
但总的来说,动能守恒定律保证了系统的总动能不变。
3. 弹性碰撞和非弹性碰撞在台球运动中,碰撞的性质对于球体之间的运动影响很大。
根据碰撞时球体之间相对运动状态的不同,碰撞可以分为弹性碰撞和非弹性碰撞。
弹性碰撞是指碰撞过程中没有能量损失的碰撞。
在弹性碰撞中,碰撞前后球体的动量和动能保持不变。
当一个球以一定速度与另一个球发生弹性碰撞时,碰撞后两球会以相同的速度分开,且它们的动量和动能都不变。
非弹性碰撞是指碰撞过程中有能量损失的碰撞。
在非弹性碰撞中,碰撞后球体的动量和动能会发生改变。
当一个球以一定速度与另一个球发生非弹性碰撞时,碰撞后两球可能会黏在一起,甚至其中一个球的速度减慢,而另一个球的速度增加。
【doc】台球运动中的力学问题

台球运动中的力学问题第16卷第3期1996年9月天津师大(自然科学版)V o1.16No319969 JOURNALOFT1ANJINNORMALUNIVERSITY(NATURALSCIENCEEDITION) i一7z台球运动中的力学问题.垂墓一t天津广播电视大学)(二)弓/;lA摘要本文运用碰撞刚体平面平行运动等理论具体分析了台球运动中,杆球与靶球的碰撞问题;由于击球部位不同,杆球的运动状态有何区别;如何确定台球桌面内侧垫边的高度等问题以期调动学生的学习兴趣,帮助学生掌握相关的知识,加深对理论的理解,提高台球运动水平关键词壁蕉角动量纯滑动纯滚动分类号031330引言莒王謇连,力学哒碰撞.台球运动中蕴含着许多科学道理,理工科学生在学习了力学后,运用碰撞的知识和刚体平面平行运动的理论,去分析在台球运动中所碰到的实际问题是非常有趣的在进行台球运动中经常会面临这样一些问题:以杆球(受杆冲击的球)去碰靶球时, 如何瞄准,使杆球以多大速度出射,方可使靶球落人袋中;用杆击杆球,冲击位置位于何处会发生纯滑动,经过多长时间,在球心前移了多长的距离后会由滑动变为纯滚动;台球桌面内侧垫边高度怎样取值才能满足某些特定的要求.本文拟探讨这些实际问题并给出相应的结论1台球的弹性碰撞质心速度为的杆球与静止的靶球发生弹性碰撞两球半径均为质量均为设的方向与靶球球心阃的距离为d,如图l(a)所示确定碰撞后杆球与靶球的质心速度,并作相应的讨论.因为两球作弹性碰撞,由动量守恒和机械能守恒可以写出+V一2=V—+VV因此?=0即垂直于,两球离开碰撞点时质心的运动方向互成直角由图l(b)可知:本文于1995年3,q收到,修改稿于1996年2月收到66天津师大(自然科学版)996薤V】Vcos:x】=V/2Rr——一V=Vcoso~一=,/1一(d/2R)(1)当0<d<2R时,为一般斜碰撞.设靶球与球袋的距离为s应满足:V,=i为靶球与台球桌面问的滑动摩擦系数.把(3)式代人(2)式,根据由实际情况确定的S,d的值解出V的数值,即为使靶球人袋应给予杆球质心的初速度.(2)当d=O时,两球为对心碰撞,此时V.一0,V1:V,:=O.碰后杆球停下,靶球以速度进.欲使靶球落人袋中,可用(3)式算出应给予杆球质心的初速度.(1)(2)要使靶球人袋,(3)fb1杆球与靶球的弹性碰撞(3)当≈2R时,即所谓擦边时,2≈9O.,l≈0..但V2≈0而Vl≈V.此时靶球仅以很小的速度被弹出,要使靶球落人袋中.碰撞前杆球质心速度V必须足够大.(4)上述两球的碰撞若为非弹性的,依动量守恒和恢复系数e的意义可以写出V】+V2:V(一)?式中为碰撞瞬间两球连心线上的单位矢量从这两个关系式可以得出+<90.的结论.两球离开碰撞点时,质心的运动方向互成锐角2杆球受杆冲击后的运动一个质量为Ⅲ,半径为只的均质杆球.置于水平桌面上,在包含球心的铅直面内,该球受到球杆沿水平方向的冲力,力的作用点相对桌面的高度为h杆球受杆冲击后,质心速度为V,球绕着过质心的水平轴转动的角速度为c..为了描述杆球的运动,建立0一轴以确定其质心的运动,建立质心坐标系来描述球绕质心轴的转动,并规定顺时针方向为正向f如图2所示)设杆对球的冲量为在杆对杆球冲击的短暂时问内,可以忽略摩擦力的冲量及其力矩.由质心动量定理和相对于质心的角动量定理,并考虑初始条件(f:0时,=0,由=0),得到第3期王云英:台球运动中的力学问题』mVDH^一R)=.,∞0'1考虑球对通过质心的水平轴的转动惯量J=;mR解得1∞05(^一R)v0/(2R)球与桌面相切的点处的速度为VV=V0一R∞0=(7R一5h)V0/(2R)根据(6),(7)两式可以判定:由于击球点高度不同球相撞后,杆球也将处于不同的状态.f4)(5)(7)杆球将作不同的运动.杆球与靶当h=R时,∞=0,V>0杆球受杆冲击后的瞬间作纯滑动,此后能否作纯滚动,何时作纯滚动,将在后面列专题讨论.须指出,此时它若与静止的靶球发生对心碰撞,靶球将以速度前进,而杆球将静止不动.当h<R时,∞<0,V>0,杆球若与静止的靶球发生对心碰撞,因杆球质心速度变为零而角速度保持不变,所以杆球与桌面的切点的速度V=RI∞I,沿x轴负方向的摩擦力将使杆球向后加速运动.当h>R时,∞>0,V>0,杆球若与静止的靶球发生对心碰撞,因杆球质心速度变为零,而角速度保持不变,所以V=一R沿x轴正方向的摩擦力使杆球向前加速运动.在h>R的条件下,受杆冲击后,杆球的运动又可分为三种情况:^当^=÷R时,V=0,此时无滑动摩擦力,杆球将保持质心速度为V.,绕过质心的水平轴转动的角速度为∞作纯滚动.当h>R时,V<0,此时它且滑且滚,滑动摩擦力沿着轴正方向,摩擦力的作用是使质心速度土不断增加,而使转动角速度巾不断减小,当=R巾时变为纯滚动.当R<h<;R时,V>0,此时它且滚且滑,滑动摩擦力沿着x轴负方向,摩擦力J 的作用是使得不断减小,而使得不断地增加,当=R巾时变为纯滚动.3杆球受杆冲击后,由纯滑动向纯滚动的转变质量为m,半径为R的均质杆球置于水平桌面上,在包含球心的铅直面内,用球杆沿着水平方向对着球心冲击,球心初速度为,若球与桌面间的滑动摩擦系数为,则杆球受杆冲击后开始作纯滑动,由于摩擦力厂的作用,将使质心速度不断地减小,而绕质68?天津师大(自然科学版)1996年心轴顺时转动的角速度由零开始不断地增加.当R由时,杆球作纯滚动.此时滑动摩擦力消失.在杆球作纯滚动前,列出如F关系式:一fmxcfRJc中f{一umg式中,一R并考虑初始条件"一.时一o,一,.,一0),可以得到质心速度表达式膏=.一flgt(8)质心位置表达式XC—V o卜-ktg}(9)杆球绕质心轴转动的角速度表达式由=f(1o)投f,时杆球开始作纯滚动,由杆球作纯滚动的条件可列出=解得=2V o..越小或越大则.越小.此时质心速度=;.质心向前移动的距离一丽1.2v~即杆球受杆冲击后最初运作纯滑动,经历了;的时间,质心向前移动等的距离以后变为纯滚动,此时其质心的平动速度为;.4如何确定台球桌面垫边的高度一个半径为R,质量为m的台球与台球桌内侧的橡皮垫边相碰,设作用于台球的冲量是沿着水平方向的不计球与桌面问的摩擦.欲使台球在与垫边碰撞前后均作纯滚动,垫边的高度就不能任意取值.为确定橡皮垫边的高度,可假设碰撞前台球质心速度为,沿轴负方向,此时它绕质心轴转动的角速度为∞,∞沿逆时针方向碰撞后,质心速度为,沿着第3期王云英:台球运动中的力学问题.69轴正方向,此时台球绕质心轴转动的角速度为,沿顺时针绕向如图3所示图2受水平力冲击的杆球图3台球与桌面垫边的碰撞由质心动量定理和对质心轴的角动量定理可列出ImVc一(一m[vcI)(11)(h—R),=JoJ一,f—I叫)(12)式中,:R,考虑台球作纯滚动的条件:V=RIVI=RI叫1可以解得h=÷RJ本文介绍了几种击球方式,分析了球被杆冲击后的运动特点,予示了杆球与靶球相撞后各自的运动趋势.人们可以在自己的实践中去检验它的正确性.注意灵活地运用力学规律,必将有益于提高台球运动水平,收到理论联系实际的效果.参考文献1【日】卢田盛和理论物理基础系列丛书第一册.任萍译.北京:北京师范大学出版社,1989.166~1682叶善专台球的运动和刚体平面平行运动.工科物理1994(2):17~18 SoMEMECHANlCALPRoBLEMSlNTHEBlLLlARDSPoRTWangYunying(TianjinTVUniversilv) Abstractingthetheoriesofcollisionandthetranslationofrigidbody,thispaperanalyzesthecollisionbetweenstick—ballandtarget-ballinthebilliardsport, thedifference(下转第72页)72天津师大学撤{自然科学版)1996正参考文献1彭崇慧,张锡喻络合滴定原理北京:北京大学出版社.198177~862彭崇慧,冯建章,张锡瑜定量分析化学筒明教程.北京:北京大学出版社.1985163~1673SkoogDA,WestDMFundamentalsofPublishing,1982.276--282 STUDIESONTHEOPTIMUMpHANDpH RANGEFORTlTRATIoNoFSoLUTIoN CoNTAINlNGSEVERALKlNDSoFloNSKangXiuwen(DepartmentofChemistry,Y aoXingmingTianjinNormalUniversity) AbstractAeoordingtothestudiesoncomplexometrletitrationofthesolutionscon- tainingseveralkinds,theregularityoftheoptimumpHandpHrangeoffourkindsof titrationhasbeensummarizedKeywordslogKMYPMe.PMEppH(上接第69页) ofkineticconditionofstick—ballbecauseofthedifferenceofhittingpositionandhowto determinetheheightofflangeofbilliardtable.Thus,itwillpromotethestudyinginterestof studen~,helpthemgraspreleventknowledge,improvetheircomprehesionoftheories,en? hancethebilliardsportplayinglevelandachievethegoalofcombinationoftheoryand practice. Keywordscollisionangularmomentumpureslidingpureroiling一-IIj。
球的对心碰撞及其实例分析

球的对心碰撞及其实例分析碰撞问题既是高中教学的重点和难点,也是高考命题的热点。
分析研究碰撞问题,对于解决力学中打夯、锻压、击球等问题,解决热学中气体分子间及气体分子与器壁间的相互作用问题,解释生活自然中的一些常见现象,以及较好地解答高考中的力学综合题等,都有十分重要的作用。
下面以球的对心碰撞为例,对碰撞现象作一些分析。
(一) 完全弹性碰撞在碰撞中,一种简单的情形是,两个等大而不同质量的小球,碰撞前后处在同一水平直线上运动,这就是球的对心碰撞。
若碰撞前后系统的动能不发生变化,就叫完全弹性碰撞。
用m 1和m 2分别表示两球的质量, 用v 10和v 20分别表示两球碰撞前的速度,用v 1和v 2分别表示两球碰撞后的速度,据动量守恒定律有m 1 v 10+ m 2 v 20= m 1v 1+m 2v 2……①由于是完全弹性碰撞,故碰撞前后动能守恒:21 m 1v 102+ 21m 2v 202= 21m 1v 12+ 21m 2v 22……② 联立①②两式可求得两小球碰撞后的速度分别为v 1= (2121m m m m +-)v 10 + (2122m m m +)v 20……③ v 2= (2122m m m +)v 10 +(2112m m m m +-) v 20……④ 根据③④式我们可做以下讨论:讨论1:当m 1=m 2,即对心碰撞的两球质量相等时可得v 1=v 20, v 2=v 10,即二球经过碰撞相互交换速度。
若v 20=0,则v 1=0 ,v 2=v 10,即m 1以一定的速度去碰撞静止的m 2,结果m 1会突然停止,而m 2“接过”m 1的速度前进。
这就是在儿童打弹子或成人打台球中经常看到的现象。
讨论2:当m 1<<m 2 且v 20=0,即用小质量的球去碰很大质量且静止的球时先将v 20=0代入③④式得到 v 1= (2121m m m m +-)v 10 , v 2= (2122m m m +)v 10 再将条件m 1<<m 2代入上述两式得到 v 1 ≈-v 10 , v 2≈0这说明球2仍然静止不动,而球1则以碰撞前等大的速率反向弹回。
台球比赛中的球道计算技巧如何球的运动路径

台球比赛中的球道计算技巧如何球的运动路径在台球比赛中,计算球道是一项基础且必要的技巧。
准确计算球的运动路径有助于选手提高击球技术,精确打进目标球袋。
本文将介绍一些基本的球道计算技巧,帮助读者更好地掌握这项技能。
一、角度计算在台球比赛中,球道的角度是决定球运动轨迹的重要因素。
为了计算球的运动路径,首先要对球道的角度有清晰的认识。
通常情况下,球道的角度越小,球的运动路径越曲线,角度越大,球的运动路径越直线。
为了准确计算球道的角度,选手可以通过以下方法进行估算:1. 视觉估算:用眼睛判断球道的大致角度。
在台球比赛中,选手通常会利用视觉来估算球道的角度,然后根据这个角度进行击球。
2. 使用球杆辅助:在进行角度计算时,选手可以利用球杆进行辅助。
将球杆放在目标球与袋口之间,调整角度,直到找到最佳击球位置。
3. 计算角度:如果选手想要更精确地计算球道的角度,可以使用三角函数来进行计算。
通过辅助计算,选手可以准确地计算出球道的角度。
二、速度计算除了角度,速度也是影响球道计算的重要因素。
在进行球道计算时,选手要根据击球力度和目标球的距离来合理调整速度,以确保球在运动过程中保持理想的轨迹。
以下是一些常用的速度计算技巧:1. 击球力度:选手在击球时应根据球的距离和目标球袋的位置来调整力度。
通常情况下,目标球离球袋越远,选手就需要施加更大的力量。
2. 触球点的高度:球的触球点也会对速度产生影响。
通常情况下,当选手将球击打在上方时,球的速度会较快;而将球击打在下方时,球的速度会较慢。
3. 碰撞角度:当球与其他球碰撞时,碰撞角度也会对速度产生影响。
碰撞角度越大,速度减慢的程度越大;反之,速度减慢的程度越小。
三、旋转计算除了角度和速度,球的旋转也是影响球道计算的一个重要因素。
球的旋转会使球运动时产生自转和滚动,从而进一步改变球的运动路径。
以下是一些常用的旋转计算技巧:1. 上旋和下旋:上旋是指球在运动时顶点方向向上,下旋则相反。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
论台球碰撞中的力学问题摘要:本文利用刚体平面平行运动的有关理论对(台球)运动中的一些力学问题作了具体的分析,首先以在理想状态下台球在桌面上的弹性碰撞为切入点,思考并找到计算两球碰撞后运动状态的方法;再由刚体平面平行运动知识对(台球)在桌面上运动时的速度和加速度分别作了具体的分析和推理。
关键词:台球;碰撞;平面运动;速度;加速度;相互作用力;目录引言 (3)1理想状态下母球1与目标球2的弹性碰撞 (3)1.1 母球1与目标球2发生正碰 (4)1.2目标球2与母球1的斜碰 (4)1.3 母球与目标球相切 (4)2 球杆击球后台球的运动 (5)3 受杆冲击后台球上各点速度的分析 (6)3.1 台球在运动中的速度分析 (6)3.2 球杆击球后在桌面上母球任一点速度的两种计算方法的讨论 (8)3.2.1 运动分解法(简称基点法) (8)3.2.2 瞬时速度中心法(简称瞬心法) (9)4 在运动中台球上各点加速度的分析 (11)4.1 运动分解法(或基点法) (11)4.2 瞬时加速度中心法 (13)5 小结 (14)6 参考文献 (15)引言台球作为一项绅士运动广为流传,传入我国后,到现在台球已经在我国广为普及。
我作为一个台球爱好者,在学习了力学之后,对台球运动中蕴含的许多碰撞和刚体平面平行运动的理论产生了浓厚的兴趣也进行了简单的分析研究。
本文就台球碰撞及运动中所包含的一些力学问题作了简单的分析。
1 理想状态下母球1与目标球2的弹性碰撞目标球2起初在桌面上处于静止状态,母球1以(质心速度为)v 的速度与静止的靶球2发生碰撞(弹性碰撞),两球质量都为m 且半径均为R 。
设v 的方向与目标球球心间的距离为d ,碰撞后母球1与目标球2的质心速度分别为1v 、2v 。
下面我们对两球的碰撞作相应的讨论。
由于两球所作碰撞时间极短几乎没有动量和能量的损失弹性碰撞,由动量及能量相关守恒律知:12m m mv v v +=22212111222mv mv mv += 解得120νν⋅=(即1ν垂直于2ν),故母球1与目标球2碰撞完成并彼此离开的时候,两球的即速度总是相互垂直。
当靶球2被母球1撞击时,在碰撞瞬间,母球1将其一部分动量分给了(变慢的)靶球2,而将剩余部分动量传送给目标球,两球速度大小的改变量与两球滚动的距离成正相关(转化法,利用为代替速度大小)。
下面以平面碰撞来推导公式,只单作纯地计算母球动量的传递方式及传递的量,不考碰撞产生的热所消耗的能量、空气阻力对球能量的消耗,球发生转动的能量以及桌面阻力对球消耗的能量,如图1所示: 1cos 2vdv v R=∂= (1)2cos v v θ==(2) 1.1 母球1与目标2球发生正碰当d=0时,母球与目标球发生的是正碰,母球1的速变为零,目标球2以母球1原来的速度沿着母球1的运动方向继续运动。
得 : 212mv lmg μ=2v v =即:要使目标球落袋,母球应具有的质心加速度大小为v = 1.2 目标球2与母球1的一般斜碰当0< d < 2R 时, 为一般斜碰撞. 设目标球2与球袋距离为l ,要使目标球入袋, 则由能量守恒定律得:212m v l m gμ=2v =(μ为台球与桌面台泥之间的滑动摩擦系数)。
将2v =2)式中,测量l 、的值,并代入解得v 的数值,即为母球1为使目标球落袋应有的质心的初速度。
1.3 母球1与目标2球相切当d=2R 时,母球与目标球相切,要使目标球落袋,母球必须被用力打出,即母球质心初速度v 须足够的大。
2 球杆击球后台球的运动设:台球的质量为m ,其半径为R ,当球杆撞击球时,球杆对母球有一水平方向作 用力使母球产生水平动量;如图2所示。
球杆打击母球的冲量为I ,不计摩擦力及其他阻力产生的冲量,则有o I Mv =o v 为母球受球杆撞击后开始运动的速度。
由于受到冲力(冲力矩)的作用,与此同时母球也发生了转动,假设球杆作用点距桌面的竖直距离为h ,则以质心为参考点对质心的力矩为I (h-R ),有下面地关系式 ()o h R J ω-=o ω是母球受冲击后产生的角速度,J 代表母球的转动惯量,且 225J MR =所以: 2()5()2o h R I h R I J MR ω--== 或 25()2o o h R v Rω-=由以上两式得受球杆冲击后母球与桌面接触点P 的速率。
227575522oP o o o R h R h I Mv MR v v R I v RM Rω--==-== (1)当h=7/5R 时,母球无滑动地作纯滚动,不会产生滑动摩擦力,只有滚动的阻力。
(2)当h>7/5R 时,母球既滑动又滚动的运动,且滑动摩擦力使质心产生加速度,使之质心的速度增加,并使它的转动角速度变小,直到母球作纯滚动为止。
(3)当h<7/5R 时,母球作既滑动又滚动的运动,滑动摩擦力产生转矩产生角加速度使它转动角速度加快、质心速率则会由于总能量不会增加而变慢,直到母球只滚动而没有滑动。
3 台球上个点在杆撞击后的速度分析 3.1 台球在运动过程中的速度的分析台球可以看作刚体,利用其定义:(刚体的平面平行的运动:刚体内任一点与固定平面始终保持一定距离的运动称为刚体平面平行运动)。
在球杆击球后,台球在桌面上做的是平行运动,遵循其相关的规律。
由刚体平面运动的特性可得,作一平面L 与固定平面(台球桌面)0L 平行,与台球相交。
假设该平面内的点运动在其自身所在平面内,在该平面内作坐标系OXY 。
只要确定图形,上任意一条线段AB 的位置,就可确定图形C,在坐标系中的具体位置。
因为图形上任何第三点至A 、B 两点的距离都不变,当线段AB 的位置确定后,其余各点的位置也就完全确定了。
线段AB 的位置完全由A 点的坐标A x 、A y (或矢径A r )和自ox 轴到线段AB 所量的ϕ角所确定。
当图形运动时,角ϕ、坐标A y 和A x 全部是随时间t 变化的连续函数,即: 1()A x f t =2()A y f t =3()f t ϕ=由上式可以推出台球在任一时刻的位置及任何一点的运动情况。
在这儿用点的相关的运动知识。
任意点M 的矢径如图4所示:'M A r r r =+ (1)'r 表示M 点对于A 点的矢径。
因台球不会变形,'r 的模'r AM =和角MAB ∂=∠均 为常数(C ),M 点的方程为:'cos()M A x x r ϕα=++ (2)'sin()M A y y rϕα=++将上式对t 求一次导,可得出点M 的速度V,在各坐标轴上的投影: 'sin()M A x x r ϕϕ=-+∂ (3) 'cos()M A y y r ϕϕ=++∂ 上式对时间求导,在坐标轴上的投影表示为:'2'cos()sin()M A x x r r ϕϕαϕϕα=-+-+ (4)'2'sin()cos()M A y y r r ϕϕαϕϕα=-+++由此可知,从点的运动学看,只要知道台球的运动情况及表达式,用求导函数的方法就可求得台球上任一点的速度与角速度。
所求得的结果的物理意义可作如:从以上式子中得知,式的右端第一个数表示加速度,以后各项表示图形上M 点相对于以A 点为原点的平动坐标系的运动。
因此,用点的复合运动的方法来分析台球运动的问题。
由刚体平面运动方程: 1()A x f t =2()A y f t =图43()f t ϕ=可以得到两种特殊情形:a 、当ϕ=常数时,而1()A x f t =、2()A y f t =。
则线段AB 的方向和位置保持不变。
这表示台球在平面内作平动。
b 、当A x 和A y 都为常数,而角ϕ随时间变化,即3()f t ϕ=。
这表示图形绕垂直于平面的固定轴A 转动。
3.2 球杆击球后在桌面上母球任一点速度的两种计算方法的讨论 3.2.1 运动的分解随着母球运动的分解,对母球上任意点的运动也作相应地分解,利用点的复合运动的有关方程及分析方法,可以求出母球1上任一点的速度。
如图5,选取运动的母球上任一点A 选为基点来分解运动。
令某A 点瞬时的线速度A v ,母球的瞬时角速度为ω,,母球上任一点M 的绝对速度为:M e r v v v =+因动坐标系随基点平动,故质心速度e A v v =。
又因M 点的相对运动是以基点为中心的圆周运动,故速度'r v r ω=⨯,'r 是由基点A 引向M 点的矢径,r v 的方向与'r 垂直。
因此,M 点的速度为 M r v v r ω=+⨯此式表明母球上任一点M 的速度等于基点的速度和M 点对以基点为原点的平动坐标系的相对速度的矢量和。
A 图5因母球中心O 点速度顺心是已知的,故选O建立平动坐标系O 'x 'y ,将母球的平面运动分解为平面运动和转动,则母球上任一点的运动可相应的加以分解,(质量中心)运动为 动坐标系O 'x 'y ,随O 点的平动。
根据相关定理,母球上点M 的速度可表示成: M o r v v v =+相对速度r v 大小为R ω,方向垂直于半径。
对于ω,利用母球无滑动的滚动的条件,它与地面的接触点C 的速度为零,即 0C o r v v v =+= 因此 or v v R Rω== 由图可知,ω为角速度。
求得ω后,各质点的速度就很容易求得,其关系如下: 2A o v v = B o v D o v = 各点运动的方向如上图6所示。
3.2.2 瞬时速度中心法,简称瞬心法用式M r v v r ω=+⨯线AC 上必有一点C 在此瞬时的速度为零, 如图7所示,则由A 到C 点的矢径'C r 满足以下条 件:图6'0C A C v v r ω=+⨯= 'C A r v ω⨯=-或写成 Av AC ω=,0ω≠,A AC v ⊥C 点称为台球的瞬时速度中心,简称瞬心。
如果在此瞬时选择瞬心C 为基点来分析台球式M r v v r ω=+⨯就变为''M C M Mv v r r ωω=+⨯=⨯ 这里'M r 是M 点对于瞬心C 的矢径,如图7所示,ω是台球的角速度。
换句话说,这时质心速度为零,只剩下 台球绕瞬心C 转动的相对速度;或者说台球的 瞬时运动是绕瞬心C 以角速度ω的转动。
此瞬时台球上各点速度的分布情形如右图8所示,它与刚体绕定轴转动时各点速度的分布情形相同。
但台球的运动与刚体绕定轴转动并不相同,因C 点不是固定点,它只是在这一瞬时速度为零。
因为不同的瞬时,瞬心C 的位置不同,故台球的平面运动可以看成是绕一系列的瞬心作瞬时转动。
