方波信号的傅里叶变换_图文
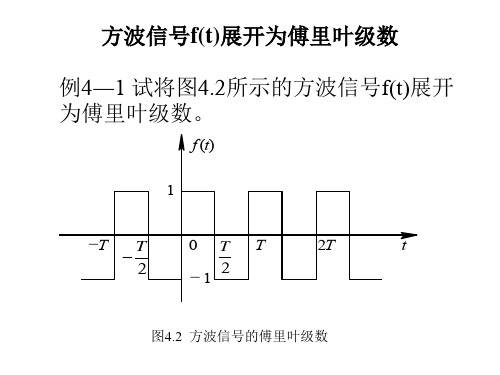
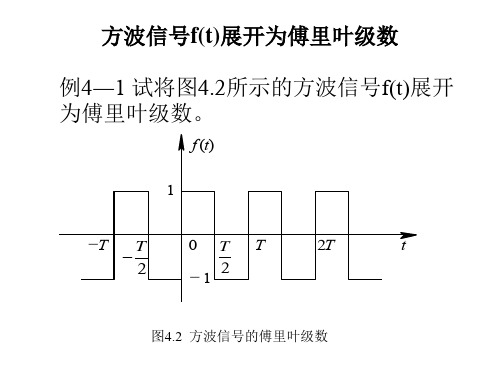
方波信号f(t)展开为傅里叶级数.ppt
01j
1
jarctan
ea
a22
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
f (t) eatu(t),a 0
F() f (t)e jtdt eat e jtdt
1
j
2 T
2
f (t)cos(2nft)dt
2 T
0 T
2
(1)cos(2nft)dt 2
T
T 2 0
1 cos(2nft)dt
2 T
1
2 nf
[ sin(2 nft)]
0 T
2
2 T
1
2 nf
[sin(2 nft)]
T
2 0
0
bn
2 T
T
2 T
2
f (t)sin(2nft)dt
2 T
o 2
τ 2
t
(a )
F(j )
2
-
4
-
2
o
4
(b )
F( )
( )
-
4
-
2
o
2 4
-
4
-
2
o 2 4
-
(c)
(d )
图 3.4-1 (a) 门函数; (b) 门函数的频谱; (c) 幅度谱; (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
g(t)
F()
1
- 2/
2/
-/ 2 0 / 2
t
方波信号f展开为傅里叶级数
f (t)sin(2nft)dt
2
T
0 T
2
(1)sin(2nft)dt 2
T
T 2 0
1 sin(2nft)dt
2 T
1 [cos(2nft)] 2 nft
0 T
2
2 T
1
2 nf
[ cos(2 nft)]
T
2 0
2 (1 n ) n
0,
2
-4
-
2
o
4
(b )
F( )
( )
-4 -2 o
2 4
-4 -2
o 2 4
-
(c)
(d )
图 3.4-1 (a) 门函数; (b) 门函数的频谱; (c) 幅度谱; (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
15 °
10 °
o
2
3
4 5
6
(b )
图 3.3-1 例 3.3-1
(a) 振幅谱; (b) (b) 相位谱
|F n |
2
1 .5
1 .5
1
1
1
0 .4 0 .2
0 .4 0 .2
- 6- 5 - 4- 3- 2 - o
2 3 4 5 6
(a )
n 45°
li m0 a2
2a
2
0
0 0
(4―45) (4―46)
lim
0
2
方波信号傅里叶变换

例 3.4-4
所示信号的频谱函数为
j
2 2 2
,从而有
Sgn(t) 1
X()
o
t
o
-1
(a) (b)
图 3.4-7 符号函数Sgn(t) (a)Sgn(t)的波形; (b) 频谱
符号函数的频谱
例4―7求符号函数的频谱。 解 符号函数简记为sgn(t),它的定义为
1 t 0 sgn(t) 0 t 0 1 t 0
(b)
图 3.4-2 单边指数函数e-αt
(a) 单边指数函数e-αt; (b) e-αt的幅度谱
解
F(j) f(t)ejtdt etejtdt
e(j)t
(j)
01j
1
jarctan
ea
a22
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
- 30°
- 20°
- 30°
- 45°
- 45° (b )
图 3.3-2 例 3.3-1 信号的 (a) 振幅谱; (b) 相位谱
单边指数函数f(t)的频谱函数
例 3.4-2 求指数函数f(t)的频谱函数。
f
(t)
e at
t 0
0
t 0
f (t)
1 e-t (>0)
(0)
F()
1
o
t
o
(a)
fo (t)
e a t
e
a
t
t0 t0
Fe()
et
ejt
0
e(j)tdt
0
e(j)tdt 222
Fo()
0
方波傅里叶变换

方波傅里叶变换在信号处理中,傅里叶变换是一种重要的数学工具,用于将一个信号分解为其频谱成分。
而方波傅里叶变换则是傅里叶变换的一种特殊形式,用于分析方波信号的频谱特性。
方波是一种典型的周期信号,其波形呈现出由高电平和低电平交替组成的矩形形状。
方波信号在数字电路和通信系统中广泛应用,因其简单明了的特点,能够有效地携带和传输信息。
傅里叶变换通过将一个信号分解为一系列正弦和余弦函数的叠加,将信号从时域转换到频域。
对于方波信号而言,傅里叶变换能够揭示其频谱特性,即方波信号中包含的各个频率成分。
方波信号的频谱图呈现出一系列垂直的频谱线,这些频谱线对应着方波信号中不同的频率成分。
方波信号的频率谱是离散的,且只包含奇次谐波。
由于方波信号是一个周期为T的信号,其频谱中的频率成分由基波频率和其奇次谐波频率构成。
在方波信号的频谱中,基波频率对应着方波信号的周期,即1/T。
而奇次谐波频率则是基波频率的整数倍。
这意味着方波信号的频谱中只包含了奇次谐波成分,如3倍频、5倍频等。
方波傅里叶变换的结果可以用于分析方波信号的频谱特性,从而了解信号中包含的各个频率成分。
通过傅里叶变换,我们可以得到方波信号的频率谱图,进而分析信号的频谱分布和能量分布。
方波傅里叶变换在实际应用中有着广泛的应用。
例如,在通信系统中,方波信号被广泛应用于数字调制和解调、编码和解码等方面。
通过对方波信号的频谱分析,可以了解信号的频率特性,从而设计合适的调制和解调方式,实现高效的数据传输。
方波傅里叶变换还在数字电路设计中起着重要的作用。
在数字电路中,方波信号被用作时钟信号,用于同步和控制电路的工作。
通过对方波信号的频谱分析,可以确定时钟信号的频率范围,从而确保电路的正常工作。
方波傅里叶变换是一种用于分析方波信号频谱特性的重要工具。
通过傅里叶变换,我们可以了解方波信号中包含的各个频率成分,从而在信号处理、通信系统和数字电路设计等领域中应用。
方波傅里叶变换的研究和应用将进一步推动信号处理技术的发展,并为实际应用带来更多的创新和改进。
傅里叶变换 正弦波 分解 方波

傅里叶变换正弦波分解方波傅里叶变换是一种非常重要的数学工具,可以将一个信号分解成不同频率的正弦波的叠加。
而其中一种特殊的信号,方波,可以通过傅里叶变换来进行分解和理解。
正弦波是一个周期性的波形,具有不同的频率和振幅。
傅里叶变换可以将任意一个周期性的信号分解成多个正弦波。
这是因为正弦波具有唯一的频率,可以表示任意周期性信号的一个重要组成部分。
通过傅里叶变换,我们可以知道一个信号包含哪些频率的正弦波,以及每个正弦波的振幅。
方波是一种非常特殊的波形,它在每个周期内都有两个不同的振幅值。
在傅里叶变换中,方波可以看作是多个正弦波的叠加。
具体地说,一个方波信号可以拆解成一个基频为f的正弦波和其奇数倍频的正弦波的叠加。
这是因为方波信号的周期性导致其可以用不同频率的正弦波分解。
通过傅里叶变换分解方波信号,我们可以得到其包含的不同频率的正弦波,并且可以知道每个正弦波的振幅。
这种分解和分析的方法非常有意义。
首先,我们可以了解方波信号的频率组成成分,进一步理解信号的特性和波动规律。
其次,我们可以根据每个正弦波的振幅来合成原始的方波信号。
这种合成是通过将不同频率的正弦波按照其振幅进行叠加而实现的。
通过合成,我们可以得到与原始方波信号非常相似的近似信号。
这种信号合成的方法在通信、音频处理和图像处理等领域中非常实用。
在实际应用中,傅里叶变换和方波信号的分解是非常有指导意义的。
首先,当我们需要分析一个信号的频率特性时,可以通过傅里叶变换将其分解成不同频率的正弦波,从而获得有关信号频率特性的重要信息。
其次,当我们需要合成一个复杂的周期性信号时,可以根据傅里叶变换的结果,通过合成不同频率和振幅的正弦波来重建原始信号。
这种技术在信号处理、音频合成和图像合成等领域中得到了广泛应用。
综上所述,傅里叶变换是一个非常有用的工具,可以将一个信号拆解成不同频率的正弦波。
方波信号作为一种特殊的周期性信号,可以通过傅里叶变换来进行分解和合成。
通过这种分解和合成的方法,我们可以了解信号的频率特性,并且可以进行信号的重建和合成。
方波信号的傅里叶变换

0
(4―40) (4―41)
F ( )
1
12
- 0
(a)
argF()
2
4
- 0
-
4
-
2
(b)
图4.7 单边指数信号及其频谱
偶对称双边指数函数的频谱函数
例 3.4-3 求图 3.4-3(a)所示双边指数函数的频谱函数。
f (t)
1
et
e-t >0)
o
t
(a)
F(j )
2
o
(b)
图 3.4-3 (a) 双边指数函数; (b) 频谱
1
j arctan
e
a
a2 2
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
f (t) eatu(t), a 0
F ( ) f (t)e jtdt eat ge jtdt
1
j
e
t
u(t)]
lim[e
0
t
u(t)]
lim
0
a2
2a
2
0
0 0
(4―45) (4―46)
lim
0
2 2 2
d
lim
0
1
2
(
)2
d
(
)
lim 2 arctan
0
2
[1] 2 ()
1 2 ()
(4―47)
(4―48) (4―49)
f (t) 1
0
t
(a)
F()
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4―45)
(4―46)
(4―47)
(4―48) (4―49)
图4.9 单位直流信号及其频谱
符号函数Sgn(t)的频谱函数
例 3.4-7 求符号函数Sgn(t)的频谱函数。
考察例 3.4-4 所示信号f(t)
当α→0时,其极限为符号函数Sgn(t)。因而可以用求f(t)的频 谱函数F(jω)当α→0的极限的方法来求得Sgn(t)的频谱函数。
图 3.8-2 例 3.8-2 (a) 系统组成; (b) s(t)的波形
先求f(t)的傅里叶变换F(jω),由于
再求s(t)的傅里叶变换S(jω)。由于s(t)为周期信号,T=1ms,则 , 因而有
图 3.8-3 y(t)的求解
图 3.4-4 例 3.4-4 (a) 信号f(t); (b) 频谱
解 图示信号f(t)可表示为
(a>0)
门函数的频谱函数
例 3.4-1 图 3.4-1(a)所示矩形脉冲一般称为门函数。其宽度 为τ, 高度为1,通常用符号gτ(t)来表示。试求其频谱函数。
解 门函数gτ(t)可表示为
Байду номын сангаас
图 3.4-1 (a) 门函数; (b) 门函数的频谱; (c) 幅度谱; (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6(a)所 示的门函数。其定义为
gτ(t)的傅里叶变换为
(4―36)
(4―37) (4―38) (4―39)
δ(t)的频谱函数
例 3.4-5 求单位冲激函数δ(t)的频谱函数。
图 3.4-5 信号δ(t) (a) 单位冲激信号δ(t); (b) δ(t)的频谱
解
可见,冲激函数δ(t)的频谱是常数1。也就是说,δ(t)中包含了 所有的频率分量, 而各频率分量的频谱密度都相等。 显然 , 信号δ(t)实际上是无法实现的。
根据分配函数关于δ(t)的定义, 有
冲激信号δ(t)的频谱
(4―75)
直流信号1的频谱函数
例 3.4-6 求直流信号1的频谱函数。
图 3.4-6 直流信号f(t) (a) 直流信号f(t); (b) 频谱
解 直流信号1可表示为
单位直流信号的频谱
例4―6 求单位直流信号的频谱。
解 幅度为1的单位直流信号可表示为
f(t)=1,-∞<t<∞
(4―44)
它可以看作是双边指数信号在α取极限趋近0时的一个 特例,即
已经知道
用频域分析法求响应
例 3.8-1 已知激励信号f(t)=(3e-2t-2)ε(t),试求图 3.8-1 所示 电路中电容电压的零状态响应uCf(t)。
图 3.8-1 例 3.8-1 的图
注意到δ(ω)的取样性质,并为了较方便地求得UCf(jω)的 逆变换,将UCf(jω)按如下形式整理:
例 3.4-4 所示信号的频谱函数为
,从而有
图 3.4-7 符号函数Sgn(t) (a)Sgn(t)的波形; (b) 频谱
符号函数的频谱
例4―7求符号函数的频谱。 解 符号函数简记为sgn(t),它的定义为
(4―50)
图4.10 符号函数及其频谱
符号函数sgn(t)也可看作是下述函数在α取极限趋近0时的一 个特例:
图 3.4-2 单边指数函数e-αt (a) 单边指数函数e-αt; (b) e-αt的幅度谱
解 其振幅频谱及相位频谱分别为
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
(4―40)
(4―41)
图4.7 单边指数信号及其频谱
偶对称双边指数函数的频谱函数
例 3.4-3 求图 3.4-3(a)所示双边指数函数的频谱函数。
图 3.5-2 (a) f(t)的波形; (b) 频谱
解 图3.5-2(a)所示高频脉冲信号f(t)可以表述为门函数 gτ(t)与cos ω0t相乘,即
高频脉冲信号的频谱函数
例4―13 求高频脉冲信号 p(t)=gτ(t)·cosω0t 的频谱函数
解 由于
故有 根据频移特性有
图4.14 频移特性
梯形信号f(t)的频谱函数
例 3.5-4 求图 3.5-5(a)所示梯形信号f(t)的频谱函数。
解 若直接按定义求图示信号的频谱,会遇到形如te-jωt的繁 复积分求解问题。而利用时域积分性质,则很容易求解。
将f(t)求导,得到图 3.5-5(b)所示的波形f1(t),将f1(t)再求导 , 得到图 3.5-5(c)所示的f2(t), 显然有
可知,其基波频率Ω=π(rad/s),基本周期T=2 s,ω=2π、3π、 6 π分别为二、 三、六次谐波频率。且有
其余
图 3.3-1 例 3.3-1
(a) 振幅谱; (b) 相位谱
图 3.3-2 例 3.3-1 信号的
(a) 振幅谱; (b) 相位谱
单边指数函数f(t)的频谱函数 例 3.4-2 求指数函数f(t)的频谱函数。
图 3.5-1 例 3.5-1 (a) f(t)的波形; (b) 相位谱
解
尺度变换求频谱
例4―11 已知
求gτ(2t)的频谱函数 解 根据傅里叶变换的尺度变换性
质,gτ(2t)的频谱函数为
图4.13 尺度变换
利用奇偶虚实性求频谱 例4―9利用奇偶虚实性求图4.11单边指数信 号f(t)=2e-αt u(t)的频谱。
方波信号的傅里叶变换_图文.ppt
解 我们将信号按式(4―6)分解成傅里叶级数,
并按式(4 及c。
―
7)、(4―8)、(4―9)分别计算an,
bn
例 3.3-1
振幅谱和相位谱例题
试画出f(t)的振幅谱和相位谱。
解 f(t)为周期信号,题中所给的f(t)表达式可视为f(t)的傅里 叶级数展开式。据
图 3.4-3 (a) 双边指数函数; (b) 频谱
偶对称双边指数信号的频谱
例4―5 求双边指数信号的频谱。 解 双边指数信号是指
从频谱函数的定义式出发
(4―42)
(4―43)
图4.8 双边指数信号及其频谱
奇对称双边指数函数的频谱函数
例 3.4-4 求图 3.4-4(a)所示信号f(t)的频谱函数。
(其中α>0)
(4-51)
阶跃函数ε(t)的频谱函数
例 3.4-8 求阶跃函数ε(t)的频谱函数。 解 由阶跃函数ε(t)的波形容易得到
从而就可更为方便地求出ε(t)的频谱函数, 即
图 3.4-8 (a) ε(t)的波形; (b) 频谱
门(平移后)信号的频谱函数
例 3.5-1 求图 3.5-1(a)所示信号的频谱函数。
图4.11 单边指数信号及其频谱
解 从波形图(a)上可见,单边指数信号 f(t)是非偶非奇函数,但可分解为如图(b), (c)所示的偶函数和奇函数两部分,见下式 。
其中
f(t)=2e-αt u(t)=fe(t)+fo(t)
高频脉冲信号f(t) 的频谱
例 3.5-2 求高频脉冲信号f(t)(图 3.5-2(a))的频谱。
用频域法求响应
例4―20如图4.19所示,试分析单位阶跃信 号u(t)通过RC高通网络传输后的波形。
图 4.19
解 显然,当输入信号uS(t)为复指数信号e jωt时 ,如图有
则按H(ω)的定义有 对于单位阶跃信号u(t)而言,此时
最后一步考虑了冲激函数的取样性质。因此
用频域分析法求响应
例 3.8-2 如图 3.8-2(a)所示系统,已知乘法器的输入 s(t)的波形如图 3.8-2(b)所示,系统函数
例4―2求冲激信号δ(t)的频谱。 解 由频谱函数的定义式有
(4―34)
(4―35)
图4.5 冲激信号及其频谱
移位冲激函数δ(t-t0)的频谱函数
例4―12求移位冲激函数δ(t-t0)的频谱函数。 解 由于已知冲激函数δ(t)的频谱函数为1,
求移位冲激函数δ(t-t0)的频谱函数,此时可利 用傅里叶变换的时移特性式(4―74)。
周期冲激函数序列δT(t)的频谱
例 3.6-2 图3.6-2(a)为周期冲激函数序列δT(t),其周期为 T,δT(t)可表示为
m为整数
图 3.6-2 周期冲激序列及其频谱
解 先求δT(t)的复振幅Fn:
设一周期信号fT(t),其周期为T,fT(t)中位于第一个周期 的信号若为fa(t),则不难得到
图 3.5-5
据时移性质有
图 3.5-6 另一种梯形信号
梯形脉冲的傅里叶变换
例4―14 求图4.15所示梯形脉冲的傅里叶变换。
图4.15 梯形脉冲的傅里叶变换
解 梯形脉冲可看作是两个不同宽度的矩形脉冲 f1(t)与f2(t)的卷积,如图4.15所示。 f(t)=f1(t)*f2(t) 而矩形脉冲的傅里叶变换已在例4―3中求出,具体来说
图4.16 半波正弦脉冲
图4.17 三角形脉冲及其一、二街导的波形
周期矩形脉冲f(t)的频谱函数
例 3.6-1 求图 3.6-1(a)所示周期矩形脉冲f(t)的频谱函数F(jω)。
图 3.6-1 (a) f(t)的波形; (b) 复振幅Fn; (c) 频谱函数F(jω)
解 周期矩形脉冲f(t)的复振幅Fn为
