《材料力学 》第五章 课后习题参考答案
材料力学第3版习题答案
材料力学第3版习题答案第一章：应力分析1. 某材料在单轴拉伸下的应力-应变曲线显示，当应力达到200 MPa 时，材料发生屈服。
若材料在该应力水平下继续加载，其应力将不再增加，但应变继续增加。
请解释这一现象，并说明材料的屈服强度是多少？答案：这种现象表明材料进入了塑性变形阶段。
在单轴拉伸试验中，当应力达到材料的屈服强度时，材料的晶格结构开始发生滑移，导致材料的变形不再需要额外的应力增加。
因此，即使继续加载，应力保持不变，但应变会因为材料内部结构的重新排列而继续增加。
在本例中，材料的屈服强度是200 MPa。
第二章：材料的弹性行为2. 弹性模量是描述材料弹性行为的重要参数。
若一块材料的弹性模量为210 GPa，当施加的应力为30 MPa时，其应变是多少？答案：弹性模量（E）与应力（σ）和应变（ε）之间的关系由胡克定律描述，即σ = Eε。
要计算应变，我们可以使用公式ε =σ/E。
将给定的数值代入，得到ε = 30 MPa / 210 GPa =1.43×10^-4。
第三章：材料的塑性行为3. 塑性变形是指材料在达到屈服点后发生的永久变形。
如果一块材料在单轴拉伸试验中，其屈服应力为150 MPa，当应力超过这个值时，材料将发生塑性变形。
请解释塑性变形与弹性变形的区别。
答案：塑性变形与弹性变形的主要区别在于材料在去除外力后是否能够恢复原状。
弹性变形是指材料在应力作用下发生的形状改变，在应力移除后能够完全恢复到原始状态，不留下永久变形。
而塑性变形是指材料在应力超过屈服点后发生的不可逆的永久变形，即使应力被移除，材料的形状也不会恢复到原始状态。
第四章：断裂力学4. 断裂韧性是衡量材料抵抗裂纹扩展的能力。
如果一块材料的断裂韧性为50 MPa√m，试样的尺寸为100 mm×100 mm×50 mm，试样中存在一个长度为10 mm的初始裂纹。
请计算在单轴拉伸下，材料达到断裂的临界应力。
工程力学--材料力学(北京科大、东北大学版)第4版第五章习题答案
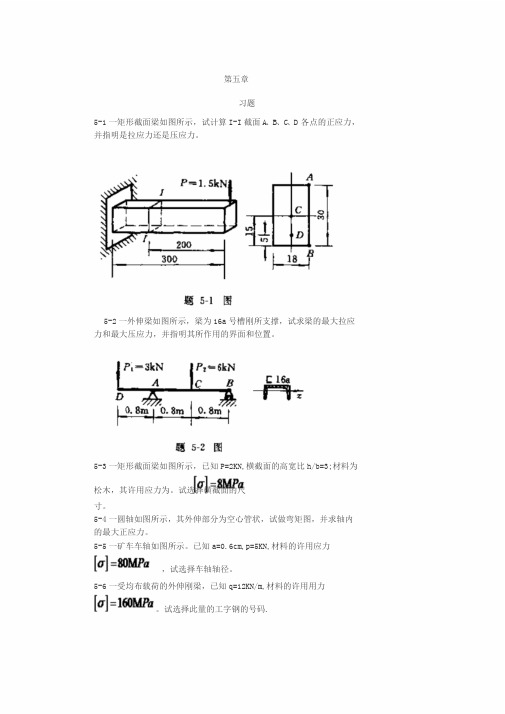
第五章习题5-1一矩形截面梁如图所示，试计算I-I截面A、B、C、D各点的正应力，并指明是拉应力还是压应力。
5-2一外伸梁如图所示，梁为16a号槽刚所支撑，试求梁的最大拉应力和最大压应力，并指明其所作用的界面和位置。
5-3一矩形截面梁如图所示，已知P=2KN,横截面的高宽比h/b=3;材料为松木，其许用应力为。
试选择横截面的尺寸。
5-4一圆轴如图所示，其外伸部分为空心管状，试做弯矩图，并求轴内的最大正应力。
5-5一矿车车轴如图所示。
已知a=0.6cm,p=5KN,材料的许用应力，试选择车轴轴径。
5-6一受均布载荷的外伸刚梁，已知q=12KN/m,材料的许用用力。
试选择此量的工字钢的号码.5-7图示的空气泵的操纵杆右端受力为8.5KN,截面I-I和II-II位矩形，其高宽比为h/b=3，材料的许用应力。
试求此二截面的尺寸。
5-8图示为以铸造用的钢水包。
试按其耳轴的正应力强度确定充满钢水所允许的总重量，已知材料的许用应力，d=200mm.5-9求以下各图形对形心轴的z的惯性矩。
5-10横梁受力如图所试。
已知P=97KN,许用应力。
校核其强度。
5-11铸铁抽承架尺寸如图所示，受力P=16KN。
材料的许用拉应力。
许用压应力。
校核截面A-A的强度，并化出其正应力分布图。
5-12铸铁T形截面如图所示。
设材料的许用应力与许用压应力之比为，试确定翼缘的合理跨度b.5-13试求题5-1中截面I-I上A、B、C、D各点处的切应力。
5-14制动装置的杠杆，在B处用直径d=30mm的销钉支承。
若杠杆的许用应力，销钉的，试求许可载荷和。
5-15有工字钢制成的外伸梁如图所示。
设材料的弯曲许用应力，许用且应力，试选择工字钢的型号。
5-16一单梁吊车由40a号工字钢制成，在梁中段的上下翼缘上各加焊一块的盖板，如图所示。
已知梁跨长=8m,=5.2m,材料的弯曲许用应力，许用且应力。
试按正应力强度条件确定梁的许可载荷，并校核梁的切应力。
材料力学习题册答案-第5章 弯曲应力
第 五 章 弯 曲 应 力一、是非判断题1、设某段梁承受正弯矩的作用，则靠近顶面和靠近底面的纵向纤维分别是伸长的和缩短的。
（ × ）2、中性轴是梁的横截面与中性层的交线。
梁发生平面弯曲时，其横截面绕中性轴旋转。
（ √ ）3、 在非均质材料的等截面梁中，最大正应力maxσ不一定出现在maxM的截面上。
（ × ）4、等截面梁产生纯弯曲时，变形前后横截面保持为平面，且其形状、大小均保持不变。
（ √ ）5、梁产生纯弯曲时，过梁内任一点的任一截面上的剪应力都等于零。
（ × ）6、控制梁弯曲强度的主要因素是最大弯矩值。
（ × ）7、横力弯曲时，横截面上的最大切应力不一定发生在截面的中性轴上。
（ √ ）@二、填空题1、应用公式zMy I 时，必须满足的两个条件是 满足平面假设 和 线弹性 。
2、跨度较短的工字形截面梁，在横力弯曲条件下，危险点可能发生在 翼缘外边缘 、 翼缘腹板交接处 和 腹板中心 处。
3、 如图所示的矩形截面悬臂梁，其高为h 、宽为b 、长为l ，则在其中性层的水平剪力=S FbhF23 。
4、梁的三种截面形状和尺寸如图所示，则其抗弯截面系数分别为226161bH BH -、xH Bh BH 66132- 和 Hbh BH 66132- 。
三、选择题1、如图所示，铸铁梁有A ，B ，C 和D 四种截面形状可以供选取，根据正应力强度，采用（ C ）图的截面形状较合理。
2、 如图所示的两铸铁梁，材料相同，承受相同的载荷F。
则当F 增大时，破坏的情况是 （ C ）。
A 同时破坏 ；B （a ）梁先坏 ；C （b ）梁先坏3、为了提高混凝土梁的抗拉强度，可在梁中配置钢筋。
若矩形截面梁的弯矩图如图所示，则梁内钢筋（图中虚线所示）配置最合理的是（D ）ABCDHABC D?四、计算题&1、长为l 的矩形截面梁，在自由端作用一集中力F ，已知m h 18.0=，m b 12.0=，m y 06.0=，m a 2=，kN F 1=，求C 截面上K 点的正应力。
工程力学--材料力学（北京科大、东北大学版）第4版第五章习题答案
⼯程⼒学--材料⼒学（北京科⼤、东北⼤学版）第4版第五章习题答案第五章习题5-1⼀矩形截⾯梁如图所⽰，试计算I-I截⾯A、B、C、D各点的正应⼒，并指明是拉应⼒还是压应⼒。
5-2⼀外伸梁如图所⽰，梁为16a号槽刚所⽀撑，试求梁的最⼤拉应⼒和最⼤压应⼒，并指明其所作⽤的界⾯和位置。
5-3⼀矩形截⾯梁如图所⽰，已知P=2KN,横截⾯的⾼宽⽐h/b=3;材料为松⽊，其许⽤应⼒为。
试选择横截⾯的尺⼨。
5-4⼀圆轴如图所⽰，其外伸部分为空⼼管状，试做弯矩图，并求轴内的最⼤正应⼒。
5-5 ⼀矿车车轴如图所⽰。
已知 a=0.6cm,p=5KN,材料的许⽤应⼒，试选择车轴轴径。
5-6 ⼀受均布载荷的外伸刚梁，已知q=12KN/m,材料的许⽤⽤⼒。
试选择此量的⼯字钢的号码.5-7 图⽰的空⽓泵的操纵杆右端受⼒为8.5KN,截⾯I-I和II-II位矩形，其⾼宽⽐为h/b=3，材料的许⽤应⼒。
试求此⼆截⾯的尺⼨。
5-8 图⽰为以铸造⽤的钢⽔包。
试按其⽿轴的正应⼒强度确定充满钢⽔所允许的总重量，已知材料的许⽤应⼒，d=200mm.5-9 求以下各图形对形⼼轴的z的惯性矩。
5-10 横梁受⼒如图所试。
已知P=97KN,许⽤应⼒。
校核其强度。
5-11 铸铁抽承架尺⼨如图所⽰，受⼒P=16KN。
材料的许⽤拉应⼒。
许⽤压应⼒。
校核截⾯A-A的强度，并化出其正应⼒分布图。
5-12 铸铁T形截⾯如图所⽰。
设材料的许⽤应⼒与许⽤压应⼒之⽐为，试确定翼缘的合理跨度b.5-13 试求题5-1中截⾯I-I上A、B、C、D各点处的切应⼒。
5-14 制动装置的杠杆，在B处⽤直径d=30mm的销钉⽀承。
若杠杆的许⽤应⼒，销钉的，试求许可载荷和。
5-15 有⼯字钢制成的外伸梁如图所⽰。
设材料的弯曲许⽤应⼒，许⽤且应⼒，试选择⼯字钢的型号。
5-16 ⼀单梁吊车由40a号⼯字钢制成，在梁中段的上下翼缘上各加焊⼀块的盖板，如图所⽰。
已知梁跨长=8m,=5.2m,材料的弯曲许⽤应⼒，许⽤且应⼒。
材料力学习题解答[第五章]
![材料力学习题解答[第五章]](https://img.taocdn.com/s3/m/5c357285a0116c175f0e48fd.png)
5-1构件受力如图5-26所示。
试：(1)确定危险点的位置；(2)用单元体表示危险点的应力状态（即用纵横截面截取危险点的单元体，并画出应力）。
题5-1图解：a) 1) 危险点的位置：每点受力情况相同，均为危险点；2）用单元体表示的危险点的应力状态见下图。
b) 1) 危险点的位置：外力扭矩3T与2T作用面之间的轴段上表面各点；2）应力状态见下图。
c) 1) 危险点：A点，即杆件最左端截面上最上面或最下面的点；2）应力状态见下图。
d) 1）危险点：杆件表面上各点；2）应力状态见下图。
5-2试写出图5-27所示单元体主应力σ1、σ2和σ3的值，并指出属于哪一种应力状态（应力单位为MPa）。
10题5-2图解：a)1σ=50 MPa,2σ=3σ=0,属于单向应力状态AAT （a）（c）（d）364dFlπτ=a) b) c) d)a) b) c)b) 1σ=40 MPa, 2σ=0, 3σ=－30 MPa ，属于二向应力状态 c) 1σ=20 MPa, 2σ=10 MPa, 3σ=－30 MPa ，属于三向应力状态5-3已知一点的应力状态如图5-28所示（应力单位为MPa ）。
试用解析法求指定斜截面上的正应力和切应力。
题5-3图解：a) 取水平轴为x 轴，则根据正负号规定可知： x σ=50MPa , y σ=30MPa , x τ=0, α=－30 带入式（5-3），（5-4）得 ατασσσσσα2sin 2cos 22x yx yx --++==45MPaατασστα2cos 2sin 2x yx +-== -8.66MPab) 取水平轴为x 轴，根据正负号规定：x σ= -40MPa , y σ=0 , x τ=20 MPa , α=120带入公式，得：240sin 20240cos 20402040---++-=ασ=7.32MPa x τ= 240cos 20240sin 2040+--=7.32MPac) 取水平轴为x 轴，则x σ= -10MPa , y σ=40MPa , x τ= -30MPa,α=30代入公式得：60sin )30(60cos 2401024010----++-=ασ=28.48MPa x τ= 60cos 3060sin 24010---=-36.65MPa5-4已知一点的应力状态如图5-29所示（应力状态为MPa ）。
材料力学-第五章
合理布置载荷
F
小结
1、熟练求解各种形式静定梁的支 座反力 2、明确剪力和弯矩的概念，理解 剪力和弯矩的正负号规定 3、熟练计算任意截面上的剪力和 弯矩的数值
4、熟练建立剪力方程、弯矩方程， 正确绘制剪力图和弯矩图
5.7 总结 回顾
毛和业，怎样快速绘制剪力图和弯
矩图，黔南民族师范学院学报， 2005，3：81-83
（ -）
1kN.m
A
FAY
1.5m
C
1.5m
D
2kN
1.5m
B
FBY
4 ．从 A 截面左测开始画 弯矩图。 从A左到A右 从A右到C左 从C左到C右 从C右到D左 从D左到D右
1.11
（+）
Fs（ kN） 0.89 M（ kN.m）
（ -）
0.330
（-）
1.330
（ -）
1.665
从D右到B左
从B左到B右
2
FS
FS x
x
0 x l 0 x l
M
ql2 / 8
依方程画出剪力图和弯矩图 ql / 2 由剪力图、弯矩图可见。最 大剪力和弯矩分别为
x
FS max＝ql
M max＝ql2 / 2
5.4
y
剪力图和弯矩图（将剪力方程和弯矩方程具体化）
q
例题 简支梁受均布载荷作用
FS ql / 2
( 2)在有均布载荷作用的 段上, 剪力图为倾斜直线, 直线由左上向右下倾斜; 弯矩图为抛物线, 抛物线 开口与均布载荷的方向一 致。
M 3ql2 / 32 x
ql2 / 8
材料力学第五章剪切和挤压的实用计算
> A[s]:=Pi*d*delta:
> d:=25e-3: tao[u]:=300e6: delta:=10e-3:
> ineq:=evalf(ineq,4);
ineq := 235600.F
答：需要 235.6kN 的冲剪力。
#清零。 #剪切强度条件 #剪切面积。 #已知条件。 #冲孔所需要冲剪力的数值。
图5-2连接轴与轮的键的工程实例
（1）作用于构件某一截面两侧的外力，大小相等，方向相反，作用线相距很近且垂 直于轴线。
（2）处于两个平行外力之间的截面，发生相对错动变形。 把有错动变形趋势的截面为剪切面，剪切面上的内力与截面相切，称为剪力， 用 FS 表示。
图5-3钢杆剪切实例
5.2剪切的实用计算
式中 bs 为材料的许用挤压应力，一般 bs 1.7 ~ 2 。
(a)
(b) (c)
图5-4圆孔及铆钉挤压应力的分布
当连接件与被连接件的接触面为平面时，如键连接，此时挤压面的面积 就是连接与被连接件的接触面积。
对于像销钉一类的连接件，它们的承压面实际上是半个圆柱面。在实用
> SOL1:=solve({eq1},{Fs}): > Fbs:=F: > tau:=Fs/A[s]: > tau:=subs(SOL1,tau): > sigma[bs]:=F/A[bs]: > A[s]:=Pi/4*d^2: > A[bs]:=delta1*d: > delta1:=1.5*delta: > d:=20e-3: delta:=8e-3: F:=15e3: > tau:=evalf(tau,4);
计算中通常是用半个圆柱面在垂直于总挤压作用线平面上的投影作为挤压 面的计算面积。这样得到的挤压应力更接近于挤压应力的最大值，因而可 以使设计更趋于安全。
《材料力学》 第五章 弯曲内力与弯曲应力
第五章 弯曲内力与应力 §5—1 工程实例、基本概念一、实例工厂厂房的天车大梁，火车的轮轴，楼房的横梁，阳台的挑梁等。
二、弯曲的概念：受力特点——作用于杆件上的外力都垂直于杆的轴线。
变形特点——杆轴线由直线变为一条平面的曲线。
三、梁的概念：主要产生弯曲变形的杆。
四、平面弯曲的概念：受力特点——作用于杆件上的外力都垂直于杆的轴线，且都在梁的纵向对称平面内（通过或平行形心主轴且过弯曲中心）。
变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平面曲线。
五、弯曲的分类：1、按杆的形状分——直杆的弯曲；曲杆的弯曲。
2、按杆的长短分——细长杆的弯曲；短粗杆的弯曲。
3、按杆的横截面有无对称轴分——有对称轴的弯曲；无对称轴的弯曲。
4、按杆的变形分——平面弯曲；斜弯曲；弹性弯曲；塑性弯曲。
5、按杆的横截面上的应力分——纯弯曲；横力弯曲。
六、梁、荷载及支座的简化（一）、简化的原则：便于计算，且符合实际要求。
（二）、梁的简化：以梁的轴线代替梁本身。
（三）、荷载的简化：1、集中力——荷载作用的范围与整个杆的长度相比非常小时。
2、分布力——荷载作用的范围与整个杆的长度相比不很小时。
3、集中力偶（分布力偶）——作用于杆的纵向对称面内的力偶。
（四）、支座的简化：1、固定端——有三个约束反力。
2、固定铰支座——有二个约束反力。
3、可动铰支座——有一个约束反力。
（五）、梁的三种基本形式：1、悬臂梁：2、简支梁：3、外伸梁：（L 称为梁的跨长） （六）、静定梁与超静定梁静定梁：由静力学方程可求出支反力，如上述三种基本形式的静定梁。
超静定梁：由静力学方程不可求出支反力或不能求出全部支反力。
§5—2 弯曲内力与内力图一、内力的确定（截面法）：[举例]已知：如图，F ，a ，l 。
求：距A 端x 处截面上内力。
解：①求外力la l F Y l FaF m F X AYBY A AX)(F, 0 , 00 , 0-=∴==∴==∴=∑∑∑ F AX =0 以后可省略不求 ②求内力xF M m l a l F F F Y AY C AY s ⋅=∴=-==∴=∑∑ , 0)( , 0∴ 弯曲构件内力：剪力和弯矩1. 弯矩：M ；构件受弯时，横截面上存在垂直于截面的内力偶矩。
材料力学课后习题答案5章
保留有限量，略去一阶和二阶微量后，得
足标 C 系指梁微段右端面的形心，对题图(b)亦同。 根据题图 b，由
∑F
略去微量 qdx 后，得
y
=0 ，FS左 + qdx − FS右 = 0
FS右 = FS左
仍据题图 b，由
(c)
∑M
C
=0 ，M 右 − M e − qdx(
dx ) − FS左 dx − M 左 = 0 2
11l 处有 FS2 = 0 ， M 2 有极大值，其值为 24 121 2 M 2 max = M max = ql 1152
(d)解：1．建立剪力、弯矩方程
8
图 5-9d 坐标如图 5-9d(1)所示，由截面法易得剪力、弯矩方程分别为
q( x1 ) ⋅ x1 qx 2 =− 1 2 l ql FS2 = − + qx2 4 qx 3 M1 = − 1 3l q 2 ql l M 2 = x2 − ⋅ ( + x2 ) 2 4 6 FS1 = −
2 q0l q 0 x2 FS = − + 4 l q x3 ql M = 0 x2 − 0 2 4 3l
l (0 ≤ x2 ≤ ) 2 l (0 ≤ x2 ≤ ) 2
(e) (f)
3．画剪力、弯矩图 依据式(c)和(e)可绘剪力图，如图 5-9b(2)所示；依据式(d)和(f)可绘弯矩图，如图 5-9b(3) 所示。 (c)解：1．求支反力
=0 ，FS左 + F + qdx − FS右 = 0
保留有限量，略去微量 qdx 后，得
FS右 − FS左 = F
为了更一般地反映 F 作用处剪力的突变情况（把向下的 F 也包括在内） ，可将上式改写为
材料力学性能-第五章-其它疲劳类型(1)
第五章 金属的疲劳
不论是循环硬化材料还是循环软化
材料，应力－应变回线只有在循环周次
达到一定值后才是闭合的—达到稳定状
态。对于每一个固定的应变幅，都能得
到相应的稳定的滞后回线，将不同应变
幅的稳定滞后回线的顶点连接起来，就
得到图5-47所示的循环应力－应变曲线。
2021年10月21日 星期四
第五章 金属的疲劳
时控制材料疲劳行为的已不是名义应力，而是塑
性变形区的循环塑性应变，所以，低周疲劳实质
上是循环塑性应变控制下的疲劳。
2021年10月21日 星期四
第五章 金属的疲劳
由于塑性变形的存在，应力
B
应变之间不再呈直线关系，
A
循环稳定后形成如图5-44所 示的封闭回线。
E
C
O
开始加载：O A B；
卸载：B C； 反向加载：C D； 反向卸载：D E； 再次拉伸：E B；
从而产生循环硬化。在冷加工后的金属中，充
满位错缠结和障碍，这些障碍在循环加载中被
破坏，或在一些沉淀强化不稳定的合金中，由
于沉淀结构在循环加载中被破坏均可导致循环
软化。
2021年10月21日 星期四
第五章 金属的疲劳
二、低周疲劳的应变－寿命(-N)曲线
低周疲劳时总应变幅t包括弹性应变幅e和
塑性应变幅p，即t＝e＋p。Manson和Coffin
2021年10月21日 星期四
第五章 金属的疲劳
在双对数坐标图上，上式等号右端两项是两条
直线，分别代表弹性应变幅-寿命线和塑性应变幅
寿命线，两条直线叠加成总应变幅-寿命线，如图5-
48所示。
直线交点对应的寿命称为过渡寿 命。交点左侧塑性应变幅起主导作 用，材料疲劳寿命由塑性控制；交 点右侧弹性应变幅起主导作用，材 料疲劳寿命由强度决定。因此，在 选择材料和确定工艺时，要弄清机 件承受哪一类疲劳。
05工程力学（静力学和材料力学）第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩
eBook工程力学（静力学与材料力学）习题详细解答（教师用书）(第5章)范钦珊 唐静静2006-12-18第5章轴向拉伸与压缩5－1试用截面法计算图示杆件各段的轴力，并画轴力图。
解：(a)题(b)题(c)题(d)题习题5－1图F NxF N(kN)x-3F Nx A5－2 图示之等截面直杆由钢杆ABC 与铜杆CD 在C 处粘接而成。
直杆各部分的直径均为d ＝36 mm ，受力如图所示。
若不考虑杆的自重，试求AC 段和AD 段杆的轴向变形量AC l Δ和AD l Δ解：()()N N 22ssππ44BCAB BC AB ACF l F l l d dE E Δ=+33321501020001001030004294720010π36.××+××=×=××mm ()3N 232c100102500429475286mm π10510π364..CDCD AD AC F l l l d E ΔΔ×××=+=+=×××5－3 长度l ＝1.2 m 、横截面面积为1.10×l0－3 m 2的铝制圆筒放置在固定的刚性块上；-10F N x习题5－2图刚性板固定刚性板A E mkN习题5－4解图直径d ＝15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上；铝制圆筒的轴线与钢杆的轴线重合。
若在钢杆的C 端施加轴向拉力F P ，且已知钢和铝的弹性模量分别为E s ＝200GPa ，E a ＝70GPa ；轴向载荷F P ＝60kN ，试求钢杆C 端向下移动的距离。
解： a a P A E l F u u ABB A −=−（其中u A = 0）∴ 935.0101010.11070102.1106063333=×××××××=−B u mm钢杆C 端的位移为33P 32s s601021100935450mm π20010154...BC C B F l u u E A ×××=+=+=×××5－4 螺旋压紧装置如图所示。
材料力学第五章梁的剪力图与弯矩图
29
§5-3
剪力和弯矩及其方程
为了建立剪力方程和弯矩方程，必须首先 建立Oxy坐标系。其中O为坐标原点，x坐 标轴与梁的轴线一致，坐标原点O一般取 在梁的左端，x坐标轴的正方向自左向右， y坐标轴铅垂向上。
30
§5-3
剪力和弯矩及其方程
建立剪力方程和弯矩方程，需要根据梁上的外 力（包括载荷和约束力）作用状况，确定控制 面，从而确定要不要分段，以及分几段建立剪 力方程和弯矩方程。
FBy
F 0 M 0
y A
FAy FBy 2F
FSE O FAy ME
FBy
F 5F FAy 3 3
分析右段得到：
FBy
O
ME FSE
F
FBy
y
0
FSE FBy 0
M
o
0
3a M E FBy Fa 2
27
§5-3 剪力和弯矩及其方程
F FBy 3
3、平面弯曲（对称弯曲）：若梁上所有外力都作用在纵向对称面内，
梁变形后轴线形成的曲线也在该平面内的弯曲。
4、非对称弯曲：若梁不具有纵向对称面，或梁有纵向对称面上但外力
并不作用在纵向对称面内的弯曲。
13
工程实际中的弯曲问题简图
P
P P P
P P P
P
14
平面弯曲
•具有纵向对称面 •外力都作用在此面内 •弯曲变形后轴线变成对称面内的平面曲线
M M M
M
弯矩为正
弯矩为负
22
梁的控制面
集中力作用点两侧的截面
集中力偶作用点两侧的截面 集度相同的均布载荷起点和终点截面处
23
材料力学习题及答案
材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。
解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。
1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。
解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量，并确定其大小。
图中之C点为截面形心。
解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。
解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。
材料力学练习册5-6详细答案
第五章弯曲应力5-1 直径为d的金属丝，环绕在直径为D的轮缘上。
试求金属丝内的最大正应变与最大正应力。
已知材料的弹性模量为E。
解：5-2 图示直径为d的圆木，现需从中切取一矩形截面梁。
试问：(1) 如欲使所切矩形梁的弯曲强度最高，h和b应分别为何值；(2) 如欲使所切矩形梁的弯曲刚度最高，h和b应分别为何值；解：(1) 欲使梁的弯曲强度最高，只要抗弯截面系数取极大值，为此令(2) 欲使梁的弯曲刚度最高，只要惯性矩取极大值，为此令5-3 图示简支梁，由№18工字钢制成，在外载荷作用下，测得横截面A 底边的纵向正应变ε=3.0×10-4，试计算梁内的最大弯曲正应力。
已知钢的弹性模量E =200GPa ，a =1m 。
解：梁的剪力图及弯矩图如图所示，从弯矩图可见：5-4 No.20a 工字钢梁的支承和受力情况如图所示。
若[]MPa 160=σ，试求许可载荷F 。
5-5 图示结构中，AB 梁和CD 梁的矩形截面宽度均为b 。
如已知AB 梁高为1h ，CD 梁高为2h 。
欲使AB 梁CD 梁的最大弯曲正应力相等，则二梁的跨度1l 和2l 之间应满足什么样的关系？若材料的许用应力为[σ]，此时许用载荷F 为多大？5-6 某吊钩横轴，受到载荷kN 130F =作用，尺寸如图所示。
已知mm 300=l ，mm 110h =，mm 160b =，mm 75d 0=，材料的[]MPa 100=σ，试校核该轴的强度。
5-7 矩形截面梁AB，以固定铰支座A及拉杆CD支承，C点可视为铰支，有关尺寸如图所示。
设拉杆及横梁的[]MPaσ，试求作用于梁B端的许可载荷F。
=1605-8 图示槽形截面铸铁梁，F=10kN，M e=70kN·m，许用拉应力[σt]=35MPa，许用压应力[σc]=120MPa。
试校核梁的强度。
解：先求形心坐标，将图示截面看成一大矩形减去一小矩形惯性矩弯矩图如图所示，C截面的左、右截面为危险截面。
材料力学第五版课后习题答案详解
Microsoft Corporation孙训方材料力学课后答案[键入文档副标题]lenovo[选取日期]第二章轴向拉伸和压缩2-12-22-32-42-52-62-72-82-9下页2-1试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。
（a）解：；；（b）解：；；（c）解：；。
(d)解：。
返回2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。
若横截面面积，试求各横截面上的应力。
解：返回2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。
若横截面面积，，，并求各横截面上的应力。
解：返回2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6)图示拉杆承受轴向拉力，杆的横截面面积。
如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。
解：2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。
如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。
解：（压）（压）返回2-7(2-9)一根直径、长的圆截面杆，承受轴向拉力，其伸长为。
试求杆横截面上的应力与材料的弹性模量E。
解：2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。
已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。
解：横截面上的线应变相同因此返回2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。
材料力学简明教程(景荣春)课后答案第五章
材料力学简明教程(景荣春)课后答案第五章5-1 最大弯曲正应力是否一定发生在弯矩值最大的横截面上?答不一定。
最大弯曲正应力发生在弯矩与弯曲截面系数比值最大的横截面上。
5-2 矩形截面简支梁承受均布载荷q作用，若梁的长度增加一倍，则其最大正应力是原来的几倍？若截面宽度缩小一倍，高度增加一倍，则最大正应力是原来的几倍？答若梁的长度增加一倍，则其最大正应力是原来的4倍；若截面宽度缩小一倍，高度增加一倍，则最大正应力是原来的1/2倍。
5-3 由钢和木胶合而成的组合梁，处于纯弯状态，如图。
设钢木之间胶合牢固不会错动，已知弹性模量EsEw，则该梁沿高度方向正应力分布为图a，b，c，d中哪一种。
思考题5-3图答(b)5-4 受力相同的两根梁，截面分别如图，图a中的截面由两矩形截面并列而成（未粘接），图b中的截面由两矩形截面上下叠合而成（未粘接）。
从弯曲正应力角度考虑哪种截面形式更合理？思考题5-4图答(a)5-5从弯曲正应力强度考虑，对不同形状的截面，可以用比值理性和经济性。
比值请从W来衡量截面形状的合AW较大，则截面的形状就较经济合理。
图示3种截面的高度均为h，A W的角度考虑哪种截面形状更经济合理？A思考题5-5图答(c)5-6 受力相同的梁，其横截面可能有图示4种形式。
若各图中阴影部分面积相同，中空部分的面积也相同，则哪种截面形式更合理？思考题5-6图答(b)（从强度考虑，(b),(c)差不多，从工艺考虑，(b)简单些）*FSSz5-7 弯曲切应力公式τ=的右段各项数值如何确定？Izb答FS为整个横截面上剪力；Iz为整个横截面对中性轴的惯性矩；b 为所求切应力所在位置横截面的宽度；Sz为横截面上距中性轴为y（所求切应力所在位置）的横线以下面积（或以上面积）对中性轴静矩的绝对值。
5-8 非对称的薄壁截面梁承受横向力作用时，怎样保证只产生弯曲而不发生扭转变形？答使梁承受的横向力过弯曲中心，并与形心主惯性轴平行。
工程力学--材料力学(北京科大、东北大学版)第4版第五章习题答案
工程力学--材料力学(北京科大、东北大学版)第4版第五章习题答案-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII第五章习题5-1一矩形截面梁如图所示，试计算I-I截面A、B、C、D各点的正应力，并指明是拉应力还是压应力。
5-2一外伸梁如图所示，梁为16a号槽刚所支撑，试求梁的最大拉应力和最大压应力，并指明其所作用的界面和位置。
5-3一矩形截面梁如图所示，已知P=2KN,横截面的高宽比h/b=3;材料为松木，其许用应力为。
试选择横截面的尺寸。
5-4一圆轴如图所示，其外伸部分为空心管状，试做弯矩图，并求轴内的最大正应力。
5-5 一矿车车轴如图所示。
已知 a=,p=5KN,材料的许用应力，试选择车轴轴径。
5-6 一受均布载荷的外伸刚梁，已知q=12KN/m,材料的许用用力。
试选择此量的工字钢的号码.5-7 图示的空气泵的操纵杆右端受力为,截面I-I和II-II位矩形，其高宽比为h/b=3，材料的许用应力。
试求此二截面的尺寸。
5-8 图示为以铸造用的钢水包。
试按其耳轴的正应力强度确定充满钢水所允许的总重量，已知材料的许用应力，d=200mm.5-9 求以下各图形对形心轴的z的惯性矩。
5-10 横梁受力如图所试。
已知P=97KN,许用应力。
校核其强度。
5-11 铸铁抽承架尺寸如图所示，受力P=16KN。
材料的许用拉应力。
许用压应力。
校核截面A-A的强度，并化出其正应力分布图。
5-12 铸铁T形截面如图所示。
设材料的许用应力与许用压应力之比为，试确定翼缘的合理跨度b.5-13 试求题5-1中截面I-I上A、B、C、D各点处的切应力。
5-14 制动装置的杠杆，在B处用直径d=30mm的销钉支承。
若杠杆的许用应力，销钉的，试求许可载荷和。
5-15 有工字钢制成的外伸梁如图所示。
设材料的弯曲许用应力，许用且应力，试选择工字钢的型号。
5-16 一单梁吊车由40a号工字钢制成，在梁中段的上下翼缘上各加焊一块的盖板，如图所示。
材料力学 第5章习题答案
图 5−4
（A）Nmax = 60kN，Nmin = 15kN （B）Nmax = 60kN，Nmin = −15kN （C）Nmax = 30kN，Nmin = −30kN （D）Nmax = 90kN，Nmin = −60kN 解：用直接法求轴力可得 NAB = −30kN，
NBC = 30kN，NCD = −15kN，NDE = 15kN。 答案：（C）
）。
图 5−1
第二节 轴 向 拉 伸 与 压 缩
5-2 （2010 年） 等截面杆轴向受力如图 5−2 所示。杆的最大轴力是（ ）kN。
（A）8
（B）5
（C）3
（D）13
解：用直接法求轴力，可得左段轴力为−3kN，而右段轴力为 5kN。
答案：（B）
图 5−2
5-3 （2006 年） 如图 5−3 所示变截面杆中，AB 段、BC 段的轴力为（ ）。
解：由于 A 是斜截面 m−m 的面积，轴向拉力 P 沿斜截面是均匀分布的，所以 σ = P A
应为斜截面上沿轴线方向的总应力，而不是垂直于斜截面的正应力。 答案：（C）
93
5-7 （2005 年） 有一横截面面积为 A 的圆截面杆件受轴向拉力作用，在其他条件不变时，
若将其横截面改为面积仍为 A 的空心圆，则杆的（ ）。
第五章 材 料 力 学
第一节 概 论
5-1 （2009 年） 在低碳钢拉伸实验中，冷作硬化现象发生在（ （A）弹性阶段 （B）屈服阶段 （C）强化阶段 （D）局部变形阶段 解：低碳钢拉伸实验时的应力—应变曲线如 图 5−1 所示。当材料拉伸到强化阶段（ce 段）后，卸除荷载时，应力和应变按直 线规律变化，如图 5−1 中直线 dd′。当 再次加载时，沿 d′d 直线上升，材料的 比例极限提高到 d 而塑性减少，此现象 称为冷作硬化。 答案：（C）