高一数学必修二立体几何测试题
高一数学(必修二)立体几何初步单元测试卷及答案

高一数学(必修二)立体几何初步单元测试卷及答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图所示,己知正方形O A B C ''''的边长为1,它是水平放置的一个平面图形的直观图,则其原图形的周长为( )A.8B.22C.4D.223+2.下列说法正确的是( ) A.三点确定一个平面B.圆心和圆上两个点确定一个平面C.如果两个平面相交有一个交点,则必有无数个公共点D.如果两条直线没有交点,则这两条直线平行3.正方体1111ABCD A B C D -中,P ,Q ,R 分别是AB ,AD ,11B C 的中点,那么正方体中过P ,Q ,R 的截面图形是( ) A.三角形B.四边形C.五边形D.六边形4.某圆柱的高为2,其正视图如图所示,圆柱上下底面圆周及侧面上的点A ,B ,D ,F ,C 在正视图中分别对应点A ,B ,E ,F ,C ,且3AE EF =,2BF BC =,异面直线AB ,CD 所成角的正弦值为45,则该圆柱的外接球的表面积为( )A.20πB.16πC.12πD.10π5.在《九章算术·商功》中将正四面形棱台体(棱台的上、下底面均为正方形)称为方亭.在方亭1111ABCD A B C D -中,1124AB A B ==,四个侧面均为全等的等腰梯形且面积之和为122( ) 282B.283142D.1436.异面直线是指( ) A.空间中两条不相交的直线B.分别位于两个不同平面内的两条直线C.平面内的一条直线与平面外的一条直线D.不同在任何一个平面内的两条直线7.如图,在正方体1111ABCD A B C D -中,E ,F 分别是11A D ,11B C 的中点,则与直线CF 互为异面直线的是( )A.1CCB.11B CC.DED.AE8.下列说法中正确的是( ) A.三点确定一个平面 B.四边形一定是平面图形 C.梯形一定是平面图形D.两个不同平面α和β有不在同一条直线上的三个公共点二、多选题(本题共4小题,每小题5分,共20分。
(word版)高一数学必修2立体几何测试题

高一数学必修2立体几何测试题第一卷一、选择题〔每题3分,共30分〕1、线段AB在平面内,那么直线AB与平面的位置关系是A、ABB、ABC、由线段AB的长短而定D、以上都不对2、以下说法正确的选项是A、三点确定一个平面B、四边形一定是平面图形C、梯形一定是平面图形D、平面和平面有不同在一条直线上的三个交点3、垂直于同一条直线的两条直线一定A、平行B、相交C、异面D、以上都有可能4、在正方体ABCD A1B1C1D1中,以下几种说法正确的选项是A、AC11ADB、D1C1ABC、AC1与DC成45o角D、AC11与B1C成60o角5l∥平面,直线a ,那么l与a的位置关系是、假设直线A、l∥aB、l与a异面C、l与a相交D、l与a没有公共点6、以下命题中:〔1〕平行于同一直线的两个平面平行;〔2〕平行于同一平面的两个平面平行;〔3〕垂直于同一直线的两直线平行;〔4〕垂直于同一平面的两直线平行.其中正确的个数有A、1B、2C、3D、47、在空间四边形ABCD各边AB、BC、CD、DA上分别取E、F、G、H四点,如果与EF、GH能相交于点P,那么A、点P不在直线AC上B、点P必在直线BD上C、点P必在平面ABC内D、点P必在平面ABC外8、a,b,c表示直线,M表示平面,给出以下四个命题:①假设a∥M,b∥M,那么a∥b;②假设b M,a∥b,那么a∥M;③假设a⊥c,b⊥c,那么a∥b;④假设a⊥M,b⊥M,那么a∥b.其中正确命题的个数有A、0个B、1个C、2个D、3个9、二面角AB 的平面角是锐角,内一点C到的距离为3,点C到棱AB的距离为4,那么tan的值等于133737 A、B、C、D、4577A '10、如图:直三棱柱ABC —111的体积为V,点P、AA1 ABC Q分别在侧棱P和CC1上,AP=C1Q,那么四棱锥B—APQC的体积为V V V VA、B、C、D、2345A二、填空题〔每题4分,共16分〕11、等体积的球和正方体,它们的外表积的大小关系是S球_____S正方体(填〞大于、小于或等于〞).12、正方体ABCD A1B1C1D1中,平面AB1D1和平面BC1D的位置关系为13、PA垂直平行四边形ABCD所在平面,假设PCA1 BD,平行那么四边形ABCD一定是D .B114、如图,在直四棱柱ABC1-ABCD中,当底面四边形ABCD111满足条件_________时,有A1B⊥B1D1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)D第二卷一、选择题〔每题3分,共30分〕A 题号123456789答案C' B'Q C BD1 C1 CB 10二、填空题〔每题4分,共16分〕11、12、13、14、三、解答题(共54分,要求写出主要的证明、解答过程)15、圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.(7分)16、E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点,且EH∥FG.求证:EH∥BD.(8分)AE HBDFGC217、 ABC 中 ACB90o ,SA 面ABC ,AD SC ,求证:AD 面SBC .(8分)SDA BC18、一块边长为 10cm 的正方形铁片按如下列图的阴影局部裁下 ,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器 ,试建立容器的容积 V 与x 的函数关系式,并求出函数的定义域 .(9分)E10DC 5OFABx19、正方体ABCDA 1B 1C 1D 1,O 是底ABCD 对角线的交点.D 1C 1求证:(1)C 1O ∥面ABD ;(2)AC 面ABD .(10分)A 1B 111 1 11DCOAB20、△BCD 中,∠BCD=90°,BC=CD=1,AB ⊥平面BCD ,A∠ADB=60°,E 、F分别是 AC 、AD 上的动点,且AE AF 1).AC (0EAD〔Ⅰ〕求证:不管λ为何值,总有平面BEF ⊥平面ABC ; CF〔Ⅱ〕当λ为何值时,平面BEF ⊥平面ACD ?(12分)DB3高一数学必修2立体几何测试题参考答案一、选择题〔每题5分,共60分〕ACDDD BCBDB二、填空题〔每题4分,共16分〕11、小于12、平行13、菱形14、对角线A1C1与B1D1互相垂直三、解答题〔共74分,要求写出主要的证明、解答过程〕15、解:设圆台的母线长为l,那么1分圆台的上底面面积为S上2242分圆台的上底面面积为S下2253分5所以圆台的底面面积为S S上S下294分又圆台的侧面积S侧(25)l7l5分于是7l256分即l 297分为所求.7面BCD,FG面BCD16、证明:QEHPFG,EH∴EH∥面BCD4分又QEH面BCD,面BCDI面ABD BD,∴EH∥BD8分17、证明:Q ACB90o BC AC1分又SA面ABC SA BC3分BC面SAC4分BC AD6分又SCAD,SCIBCCAD面SBC8分18、解:如图,设所截等腰三角形的底边边长为xcm.在Rt△EOF中, EF5cm,OF 1xcm,2分2所以EO251x2,5分4于是V 1x2251x27分34依题意函数的定义域为{x|0x10}9分419、证明:〔1〕连结A1C1,设AC11IB1D1O1连结AO1,QABCD A1B1C1D1是正方体A1ACC1是平行四边形∴A1C1∥AC且A1C1AC1分又O1,O分别是A1C1,AC的中点,∴O1C1∥AO且O1C1AOAOC1O1是平行四边形3分∴C1OPAO1,AO1面AB1D1,C1O面AB1D1∴C1O∥面AB1D1〔2〕QCC1面A1B1C1D1CC1B1D!又QA1C1B1D1,B1D1面AC11C即AC1B1D1同理可证A1C AB1,又D1B1I AB1B1A1C面AB1D120、证明:〔Ⅰ〕∵AB⊥平面BCD,∴AB⊥CD,CD⊥BC且AB∩BC=B,∴CD⊥平面ABC.又AE AF1),AC(0AD分分分分分分分∴不管λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF平面BEF,∴不管λ为何值恒有平面BEF⊥平面ABC.5分〔Ⅱ〕由〔Ⅰ〕知,BE⊥EF,又平面BEF⊥平面ACD,∴BE⊥平面ACD,∴BE⊥AC.7分BC=CD=1,∠BCD=90°,∠ADB=60°,∴BD2,AB2tan606,9分AC AB2BC27,由AB2=AE·AC得AE6,AE6,11分7AC7故当612分时,平面BEF⊥平面ACD.75。
高一数学必修二立体几何测试题-----2013

高一数学必修二立体几何测试题一:选择题(4分10题) 1.下面四个条件中,能确定一个平面的条件是()A.空间任意三点B.空间两条直线C.空间两条平行直线D. 一条直线和一个点2. h , l 2 , I 3是空间三条不同的直线,则下列命题正确的是()•A . I ,l 2 , l 2l 3 I ,//l 3B . I , I 2 ,I 2//I 3I ,I 3C . I 2 //I 3//I 3l , , I 2 ,13 共面D. h , l2 ,I 3共点I , , I 2 , I 3 共面3.已知 m n 是两条不同的直线,,,是三个不同的平面, 下列命题中正确的是:A. 若,,则 〃B .若 m, n ,则 m II nC. 若 m II , n 〃 ,贝 U m II n D .若 m // , m II ,则//4.在四面体A.0个 P ABC 的四个面中,是直角三角形的面至多有(BH个C. 3个D .4)个5, 下列命题中错说的是A •如果平面平面,那么平面内一定存在直线平行于平面B .如果平面a 不垂直于平面 ,那么平面内一定不存在直线垂直于平面D .如果平面 平面,那么平面内所有直线都垂直于平面6.如图所示正方体 AC ,,下面结论错误的是( )A. BD// 平面 CB 1D 1B. AC , BDC. AC ,平面 CB , D ,D.异面直线 AD 与CB ,角为607. 已知圆锥的全面积是底面积的 3倍,那么该圆锥的侧面展C .如果平面平面,平面 平面 l ,那么I 平面AB开图扇形的圆心角是(A. ,20B. ,50C. ,80D. 240A. AB BCB. AC BDC. CD 平面 ABCD.平面 ABC个点到这四个点距离相等,则这个距离是14. 一正方体内接于一个球,经过球心作一个截面,则截面的可能图形为 ________ (只填写序号).平面ACD9某几何体的三视图如图所示, 则该几何体的表面积为()D. 240A iC 1B i第10题10.如图所示点P 为三棱柱 ABC A 1B 1C 1侧棱AA 1上一动点,若四棱锥 P BCC 1B 1的体积为V ,则三棱柱ABC A 1B 1C 1的体积为()A . 2V B.V C. 4V D. 3V32二•填空题(5分4题)11.如图所示正方形 O'A'BC 的边长为2cm, 它是一个水平放置的一个平面图形的直观图, 则原图形的周长是 ________ , 面积是 __________ /」A f12.已知m,l是直线,是平面,给出下列命题正确的是(1)若I 垂直于 内的两条相交直线, 则I(2)若|平行于 ,则|平行于内所有直线;13.三棱锥 ,1 ,1,且I m,则;4) 若I ,且I ,则,且 II ,贝 y m // I .P-ABC 中,PA PB, PC 两两垂直,PA=1, PB PC . 2,已知空间中有左视图3 2 3俯视图C三•解答题15.已知圆台的上下底面半径分别为2,6 ,且侧面面积等于两底面面积之和,求该圆台的母线长,侧面积及体积•P ABCD的直观图;(2) 求四棱锥PABCD的表面积;17 .如图,已知PA 圆0所在的平面,AB是圆0的直径,AB 2,C是圆0上的一点,且AC BC ,PC与圆0所在的平面成45角,E是PC中点,F为PB 的中点•(1)求证:EF//面ABC ; ⑵求证:EF 面PAC ;⑶求三棱锥B PAC的体积16.已知四棱锥P ABCD的三视图如下:(1)画出四棱锥(3)求四棱锥PABCD的体积;18,如图,在三棱锥S ABC 中,平面SAB 平面SBC , ABBC , AS AB ,过 A 作AF 求证: SB ,垂足为F ,点E , G 分别是棱SA , (1)平面EFG 〃平面ABC ; (2)BC SA .19.如图 1,在 Rt ABC 中, C 90o ,D,E 分 别为AC, AB 的中点,点F 为线段CD 上的一点, 将 AF CD ,如图 2。
高一数学立体几何初步测试题及答案必修2答案

高一立体几何初步测试题答案参考答案及评分标准一、选择题 1 2 3 4 5 6 7 8 9 10 B B A B C A C D B B 二、填空题11. 2215()(5)252x y -+-=或2215()(5)252x y +++= 12. 3090α︒︒<<13. 20x -= 14. 22(1)1x y +-= 15. 2或-2 16. 240x y -+=; 25270x y -+= 三、解答题17. 解:解方程组2222(1)(3)20,10,x y x y ⎧-+-=⎪⎨+=⎪⎩得交点坐标为(3,1)-,(3,1)-. …5分 设所求圆的圆心坐标为(2,)a a -,=解得37a =-,r =, …5分因此,圆的方程为222610077x y x y +++-=. …2分 18. 解:设点P 的坐标为(,0)a (0)a >,点P 到直线AB 的距离为d . 由已知,得2211(31)(42)1022ABP S AB d d ∆==-+-=. …4分 解得d =…6分由已知易得,直线AB 的方程为10x y -+=. 所以d == …10分解得9a =,或11a =-(舍去). …12分 所以点P 的坐标为(9,0). …14分 19. 解:由已知得圆C 的圆心为(0,7)C ,半径为5r =. …3分如图所示,(25,18)M 关于x 轴的对称点为(25,18)M '-, …6分 所求反射光线过点M ',C ,所以所求直线方程为70187250y x --=---, 即70x y +-=. …9分 20. 设圆C 的方程为222()()x a y b r -+-=(0)r >,则圆心是(,)C a b ,半径是r . 因为圆C 截得y 轴所得的弦长为4,所以224r a =+. …4分 因为圆C 被x 轴分成两段圆弧,其弧长之比为3:1,所以2r b =. …8分 因为圆心(,)C a b 在直线y x =,所以b a =。
【高一数学】必修2立体几何测试题(含答案)

高一数学立体几何(必修2)期末测试卷一、选择题1、线段AB 在平面α内,则直线AB 与平面α的位置关系是 ( )A 、AB α⊂ B 、AB α⊄C 、由线段AB 的长短而定D 、以上都不对2、下列说法正确的是A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点 3、垂直于同一条直线的两条直线一定 ( )A 、平行B 、相交C 、异面D 、以上都有可能 4、在正方体1111ABCD A B C D -中,下列几种说法正确的是 ( )A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45角D 、11AC 与1B C 成60角5、若直线l ∥平面α,直线a α⊂,则l 与a 的位置关系是 ( )A 、 l ∥αB 、l 与a 异面C 、l 与a 相交D 、l 与a 没有公共点 6、下列命题中:(1)、平行于同一直线的两个平面平行;(2)、平行于同一平面的两个平面平行;(3)、垂直于同一直线的两直线平行;(4)、垂直于同一平面的两直线平行.其中正确的个数有 ( ) A 、1 B 、2 C 、3 D 、47、a ,b ,c 表示直线,M 表示平面,给出下列四个命题:①若a ∥M ,b ∥M ,则a ∥b ;②若b ⊂M ,a ∥b ,则a ∥M ;③若a ⊥c ,b ⊥c ,则a ∥b ;④若a ⊥M ,b ⊥M ,则a ∥b .其中正确命题的个数有( ) A 、0个 B 、1个 C 、2个 D 、3个8.正方体ABCD —A 1B 1C 1D 1中,P 在侧面BCC 1B 1及其边界上运动,且总保持AP ⊥BD 1 ,则动点P 的轨迹是( )A 、线段B 1C B 、 BB 1中点与CC 1中点连成的线段 C 、线段BC 1D 、 BC 中点与B 1C 1中点连成的线段二、填空题9、直线AB 、AD ⊂α,直线CB 、CD ⊂β,点E ∈AB ,点F ∈BC ,点G ∈CD ,点H ∈DA ,若直线EH∩直线FG=M ,则点M 在 上10、已知△ABC 中,A ∈α,BC ∥α,BC=6,∠BAC=90︒,AB 、AC 与平面α分别成30︒、45︒的角.则BC 到平面α的距离为三、解答题11、已知平面α∥β,直线AB β⊄,且直线AB ∥α,求证:AB ∥β12、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.求证:(1)C 1O ∥面11AB D ; (2 )1AC ⊥面11AB D .D 1ODB AC 1B 1A 1CBACBANM CBAC 1B 1A 113、已知矩形ABCD 所在平面外一点P ,PA ⊥平面ABCD ,E 、F 分别是 AB 、PC 的中点. (1) 求证:EF ∥平面PAD ; (2) 求证:EF ⊥CD ;15、如图,在矩形ABCD 中,AB=33,BC=3,沿对角线BD 将BCD 折起,使点C 移到点C ’,且C ’在平面ABD的射影O 恰好在AB 上。
(完整版)高中数学必修2立体几何考题(附答案)

高中数学必修2立体几何考题13.如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1,B1C1的中点.问:(1)AM和CN是否是异面直线?说明理由;(2)D1B和CC1是否是异面直线?说明理由.解析:(1)由于M、N分别是A1B1和B1C1的中点,可证明MN∥AC,因此AM与CN不是异面直线.(2)由空间图形可感知D1B和CC1为异面直线的可能性较大,判断的方法可用反证法.探究拓展:解决这类开放型问题常用的方法有直接法(即由条件入手,经过推理、演算、变形等),如第(1)问,还有假设法,特例法,有时证明两直线异面用直线法较难说明问题,这时可用反证法,即假设两直线共面,由这个假设出发,来推证错误,从而否定假设,则两直线是异面的.解:(1)不是异面直线.理由如下:∵M、N分别是A1B1、B1C1的中点,∴MN∥A1C1.又∵A1A∥D1D,而D1D綊C1C,∴A1A綊C1C,∴四边形A1ACC1为平行四边形.∴A1A∥AC,得到MN∥AC,∴A、M、N、C在同一个平面内,故AM和CN不是异面直线.(2)是异面直线.理由如下:假设D1B与CC1在同一个平面CC1D1内,则B∈平面CC1D1,C∈平面CC1D1.∴BC⊂平面CC1D1,这与在正方体中BC⊥平面CC1D1相矛盾,∴假设不成立,故D1B与CC1是异面直线.14.如下图所示,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为面BCC1B1的中心.(1)过O作一直线与AN交于P,与CM交于Q(只写作法,不必证明);(2)求PQ的长(不必证明).解析:(1)由ON∥AD知,AD与ON确定一个平面α.又O、C、M三点确定一个平面β(如下图所示).∵三个平面α,β和ABCD两两相交,有三条交线OP、CM、DA,其中交线DA与交线CM不平行且共面.∴DA与CM必相交,记交点为Q.∴OQ是α与β的交线.连结OQ与AN交于P,与CM交于Q,故OPQ即为所作的直线.(2)解三角形APQ可得PQ=14 3.15.如图,在直三棱柱ABC-A1B1C1中,AB=BC=B1B=a,∠ABC=90°,D、E分别为BB1、AC1的中点.(1)求异面直线BB1与AC1所成的角的正切值;(2)证明:DE为异面直线BB1与AC1的公垂线;(3)求异面直线BB1与AC1的距离.解析:(1)由于直三棱柱ABC-A 1B1C1中,AA1∥BB1,所以∠A1AC1就是异面直线BB1与AC1所成的角.又AB=BC=B1B=a,∠ABC=90°,所以A1C1=2a,tan∠A1AC1=2,即异面直线BB1与AC1所成的角的正切值为 2.(2)证明:解法一:如图,在矩形ACC1A1中,过点E作AA1的平行线MM1分别交AC、A1C1于点M、M1,连结BM,B1M1,则BB1綊MM1.又D、E分别是BB1、MM1的中点,可得DE綊BM.在直三棱柱ABC-A1B1C1中,由条件AB=BC得BM⊥AC,所以BM⊥平面ACC1A1,故DE⊥平面ACC1A1,所以DE⊥AC1,DE⊥BB1,即DE为异面直线BB1与AC1的公垂线.解法二:如图,延长C1D、CB交于点F,连结AF,由条件易证D是C1F的中点,B是CF的中点,又E是AC1的中点,所以DE∥AF.在△ACF中,由AB=BC=BF知AF⊥AC.在直三棱柱ABC-A1B1C1中,AA1⊥平面ABC,所以AF⊥AA1,故AF⊥平面ACC1A1,故DE⊥平面ACC1A1,所以DE⊥AC1,DE⊥BB1,即DE为异面直线BB1与AC1的公垂线.(3)由(2)知线段DE的长就是异面直线BB1与AC1的距离,由于AB=BC=a,∠ABC=90°,所以DE=2 2a.反思归纳:两条异面直线的公垂线是指与两条异面直线既垂直又相交的直线,两条异面直线的公垂线是惟一的,两条异面直线的公垂线夹在两条异面直线之间的线段的长度就是两条异面直线的距离.证明一直线是某两条异面直线的公垂线,可以分别证明这条直线与两条异面直线垂直.本题的思路是证明这条直线与一个平面垂直,而这一平面与两条异面直线的位置关系是一条直线在平面内,另一条直线与这个平面平行.16.如图所示,在正方体ABCD-A1B1C1D1中,O,M分别是BD1,AA1的中点.(1)求证:MO是异面直线AA1和BD1的公垂线;(2)求异面直线AA1与BD1所成的角的余弦值;(3)若正方体的棱长为a,求异面直线AA1与BD1的距离.解析:(1)证明:∵O是BD1的中点,∴O是正方体的中心,∴OA=OA 1,又M为AA1的中点,即OM是线段AA1的垂直平分线,故OM⊥AA1.连结MD1、BM,则可得MB=MD1.同理由点O为BD1的中点知MO⊥BD1,即MO 是异面直线AA 1和BD 1的公垂线. (2)由于AA 1∥BB 1,所以∠B 1BD 1就是异面直线AA 1和BD 1所成的角. 在Rt △BB 1D 1中,设BB 1=1,则BD 1=3,所以cos ∠B 1BD 1=33,故异面直线AA 1与BD 1所成的角的余弦值等于33.(3)由(1)知,所求距离即为线段MO 的长,由于OA =12AC 1=32a ,AM =a 2,且OM ⊥AM ,所以OM =22a .13.如图所示,正方体ABCD -A 1B 1C 1D 1中,侧面对角线AB 1,BC 1上分别有两点E 、F ,且B 1E =C 1F ,求证:EF ∥ABCD .证明:解法一:分别过E 、F 作EM ⊥AB 于M ,FN ⊥BC 于N ,连结MN .∵BB 1⊥平面ABCD , ∴BB 1⊥AB ,BB 1⊥BC , ∴EM ∥BB 1,FN ∥BB 1, ∴EM ∥FN .又B 1E =C 1F ,∴EM =FN ,故四边形MNFE 是平行四边形, ∴EF ∥MN ,又MN 在平面ABCD 中, 所以EF ∥平面ABCD .解法二:过E 作EG ∥AB 交BB 1于G ,连结GF ,则B 1E B 1A =B 1GB 1B,∵B 1E =C 1F ,B 1A =C 1B , ∴C 1F C 1B =B 1G B 1B,∴FG ∥B 1C 1∥BC . 又EG ∩FG =G ,AB ∩BC =B , ∴平面EFG ∥平面ABCD , 而EF ⊂平面EFG , ∴EF ∥平面ABCD .14.如下图,在四棱锥P -ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD =DC .过BD 作与P A 平行的平面,交侧棱PC 于点E ,又作DF ⊥PB ,交PB 于点F .(1)求证:点E 是PC 的中点; (2)求证:PB ⊥平面EFD .证明:(1)连结AC ,交BD 于O ,则O 为AC 的中点,连结EO . ∵P A ∥平面BDE ,平面P AC ∩平面BDE =OE ,∴P A ∥OE . ∴点E 是PC 的中点;(2)∵PD ⊥底面ABCD 且DC ⊂底面ABCD ,∴PD ⊥DC ,△PDC 是等腰直角三角形,而DE 是斜边PC 的中线, ∴DE ⊥PC ,①又由PD ⊥平面ABCD ,得PD ⊥BC .∵底面ABCD 是正方形,CD ⊥BC ,∴BC ⊥平面PDC .而DE ⊂平面PDC .∴BC ⊥DE .②由①和②推得DE ⊥平面PBC .而PB ⊂平面PBC , ∴DE ⊥PB ,又DF ⊥PB 且DE ∩DF =D , 所以PB ⊥平面EFD .15.如图,l 1、l 2是互相垂直的异面直线,MN 是它们的公垂线段.点A 、B 在l 1上,C 在l 2上,AM =MB =MN .(1)求证AC ⊥NB ; (2)若∠ACB =60°,求NB 与平面ABC 所成角的余弦值.证明:(1)如图由已知l 2⊥MN ,l 2⊥l 1,MN ∩l 1=M ,可得l 2⊥平面ABN .由已知MN ⊥l 1,AM =MB =MN ,可知AN =NB 且AN ⊥NB . 又AN 为AC 在平面ABN 内的射影, ∴AC ⊥NB .(2)∵Rt △CNA ≌Rt △CNB ,∴AC =BC ,又已知∠ACB =60°,因此△ABC 为正三角形. ∵Rt △ANB ≌Rt △CNB ,∴NC =NA =NB ,因此N 在平面ABC 内的射影H 是正三角形ABC 的中心.连结BH ,∠NBH 为NB 与平面ABC 所成的角.在Rt △NHB 中,cos ∠NBH =HB NB =33AB22AB =63.16.如图,在四面体ABCD 中,CB =CD ,AD ⊥BD ,点E 、F 分别是AB 、BD 的中点.求证:(1)直线EF ∥平面ACD ; (2)平面EFC ⊥平面BCD .命题意图:本小题主要考查直线与平面、平面与平面的位置关系,考查空间想象能力、推理论证能力.证明:(1)在△ABD 中,∵E 、F 分别是AB 、BD 的中点,所以EF ∥AD . 又AD ⊂平面ACD ,EF ⊄平面ACD ,∴直线EF ∥平面ACD . (2)在△ABD 中,∵AD ⊥BD ,EF ∥AD ,∴EF ⊥BD .在△BCD 中,∵CD =CB ,F 为BD 的中点,∴CF ⊥BD .∵EF ⊂平面EFC ,CF ⊂平面EFC ,EF 与CF 交于点F ,∴BD ⊥平面EFC . 又∵BD ⊂平面BCD ,∴平面EFC ⊥平面BCD .13.如图,在四棱锥P -ABCD 中,底面ABCD 是边长为a 的正方形,P A ⊥平面ABCD ,且P A =2AB .(1)求证:平面P AC ⊥平面PBD ; (2)求二面角B -PC -D 的余弦值. 解析:(1)证明:∵P A ⊥平面ABCD , ∴P A ⊥BD .∵ABCD 为正方形,∴AC ⊥BD .∴BD ⊥平面P AC ,又BD 在平面BPD 内,∴平面P AC ⊥平面BPD . (2)在平面BCP 内作BN ⊥PC ,垂足为N ,连结DN , ∵Rt △PBC ≌Rt △PDC , 由BN ⊥PC 得DN ⊥PC ;∴∠BND 为二面角B -PC -D 的平面角,在△BND 中,BN =DN =56a ,BD =2a ,∴cos ∠BND =56a 2+56a 2-2a 253a 2=-15.14.如图,已知ABCD -A 1B 1C 1D 1是棱长为3的正方体,点E 在AA 1上,点F 在CC 1上,G 在BB 1上,且AE =FC 1=B 1G =1,H 是B 1C 1的中点.(1)求证:E 、B 、F 、D 1四点共面; (2)求证:平面A 1GH ∥平面BED 1F . 证明:(1)连结FG .∵AE =B 1G =1,∴BG =A 1E =2, ∴BG 綊A 1E ,∴A 1G 綊BE . ∵C 1F 綊B 1G ,∴四边形C 1FGB 1是平行四边形. ∴FG 綊C 1B 1綊D 1A 1,∴四边形A 1GFD 1是平行四边形. ∴A 1G 綊D 1F ,∴D 1F 綊EB , 故E 、B 、F 、D 1四点共面.(2)∵H 是B 1C 1的中点,∴B 1H =32.又B 1G =1,∴B 1G B 1H =32.又FC BC =23,且∠FCB =∠GB 1H =90°, ∴△B 1HG ∽△CBF ,∴∠B 1GH =∠CFB =∠FBG , ∴HG ∥FB .又由(1)知A 1G ∥BE ,且HG ∩A 1G =G , FB ∩BE =B ,∴平面A 1GH ∥平面BED 1F .15.在三棱锥P -ABC 中,P A ⊥面ABC ,△ABC 为正三角形,D 、E 分别为BC 、AC 的中点,设AB =P A =2.(1)求证:平面PBE ⊥平面P AC ;(2)如何在BC 上找一点F ,使AD ∥平面PEF ,请说明理由; (3)对于(2)中的点F ,求三棱锥B -PEF 的体积. 解析:(1)证明:∵P A ⊥面ABC ,BE ⊂面ABC , ∴P A ⊥BE .∵△ABC 是正三角形,E 为AC 的中点, ∴BE ⊥AC ,又P A 与AC 相交, ∴BE ⊥平面P AC ,∴平面PBE ⊥平面P AC .(2)解:取DC 的中点F ,则点F 即为所求. ∵E ,F 分别是AC ,DC 的中点, ∴EF ∥AD ,又AD ⊄平面PEF ,EF ⊂平面PEF , ∴AD ∥平面PEF .(3)解:V B -PEF =V P -BEF =13S △BEF ·P A =13×12×32×32×2=34.16.(2009·天津,19)如图所示,在五面体ABCDEF 中,F A ⊥平面ABCD ,AD ∥BC ∥FE ,AB ⊥AD ,M 为CE 的中点,AF =AB =BC =FE =12AD .(1)求异面直线BF 与DE 所成的角的大小; (2)求证:平面AMD ⊥平面CDE ; (3)求二面角A -CD -E 的余弦值.解答:(1)解:由题设知,BF ∥CE ,所以∠CED (或其补角)为异面直线BF 与DE 所成的角.设P 为AD 的中点,连结EP ,PC .因为FE 綊AP ,所以F A 綊EP .同理,AB 綊PC .又F A ⊥平面ABCD ,所以EP ⊥平面ABCD .而PC ,AD 都在平面ABCD 内,故EP ⊥PC ,EP ⊥AD .由AB ⊥AD ,可得PC ⊥AD .设F A =a ,则EP =PC =PD =a ,CD =DE =EC =2a .故∠CED =60°.所以异面直线BF 与DE 所成的角的大小为60°.(2)证明:因为DC =DE 且M 为CE 的中点,所以DM ⊥CE .连结MP ,则MP ⊥CE .又MP ∩DM =M ,故CE ⊥平面AMD .而CE ⊂平面CDE ,所以平面AMD ⊥平面CDE .(3)设Q 为CD 的中点,连结PQ ,EQ .因为CE =DE ,所以EQ ⊥CD .因为PC =PD ,所以PQ ⊥CD ,故∠EQP 为二面角A -CD -E 的平面角.由(1)可得,EP ⊥PQ ,EQ =62a ,PQ =22a .于是在Rt △EPQ 中,cos ∠EQP =PQ EQ =33.所以二面角A -CD -E 的余弦值为33.13.(2009·重庆)如图所示,四棱锥P -ABCD 中,AB ⊥AD ,AD ⊥DC ,P A ⊥底面ABCD ,P A =AD =DC =12AB =1,M 为PC 的中点,N 点在AB 上且AN =13NB .(1)求证:MN ∥平面P AD ;(2)求直线MN 与平面PCB 所成的角.解析:(1)证明:过点M 作ME ∥CD 交PD 于E 点,连结AE .∵AN =13NB ,∴AN =14AB =12DC =EM .又EM ∥DC ∥AB ,∴EM 綊AN , ∴AEMN 为平行四边形,∴MN ∥AE ,∴MN ∥平面P AD .(2)解:过N 点作NQ ∥AP 交BP 于点Q ,NF ⊥CB 于点F . 连结QF ,过N 点作NH ⊥QF 于H ,连结MH , 易知QN ⊥面ABCD ,∴QN ⊥BC ,而NF ⊥BC , ∴BC ⊥面QNF ,∵BC ⊥NH ,而NH ⊥QF ,∴NH ⊥平面PBC ,∴∠NMH 为直线MN 与平面PCB 所成的角.通过计算可得MN =AE =22,QN =34,NF =342,∴NH =QN ·NF QF =ON ·NF QN 2+NF 2=64,∴sin ∠NMH =NH MN =32,∴∠NMH =60°,∴直线MN 与平面PCB 所成的角为60°. 14.(2009·广西柳州三模)如图所示,已知直平行六面体ABCD -A 1B 1C 1D 1中,AD ⊥BD ,AD =BD =a ,E 是CC 1的中点,A 1D ⊥BE .(1)求证:A 1D ⊥平面BDE ;(2)求二面角B -DE -C 的大小.解析:(1)证明:在直平行六面体ABCD -A 1B 1C 1D 1中, ∵AA 1⊥平面ABCD ,∴AA 1⊥BD . 又∵BD ⊥AD ,∴BD ⊥平面ADD 1A 1,即BD ⊥A 1D . 又∵A 1D ⊥BE 且BE ∩BD =B , ∴A 1D ⊥平面BDE .(2)解:如图,连B 1C ,则B 1C ⊥BE , 易证Rt △BCE ∽Rt △B 1BC ,∴CE BC =BC B 1B,又∵E 为CC 1中点, ∴BC 2=12BB 21.BB 1=2BC =2a .取CD 中点M ,连结BM ,则BM ⊥平面CC 1D 1C , 作MN ⊥DE 于N ,连NB ,由三垂线定理知:BN ⊥DE ,则∠BNM 是二面角B -DE -C 的平面角.在Rt △BDC 中,BM =BD ·BC DC =22a ,Rt △CED 中,易求得MN =1010a ,Rt △BMN 中,tan ∠BNM =BMMN=5,则二面角B -DE -C 的大小为arctan 5.15.如图,已知正方体ABCD -A 1B 1C 1D 1中,E 为AB 的中点.(1)求直线B 1C 与DE 所成的角的余弦值; (2)求证:平面EB 1D ⊥平面B 1CD ; (3)求二面角E -B 1C -D 的余弦值.解析:(1)连结A 1D ,则由A 1D ∥B 1C 知,B 1C 与DE 所成的角即为A 1D 与DE 所成的角.连结A 1E ,由正方体ABCD -A 1B 1C 1D 1,可设其棱长为a ,则A 1D =2a ,A 1E =DE =52a ,∴cos ∠A 1DE=A 1D 2+DE 2-A 1E 22·A 1D ·DE =105.∴直线B 1C 与DE 所成角的余弦值是105. (2)证明取B 1C 的中点F ,B 1D 的中点G ,连结BF ,EG ,GF . ∵CD ⊥平面BCC 1B 1,且BF ⊂平面BCC 1B 1,∴DC ⊥BF . 又∵BF ⊥B 1C ,CD ∩B 1C =C , ∴BF ⊥平面B 1CD .又∵GF 綊12CD ,BE 綊12CD ,∴GF 綊BE ,∴四边形BFGE 是平行四边形, ∴BF ∥GE ,∴GE ⊥平面B 1CD . ∵GE ⊂平面EB 1D ,∴平面EB 1D ⊥平面B 1CD . (3)连结EF .∵CD ⊥B 1C ,GF ∥CD ,∴GF ⊥B 1C . 又∵GE ⊥平面B 1CD ,∴EF ⊥B 1C ,∴∠EFG 是二面角E -B 1C -D 的平面角. 设正方体的棱长为a ,则在△EFG 中,GF =12a ,EF =32a ,∴cos ∠EFG =FG EF =33,∴二面角E -B 1C -D 的余弦值为33.16.(2009·全国Ⅱ,18)如图所示,直三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,D 、E 分别为AA 1、B 1C 的中点,DE ⊥平面BCC 1.(1)求证:AB =AC ;(2)设二面角A -BD -C 为60°,求B 1C 与平面BCD 所成的角的大小. 解析:(1)证明:取BC 中点F ,连结EF ,则EF 綊12B 1B ,从而EF 綊DA .连结AF ,则ADEF 为平行四边形,从而AF ∥DE .又DE ⊥平面BCC 1,故AF ⊥平面BCC 1,从而AF ⊥BC ,即AF 为BC 的垂直平分线,所以AB =AC .(2)解:作AG ⊥BD ,垂足为G ,连结CG .由三垂线定理知CG ⊥BD ,故∠AGC 为二面角A -BD -C 的平面角.由题设知,∠AGC =60°.设AC =2,则AG =23.又AB =2,BC =22,故AF = 2.由AB ·AD =AG ·BD 得2AD =23·AD 2+22,解得AD =2,故AD =AF .又AD ⊥AF ,所以四边形ADEF 为正方形.因为BC ⊥AF ,BC ⊥AD ,AF ∩AD =A ,故BC ⊥平面DEF ,因此平面BCD ⊥平面DEF . 连结AE 、DF ,设AE ∩DF =H ,则EH ⊥DF ,EH ⊥平面BCD .连结CH ,则∠ECH 为B 1C 与平面BCD 所成的角.因ADEF 为正方形,AD =2,故EH =1,又EC =12B 1C =2,所以∠ECH =30°,即B 1C 与平面BCD 所成的角为30°.13.在正四棱柱ABCD -A 1B 1C 1D 1中,底面边长为22,侧棱长为4,E 、F 分别为棱AB 、BC 的中点.(1)求证:平面B 1EF ⊥平面BDD 1B 1; (2)求点D 1到平面B 1EF 的距离d .分析:(1)可先证EF ⊥平面BDD 1B 1.(2)用几何法或等积法求距离时,可由B 1D 1∥BD ,将点进行转移:D 1点到平面B 1EF 的距离是B 点到它的距离的4倍,先求B 点到平面B 1EF 的距离即可.解答:(1)证明:⎭⎪⎬⎪⎫EF ⊥BD EF ⊥B 1B ⇒EF ⊥平面BDD 1B 1⇒平面B 1EF ⊥平面BDD 1B 1.(2)解:解法一:连结EF 交BD 于G 点. ∵B 1D 1=4BG ,且B 1D 1∥BG ,∴D 1点到平面B 1EF 的距离是B 点到它的距离的4倍. 利用等积法可求.由题意可知,EF =12AC =2,B 1G =17.S △B 1EF =12EF ·B 1G =12×2×17=17,S △BEF =12BE ·BF =12×2×2=1.∵VB -B 1EF =VB 1-BEF ,设B 到面B 1EF 的距离为h 1,则13×17×h 1=13×1×4,∴h 1=41717.∴点D 1到平面B 1EF 的距离为h =4h 1=161717.解法二:如图,在正方形BDD 1B 1的边BD 上取一点G ,使BG =14BD ,连结B 1G ,过点D 1作D 1H ⊥B 1G 于H ,则D 1H 即为所求距离.可求得D 1H =161717(直接法).14.如图直三棱柱ABC -A 1B 1C 1中,侧棱CC 1=2,∠BAC =90°,AB =AC =2,M 是棱BC 的中点,N 是CC 1中点.求:(1)二面角B 1-AN -M 的大小; (2)C 1到平面AMN 的距离. 解析:(1)∵∠BAC =90°,AB =AC =2,M 是棱BC 的中点, ∴AM ⊥BC ,BC =2,AM =1. ∴AM ⊥平面BCC 1B 1.∴平面AMN ⊥平面BCC 1B 1.作B 1H ⊥MN 于H ,HR ⊥AN 于R ,连结B 1R , ∴B 1H ⊥平面AMN .又由三垂线定理知,B 1R ⊥AN .∴∠B 1RH 是二面角B 1-AN -M 的平面角. 由已知得AN =3,MN =2,B 1M =5=B 1N ,则B 1H =322,又Rt △AMN ∽Rt △HRN ,RH AM =HN AN ,∴RH =66.∴B 1R =143,∴cos ∠B 1RH =RH B 1R =714.∴二面角B 1-AN -M 的大小为arccos 714.(2)∵N 是CC 1中点,∴C 1到平面AMN 的距离等于C 到平面AMN 的距离. 设C 到平面AMN 的距离为h , 由V C -AMN =V N -AMC 得13×12·MN ·h =13×12AM ·MC . ∴h =22.15.(2009·北京海淀一模)如图所示,四棱锥P -ABCD 中,P A ⊥平面ABCD ,底面ABCD 为直角梯形,且AB ∥CD ,∠BAD =90°,P A =AD =DC =2,AB =4.(1)求证:BC ⊥PC ;(2)求PB 与平面P AC 所成的角的正弦值; (3)求点A 到平面PBC 的距离.解析:(1)证明:如图,在直角梯形ABCD 中, ∵AB ∥CD ,∠BAD =90°,AD =DC =2, ∴∠ADC =90°,且AC =2 2. 取AB 的中点E ,连结CE ,由题意可知,四边形ABCD 为正方形, ∴AE =CE =2.又∵BE =12AB =2.∴CE =12AB ,∴△ABC 为等腰直角三角形, ∴AC ⊥BC .又∵P A ⊥平面ABCD ,且AC 为PC 在平面ABCD 内的射影, BC ⊂平面ABCD ,由三垂线定理得, BC ⊥PC .(2)由(1)可知,BC ⊥PC ,BC ⊥AC ,PC ∩AC =C , ∴BC ⊥平面P AC .PC 是PB 在平面P AC 内的射影,∴∠CPB 是PB 与平面P AC 所成的角.又CB =22, PB 2=P A 2+AB 2=20,PB =25,∴sin ∠CPB =BC PB =105,即PB 与平面P AC 所成角的正弦值为105.(3)由(2)可知,BC ⊥平面P AC ,BC ⊂平面PBC , ∴平面PBC ⊥平面P AC .过A 点在平面P AC 内作AF ⊥PC 于F , ∴AF ⊥平面PBC ,∴AF 的长即为点A 到平面PBC 的距离.在直角三角形P AC 中, P A =2,AC =22,PC =23,∴AF =263.即点A 到平面PBC 的距离为263.16.(2009·吉林长春一模)如图所示,四棱锥P -ABCD 的底面是正方形,P A ⊥底面ABCD ,P A =2,∠PDA =45°,点E 、F 分别为棱AB 、PD 的中点.(1)求证:AF ∥平面PCE ;(2)求二面角E -PD -C 的大小; (3)求点A 到平面PCE 的距离.解析:(1)证明:如图取PC 的中点G ,连结FG 、EG , ∴FG 为△PCD 的中位线,∴FG =12CD 且FG ∥CD .又∵底面四边形ABCD 是正方形,E 为棱AB 的中点,∴AE =12CD 且AE ∥CD ,∴AE =FG 且AE ∥FG .∴四边形AEGF 是平行四边形, ∴AF ∥EG .又EG ⊂平面PCE ,AF ⊄平面PCE , ∴AF ∥平面PCE .(2)解:∵P A ⊥底面ABCD , ∴P A ⊥AD ,P A ⊥CD . 又AD ⊥CD , P A ∩AD =A , ∴CD ⊥平面P AD . 又∵AF ⊂平面P AD , ∴CD ⊥AF .又P A =2,∠PDA =45°, ∴P A =AD =2.∵F 是PD 的中点,∴AF ⊥PD . 又∵CD ∩PD =D , ∴AF ⊥平面PCD .∵AF ∥EG ,∴EG ⊥平面PCD . 又GF ⊥PD ,连结EF ,则∠GFE 是二面角E -PD -C 的平面角. 在Rt △EGF 中,EG =AF =2,GF =1,∴tan ∠GFE =GEGF= 2.∴二面角E -PD -C 的大小为arctan 2. (3)设A 到平面PCE 的距离为h ,由V A -PCE =V P -ACE ,即13×12PC ·EG ·h =13P A ·12AE ·CB ,得h =63,∴点A 到平面PCE 的距离为63.13.(2009·陕西,18)如图所示,在直三棱柱ABC -A 1B 1C 1中,AB =1,AC =AA 1=3,∠ABC =60°.(1)求证:AB ⊥A 1C ;(2)求二面角A -A 1C -B 的大小.解析:(1)证明:∵三棱柱ABC -A 1B 1C 1为直三棱柱, ∴AB ⊥AA 1,在△ABC 中,AB =1,AC =3,∠ABC =60°,由正弦定理得∠ACB =30°, ∴∠BAC =90°,即AB ⊥AC .∴AB ⊥平面ACC 1A 1,又A 1C ⊂平面ACC 1A 1,∴AB ⊥A 1C .(2)解:如图,作AD ⊥A 1C 交A 1C 于D 点,连结BD ,由三垂线定理知BD ⊥A 1C ,∴∠ADB 为二面角A -A 1C -B 的平面角.在Rt △AA 1C 中,AD =AA 1·AC A 1C =3×36=62,在Rt △BAD 中,tan ∠ADB =AB AD =63, ∴∠ADB =arctan63,即二面角A -A 1C -B 的大小为arctan 63. 14.如图,三棱柱ABC -A 1B 1C 1的底面是边长为a 的正三角形,侧面ABB 1A 1是菱形且垂直于底面,∠A 1AB =60°,M 是A 1B 1的中点.(1)求证:BM ⊥AC ;(2)求二面角B -B 1C 1-A 1的正切值; (3)求三棱锥M -A 1CB 的体积.解析:(1)证明:∵ABB 1A 1是菱形,∠A 1AB =60°⇒△A 1B 1B 是正三角形, ⎭⎪⎬⎪⎫∵M 是A 1B 1的中点,∴BM ⊥A 1B 又∵平面AA 1B 1B ⊥平面A 1B 1C 1 ⇒BM ⊥平面A 1B 1C 1. ⎭⎪⎬⎪⎫∴BM ⊥A 1C 1又∵AC ∥A 1C 1⇒BM ⊥AC .⎭⎪⎬⎪⎫(2)过M 作ME ⊥B 1C 1且交于点E ,∵BM ⊥平面A 1B 1C 1,⇒BE ⊥B 1C 1,∴∠BEM 为所求二面角的平面角, △A 1B 1C 1中,ME =MB 1·sin60°=34a ,Rt △BMB 1中,MB =MB 1·tan60°=32a , ∴tan ∠BEM =MBME=2,∴所求二面角的正切值是2.(3)VM -A 1CB =12VB 1-A 1CB =12VA -A 1CB =12VA 1-ABC =12×13×34a 2·32a =116a 3.15.(2009·广东汕头一模)如图所示,已知△BCD 中,∠BCD =90°,BC =CD =1,AB ⊥平面BCD ,∠ADB =60°,E 、F 分别是AC 、AD 上的动点,且AE AC =AFAD=λ(0<λ<1).(1)求证:不论λ为何值,总有EF ⊥平面ABC ;(2)若λ=12,求三棱锥A -BEF 的体积.解析:(1)证明:∵AB ⊥平面BCD , ∴AB ⊥CD .又∵在△BCD 中,∠BCD =90°, ∴BC ⊥CD .∵又AB ∩BC =B ,∴CD ⊥平面ABC .又∵在△ACD 中,E 、F 分别是AC 、AD 上的动点,且AE AC =AFAD=λ(0<λ<1),∴不论λ为何值,都有EF ∥CD , ∴EF ⊥平面ABC .(2)在△BCD 中,∠BCD =90°,BC =CD =1, ∴BD = 2.又∵AB ⊥平面BCD , ∴AB ⊥BC ,AB ⊥BD .又∵在Rt △ABD 中,∠ADB =60°, ∴AB =BD ·tan60°=6, 由(1)知EF ⊥平面ABC , ∴V A -BEF =V F -ABE =13S △ABE ·EF =13×12S △ABC ·EF =16×12×1×6×12=624. 故三棱锥A -BEF 的体积是624.16.在四棱锥P -ABCD 中,侧面PDC 是边长为2的正三角形,且与底面垂直,底面ABCD 是面积为23的菱形,∠ADC 为菱形的锐角.(1)求证:P A ⊥CD ;(2)求二面角P -AB -D 的大小; (3)求棱锥P -ABCD 的侧面积;解析:(1)证明:如图所示,取CD 的中点E ,由PE ⊥CD ,得PE ⊥平面ABCD ,连结AC 、AE .∵AD ·CD ·sin ∠ADC =23, AD =CD =2,∴sin ∠ADC =32,即∠ADC =60°,∴△ADC 为正三角形,∴CD ⊥AE . ∴CD ⊥P A (三垂线定理).(2)解:∵AB ∥CD ,∴AB ⊥P A ,AB ⊥AE , ∴∠P AE 为二面角P -AB -D 的平面角. 在Rt △PEA 中,PE =AE ,∴∠P AE =45°. 即二面角P -AB -D 的大小为45°. (3)分别计算各侧面的面积: ∵PD =DA =2,P A =6,∴cos ∠PDA =14,sin ∠PDA =154.S △PCD =3,S △P AB =12AB ·P A =12·2·2·3=6,S △P AD =S △PBC =12PD ·DA ·sin ∠PDA =152.∴S P -ABCD 侧=3+6+15.13.把地球当作半径为R 的球,地球上A 、B 两地都在北纬45°,A 、B 两点的球面距离是π3R ,A 点在东经20°,求B 点的位置. 解析:如图,求B 点的位置即求B 点的经度,设B 点在东经α,∵A 、B 两点的球面距离是π3R .∴∠AOB =π3,因此三角形AOB 是等边三角形,∴AB =R ,又∵∠AO 1B =α-20°(经度差)问题转化为在△AO 1B 中借助AO 1=BO 1=AO cos45°=22R ,求出∠AO 1B =90°,则α=110°,同理:B 点也可在西经70°,即B 点在北纬45°东经110°或西经70°.14.在球心同侧有相距9cm 的两个平行截面,它们的面积分别为49πcm 2和400πcm 2,求球的表面积和体积.解析:如图,两平行截面被球大圆所在平面截得的交线分别为AO 1、BO 2,则AO 1∥BO 2. 若O 1、O 2分别为两截面圆的圆心,则由等腰三角形性质易知OO 1⊥AO 1,OO 2⊥BO 2, 设球半径为R ,∵πO 2B 2=49π, ∴O 2B =7cm ,同理O 1A =20cm. 设OO 1=x cm ,则OO 2=(x +9)cm. 在Rt △OO 1A 中,R 2=x 2+202, 在Rt △OO 2B 中,R 2=(x +9)2+72, ∴x 2+202=72+(x +9)2,解得x =15cm. ∴R =25cm ,∴S 球=2500πcm 2,V 球=43πR 3=625003πcm 3.15.设A 、B 、C 是半径为1的球面上的三点,B 、C 两点间的球面距离为π3,点A 与B 、C 两点间的球面距离均为π2,O 为球心,求:(1)∠AOB 、∠BOC 的大小; (2)球心O 到截面ABC 的距离.解析:(1)如图,因为球O 的半径为1,B 、C 两点间的球面距离为π3,点A 与B 、C 两点间的球面距离均为π2,所以∠BOC =π3,∠AOB =∠AOC =π2, (2)因为BC =1,AC =AB =2,所以由余弦定理得cos ∠BAC =34,sin ∠BAC =74,设截面圆的圆心为O 1,连结AO 1,则截面圆的半径r =AO 1,由正弦定理得r =BC 2sin ∠BAC=277,所以OO 1=OA 2-r 2=217.16.如图四棱锥A -BCDE 中,AD ⊥底面BCDE ,AC ⊥BC ,AE ⊥BE . (1)求证:A 、B 、C 、D 、E 五点共球; (2)若∠CBE =90°,CE =3,AD =1,求B 、D 两点的球面距离. 解析:(1)证明:取AB 的中点P ,连结PE ,PC ,PD ,由题设条件知△AEB 、△ADB 、△ABC 都是直角三角形.故PE =PD =PC =12AB =P A =PB .所以A 、B 、C 、D 、E 五点在同一球面上. (2)解:由题意知四边形BCDE 为矩形, 所以BD =CE =3,在Rt △ADB 中,AB =2,AD =1,∴∠DPB =120°,D 、B 的球面距离为23π.17.(本小题满分10分)如图,四棱锥S —ABCD 的底面是正方形,SA ⊥底面ABCD ,E 是SC 上一点.(1)求证:平面EBD ⊥平面SAC ;(2)假设SA =4,AB =2,求点A 到平面SBD 的距离;解析:(1)∵正方形ABCD ,∴BD ⊥AC ,又∵SA ⊥平面ABCD ,∴SA ⊥BD ,则BD ⊥平面SAC ,又BD ⊂平面BED ,∴平面BED ⊥平面SAC .(2)设AC ∩BD =O ,由三垂线定理得BD ⊥SO .AO =12AC =122AB =12·2·2=2,SA =4,则SO =SA 2+AO 2=16+2=32,S △BSD =12BD ·SO =12·22·32=6.设A 到面BSD 的距离为h ,则V S -ABD =V A -BSD ,即13S △ABD ·SA =13S △BSD ·h ,解得h =43,即点A 到平面SBD 的距离为43. 18.(本小题满分12分)如图,正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2AB =4,点E 在C 1C 上且C 1E =3EC .(1)证明A 1C ⊥平面BED ;(2)求二面角A 1-DE -B 的大小. 解析:依题设知AB =2,CE =1,(1)证明:连结AC 交BD 于点F ,则BD ⊥AC . 由三垂线定理知,BD ⊥A 1C .在平面A 1CA 内,连结EF 交A 1C 于点G ,由于AA 1FC =AC CE=22,故Rt △A 1AC ∽Rt △FCE ,∠AA 1C =∠CFE ,∠CFE 与∠FCA 1互余. 于是A 1C ⊥EF .A 1C 与平面BED 内两条相交直线BD 、EF 都垂直. 所以A 1C ⊥平面BED .(2)作GH ⊥DE ,垂足为H ,连结A 1H . 由三垂线定理知A 1H ⊥DE ,故∠A 1HG 是二面角A 1-DE -B 的平面角. EF =CF 2+CE 2=3,CG =CE ×CF EF =23.EG =CE 2-CG 2=33.EG EF =13,GH =13×EF ×FD DE =215. 又A 1C =AA 21+AC 2=26,A 1G =A 1C -CG =563, tan ∠A 1HG =A 1GHG=5 5.所以二面角A 1-DE -B 的大小为arctan5 5.19.(本小题满分12分)如图,四棱锥S -ABCD 的底面是直角梯形,∠ABC =∠BCD =90°,AB =BC =SB =SC =2CD =2,侧面SBC ⊥底面ABCD .(1)由SA 的中点E 作底面的垂线EH ,试确定垂足H 的位置; (2)求二面角E -BC -A 的大小.解析:(1)作SO ⊥BC 于O ,则SO ⊂平面SBC , 又面SBC ⊥底面ABCD , 面SBC ∩面ABCD =BC , ∴SO ⊥底面ABCD ①又SO ⊂平面SAO ,∴面SAO ⊥底面ABCD , 作EH ⊥AO ,∴EH ⊥底面ABCD ② 即H 为垂足,由①②知,EH ∥SO , 又E 为SA 的中点,∴H 是AO 的中点. (2)过H 作HF ⊥BC 于F ,连结EF , 由(1)知EH ⊥平面ABCD ,∴EH ⊥BC ,又EH ∩HF =H ,∴BC ⊥平面EFH ,∴BC ⊥EF ,∴∠HFE 为面EBC 和底面ABCD 所成二面角的平面角. 在等边三角形SBC 中,∵SO ⊥BC , ∴O 为BC 中点,又BC =2.∴SO =22-12=3,EH =12SO =32,又HF =12AB =1,∴在Rt △EHF 中,tan ∠HFE =EH HF =321=32,∴∠HFE =arctan 32.即二面角E -BC -A 的大小为arctan 32.20.(本小题满分12分)(2010·唐山市高三摸底考试)如图,在正四棱柱ABCD -A 1B 1C 1D 1中,AB =1,AA 1=2,N 是A 1D 的中点,M ∈BB 1,异面直线MN 与A 1A 所成的角为90°.(1)求证:点M 是BB 1的中点;(2)求直线MN 与平面ADD 1A 1所成角的大小;(3)求二面角A -MN -A 1的大小.解析:(1)取AA 1的中点P ,连结PM ,PN .∵N 是A 1D 的中点,∴AA 1⊥PN ,又∵AA 1⊥MN ,MN ∩PN =N , ∴AA 1⊥面PMN .∵PM ⊂面PMN ,∴AA 1⊥PM ,∴PM ∥AB , ∴点M 是BB 1的中点.(2)由(1)知∠PNM 即为MN 与平面ADD 1A 1所成的角.在Rt △PMN 中,易知PM =1,PN =12,∴tan ∠PNM =PMPN=2,∠PNM =arctan2.故MN 与平面ADD 1A 1所成的角为arctan2.(3)∵N 是A 1D 的中点,M 是BB 1的中点,∴A 1N =AN ,A 1M =AM , 又MN 为公共边,∴△A 1MN ≌△AMN .在△AMN 中,作AG ⊥MN 交MN 于G ,连结A 1G ,则∠A 1GA 即为二面角A -MN -A 1的平面角.在△A 1GA 中,AA 1=2,A 1G =GA =305,∴cos ∠A 1GA =A 1G 2+GA 2-AA 212A 1G ·GA =-23,∴∠A 1GA =arccos(-23),故二面角A -MN -A 1的大小为arccos(-23).21.(2009·安徽,18)(本小题满分12分)如图所示,四棱锥F -ABCD 的底面ABCD 是菱形,其对角线AC =2,BD = 2.AE 、CF 都与平面ABCD 垂直,AE =1,CF =2.(1)求二面角B -AF -D 的大小;(2)求四棱锥E -ABCD 与四棱锥F -ABCD 公共部分的体积. 命题意图:本题考查空间位置关系,二面角平面角的作法以及空间几何体的体积计算等知识.考查利用综合法或向量法解决立体几何问题的能力.解答:(1)解:连接AC 、BD 交于菱形的中心O ,过O 作OG ⊥AF ,G 为垂足,连接BG 、DG .由BD ⊥AC ,BD ⊥CF 得BD ⊥平面ACF ,故BD ⊥AF .于是AF ⊥平面BGD ,所以BG ⊥AF ,DG ⊥AF ,∠BGD 为二面角B -AF -D 的平面角.由FC ⊥AC ,FC =AC =2,得∠F AC =π4,OG =22.由OB ⊥OG ,OB =OD =22,得∠BGD =2∠BGO =π2.(2)解:连接EB 、EC 、ED ,设直线AF 与直线CE 相交于点H ,则四棱锥E -ABCD 与四棱锥F -ABCD 的公共部分为四棱锥H -ABCD .过H 作HP ⊥平面ABCD ,P 为垂足. 因为EA ⊥平面ABCD ,FC ⊥平面ABCD ,所以平面ACEF ⊥平面ABCD ,从而P ∈AC ,HP ⊥AC . 由HP CF +HP AE =AP AC +PC AC =1,得HP =23. 又因为S 菱形ABCD =12AC ·BD =2,故四棱锥H -ABCD 的体积V =13S 菱形ABCD ·HP =229.22.(2009·深圳调考一)(本小题满分12分)如图所示,AB 为圆O 的直径,点E 、F 在圆O 上,AB ∥EF ,矩形ABCD 所在平面和圆O 所在的平面互相垂直.已知AB =2,EF =1.(1)求证:平面DAF ⊥平面CBF ;(2)求直线AB 与平面CBF 所成角的大小;(3)当AD 的长为何值时,二面角D -FE -B 的大小为60°? 解析:(1)证明:∵平面ABCD ⊥平面ABEF ,CB ⊥AB , 平面ABCD ∩平面ABEF =AB , ∴CB ⊥平面ABEF .∵AF ⊂平面ABEF ,∴AF ⊥CB , 又∵AB 为圆O 的直径,∴AF ⊥BF , ∴AF ⊥平面CBF .∵AF ⊂平面DAF ,∴平面DAF ⊥平面CBF . (2)解:根据(1)的证明,有AF ⊥平面CBF , ∴FB 为AB 在平面CBF 上的射影,因此,∠ABF 为直线AB 与平面CBF 所成的角. ∵AB ∥EF ,∴四边形ABEF 为等腰梯形, 过点F 作FH ⊥AB ,交AB 于H .AB =2,EF =1,则AH =AB -EF 2=12.在Rt △AFB 中,根据射影定理AF 2=AH ·AB ,得AF =1,sin ∠ABF =AF AB =12,∴∠ABF =30°,∴直线AB 与平面CBF 所成角的大小为30°.(3)解:过点A 作AM ⊥EF ,交EF 的延长线于点M ,连结DM . 根据(1)的证明,DA ⊥平面ABEF ,则DM ⊥EF , ∴∠DMA 为二面角D -FE -B 的平面角, ∠DMA =60°.在Rt △AFH 中,∵AH =12,AF =1,∴FH =32. 又∵四边形AMFH 为矩形,∴MA =FH =32. ∵AD =MA ·tan ∠DMA =32·3=32. 因此,当AD 的长为32时,二面角D -FE -B 的大小为60°.。
立体几何测试题

高一数学必修2立体几何测试题试卷满分:150分 考试时间:120分钟第Ⅰ卷一、选择题(每小题5分,共60分)1、下列说法正确的是 ( )A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点2.有一个几何体的三视图如下图所示, 这个几何体应是一个( )A 、棱台B 、棱锥C 、棱柱D 、都不对 3、在正方体1111ABC D A B C D -中,下列几种说法正确的是 A 、11A C AD ⊥ B 、11D C AB ⊥ C 、1AC 与D C 成45 角 D 、11A C 与1B C 成60 角 4、正三棱锥ABCS—的侧棱长和底面边长相等, 如果E 、F 分别为SC ,AB 的中点,那么异面直线EF 与SA 所成角为 ( ) A .090 B .060 C .045 5、下列命题中:正确的个数有 ( ) (1)、平行于同一直线的两个平面平行; (2)、平行于同一平面的两个平面平行; (3)、垂直于同一直线的两直线平行; (4)、垂直于同一平面的两直线平行.A 、1B 、2C 、3D 、46、一个水平放置的平面图形的斜二测直观图是一个底角为45,腰和上底边均为1的等腰梯形,则这个平面图形的面积是 ( )A. 2221+B. 22+C. 21+D.221+7、设a 、b 是两条不同的直线,α、β是两个不同的平面,则下列四个命题:①若b a ⊥,α⊥a ,α⊄b ,则α//b ;②若α//a , βα⊥,则β⊥a ; ③若β⊥a ,βα⊥,则α//a 或α⊂a ;④若b a ⊥,α⊥a ,β⊥b ,则βα⊥ 其中A .0 B .1 C .2 D .3B 1C 1A 1D 1BACD8、给出下列关于互不相同的直线 和平面 的四个命题: (1),,,m A A l m ∉=⊂点αα 则l 与m 不共面;(2)l 、m 是异面直线,ααα⊥⊥⊥n m n l n m l 则且,,,//,//; (3)若m l m l //,//,//,//则βαβα;(4)若ββαα//,//,,,m l A m l m l 点=⊂⊂ ,则βα//,其中为错误的命题是( )个. A.1个 B.2个 C.3个 D.4个9、下列各图是正方体或正四面体,P ,Q ,R ,S 分别是所在棱的中点,这四个点中不共面的一个图是PPRSSPRRSSPPPQRSSP P QRRSSA 、B 、C 、D 、10、在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是A 、23 B 、76 C 、45 D 、56 11、 已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧且相距是1,那么这个球的半径是( )A.4B.3C.2D.512、如图:直三棱柱ABC —A 1B 1C 1的体积为V ,点P 、Q 分别在侧棱AA 1和CC 1上,AP=C 1Q ,则四棱锥B —APQC 的体积为A 、2V B 、3V C 、4V D 、5V二、填空题(每小题4分,共16分)13、等体积的球和正方体,它们的表面积的大小关系是S 球_____S 正方体(填”大于、小于或等于”).14、正方体1111ABC D A B C D -中,平面11A B D 和平面1B C D 的位置关系为 15、已知P A 垂直平行四边形A B C D 所在平面,若PC BD ⊥,平行则四边形A B C D 一定是 .16、如图,在直四棱柱A 1B 1C 1 D 1-ABCD 中,当底面四边形ABCD 满足条件_________时,有A 1 B ⊥B 1 D 1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)QPC'B'A'CBAH G FE DBACSDCBA高一数学必修2立体几何测试题第Ⅱ卷一、选择题:1---5___________, 6------10__________, 11---12________二、填空题:13、__________ 14、_____________ 15、__________ 16、___________ 三、简答题:17、已知E 、F 、G 、H 为空间四边形ABCD 的边AB ,BC ,CD ,DA 上的点,且EH ∥FG 。
高一数学必修2立体几何精选30题
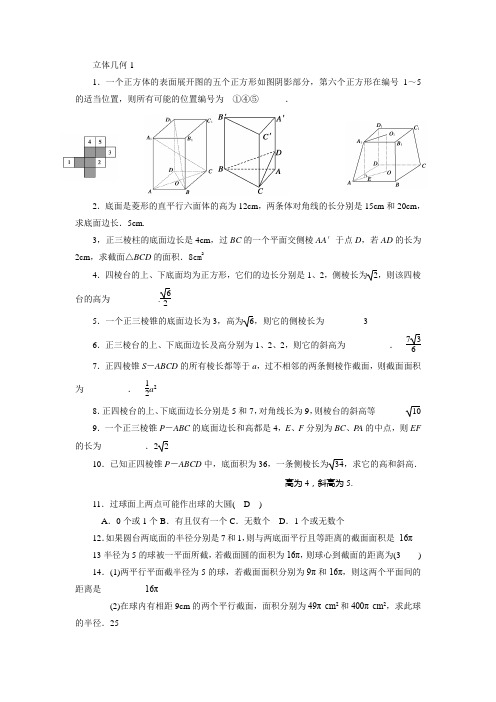
立体几何11.一个正方体的表面展开图的五个正方形如图阴影部分,第六个正方形在编号1~5的适当位置,则所有可能的位置编号为__①④⑤______.2.底面是菱形的直平行六面体的高为12cm ,两条体对角线的长分别是15cm 和20cm ,求底面边长.5cm.3,正三棱柱的底面边长是4cm ,过BC 的一个平面交侧棱AA ′于点D ,若AD 的长为2cm ,求截面△BCD 的面积.8cm 24.四棱台的上、下底面均为正方形,它们的边长分别是1、2,侧棱长为2,则该四棱台的高为_______ .62 5.一个正三棱锥的底面边长为3,高为6,则它的侧棱长为______ 36.正三棱台的上、下底面边长及高分别为1、2、2,则它的斜高为__________. 7367.正四棱锥S -ABCD 的所有棱长都等于a ,过不相邻的两条侧棱作截面,则截面面积为__________. 12a 2 8.正四棱台的上、下底面边长分别是5和7,对角线长为9,则棱台的斜高等_______109.一个正三棱锥P -ABC 的底面边长和高都是4,E 、F 分别为BC 、P A 的中点,则EF 的长为__________.2 210.已知正四棱锥P -ABCD 中,底面积为36,一条侧棱长为34,求它的高和斜高.高为4,斜高为5.11.过球面上两点可能作出球的大圆( D )A .0个或1个B .有且仅有一个C .无数个D .1个或无数个12.如果圆台两底面的半径分别是7和1,则与两底面平行且等距离的截面面积是_16π__ 13半径为5的球被一平面所截,若截面圆的面积为16π,则球心到截面的距离为(3 )14.(1)两平行平面截半径为5的球,若截面面积分别为9π和16π,则这两个平面间的距离是__________16π(2)在球内有相距9cm 的两个平行截面,面积分别为49π cm 2和400π cm 2,求此球的半径.2515.已知圆柱的底面半径是20cm ,高是15cm ,则平行于圆柱的轴且与此轴相距12cm的截面面积是________.480cm 216过球半径的中点,作一垂直于这个半径的截面,截面面积为48πcm 2,则球的半径为________.8cm17.一个圆台的母线长为12cm ,两底面的面积分别为4π cm 2和25π cm 2,求:(1)圆台的高315;(2)截得此圆台的圆锥的母线长.20(18.圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392cm 2,母线与轴的夹角是45°,求这个圆台的高、母线长和两底面半径.7cm 、21cm. 14 2 1419.水平放置的△ABC 的斜二测直观图如图所示,已知A ′C ′=3,B ′C ′=2,则AB 边上的中线的实际长度 52_____.20.如图,正方形O ′A ′B ′C ′的边长为a cm(a >0),它是一个水平放置的平面图形的直观图,则它的原图形OABC 的周长是_8a _________21.如图是一个空间几何体的三视图,该几何体是________.表面积 体积公式,,,,22.圆台的母线长是3cm ,侧面展开后所得扇环的圆心角为180°,侧面积为10πcm 2,则圆台的高为________,上、下底面半径分别为________、________.332cm 1112cm 2912cm 23.圆台的上、下底面半径分别是10cm 和20cm ,它的侧面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?1100π24.一个正四面体的所有棱长都为2,四个顶点在同一球面上,求此球的表面积.3π. 25,正六棱台的斜高为33cm ,两底面边长的差为10cm ,全面积为4803cm 2,求两底面的边长.上底面边长为4cm ,下底面边长为14cm26.一个圆柱的高缩小为原来的1n,底面半径扩大为原来的n 倍,则所得的圆柱的体积为原来的________.n 倍27.已知ABCD -A 1B 1C 1D 1是棱长为a 的正方体,E 、F 分别为棱AA 1与CC 1的中点,求四棱锥A 1-EBFD 1的体积 a 36. 28.求棱长都为a 的正四棱锥的体积26a 329,棱台的上底面积为16,下底面积为64,求棱台被它的中截面分成的上、下两部分体积之比.8:27:6430.正方体内切球和外接球的半径比和体积比________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
A
1
P
1一 :选择题(4分10⨯题)
1.下面四个条件中,能确定一个平面的条件是( )
A . 空间任意三点 B.空间两条直线 C.空间两条平行直线 D.一条直线和一个点
2.1l ,2l ,3l 是空间三条不同的直线,则下列命题正确的是( ).
A.12l l ⊥,23l l ⊥13//l l ⇒
ﻩ
B.12l l ⊥,23//l l ⇒13l l ⊥
C.233////l l l ⇒1l ,2l ,3l 共面ﻩ ﻩ
D.1l ,2l ,3l 共点⇒1l ,2l ,3l 共面
3.已知m,n是两条不同的直线,,,αβγ是三个不同的平面,下列命题中正确的是:
A.若,αγβγ⊥⊥,则α∥β B.若,m n αα⊥⊥,则m ∥n C .若m ∥α,n ∥α,则m ∥n D .若m ∥α,m ∥β,则α∥β 4.在四面体ABC P -的四个面中,是直角三角形的面至多有( )
A .0 个 B.1个 C. 3个 D .4个 5,下列命题中错误..的是ﻩﻩ
A .如果平面αβ⊥平面,那么平面α内一定存在直线平行于平面β
ﻩB.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
C .如果平面αγ⊥平面,平面βγ⊥平面,l =βα ,那么l γ⊥平面
ﻩD.如果平面αβ⊥平面,那么平面α内所有直线都垂直于平面β 6.如图所示正方体1AC ,下面结论错误的是( ) A. 11//D CB BD 平面 B . BD AC ⊥1
C . 111
D CB AC 平面⊥ D . 异面直线1CB AD 与角为︒
60
7.已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角是( )
A. ︒120 B. ︒150 C. ︒180 D . ︒
240
8.把正方形ABCD 沿对角线BD 折成直二面角后,下列命题正确的是( )
A. BC AB ⊥ B . BD AC ⊥ C . ABC CD 平面⊥ D . ACD ABC 平面平面⊥ 9某几何体的三视图如图所示,则该几何体的表面积为( )
.A 180 .B 200 .C 220 .D 240
左视图
10.如图所示点P 为三棱柱111C B A ABC -侧棱1AA 上一动点,若四棱锥11B BCC P -的体积为V ,则三棱柱111C B A ABC -的体积为( ) A .V 2 B. V 3 C.
3
4V
D. 23V
二.填空题(5分4⨯题)
11.如图所示正方形''''C B A O 的边长为2c m, 它是一个水平放置的一个平面图形的直观图,
则原图形的周长是______, 面积是_________.
12.已知l m , 是直线,βα,是平面,给出下列命题正确的是________________. (1)若l 垂直于α内的两条相交直线,则α⊥l (2)若l 平行于α,则l 平行于α内所有直线; (3) ;则且βαβα⊥⊥⊂⊂,,,m l l m (4) ;则且若βααβ⊥⊥⊂,,l l (5) αβα且,,⊂⊂l m //m ,则β//l .
13.三棱锥P-ABC 中,P A,PB,P C两两垂直,PA=1,2=
=PC PB ,已知空间中有一
个点到这四个点距离相等,则这个距离是 ___________.
14.一正方体内接于一个球,经过球心作一个截面,则截面的可能图形为________(只填写序号).
三.解答题
15.已知圆台的上下底面半径分别为2,6,且侧面面积等于两底面面积之和,求该圆台的母线长,侧面积及体积.
16. 已知四棱锥ABCD P -的三视图如下:
1)画出四棱锥ABCD P -的直观图 2)求四棱锥ABCD P -的体积; 3求四棱锥ABCD P -的表面积;
B
17.如图,已知O PA 圆⊥所在的平面,AB 是O 圆的直径,2=AB ,O C 是圆上的一点,且
BC AC =,角所在的平面成与圆 45O PC ,PC E 是中点,PB F 为的中点.
(1)求证:EF //面ABC ; (2)求证:PAC EF 面⊥; (3)求三棱锥PAC B -的体积
18,如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点.
求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.
19. 如图1,在Rt ABC ∆中,90C ∠=,,D E 分别为
,AC AB 的中点,点F 为线段CD 上的一点,将ADE ∆沿
DE 折起到1A DE ∆的位置,使1A F CD ⊥,如图2。
(Ⅰ)求证://DE 平面1A CB ; (Ⅱ)求证:1A F BE ⊥;
(Ⅲ)线段1A B 上是否存在点Q ,使1
AC ⊥平面DEQ ?说明理由。
A B C
S
G F E 图2
图1
F
高一立体几何测试答案
一:1-5;C BB DD 6-10;DCBDD
二:11._16cm_; 82
2cm ____12._1,4____13.
2
5
; 14. ①②③ 15.母线长为5,侧面积为40π,高为3,体积为52π.
16.(1)
(2)由直观图可知此空间几何体为四棱锥,由正视图可知高为2, 所以3
22)11(31=⨯⨯=
-ABCD P V (3)由题意可知是直角三角形,PCB PCD ∆∆, 由勾股定理逆定理可知是直角三角形,PAD PAB ∆∆,
所以.53)512
1
()5121()
212
1
()2121()11(+=⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯=++++=PAD PAB PCB PCD ABCD S S S S S S 表
3
2
2)2221(31)(31,2,2)3(.
,//,,;,,;
)2(.
//,,//)1.(17=
⨯⨯⨯=⨯=∴===-∴⊥⊥∴⊥∴=⊥∴⊂⊥⊥∴⊂⊄∆∆-BC S V PA BC AC PAC B BC PAC BC PAC EF EF BC PAC BC C CA BC BC PA ACB BC ACB PA CA BC O AB ABC EF ABC BC ABC EF BC EF EF PBC PAC PAC B 的高;是三棱锥面问知由第面又面面面的直径,是圆平面所以平面平面为中位线,所以中,证明:在 18.证:(1)
SA BA =,AF SB ⊥,SF BF ∴=,由题SE EA =,//EF AB ∴,EF ⊄平面
ABC AB ⊂平面ABC ,//EF ∴平面ABC ,同理//EG 平面ABC ,EF 与EG 为平面EFG 内的
两条相交直线,∴平面//EFG 平面ABC , (2)
平面⊥SAB 平面SBC 于SB ,AF ⊂平面SAB ,AF ∴⊥平面SBC ,AF BC ∴⊥,
又BC AB ⊥且AB 与AF 为平面SAB 内的两条相交直线,BC SA ∴⊥。
19.(1)因为D,E分别为AC,AB的中点,所以DE∥BC.又因为DE⊄平面A1CB,所以DE∥平面A1CB. (2)由已知得AC⊥BC且DE∥BC,所以DE⊥AC.所以DE⊥A1D,DE⊥CD.所以DE⊥平面A1DC.而A1F ⊂平面A1DC,
所以DE⊥A1F.又因为A1F⊥CD,所以A1F⊥平面BCDE.所以A1F⊥BE
(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如图,
分别取A1C,A1B的中点P,Q,则PQ∥BC.
又因为DE∥BC,所以DE∥PQ.所以平面DEQ即为平面DEP.
由(2)知DE⊥平面A1DC,所以DE⊥A1C.
又因为P是等腰三角形DA1C底边A1C的中点,
所以A1C⊥DP,所以A1C⊥平面DEP,从而A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.。
