【决赛】2014年迎春杯六年级试卷

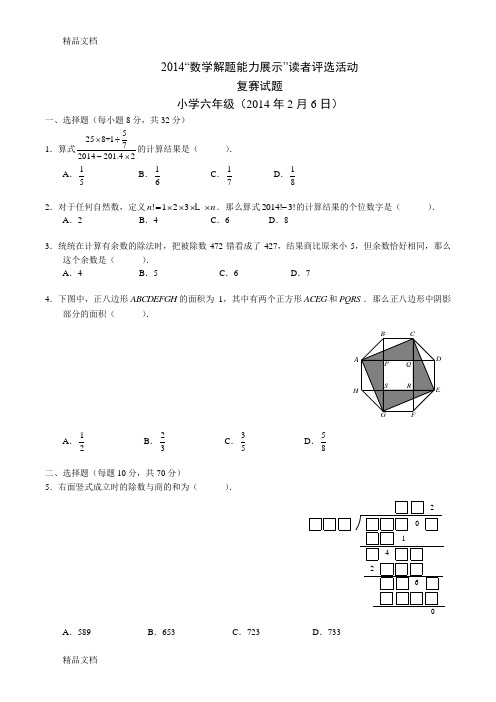
2014“数学解题能力展示”读者评选活动复赛试题小学六年级一、选择题（每小题8分，共32分）1．算式5258+172014201.42⨯÷-⨯的计算结果是（ ）．A ．15B ．16C ．17D ．182．对于任何自然数，定义!123n n =⨯⨯⨯⨯L ．那么算式2014!3!-的计算结果的个位数字是（ ）．A ．2B ．4C ．6D ．83．统统在计算有余数的除法时，把被除数472错看成了427，结果商比原来小5，但余数恰好相同，那么这个余数是（ ）．A ．4B ．5C ．6D ．74．下图中，正八边形ABCDEFGH 的面积为1，其中有两个正方形ACEG 和PQRS ．那么正八边形中阴影部分的面积（ ）．H AA ．12B ．23C ．35D ．58二、选择题（每题10分，共70分）5．右面竖式成立时的除数与商的和为（ ）．12642A ．589B ．653C ．723D ．736．甲乙丙三人进行一场特殊的真人CS 比赛，规定：第一枪由乙射出，射击甲或者丙，以后的射击过程中，若甲被击中一次，则甲可以有6发子弹射击乙或丙，若乙被击中一次，则乙可以有5发子弹射击甲或丙，若丙被击中一次，则丙可以有4发子弹射击甲或乙，比赛结束后，共有16发子弹没有击中任何人？则甲乙丙三人被击中的次数有（ ）种不同的情况． A ．1 B ．2 C ．3 D ．47．甲乙二人进行下面的游戏．二人先约定一个整数N ，然后由甲开始，轮流把1，2，3，4，5，6，7，8，9这九个数字之一填入下面任一方格中：□□□□□□，每一方格只填入一个数字，形成一个数字可以重复的六位数．若这个六位数能被N 整除，乙胜；否则甲胜．当N 小于15时，使得乙有必胜策略的N 有（ ）．A ．5B ．6C ．7D ．88．在纸上任意写一个自然数，把这张纸旋转180度，数值不变，如0、11、96、888等，我们把这样的数称为“神马数”．在所有五位数中共有（ ）个不同的“神马数”． A ．12 B ．36 C ．48 D ．609．如图，第（1）个多边形由正三角形“扩展”而来，边数记为3a ，第（2）个多边形由正方形“扩展”而来，边数记为4a ，……，依此类推，由正n 边形“扩展”而来的多边形的边数记为n a （3n ≥ ），则34511112014++++6051n a a a a =L ，那么n =（ ）．(4)(3)(2)(1)A ．2014B ．2015C ．2016D ．201710．如右图所示，五边形ABCDEF 面积是2014平方厘米，BC 与CE 垂直于C 点，EF 与CE 垂直于E 点，四边形ABDF 是正方形，:3:2CD DE =．那么，三角形ACE 的面积是 （ ）平方厘米．FECB AA ．1325B ．1400C ．1475D ．150011．甲乙两车分别从A、B两地同时出发，相向而行，甲车的速度大于乙车．甲行驶了60千米后和乙车在C点相遇．此后甲车继续向前行驶，乙车掉头与甲车同向行驶．那么当甲车到达B地时，甲乙两车最远相距（）千米．A．10 B．15 C．25 D．30三、选择题（每题12分，共48分）12．在“爸爸去哪儿”的节目中有一个任务，五个参加任务的孩子（天天、石头、Kimi、Cindy、Angela）需要换爸爸（每个小朋友可以选择除了自己爸爸之外其他四位父亲中的任何一位），那么最终五人有（）种不同的选择结果．A．40 B．44 C．48 D．5213．老师在黑板上从1开始将奇数连续地写下去，写了一长串数后，擦去了其中的两个数，将这些奇数隔成了3串，已知第二串比第一串多1个数，第三串比第二串多1个数，且第三串奇数和为4147，那么被划去的两个奇数的和是（）．A．188 B．178 C．168 D．15814．从一张大方格纸上剪下5个相连的方格（只有一个公共顶点的两个方格不算相连），要使剪下的图形可折叠为一个无盖的正方体，则共可以剪出（）种不同的图形（经过旋转或翻转相同的图形市委同一种）．A．8 B．9 C．10 D．1115．老师把某个两位数的六个不同约数分别告诉了A F:六个聪明诚实的同学．A和B同时说：“我知道这个数是多少了．”C和D同时说：“听了他们两人的话，我也知道这个两位数是多少了．”E：“听了他们的话，我知道我的数一定比F的大．”F：“我拿的数的大小在C和D之间．”那么六个人拿的数之和是（）A．141 B．152 C．171 D．1752014“数学解题能力展示”读者评选活动复赛试题小学六年级参考答案部分解析一、选择题（每小题8分，共32分）1．算式5258+172014201.42⨯÷-⨯的计算结果是（）．A．15B．16C．17D．18【考点】计算【难度】☆☆【答案】D【解析】5258+1200 1.4201.41 72014201.42201.410201.42201.488⨯÷+=== -⨯⨯-⨯⨯2．对于任何自然数，定义!123n n=⨯⨯⨯⨯L．那么算式2014!3!-的计算结果的个位数字是（）．A．2 B．4 C．6 D．8【考点】定义新运算【难度】☆☆【答案】B【解析】2014!个位数字是0，3!1236=⨯⨯=，所以2014!3!-个位是4．3．童童在计算有余数的除法时，把被除数472错看成了427，结果商比原来小5，但余数恰好相同，那么这个余数是（）．A．4 B．5 C．6 D．7【考点】整除同余【难度】☆☆【答案】A【解析】除数=(472427)59-÷=，4724(mod9)≡，所以余数是4．4．下图中，正八边形ABCDEFGH 的面积为1，其中有两个正方形ACEG 和PQRS ．那么正八边形中阴影部分的面积（ ）．H AA ．12B ．23C ．35D ．58【考点】几何 【难度】☆☆☆ 【答案】A【解析】等积变形．H AAH H A所以刚好各占一半．二、选择题（每题10分，共70分）5．右面竖式成立时的除数与商的和为（ ）．12642A ．589B ．653C ．723D ．733 【考点】数字谜 【难度】☆☆☆ 【答案】C【解析】首先根据倒数第三行可以确定0A =，4B =；241ECB A 60D22112611322440854815252824160120再根据顺数第三行最后一位为1可以确定，第一行D 和C 的取值为（1，1）或（3，7）或（9，9）或（7，3），根据尝试只有（1，1）符合题意．再依次进行推理，可得商和除数分别为：142和581．6．甲乙丙三人进行一场特殊的真人CS 比赛，规定：第一枪由乙射出，射击甲或者丙，以后的射击过程中，若甲被击中一次，则甲可以有6发子弹射击乙或丙，若乙被击中一次，则乙可以有5发子弹射击甲或丙，若丙被击中一次，则丙可以有4发子弹射击甲或乙，比赛结束后，共有16发子弹没有击中任何人？则甲乙丙三人被击中的次数有（ ）种不同的情况． A ．1 B ．2 C ．3 D ．4 【考点】不定方程 【难度】☆☆☆ 【答案】B【解析】设甲乙丙分别被击中x 、y 、z 次则三人分别发射6x 、51y +，4z 次[6(51)4]()16x y z x y z +++-++=化简得54315x y z ++=7．甲乙二人进行下面的游戏．二人先约定一个整数N ，然后由甲开始，轮流把1，2，3，4，5，6，7，8，9这九个数字之一填入下面任一方格中：□□□□□□，每一方格只填入一个数字，形成一个数字可以重复的六位数．若这个六位数能被N 整除，乙胜；否则甲胜．当N 小于15时，使得乙有必胜策略的N 有（ ）．A ．5B ．6C ．7D ．8 【考点】数论 【难度】☆☆☆ 【答案】B【解析】若N 是偶数，甲只需第一次在个位填个奇数，乙必败只需考虑N 是奇数．1N =，显然乙必胜．39N =，，乙只需配数字和1-8，2-7，3-6，4-5，9-9即可．5N =，甲在个位填不是5的数，乙必败．71113N =，，，乙只需配成100171113abcabc abc abc =⨯=⨯⨯⨯．8．在纸上任意写一个自然数，把这张纸旋转180度，数值不变，如0、11、96、888等，我们把这样的数称为“神马数”．在所有五位数中共有（ ）个不同的“神马数”． A ．12 B ．36 C ．48 D ．60 【考点】数论 【难度】☆☆☆ 【答案】D【解析】设这个数为ABCBA ，A 位可以填11,88,69,96，4种情况，B 位可以填00,11,88,69,96，5种情况，C 位可以填0,1,8，3种情况，453=60⨯⨯（个）．9．如图，第（1）个多边形由正三角形“扩展”而来，边数记为3a ，第（2）个多边形由正方形“扩展”而来，边数记为4a ，……，依此类推，由正n 边形“扩展”而来的多边形的边数记为n a （3n ≥ ），则34511112014++++6051n a a a a =L ，那么n =（ ）．(4)(3)(2)(1)A ．2014B ．2015C ．2016D ．2017 【考点】找规律 【难度】☆☆☆ 【答案】C【解析】33(22)34a =⨯+=⨯，44(23)45a =⨯+=⨯，55(24)56a =⨯+=⨯，……(21)(1)n a n n n n =⨯+-=+ ，34511111111120143445(1)316051n a a a a n n n ++++=+++=-=⨯⨯⨯++L L ，12017n +=，2016n = ．10．如右图所示，五边形ABCDEF 面积是2014平方厘米，BC 与CE 垂直于C 点，EF 与CE 垂直于E 点，四边形ABDF 是正方形，:3:2CD DE =．那么，三角形ACE 的面积是 （ ）平方厘米．FEDCB AA ．1325B ．1400C ．1475D ．1500 【考点】几何 【难度】☆☆☆ 【答案】A【解析】作正方形ABCD 的“弦图”，如右图所示，IH GFEDCBA假设CD 的长度为3a ，DE 的长度为2a ，那么3BG a =，2DG a =，根据勾股定理可得2222229413BD BG DG a a a =+=+=，所以，正方形ABDF 的面积为213a ；因为CD EF =，BC DE =，所以三角形BCD 和三角形DEF 的面积相等为23a ； 又因为五边形ABCEF 面积是2014平方厘米，所以222136192014a a a +==，解得2106a =， 三角形ACE 的面积为：2255522a a a ⨯÷=，即2510613252⨯=．11．甲乙两车分别从A 、B 两地同时出发，相向而行，甲车的速度大于乙车．甲行驶了60千米后和乙车在C 点相遇．此后甲车继续向前行驶，乙车掉头与甲车同向行驶．那么当甲车到达B 地时，甲乙两车最远相距（ ）千米．A ．10B ．15C ．25D ．30 【考点】行程问题 【难度】☆☆☆ 【答案】A【解析】假设甲走60千米时，乙走了a 千米，甲到达B 地时，乙车应走26060a a a ⨯=千米，此时甲、乙相差最远为1(60)6060a a a a -=⨯-⨯，和一定，差小积大，60a a -=，30a =．甲、乙最远相差900301560-=（千米）．三、选择题（每题12分，共48分）12．在“爸爸去哪儿”的节目中有一个任务，五个参加任务的孩子（天天、石头、Kimi 、Cindy 、Angela ）需要换爸爸（每个小朋友可以选择除了自己爸爸之外其他四位父亲中的任何一位），那么最终五人有（ ）种不同的选择结果．A ．40B ．44C ．48D ．52 【考点】排列组合 【难度】☆☆☆【答案】B【解析】设五个爸爸分别是A B C D E 、、、、，五个孩子分别是a b c d e 、、、、，a 有4种选择，假设a选择B ， 接着让b 选择，有两种可能，选择A 和不选择A ，（1）选择A ，c d e 、、 选择三个人错排，（2）不选择A ，则b c d e 、、、 选择情况同4人错排．所以5434()S S S =⨯+ 同理4323()S S S =⨯+ ，3212()S S S =⨯+，而10S =（不可能排错），21S =，所以32S =，49S =，544S =．13．老师在黑板上从1开始将奇数连续地写下去，写了一长串数后，擦去了其中的两个数，将这些奇数隔成了3串，已知第二串比第一串多1个数，第三串比第二串多1个数，且第三串奇数和为4147，那么被划去的两个奇数的和是（ ）．A ．188B ．178C ．168D ．158 【考点】数论 【难度】☆☆☆ 【答案】C【解析】设第一段有n 个，则第2段有1n +个，第一个擦的奇数是21n +，第二个擦的奇数是45n +，和为66n +，是6的倍数．只有168符合．14．从一张大方格纸上剪下5个相连的方格（只有一个公共顶点的两个方格不算相连），要使剪下的图形可折叠为一个无盖的正方体，则共可以剪出（ ）种不同的图形（经过旋转或翻转相同的图形视为同一种）．A ．8B ．9C ．10D ．11 【考点】立体几何 【难度】☆☆☆ 【答案】A 【解析】如下图15．老师把某个两位数的六个不同约数分别告诉了A F :六个聪明诚实的同学．A 和B 同时说：“我知道这个数是多少了．”C和D同时说：“听了他们两人的话，我也知道这个两位数是多少了．”E：“听了他们的话，我知道我的数一定比F的大．”F：“我拿的数的大小在C和D之间．”那么六个人拿的数之和是（）A．141 B．152 C．171 D．175【考点】数论【难度】☆☆☆☆【答案】A【解析】（1）这个数的因数个数肯定不低于6个（假定这个数为N，且拿到的6个数从大到小分别是A B C D E F、、、、、）（2）有两个人同时第一时间知道结果，这说明以下几个问题：第一种情况：有一个人知道了最后的结果，这个结果是怎么知道的呢？很简单，他拿到的因数在5099:之间（也就是说A的2倍是3位数，所以A其实就是N）第二种情况：有一个人拿到的不是最后结果，但是具备以下条件：1）这个数的约数少于6个，比如：有人拿到36，单他不能断定N究竟是36还是72．2）这个数小于50，不然这个数就只能也是N了．3）这个数大于33，比如：有人拿到29，那么他不能断定N是58还是87；这里有个特例是27，因为272=54⨯，因数个数少于6个，所以如果拿到⨯，因数个数不少于6个；273=8127可以判断N只能为54）4）这个数还不能是是质数，不然不存在含有这个因数的两位数．最关键的是，这两人的数是2倍关系但是上述内容并不完全正确，需要注意还有一些“奇葩”数：17、19、23也能顺利通过第一轮．因此，这两个人拿到的数有如下可能：（54，27）（68，34）（70，35）（76，38）（78，39）（92，46）（98，49）（3）为了对比清晰，我们再来把上面所有的情况的因数都列举出来：（54，27，18，9，6，3，2，1）（68，34，17，4，2，1）（×）（70，35，14，10，7，5，2，1）（76，38，19，4，2，1）（×）（78，39，26，13，6，3，2，1）（92，46，23，4，2，1）（×）（98，49，14，7，2，1）对于第一轮通过的数，我们用红色标注，所以N不能是68、76、92中的任意一个．之后在考虑第二轮需要通过的两个数．用紫色标注的6、3、2、1，因为重复使用，如果出现了也不能判断N是多少，所以不能作为第二轮通过的数．用绿色标注的14和7也不能作为第二轮通过的数，这样N也不是98．那么通过第二轮的数只有黑色的数．所以N只能是54、70、78中的一个．我们再来观察可能满足E和F所说的内容：（54，27，18，9，6，3，2，1）（70，35，14，10，7，5，2，1）（78，39，26，13，6，3，2，1）因为F说他的数在C和D之间，我们发现上面的数据只有当70、(10N=的时候，7F=，在C D和5)之间，是唯一满足条件的一种情况．又因为E确定自己比F的大，那么他拿到的数一定是该组中剩余数里最大的．所以E拿到的是14（70N=）．所以70N=，六个人拿的数之和为：70+35+14+10+7+5=141．。