材力习题集
机械工程材料习题集

机械工程材料习题集第一章材料的性能一、是非题(1)一切材料的硬度越高,其强度也越高。
( )(2)静载荷是指大小不可变的载荷,反之则一定不是静载荷。
( ) (3)所有的金属材料均有明显的屈服现象。
( ) (4)HRC测量方便,能直接从刻度盘上读数。
( )(5)生产中常用于测量退火钢、铸铁及有色金属的硬度方法为布氏硬度法。
( )(6)材料的强度高,其塑性不一定差。
( )(7)材料抵抗小能量多次冲击的能力主要取决于材料的强度。
( )(8)只要零件的工作应力低于材料的屈服强度,材料不会发生塑性变形,更不会断裂。
( )(9)蠕变强度是材料的高温性能指标。
( )(10)断裂韧性是反应材料抵抗裂纹失稳扩展的性能指标。
( )二、选择题(1)机械零件在正常工作情况下多数处于( )。
A.弹性变形状态 B.塑性变形状态 C.刚性状态 D.弹塑性状态(2)下列四种硬度的表示方法中,最恰当的是( )。
A.600~650 HBSB.12~15 HRC C.:170~230 HBS D.80~90 HRC(3)工程上希望材料的屈服比高些,目的在于( )。
A.方便设计 B.便于施工C.提高使用中的安全系数 D.提高材料的有效利用率 (4)ak值小的金属材料表现为( )。
A.塑性差 B.强度差 C.疲劳强度差 D.韧性差 (5) 下面( )不是洛氏硬度法的优点。
A.测量迅速简便 B.压痕小c.适应于成品零件的检测 D.硬度范围的上限比布氏、维氏硬度高(6)国家标准规定,对于钢铁材料进行疲劳强度试验时,取应力循环次数为( ) 所对应的应力作为疲劳强度。
A.10 B.10 C.10 D.10(7)涂层刀具表面硬度宜采用( )法进行测量。
A.布氏硬度(HBS) B.布氏硬度(HBW) C.维氏硬度 D.洛氏硬度三、填空题(1)材料常用的塑性指标有和,其中用 ___ 来表示塑性更接近材料的真实变形。
6789(2)在外力作用下,材料抵抗和的能力称为强度。
汽车材料习题集及答案

汽车材料习题集及答案目录第一章金属材料的力学性能--------------------------------(3)第二章钢铁材料----------------------------------------------------------------(4)第三章有色金属及其合金---------------------------------(8)第四章非金属材料-------------------------------------------------------------(9)第五章汽车零件的选材------------------------------------------------------(11)第六章汽车燃料---------------------------------------------------------------(11)第七章车用润滑油及特种液------------------------------------------------(13)第八章汽车轮胎---------------------------------------------------------------(15)第九章汽车美容材料---------------------------------------------------------(16)习题答案------------------------------------------------------------------------(16)第一章金属材料的力学性能一、名词解释1.金属的使用性能:1.指金属材料在正常使用条件下所具备的性能。
它包括力学、物理、化学三方面的性能2.金属的工艺性能:指机械零件在制造加工过程中,金属材料所具备的性能。
它包括铸造、压力加工、焊接、切削、热处理等加工过程中的性能。
工程材料习题集

工程材料习题集绪论1.一铜棒的最大拉应力为70MPa,若要承受2000kgf的载荷,它的直径是多少?2.有一直径15mm的钢棒所能承受的最大载荷为11800kgf,问它的强度是多少。
3.一根2米长的黄铜棒温度升高80℃,伸长量是多少?要使该棒有同样的伸长,问需要作用多少力?(黄铜线膨胀系数为20×10-6/℃,平均弹性模量为110000MPa)4.一根焊接钢轨在35℃时铺设并固定,因此不能发生收缩。
问当温度下降到9℃时,钢轨内产生的应力有多大?(钢的线膨胀系数为12×10-6/℃,弹性模量为206000MPa)5.零件设计时,选取σ0.2(σS)还是选取σb,应以什么情况为依据?6.δ与ψ这两个指标,哪个能更准确地表达材料的塑性?并说明以下符号的意义和单位:σe;σs(σ0.2);σb;δ;ψ;σ-1;ɑk7.常用的测量硬度的方法有几种?其应用范围如何?8.有一碳钢制支架刚性不足,有人要用热处理强化方法;有人要另选合金钢;有人要改变零件的截面形状来解决。
哪种方法合理?为什么?参考答案:1.18.9mm 2.871MPa 3.3.2mm,176MPa 4.64.3MPa第一章金属的结构与结晶1.金属中常见的晶体结构类型有哪几种?α-Fe、γ-Fe、A1、Cu、Ni、Pb、Cr、V、Mg、Zn 各属何种晶体结构?2.单晶体与多晶体有何差别?为什么单晶体具有各向异性,而多晶体材料通常不表现出各向异性?3.简述金属常见的三种晶体结构的基本特点。
4.晶体缺陷有哪些?对材料有哪些影响?对所有的材料都有影响吗?5. 分别说明以下概念:晶格;晶胞;晶格常数;致密度;配位数;晶面;晶向;单晶体;多晶体;晶粒;晶界;各向异性;同素异构。
6.在立方晶格中,如果晶面指数和晶向指数的数值相同,该晶面与晶向间存在着什么关系?7. 何谓过冷度?为什么结晶需要过冷度?它对结晶后晶粒大小有何影响?8. 何谓同素异构转变?纯铁在常压下有哪几种同素异构体?各具有何种晶体结构?1.金属结晶的基本规律是什么?结晶过程是怎样进行的?2.过冷度与冷却速度有何关系?它对金属结晶后的晶粒大小有何影响?3.如果其它条件相同,试比较在下列条件下,铸件晶粒的大小:(1)砂型铸造与金属铸造;(2)厚壁铸件与薄壁铸件;(3)加变质剂与不加变质剂;(4)浇注时振动与不振动。
建筑材料习题集(习题、答案部分)

第一篇试题第一单元绪论一、名词解释1.技术标准2.建筑结构材料3.建筑功能材料二、填空题1.根据建筑材料的化学成分,建筑材料可分为________、________、________三大类。
2.根据建筑材料在建筑物中的部位或使用功能,大体可分为_ ___、_ __、___三大类。
3.建筑材料的技术标准主要包括_______ 、 _________两方面的内容。
4.我国常用的技术标准有________、________、________、________四级。
5.建筑材料的技术标准的一般表示方法是由_____、______、_______、____四位组成。
6.为组织现代社会化大生产,加强科学管理与使用,建筑材料的生产必须_____、_____。
7.建筑材料的研制与开发,应朝着_____、_____、_____、_______、_____等方向发展。
8.2008年我国水泥产量再创历史新高,达______ ,是美国水泥产量的约______ 倍,遥遥领先其它国家,居世界第一位。
三、单项选择题1.以下哪种材料不属于常用的三大建筑材料()。
A、水泥B、玻璃C、钢材D、木材2.以下不是复合材料的是()。
A、混凝土B、灰砂砖C、铝合金D、三合板3.目前,()是最主要的建筑材料。
A、钢筋混凝土及预应力钢筋混凝土B、建筑塑料C、铝合金材料D、建筑陶瓷四、简答题1.为什么建筑材料大多为复合材料?第二单元建筑材料的基本性质一、名词解释1.材料的空隙率2.材料的堆积密度3.材料的强度4.材料的耐久性二、填空题1.材料的密度是指_ ______,是一_____值,只与材料的组成成分与结构有关。
2.材料的表观密度是指___ _________。
3.材料的吸水性是指材料在________。
对选定的材料而言,吸水率是一______值。
4.材料的吸湿性是指材料在________的性质。
对选定的材料而言,含水率是一_____值,与大气的温、湿度等因素有关。
材力习题集
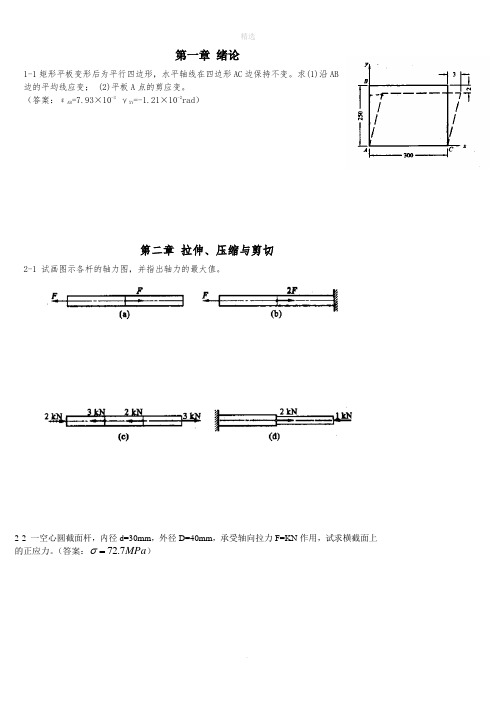
第一章 绪论1-1矩形平板变形后为平行四边形,水平轴线在四边形AC 边保持不变。
求(1)沿AB边的平均线应变; (2)平板A 点的剪应变。
(答案:εAB =7.93×10-3 γXY =-1.21×10-2rad )第二章 拉伸、压缩与剪切2-1 试画图示各杆的轴力图,并指出轴力的最大值。
2-2 一空心圆截面杆,内径d=30mm ,外径D=40mm ,承受轴向拉力F=KN 作用,试求横截面上的正应力。
(答案:MPa 7.72=σ)2-3 题2-1 c 所示杆,若该杆的横截面面积A=502mm ,试计算杆内的最大拉应力与最大压应力(答案:MPa t 60max ,=σ MPa c 40max ,=σ)2.4图示轴向受拉等截面杆,横截面面积A=5002mm ,载荷F=50KN 。
试求图示截面m-m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
(答案:MPa MPa MPa MPa 50 ; 100 ; 24.49 ; 32.41max max ==-==τστσαα)2.5如图所示,杆件受轴向载荷F 作用。
该杆由两根木杆粘接而成,若欲使粘接面上的正应力为其切应力的二倍,则粘接面的方位角θ应为何值(答案: 6.26=θ) 2.6 等直杆受力如图所示,试求各杆段中截面上的轴力,并绘出轴力图。
2.7某材料的应力-应变曲线如图所示,图中还同时画出了低应变去区的详图,试确定材料的弹性模量E 、屈服极限s σ、强度极限b σ、与伸长率δ,并判断该材料属于何种类型(塑性或脆性材料)。
2.8某材料的应力-应变曲线如图所示,试根据该曲线确定: (1)材料的弹性模量E 、比例极限P σ与屈服极限2.0σ; (2)当应力增加到MPa 350=σ时,材料的正应变ε, 以及相应的弹性应变e ε与塑性应变p ε2.9图示桁架,杆1与杆2的横截面均为圆形,直径分别为d1=30mm 与d2=20mm ,两杆材料相同,许用应力[]σ=160MPa ,该桁架在节点A 处承受铅垂方向的载荷F=80KN 作用。
付华-材料性能学-部分习题答案1

第一章材料的弹性变形一、填空题:1.金属材料的力学性能是指在载荷作用下其抵抗变形或断裂的能力。
2. 低碳钢拉伸试验的过程可以分为弹性变形、塑性变形和断裂三个阶段。
3. 线性无定形高聚物的三种力学状态是玻璃态、高弹态、粘流态,它们的基本运动单元相应是链节或侧基、链段、大分子链,它们相应是塑料、橡胶、流动树脂(胶粘剂的使用状态。
二、名词解释1.弹性变形:去除外力,物体恢复原形状。
弹性变形是可逆的2.弹性模量:拉伸时σ=EεE:弹性模量(杨氏模数)切变时τ=GγG:切变模量3.虎克定律:在弹性变形阶段,应力和应变间的关系为线性关系。
4.弹性比功定义:材料在弹性变形过程中吸收变形功的能力,又称为弹性比能或应变比能,表示材料的弹性好坏。
三、简答:1.金属材料、陶瓷、高分子弹性变形的本质。
答:金属和陶瓷材料的弹性变形主要是指其中的原子偏离平衡位置所作的微小的位移,这部分位移在撤除外力后可以恢复为0。
对高分子材料弹性变形在玻璃态时主要是指键角键长的微小变化,而在高弹态则是由于分子链的构型发生变化,由链段移动引起,这时弹性变形可以很大。
2.非理想弹性的概念及种类。
答:非理想弹性是应力、应变不同时响应的弹性变形,是与时间有关的弹性变形。
表现为应力应变不同步,应力和应变的关系不是单值关系。
种类主要包括滞弹性,粘弹性,伪弹性和包申格效应。
3.什么是高分子材料强度和模数的时-温等效原理?答:高分子材料的强度和模数强烈的依赖于温度和加载速率。
加载速率一定时,随温度的升高,高分子材料的会从玻璃态到高弹态再到粘流态变化,其强度和模数降低;而在温度一定时,玻璃态的高聚物又会随着加载速率的降低,加载时间的加长,同样出现从玻璃态到高弹态再到粘流态的变化,其强度和模数降低。
时间和温度对材料的强度和模数起着相同作用称为时=温等效原理。
四、计算题:气孔率对陶瓷弹性模量的影响用下式表示:E=E0 (1—1.9P+0.9P2)E0为无气孔时的弹性模量;P为气孔率,适用于P≤50 %。
材力习题集.
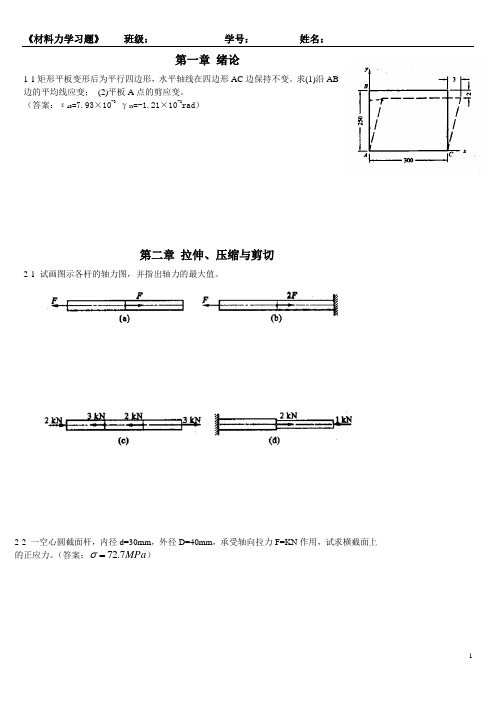
第一章 绪论1-1矩形平板变形后为平行四边形,水平轴线在四边形AC 边保持不变。
求(1)沿AB边的平均线应变; (2)平板A 点的剪应变。
(答案:εAB =7.93×10-3 γXY =-1.21×10-2rad )第二章 拉伸、压缩与剪切2-1 试画图示各杆的轴力图,并指出轴力的最大值。
2-2 一空心圆截面杆,内径d=30mm ,外径D=40mm ,承受轴向拉力F=KN 作用,试求横截面上的正应力。
(答案:MPa 7.72=σ)2-3 题2-1 c 所示杆,若该杆的横截面面积A=502m m ,试计算杆内的最大拉应力与最大压应力(答案:MPa t 60max ,=σ MPa c 40max ,=σ)2.4图示轴向受拉等截面杆,横截面面积A=5002m m ,载荷F=50KN 。
试求图示截面m-m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
(答案:MPa MPa MPa MPa 50 ; 100 ; 24.49 ; 32.41max max ==-==τστσαα)2.5如图所示,杆件受轴向载荷F 作用。
该杆由两根木杆粘接而成,若欲使粘接面上的正应力为其切应力的二倍,则粘接面的方位角θ应为何值(答案: 6.26=θ)2.6 等直杆受力如图所示,试求各杆段中截面上的轴力,并绘出轴力图。
2.7某材料的应力-应变曲线如图所示,图中还同时画出了低应变去区的详图,试确定材料的弹性模量E 、屈服极限s σ、强度极限b σ、与伸长率δ,并判断该材料属于何种类型(塑性或脆性材料)。
2.8某材料的应力-应变曲线如图所示,试根据该曲线确定: (1)材料的弹性模量E 、比例极限P σ与屈服极限2.0σ; (2)当应力增加到MPa 350=σ时,材料的正应变ε, 以及相应的弹性应变e ε与塑性应变p ε2.9图示桁架,杆1与杆2的横截面均为圆形,直径分别为d1=30mm 与d2=20mm ,两杆材料相同,许用应力[]σ=160MPa ,该桁架在节点A 处承受铅垂方向的载荷F=80KN 作用。
郑大材料力学习题集
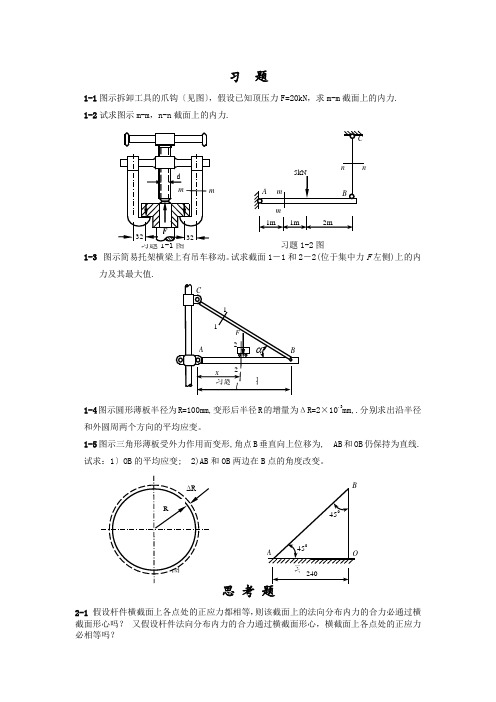
习 题1-1图示拆卸工具的爪钩〔见图〕,假设已知顶压力F=20kN ,求m-m 截面上的内力. 1-2试求图示m-m ,n-n 截面上的内力.习题1-2图 1-3 图示简易托架横梁上有吊车移动。
试求截面1-1和2-2(位于集中力F 左侧)上的内力及其最大值.1-4图示圆形薄板半径为R=100mm,变形后半径R 的增量为ΔR=2×10.3mm,.分别求出沿半径和外圆周两个方向的平均应变。
1-5图示三角形薄板受外力作用而变形,角点B 垂直向上位移为, AB 和OB 仍保持为直线.试求:1〕OB 的平均应变; 2)AB 和OB 两边在B 点的角度改变。
考 2-1 假设杆件横截面上各点处的正应力都相等,则该截面上的法向分布内力的合力必通过横截面形心吗? 又假设杆件法向分布内力的合力通过横截面形心,横截面上各点处的正应力必相等吗?A 、B 两点间距离为a,材料的横向变形系数ν。
试证明该两点距离改变量为aAB νεδ-=。
2-3试说明公式A F N =σ, EA lF l N=∆的应用条件,并说明E 的物理意义和量纲。
2-4 三根杆件尺寸相同但材料不同,材料的εσ-曲线如下图,试问哪一种〔1〕强度高?〔2〕刚度大?〔1〕塑性好? 2-5 杆件弹性模量E =210GPa ,比例极限σp =200MPa; 在轴向拉力作用下,纵向线应变为ε=8×10—4,求此时横截面上的正应力。
假设拉力加大使杆件的纵向线应变增加到ε=5×10—3,问此时横截面上的正应力能否再由胡克定律确定? 2-6 假设已测得受力物体内x 和y 两方向均有线应变,问在x 和y 两方向是否都必有正应力? 假设测得x 和y 两方向均无线应变,则在x 和y 两方向是否都必无正应力? 2-7 低碳钢试样的拉伸图中,拉断时的应力为何比强度极限低?2-8 两根杆件,同样材料制成但横截面积不同,它们的强度极限相同吗? 2-9 脆性材料制成的轴向拉伸矩形截面杆,假设有方向平行于轴线的裂纹,问杆的强度是否因此降低?假设裂纹方向垂直于轴线,杆的强度是否因此降低?2-10 在图示杆系中,钢杆1和铜杆2的许用应力分别为[]1σ和[]2σ,横截面面积分别为A 1 和A 2 ;且[]1σ>[]2σ,而A 2 >A 1; 能断定铜杆2先破坏吗?假设根据节点C 的平衡条件ΣY=0求结构的许可荷载,则02201130cos ][45cos ][][A A F σσ+=,这种结论对吗?思考题2-4图时到达材料的许用应力值?习题Array 2-2 图示托架的AC横梁上有吊车移动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章绪论1-1矩形平板变形后为平行四边形,水平轴线在四边形AC边保持不变。
求(1)沿AB边的平均线应变;(2)平板A点的剪应变。
(答案:εAB=7.93×10-3γXY=-1.21×10-2rad)第二章拉伸、压缩与剪切2-1 试画图示各杆的轴力图,并指出轴力的最大值。
2-2 一空心圆截面杆,内径d=30mm,外径D=40mm,承受轴向拉力F=KN作用,试求横截面上的正应力。
(答案:MPa7.72=σ)2-3 题2-1 c 所示杆,若该杆的横截面面积A=502mm ,试计算杆内的最大拉应力与最大压应力(答案:MPa t 60max ,=σ MPa c 40max ,=σ)2.4图示轴向受拉等截面杆,横截面面积A=5002mm ,载荷F=50KN 。
试求图示截面m-m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
(答案:MPa MPa MPa MPa 50 ; 100 ; 24.49 ; 32.41max max ==-==τστσαα)2.5如图所示,杆件受轴向载荷F 作用。
该杆由两根木杆粘接而成,若欲使粘接面上的正应力为其切应力的二倍,则粘接面的方位角θ应为何值(答案: ο6.26=θ)2.6 等直杆受力如图所示,试求各杆段中截面上的轴力,并绘出轴力图。
2.7某材料的应力-应变曲线如图所示,图中还同时画出了低应变去区的详图,试确定材料的弹性模量E 、屈服极限s σ、强度极限b σ、与伸长率δ,并判断该材料属于何种类型(塑性或脆性材料)。
2.8某材料的应力-应变曲线如图所示,试根据该曲线确定: (1)材料的弹性模量E 、比例极限P σ与屈服极限2.0σ; (2)当应力增加到MPa 350=σ时,材料的正应变ε, 以及相应的弹性应变e ε与塑性应变p ε2.9图示桁架,杆1与杆2的横截面均为圆形,直径分别为d1=30mm 与d2=20mm ,两杆材料相同,许用应力[]σ=160MPa ,该桁架在节点A 处承受铅垂方向的载荷F=80KN 作用。
试校核该桁架的强度(答案: MPa MPa 8.131 , 9.8221==σσ)2.10图示桁架,杆1为圆截面钢杆,杆2为方截面木杆,在节点A 处承受铅垂方向的载荷F 作用,试确定钢杆的直径d 与木杆截面的边宽b 。
已知载荷F=50KN,钢的许用应力[]σ=160MPa 木杆的许用应力[]w σ=10MPa (答案:d ≥20mm ,b ≥84.1mm )2.11 题2.9所述桁架,试确定载荷F 的许用值[]F 。
(答案:[]F =97.1KN )2.12某钢的拉伸试件,直径d=10mm ,标距mm l 500=。
在试验的比例阶段测得拉力增量KN F 9=∆,对应伸长量mm l 028.0)(=∆∆,屈服点时拉力KN F s 17=,拉断前最大拉力KN F b 32=,拉断后量得标距1l =62mm ,断口处直径d1=6.9mm ,试计算该钢的E 、s σ、b σ、δ和ψ值。
2.13 图示杆件AB 段截面21200mm A =,BC 段截面22300mm A =,E=200GPa ,mm l 100=,求各段截面的应力。
2.14 图示支架,杆AB 为钢杆,横截面A1=6002mm ,许用应力[]MPa 1001=σ;杆BC 为木杆, 横截面A2=200×2210mm ,许用应力[]MPa 52=σ,试确定支架的许可载荷[]G 。
答案:对于钢杆KN G 9.1031=2.15图所示等截面钢杆AB ,已知其截面面积A=23102mm ⨯在杆轴线C 处作用F=120KN 的轴向力,试求杆件各段横截面上的应力。
2.16 图示结构横杆AB 为刚性杆,不计其变形。
已知杆1、2的材料、截面面积和杆长均相同,A=[]MPa mm 100 , 2002=σ,试求结构的许可载荷[]F 。
( 答案:[]F =30KN )2.17 木杆的横截面为边长a=200mm 的正方形,在BC 段开一长为l ,宽为2/a 的槽,杆件受力如图。
试绘全杆的轴力图,并求出各段横截面上的正应力(不考虑槽孔角点处应力集中的影响)。
2.18直杆受力如图,已知a=1m ,直杆的横截面面积为A=4002mm ,材料的弹性模量MPa E 5102⨯=。
试求各段的伸长(或缩短),并计算全杆的总伸长。
2.19 一正方形混凝土短柱,受轴向压力F 的作用,如图所示。
柱高l ,截面每边长a=400mm 。
柱内埋有直径d=30mm 的钢筋四根。
已知柱受压后混凝土内截面上的正应力MPa 6=混σ。
试求钢筋中的应力和外部轴向压力F 的值。
假设钢筋与混凝土的弹性模量之比15/混=钢E E 。
(答案:F=1200KN ,MPa 90=钢σ)2.20刚性梁AB 放在三根材料相同、截面积都为2400cm A =的支柱上。
因制造不准确,中间柱短了mm 5.1=∆,材料的E=1.4MPa 410⨯, 求梁上受集中力P=720KN 时三柱内的应力。
(答案:MPa MPa 0.2 0.8231-=-==σσσ) 2.21阶梯形杆上端固定,下端与地面留有空隙mm 08.0=∆。
上段是铜杆,A1=2E , 20A ; 10E , 40222512===cm MPa cm 下段是钢杆,MPa 510⨯,在两段交界处受P 力作用。
试问:(1)P 力为多少时空隙消失?(2)P=500KN 时,各段杆的应力。
(3)温度再上升C ο20,求各段杆的应力。
(答案: 1) P=32KN ;2)MPa MPa 78 , 8621-==σσ ;3)MPa MPa 5.131 , 3.5921-==σσ )2.22 图示轴与齿轮用普通平键联接,已知d=70mm ,b=20mm ,h=12mm ,轴传递的转矩m KN M ⋅=2,键的许用切应力[]MPa 60=τ,许用积压应力[]100MPa jy =σ,试设计键的长度l 。
(答案:l =95.2mm )2.23 图所示螺钉受拉力F 作用。
已知材料的许用切应力[]τ和许用拉应力[]σ的关系为[][]στ6.0=,求螺钉直径d 和顶头高度h 的合理比值。
(答案:d/h=2.4)2-25图示结构杆1与杆2的弹性模量均为E ,横截面面积均为A ,梁BD 为刚体,试求在下列两种情况下,画变形图,建立补充方程。
2.24硬质铝板的厚度为6mm ,材料的剪切强度极限MPa b 220=τ。
为了将其冲成图示形状,求冲床的最小冲剪力。
(答案:KN F 150min =)2-26图示接头,承受轴向载荷F作用,试校核接头的强度。
已知,载荷F=80kN,板宽b=80mm,板厚δ=10mm,铆钉直径d=15mm,许用应力[σ]=160MPa,许用切应力[τ]=120MPa,许用挤压应力[σbs]=340MPa,板件与铆钉的材料相同。
答:σ=125MPa; τ=99.5MPa;σbs=125MPa第三章扭转3-1作图示各轴的扭矩图。
3-2试分析图示圆截面轴扭转时横截面的切应力分布,哪些是正确的?哪些是错误的?3-3图示船用推进器,一端是实心的,直径d 1=28cm ;另一端是空心的,内径d=14.8cm外径D=29.6cm 。
若[τ]=50MPa ,试求此轴允许传递的最大外力偶矩。
答:3-4如图所示,驾驶盘的直径d 1=520mm ,加在盘上的力F=300N ,盘下面竖轴所用材料的许用应力[τ]=60MPa 。
(1)当竖轴为实心轴时,试设计轴的直径d(2)如采用空心轴.且内外径之比a=0.8,试设计轴的外径D(3)比较实心轴与空心轴的重量。
答:(1)d=23.66mm (2)D=28.2mm (3)Q 实/Q 空=1.955[]mkN M ⋅=2163-5如图所示,传动轴的转速为n=200r/min,由主动轮B输入功率P B=60kW,由从动轮A、C和D分别输出功率为P A=18kW,P C=12kW,P D=30kW,若[τ]=20MPa,[θ]=0.50/m,G=82GPa,试按强度和刚度条件选定轴的直径答:T max=2005.5Nm ,按强度条件确定d=79.9mm, 按刚度条件确定d=73.1mm,;可选直径约为80mm3-6如图所示圆轴的直径d=50mm,作用外力偶矩M=2kNm,材料的切变模量G=80GPa。
要求:1)求横截面上最大切应力和单位轴长的相对扭转角;2)已知r B=15mm,求横截面上A、B、c三点的切应变。
答:1)τmax=81.5MPa , θ=2.30/m ; 2) τA=81.5MPa , γA=1.02×10-3;3) τB=48.9MPa , γB=0.61×10-3; 4) τC=0 , γC=0;3-7如图所示阶梯轴上的作用外力偶矩M1=3kNm,M2=lkNm直径d1=50mm,d2=40mm.l=100mm,材料的切变模量G=80GPa。
试求:1)画轴的扭矩图;2)求轴的最大切应力τmax;3)求c截面相对于A截面的扭转角φAC 。
答:τmax=80MPa;φAB=0.004rad;φBC=-0.005rad;φAC=-0.001rad.。
3-8某钢制实心圆截面传动轴的转速n=300r/min,传递的功率P=60kW,轴的[τ]=60MPa,材料的切变模量G=80GPa,轴的许用扭转角[θ]=0.50/m,m,试按强度和刚度准则设计轴径d 。
答:d=72.65mm3-9图示传动轴,已知轴的转速n=l00r/min,d=80mm,试求:1)轴的扭矩图;2)轴的最大切应力;3)截面上半径为25mm圆周处的切应力;4)从强度角度分析三个轮的布置是否合理?若不合理,试重新布置。
答:2)τmax=46.63MPa 3)τ1=29.14MPa3-10一阶梯型圆截面杆,两端固定后,在C处受一扭转力偶矩T 。
已知T、GI P及a。
试求支反力偶矩M A和M B3-11图示圆截面轴,直径为d、材料的切变模量为G、截面B的转角为φB。
试求所加扭力偶矩M之值3-12图示两端固定的圆截面轴,承受扭力矩M作用,若许用切应力[τ]=60MPa,试确定许用扭力偶矩[M]。
附录:平面图形几何性质附-1图示平行四边形截面。
高为h ,底为b ,试计算该截面对水平形心轴z 的惯性矩。
312Z bh I ⎛⎫= ⎪⎝⎭附-2试计算图示截面对水平形心轴z 的惯性矩。
44124Z a R I π=-附-3试计算图示截面对水平形心轴z 的惯性矩。
941.7310Z I mm =⨯附-4试求图示截面的主形心轴的位置与主形心惯性矩。
74849.8310, 2.1310,28.5Z y I m I m α--⎛⎫ ⎪⎝⎭=⨯=⨯=-o第四章 弯曲内力4-1.图示各梁中a q ,均为已知,试求指定截面上的剪力和弯矩。
