北京市朝阳区2012-2013学年度高三年级第一学期期中统一考试(文史类)
北京市朝阳区2013届高三上学期期中练习 历史 Word版

北京市朝阳区2012—2013学年度高三年级第一学期期中统一考试历史试题(考试时间90分钟,满分100分))一、选择题:共32小题。
每小题1.5分,共48分。
在下列各题的四个选项中,选出最符合题目要求的一项。
1.下图中的“示”指“祖先”,“示”与“司”合起来表示“世世代代专门祭祀祖先的庙堂”。
与“祠”紧密相关的制度为A.王位世袭制B.分封制C.宗法制D.世卿世禄制2.“民舍本而事末则其产约(财产轻便),其产约则轻(容易)迁徙,轻迁徙则国家有患,皆有远志,无有居心。
”这段话主张A.民贵君轻B.重农抑商C.农商并重D.寓兵于农3.这是一位生活于公元前4世纪前后的伟大的思想家,后成为仅次于孔子的一代儒学宗师。
他的思想中一个重要的内容是A.克己复礼B.仁者无敌C.天人感应D.格物致知4.梁启超称《诗经》的许多篇章乃是“中国最初之史”。
下列对其理解正确的是A.为研究夏商社会生活留下了宝贵素材B.以华丽的文采表现出大一统时代的气度C.反映了周朝从建立到结束的兴衰过程D.提供了研究前11~前6世纪的重要资料5.下面各项与“土”相关的解读中,不准确的是A.“普天之下,莫非王土”实为一种名义上的土地国有制度B.“六合之内,皇帝之土”是指皇帝对全国拥有至高的主权C.“惩戒亡秦孤立之败,于是剖裂疆土……”即废除郡县制D.“王在,礼治在,军令行,是王道乐土”意在维护封建正统6.汉宣帝(西汉第十位皇帝)曾说:“汉家自有制度,本以霸王道杂之,奈何纯用德教,用周政乎?”这表明汉代统治者的主张是A.以道家无为而治为指导思想B.以兼爱非攻尚贤为治国理念C.权势法制与伦理劝导相结合D.推崇理学扶为官方统治哲学7.东晋南朝时谢灵运的田庄“春秋有待,朝夕须资。
既耕以饭,亦桑贸衣。
艺菜当肴,采药救颓”。
孔灵符“立墅,周围三十三里,水陆地二百六十五顷,含带二山,又有果园九处”。
这说明田庄A.占田过限,违制兼并B.封疆裂土,富甲天下C.分工明确,交换频繁D.相对独立,自给自足8.在灌钢法的发明为世界冶炼技术做出划时代贡献的同时,制瓷业中的新品种在逐步走向成熟,为后期瓷器的发展提供了更广阔的平台。
北京市朝阳区2013届高三上学期期末考试数学文试题

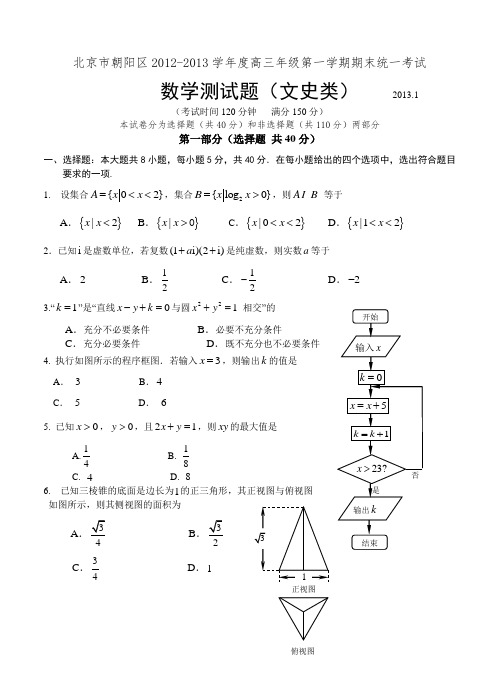
北京市朝阳区2012-2013学年度高三年级第一学期期末统一考试数学测试题(文史类) 2013.1(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1. 设集合{02}A x x =<<,集合2{log 0}B x x =>,则AB 等于A .{}|2x x <B .{}|x x >0C .{}|02x x <<D .{}|12x x <<【答案】D【KS5U 解析】2{log 0}{1}B x x x x =>=>,所以AB {}|12x x =<<,选D.2.已知i 是虚数单位,若复数(1i)(2i)a ++是纯虚数,则实数a 等于A .2B .12C .12-D .2- 【答案】A【KS5U 解析】(1)(2)2(12a i i a a i ++=-++,要使复数为纯虚数,所以有20,120a a -=+≠,解得2a =,选A.3.“1k =”是“直线0x y k -+=与圆221x y += 相交”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A【KS5U 解析】要使直线0x y k -+=与圆221x y += 相交,则有圆心到直线的距离1d =≤。
即k ≤k ≤≤“1k =”是“直线0x y k -+=与圆221x y += 相交”的充分不必要条件,选A.4. 执行如图所示的程序框图.若输入3x =,则输出k 的值是A . 3B .4C . 5D . 6 【答案】C【KS5U 解析】第一次循环358,1x k =+==;第二次循环8513,2x k =+==;第三次循环13518,3x k =+==;第四次循环18523,4x k =+==;第五次循环23528,5x k =+==,此时满足条件输出5k =,选C.5. 已知0x >,0y >,且21x y +=,则xy 的最大值是A.14 B. 18C. 4D. 8 【答案】B【KS5U 解析】因为21x y +=≥所以18xy ≤,当且仅当122x y ==,即11,42x y ==取等号,所以选B.6. 已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为A .4 B .2C .34D .1【答案】C【KS5U 解析】由正视图与俯视图可知,该几何体为正三棱锥,侧视图为,1324=。
2013北京市朝阳区高三(上)期中历 史

2013北京市朝阳区高三(上)期中历史2013.11(考试时间90分钟,满分100分)第Ⅰ卷(选择题共48分)注意事项:(1)每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不涂在答题卡上,只答在试卷上无效。
(2)每小题1.5分,满分48分;在每题给出的四个选项中,只有一项是最符合题目要求的。
1.“西周政治里有着浓厚的贵族色彩,形成了‘共主’名义下的地方分权体制。
”这表明( ) A.周天子通过垄断神权以强化王权B.周天子掌握了高度集中的政治权力C.西周等级分封制以宗法制为核心D.西周形成中央垂直管理地方的制度2.在“法”与“德”关系上,某位思想家主张先德后刑、先教后杀,认为有礼之法才是良法,无礼之法是恶法,“故非礼,是无法也”。
材料表明这位思想家属于( )A.道家 B.儒家C.法家 D.墨家3.秦朝的郡县制( )A.起源于先秦时期的分封制B.消除了地方割据的经济基础C.有利于中央对地方的控制D.其行政长官受到刺史的监督4.明万历年间,福建泉州府佃农“朝登垅亩,夕贸市廛”;浙江秀水县佃农用上等米换白银,用中下等米来抵租。
这一现象的出现突出反映了( )A.农村资本主义生产关系的初步发展B.农民反封建斗争的水平提高C.农民能够支配自己全部的劳动产品D.农业与市场的经济联系加强5.观察1843年与1858年进口棉花及棉纺织品税率比较表货物单位1843年税率1858年税率棉花担6.54% 5.72%印花布匹14.25% 4.98%棉纱担6.94% 4.86%这一现象造成( )A.耕织结合的小农经济完全解体B.中国传统的经济结构发生变化C.列强控制了中国棉纺织业命脉D.中国民族棉纺织企业大量破产6.近代中国历史上的某位人士自我评价说:“予少年科第,壮年戎马,中年封疆,晚年洋务,一路扶摇,遭遇不为不幸,自问亦未有何等陨越,乃无端发生中日交涉,至一生事业,扫地无余……半生名节,被后生辈描画都尽。
北京市朝阳区2012~2013学年度高三年级第一学期期中练习

北京市朝阳区2012~2013学年度高三年级第一学期期中练习物理试卷2012.11(考试时间90分钟 满分100分)一、本题共13小题,每小题3分,共39分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.卢瑟福提出原子的核式结构模型,这一模型建立的基础是A .对阴极射线的研究B .天然放射现象的发现C .α粒子散射实验D .氢原子光谱的发现【答案】C较易,考查α粒子散射实验的理解,要求知道选项中的四个实验事实的发现的意义。
考查:理解能力。
理解知识的意义,把握物理情景的本质特征,并能将知识与情景联系起来的能力。
2.用一束紫光照射某金属时不能发生光电效应,若要使该金属发生光电效应,可采取的措施是A .增大该紫光的强度B .延长该紫光的照射时间C .改用频率更高的电磁波照射D .改用波长更长的光照射【答案】C较易。
考查光电效应的规律。
要求知道光的能量有光的频率决定。
考查:理解能力。
根据研究对象及运动(变化)的特点,正确选用物理量、物理规律描述其物理状态、物理过程。
3.能源是社会发展的基础,发展核能是解决能源问题的途径之一。
目前各国核电站应用的可能核反应方程是A .23411120H+H He+n −−→B .235114192192056360U+n Ba+Kr+3n −−→C .234234090911Th Pa+e -−−→D .238234492902U Th+He −−→【答案】B较易。
考查核裂变反应方程以及各国核电站应用的核材料。
要求能鉴别什么是裂变反应。
考查:理解能力。
明确物理概念和规律的适用对象、适用条件、适用范围,及与其他物理概念和规律的区别和联系。
4.如图所示为波尔理论中氢原子能级图。
当氢原子从n=4的激发态向较低能级跃迁时,放出光子的能量可能是 A .13.6eV B .10.2 eV C .3.4 eV D .1.51eV 【答案】B较易。
考查波尔理论,氢原子跃迁的规律。
北京市朝阳区2012-2013学年度高三年级第一学期期中统一考试

北京市朝阳区2012-2013学年度高三年级第一学期期中统一考试数学试卷(理工类) 2012.11(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1. 已知全集{}1,2,3,4,5,6U =, 集合{}1,3,5A =, {}1,2B =, 则A I (U ðB )等于( ) A .∅ B .{}5 C .{}3 D .{}3,52. 已知数列{}n a 是各项均为正数的等比数列,若2342,216a a a =+=,则n a 等于( )A .22-nB .32n -C .12-n D .n23.已知平面向量a ,b 满足||1=a ,||2=b ,且()+⊥a b a ,则a 与b 的夹角为( )A .56π B .23π C . 3π D .6π 4.曲线e ()1xf x x =-在0x =处的切线方程为( )A .10x y --=B .10x y ++=C .210x y --=D .210x y ++=5.在ABC ∆中,M 是BC 的中点,3AM =,点P 在AM 上,且满足2AP PM =u u u r u u u u r,则()PA PB PC ⋅+u u u r u u u r u u u r的值为( )A .4-B .2-C .2D .46.函数33,0,(),0x x f x x x --<⎧=⎨≥⎩的图象与函数()ln(1)g x x =+的图象的交点个数是( )A .1B .2C .3D .47.函数()f x 是定义域为R 的可导函数,且对任意实数x 都有()(2)f x f x =-成立.若当1x ≠时,不等式(1)()0x f x '-⋅<成立,设(0.5)a f =,4()3b f =,(3)c f =,则a ,b ,c 的大小关系是( )A .B .C .D .8.已知数列{}n a 是各项均为正数且公比不等于1的等比数列.对于函数()y f x =,若数列b ac >>c b a >>a b c >>b c a >>{}ln ()n f a 为等差数列,则称函数()f x 为“保比差数列函数”.现有定义在(0,)+∞上的如下函数:①1()f x x=, ②2()f x x =, ③()e x f x =,④()f x = 则为“保比差数列函数”的所有序号为( )A .①②B .③④C .①②④D .②③④第二部分(非选择题 共110分)9.10.10S 11.12. 13. f 14.15. (Ⅰ)求△ABC 的面积; (Ⅱ)求sin()C A -的值. 16.(本小题满分14分)设数列{}n a 的前n 项和为n S .已知11a =,131n n a S +=+,n *∈N . (Ⅰ)写出23,a a 的值,并求数列{}n a 的通项公式;(Ⅱ)记n T 为数列{}n na 的前n 项和,求n T ;(Ⅲ)若数列{}n b 满足10b =,12log (2)n n n b b a n --=≥,求数列{}n b 的通项公式.17.(本小题满分13分)函数()sin()(0,0,||)2f x A x A ωϕωϕπ=+>><部分图象如图所示. 18.19.20.给定一个n 项的实数列12,,,(N )n a a a n *∈L ,任意选取一个实数c ,变换()T c 将数列12,,,n a a a L 变换为数列12||,||,,||n a c a c a c ---L ,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c 可以不相同,第(N )k k *∈次变换记为()k k T c ,其中k c 为第次变换时选择的实数.如果通过k 次变换后,数列中的各项均为0,则称11()T c ,22()T c ,…,()k k T c 为 “k 次归零变换”.k(Ⅰ)对数列:1,3,5,7,给出一个 “k 次归零变换”,其中4k ≤; (Ⅱ)证明:对任意n 项数列,都存在“n 次归零变换”;(Ⅲ)对于数列231,2,3,,nn L ,是否存在“1n -次归零变换”?请说明理由.北京市朝阳区2012-2013学年度第一学期高三年级期中练习 数学试卷答案(理工类) 2012.11又由正弦定理得,,所以,. ……………………9分因为,所以为锐角,所以,. ……………………11分sin sin C A 2sin 3sin 39a CA c===g a b <A 7cos 9A ===所以, . …………………………………13分16. (本小题满分14分)解:(Ⅰ)由已知得,,. ……………………………………………2分由题意,,则当时,.两式相减,得(). ……………………………………………3分分 分.17.因为,所以. ………………………………………………………4分所以函数的解析式为.………………………………5分 函数的单调递增区间为.…………………………7分sin()sin cos cos sin C A C A C A -=-gg 71393927=-⨯=24a =316a =131n n a S +=+2n ≥131n n a S -=+14n n a a +=2n ≥n ||2ϕπ<6ϕπ=()f x ()2sin(2)6f x x π=+()f x [,]()36k k k πππ-π+∈Z(Ⅱ)因为…………………………8分. ………………………10分18. 解:分分分( 由,得,所以当 时, 均恰有一个零点在上.………………7分(2)当,即时,在上必有零点. ………………………………………8分(3)若在上有两个零点, 则()()2cos 22sin(2)2cos 26g x f x x x xπ=+=++2sin 2cos2cos 2sin 2cos 266x x x ππ=++23cos 2x x =+)3x π=+[,]x ππ∈-502x ππ≤+≤0,1,2a =--()y f x =[]1,1-(1)(1)(7)(1)0f f a a -=-+≤g 17a -≤≤()y f x =[]1,1-()y f x =[]1,1-或…………………12分解得或.19.(Ⅱ)因为对于任意正实数,不等式成立,即恒成立.因为,由(Ⅰ)可知当时,函数有最小值.…7分所以,解得.0,8(1)(2)0,111,(1)0,(1)0a a a a f f >⎧⎪∆=++>⎪⎪-<-<⎨⎪-≥⎪⎪≥⎩0,8(1)(2)0,111,(1)0,(1)0.a a a a f f <⎧⎪∆=++>⎪⎪-<-<⎨⎪-≤⎪⎪≤⎩7a ≥2a <-x ()2f x a ≥x x a a ln 2+≤0>a a x 1=()ln f x a x x 1=+a a a a a a a f ln 1ln )1(-=+=a a a x f a ln )(2min -=≤10e a <≤故所求实数的取值范围是.………………………………………9分(Ⅲ)因为,.分(1分(2分综,.……………………………………………………14分20.(本小题满分13分)解:(Ⅰ)方法1::3,1,1,3;:1,1,1,1;:0,0,0,0.方法2::1,1,3,5;:1,1,1,3;:1,1,1,1;:0,0,0,0..……4分(Ⅱ)经过次变换后,数列记为,.a1(0,]e121212()ln22x x x xf ax x++2=++121212()()1(ln ln)22f x f xa x a xx x+11=+++1212121[ln(]x x x xa x x a++=)+=2)()()2(2121xfxfxxf+<+1(4)T2(2)T3(1)T1(2)T2(2)T3(2)T4(1)Tk()()()12,,,k k kna a aL1,2,k=L取,则,即经后,前两项相等;取,则,即经后,前3项相等;… …时,;此变换步数也不是最小.由以上分析可知,如果某一数列经最少的次数的“归零变换”,每一步所取的满足.以下用数学归纳法来证明,对已给数列,不存在“次归零变换”. (1)当时,对于1,4,显然不存在 “一次归零变换” ,结论成立.1121)2c a a =(+(1)(1)12121||2a a a a ==-11()T c (1)(1)2231()2c a a =+(2)(2)(2)(1)(1)123321||2a a a a a ===-22()T c ()k k T c (1)(1)11()k k k k k c a a --+=+j c ||i a (j j T 12j n ic 1212min{,,,}max{,,,}n i n a a a c a a a ≤≤L L 1n -2n =(由(Ⅱ)可知,存在 “两次归零变换”变换:) (2)假设时成立,即不存在“次归零变换”.当时,假设存在“次归零变换”. 此时,对也显然是“次归零变换”,由归纳假设以及前面的讨论不难知不存在“次归零变换”,则是最少的变换次数,每一次变换一定满足,.因为所以,绝不可能变换为0,与归纳假设矛盾.所以,当时不存在“次归零变换”.由(1)(2)命题得证. ………………………………………13分1253(),()22T T n k =231,2,3,,kk L 1k -1n k =+2311,2,3,,,(1)k k k k ++L k 231,2,3,,kk L k 231,2,3,,kk L 1k -k ic 1ki c k ≤≤1,2,,i k =L 111212|||(1)|||(1)()k k k k k c c c k c c c +++----=+-+++L L L 1(1)0k k k k k +≥+->g 1(1)k k ++1n k =+k。
北京市朝阳区2013届高三上学期期中练习历史含答案

北京市旭日区2012—2013 学年度高三年级第一学期期中一致考试历史试题(考90 分,分100 分))一、:共32 小。
每小 1.5 分,共 48 分。
在以下各的四个中,出最切合目要求的一。
1.下中的“示”指“先人”,“示” 与“司” 合起来表示“子子孙孙祭祀先人的堂”。
与“祠” 密有关的制度A .王位世制B.分封制C.宗法制 D .世卿世禄制【答案】 C【分析】观察中国古代的宗法制。
宗法制是把血关系与政治关系合起来的一种政治举措,此中心是嫡子承制,其影响深。
祭祖、着重血关系是宗法制影响的详细体。
2.“民舍本而事末其(便),其(简单)迁移,迁移国家有患,皆有志,无有存心。
” 段主A .民君B.重抑商C.商并重 D .寓兵于【答案】 B【分析】观察中国古代的重抑商政策。
剖析资料,人民从事商不利于社会定,不利于治,重抑商,将民固定在土地上。
3.是一位生活于公元前 4 世前后的大的思想家,后成次于孔子的一代儒学宗。
他的思想中一个重要的内容是A .克己复礼B.仁者无C.天人感 D .格物致知【答案】 B【分析】观察中国思想。
干思想家地位次于孔子,可知人是圣——孟子,提出仁者无的思想主。
4.梁启超称《》的多篇章乃是“中国最先之史”A .研究夏商社会生活留下了宝素材C.反应了周代从成立到束的衰程。
以下其理解正确的选项是B.以的文采表出大一代的心胸D .供给了研究前11~前 6 世的重要料【答案】 D【分析】《》是中国最早的歌集,收入自西周初年至春秋中叶大五百多年的歌(前11 世至前 6 世),合干可出D。
5.下边各与“土”有关的解中,不正确的是A.“普天之下,难道王土” 一种名上的土地国有制度B.“六合以内,皇帝之土”是指皇帝全国有至高的主D.“王在,礼治在,令行,是王道土”意在封建正【答案】 C【分析】观察中国古代文明,“ 戒亡秦孤立之,于是剖裂疆土⋯⋯”指西初年汲取秦代亡教,分封同姓侯王,但没有除郡制,初行郡国并行制。
北京市朝阳区2012届高三数学上学期期中考试试题 文 新人教A版

北京市朝阳区2011-2012学年度高三年级第一学期期中统一考试数学试卷(文史类)(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分注意事项:1.答第一部分前,考生务必将自己的姓名、考试科目涂写在答题卡上.考试结束时,将试题卷和答题卡一并交回.2.第一部分每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.第二部分不能答在试题卷上,请答在答题卡上.第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.设集合{}260M x x x =+-<,{}13N x x =≤≤,则MN 等于( )A .[)1,2B .[]1,2C .(]2,3D .[]2,32. 已知向量a ,b 满足|a | = 8,|b | = 6, a ·b = 24,则a 与b 的夹角为( )A .30︒B .60︒C .90︒D .120︒3. 已知函数()2sin()f x x ωϕ=+(0,0π)ωϕ><<的图象如图所示,则ω等于( )A .13 B .1 C .32D .24.已知等差数列{}n a 的前n 项和为n S ,且369315a a a ++=,则11S 等于( )A .78B .66C .55D .335.命题“,sin 1x x ∀∈≤R ”的否定是( )A .,sin 1x x ∃∈≥RB .,sin 1x x ∀∈>RC .,sin 1x x ∀∈≥RD .,sin 1x x ∃∈>R 6. 函数x x x f ln )(+=的零点所在的大致区间为( )A .()0,1B .()1,2C .()1,eD .()2,e 7. “1a >”是“对任意的正数x ,不等式21ax x+≥成立”的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件8.设集合{}0123,,,S A A A A =,在S 上定义运算⊕:ij k A A A ⊕=,其中k 为i j +被4除的余数,,0,1,2,3i j =,则使关系式0()i i j A A A A ⊕⊕=成立的有序数对(,)i j 的组数为( ) A .4 B .3 C .2 D .1第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9.已知π3(,π),sin ,25αα∈=则tan α= . 10.已知等比数列{}n a 各项均为正数,前n 项和为n S ,若22a =,1516a a =,则3a = ;5S = .11. 在ABC ∆中,角,,A B C 所对的边分别为,,a b c .若5,2a b c ===, 则cos B = .12. 在ABC ∆中,已知(2,1)AB =,(3,)AC k =()k ∈R ,则BC =__;若90B ∠=︒,则k =__ _.13.已知函数2,20,()2cos ,0.x x f x x x ⎧-≤≤=⎨<≤π⎩若方程()f x a =有解,则实数a 的取值范围是 .14.设函数()1f x x α=+(α∈Q )的定义域为[][],,b a a b --,其中0a b <<,且()f x 在[],a b 上的最大值为6,最小值为3,则()f x 在[],b a --上的最大值与最小值的和为 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本小题满分13分)设集合{|(1)0,M x x x a =--<a ∈R },集合2{|230}N x x x =--≤. (Ⅰ)当1a =时,求M N ;(Ⅱ)若M N ⊆,求实数a 的取值范围.16. (本小题满分13分)已知向量a =(sin ,cos())x x π-,b =(2cos ,2cos )x x ,函数()1f x =⋅a b+. (Ⅰ)求π()4f -的值;(Ⅱ)求()f x 在π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值,并求出相应的x 的值.17. (本小题满分13分)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且3cos 4B =. (Ⅰ)求2sinsin 22BB +的值;(Ⅱ)若b =ac 取最大值时,求ABC ∆的面积.18.(本小题满分13分)在递增数列}{n a 中,n S 表示数列}{n a 的前n 项和,11a =,1n n a a c +=+(c 为常数,n *∈N ),且123,,a a S 成等比数列.(Ⅰ)求c 的值;(Ⅱ)若12()3nn n b a +=⋅-,*n ∈N ,求242n b b b +++.19.(本小题满分14分)设函数221()22x a f x ax -=-+,R a ∈.(Ⅰ)若2]x ∀∈,关于x 的不等式24()2a f x -≥恒成立,试求a 的取值范围;(Ⅱ)若函数()f x 在区间[0,4]上恰有一个零点,试求a 的取值范围.20. (本小题满分14分) 已知函数21()ln (1)2f x x ax a x =-+-(a ∈R 且0a ≠). (Ⅰ)求函数()f x 的单调区间;(Ⅱ) 记函数()y F x =的图象为曲线C .设点11(,)A x y ,22(,)B x y 是曲线C 上的不同两点,如果在曲线C 上存在点00(,)M x y ,使得:①1202x x x +=;②曲线C 在M 处的切线平行于直线AB ,则称函数()F x 存在“中值相依切线”. 试问:函数()f x 是否存在“中值相依切线”,请说明理由.北京市朝阳区2011-2012学年度高三年级第一学期期中统一考试数学试卷(文史类)答案 2011.11一、选择题:注:若有两空,则第一个空3分,第二个空2分.三、解答题: (15)(本小题满分13分)解:(Ⅰ)当1a =时,不等式化为(2)0x x -<,则{|02}M x x =<<.又{}13N x x =-≤≤,因此{}13MN x x =-≤≤. ………………6分(Ⅱ)若1a <-,{|10},M x a x =+<<若M N ⊆,则有110a -≤+<,解得21a -≤<-. ………………8分若1a =-,,{|13}M N x x φ==-≤≤,此时M N ⊆成立; ………………10分 若1a >-,{|01},{|13}M x x a N x x =<<+=-≤≤,若M N ⊆,则有013a <+≤, 解得12a -<≤. ………………12分 综上,a 的取值范围是[2,2]-. ………………13分(16)(本小题满分13分)解:(Ⅰ)()1f x =⋅+a b =22sin cos 2cos 1xx x -+=sin 2cos2x x -, …………4分则π()14f -=-. ………………6分(Ⅱ)()f x =sin 2cos2x x -)4x π-. ………………7分因为π0,2x ⎡⎤∈⎢⎥⎣⎦,所以π3π2,444x π⎡⎤-∈-⎢⎥⎣⎦. ………………9分则当242x ππ-=时,即8x 3π=时,()f x ; ………………11分当244x ππ-=-时,即0x =时,()f x 的最小值是1-. ………………13分 (17)(本小题满分13分) 解:(Ⅰ)因为3cos 4B =,所以sin 4B =. ………………1分则21sinsin 2(1cos )2sin cos 22B B B B B +=-+=18+3244⨯=18+.…5分 (Ⅱ)由已知得2223cos 24a cb B ac +-==, …………7分又因为b =所以,22332a c ac +-=. …………8分 又因为223322a c ac ac +=+≥, 所以6ac ≤,当且仅当a c ==ac 取得最大值. …………11分此时11sin 62244ABC S ac B ∆==⨯⨯= 所以当ac 取最大值时,ABC ∆的面积为4. ……………13分 (18)(本小题满分13分)解:(Ⅰ)11,1,n n a a c a c +=+=为常数, 所以1(1).n a n c =+-则231,1(1)(12)33.a c S c c c =+=++++=+ ………………3分 又123,,a a S 成等比数列,所以2(1)33c c +=+,解得1c =-或2c =.由于}{n a 是递增数列,舍去1c =-,故2c =. ………………6分(Ⅱ)由(Ⅰ)得21n a n =-,*n ∈N .所以12()(21)3nn b n =⋅---,2212()(41)3nn b n =⋅---. ……………8分从而 242n b b b +++21[1()](341)991219n n n -+-=-- 211(1)249n n n =---,*n ∈N . ………………13分(19)(本小题满分14分)解:(Ⅰ) 依题得:2]x ∀∈,不等式232x ax +≥恒成立,则322x a x ≤+.…2分设3()22x g x x=+,则min ()a g x ≤即可. ………………3分又3()22x g x x =+≥=x =,min ()g x g ==所以a的取值范围是(-∞. ………………6分 (Ⅱ)二次函数()f x 的图象开口向上,对称轴是直线x a =. ………………7分依题意得:当2a ≤时,只需满足(0)0,(4)0,f f <⎧⎨>⎩即2210,8150,a a a ⎧-<⎨-+>⎩解得11a -<<, ………………10分当1a =-时满足题意,1a =时不满足题意,则11a -≤< . ……………11分当2a >时,只需满足(0)0,(4)0,f f >⎧⎨<⎩即2210,8150,a a a ⎧->⎨-+<⎩解得35a <<. …………12分当5a =时满足题意,3a =时不满足题意,则35a <≤. …………13分 综上所述, a 的取值范围是[1,1)(3,5]-. …………14分(20)(本小题满分14分)解:(Ⅰ)显然函数()f x 的定义域是(0,)+∞. …………1分由已知得,1(1)()1'()1a x x a f x ax a x x-+=-+-=-. …………2分 ⑴当0a >时, 令'()0f x >,解得01x <<; 令'()0f x <,解得1x >.所以函数()f x 在(0,1)上单调递增,在(1,)+∞上单调递减. …………3分 ⑵当0a <时,①当11a -<时,即1a <-时, 令'()0f x >,解得10x a<<-或1x >; 令'()0f x <,解得11x a-<<.所以,函数()f x 在1(0,)a -和(1,)+∞上单调递增,在1(,1)a-上单调递减;…………4分②当11a -=时,即1a =-时, 显然,函数()f x 在(0,)+∞上单调递增; ………5分 ③当11a ->时,即10a -<<时, 令'()0f x >,解得01x <<或1x a>-;令'()0f x <,解得11x a<<-. 所以,函数()f x 在(0,1)和1(,)a -+∞上单调递增,在1(1,)a-上单调递减. …………6分 综上所述,⑴当0a >时,函数()f x 在(0,1)上单调递增,在(1,)+∞上单调递减; ⑵当1a <-时,函数()f x 在1(0,)a -和(1,)+∞上单调递增,在1(,1)a-上单调递减; ⑶当1a =-时,函数()f x 在(0,)+∞上单调递增; ⑷当10a -<<时,函数()f x 在(0,1)和1(,)a -+∞上单调递增,在1(1,)a-上单调递减. ……………7分 (Ⅱ)假设函数()f x 存在“中值相依切线”.设11(,)A x y ,22(,)B x y 是曲线()y f x =上的不同两点,且120x x <<, 则211111ln (1)2y x ax a x =-+-,222221ln (1)2y x ax a x =-+-. 2121ABy y k x x -=-22212121211(ln ln )()(1)()2x x a x x a x x x x ---+--=- 211221ln ln 1()(1)2x x a x x a x x -=-++-- …………8分曲线在点00(,)M x y 处的切线斜率0()k f x '=12()2x x f +'=12122(1)2x x a a x x +=-⋅+-+, …………9分 依题意得:211221ln ln 1()(1)2x x a x x a x x --++--12122(1)2x x a a x x +=-⋅+-+.化简可得:2121ln ln x x x x --122x x =+,即21lnx x =21212()x x x x -+21212(1)1x x x x -=+. …………11分设21x t x = (1t >),上式化为:2(1)4ln 211t t t t -==-++, 即4ln 21t t +=+. …………12分 令4()ln 1g t t t =++,214'()(1)g t t t =-+=22(1)(1)t t t -+.因为1t >,显然'()0g t >,所以()g t 在(1,)+∞上递增, 显然有()2g t >恒成立. 所以在(1,)+∞内不存在t ,使得4ln 21t t +=+成立. 综上所述,假设不成立.所以,函数()f x 不存在“中值相依切线”. ……………14分。
北京市朝阳区2013届高三上学期期末考试数学文试题
北京市朝阳区2012-2013学年度高三年级第一学期期末统一考试数学测试题(文史类) 2013.1(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1. 设集合{02}A x x =<<,集合2{log 0}B x x =>,则AB 等于A .{}|2x x <B .{}|x x >0C .{}|02x x <<D .{}|12x x <<2.已知i 是虚数单位,若复数(1i)(2i)a ++是纯虚数,则实数a 等于A .2B .12C .12-D .2-7. 已知函数e ,0,()21,0x a x f x x x ⎧+≤=⎨->⎩(a ∈R ),若函数()f x 在R 上有两个零点,则a 的取值范围是A .(),1-∞-B .(),0-∞C .()1,0-D .[)1,0-8. 在棱长为1的正方体1111ABCD A BC D -中,1P,2P 分别为线段AB ,1BD (不包括端点)上的动点,且线段12P P 平行于平面11A ADD ,则四面体121PP AB 的体积的最大值是 A .124 B .112C .16 D .12第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上. 9. 已知数列1,,9a 是等比数列,数列121,,,9b b 是等差数列,则12a b b +的值为 .10.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且222b c a bc +-=,则A = .11.若关于x ,y 的不等式组10,10,10x y x ax y +-≥⎧⎪-≤⎨⎪-+≥⎩(a 为常数)所表示的平面区域的面积等于2,则a 的值为 .12.已知双曲线中心在原点,一个焦点为)0,5(1-F ,点P 在双曲线上,且线段1PF 的中点坐标为(0,2),则此双曲线的方程是 ,离心率是 .13.在直角三角形ABC 中,90ACB ∠=︒,2AC BC ==,点P 是斜边AB 上的一个三等分点,则CP CB CP CA ⋅+⋅= .14. 将连续整数1,2,,25填入如图所示的5行5列的表格中,使每一行的数字从左到右都成递增数列,则第三列各数之和的最小值为 ,最大值为 .A 1B 1CBD 1C 1ADE三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本小题满分13分)已知函数2()sincos cos 1222x x xf x =+-. (Ⅰ)求函数()f x 的最小正周期及单调递减区间; (Ⅱ)求函数()f x 在[,]π3π42上的最小值.16. (本小题满分14分)在长方体1111ABCD-A BC D 中,12AA=AD=,E 是棱CD 上的一点. (Ⅰ)求证:1AD ⊥平面11A B D ; (Ⅱ)求证:11B E AD ⊥;(Ⅲ)若E 是棱CD 的中点,在棱1AA 上是否存在点P ,使得DP ∥平面1B AE ?若存在,求出线段AP 的长;若不存在,请说明理由. 17. (本小题满分13分)某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:(Ⅰ)写出,,,a b x y 的值;(Ⅱ)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参组别 分组 频数频率第1组 [50,60) 8 0.16 第2组 [60,70) a ▓ 第3组 [70,80) 20 0.40 第4组 [80,90) ▓ 0.08 第5组[90,100]2 b合计▓▓频率分布表频率频率分布直方图加环保知识的志愿宣传活动.(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率; (ⅱ)求所抽取的2名同学来自同一组的概率.18. (本小题满分13分)已知函数1()()2ln ()f x a x x a x=--∈R .(Ⅰ)若2a =,求曲线()y f x =在点(1,(1))f 处的切线方程; (Ⅱ)求函数()f x 的单调区间.19. (本小题满分14分)已知直线:1()l x my m =+∈R 与椭圆()22:109x y C t t +=>相交于,E F 两点,与x 轴相交于点B ,且当0m =时,83EF =. (Ⅰ)求椭圆C 的方程;(Ⅱ)设点A 的坐标为(3,0)-,直线AE ,AF 与直线3x =分别交于M ,N 两点.试判断以MN 为直径的圆是否经过点B ?并请说明理由.20. (本小题满分13分)将正整数21,2,3,4,,n (2n ≥)任意排成n 行n 列的数表.对于某一个数表,计算各行和各列中的任意两个数,a b (a b >)的比值ab,称这些比值中的最小值为这个数表的“特征值”. (Ⅰ)当2n =时,试写出排成的各个数表中所有可能的不同“特征值”;(Ⅱ)若ij a 表示某个n 行n 列数表中第i 行第j 列的数(1i n ≤≤,1j n ≤≤),且满足(1),(1),ij i j i n i j a i n i j n i j +--<⎧=⎨+-+-≥⎩, ,请分别写出3,4,5n =时数表的“特征值”,并由此归纳此类数表的“特征值”(不必证明); (Ⅲ)对于由正整数21,2,3,4,,n 排成的n 行n 列的任意数表,若某行(或列)中,存在两个数属于集合222{1,2,,}n n n n n -+-+,记其“特征值”为λ,求证:1.n n λ+<北京市朝阳区2012-2013学年度高三年级第一学期期末统一考试数学测试题答案(文史类) 2013.1二、填空题:(注:两空的填空,第一空3分,第一空2分) 三、解答题:(15)(本小题满分13分) 解:(Ⅰ)1cos ()sincos 1222x x xf x +=+- 111sin cos 222x x =+- …………………………………………2分1).242x π=+- ……………………………………………4分所以函数()f x 的最小正周期为2π. …………………………………………6分由322242k x kππππ+≤+≤π+,k ∈Z ,则52244k x k πππ+≤≤π+. 则函数()f x 单调减区间是5[2,2]44k k πππ+π+,k ∈Z . ………………9分 (Ⅱ)由x π3π≤≤42,得7244x πππ≤+≤. ………………………………………11分则当342x ππ+=,即54x π=时,()f x 取得最小值12-. …………………13分 (16)(本小题满分14分)解:(Ⅰ)在长方体1111ABCD-A BC D 中,因为11A B ⊥面11A D DA ,所以111A B AD ⊥. ………………………………………………………………2分 在矩形11A D DA 中,因为12AA=AD=,所以11AD A D ⊥.……………………4分 所以1AD ⊥面11A B D . ………………………………………………………5分 (Ⅱ)因为E CD ∈,所以1B E ⊂面11A B CD ,由(Ⅰ)可知,1AD ⊥面11A B CD , …………………………………………7分 所以11B E AD ⊥. …………………………………………………………………8分 (Ⅲ)当点P 是棱1AA 的中点时,有DP ∥平面1B AE . ………………………9分 理由如下:在1AB 上取中点M ,连接PM,ME . 因为P 是棱1AA 的中点,M 是1AB 的中点, 所以PM ∥11A B ,且1112PM A B =.……10分 又DE ∥11A B ,且1112DE A B =. 所以PM ∥DE ,且PM DE =, 所以四边形PMED 是平行四边形,所以DP ∥ME .…………………………11分 又DP ⊄面1B AE ,ME ⊂面1B AE ,所以DP ∥平面1B AE . …………………………………………………………13分 此时,1112AP A A ==. …………………………………………………………14分 (17)(本小题满分13分)解:(Ⅰ)由题意可知,16,0.04,0.032,0.004a b x y ====.……………………4分 (Ⅱ)(ⅰ)由题意可知,第4组共有4人,记为,,,A B C D ,第5组共有2人,记为,X Y . 从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有,,,,,,,A B A C A D B C B D C D A X A Y ,,,,,,,BX BY CX CY DX DY XY A 1B 1CBD 1C 1ADEPM共15种情况.…………………………………………………………………………6分 设“随机抽取的2名同学中至少有1名同学来自第5组”为事件E , …………7分 有,AX AY ,,,,,,,BX BY CX CY DX DY XY 共9种情况. ……………8分 所以随机抽取的2名同学中至少有1名同学来自第5组的概率是93()155P E ==. 答:随机抽取的2名同学中至少有1名同学来自第5组的概率35. ……………10分 (ⅱ)设“随机抽取的2名同学来自同一组”为事件F ,有,,,,,,AB AC AD BC BD CD XY 共7种情况. …………………………………………………………………………11分 所以7()15P F =答:随机抽取的2名同学来自同一组的概率是715. ………………………………13分 (18)(本小题满分13分)解:222122()(1)ax x a f x a x x x -+'=+-=, ……………………………………………1分令2()2h x ax x a =-+.(Ⅰ)当2a =时,函数1()2()2ln f x x x x =--,(1)0f =,212()2(1)f x x x '=+-.曲线()y f x =在点(1,(1))f 处的切线的斜率为(1)2f '=. …………………………2分 从而曲线()y f x =在点(1,(1))f 处的切线方程为02(1)y x -=-,即220x y --=. ………………………………………………………………4分 (Ⅱ)函数()f x 的定义域为(0,)+∞. 设2()2h x ax x a =-+, (1)当0a ≤时,2()20h x ax x a =-+<在(0,)+∞上恒成立,则()0f x '<在(0,)+∞上恒成立,此时()f x 在(0,)+∞上单调递减.……………6分(2)当0a >时,244a ∆=-,(ⅰ)若01a <<,由()0f x '>,即()0h x >,得0x <<或x >;……………8分由()0f x '<,即()0h x <x <<.………………………9分所以函数()f x的单调递增区间为和)+∞,单调递减区间为11()a a. ……………………………………11分(ⅱ)若1a ≥,()0h x ≥在(0,)+∞上恒成立,则()0f x '≥在(0,)+∞上恒成立,此时()f x 在(0,)+∞上单调递增. ………………………………………………………………13分 (19)(本小题满分14分)解:(Ⅰ)当0m =时,直线l 的方程为1x =,设点E 在x 轴上方,由221,91x y tx ⎧+=⎪⎨⎪=⎩解得(1,E F .所以83EF ==,解得2t =. ……………………………………………3分 所以椭圆C 的方程为22192x y +=. ………………………………………………4分 (Ⅱ)由221,921x y x my ⎧+=⎪⎨⎪=+⎩得22(29)4160m y my ++-=,显然m ∈R . …………5分 设1122(,),(,)E x y F x y ,则121222416,2929m y y y y m m --+==++. ……………6分 111x my =+,221x my =+.又直线AE 的方程为11(3)3y y x x =++, 11(3),33y y x x x ⎧=+⎪+⎨⎪=⎩解得116(3,)3y M x +, 同理得226(3,)3y N x +.所以121266(2,),(2,)33y y BM BN x x ==++, …………………………………………9分 又因为121266(2,)(2,)33y y BM BN x x ⋅=⋅++ 12121212363644(3)(3)(4)(4)y y y y x x my my =+=+++++ 1212212124(4)(4)364()16my my y y m y y m y y +++=+++ 2222216(436)164164(29)3216(29)m m m m m -+-⨯+⨯+=-++ 22264576641285769m m m ---++=0=.…………………13分 所以BM BN ⊥,所以以MN 为直径的圆过点B . ………………………………14分(20)(本小题满分13分) 证明:(Ⅰ)显然,交换任何两行或两列,特征值不变.可设1在第一行第一列,考虑与1同行或同列的两个数只有三种可能,2,3或2,4或3,4. 得到数表的不同特征值是32或4.3……………………………………………3分(Ⅱ)当3n =时,数表为此时,数表的“特征值”为4.3……………………………………………………4分当4n =时,数表为此时,数表的“特征值”为54. ………………………………………………………5分 7 1 4 5 8 2 3 6 913 1 5 9 10 14 2 6 7 11 15 3 4 8 12 1621 1 6 11 16 17 22 2 7 12 13 18 23 3 8当5n =时,数表为此时,数表的“特征值”为65. …………………………………………………………6分 猜想“特征值”为1n n+. …………………………………………………………………7分 (Ⅲ)设,a b (a b >)为该行(或列)中最大的两个数,则221a nb n n λ≤≤-+,因为2332221(1)10,1(1)(1)n n n n n n n n n n n n n +-+-==-<-+-+-+ 所以2211n n n n n +<-+,从而1.n n λ+<…………………………………………13分9 14 19 24 4 510 15 20 25。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市朝阳区2012-2013学年度高三年级第一学期期中统一考试
数学试卷(文史类) 2012.11
(考试时间120分钟 满分150分)
本试卷分为选择题(共40分)和非选择题(共110分)两部分
第一部分(选择题 共40分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出
符合题目要求的一项.
1. 已知全集{}1,2,3,4,5,6U =, 集合{}1,3,5A =, {}1,2B =, 则A (U
ðB )等于 A .∅ B .{}5 C .{}3 D .{}3,5 2. 曲线321y x x x =-=-在处的切线方程为 A .20x y ++=
B .20x y +-=
C .20x y -+=
D .20x y --=
3. 已知平面向量a ,b 满足||1=a ,||2=b ,且()+⊥a b a ,则a 与b 的夹角是
A .
56π B .23π C .3π D . π
6
4. 已知数列{}n a 是各项均为正数的等比数列,若2342,216a a a =+=,则n a 等于
A .2
2
-n
B .32
n
- C .1
2
-n D .n
2
5. 已知角α的终边经过点(3,4)(0)a a a ->,则sin 2α等于
A .725-
B .1225-
C .2425
D .24
25
- 6. 在ABC ∆中,M 是BC 的中点,3AM =,点P 在AM 上,且满足2AP PM =
,
则()PA PB PC ⋅+
的值为
A. 4-
B.2-
C.2
D. 4 7. 函数3
3,0,
(),0
x x f x x x --<⎧=⎨
≥⎩的图象与函数()ln(1)g x x =+的图象的交点个数是 A .1
B .2
C .3
D .4
8.已知数列{}n a 是各项均为正数且公比不等于1的等比数列.对于函数()y f x =,若数列
{}ln ()n f a 为等差数列,则称函数()f x 为“保比差数列函数”. 现有定义在(0,)+∞上的如
下函数:
①1
()f x x
=
, ②2()f x x =, ③()e x f x =,
④()f x = 则为“保比差数列函数”的所有序号为
A .①②
B .③④
C .①②④
D .②③④
第二部分(非选择题 共110分)
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.
9. 已知1
cos()2
απ-=
,且α为第二象限的角,则sin α= ,tan α= . 10. 已知集合{|2}A x x =∈<R ,B ={x ∈R ∣}1282
x
≤<,则A B = .
11. 设n S 为等差数列{}n a 的前n 项和,若34674,16
a a a a +=+=,则公差d = ,9S = .
12. 在ABC ∆中,若4BA BC ⋅=
,ABC ∆的面积为2,则角B = .
13. 已知函数()y f x =满足:(1)=f a (01a <≤),且()1
,()1,()
(1)2(),()1,
f x f x f x f x f x f x -⎧>⎪
+=⎨⎪≤⎩则
(2)=f (用a 表示);若1
(3)=
(2)
f f ,则a = . 14. 已知函数()f x 是定义在R 上的奇函数,且在定义域上单调递增.当[)1,x a ∈-+∞时,不等式(2)()0f x a f x -+>恒成立,则实数a 的取值范围是 .
三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本小题满分13分)
设△ABC 的内角,,A B C 所对的边分别为,,a b c ,已知12,3,cos 3
a b C ===
. (Ⅰ)求△ABC 的面积;
(Ⅱ)求sin()C A -的值. 16. (本小题满分13分)
设数列{}n a 的前n 项和为n S ,已知11a =,131n n a S +=+,n *∈N . (Ⅰ)写出23,a a 的值,并求出数列{}n a 的通项公式; (Ⅱ)求数列{}n na 的前n 项和n T .
17. (本小题满分13分)
函数()sin()(0,0,||)2
f x A x A ωϕωϕπ
=+>><部分图象如图所示.
(Ⅰ)求()f x 的最小正周期及解析式;
(Ⅱ)设()()2cos 2g x f x x =-,求函数()g x 在区间[0,]2
π
上的最大值和最小值.
18. (本小题满分14分)
函数2()243f x ax x a =+--,a ∈R .
(Ⅰ)当1a =时,求函数()f x 在[]1,1-上的最大值;
(Ⅱ)如果函数()f x 在区间[]1,1-上存在零点,求a 的取值范围. 19. (本小题满分14分)
设函数()e x f x x a =-,a ∈R .
(Ⅰ)求函数()f x 单调区间;
(Ⅱ)若x ∀∈R ,()0f x ≤成立,求a 的取值范围.
20. (本小题满分13分)
给定一个n 项的实数列12,,,(N )n a a a n *∈ ,任意选取一个实数c ,变换()T c 将数列12,,,n a a a 变换为数列12||,||,,||n a c a c a c --- ,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c 可以不相同,第(N )k k *∈次变换记为()k k T c ,其中k c 为第k 次变换时选择的实数.如果通过k 次变换后,数列中的各项均为0,则称11()T c ,
22()T c ,…,()k k T c 为 “k 次归零变换”
(Ⅰ)对数列:1,2,4,8,分别写出经变换1(2)T ,2(3)T ,3(4)T 后得到的数列; (Ⅱ)对数列:1,3,5,7,给出一个 “k 次归零变换”,其中4k ≤; (Ⅲ)证明:对任意n 项数列,都存在“n 次归零变换”.。
