山大 信号与系统 2008 试卷
信号与系统试卷及参考答案

试卷及答案信号与系统试卷(1)(满分:100分,所有答案一律写在答题纸上)考试班级学号姓名成绩考试日期:年月日,阅卷教师:考试时间120分钟,试卷题共2页一一线性非时变离散系统,具有一初始状态x(0),当激励为时f(k),响应为y(k)=((1/2)k+1)u(k);若初始状态不变,当激励为-f(k)时,响应y(k)=((-1/2)k-1)u(k)为;试求当初始状态2x(0)为,激励为4f(k)时,系统的响应?(10分)二绘出下列函数的图形(1).已知一连续时间信号x(t)如图所示,试概略画出信号y(t)=x(2-t/3)的波形图。
(8分)t(2). 试概略画出信号y(t)=u(t 2-4) 的波形图。
(8分)三 计算下列函数(1). y(t)=⎰-44(t 2+3t+2)(δ(t)+2δ(t-2))dt (4分) (2). f(t)=e -2t u(t), h(t)= e -2t u(t), y(t)=f(t)*h (t) (8分)(3). f(k)=1, k=0,1,2,3, h(k)=1, k=0,1,2,3, y(k)=f(k)*h (k) (8分) (4) 已知f(t)=e -2t u(t), 求y(t)=[t f(2t)] 的富立叶变换 (8分) (5)y’(t)+2y(t)=δ(t)+u(t), y(0)=0, 试求y(t)=? (8分) (6). y(k)-y(k-1)-2y(k-2)=u(k)+2u(k-2), y(-1)= 2,y(-2)= -1/2, 试求零输入响应y x (k)=? 零状态响应y f (k)=? (8分)四 一线性非时变因果系统,当激励为u(t)时,响应为)]2()([cos )(cos )(ππ---+=-t u t u t t tu e t g t ,求当激励f(t)=δ(t)时的响应)(t h 。
(10分)五 某一子系统,当输入f(t)=e -t u(t)时,零状态响应y f (t) = (1/2 e -t - e -2t +1/2e -3t )u(t), 试求将两个这样的子系统串联时,总系统的冲激响应。
山大信号与系统答案

第一章习题新闻来源:山东大学信息学院点击数:707 更新时间:2009-4-5 0:13 1—1 画出下列各函数的波形图。
(1)(2)(3)(4)1—2 写出图1各波形的数学表达式图1(1) (2)(3) 全波余弦整流(4) 函数1—3 求下列函数的值。
(1)(2)(3)(4)(5)1—4 已知,求,。
1—5 设,分别是连续信号的偶分量和奇分量,试证明1—6 若记,分别是因果信号的奇分量和偶分量,试证明,1—7 已知信号的波形如图2所示,试画出下列函数的波形。
(1)(2)图 21—8 以知的波形如图3所示,试画出的波形.图31—9 求下列各函数式的卷积积分。
(1),(2),1—10 已知试画出的波形并求。
1—11 给定某线性非时变连续系统,有非零初始状态。
已知当激励为时,系统的响应为时,系统的响应则为。
试求当初始状态保持不变,而激励为时的系统响1—12 设和分别为各系统的激励和响应,试根据下列的输入—输出关系,确定下列各⑴⑵(3)(4)第一章习题答案新闻来源:山东大学信息学院点击数:623 更新时间:2009-4-5 23:181-1 (1)(2)(3)(4)1-2(1)、(2)、或或(3)(4) =1-3(1)(2)(3)(4)(5)01-4 ,1-7 (1)(2)1-81-9(1)(2)1-101-111-12 (1)非线性、时不变系统。
(2)线性、时变系统。
(3)线性、时不变系统。
(4)线性、时变系统。
上一篇:没有上一篇资讯了下一篇:没有下一篇资讯了第二章习题新闻来源:山东大学信息学院点击数:412 更新时间:2009-4-9 22—1 已知给定系统的齐次方程是,分别对以下几种初始状态求解系1),2),3),2—2 已知系统的微分方程是当激励信号时,系统的全响应是,试确定系统的零输入2—3 已知系统的微分方程是该系统的初始状态为零。
1)若激励,求响应。
2)若在时再加入激励信号,使得时,,求系数。
山大信号与系统答案

第一章习题新闻来源:山东大学信息学院点击数:707 更新时间:2009-4-5 0:13 1—1 画出下列各函数的波形图。
(1)(2)(3)(4)1—2 写出图1各波形的数学表达式图1(1) (2)(3) 全波余弦整流(4) 函数1—3 求下列函数的值。
(1)(2)(3)(4)(5)1—4 已知,求,。
1—5 设,分别是连续信号的偶分量和奇分量,试证明1—6 若记,分别是因果信号的奇分量和偶分量,试证明,1—7 已知信号的波形如图2所示,试画出下列函数的波形。
(1)(2)图 21—8 以知的波形如图3所示,试画出的波形.图31—9 求下列各函数式的卷积积分。
(1),(2),1—10 已知试画出的波形并求。
1—11 给定某线性非时变连续系统,有非零初始状态。
已知当激励为时,系统的响应为时,系统的响应则为。
试求当初始状态保持不变,而激励为时的系统响1—12 设和分别为各系统的激励和响应,试根据下列的输入—输出关系,确定下列各⑴⑵(3)(4)第一章习题答案新闻来源:山东大学信息学院点击数:623 更新时间:2009-4-5 23:181-1 (1)(2)(3)(4)1-2(1)、(2)、或或(3)(4) =1-3(1)(2)(3)(4)(5)01-4 ,1-7 (1)(2)1-81-9(1)(2)1-101-111-12 (1)非线性、时不变系统。
(2)线性、时变系统。
(3)线性、时不变系统。
(4)线性、时变系统。
上一篇:没有上一篇资讯了下一篇:没有下一篇资讯了第二章习题新闻来源:山东大学信息学院点击数:412 更新时间:2009-4-9 22—1 已知给定系统的齐次方程是,分别对以下几种初始状态求解系1),2),3),2—2 已知系统的微分方程是当激励信号时,系统的全响应是,试确定系统的零输入2—3 已知系统的微分方程是该系统的初始状态为零。
1)若激励,求响应。
2)若在时再加入激励信号,使得时,,求系数。
2008-06电科《信号与系统》A卷试题及答案
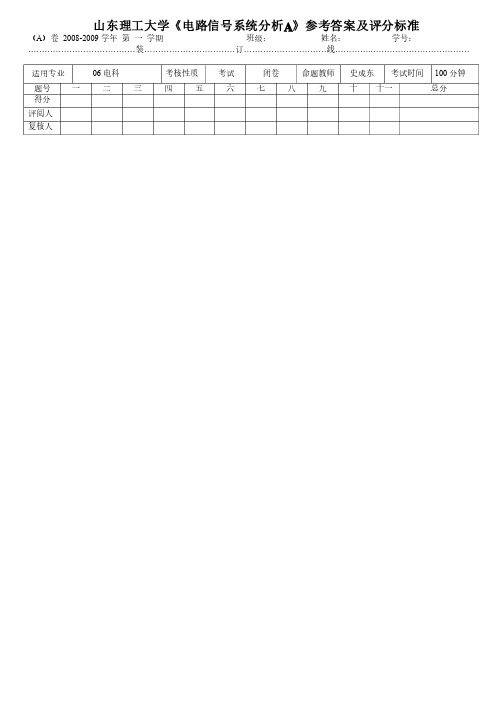
山东理工大学《电路信号系统分析A 》参考答案及评分标准(A )卷)卷 2008-2009学年学年 第 一 学期学期 班级:班级: 姓名:姓名: 学号:学号:…………………………………装……………………………订…………………………线………….………………………………适用专业适用专业 06电科电科 考核性质考核性质 考试考试 闭卷闭卷 命题教师命题教师 史成东史成东 考试时间考试时间 100分钟分钟 题号题号 一二三 四 五 六 七 八 九 十 十一十一 总分总分 得分得分评阅人评阅人复核人复核人一、计算题(每题3分)分)()()822cos2)1(41-=-å=k k k k kd p(2) 144)z (22+=z z F()51)122()3(1023-=-¢+-+ò¥-dt t t t t d)()()4(32t ee tte ---=(5) )()(2w g w F p = (6) (6) )10()10()(++-=w s w s w F a a 二、填空(22分)分)1、已知f 1(k)={3,2,1}-1, f 2(k)={1,2,3}-1,y(k)= f 1(k)*f 2(k) 则y(-1)= 8 ,y(2)= 3 (4分)分)2、若f(t)ε(t)的拉氏变换为()11+=s s F ,则该信号拉氏变换的收敛域ROC: σ〉-1 该信号的频谱密度函数该信号的频谱密度函数F(jω)=11+w j (4分)分) 3、若门脉冲串的波形如右图,τ=1秒,T=10秒,秒,则该脉冲串的频谱n F =10101p n Sa基波频率W =5p(4分)分) 4、在对连续信号均匀抽样时,若采样角频率为w s ,信号最高截止频率为w m ,,则采样后信号频谱不产生失真的条件为:__w s ³2w m ______。
(2分)分)5. 因果信号f(k)f(k)的拉氏变换为的拉氏变换为 )1(1)z (22--=z z F 则)0(+f =____0_____=____0_____。
信号与系统试题及答案

信号与系统试题1第一部分 选择题(共32分)一、单项选择题(本大题共16小题,每小题2分,共32分。
在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内)1.积分e d t --∞⎰2τδττ()等于( )A .δ()tB .ε()tC .2ε()tD .δε()()t t +2.已知系统微分方程为dy t dt y t f t ()()()+=2,若y f t t t (),()sin ()012+==ε,解得全响应为y t e t t ()sin()=+-︒-54242452,t ≥0。
全响应中24245sin()t -︒为( ) A .零输入响应分量 B .零状态响应分量C .自由响应分量D .稳态响应分量3.系统结构框图如图示,该系统的单位冲激响应h(t)满足的方程式为( )A .dy t dt y t x t ()()()+= B .h t x t y t ()()()=- C .dh t dt h t t ()()()+=δ D .h t t y t ()()()=-δ4.信号f t f t 12(),()波形如图所示,设f t f t f t ()()*()=12,则f()0为( )A .1B .2C .3D .45.已知信号f t ()的傅里叶变换F j ()()ωδωω=-0,则f t ()为( )A .120πωe j t B .120πωe j t - C .120πεωe t j t () D .120πεωe t j t -()6.已知信号f t ()如图所示,则其傅里叶变换为( )A .τωττωτ2422Sa Sa ()()+B .τωττωτSa Sa ()()422+ C .τωττωτ242Sa Sa ()()+ D .τωττωτSa Sa ()()42+7.信号f t 1()和f t 2()分别如图(a )和图(b)所示,已知 [()]()f t F j 11=ω,则f t 2()的 傅里叶变换为( )A .F j e j t 10()--ωωB .F j e j t 10()ωω-C .F j e j t 10()-ωωD .F j e j t 10()ωω8.有一因果线性时不变系统,其频率响应H j j ()ωω=+12,对于某一输入x(t)所得输出信号的傅里叶变换为Y j j j ()()()ωωω=++123,则该输入x(t)为( ) A .--e t t 3ε()B .e t t -3ε()C .-e t t 3ε()D .e t t 3ε()9.f t e t t ()()=2ε的拉氏变换及收敛域为( )A .122s s +>-,Re{} B .122s s +<-,Re{} C .122s s ->,Re{} D .122s s -<,Re{} 10.f t t t ()()()=--εε1的拉氏变换为( ) A .11s e s ()--B .11s e s ()-C .s e s ()1--D .s e s ()1-11.F s s s s s ()Re{}=+++>-25622的拉氏反变换为( )A .[]()e e t t t --+322εB .[]()e e t t t ---322εC .δε()()t e t t +-3D .e t t -3ε()12.图(a )中ab 段电路是某复杂电路的一部分,其中电感L 和电容C 都含有初始状态,请在图(b )中选出该电路的复频域模型。
2008信号2-2_06

两个子系统并联
x(t )
h1 (t)
x(t ) h (t ) 1
∑
x(t ) h2 (t )
y(t ) = x(t ) [h (t ) + h2 (t )] 1
h2 (t)
x(t )
h1 (t) + h2 (t)
y(t )
(3) 结合律
[ x(t ) h (t )] h2 (t ) = x(t ) [h (t ) h2 (t )] 1 1
4 5 0 1 2 3 -2 t
x 例:已知 (t ) = e , h(t ) = e ε (t ), 求x(t ) h(t )
2t t
x 解: (t ) h(t ) = ∫ x(τ )h(t τ )dτ
∞
∞
=∫ e e
∞
∞
2τ
(t τ )
1
t
-1
0
( t +1)
t
x 解: (t ) = 1+ ε (t 1), h(t ) = e
ε (t + 1)
y(t ) = x(t ) h(t )
= 1 e
( t +1)
ε (t + 1) + ε (t 1) e
( t +1)
ε (t + 1)
=e
( t +1)
ε (t + 1) 1+ e
t 1
t
y'(t ) = ∫ e dτ ε (t ) =(1 e )ε (t ),
τ t 0
t
y(t ) = ∫ (1 e )dτ ε (t ) = (t + e 1)ε (t )
t t 0
大学考试试卷《信号与系统》及参考答案

信号与系统一、单项选择题(本大题共46分,共 10 小题,每小题 4.599999 分)1. 若一因果系统的系统函数为则有如下结论——————————() A. 若,则系统稳定 B. 若H(s)的所有极点均在左半s平面,则系统稳定 C. 若H(s)的所有极点均在s平面的单位圆内,则系统稳定。
2. 连续信号,该信号的拉普拉斯变换收敛域为()。
A.B.C.D.3. 连续信号与的乘积,即*=( )A.B.C.D.4. 已知f(t),为求f(t0−at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A. f(-at)左移t0 B. f(-at) 右移tC. f(at) 左移D. f(at)右移5. 已知 f(t),为求f(t0-at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A.B. f(at) 右移t0 C. f(at) 左移t/a D. f(-at) 右移t/a6. 系统函数H(s)与激励信号X(s)之间——() A. 是反比关系; B. 无关系; C. 线性关系; D. 不确定。
7. 下列论断正确的为()。
A. 两个周期信号之和必为周期信号; B. 非周期信号一定是能量信号; C. 能量信号一定是非周期信号; D. 两个功率信号之和仍为功率信号。
8. 的拉氏反变换为()A.B.C.D.9. 系统结构框图如下,该系统单位冲激响应h(t)的表达式为()A.B.C.D.10. 已知,可以求得—————()A.B.C.D.二、多项选择题(本大题共18分,共 3 小题,每小题 6 分)1. 线性系统响应满足以下规律————————————() A. 若起始状态为零,则零输入响应为零。
B. 若起始状态为零,则零状态响应为零。
C. 若系统的零状态响应为零,则强迫响应也为零。
D. 若激励信号为零,零输入响应就是自由响应。
2. 1.之间满足如下关系———————()A.B.C.D.3. 一线性时不变因果系统的系统函数为H(s),系统稳定的条件是——()A. H(s)的极点在s平面的单位圆内B. H(s)的极点的模值小于1C. H (s)的极点全部在s平面的左半平面D. H(s)为有理多项式。
《信号与系统》试卷及答案1

1、画出系统的模拟方框图;
2、由模拟方框图写出系统的状态方程。
解:(10分)
1、因为
所以该系统的直接型模拟方框图如下
2、状态变量按上图所示选取,可得系统的状态方程为
东莞理工学院(本科)试卷(B卷)
2004—2005学年第二学期
一、已知 ,试画出 、 的波形。(10分)
2、状态变量按上图所示选取,可得系统的状态方程为
稳定的。(5分)
东莞理工学院(专科)试卷(A卷)
2008--2009学年第1学期
《信号与系统》试卷
一、计算下列积分(共12分,每题6分)
1、 ;2、
解:(12分)
1、 ;
2、
二、已知 ,画出 的波形(12分)
解:(12分)
由题知 的表达式为
所以 的表达式为
解:(11分)
因为
所以
故被抽样信号的最大角频率为 ,即 。根据抽样定理,其无失真抽样的最小抽样频率为 。
九、判断下列因果系统的稳定性(12分)
1、 ;2、
解:(12分)
1、由题知
系统的极点为 , 。由于系统的两个极点都位于 左半平面,所以该系统是稳定的。
2、由题知该离散系统的极点为 , 。由于 ,所以 位于 平面上单位圆外,故该离散系统不稳定。
解:(10分)
因为
所以
令 ,有
故
从而有
,
由抽样定理可得
六、已知某离散 系统的单位脉冲响应为(10分)
求该系统的系统函数 。
解:(10分)
由题意知
所以
七、已知某离散 系统的系统函数如下(10分)
试分析该系统的稳定性。
解:(10分)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Signal and system test paper B (08-09)一、PART 1 CHOOSING THE BEST ANSWER (25 points)1.The following signals are shown below, the ______is periodic signal.A.x(t)=costu(t)B.x[n]=cos(1/4)nC.X(Ω)=The Fourier transform of x[n]2.The Fourier transform of periodic signal x T(t) is_______ .A. discrete values c kB. impulse train(冲激序列)C. continuous function3.The frequency transfer function of the ideal filter is given by│H(ω)│=0 for -B≤│ω│≤B,│H(ω)│=1 for │ω│≥Bthe ideal filter is_________.A. a high-pass filterB. a band-stop filterC. a low-pass filter4.The input/output relationship of the discrete-time system in time domain is______.A. The Fourier transform representation and the convolution model.B. The input/output differential equation and the convolution model.C. The input/output difference equation and the convolution model.5.The rectangular pulse train is periodic signal with fundamental period T. Theamplitude spectrum is |Ck|. When T becomes large, Then________A. |Ck| becomes larger and the line spectrum interval (谱线间隔) becomeslargerB. |Ck| becomes smaller and the line spectrum interval becomes largerC. |Ck| becomes smaller and the line spectrum interval becomes smaller6.Suppose that x(t) is given by x(t)={x1(t) t1≤t﹤t2 and x2(t) t≥t2}.The signal x(t) can be expressed _______.A. x(t)=x1(t)[u(t-t1)- u(t-t2)]+ x2(t)[u(t-t1)- u(t-t2)]B. x(t)=x1(t)[u(t-t1)- u(t-t2)]+ x2(t)u(t-t2)C.x(t)=[x1(t) + x2(t)][u(t-t1)- u(t-t2)]7.The discrete-time system hes the relationship with the input and theoutput .y[n]= nx[n].To determined the system are _______.A. linear,causal,time varying , memorylessB. nonlinear,causal,time varying, memoryC. linear,causal, time invariant, memoryless8. The magnitude function of the ideal lowpass filter is 1 for|ω|<B, the time delay is t d for all frequency. The input signal tothe ideal lowpass filter is δ(t), the Fourier transform Y(ω) of theresponse y(t) is ______.A. 1, for allω.B. d-j ωt e ,for |ω|<BC. 1, for |ω|<B9. The relationship between the DTFT and DFT is _________.A. DTFT=DFTB.Ω=2π/N DFT=DTFT| C. Ω=2πk/N DFT=DTFT|, k=0,1…N -1 10. For a stable linear time-invariant system, the steady state response must inthe______.A. zero input responseB. zero state responseC. zero input and zero state response二 、ANSWER THE FOLLOWING QUESTIONS (40 points)、1. Compute the following expression:A: ⎰+∞∞-2(t 3+4) δ(1-t)dtB: {t[u(t)-u(t-2)]}’C: u(t)*u(t)2. Given a system y(t)=x 2(t),determine whether the continuous-time system iscausal or noncausal ,has memory or is memeoryless,is linear or nonlinear,istime invariant or time varying.Justify your answer.3. A linear time invariant system, when input 1x (t)=u(t), the response is-2t 1y (t)=(1-e )u(t), when input 2x (t)=cos(2t), the response is 2y (t)=cos(2t-/4)π, Findthe response when input the following signals.A: x(t)=u(t-1)+2cos(2t-4)B: x(t)=(t)+tu(t)δ4. Plot the magnitude function of the ideal lowpass filter ,if the input signal tothe i deal lowpass filte is δ(t) ,the response is y(t), the Fourier transform isY(ω),plot the |Y(ω)|.5. Compute the reverse transform of the following signals. A: 2s+2X(s)=s +7s+12B: -s 22se X(s)=(s+1)+1006. For the following linear time-invariant continuous-time systems, determine ifthe system is stable, marginally stable or unstable. A: 2s-4H(s)=s +7sB: -2t h(t)=e u(t) C: dy(t)-2y(t)=x(t)dt7. For the following ideal lowpass filter .the frequency response functionH(ω)=2[u(ω+π)-u(ω-π)]e -j3w .if x(t)=sin2t+pute the y(t).y (t )x (t )8. Plot the magnitude function of the ideal lowpass, ideal highpass, idealbandpass, ideal bandstop filter.三 、PART 3 COMPUTE AND ANSWER THE FOLLOWING QUESTIONS(35 points)1.Given an input of x(t)=4+2cos(10t+∏/4)+3 cos(30t+∏/2) .find the outputy(t) to each of the following filters.2.Given a bandlimited signal x(t) ,the Fourier transform X(ω) is shown in Fig. A. The system is shown in Fig. B.- Fig APlot the A(ω),B(ω) and Y(ω).{ Note: x(t)cos ω0t<--->1/2 [X(ω+ω0)+ X(ω-ω0)] }3. Given two signals x1(t)=x2(t) = compute theconvo lution y(t)=x1(t)*x2(t) and the Fourier transform Y(ω), plot the waveform of y(t) and |Y(ω)|.4.Given the frequency response function of the ideal lowpass filterH(ω)={ 1, |ω|<ωc and 0 ,|ω|>ωc } .the input signal x(t)=sinat/Пt. Compute and analyse the following questions.(a).if a < ωc,the filter output y(t).(b).if a > ωc,the filter output y(t).(c).which case come into being the output distortion.(where x(t)=sinat/Пt ---取样函数)5. For a linear time-invariant continuous-time system are connected as shown below. Compute the transfer function of the system and find theβ value if the system is stable2121,1,0{<≤-t t other all。
