清华大学-理论力学-习题解答-2-09
理论力学答案完整版(清华大学出版社)1

本章要点:
一、 三个概念:力、力矩和力偶 1 力: 力的定义、力的三要素、集中力、分布力;
力的投影:直接投影法和二次投影法;力在平行轴上的投影都相等; 力的合成:平行四边形法则、三角形法则、多边形法则; 合力投影定理 2 力矩:力对点之矩的定义、力对点之矩的三要素、对点的合力矩定理; 力对轴之矩的定义、力对轴之矩和对点之矩的关系、对轴的合力矩定理; 3 力偶:力偶的定义、力偶的三要素、力偶的等效条件; 力偶系的合力偶等于分力偶的矢量和.
解:ξ 轴与 y 轴的交点为 B,合力对 B 点的力矩为 M B = FRx 3k − FRz 3i ;
ξ 轴方向的单位向量为:ξˆ = 1 (3i − 2k )。
13
利用力对点吱矩与力对轴之矩的关系有:
Mξ = M B ⋅ξˆ = −513.4 (N) 。
1-4 图示平面 Π 在各坐标轴上的截矩分别为 a,b, c ,且 a = b 。计算图示力 F 和力偶 M
解:(a)图示三铰拱,BC 半拱为二力构件,约束力一定是沿 BC 连线作用,铰链 A 处的约 束力方向由三力平衡汇交定理确定。
题 1-7(a)图 (b)图示三铰拱,铰链 A、B 和 C 三处的约束力方向都不能确定,因此用两个分力力表示。
3
题 1-7(b)图 (c)图示三铰拱,BC 半拱为二力构件,约束力一定是沿 BC 连线作用,AC 半拱上除约束 力外仅有力偶作用,因力偶只能与力偶平衡,因此 A、C 处的约束力必互相平行并组成力偶。
题 1-9(d力的大小为:
其中: cosϕ1
=
3 13 13
, cosγ 2
=
22 11
;ϕ2
=
45o
。
FR = FR2x + FR2y + FR2z = 645 (N) ;
清华大学版理论力学课后习题答案大全-----第5章点的复合运动分析
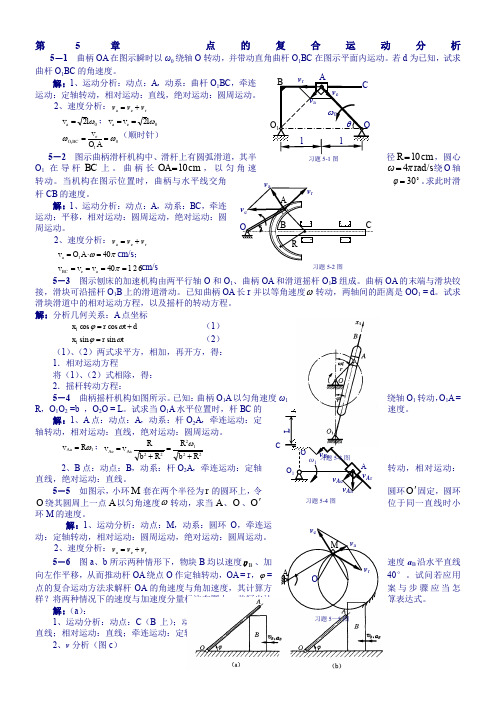
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴30=φ。
求此时滑转动。
当机构在图示位置时,曲柄与水平线交角杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v += πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程 将(1)、(2)式相除,得: 2.摇杆转动方程:5-4 曲柄摇杆机构如图所示。
已知:曲柄O 1A 以匀角速度ω1绕轴O 1转动,O 1A = R ,O 1O 2 =b ,O 2O = L 。
试求当O 1A 水平位置时,杆BC 的速度。
解:1、A 点:动点:A ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
理论力学答案完整版(清华大学出版社)9

F1 = F1(sinϑ i − cosϑ j) , F2 = F2i
点 A 和 B 的坐标及其变分为
rA = −(l1 − l2 )cosϑ i + (l1 + l2 )sinϑ j
,
rB = −2l1 cosϑ i
δrA = (l1 − l2 )sinϑ ⋅δϑ i + (l1 + l2 )cosϑ ⋅δϑ j ,
Fδ re − G1δ ra = 0 按速度合成定理,虚位移存在如下关系:δ ra = δ re tan β ,于是
(a)
题 9-9 图
导出 F = G1 tan β .
(2)水平面有摩擦时,当水平力 F 较小,斜面 D 有向左运动趋势,此时摩擦力方向向右,
临界平衡时,虚功方程为
(F + ) Fmax δ re − G1δ ra = 0 , 其中 Fmax = (G1 + G2 ) f 。求得: F ≥ G1 tan β − (G1 + G2 ) f .
i =1
解题要领 1) 对于自由度不为零的系统,求其平衡时主动力满足的关系可用虚功原理. 2) 对于自由度为零的系统,为求其约束力,可以依次解除一个约束,使自由度为 1,即将
此约束力作为主动力应用虚功原理. 3) 独立的坐标变分个数与系统的自由度相同,可以用解析或虚速度的方法建立不独立的坐
标变分满足的关系.
三 广义坐标表示的虚位移原理
广义坐标:确定质点系位形的独立坐标。
虚功原理的广义坐标表述:受理想约束的质点系,其平衡的充分必要条件是系统所有与广义
坐标对应的广义力为零
Qj = 0 ( j = 1,2,L, m)
∑ 其中
Qj
=
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
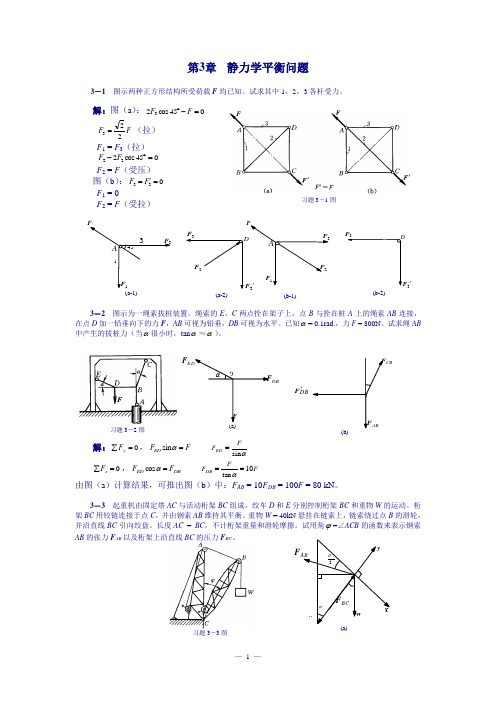
F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
清华理论力学课后答案2

kh da
(b)
w.
co
m
4
三角块 V4
V4 = 2 × 3 × 3 ÷ 2 = 9
(1, 7, 1)
2-5 均质折杆及尺寸如图示,求此折杆形心坐标。 解: 将图示折杆简化为折线计算。 折杆有 5 段直线组成, 每一段的长度及形心坐标如表所示。 按形心计算公式,有
xc =
∑iLi xi 200 × (−100) + 100 × (−50) + 100 × 0 + 200 × 100 + 100 × 200 = 200 + 100 + 100 + 200 + 100 ∑iLi = 21.43(mm)
kh da
,
w.
FRx ' = F1 cos 45� − F2 cos 45� = 0 ,
�
co
在坐标轴上的投影为
m
解: 各力均在与坐标平面平行的面内, 且与所在平面的棱边成 45°角。 将力系向 A 点简化, 主矢 FR '
a b c + + = 0。 F1 F2 F3
当主矢与主矩平行时,力系能简化为力螺旋,即从 FR '× M O = 0 得,
yc =
答
案
网
(200,100,-50)
ww w.
3
kh da
题 2-5 图
w.
co
m
题 2-6 图
解: 由对称性知,该图形的形心一定在 x 轴上,即 yc = 0 。用负面积法计算其横坐标。此平面图
按形心计算公式,有
xc =
2-7 工字钢截面尺寸如图示,求此截面的形心坐标。
题 2-7 图
清华大学-理论力学-习题解答-2-23

2-23 在圆周轮传动装置中,半径为R 的主动齿轮以角速度0ω和角加速度0ε作反时针转向的转动,长为R 3的曲柄以同样的角速度和角加速度绕其轴作顺时针转向的转动,M 点位于半径为R 的从动齿轮上,且在垂直于曲柄的直径末端,如图所示,求M 点的速度和加速度。
解:由于在齿轮接触的点速度必须相等,所以以A 点为中心旋转的齿轮的旋转角速度也为0ω。
M 点的牵连速度为03e R ω=−V j ,相对速度为0r R ω=V i ,所以M 点的速度为:
003M R R ωω=−V i j
M 点的牵连加速度,即A 点的加速度为20033e R R εω=−−a j i ,M 点的相对于A 点的加速度为
200r R R εω=+a i j ,所以M 点的加速度为:
220000(3)(3)M R R R R εωωε=−+−a i j。
清华大学理论力学课后习题答案大全

第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕcos )(r R x A += (1) ϕsin )(r R y A +=(2)α为常数,当t = 0时,0ω=0ϕ= 0 221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R = ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R yt r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:RvR v A A ==ωR v R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度=12 rad/s ,=30,=60,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
习题6-1图A BCv 0h习题6-2图 P ABv CA BCv o h习题6-2解图习题6-3解图习题6-3图 v A = vv B = v习题6-6图习题6-6解图解:杆BC 的瞬心在点P ,滚子O 的瞬心在点D BDv B ⋅=ωBPBD BP v B BC ⋅==ωω ︒︒⨯=30sin 27030cos 36012 rad/s 8=PC v BC C ⋅=ωm/s 87.130cos 27.08=︒⨯=6-5 在下列机构中,那些构件做平面运动,画出它们图示位置的速度瞬心。
理论力学解答(清华版)

第一章 静力学基本概念1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量B.自由矢量C.定位矢量1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相反,则其合力可表为( C )。
A.1F –2FB.2F - 1FC.1F +2F图1-18 图1-191-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6B. 70.0C. 136.6D.25.91-4 力的可传性只适用于 A 。
A. 刚体B. 变形体1-5 加减平衡力系公理适用于 C 。
A. 刚体;B. 变形体;C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0B. F/2C. F/6D.-F/31-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为: Fx = -402N ,Fy = 302N ,Fz = 502 N 。
图1-20 图1-21第二章力系的简化2-1.通过A(3,0,0),B(0,4,5)两点(长度单位为米),且由A指向B的力F,在z轴上投影为,对z轴的矩的大小为。
答:F/2;62F/5。
2-2.已知力F的大小,角度φ和θ,以及长方体的边长a,b,c,则力F在轴z和y上的投影:Fz= ;Fy= ;F对轴x的矩M x(F)= 。
答:Fz=F·sinφ;Fy=-F·cosφ·cosφ;Mx(F)=F(b·sinφ+c·cosφ·cosθ)图2-40 图2-412-3.力通过A(3,4、0),B(0,4,4)两点(长度单位为米),若F=100N,则该力在x轴上的投影为,对x轴的矩为。
