哈工大理论力学07考试题及答案a
理论力学复习试题和答案(哈工大版)

C :作用于质点系的约束反力主矢恒等于零; D:作用于质点系的主动力主矢恒等于零;
..
..
6、 若作用在 A 点的两个大小不等的力 F 1 和 F 2,沿同一直
反。则其合力可以表示为
③
。
① F 1- F 2; ② F 2- F 1; ③ F 1+ F 2;
7、 作用在一个刚体上的两个力 F A、 F B,满足 F A=- F B 的条件,则该二力可能是②
( √) (× )
14、 已知质点的质量和作用于质点的力,质点的运动规律就完全确定。
(× )
15、 质点系中各质点都处于静止时,质点系的动量为零。于是可知如果质点
系的动量为零,则质点系中各质点必都静止。
(×)
16、 作 用 在 一 个 物 体 上 有 三 个 力 , 当 这 三 个 力 的 作 用 线 汇 交 于 一 点 时 , 则 此 力 系 必 然 平 衡 。
..
..
..
..
2、图示平面结构,自重不计。 求支座 A 的约束反力。
B 处为铰链联接。已知: P = 100 kN , M = 200 kN · m, L1 = 2m , L2 = 3m 。试
3、 一 水平 简支梁 结 构, 约 束和载 荷如 图 所示 , 求支座
q A
D
M B
E
P C
A和
B 的约束反力。
一、 是非题
1、 力 有 两 种 作 用 效 果 , 即 力 可 以 使 物 体 的 运 动 状 态 发 生 变 化 , 也 可 以 使 物 体 发 生 变 形 。
( √)
2、 在理论力学中只研究力的外效应。
( √)
3、 两端用光滑铰链连接的构件是二力构件。
(彩色版第七版)理论力学哈工大课后题答案
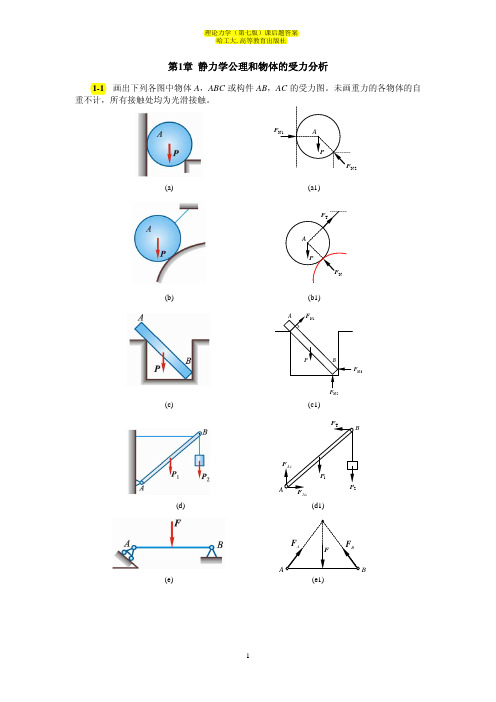
第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体A ,ABC 或构件AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
2F(a)(a1)(b) (b1)2N F 3N(c) (c1)Ax(d) (d1)B(e) (e1)Bq(f) (f1)(g)1F 2(h)(h1)Ax(i)(i1)(j)(j1)F(k) (k1)BA F FF ′ (l) (l2) (l3)图1-11-2画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所有接触处均为光滑接触。
22N(a1)2AxFAx(a2)3N(b)(b1)N3′(b2) (b3)1N2AxF(c)(c1)1N2N2Ax(c2)(c3)(d) (d1)CDy(d2)(d3)CxBxByF By′(e) (e1)(e2) (e3)ByBxAx(f) (f1)AxBx F′(f2)(f3)FB(g) (g1)BCx′F(g3)(h)(h1)FFAxC(i) (i1) (i2)F(i3)(i4)AyFFFCy (j) (j1)(j2) 2TFDx3TEyFCyEx′(j3) (j4) (j5)BBDECyF(k)(k1)BBCx (k2) (k3) DEA1F(l) (l1) (l2)A C E(l3) (l4)或CDxFEyFEy(l2)’(l3)’ (l4)’F′(m)(m1)EADFH2FAD′(m2) (m3)BN(n)q3N(n2)G(o)(o1)BADB(o2) (o3) (o4)图1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心A ,B 和C 处受3个力作用,如图2-1a 所示。
N 1001=F ,沿铅直方向;N 503=F ,沿水平方向,并通过点A ;N 502=F ,力的作用线也通过点A ,尺寸如图。
求此力系的合力。
(a)(b)图2-1解 (1) 几何法作力多边形abcd ,其封闭边ad 即确定了合力F R 的大小和方向。
理论力学(哈工第七版) 课后练习答案 第三部分
A
ϕ
O
r ϕ
M
W=
2π
∫ 4ϕ dϕ + (m
0
− mB ) g ⋅ 2π r
A B
A mAg
= 8π 2 + (mA − mB ) g ⋅ 2π r = 8π 2 + 1× 9.8 × 2π × 0.5 = 110 (J)
B
mBg
(a)
(b)
7
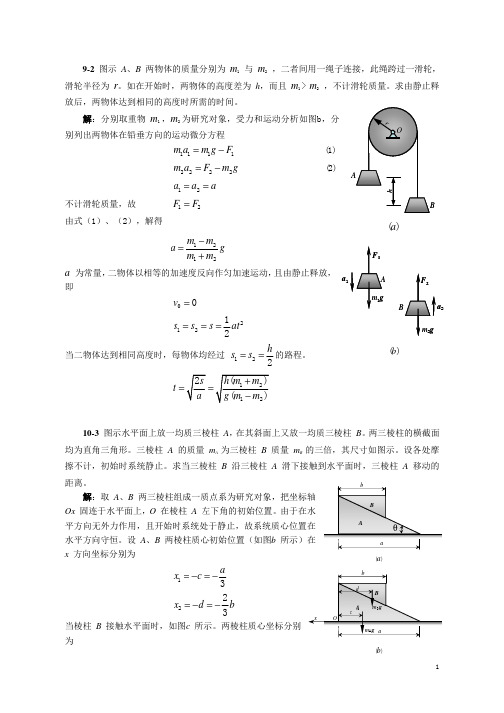
12-4 图示坦克的履带质量为 m,两个车轮的质量均为 m1。车轮被看成均质圆盘,半径为 R, 两车轮间的距离为 πR。设坦克前进速度为 v,计算此质点系的动能。 解:系统的动能为履带动能和车轮动能之和。将履带分为四部 分,如图b 所示。履带动能:
O
P2 P aB − 1 a A = FN − P 1−P 2 g g
其中, a A = a , aB = 解得
A
a 2 1 (2 P 1−P 2 )a 2g
B
(a)
FN = P 1+P 2 −
v FN
O
v P 1
A
v aA
v aB B
v P2
(b)
11-1 质量为 m 的点在平面 Oxy 内运动,其运动方程为
得
G1
320
B C
SB
S A = 170 mm S B = 90 mm
(b)
2
10-12 图示滑轮中,两重物 A 和 B 的重量分别为 P1 和 P2。如物体 A 以加速度 a 下降, 不计滑轮质量,求支座 O 的约束力。 解:对整体进行分析,两重物的加速度和支座 O 的约束力如图b 所示。由 动量定理知:
整体受力和运动分析如图b因为0xf所以x方向系统守恒有21cos0brbmvmvv??解得121cosbrmmvvm1所以该系统动能为设此时三棱柱a沿三棱柱b下滑的距离为s则其重力作的功为1sinwmgs??系统动能22b211221sin12cosmmtmmvm由系统动能定理tw即1sinwmgs??上式对时间求导并注意到rdsdtv整理后得22112121sinsincosbbrmmmmvamgvm?????得2b2a212b2b2r2122b21122
理论力学第7版(哈工大)第3章习题

《理论力学》第二章作业习题2-1解:根据题意,取滑轮B 为研究对象,其受力情况如上图所示:物体对其有一铅直向下的拉力P , 沿DB 有一与物体重量相等的拉力P,拉杆AB 的作用力A B F 和支杆CB 的作用力C B F。
建立图示坐标系,列平衡方程0X YF F ⎧=⎪⎨=⎪⎩∑∑co s 30sin 300sin 30co s 300o oA B C B o oC B F F P P F P ⎧++=⎨++=⎩解之得54.64()74.64()A B C B F kN F kN =⎧⎨=-⎩答:拉杆AB 和支杆CB 所受的的力分别为54.64kN (拉)和74.64 kN (压)。
习题2-6解:(1) 取构件BC 为研究对象,其受力情况如上图(a)所示:由于其主动力仅有一个力偶M ,那末B 、C 处所受的约束力BF、CF 必定形成一个阻力偶与之平衡。
列平衡方程()0B M F =∑C M F l -=所以C M F l=(2) 取构件ACD 为研究对象,其受力情况如上图(b)所示:C 处有一约束力C F '与BC 构件所受的约束力C F 互为作用力与反作用力关系,在D 处有一约束力D F,方向向上;在A 处有一约束力A F,其方向可根据三力汇交定理确定,根据构件尺寸,A F与水平方向成45度角。
列平衡方程X F =∑sin 450oA C F F '-=所以222A C C M F F F l'===答:支座A的约束力为2M l,其方向如上图(b)所示。
习题2-9解:主矢RF在各坐标轴上的投影:)(6.4375210121321N F F F F x -=---=∑)(6.1615110321321N F F F F y -=+--=∑力系对O 点的主矩:).(42.21439805120021100)(31mm N F F F F MMOO=-+==∑由于主矢在各坐标轴上的投影均为负值而主矩为正值,合力的作用线应在原点O的左侧且方向向左下方,其大小为()())(5.46622N F F F YXR =+=∑∑其与O 点的距离为:)(96.455.46642.21439mm F M d R O=='=答:力系向O点简化的结果得一方向向左下方的主矢ji F R6.1616.437--='和一沿顺时针方向的力偶,力偶矩为21439.42Nmm; 力系的合力的大小为466.5N ,处于原点O 的左侧且与O 点的距离为45.96mm (如图)。
哈尔滨工业大学理论力学课后习题答案
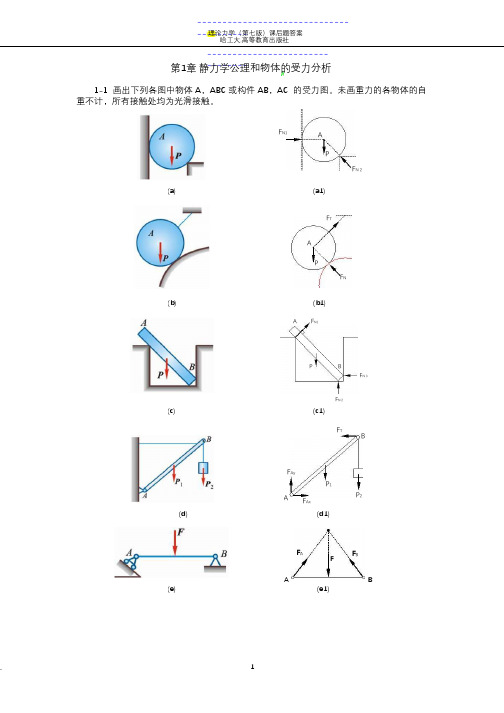
.----------------------------------------理论力学(第七版)课后题答案 哈工大.高等教育出版社 -------------------------------- 第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
F N1A PF N 2(a) (a1)F TA PF N(b)(b1)AF N1P BF N 3F N 2(c) (c1)F TBF AyP 1P 2AF Ax(d) (d1)F AF BFAB(e)(e1)qFF Ay F BF AxA B(f) (f1)FBC F CAF A(g) (g1)F Ay FCCA F Ax BP1 P2(h) (h1)BFCF CF AxDAF Ay(i) (i1)(j) (j1)BF B FCPF AyF AxA(k) (k1)F CAF AB 2 F AC CA2 F ABBF ACF BAA P (l) (l1)(l2)(l3)图 1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
F N 2C2 F P 2(a1) F N1N(a)BF N1BC F N 2F NP 2P1P1F AyF Ay F AxF AxAA(a2) (a3)F N1AP1F N3B P 2F N 2(b) (b1)2 F NF N3F N1ABP 2P1F N F N 2(b2)(b3)F AyF AxA C D F N2BP 2P 1F N1(c)(c1)F AyF TAF AxD2 F F N2TBP 1F N1P 2(c2)(c3)F AyF BqBAF AxCDF C(d)(d1)F DyF AyF BqqD2 FDxBAF AxCF Dx D 2 FDyF C(d2) (d3)F Ay2 FBxqBF AyF AxqAB 2F ByF AxF CxC F CyP F BxAB PF Cx (e1)CF ByF Cy(e)(e2)(e3)F 1CF 2F AyF ByABF AxF Bx(f)(f1)F Cx2 FCxCCF 1F CyF 2 F 2F AyCyF ByAF BxF Ax B(f2)(f3)F BF AyCBAF AxP(g)(g1)2 F CyF T2 FCxCF AyF BF TDCF AxBAF Cx P (g2)(g3)DF 1F CyF B2 F 2F BBCF CxBF Ay AF Ax(h)(h1)(h2)A F AxF AyF CyF CxC2 A F EF CyF F OyCDF OxF Cx 2EOB(i)(i1)(i2)A A2 F Ax2 FE2 F AyFEC D F ByF ByF OyF BxF OxF BxOBB (i3)(i4)F AyDE F CxF TA F AxF ByC CHF By F Cy BPF BxF BxB(j)(j1)(j2)F Ay F Dy 22 F Ey2 F CF Cx 2 E F AxT 2 D F T 22FExF ExA D F Dx 2E F DxF T3F T12FCyF DyF Ey(j3)(j4)(j5)EFF BCED2 BF Cx⎝2 2 F DEF Cy(k)(k1)F BF FC BF Cx⎝EC F Cy90︒ ⎝FDED DF AyF AyAAF AxF Ax(k2) (k3)F B2 FBF 1F DBBDCAF AF C(l)(l1)(l2)F 22 DF DF 1F 2DBAC EE F EF AF C F E(l3)(l4)或2 2 F DyF2F 1F F Dy F 2F 1B 2 DF DxF DxBBD D F ExA C E C E F ExF CF EyF AF CF Ey(l2)’(l3)’(l4)’2 F ADAF CyF CxCF 1B(m)(m1)F ADDF ADHEF 2A DF EF HF AD 2(m2)(m3)F N AAF kF N BF OyF OxBO(n) (n1)F N1B Dq2 F BF N 2F N3(n2)FB D FF C F EF AF G GCEA(o)(o1)FBB DFDF BF E F FF C F D2 FEA F AF B 2CD(o2)(o3) (o4) 图 1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ,B 和 C 处受 3个力作用,如图 2-1a 所示。
理论力学复习试题和答案(哈工大版)

一、是非题1、力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
(√)2、在理论力学中只研究力的外效应。
(√)3、两端用光滑铰链连接的构件是二力构件。
(×)4、作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
(√)5、作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
(×)6、三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
(×)7、平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
(√)8、约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
(×)9、在有摩擦的情况下,全约束力与法向约束力之间的(应是最大)夹角称为摩擦角。
(×)10、用解析法求平面汇交力系的平衡问题时,所建立的坐标系x,y轴一定要相互垂直。
(×)11、一空间任意力系,若各力的作用线均平行于某一固定平面,则其独立的平衡方程最多只有3个。
(×)12、静摩擦因数等于摩擦角的正切值。
(√)13、一个质点只要运动,就一定受有力的作用,而且运动的方向就是它受力方向。
(×)14、已知质点的质量和作用于质点的力,质点的运动规律就完全确定。
(×)15、质点系中各质点都处于静止时,质点系的动量为零。
于是可知如果质点系的动量为零,则质点系中各质点必都静止。
(×)16、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
(×)17、力对于一点的矩不因力沿其作用线移动而改变。
(√)18、在自然坐标系中,如果速度υ = 常数,则加速度α = 0应是切线方向加速度为零。
(×)19、设一质点的质量为m,其速度 与x轴的夹角为α,则其动量在x轴上的投影为mvx =mvcos a。
(√)20、用力的平行四边形法则,将一已知力分解为F1和F2两个分力,要得到唯一解答,必须具备:已知F1和F2两力的大小;或已知F1和F2两力的方向;或已知F1或F2中任一个力的大小和方向。
哈尔滨工业大学理论力学课后习题答案

.----------------------------------------理论力学(第七版)课后题答案 哈工大.高等教育出版社 -------------------------------- 第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
F N1A PF N 2(a) (a1)F TA PF N(b)(b1)AF N1P BF N 3F N 2(c) (c1)F TBF AyP 1P 2AF Ax(d) (d1)F AF BFAB(e)(e1)qFF Ay F BF AxA B(f) (f1)FBC F CAF A(g) (g1)F Ay FCCA F Ax BP1 P2(h) (h1)BFCF CF AxDAF Ay(i) (i1)(j) (j1)BF B FCPF AyF AxA(k) (k1)F CAF AB 2 F AC CA2 F ABBF ACF BAA P (l) (l1)(l2)(l3)图 1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
F N 2C2 F P 2(a1) F N1N(a)BF N1BC F N 2F NP 2P1P1F AyF Ay F AxF AxAA(a2) (a3)F N1AP1F N3B P 2F N 2(b) (b1)2 F NF N3F N1ABP 2P1F N F N 2(b2)(b3)F AyF AxA C D F N2BP 2P 1F N1(c)(c1)F AyF TAF AxD2 F F N2TBP 1F N1P 2(c2)(c3)F AyF BqBAF AxCDF C(d)(d1)F DyF AyF BqqD2 FDxBAF AxCF Dx D 2 FDyF C(d2) (d3)F Ay2 FBxqBF AyF AxqAB 2F ByF AxF CxC F CyP F BxAB PF Cx (e1)CF ByF Cy(e)(e2)(e3)F 1CF 2F AyF ByABF AxF Bx(f)(f1)F Cx2 FCxCCF 1F CyF 2 F 2F AyCyF ByAF BxF Ax B(f2)(f3)F BF AyCBAF AxP(g)(g1)2 F CyF T2 FCxCF AyF BF TDCF AxBAF Cx P (g2)(g3)DF 1F CyF B2 F 2F BBCF CxBF Ay AF Ax(h)(h1)(h2)A F AxF AyF CyF CxC2 A F EF CyF F OyCDF OxF Cx 2EOB(i)(i1)(i2)A A2 F Ax2 FE2 F AyFEC D F ByF ByF OyF BxF OxF BxOBB (i3)(i4)F AyDE F CxF TA F AxF ByC CHF By F Cy BPF BxF BxB(j)(j1)(j2)F Ay F Dy 22 F Ey2 F CF Cx 2 E F AxT 2 D F T 22FExF ExA D F Dx 2E F DxF T3F T12FCyF DyF Ey(j3)(j4)(j5)EFF BCED2 BF Cx⎝2 2 F DEF Cy(k)(k1)F BF FC BF Cx⎝EC F Cy90︒ ⎝FDED DF AyF AyAAF AxF Ax(k2) (k3)F B2 FBF 1F DBBDCAF AF C(l)(l1)(l2)F 22 DF DF 1F 2DBAC EE F EF AF C F E(l3)(l4)或2 2 F DyF2F 1F F Dy F 2F 1B 2 DF DxF DxBBD D F ExA C E C E F ExF CF EyF AF CF Ey(l2)’(l3)’(l4)’2 F ADAF CyF CxCF 1B(m)(m1)F ADDF ADHEF 2A DF EF HF AD 2(m2)(m3)F N AAF kF N BF OyF OxBO(n) (n1)F N1B Dq2 F BF N 2F N3(n2)FB D FF C F EF AF G GCEA(o)(o1)FBB DFDF BF E F FF C F D2 FEA F AF B 2CD(o2)(o3) (o4) 图 1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ,B 和 C 处受 3个力作用,如图 2-1a 所示。
哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案

tan θ =
r sin ϕ h − r cos ϕ
sin ω 0 t h − cos ω 0 t r ]
图 7-5
注意到 ϕ = ω 0 t ,得
θ = tan −1 [
(2)
自 B 作直线 BD 垂直相交 CO 于 D,则
tan θ =
r sin ω 0 t BD = DO h − r cos ω 0 t
80
理论力学(第七版)课后题答案 哈工大.高等教育出版社
7-6 如图 7-6 所示,摩擦传动机构的主动轴 I 的转速为 n = 600 r/min 。轴 I 的轮盘与轴Ⅱ的轮 盘接触,接触点按箭头 A 所示的方向移动。距离 d 的变化规律为 d = 100 − 5t ,其中 d 以 mm 计, t 以 s 计。已知 r = 50 mm , R = 150 mm 。求: (1)以距离 d 表示轴 II 的角加速度; (2)当 d = r 时,轮 B 边缘上 1 点的全加速度。 解 (1)两轮接触点的速度以及切向加速度相同
∠CBO =
π , x B = 2 R cos ϕ 2 & B = 2 R + vt (↓) x B (0) = 2 R , x
(2 R) 2 − x B
2
vt vt 1 2 − 2 2 − ( )2 R R 2R 2 v v , vC = 2 Rω = − ω =− 2 R sin ϕ sin ϕ sin ϕ = =
两边对时间 t 求导:
vt l
& sec 2 ϕ = , ϕ & = cos 2 ϕ , ϕ && = − ϕ
当ϕ =
v l
v l
2v & cos ϕ sin ϕ ⋅ ϕ l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六、 (本题 10 分) 解: 杆刚离开地面上仍为平行移动, 地 面约束力为零。以杆为研究对象,杆的受 力分析如图并加上惯性力。 (1 分)
FgC = ma
(1 分)
(1 分)
由动静法得: ∑ M A ( F ) = 0 ⇒ mar sin 30 0 − mgr cos 30 0 = 0 (1 分) 得: a = 3 g (1 分)
三、基本计算题(共 20 分)
r 1、图示结构中,A, C, D 三处均为铰链约束。横杆 AB 在 B 处承受集中载荷 F1 , r 结构各部分尺寸均示于图中,若已知 F1 和 l,试求杆 CD 的受力以及 A 处的约束
力。 (6 分)
2 、图示均质细杆和均质圆盘焊接而成,质量皆为 5Kg,杆长 l=0.8m,圆盘半径 r=0.2m,求:系统对于 悬挂点 O 轴的转动惯量。 (6 分)
XA
SCD (1 分)
2、 (本题 6 分)
解: I o杆 =
I o盘 =
1 1 l ml 2 + m = ml 2 (2 分) 12 3 m 1 2 mr + m(l + r ) 2 (2 分) 2
1 1 × 5 × 0 .8 2 + × 5 × 0 .2 2 + 5 × ( 0 .8 + 0 .2 ) 2 3 2
P
G
2、鼓轮半径 R=0.5m,物体的运动方程为 x=5t2(t 以 s 计,x 以 m 计) ,则鼓轮 的角速度ω= ,角加速度α= 。
R
x
x
3、平面图形上任意两点的加速度 aA、aB 与 A、B 连线垂直,且 aA ≠ aB,则该瞬 时,平面图形的角速度ω=
aA A
和角加速度 α 应为
aB B
1、F= 100N 方向如图示,若将 F 沿图示 x,y 方向分解,则 x 向分力大小为
2、 某平面任意力系 F1 =4KN, F2=3 KN, 如图所示, 若向 A 点简化, 则得到 ( A.F’=3 KN,M=0.2KNm B.F’=4KN,M=0.3KNm C.F’=5 KN,M=0.2KNm D.F’=6 KN,M=0.3 KNm
牵连运动:圆周运动, ve = O1 Aω 1 (1 分) 速度矢量图如右图所示。根据点的速度合成定理 v a = ve + v r (1 分) 得:
v a = ve / cos 30 0 (1 分)
ω2 =
va ve O1 Aω1 = = = ω1 = 3rad / s 0 O2 A O2 A cos 30 O2 A cos 30 0
。
4、直杆 0A 在平面内以角速度 ω 绕 O 轴逆时针转动,滑块 M 以 vr 相对杆运动, 图示瞬时,科氏加速度大小 ac=( )
vr M 45
5. 如图所示,质量为 m,半径为 R 的均质圆盘绕过 O 点的水平轴做定轴转动,图 示瞬时圆盘角速度为ω,角加速度为ε,则其对 O 轴的转动惯量为 ; 动能为 。
F1 O2 0.2m A 0.2m O1 F2
3、实验测定摩擦系数的方法,把物体放在斜面上,逐渐从零起增大斜面的倾角 φ 直到物体刚开始下滑为止,这时的 φ 就是对应的摩擦角 φf,求得摩擦系数为 ( ) A. fs=tanφf,B. fs=cosφf C. fs=cotφf D. fs=secφf 4、直角杆自重不计,其上作用一力偶矩为 M 的力偶,图(a)与图(b)相比, B 点约束反力的关系为( A、大于 B、小于 C、相等 D、不能确定
(d)
6、杆 AB 的两端可分别沿水平、铅直滑道运动,已知 B 端的速度为 vB,则图示 瞬时 B 点相对于 A 点的速度为____________________。 A) vB sinθ; B) vB cosθ; C) vB ⁄ sinθ; D) vB ⁄ cosθ.
7. 如图所示质量弹簧系统,两弹簧刚度系数 为 k1,k2,物块质量为 m,则系统固有频率为(
∑X =0
3 F = FgA + FgC + Fs = m A + m 3 g (1 分) 2
七、 (本题 10 分) 解:图示机构为单自由度系统,取角度 ϕ 为广义坐标。 (1 分)
y A = l tan ϕ
y C = a sin ϕ
xC = a cos ϕ (1 分)
上述坐标对 ϕ 求变分得
(1 分)
四、计算题(本题 15 分) 解:以均质盘为研究对象,受力和运动分析 如右图,由转动微分方程
( e) ICε = M C (2 分)
T
aoy
ε
aox
3 2g 得: mR 2 ε = mgR (3分) ⇒ ε = (1 分) 2 3R 由质心运动定理得:
mg
(2 分)
T − mg = − maoy (3 分)
2 g (2 分) 3 2 4 T = mg − ma oy = m( g − g ) = g (kN ) (2 分) 3 3 a oy = Rε =
五、 (本题 15 分) 解:因 BC 杆件作曲线平移, (2 分) 故 vC = v B (2 分)
OA 杆作圆周运动: v A = OAω (2 分)
L B M
) 。
2L A B M A 2L
L
(a) (b) a,如图所 5、圆轮绕固定轴 O 转动,某瞬时轮缘上一点的速度为 v,加速度为
示。试问哪些情况是不可能的?(
)
A、(a)、(b)
v
B、(b)、(c)
a O v
C、(c)、(d)
a v O a O v O
D、(a)、(d)
a
(a)
(b)
(c)
理论力学
试题 A 卷
2007 ~2008 学年 第 1 学期
一 二 三 四 五 六 七 八 — 一、单选题 ( A) B) C) D) 九 — 十 — 总分
将正确答案的序号填入题后括号内。 (本题 14 分,每小题 2 分) ) 。 86.6 N; 70.7 N; 136.6 N; 25.9 N。 )
3、0; (a B − a A ) / AB
三、基本计算题
1, (本题 6 分)
解:以 AB 为研究对象,受力分析如右图。
∑ X = 0 由静力学平衡方程 ∑ Y = 0 (1 分) ∑ M A = 0
YA
l/2
l/2
F1
X A + S CD cos 45 0 = 0 (1分) 得 S CD sin 45 0 − Y A − F1 = 0 (1分) l S CD sin 45 0 − F1l = 0 (1分) 2 S CD = 2 2 F1 解方程得: X A = −2 F1 (1 分) Y = F 1 A
A.
分别 ) 。
k1k2 ; (k1 + k 2 )m
B.
k1 + k2 ; k1k2 m
C. ( k1 + k2 ) m ;
D.
m 。 k1 + k2
二、填空题
将正确答案填入空内。 (本题 16 分,每空 2 分)
1 、图示物块重 G=100N,用水平力 P 将它压在铅垂墙上,P=400N,物块与墙间 静摩擦系数 fS=0.3,物块与墙间的摩擦力为 F= 。
v BA vB
vA
(3 分)
杆件 AB 作平面运动,以点 A 为基点, 速度分析如右图,有 r v B = v A + v BA (2 分)
v B sin 30 0 = v A ⇒ v B = 2v A (3 分) vC = v B = 2v A = 2OAω = 2 × 0.3 × 10 = 6(m / s ) (1 分)
质量为 m,杆端 A 与轮心为光滑铰链连接。如在 A 处加以水平力 F,使轮沿水 平面作纯滚动。问力 F 为多大,方能使杆 B 端刚好离开地面?
七、计算题 (本题 10 分)
(限用虚位移原理求解)图示机构中,当曲柄 OC 绕 O 轴摆动时,滑块 A
沿曲柄滑动,从而带动杆 AB 在铅直导槽内移动,几何尺寸如图所示,不计各杆 自重, 不计摩擦。 求机构平衡时 F1 与 F2 的关系。
l 2 2 F2 cos 2 ϕ − F1a cos ϕ − F1 a sin ϕ δϕ = 0 (1 分)
因 δϕ 为任意值,有
F2
l − F1 a cos 2 ϕ − F1 a sin 2 ϕ = 0 (1 分) 2 cos ϕ
得: F1 =
F2 l F1 a cos 2 ϕ 或 F = 2 l a cos 2 ϕ
δy A =
l δϕ cos 2 ϕ
δy C = a cos ϕδϕ (1 分) δxC = − a sin ϕδϕ
由虚位移原理
∑ ( X δx
i
i
+ Yi δy i + Z i δz i ) = 0 (2 分)
得: F2δy A − F1 cos ϕδy C + F1 sin ϕδxC = 0 (2 分)
(1 分)
五计算题(本题 15 分) 已知曲柄 OA 以角速度 ω=10rad/s 逆时针转动,OA=0.3m,L1=L2,且 L1//L2 当 BC 运动到与 O 在同一水平线上时,AB 垂直于 OA,求此瞬时 C 点的速度。
60o
60o
60o
六、计算题 (本题 10 分)
(限用达朗贝尔原理求解)均质圆盘质量为 mA, 半径为 r, 均质杆长 l=2r,
C
O
一、单选题(本题 14 分,每小题 2 分) 1、A; 2、C ; 3、A; 4、B; 5、D; 6、D; 7、 A
二、填空题(本题 16 分,每空 2 分) 1、100N;
4、 2ωv r ;
