带参数GPS水准拟合实现跨河高程传递

合集下载

GPS跨河水准测量的理论与实践

GPS定位技术运用于跨河水准测量的理论与实践目录第一节： GPS 定位技术运用于跨河水准测量的理论依据 (1)第二节 GPS 定位技术运用于跨河水准测量的适用范围 (5)第三节 GPS 定位技术运用于跨河水准测量的布点要求 (5)第四节 GPS 技术运用于跨河水准测量中GPS 观测及数据处理 (7)第五节 GPS 定位技术运用于淮扬镇新建铁路项目跨河水准测量 (9)第一节：GPS 定位技术运用于跨河水准测量的理论依据1GPS大地高，水准测量的正常高，高程异常GPS 测量是以 WGS-84 椭球面为基准,在WGS-84 地心坐标系中进行的,所提供的高程为相对于 WGS-84 椭球的大地高 ,遗憾的是相对于 WGS-84 椭球的 GPS大地高是没有物理意义的,只是一个假定的高程系统,而实际工程应用中采用的是以似大地水准面为基准的正常高系统。

所以 ,在实际应用中一般要将 GPS 大地高转化为目前我国使用的正常高(我国现有的高程资料基本属于黄海 56 高程系或 85 高程系 )。

进行 GPS 高程转换要考虑 WGS-84 椭球和本地参考椭球的差异以及大地水准面和似大地水准面相对本地参考椭球的高差 ,即大地水准面高和高程异常。

大地高、正常高和高程异常之间有如下关系 :ξH G=H N+其中 ,HG 为大地高 ;HN 为正常高 ; ξ为高程异常，高程异常，即同一测站点以 WGS-84 为基准的 GPS大地高与以似大地水准面为基准的正常高之间的高程异常。

其几何关系见下图⒉高程异常变化值，高程异常变化率高程异常变化值：当测区中某一个点 A 既用 GPS 定位技术测得其GPS大地高 HGA ，又用常规高程测量方法测得其正常高 HNA, 我们就可以求出 A 点的高程异常值；ξA=H GA-H NA同样，当测区中某一个点 B 既用 GPS 定位技术测得其 GPS 大地高 HGB，又用常规高程测量方法测得其正常高 HNB, 我们就可以求出 B 点的高程异常值。

GPS水准法在海岛间高程传递的应用

GPS水准法在海岛间高程传递的应用摘要：结合所承担的地形项目，利用GPS水准法进行海岛间高程传递。

结果表明，在一些项目中，GPS水准法完全能满足精度要求，能提高工作效率和经济效益。

关键词：GPS水准法；高程异常；曲线拟合法1引言浙江省是我国海岛较多的省份之一，海洋资源丰富。

为了开发海洋资源，维护海洋权利，迫切需要确定每个海岛的地理位置。

众所周知，由于历史原因及技术的落后，海岛的大地基准和高程基准与大陆的基准未统一起来。

而海岛测量与陆地不同，有其自身的特点。

目前，跨海正常高程传递方法有动力水准法、静力水准法、GPS水准法和常规三角高程法等几种。

动力水准法（验潮法）、静力水准法由于需要的工期长，成本随着海岛间的距离增加而不断增加，费时费力，国内未曾应用，国际上应用也很有限。

常规三角高程法虽然精度较高，但是受到了距离影响较大。

相对来说，GPS测量的大地高差精度较高，GPS水准法传递的正常高程，其误差源主要是高程异常误差，在数据充实，地形平坦地区精度能达到厘米级。

且GPS技术现在也日益成熟和完善，能满足海岛建设开发规划对高程基准的要求。

2.GPS水准法基本原理已知某点的正常高，且利用GPS观测该点的大地高，则可精确求得该点的高程异常，考虑到工程测量控制网的范围较小，似大地水准面的变化较平缓，因此，联测水准的GPS点，求得各点的高程异常值，再用曲线拟合的方法来近似大地水准面，以求得其他GPS点的高程异常，从而达到高程系统转换的目的。

曲线拟合法仅是将高程异常近似看作是一定范围内各点坐标的曲线函数，用已联测水准的GPS点的高程异常来拟合这个函数，在求得函数的拟合常数后，就可利用这一函数来计算其他GPS点的高程异常和正常高。

3．工程概况大陈岛位于台州市椒江区东部，台州湾东南，台州列岛中南部。

分上、下大陈，二岛相隔2.5公里水道，总面积11.89平方公里。

大陈岛属于全国风能最富集地区之一，为缓解大陈岛、椒江主城区乃至整个台州的用电问题，大陈岛拟建立风力发电场工程。

三角高程_GPS在跨河水准测量的应用

从表中数据可知 : 同岸 α最大互差 = 3107 mm / km < 13 mm / km; 不同岸 α最大互差 = 4113 mm / km < 18 mm / km[3] ,α平 = 0103065 mm / km。从 C1 - S3 桩跨河 : GPS法正常高高差 △HC1 - S3 =
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
3 C3 - C1 2. 079 67 1. 041 9 1. 104 1 0. 062 2 0. 029 91
4 C4 - C1 2. 046 99 1. 032 1 1. 099 6 0. 067 5 0. 032 98
5 C1 - S3 2. 105 09
2. 329 8 平均 : 0. 030 65
跨河三角高程采用两岸对向同时观测测点斜距及竖直角方式进行。对向同时观测可以极大地提高精度 ,
消除或减弱仪器高误差、大气垂直折射差、地球曲率误差等多项误差 [2 ] 。观测斜距时分别读取仪站与镜站的
3 收稿日期 : 2008—11—24 作者简介 :欧阳平 (1978—) ,男 ,工程师 ,主要从事测绘生产科研工作。
1 前言
当水准路线需要跨越大的水面或宽的峡谷时 ,由于视线超出常规水准测量的长度 ,就必须采用跨河水准测量的方法 ,以指定的精度等级将本岸的高程传递到对岸 [ 1 ] 。三角高程测量以其快速、简便且能保证一定精度而应用于跨河水准测量 ; GPS测量观测周期短、布网迅速、精度高、自动化程度高 ,平面精度已经得到广泛认可和应用 ,高程精度的提高也为 GPS替代水准测量成为可能 , GPS测量不受通视条件限制的优点更适用于跨河高程测量。单独的三角高程测量只能通过闭合差来检验其内符合精度 ,在本例跨河水准测量中 , 用光电测距三角高程法进行施测 ,通过相关精度分析 , 在本例中三角高程测量能达到国家三等水准测量的要求 ,并用 GPS高程测量进行外符合精度检核。

GPS水准高差拟合应用于跨河水准测量研究

移量 △h,因此必须对 ( 2) 式作相应的变化 ,即 :
H = h + △h - ξ
(3)
因为 △h对于同一个网的各点是一个常量 ,所
以我们将不单独考虑它 , 也即把 GPS 网点中起算
点的大地高的精度视为精确己知 , 而直接利用式
Байду номын сангаас
(2) 。
以上就是 GPS 水准测量的原理 , 通过 GPS 解
算得到高精度的 GPS 水准点大地高后 , 再根据已
变化 , 采用简单模型对区域大地水准面变化情况
进行拟合 ,从而求得跨越河流的 GPS 水准点 (上例
中的 B C两点 ) 之间的高程异常差值及正常高高
差。
为了提高跨河测量方法的经济技术指标 , 应
在满足精度要求的前提下采用尽可能少的 GPS 水
准点数。为此 , GPS高差拟合可采用以下几种模型。
收稿日期 : 2009 - 07 - 08 作者简介 : 王晓华 (1981 - ) ,女 ,河南永城人 ,研究方向 : GPS测量技术研究与应用。
86 淮阴工学院学报 2009年
水准标尺上读数为 A1 。设水准仪具有某一定值的 i 角误差 , 其值为正 , 由此对读数 B1 的误差影响为 △1 ,对于读数 A1 的误差影响为 △2 ,则由 I1 站所得观测结果 ,可按下式计算 b2 相对于 b1 的正确高差 , 取 I1 、I2 测站所得高差的平均值 ,即
2. 1 直线拟合模型
当河两岸 GPS 水准点呈近似直线分布 , 且区
域大地水准面近似平面时 , 设沿跨河方向 (B C ) 大地水准面剖面变化率为 α,则 :
△ζBC = a△X 式中 , XB , XC为 B , C点的 X 坐标 ( X 轴与 B , C

基于高精度GPS测量技术进行长距离跨河高程传递

第十章基于高精度 GPS测量技术进行长距离跨河高程传递10.1 概述随着GPS技术的不断发展，用GPS测量来代替传统的大地测量方法建立高精度的水利枢纽工程平面施工控制网及施工测量工作，其精度和优越性已被广大测量技术人员所认识，并得到广泛使用。

但在GPS测量代替高精度的几何水准或三角高程测量方面，还处于初级应用阶段。

由GPS相对定位获得的三维基线向量，通过GPS网平差，可求得以WGS-84椭球面为基准的高精度大地高。

而我国采用的高程系统则是以似大地水准面为基准的正常高系统，传统的几何水准或三角高程测量方法是获取以似大地水准面为基准的正常高的主要手段。

如果找出似大地水准面与椭球面这两个基准面间差距的数学表达式（似大地水准面模型），就能将GPS大地高换算成正常高，从而实现GPS测高来代替高精度的几何水准或三角高程测量。

利用GPS测量可以获得精确地大地高差的原理，测绘工作者已开始使用GPS 测量技术进行长距离跨障碍（比如河流等）的高程传递测量研究，并已获得成功应用。

《国家一、二等水准测量规范》（GB/T 12897-2006）也明确规定了GPS跨河水准测量法，致使用GPS测量代替传统的跨河水准测量来进行一、二跨河水准测量获得了法规上的支持。

由于GB/T 12897-2006强制性的规定了用于跨河水准测量时，GPS网点的场地布置图型，因此，在计算跨河点间的正常高差时，是基于线拟合的原理来实现的。

成国辉和许曦（2004年）将垂线偏差看作是似大地水准面的法线方向与参考椭球面(或平均椭球面) 的法线方向之间的夹角,故其只决定于似大地水准面的起伏形状,而与似大地水准面的绝对位置无关,即垂线偏差不会受到高程系统不同起算基准的影响。

这样,如果在河流两侧联测一定数量的GPS点的水准高,并分别拟合各自的似大地水准面形状,则可分别解求出同属于WGS284 系统的地面垂线偏差。

再根据天文水准原理,则可计算出河流两侧的高程异常差,正常高差也就相应获得。

GPS在跨河水准测量中的可行性应用

GPS在跨河水准测量中的可行性应用作者：张扬来源：《科学与财富》2015年第26期摘要：本文阐述了GPS跨河水准测量的概念、方法，并以实例验证了跨河水准测量方法的可行性。

关键词：GPS；跨河水准测量；高程异常1 前言当精密水准路线必须跨越江河或峡谷时，其视线长度将明显增长。

此时，不仅照准水准尺读数的精度显著降低，而且视准轴与水准轴不平行及大气折光的影响也急剧增大，水面上空的温度梯度与陆地上的温度梯度完全不同，使得折光影响更加复杂化。

为了顾及这些影响因素以求得可靠的成果，《国家一、二等水准测量规范》（GB 12897-1991）规定：当水准路线跨越江、河，视线长度超过100m时，应根据视线长度和仪器设备情况，选择适当的跨河水准测量发放。

2 GPS在跨河水准测量中的应用2.1 常规的跨河水准测量方法简介目前，常规的跨河水准测量方法主要有光学测微法、倾斜螺旋法、经纬仪倾角法、测距三角高程及冰上观测等几种方法。

对于长距离的跨河水准测量，由于需要观测多个测回，费时、费力，而且对角度观测的精度要求较高，经常出现返工现象。

如果在跨河水准测量中，能够利用GPS定位技术，无疑将显著提高工作效率。

2.2 GPS高程的概念GPS测量是在WGS-84地心坐标系上进行的，它所测得的高程是测站相对于WGS-84椭球面的大地高。

而水准测量测得的高程则是以水准原点为基准相对于大地面的海拔高，以大地水准面为基准的高程系统，称为正高系统。

由于地面点至大地水准面的平均重力加速度无法直接测定，所以正高是无法严格确定的。

因此，我国采用的高程系统是相对于似大地水准面的正常高系统，其高程称为正常高。

似大地水准面同大地水准面非常接近，在海洋面上是重合的，在平原地区仅差数厘米，在高程异常值较大时，最大可达数米。

正由于高程异常的差异性带来了GPS高程的不确定性。

图1 大地高、正常高、高程异常的关系示意图图1为大地、高和正常高之间的关系。

其中，为高程异常。

带参数GPS水准拟合实现跨河高程传递

带参数GPS水准拟合实现跨河高程传递邓兴升;贾莎莎;王文慧【期刊名称】《测绘工程》【年(卷),期】2011(020)004【摘要】为了解决在特大桥隧工程建设中远距离高程基准传递的难题,介绍带高程基准参数的GPS水准拟合方法,给出拟合函数、计算公式及精度估算公式.通过3个大跨度桥梁高程控制的计算实例验证方法的可靠性,证明方法能同时获得局部似大地水准面模型和高程基准参数,解算高程基准参数的精度优于公路桥位勘测设计规程中桥梁高程控制测量的限差要求.%A key problem in long span bridge and tunnel engineering is to transfer height datum across the obstacle with long distance. In order to solve the problem, GPS leveling fitting method with additional pa rameter is presented. Fitting functions and equations are given in this paper. Feasibility of the proposed method is validated by practical data of numerical engineering. The method can obtain the height datum parameter and local quasigeoid model at the same time. It is verified that parameters of the fitting model and fitting standard deviation have no connection with height datum. This method can also be used to vali date the reliability of other methods for across sea leveling surveying. Accuracy of the height datum calcu lated by the proposed method can reach the demand of national order leveling; therefore it can be applied in practical engineering.【总页数】5页(P1-4,8)【作者】邓兴升;贾莎莎;王文慧【作者单位】长沙理工大学交通运输工程学院测绘工程系,湖南长沙410004;长沙理工大学交通运输工程学院测绘工程系,湖南长沙410004;长沙理工大学交通运输工程学院测绘工程系,湖南长沙410004【正文语种】中文【中图分类】U442;P224【相关文献】1.基于数学曲面法的GPS水准拟合的研究与实现 [J], 邢锐;王猛2.GPS水准高差拟合应用于跨河水准测量研究 [J], 王晓华;徐勇3.利用 GNSS 水准实现跨河高程传递的方法及精度分析 [J], 张兴福;张永毅4.多项式拟合GPS水准高程软件设计与实现 [J], 贺永成;王文飞5.某测区GPS水准拟合算法的研究及程序实现 [J], 刘维忠;张国辉;孙盛峰因版权原因，仅展示原文概要，查看原文内容请购买。

GPS跨河水准测量技术探讨

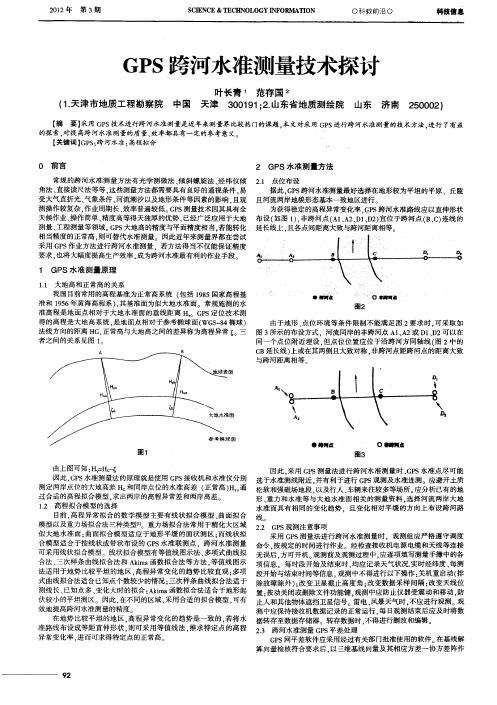
１ＧＰＳ水准测量原理
１大地高和正常高的关系．１我国目常用的高程基准为正常高系统（括１８国家高程基前包９５簟蔫碱毂ＩｉＯ聋■■慨准和１５年黄海高程系）其基准面为似大地水准面。常规施测的水９６，图２准高程是地面点相对于大地水准面的垂线距离ＧＳＰ定位技术测得的高程是大地高系统，是地面点相对于参考椭球面（Ｓ８椭球）ＷＧ一４由于地形、点位环境等条件限制不能满足图２求时．要可采取如法线方向的距离Ｈ，Ｇ正常高与大地高之间的差异称为高程异常（三图３所示的布设方式，河流同岸的非跨河点Ａ１Ａ、２或Ｄ１Ｄ２可以在、者之间的关系见图１同一个点位附近埋设，但点位位置应位于沿跨河方同轴线（２图中的ｃＢ延长线）上或在其两侧且大致对称，河点距跨河点的距离大致非跨与跨河距离相等。
山东

济南
２００５０２）
【摘要】采用ＧＳＰ技术进行跨河水准测量是近年来测量界比较热门的课题，本文对采用ＧＳＰ进行跨河水准测量的技术方法．进行了有益的探索，对提高跨河水准测量的质量、效率都具有一定的参考意义。【关键词】Ｐ；ＧＳ跨河水准；高程拟合
０前言
２ＧＰＳ水准测量方法
常规的跨河水准测量方法有光学测微法、倾斜螺旋法、经纬仪倾２１点位布设．角法、直接读尺法等等，这些测量方法都需要具有良好的通视条件．易据此，Ｐ跨河水准测量最好选择在地形较为平坦的平原、丘陵ＧＳ受大气直折光、象条件、气河流潮汐以及地形条件等因素的影响．且观且河流两岸地貌形态基本一致地区进行测操作较复杂，周期长、作业效率普遍较低。Ｐ测量技术因其具有全ＧＳ为获得稳定的高程异常变化率．Ｐ跨河水准路线应以直伸形状ＧＳ天候作业、操作简单、度高等得天独厚的优势，精已经广泛应用于大地布设（图１，如）非跨河点（１Ａ、１Ｄ）Ａ、２Ｄ、２宜位于跨河点（、）线的Ｂｃ连测量、工程测量等领域。Ｐ大地高的精度与平面精度相当．ＧＳ若能转化延长线上，点间距离大致与跨河距离相等。且各相当精度的正常高，则可替代水准测量。因此近年来测量界都在尝试采用ＧＳＰ作业方法进行跨河水准测量．若方法得当不仅能保证精度要求，也将大幅度提高生产效率．成为跨河水准最有利的作业手段

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

测
绘
工
程
第２Ｏ卷
洋动力学法，它需要相当长时间连续的潮位观测资
反映出该局部似大地水准面的基本形状，能获得就较高的精度。设区域高程异常拟合模型
—
料，周期长且需建立长期验潮站。ＧＰＳ水准法是利用ＧＰＳ水准观测值构建局部似大地水准面，用利ＧＰＳ大地高结合高程异常解算出另一岸海岛的正常高，而实现跨海高程基准传递。ＧＳ水准法方从Ｐ便实用，具有较高的精度，Ｓ重力大地水准面且ＧＰ与利用潮位观测法计算的小长山高程基准相差
二元三次十参数多项式有１模型参数及１０个
个基准参数，需要１个已知ＧＳ水准点才能解算，１Ｐ该函数在我国构造省市似大地水准面时应用较广。
误差方程形式如下：
一
ｆＢＬ～［一（＋ｃｊ（，）ＨＧＨＬ）．
高程测量方法主要包括几何水准测量、角高三程测量、Ｓ大地高测量。受视距和通视条件的限ＧＰ制，距离水准测量难以实现。而三角高程测量，远远
距离观测的分辨率太低，大气折光使得观测精度降
收稿日期：０００ —８２１—５１基金项目：国家自然科学基金资助项目（０７０８；４６４０）湖南省自然科学基金资助项目（０Ｊ００１Ｊ３９）作者简介：邓兴升（９１，高级工程师，１７一）男，博士．
ｍｅｈｄｗｉｈａｄｔｎｌｐｒｍｅｅ；ｈｉｈａｕｔｏｔｄｉｉａａａｔｒｅｇｔｄｔｍｏ
越湾
在跨海大桥的工程建设中，何将陆地的高程如基准传递到海岛，直是工程建设中面临的难点一题。在跨越大江大河的桥梁、越大山的隧道工跨
，
大气能见度的影响也使得观测十分困难。随着
国经济建设的发展，建和拟建的特大桥梁跨在距离越来越长，如东海大桥跨越３ｍ，州例０ｋ杭
建设中，高程从一侧传递到另一侧，将进行远距离的高程传递也比较困难。因此，究远距离高程基准研
第２第４期Ｏ卷２１０１年８月
测
绘
工
程
Ｖｏ．Ｏ № ．１２４
Ａｕ．，０１ｇ２１
ＥＮＧＩＮＥＥＲＩＮＧＵＲＶＥＹＩ０ＦＳＮＧＡＮＤＡＰＮＧＭＰＩ
带参数ＧＰＳ水准拟合实现跨河高程传递
邓兴升，贾莎莎，王文慧
Ｔｅｈｏｏｙｈｎｓａ４００，Ｃｈｎ）ｃｎｌｇ，Ｃａｇｈ１０４ｉａ
低我的
ＡｂｔａｔＡｅｒｂｅｉｏｇｓａｒｄｅａｄｔｎｅｎｉｅｒｎｓｔｒｎｆｒｈｉｈａｕａｒｓｈｓｒｃ：ｋｙｐｏｌｍｎｌｎｐｎｂｉｇｎｕｎｌｇｎｅｉｇｉｏｔａｓｅｅｇｔｄｔｍｃｏｓｔｅｅｏｓａｌｔｏｇｄｓａｃ．Ｉｒｅｏｓｌｅｔｅｐｏｌｍ，ＧＰＳｌｖｌｇｆｔｎｅｈｄｗｉｄｉｉｎｌａｂｔｃｅｗｉｈｌｎｉｔｎｅｎｏｄｒｔｏｖｈｒｂｅｅｅｉｉｉｇｍｔｏｔａｄｔａ — ｎｔｈｏｐｒｍｅｅｓｐｅｅｔｄＦｔｉｇｆｎｔｏｓａｄｅｕｔｏｓａｅｇｖｎｉｈｓｐｐｒＦｅｓｂｌｙｏｈｒｐｓｄａｔｒｉｒｓｎｅ．ｉｔｕｃｉｎｎｑａｉｎｒｉｅｎｔｉａｅ．ｎａｉｉｔｆｔｅｐｏｏｅｉｍｅｈｄｉａｉａｅｙｐａｔａａａｏｕｒｃｌｅｇｎｅｉｇＴｈｅｈｄｃｎｏｔｉｈｅｇｔｄｔｍｔｏｓｖｌｔｄｂｒｃｉｌｄｔｆｎｍｅｉａｎｉｅｒｎ．ｄｃｅｍｔｏａｂａｎｔｅｈｉｈａｕｐｒｍｅｅｎｏａｕｓｇｏｄｍｏｅｔｔｅｓｍｅｔｍｅＩｓｖｒｆｅｈｔｐｒｍｅｅｓｏｈｉｉｇｍｏｅａａｔｒａｄｌｃｌｑａｉｅｉｄｌａｈａｉ．ｔｉｅｉｉｄｔａａａｔｒｆｔｅｆｔｎｄｌｔａｄｆｔｉｇｓａｄｒｅｉｔｎｈｖｏｃｎｅｔｎｗｉｈｈｉｈａｕ．Ｔｈｓｍｅｈｄｃｎａｓｅｕｅｏｖｌｎｉｔｔｎａｄｄｖａｉａｅｎｏｎｃｉｔｅｇｔｄｔｍｎｏｏｉｔｏａｌｏｂｓｄｔａｉ — ｄｔｈｅｉｂｌｙｏｔｅｅｈｄｏｃｏｓｓａｌｖｌｇｓｒｅｉｇＡｃｕａｙｏｈｅｇｔｄｔｍａｃ — ａｅｔｅｒｌｉｔｆｏｈｒｍｔｏｓｆｒａｒｓｅｅｅｉｕｖｙｎ．ａｉｎｃｒｃｆｔｅｈｉｈａｕｃｌｕｌｔｄｂｈｒｐｓｄｍｅｈｄｃｎｒａｈｔｅｄｍａｄｏａｉｎｌｒｅｅｅｉｇｈｒｆｒｔａｅａｐｉｄｉａｅｙｔｅｐｏｏｅｔｏａｅｃｈｅｎｆｔａｄｒｌｖｌ；ｔｅｅｏｅｉｃｎｂｐｌｎｎｏｏｎｅｐａｔａｎｉｅｒｎ．ｒｃｉｌｇｎｅｉｇｃｅＫｅｒｓｌｎｐｎｂｉｇｎｕｎｌｅｇｎｅｉｇ；ｈｉｈｒｎｆｒｎｅａｒｓｉｅ；ＧＰｅｅｉｇｆｔｎｙｗｏｄ：ｏｇｓａｒｄｅａｄｔｎｅｎｉｅｒｎｅｇｔｔａｓｅｅｃｃｏｓｒｖｒＳｌｖｌｉｉｇｎｔ
基准参数，要７已知ＧＳ水准点才能解算。需个Ｐ
由于两者存在着２二元三次十参数多项式）
ｆＢ，）一ａＢ。ａＢ＋ａＢ＋ａＬ＋ｎＬ＋（Ｌ１＋２３４。５
口Ｌ＋口Ｂ＋ａＢ６７Ｌ８Ｌ＋ａ１１＋以０９１３１．（）３
能同时获得局部似大地水准面模型和高程基准参数，解算高程基准参数的精度优于公路桥位勘测设计规程中桥梁高程控制测量的限差要求。
关键词：特大桥隧工程；跨河高程传递；带参数ＧＰＳ水准拟合；高程基准
中图分类号：４；Ｐ２Ｕ４２２４文献标志码：Ａ文章编号：０６７４（０）４００ —４１０— ９９２１０ —０１０１
在着垂向偏差和水平倾斜差异［］１。而且重力似大
地水准面的建立，要足够多且精度足够高的重力需测量资料，而目前大面积的海域可能无法进行重然力测量［。在天文水准法中，采用多项式对两侧５］先ＧＰＳ水准分别拟合，别计算两端点的垂线偏差，分再根据天文水准测量原理，由两端点的垂线偏差和方位角计算高程异常差，到传递高程基准的目达
ＤＥＮＧｎ — ｈｎＸｉｇｓｅｇ，ＪＡｈ — ｈ，ＷＡＮＧｅ－ｕＩＳａｓａＷｎｈｉ
（ｅａｔｎｆｕｖｙｎｎｉｅｒｇｃｏｌｆａｆｎａｓｏｔｔｎＥｇｎｅｉｇｈｎｓａＵｎｖｒｉｆＳｉｃＤｐｒｍｅｔｒｅｉＥｇｎｅｉ，ＳｈｏｆｃａｄＴｒｎｐｒｉｎｉｅｒ，Ｃａｇｈｉｅｓｙｏｃｎｅ＆ｏＳｇｎｏＴｒｉａｏｎｔｅ
３３ｃ幻；Ｐ．ｍ［ＧＳ似大地水准面与重力似大地水准面
ｆＢ，）（Ｌ．
（）１
式中：为高程异常，为大地纬度，为大地经度，ＢＬ
，（・）为拟合函数，如下形式：有１－元二次六参数多项式）
问程
ＧＰＳｌｖｌｎｉｔｎｇｗｉｈａｄｔｏｌｐｒｍｅｅｏｅｅｉｇｆｔｉｔｄｉｉｎａａａｔｒｆｒ
ｈｉｈｔｔａｓｅｒｎｇａｒｓｉｅｅｇｒｎｆｒｉｃｏｓｒｖｒ
ｆＢ，）一ａＢ＋ａＢ＋ａＬ＋ａＬ＋ａＢ（Ｌｌ２３４５Ｌ＋６．
（）２
进行叠加后，得到拟合后精确的局部似大地水准面，
其精度为３３ｃ３。．ｍＬｊ
重力似大地水准面与ＧＳ水准似大地水准面Ｐ
二元二次六参数多项式有６个未知参数及１个