[套卷]四川省邛崃市高埂中学2013-2014学年高一上学期第一次月考数学试题
四川省邛崃市高一上学期半期考试数学试题

命题人:李进 审题人:张永胜本试卷分为选择题和非选择题两部分,由笫一部分(选择题)和第二部分(非选择题)组成,共4页,满分150分,考试时间120分钟。
注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3. 答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效.5. 考试结束后,只将答题卷交回。
第一部分(选择题)本部分共十个小题,每小题5分,共计50分。
(每小题的四个选项只有一项是最符合题目要求的。
)1.已知全集U={1,2,3,4,5},集合A={1,2,3}.则()A.{4,5}.B.{1,2,3}.C.{5}.D.{2,4} 2、函数f(x)=的大致图像为( )3.下列函数与y=x 是相同函数的是() A. B. C. D.y=4.函数f(x)=|x+2|的单调递减区间是()A. B. C., D.无减区间 5.下列等式成立的是()A. B..C. D..6.记a= b= c=,则a 、b 、c 的大小关系是()A.a<b<c.B.c<b<a.C.a<c<b.D.b<a<c 7.已知的取值范围是())上是单调函数,则,在区间(k kx x x f 201)(2-+=A, B,k<-4或k>0; C, D,-4<k<08.函数)34log )(21x x f -=(的定义域区间为()A.[1,.B.C.D.9.当生物死亡时,他机体内原有的碳14含量按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”,据此规律,生物体内碳14的含量P 与死亡年数t 间的函数关系式为( )A. B. C. D. 10.已知函数:,若关于x 的方程:f(x)=2k 恰有四个不等的实数根,则实数k 的取值范围为() A. B.-3<k<1. C.-6<K<2. D.k>第二部分(非选择题)本部分共十一题,共100分。
四川省成都市邛崃市高埂中学高一上学期第一次月考数学试卷

2015-2016学年四川省成都市邛崃市高埂中学高一(上)第一次月考数学试卷一.选择题(每小题5分,共60分)1.不等式(x﹣1)(2﹣x)≥0的解集是( )A.{x|1≤x≤2} B.{x|x≥1或x≤2} C.{x|1<x<2} D.{x|x>1或x<2}2.下列各组函数是同一函数的是( )A.y=﹣2 B.y=C.D.3.若函数f(x)=,则f(2)的值为( )A.2 B.3 C.4 D.54.设集合A、B是非空集合,定义A×B={x|x∈A∪B且x∉A∩B},已知A=,B={y|y=2x2},则A×B等于( )A.(2,+∞)B.∪0,1)∪(2,+∞)D.∪(2,+∞)5.函数f(x)=﹣x2+2(a﹣1)x+2在(﹣∞,4)上是增函数,则a的范围是( ) A.a≥5 B.a≥3 C.a≤3 D.a≤﹣56.若函数f(x)=在(﹣∞,+∞)上单调递增,则实数a的取值范围是( )A.(﹣,0) B.(﹣1,0)C.﹣1,0)7.如图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H 与下落时间t(分)的函数关系表示的图象只可能是( )A.B.C.D.8.已知函数f(x)是定义在区间,)C.(,) D.0,33,+∞)上分别递减和递增,则不等式x3f(x)<0的解集为( )A.(﹣∞,﹣4)∪(4,+∞)B.(﹣4,﹣1)∪(1,4)C.(﹣∞,﹣4)∪(﹣1,0)D.(﹣∞,﹣4)∪(﹣1,0)∪(1,4)二.填空题(每小题4分,共16分)13.如果集合A={x|ax2+2x+1=0}只有一个元素,则实数a的值为__________.14.若递增的一次函数f(x)满足f=4x+3,则f(x)=__________.15.设一元二次不等式ax2+bx+1>0的解集为,则ab的值是__________.16.对于实数a,b,定义运算“*”:a*b=,设f(x)=(2x﹣1)*(x﹣1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则m的取值范围是__________.三.解答题(将答案写在答题卡中相应题号的方框内,只有结果没有步骤不给分)17.已知集合A={x|1<x<3},集合B={x|2m<x<1﹣m}.(1)当m=﹣1时,求A∪B;(2)若A⊆B,求实数m的取值范围;(3)若A∩B=∅,求实数m的取值范围.18.已知函数f(x)=|x2﹣2x|.(1)在给出的坐标系中作出y=f(x)的图象;(2)根据图象写出函数f(x)的单调区间和值域;(3)若集合{x|f(x)=a}恰有三个元素,求实数a的值.19.解不等式x2﹣(a+)x+1<0(a≠0)20.(1)证明函数f(x)=x+ 在x∈4,8﹣1,10,12,+∞)C.0,10,+∞),A∩B= 因此A×B=(2,+∞),故选A.【点评】此题主要考查新定义、根式有意义的条件和集合交、并、补集的混合运算,新定义的题型是常见的题型,同学们要注意多练习这样的题.5.函数f(x)=﹣x2+2(a﹣1)x+2在(﹣∞,4)上是增函数,则a的范围是( ) A.a≥5 B.a≥3 C.a≤3 D.a≤﹣5【考点】函数单调性的性质.【专题】计算题.【分析】先将函数f(x)=﹣x2+2(a﹣1)x+2转化为:y=﹣(x﹣a+1)2﹣2a+3+a2明确其对称轴,再由函数在(﹣∞,4)上单调递增,则对称轴在区间的右侧求解.【解答】解:函数f(x)=﹣x2+2(a﹣1)x+2∴其对称轴为:x=a﹣1又∵函数在(﹣∞,4)上单调递增∴a﹣1≥4即a≥5故选A【点评】本题主要考查二次函数的性质,涉及了二次函数的对称性和单调性,在研究二次函数单调性时,一定要明确开口方向和对称轴.6.若函数f(x)=在(﹣∞,+∞)上单调递增,则实数a的取值范围是( )A.(﹣,0) B.(﹣1,0)C.﹣1,0)【考点】函数单调性的性质.【专题】函数的性质及应用.【分析】通过增函数的单调性,判断x大于等于1时一次函数的单调性,x小于1时二次函数的单调性,及以及x=1时的函数值即可得到结果.【解答】解:∵函数f(x)=在(﹣∞,+∞)上单调递增,∴,解得:a∈0,+∞)上的增函数,则满足f(2x﹣1)<f()的x的取值范围是( ) A.(,) B.,)【考点】函数单调性的性质.【专题】函数的性质及应用.【分析】由函数的单调性的性质可得0≤2x﹣1<,由此求得x的取值范围.【解答】解:∵函数f(x)是定义在区间故答案为:(﹣20,0,33,+∞)上分别递减和递增,则不等式x3f(x)<0的解集为( ) A.(﹣∞,﹣4)∪(4,+∞)B.(﹣4,﹣1)∪(1,4)C.(﹣∞,﹣4)∪(﹣1,0)D.(﹣∞,﹣4)∪(﹣1,0)∪(1,4)【考点】奇偶性与单调性的综合;不等式.【分析】利用偶函数关于y轴对称的性质并结合题中给出函数的单调区间画出函数f(x)的图象,再由x3f(x)<0得到x3与f(x)异号得出结论.【解答】解:∵f(x)是偶函数∴f(﹣x)=f(x)即f(4)=f(﹣1)=0又∵f(x)在区间与f(x)f(x)ax+b;(3)由A∩B=∅得:①若2m≥1﹣m,即时,B=∅,符合题意,②若2m<1﹣m,即时,需,或;解得,或∅,即;综上知:m≥0;即实数m的取值范围是0,12,+∞),单减区间为(﹣∞,01,20,+∞).(3)∵集合{x|f(x)=a}恰有三个元素,∴由题意得,方程f(x)=a恰有三个不等实根,结合直线y=a的图象可知,实数a的值为1.【点评】本题考查函数图象的作法、函数的单调区间及值域的求法、实数值的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.19.解不等式x2﹣(a+)x+1<0(a≠0)【考点】一元二次不等式的解法.【专题】不等式的解法及应用.【分析】不等式x2﹣(a+)x+1<0(a≠0)可化为0,令,解得a=±1.对a分类讨论:当a<﹣1或0<a<1时,当a=±1时,当a>1或﹣1<a<0时,即可得出.【解答】解:不等式x2﹣(a+)x+1<0(a≠0)可化为0,令,解得a=±1.当a<﹣1或0<a<1时,,因此原不等式的解集为.当a=±1时,a=,因此原不等式的解集为∅.当a>1或﹣1<a<0时,a>,因此原不等式的解集为.【点评】本题考查了一元二次不等式的解法,考查了分类讨论的思想方法,属于基础题.20.(1)证明函数f(x)=x+ 在x∈4,84,85,﹣1,1﹣1,1﹣1,1﹣1,1﹣1,1﹣1,10,2000,300hslx3y3h上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大.【点评】本小题主要考查由函数图象建立函数关系式和求函数最大值的问题,考查运用所学知识解决实际问题的能力.。
四川省邛崃一中2013届高三10月月考数学(理)试题

邛崃市2013届高三月考(十月)数学(理科)试题卷 时间 120分钟 总分 150分一、选择题(每小题5分,共60分)1.设集合A ={1,2,3,4},B ={3,4,5},U =A ∪B ,则∁U (A ∩B )的元素个数为A .1个B .2个C .3个D .4个2. 复数z 满足z =2-i1-i,则复数z 对应的点在 A .第一象限 B .第二象限 C. 第三象限 D. 第四象限3. 已知sin 2α=-2425,α∈⎝ ⎛⎭⎪⎫-π4,0,则sin α+cos α= A. -15 B. 15 C. -75 D. 754. 设f (x )是定义在R 上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图象,则f (2 011)+f (2 012)=A .3B .2C .1D .05.已知p :x 2-x < 0,那么命题p 的一个必要不充分条件是A .0 < x < 1B .-1< x < 1 C. 12 < x < 23D. 12< x < 26. 如图,是一个程序框图,运行这个程序, 则输出的结果为A.1321B.2113 C. 813 D. 1387. 若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于A.3B .3+2 38. 已知等差数列{a n }的前n 项和为S n ,S 9=-36,S 13=-104,等比数列{b n }中, b 5=a 5,b 7=a 7,则b 6的值为 A .±4 2B .-4 2C .4 2D .无法确定9. 从10名大学毕业生中选3人担任村长助理,则甲、乙至少有1人入选,而丙没 有入选的不同选法的种数为A .85B .56C .49D .2810. 设函数f (x )在R 上可导,其导函数为f /(x ),且函数y = (1−x ) f /(x )的图像如图所示,则下列结论中一定成立的是A .函数f (x )有极大值f (2)和极小值f (1)B .函数f (x )有极大值f (−2)和极小值f (1)C .函数f (x )有极大值f (2)和极小值f (−2)D .函数f (x )有极大值f (−2)和极小值f (2)11. 甲乙二人玩猜数字游戏,先由甲任想一数字,记为a ,再由乙猜甲刚才想的数字,把乙猜出的数字记为b ,且a ,b ∈{1,2,3},若|a -b | ≤ 1,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,则他们“心有灵犀”的概率为 A. 13B. 59C. 23D. 7912. 对实数a 和b ,定义运算“⊕”:a ⊕b =⎩⎨⎧a ,a -b ≤1b ,a -b >1.设函数f (x )=(x 2-2)⊕(x -x 2),x ∈R ,若函数y =f (x )-c 的图象与x 轴恰有两个公共点,则实数c 的取值范围是A .(-∞,-2]∪⎝ ⎛⎭⎪⎫-1,32B .(-∞,-2]∪⎝ ⎛⎭⎪⎫-1,-34C. ⎝ ⎛⎭⎪⎫-1,14∪⎝ ⎛⎭⎪⎫14,+∞ D. ⎝ ⎛⎭⎪⎫-1,-34∪⎣⎢⎡⎭⎪⎫14,+∞二、填空题(每小题4分,共16分)13.在⎝⎛⎭⎪⎫x − 2x 6的二项展开式中,常数项等于 _________ .14. 变量x ,y 满足条件:⎩⎪⎨⎪⎧x +2y -5 ≤ 0x -y -2 ≤ 0x ≥ 0,则目标函数z =2x +3y +1的最大值为____.15. 已知函数f (x ) = ||lg x ,若a < b ,且f (a ) = f (b ),则a + 2b 的取值范围是________ . 16.给出以下五个命题:①R y x ∈,,若022=+y x ,则0x =或0y =的否命题是假命题; ②函数33(0)x x y x -=+<的最小值为2;③若函数32()2f x x ax =++的图象关于点(1,0)对称,则a 的值为-3; ④若1(2)0()f x f x ++=,则函数()y f x =是以4为周期的周期函数;⑤若(1+ x )10 = a 0 +a 1x + a 2x 2 +… + a 10x 10,则 a 0 +a 1 + 2a 2 + 3a 3 + … + 10a 10=10×29. 其中真命题的序号是___________.三、解答题(共六小题,共74分) 17.(本小题满分12分)函数f (x ) = 3sin ωx cos ωx + sin 2ωx + 12 ,其图像相邻两条对称轴之间的距离为 π2. (Ⅰ)求ω的值;(Ⅱ) 若A 为△ABC 的内角,且f ⎝ ⎛⎭⎪⎫A 2 = 32,求A 的值.18.(本小题满分12分)如图,直三棱柱ABC −A 1B 1C 1中, AC = BC = 12AA 1,D 是棱AA 1的中点,DC 1⊥BD .(Ⅰ)证明:DC 1⊥BC ;(Ⅱ)求二面角A 1−BD −C 1的大小.A 1B 1C 1A BCD19. (本小题满分12分)某班50位学生期中考试数学成绩的频率分 布直方图如图所示,成绩分组区间是: [40,50)、[50,60)、[60,70)、[70,80)、 [80,90)、[90,100]. (Ⅰ)求图中 x的值;(Ⅱ)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为ξ,求ξ的分布列和数学期望. 20. (本小题满分12分)已知 f (x ) = ||ax + 1 (a ∈R),不等式 f (x )≤3 的解集为{x | −2≤x ≤1}. (Ⅰ)求a 的值;(Ⅱ)若⎪⎪⎪⎪⎪⎪f (x ) − 2f ( x 2 )≤ k 恒成立,求 k 的取值范围. 21.(本小题满分12分)已知等比数列{a n }的各项均为正数,且 2a 1 + 3a 2 = 1,a 32= 9a 2a 6. (Ⅰ) 求数列{a n }的通项公式;(Ⅱ)设 b n = log 3a 1 + log 3a 2 + … + log 3a n ,求⎩⎨⎧⎭⎬⎫1b n 的前n 项和T n ;(Ⅲ)在(Ⅱ)的条件下,求使 kn ·2n +1n +1≥ (7 − 2n )T n 恒成立的实数 k 的取值范围. 22. (本小题满分14分)已知函数)0(3ln )(≠∈--=a R a ax x a x f 且. (Ⅰ) 求函数)(x f 的单调区间;(Ⅱ)若函数)(x f y =的图像在点))2(,2(f 处的切线的倾斜角为︒45,问:m 在什么范围取值时,对于任意的[]2,1∈t ,函数g (x )=x 3 + x 2⎣⎢⎡⎦⎥⎤m 2 + f /(x )在区间)3,(t 上总存在极值? (Ⅲ)当2=a 时,设函数32)2()(-+--=xe p x p x h ,若在区间[]e ,1上至少存在一个0x ,使得)()(00x f x h >成立,试求实数p 的取值范围.邛崃市2013届高三月考(10月)数学(理科)参考答案一、1. C ;2. A ;3.B ;4. A ;5B ;6.D ;7. D ;8. A ;9. C ;10.D ;11. D ;12. B 二、填空题13.−160 14. 10 15. (3,+∞) 16.①、③、④三、解答题17.解析:(Ⅰ)f (x ) =32sin2ωx + 1 −cos2ωx 2+ 12 = 32sin2ωx − 12cos2ωx + 1 = sin ⎝ ⎛⎭⎪⎫2ωx −π6+1 ∵函数图像的相邻两条对称轴之间的距离为 π2,∴最小正周期T = π∴2π2ω= π,ω = 1. ∴f (x ) = sin ⎝ ⎛⎭⎪⎫2x − π6 + 1(2) ∵f ⎝ ⎛⎭A 2 = sin ⎝ ⎛⎭⎪⎫A − π6 + 1 = 32 ∴sin ⎝ ⎛⎭⎪⎫A − π6 = 12∵ A ∈(0,π) ∴ − π6 < A − π6 < 5π6∴ A − π6 = π6 ,故A = π3.18.解析:(Ⅰ)证明:由题设知,三棱柱的侧面为矩形.∵D 是AA 1的中点, ∴ DC = DC 1B 1 C又 AC = 12AA 1,∴ DC 12 + DC 2 = CC 12∴ DC 1⊥DC又 DC 1⊥BD ,且DC 1∩DC = D ∴ DC 1⊥平面DCB . ∴ DC 1⊥BC(Ⅱ) 解:由(Ⅰ)知,DC 1⊥BC ,又CC 1⊥BC , DC 1∩CC 1 = C 1 ∴ BC ⊥平面CDC 1∵ B 1C 1∥BC ∴B 1C 1⊥平面CDC 1∴ B 1C 1⊥A 1C 1,△A 1C 1B 1为等腰直角三角形 取A 1B 1的中点为M ,连结C 1M 、DM∵ 直棱柱的底面A 1B 1C 1⊥侧面AB 1,C 1M ⊥A 1B 1 ∴ C 1M ⊥平面AB 1,C 1M ⊥BD .由(Ⅰ)知,DC 1⊥平面DCB ,∴DC 1⊥BD又C 1M ∩DC 1 = C 1,∴BD ⊥平面C 1MD MD ⊥BD ∴∠C 1DM 是A 1−BD −C 1的平面角.在Rt △C 1MD 中,C 1M = 22A 1C 1,C 1D = DA 12 + A 1C 12 = 2A 1C 1,∴sin ∠C 1DM = C 1M C 1D = 12, ∴∠C 1DM = 30o∴二面角A 1−BD −C 1的大小为30o . 19. 解析:(Ⅰ) 由()0.00630.010.054101x ⨯+++⨯=,解得0.018x =.(Ⅱ) 分数在[)80,90、[]90,100的人数分别是500.018109⨯⨯=人、500.006103⨯⨯=人.所以ξ的取值为0、1、2.()023921236606611C C P Cξ====,()113921227916622C C P Cξ====,()20392123126622C C P Cξ====,所以ξ的数学期望是691111012112222222E ξ=⨯+⨯+⨯==.20. 解析:(Ⅰ) 由||ax +1≤3得−4≤ax ≤2, f (x )≤3的解集为{x | −2≤x ≤1},当a ≤0时,不合题意.当a > 0时,− 4a ≤x ≤2a得a = 2.……………………………………5分(Ⅱ)记h (x )= f (x ) −2f⎝⎛⎭x 2,则 h (x ) =⎩⎨⎧1, x ≤−1−4x − 3,−1<x < −12−1, x ≥ −12所以 | h (x ) |≤1,因此 k ≥1.21.解析:(Ⅰ)设数列{}n a 的公比为q (q > 0 ),由 ⎩⎨⎧2a 1 + 3a 2 = 1 a 32 = 9a 2a 6得13q =,113a =. 故数列{}n a 的通项公式为13n na =.(Ⅱ )b n =log 3a 1 + log 3a 2 + …+ log 3a n = − n (n +1)2故1b n= −2⎝⎛⎭⎪⎫1n − 1n + 1 T n = 1b 1 + 1b 2 + 1b 3 + … + 1b n= −2⎣⎢⎡⎦⎥⎤⎝ ⎛⎪⎫1 − 12 + ⎝ ⎛⎭⎪⎫12 − 13 + ⎝ ⎛⎪⎫13 − 14 + … + ⎝ ⎛⎪⎫1n − 1n +1 = − 2n n +1 所以数列 ⎩⎨⎧⎭⎬⎫1b n 的前 n 项和为 − 2n n + 1. (Ⅲ )化简得272nn k -≥对任意n N *∈恒成立设272n nn d -=,则1922n n nn d d +--=当15,,{}n n n n d d d +≥<为单调递减数列,115,,{}n n n n d d d +≤<>为单调递增数列,所以,n=5时,n d 取得最大值为332.所以, 要使272nn k -≥对任意n N *∈恒成立,332k ≥22. 解析:(Ⅰ)由x x a x f )1()('-=知当0>a 时,函数)(x f 的单调增区间是)1,0(,单调减区间是),1(+∞; 当0<a 时,函数)(x f 的单调增区间是),1(+∞,单调减区间是)1,0(.(Ⅱ)由()212a f '=-=2a ⇔=-,∴()223f x ln x x =-+-,()22f 'x x=-.故3232()'()(2)222mmg x x x f x x x x ⎡⎤=++=++-⎢⎥⎣⎦, ∴2'()3(4)2g x x m x =++-.∵ 函数)(x g 在区间)3,(t 上总存在极值,∴0)('=x g 有两个不等实根且至少有一个在区间)3,(t 内 又∵函数)('x g 是开口向上的二次函数,且02)0('<-=g , ∴ ⎩⎨⎧><0)3('0)('g t g 由4320)('--<⇔<t tm t g ,∵=)(t H 432--t t在[]2,1上单调递减,所以9)1()(min -==H t H ;∴9-<m ,由023)4(27)3('>-⨯++=m g ,解得337->m ;综上得:379.3m -<<-所以当m 在)9,337(--内取值时,对于任意的[]2,1∈t ,函数⎥⎦⎤⎢⎣⎡++=)('2)(23x f m x x x g 在区间)3,(t 上总存在极值。
高埂中学高一期中试题

高埂中学2013-2014学年高一上学期期中考试语文检测题班级:姓名:一、基础知识(12分)1. 下列词语中,加点字的读音全都正确的一项是 ( )A.濡缕(rú)杯杓(sháo)叱咤(zhà ) 瞋目(chēn)B.拜谒(yâ ) 拊心(fǔ)游说(shuì) 震慑(niâ)C.参乘(shâng) 变徵(zhǐ)创伤(chuāng) 顷刻(qīng)D.噩梦(â)浸渍(qìn)氾南(fán )给予(jǐ)2. 下列各组词语中书写无误的一项是 ( )A.慷概荆柯刀俎秦晋之好 B.邮戳戍守烦燥朝秦暮楚C.沉淀岐视屠戮图穷匕现 D.忤逆惊愕陷阱从善如流3.下面各句中,没有语病且句意明确的一句是()A.金乌炭雕工艺精湛,采用纯天然燃料着色,具有高雅、时尚、个性的艺术享受,还能吸附有毒有害气体,是一种环保艺术品。
B.坐火车到威尔士北部最高的斯诺登尼亚山峰去观赏高原风光,是威尔士最主要的一个景点。
C.王林呆在实验室里半个月,好像与世隔绝了,所以他回到家,强迫着自己看了十天的报纸。
D.纵观科学史,科学的发展与全人类的文化是分不开的,在西方是如此,在中国也是如此。
4.下面各句中,加点成语使用恰当的一项是()A.工会准备组织员工去九寨沟旅游,大家兴致勃勃,小张更是推波助澜,积极鼓励年轻人提出要搞生态自助游。
B.为了防止有毒豆制品再次流入市场,有关部门迅速采取釜底抽薪的办法,查封加工窝点,堵住了生产的源头。
C.随着国家食品安检局对奶制品查处力度的进一步加大,食品生产行业的一系列问题如雨后春笋般暴露了出来。
D.他刚从书店买来的那本书不胫而走,他的心里非常着急。
二、文言文阅读(18分)(一)楚左尹项伯者,项羽季父也,素善留侯张良。
张良是时从沛公,项伯乃夜驰之沛公军,私见张良,具告以事,欲呼张良与俱去,曰:“毋从俱死也。
”张良曰:“臣为韩王送沛公,沛公今事有急,亡去不义,不可不语。
四川省邛崃市2014届高三第一次月考数学(理)试题 word版含答案

命题人:梁应惠 审题人:戴建军本试卷分为选择题和非选择题两部分,由第一部分(选择题)和第二部分(非选择题)组成,共4页,满分150分,考试时间120分钟.注意事项:1. 答题前,考生务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2. 答选择题时,必须用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3. 答非选择题时,必须用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4. 所有题目必须在答题卡上作答,在试题卷上答题无效。
5. 考试结束后,只将答题卷交回。
第一部分(选择题)一.选择题:(每小题5分,共50分。
每小题的四个选项只有一项是最符合题要求的。
) 1. 已知全集是实数集R ,M ={x |x ≤1},N ={1,2,3,4},则(∁R M )∩N 等于( ) A .{4} B .{3,4} C .{2,3,4} D .{1,2,3,4}2.若复数z 满足z1+i=2i ,则z 对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3.已知a ,b ,c ,d 为实数,且c >d ,则“a >b ”是“a -c >b -d ”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件4. 函数y =xa x|x |(0<a <1)的图象的大致形状是( )5. ( )6. 若a >0,b >0,且函数f (x )=4x 3-ax 2-2bx +2在x =1处有极值,则ab 的最大值等于( )A .2B .3C .6D .97. 已知tan α=4,则1+cos2α+8sin 2αsin2α的值为( )A .4 3 B.654 C .4 D.2338. 2011年,哈三中派出5名优秀教师去大兴安岭地区的三所中学进行教学交流,每所中学至少派一名教师,则不同的分配方法有( )A .80种B .90种C .120种D .150种9. 函数f (x )=13ax 3+12ax 2-2ax +2a +1的图象经过四个象限,则实数a 的取值范围是( )A .-65<a <316B .-85<a <-316C .-85<a <-116D .-65<a <-31610.已知一个三角形的三边长分别是5,5,6,一只蚂蚁在其内部爬行,若不考虑蚂蚁的大小,则某时刻该蚂蚁距离三角形的三个顶点的距离均超过2的概率是( )A .2-π3B .1-π6C .2-π2D .1-π12第二部分(非选择题)二.填空题(每小题5分,共25分) 11.已知幂函数过点(2,41),则此函数f (x )=________. 12.若(1-2x )2 013=a 0+a 1x +…+a 2 013x 2 013(x ∈R ),则a 12+a 222+…+a 2 01322 013=________.13.在△ABC 中,M 是BC 的中点,AM=3,BC=10,则AB AC ⋅=________.14. 若数列{a n }满足1a n +1-1a n=d (n ∈N *,d 为常数),则称数列{a n }为调和数列.记数列⎩⎨⎧⎭⎬⎫1x n 为调和数列,且x 1+x 2+…+x 20=200,则x 5+x 16=________.15.已知定义在[1,+∞)上的函数⎪⎪⎩⎪⎪⎨⎧>≤≤--=2),2(2121,2384)(x x f x x x f 。
四川省邛崃市高埂中学2013至2014高二上学期第一次月考数学理科试题

一.选择题:(共10小题,每题5分,共50分.)1.已知直线的倾斜角为45°,在y 轴上的截距为2,则此直线方程为( )A .y x =+2.B .y x =-2C .y x =-+2D .y x =--2 2.下列说法正确的是( )A .若两个平面有三个公共点,则它们一定重合;B .一个棱锥截去一个小棱锥后,剩下部分一定是一个棱台;C .若一条直线a 有无数个点不在平面β内,则直线a //平面β; D.一个圆锥截去一个小圆锥后剩余部分是圆台。
3. 如图是由哪个平面图形旋转得到的( )A.B. C. D.4.若直线a 和b 没有公共点,则a 与b 的位置关系是( ) A .相交 B .平行 C .异面 D .平行或异面 5.三个数20.90.9,ln 0.9,2a b c ===之间的大小关系是( )A.b c a <<.B.c b a <<C.c a b << D .a c b << 6.公比为32等比数列{}n a 的各项都是正数,且5916a a =,则216log a =( ) A.4 B.5 C.6D.77. 若20,AB BC AB ABC ⋅+=∆则是 ( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .等腰直角三角形8. 设,αβ是两个不同的平面,l 是一条直线,以下命题正确的是 ( )A .若,l ααβ⊥⊥,则l β⊂B .若//,//l ααβ,则l β⊂C .若,//l ααβ⊥,则l β⊥D .若//,l ααβ⊥,则l β⊥ 9. 某四面体三视图如图所示,该四面体四个面的面积中最大的是 A. 8B.C. D. 1010. 在R 上定义运算:对x 、y R ∈,有2x y x y ⊕=+, 如果(3)1(0)a b ab ⊕=>,则11()3a b⊕ 的最小值是( ) A .4B .323 C .9 D .283二.填空题:(共5小题,每题5分,共25分.请将最简答案填在答题卷相应的位置) 11. 直观图(如右图)中,四边形O ′A ′B ′C ′为菱形且边长为2cm , 则在xoy 坐标中四边形OBCD 的面积为______cm 2. 12.不等式x +1x≤3的解集是___ _____. 13. 设,l m 是两条不同的直线,,αβ是两个不同的平面,有下列命题:①l m m α⊂∥,,则l α∥;②l m αα∥,∥则l m ∥; ③l αβα⊥⊂,,则l β⊥;④l m αα⊥⊥,,则l m ∥. 其中正确的命题的个数是 .14. 下列命题:①α内有无数条直线平行于β,则α∥β;②平行于同一直线的两个平面互相平行;③经过平面α外两点一定可以作一个平面与α平行;④平行于同一个平面的两个平面平行.其中不正确...的命题为 . 15.已知直线41y kx k =-+与曲线|1|2y =--恰有一个公共点,则实数k 的取值范围是 .三.解答题:(共6小题,共75分.请将每题的解答过程写在答题卷相应的答题框内)D'C'B'A'O'Y'X'16.(本题满分12分)如图,三棱柱ABC ﹣A 1B 1C 1中,AA 1⊥平面ABC ,D 是AB 的中点.(Ⅰ)证明:BC 1∥平面A 1CD ; (Ⅱ)设AA 1=AC=CB=2,,求三棱锥D ﹣A 1CA 的体积.17.(本题满分12分)设ABC ∆的三个内角分别为,,A B C .向量3(1,cos )(3sin cos ,)2222C C C m n ==+与共线.(Ⅰ)求角C 的大小;(Ⅱ)设角,,A B C 的对边分别是,,a b c ,且满足2cos 2a C c b +=,试判断∆ABC 的形状.18.(本题满分12分)如图,AB 是圆O 的的直径,点C 是弧AB 的中点,D ,E 分别是VB ,VC 的中点,VA ⊥平面ABC .(1)求异面直线DE 与AB 所成的角; (2)证明 :DE ⊥平面VAC . (3)若2AB VA =,求二面角A BC D --的大小。
四川省邛崃市2014-2015学年高一上学期半期考试数学试题
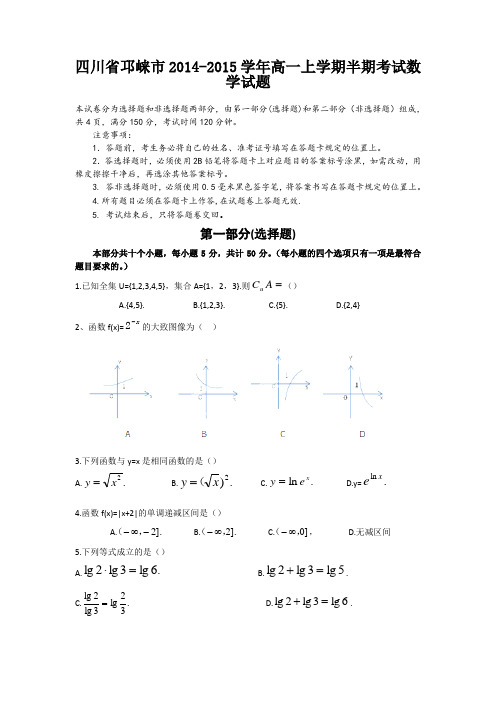
四川省邛崃市2014-2015学年高一上学期半期考试数学试题本试卷分为选择题和非选择题两部分,由笫一部分(选择题)和第二部分(非选择题)组成,共4页,满分150分,考试时间120分钟。
注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3. 答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效.5. 考试结束后,只将答题卷交回。
第一部分(选择题)本部分共十个小题,每小题5分,共计50分。
(每小题的四个选项只有一项是最符合题目要求的。
) 1.已知全集U={1,2,3,4,5},集合A={1,2,3}.则=A C u ()A.{4,5}.B.{1,2,3}.C.{5}.D.{2,4} 2、函数f(x)=x-2的大致图像为( )3.下列函数与y=x 是相同函数的是() A..2x y = B..)2x y (=C..ln x e y =D.y=.ln xe4.函数f(x)=|x+2|的单调递减区间是()A.].2-∞-,( B.].2,(∞- C.]0,(∞-, D.无减区间 5.下列等式成立的是() A..6lg 3lg 2lg =⋅ B.5lg 3lg 2lg =+.C..32lg 3lg 2lg = D.6lg 3lg 2lg =+.6.记a=,65log 2 b=.73.0 c=1.971)(,则a 、b 、c 的大小关系是() A.a<b<c. B.c<b<a. C.a<c<b. D.b<a<c 7.已知的取值范围是())上是单调函数,则,在区间(k kx x x f 201)(2-+=A,;或40-≥≤k k B,k<-4或k>0; C,;或04≥-≤k k D,-4<k<08.函数)34log )(21x x f -=(的定义域区间为()A.[1,]34. B..34,1[)C..34),(∞-D..341),( 9.当生物死亡时,他机体内原有的碳14含量按确定的规律衰减,大约每经过5730年衰减为原的一半,这个时间称为“半衰期”,据此规律,生物体内碳14的含量P 与死亡年数t 间的函数关系式为( )A.()1tP = B.()573012tP = C. ()573012t P = D.()573012P =10.已知函数:1||4)(2+-=x x x f ,若关于x 的方程:f(x)=2k 恰有四个不等的实数根,则实数k 的取值范围为() A..2123<<-k B.-3<k<1. C.-6<K<2. D.k>23-第二部分(非选择题)本部分共十一题,共100分。
四川省邛崃市高埂中学高三数学上学期一诊适应性考试试

是k=0,S=1开始 k<3? S=S .2k k=k+1 输出S 结束否 高埂中学高2016级一诊适应性考试(文科数学)第Ⅰ卷 (选择题共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1.已知集合{}1==x x M ,{}x x x N ==2,则=⋃N MA.{}1B.{}1,1-C.{}1,0D.{}1,0,1-2.复数2(1)1i i+-=A. 1i +B. 1i -+C. 1i --D. 1i -3.已知平面γβα,,,直线c b a ,,,则下列命题正确的是A. 若,,γβγα⊥⊥则βα//;B. 若,,c b c a ⊥⊥则b a //;C. 若,,αα⊥⊥b a 则b a //;D. 若,//,//ααb a 则b a //. 4.设a 、b 是实数,则“22a b >”是“0a b >>”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件5.设y x ,满足约束条件⎩⎨⎧≤-≤-≤≤0131y x x ,则y x z -=2的最大值为A.3B.2C.1D.0 6.一个棱锥的三视图如图,则该棱锥的全面积是A .4+2 6B .4+ 6C .4+2 2D .4+ 27. 执行如图所示的程序框图,输出的S 值是A. 2B. 4C. 8D. 168.定义22⨯矩阵12142334=a a a a a a a a ⎡⎤-⎢⎥⎦⎣,若22cos sin 3()cos(2)12x xf x x π⎡⎤-⎢⎥=⎢⎥+⎢⎥⎣⎦,则()f x 的图象向右平移3π个单位得到函数()g x ,则函数()g x A. 图象关于(),0π中心对称 B. 图象关于直线2x π=对称C.()g x 是周期为π的奇函数D. 在区间[,0]6π-上单调递增9.设12,F F 是双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点, P 是C 上一点,若126,PF PF a +=且12PF F ∆的最小内角为30o ,则C 的离心率为B.D.310.函数))((R x x f y ∈=满足)1()1(-=+x f x f ,且]1,1[-∈x 时,21)(x x f -=,函数⎪⎩⎪⎨⎧<->=)0(1)0(1)(x xx gx x g ,则函数)()()(x g x f x h -=在区间]5,5[-内的零点的个数为 A.9B. 8C.7D.6第Ⅱ卷 (非选择题共100分)二、填空题:本大题共5小题,每小题5分,共25分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四川省邛崃市高埂中学2013-2014学年高一上学期第一次月考数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分,考试时间120分钟。
1、答卷前,考生务必将自己的姓名、考号填写在答题卷上。
2、考试结束,只交答题卷。
第Ⅰ卷(选择题,共50分)一、选择题:(本大题共10各小题,每小题5分,共50分)在每小题给出的四个选项中,有且只有一个项是符合题目要求的。
1.已知全集{}{}{}()====N M C ,N M U U 则3,2,2,1,0,4,3,2,1,0( ) A. {}2 B. {}3 C. {}432,, D. {}4321,0,,,2.已知全集R U =,则正确表示集合{}{}0|1,0,12=+=-=x x x N M 和关系的Venn 图是( )3.下列哪组中的两个函数是相等函数( ) A. ()4444)()(x x g x x f ==, B. 2)(24)(2-=+-=x x g x x x f , C. 0)(,1)(x x g x f == D. ()()2,x x g x x f ==4.下列集合A 到集合B 的对应f 是映射的是( ) (A ){}{}1,0,1,1,0,1,A B f =-=-:A 中的数平方; (B ){}{}f B A ,1,0,1,1,0-==:A 中的数开方; (C ),,A Z B Q f ==:A 中的数取倒数; (D ),,A R B R f +==:A 中的数取绝对值.5.下列函数在区间(,0)-∞上是增函数的是( )A .2y x = B . y x =- C .xy 1= D .1+-=x y 6.下列函数中,不满足(2)2()f x f x =的是( )A .()f x x =B .()f x x x =-C .()f x x =+1D .()f x x =-7.客车从甲地以60km/h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h 的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图象中,正确的是( )A. B. C. D.8.已知集合{},10x A y y B x kx x ⎧⎫⎪⎪===-=⎨⎬⎪⎪⎩⎭,且B B A = ,则k 的值为( )A .1B .1-C .1或1-D .1或1-或09.设函数)0()(2≠++=a c bx ax x f ,对任意实数t 都有)2()2(t f t f -=+成立,则函 数值)1(-f ,)1(f ,)2(f ,)5(f 中,最小的一个不可能是( )A .)1(-fB .)1(fC .)2(fD .)5(f10. 定义运算“*”如下:2,*,,a a ba b b a b≥⎧=⎨<⎩则函数()(1*)(2*)(f x x x x x =⋅-∈[2,2])-的最大值等于( )A. 8B. 6C. 4D.1第Ⅱ卷(非选择题,共90分)二、填空题:(每小题5分,共25分)将答案直接填在答题卡上。
11.函数1()2f x x x=++的定义域为________ 12.已知函数⎩⎨⎧≥+<+=1,1,23)(2x ax x x x x f ,若a f f 4))0((=,则实数=a13.若集合}044|{2=+-=x mx x A 中只有一个元素,则m 的值为14. 设A ,B 是非空集合,定义{}B A x B A x x B A ∉∈=*且|,已知{}30|≤≤=x x A ,{}1|≥=x x B ,则=*B A ________15.已知下列命题:①若()f x 为减函数,则()f x -为增函数; ②若()(),40f f <则函数()x f 不是R 上的减函数;③若函数)(x f 的定义域为]2,0[,则函数)2(x f 的定义域为]4,0[;④设函数()x f 是在区间[]b a ,上图像连续的函数,且()()0<⋅b f a f ,则方程()0=x f 在 区间[]b a ,上至少有一实根.⑤若函数()()()221()11(1)m x m x f x m x x -+<⎧⎪=⎨-+≥⎪⎩在R 上是增函数,则m 的取值范围是12m <<; 其中正确命题的序号有 (把所有正确命题的番号都填上)三、解答题:(本大题共6小题,共75分)解答题应写出文字说明、证明过程或推演步骤。
16.(本小题满分12分)已知集合⎭⎬⎫⎩⎨⎧<+-=0532x x xA ,{}0232<+-=x x x B ,R U =.求:(1)B A ; (2)B A ; (3)B A C U )(.17.(本小题满分12分)已知函数()221x f x x =+()0x ≠.(1)求)2(f ,)21(f ,1f x ⎛⎫ ⎪⎝⎭;(2)由(1)中求得的结果,你能发现()f x 与1f x ⎛⎫ ⎪⎝⎭有什么关系吗?如果能,请求出111(1)(2)(3)f(10)f()f()f()2310f f f +++⋯++++⋯+的值。
18.(本小题满分12分)已知函数)()()(x g x f x F +=,其中()f x 、)(x g 分别为正、反比例函数,且29)2(,3)1(==F F 。
(I)求函数)(x F 的解析式; (II)判断函数)(x F 在[22, +∞)上的单调性,并用定义证明。
19.(本小题满分12分)已知函数()f x 是定义在(0,+∞)上的单调递增函数,且满足1)3(),()()(=+=f y f x f xy f 。
(1)求)1(f 的值; (2)若满足2)8()(≤-+x f x f ,求x 的取值范围。
20.(本小题满分12分)某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x (百台),其总成本为()x G (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。
销售收入()x R (万元)满足()()()⎩⎨⎧>≤≤+-=511502.44.02x x x x x R ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题: (1)写出利润函数()x f y =的解析式(利润=销售收入—总成本);(2)要使工厂有盈利,求产量x 的范围;(3)工厂生产多少台产品时,可使盈利最多?21.(本小题满分14分)已知函数2()(3)3,0.f x kx k x k k =+++≠其中为常数,且 (1)若(2)3f =,求函数()f x 的表达式;(2)在(1)的条件下,设函数()()g x f x mx =-,若()[2,2]g x -在区间上是单调函数,求实数m 的取值范围;(3)是否存在实数k 使得函数()f x 在[1,4]-上的最大值是4?若存在,求出k 的值;若不存在,请说明理由.高埂中学高2016级高一上期第一次月考数学试题参考答案一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 答案BBDADCCDBB二、填空题:11、[)2,0)(0,-+∞ 12、2 13、0或1 14、[)()0,13,+∞ 15、①、②、④ 三、解答题:16.解:A={x|532+-x x <0}={x|-5<x <23} B={x|x 2-3x+2<0}={x|1<x<2}………2分 (Ⅰ)A ∩B={x|1<x <23} …………5分(Ⅱ)A ∪B={x|-5<x<2} …………8分(Ⅲ)(uA )={x|x ≤-5或x ≥23} (uA )∩B={x|23≤x<2}………12分 17、解:(1)54212)2(f 22=+=,51)21(1)21()21(f 22=+=,2221()11()111()x f x x x==++.......5分 (2)()22211111x f x f x x x ⎛⎫+=+= ⎪++⎝⎭.......8分 ∴1)21(f )2(f =+,1)31(f )3(f =+,…,1(10)()110f f +=∴原式111(1)[(2)()][(3)()][f(10)f()]2310f f f f f =+++++⋯++11111922=+++⋯+=,.....................12分18、解:(1)设xk x g x k x f 21)(,)(==............1分 ⎩⎨⎧==⇒⎪⎩⎪⎨⎧=+==+=122922)2(3)1(212121k k k k F k k F 由 ∴x x x F 12)(+=............6分(2)设2122x x <≤,则)12(12)()(112212x x x x x F x F +-+=-=................9个212112)12)((x x x x x x --=...........9分∵2122x x <≤ ∴12,0,0212112>>>-x x x x x x .........11分 ∴)()(,0)()(1212x f x f x f x f >>-即 故函数)(x f 在[22, +∞)上为增函数...........12分 19.解(1)由题意令x=y=1结合f(xy)=f(x)+f(y)得f(1)=f(1)+f(1),f(1)=0-------------------4分(2)因为f(3)=1,所以 2=f(3)+f(3)结合f(xy)=f(x)+f(y) 所以2=f(9) -------------------6分根据题意结合函数的定义域得989109)8(080≤<⇒⎪⎩⎪⎨⎧≤≤->>⇒⎪⎩⎪⎨⎧≤->->x x x x x x x x -------------10分 所以x 的取值范围是98≤<x -------------------12分21.ⅰ)若13422k k +-<-≤,即13k ≤-时,函数()f x 在[1,4]-的最大值为2312(3)()424k k k f k k +-+-==,化简得21090k k ++=,解得19或k k =-=-,符合题意; ………………………………11分 ⅱ)若342k k +->即103k -<<时,函数()f x 在[1,4]-上单调递增,最大值为(4)164(3)320154f k k k =+++=+=,解得111203k =-<-,不合题意,舍去.13分 综上所述,存在k 使得函数()f x 在[1,4]-上的最大值是4,且19或k k =-=-.…14分。
