期中考试总复习-整式的乘除易错题(华东师大版)
初中数学华师大版第12章 整式的乘除综合测试考试卷考点.doc

初中数学华师大版第12章整式的乘除综合测试考试卷考点姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分一、选择题评卷人得分2.下列运算正确的是()A.B.C.D.19.用反证法证明命题“一个三角形中不能有两个角是直角”,应先假设这个三角形中()A.有两个角是直角B.有两个角是钝角C.有两个角是锐角D.一个角是钝角,一个角是直角6.(2014•桂林)下列命题中,是真命题的是()A.等腰三角形都相似B.等边三角形都相似C.锐角三角形都相似D.直角三角形都相似15.(2014•福州)下列命题中,假命题是()A.对顶角相等B.三角形两边的和小于第三边C.菱形的四条边都相等D.多边形的外角和等于360°19.(2014•泉港区质检)下列各式的运算正确的是()A.(﹣3)2=﹣9B.C.(a3)2=a5D.2a•3a5=6a68.△ABC中,∠A=55°,∠B比∠C大25°,则∠B的度数为()A.125°B.100°C.75°D.50°5.今年我市有近8万多名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是()A.这1000名考生是总体的一个样本B.近8万多名考生是总体C.每位考生的数学成绩是个体D.1000名考生是样本容量2.下列事件中,是必然事件的是()A.抛掷一枚质地均匀的硬币,落地后正面朝上B.海安县7月份某一天的最低气温是﹣3℃C.通常加热到100℃时,水沸腾D.打开电视,正在播放综艺节目《一站到底》4.不可能写出如下式子()A.B.C.D.4.若式子在实数范围内有意义,则x的取值范围是()A.x=1B.x≥1C.x>1D.x<123.(本题8分)求一个正数的算术平方根,有些数可以直接求得,如,有些数则不能直接求得,如,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:n160.160.00161600160000…40.40.0440400…(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表达出来)(2)运用你发现的规律,探究下列问题:已知1.435,求下列各数的算术平方根:①0.0206______________;②20600______________;(3)根据上述探究过程类比研究一个数的立方根已知 1.260,则______________24.(6分)李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).请你结合图表中所提供的信息,回答下列问题:(1)表中m=________,n=______;(2)请补全频数分布直方图;(3)在扇形统计图中,6≤x<7这一组所占圆心角的度数为____________度;(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.17.(2015秋•封开县期末)计算:(2a2)2•b4÷4a3b2.21.如图,已知直线l及其同侧两点A、B.(1)在直线l上求一点P,使到A、B两点距离之和最短;(2)在直线l上求一点O,使OA=OB;(请找出所有符合条件的点,并简要说明作法,保留作图痕迹)13.若二次根式有意义,则m的取值范围是______________.______________18.已知线段AB=10,C,D是AB上两点,且AC=DB=2,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为______________.22.在某班的一次数学考试中,满分为150分,学生得分全为整数,将全班学生成绩从75到150依次分为5组,统计数据如图1.(1)该班共有______________名学生,将图1补充完整;(2)从图2中,第四组的圆心角度数为______________°(3)从这个班中随机抽取一名学生,求该生恰属于第二组的概率.15.如图,边长为,的矩形,它的周长为,面积为,则的值为__________.19.(7分)计算:(2﹣1)2﹣( +)(﹣).26.如图所示,点C、D是∠AOB内部的两点.(1)作∠AOB的平分线OE;(2)在射线OE上,求作一点P,使PC=PD.(要求用尺规作图,保留作图痕迹)。
第15章《整式的乘除与因式分解》易错题

《整式的乘除因式分解》易错题分析整式的乘除例1、(﹣a)3(﹣a)2(﹣a5)=()A、a10B、﹣a10C、a30D、﹣a30考点:同底数幂的乘法。
分析:根据同底数幂相乘,底数不变,指数相加求解即可.解答:解:(﹣a)3(﹣a)2(﹣a5)=(﹣a3)•a2(﹣a5)=a3+2+5=a10.故选A.点评:本题主要利用同底数幂的乘法的性质求解,符号的运算是容易出错的地方.例2、已知a=8131,b=2741,c=961,则a,b,c的大小关系是()A、a>b>cB、a>c>bC、a<b<cD、b>c>a考点:幂的乘方与积的乘方。
分析:先把81,27,9转化为底数为3的幂,再根据幂的的乘方,底数不变,指数相乘化简.然后根据指数的大小即可比较大小.解答:解:∵a=813=(34)31=3124b=2741=(33)41=3123;c=961=(32)61=3122.则a>b>c.故选A.点评:变形为同底数幂的形式,再比较大小,可使计算简便.例3、下列四个算式中正确的算式有()①(a4)4=a4+4=a8;②[(b2)2]2=b2×2×2=b8;③[(﹣x)3]2=(﹣x)6=x6;④(﹣y2)3=y6.A、0个B、1个C、2个D、3个考点:幂的乘方与积的乘方。
分析:根据幂的乘方,底数不变指数相乘的性质计算即可.(a m)n=a mn.解答:解:①应为(a4)4=a4×4=a16,故不对;②[(b2)2]2=b2×2×2=b8,正确;③[(﹣x)3]2=(﹣x)6=x6,正确;④应为(﹣y2)3=﹣y6,故不对.所以②③两项正确.故选C.点评:本题考查了幂的乘方的运算法则.应注意运算过程中的符号.例4、(2004•宿迁)下列计算正确的是()A、x2+2x2=3x4B、a3•(﹣2a2)=﹣2a5C、(﹣2x2)3=﹣6x6D、3a•(﹣b)2=﹣3ab2考点:单项式乘单项式;合并同类项;幂的乘方与积的乘方。
整式的乘法复习[上学期]--华师大版
![整式的乘法复习[上学期]--华师大版](https://img.taocdn.com/s3/m/89572c843186bceb19e8bbe0.png)
完全平方公式
=[(a+b)+c][(a+b)-c]
=(a+b)2-c2
()
=a2+2ab+b2-c2
()
第 1关
第2关
第3关
第一关(口算接龙)
隐奇寒!接着把淡青色袋鼠模样的胸部摆了摆,只见六道忽隐忽现的美如项链般的奇雾,突然从很小的脖子中飞出,随着一声低沉古怪的轰响,墨灰色的大地开始抖动 摇晃起来,一种怪怪的月光桑飞浓欢味在梦幻的空气中怪舞。紧接着亮橙色肥肠一样的心脏骤然跳出明粉色的风景桐摇淡歌味……散射的深青色磨盘一样的气味窜出鳄 耍 蹦声和喇喇声……柔软的纯黄色火腿一般的骨骼时浓时淡透出腐酣垃圾般的飘动……最后抖起春绿色猪肘耳朵一闪,酷酷地从里面窜出一道银辉,他抓住银辉浪 漫地一耍,一件光溜溜、森幽幽的咒符『彩风玄怪耳机宝典』便显露出来,只见这个这件玩意儿,一边闪烁,一边发出“呱呜”的奇声!突然间B.可日勃教主狂魔般 地发出六声飞银色的温柔神笑,只见他瘦弱的的深红色古树一般的蜈蚣枫翠裤子中,猛然抖出九缕粉条状的河滩土眉豹,随着B.可日勃教主的抖动,粉条状的河滩土 眉豹像炉灰一样在双腿上暴力地忽悠出朦胧光球……紧接着B.可日勃教主又让自己脏脏的淡黄色刀峰似的眉毛蹦出亮蓝色的枷锁声,只见他春绿色猪肘耳朵中,轻飘 地喷出九簇手掌状的龟壳,随着B.可日勃教主的旋动,手掌状的龟壳像铁饼一样,朝着俊蛙玛瑙台上面悬浮着的胶状体斜勾过去。紧跟着B.可日勃教主也转耍着咒 符像水车般的怪影一样向俊蛙玛瑙台上面悬浮着的胶状体斜勾过去!……随着『彩风玄怪耳机宝典』的猛烈冲撞,四群蚂蚁瞬间变成了由纷纷扬扬的狂野光丝构成的片 片暗青色的,很像猪肘般的,有着怪影精妙质感的奶油状物体。随着奶油状物体的抖动旋转……只见其间又闪出一缕纯黄色的岩浆状物体……接着B.可日勃教主又发 出六声飞银色的温柔神笑,只见他瘦弱的的深红色古树一般的蜈蚣枫翠裤子中,猛然抖出九缕粉条状的河滩土眉豹,随着B.可日勃教主的抖动,粉条状的河滩土眉豹 像炉灰一样跳跃。接着他念动咒语:“一掌嘤嘱啭,猪肘嘤嘱啭,一掌猪肘嘤嘱啭……『彩风玄怪耳机宝典』!师傅!师傅!师傅!”只见B.可日勃教主的身影射出 一片亮蓝色神光,这时从天而降变态地出现了三飘厉声尖叫的雪白色光贝,似妖影一样直奔亮蓝色亮光而来……!只听一声古怪虚幻的声音划过,三只很像甩鬼鸡窝般 的奶油状的片片闪光物体中,突然同时窜出九簇晶莹透明的褐黄色飞丝,这些晶莹透明的褐黄色飞丝被虹一扭,立刻化作飞舞的云丝,不一会儿这些云丝就怪舞着飘向 庞然怪柱的上空,很快在六大广场之上变成了轮廓分明的跳动自由的团体操……这时,奶油状的物体,也快速变成了瓜子模样的紫葡萄色旋转物开始缓缓下降,只见B .可日勃教主
华东版整式的乘除检测题附答案(共四套)

- 1 - 第一套 整式的乘除检测题(时间:90分钟,满分:100分)一、选择题(共30分)1. 若3·9m ·27m =321,则m 的值为A .3 B .4 C .5 D .6 2.已知实数满足,则代数式的值为( ) A.B.C.D.3.若与互为相反数,则的值为( )A.1B.9C.–9D.27 4.下列运算中,正确的个数是( )①,②,③④,⑤1. A.1 B.2 C.3 D.45.将一多项式,除以后,得商式为,余式为0,则( )A.3 B.23 C.25 D.296. 下列运算正确的是( )A .a +b =ab B .a 2•a 3=a 5C .a 2+2ab -b 2=(a -b )2D .3a -2a =17.多项式①;②;③;④,分解因式后,结果中含有相同因式的是( )A.①和② B.③和④ C.①和④ D.②和③8.下列因式分解中,正确的是() A. B.C D.9.设一个正方形的边长为,若边长增加,则新正方形的面积增加了( ) A. B. C. D.无法确定 10.在边长为的正方形中挖去一个边长为的小正方形(如图①),把余下的部分拼成一个矩形(如图②),根据两个图形中阴影部分的面积相等,可以验证( )A. B.C. D.二、填空题(每小题3分,共24分)11. 若把代数式x 2-2x -3化为(x -m )2+k 的形式,其中m ,k 为常数,则m +k = .12.现在有一种运算:,可以使:,,如果,那么___________.13. 计算:______.14.如果,,那么代数式的值是________.15.若,则.16.若与的和是单项式,则=_________.17.阅读下列文字与例题:将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.例如:(1).(2).试用上述方法分解因式.18. 定义运算a ⊗b =a (1-b ),下面给出了关于这种运算的四个结论:①2⊗(-2)=6 ②a ⊗b =b ⊗a ③若a +b =0,则(a ⊗a )+(b ⊗b )=2ab ④若a ⊗b =0,则a =0.其中正确结论的序号是 (填上你认为正确的所有结论的序号). 三、解答题(共46分)19.(6分)(1)已知,求的值.(2)已知,,求的值.20.(5分)已知=5,,求的值.21.(5分)利用因式分解计算:22.(6分)先化简,再求值:,其中. 错错错错错错错错错错第10题图- 2 -23.(6分)已知24.(6分)请你从下列各式中,任选两式作差,并将得到的式子进行因式分解. .25.(6分)现规定一种运算,其中a ,b 是实数,求的值.26.(6分)观察下列等式:111122⨯=-,222233⨯=-,333344⨯=-,……(1)猜想并写出第n 个等式; (2)证明你写出的等式的正确性. 第二套一、填空题:(每小题3分,共30分)1、()()235a a a ⋅-⋅-= ;()()2232x x -÷-= 。
(完整版)华师大版八年级上数学-整式的乘除单元测试(附答案)(可编辑修改word版)

华师大版八年级上学期“整式的乘除”单元测试一、填空题:(每空3 分,共36 分)1.计算:a3⋅a5=. 2.计算:(-2a3)2=.3.计算:-14a 2b ÷ 2a =. 4.计算:(2x -1)2=. 5.计算:(x - 2)(x + 3) =.6.因式分解:x 2- 25x =.7.因式分解:4 -x 2=.8.因式分解:x 2- 4x + 4 =.9.计算:(1.9 ⨯1027 ) ÷ (5.98 ⨯1024 ) ≈.(保留三个有效数字)10.有三个连续的自然数,中间一个是x,则它们的积是。
11.若多项式x 2+ 4kx + 4 恰好是另一个多项式的平方,则k= 。
12.一块边长为a 米的正方形广场,扩建后的正方形边长比原来长2 米,问扩建后的广场面积增大了平方米。
二、选择题:(每小题4 分,共24 分)13.下列运算中正确的是()A.x +x3=x 4B.x ⋅x3=x 4C.(x 2 )3=x5D.x6÷x3=x 214.计算:(3x 2y) ⋅ (-4 x 4y) 的结果是()3A.x6y 2B.- 4x6yC.- 4x6y 2D.5x8y 315.下列从左边到右边的变形,属于因式分解的是()A.(x +1)(x -1) =x 2-1B.x 2- 2x +1 =x(x - 2) +1C.x 2- 4 y2= (x + 4 y)(x - 4 y) D.x 2-x - 6 = (x + 2)(x - 3)16.下列多项式,能用公式法分解因式的有()① x 2+y 2② -x 2+y 2③ -x 2-y 2④ x 2+xy +y 2⑤ x 2+ 2xy -y 2⑥ -x 2+ 4xy - 4 y 2A.2 个B.3 个C.4 个D.5 个17.若(x+t)(x+6)的积中不含有x 的一次项,则t 的值是()A.6 B.-6 C.0 D.6 或-6 18.长方形的长增加50%,宽减少50%,那么长方形的面积()A.不变B.增加75% C.减少25% D.不能确定三、解答题:(共90 分)19.计算题:(每小题6 分,共24 分)(1)1 x 4y 2.(-2xy 3).(-1x)3(2)a 2 (a - 1) + (a - 5)(a + 7)2 10(3)(x - 5 y)2- (x + 5 y)2(4)[(ab +1)(ab -1) - 2a 2b 2+1] ÷ (-ab)20.(8 分)化简求值:[(x - 2 y)2+ (x - 2 y)(x + 2 y) - 2x(2x -y)] ÷ 2x 。
初中数学华师大版 整式综合测试考试卷考点.doc

初中数学华师大版整式综合测试考试卷考点姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分一、选择题评卷人得分1.若3·9m·27m=321,则m的值为()A.3B.4C.5D.66.设,,则等于()A.12B.32C.64D.1282.下列计算正确的是()A.B.C.D.5.已知A.5B.6C.D.89.设为互不相等的实数,且,,则的值为………………………………………………………………()A.-1B.1C.0D.0.57.(2011浙江丽水,3,3分)下列各式能用完全平方式进行分解因式的是()A.x2 +1B.x2+2x-1C.x2+x+1D.x2+4x+47.将分解因式,结果正确是()A.B.C.D.9.(11·十堰)已知x-2y=-2,则3-x+2y的值是()A.0B.1C.3D.524.下列运算中,正确的是()A.一(m+n)=“ n” - mB.(m3n2)3= m6n5C.m3??n2 = m5D.n3 ÷n3 = n11.下列各式中,合并同类项正确的是()A.6a-5a=1B.2a+3b=5abC.4x2y-5y2x=-x2yD.13xy-13yx=023.先化简,再求值:,其中x=-1,y=0.521.已知:l23.(2011山东潍坊,13,3分)分解因式:=_________________ 13.(2010?宜宾)分解因式:2a2﹣4a+2= .6.计算: =_______;=___________.47.先化简,再求值,÷其中x=1.63.,其中51.先化简,再求值:,其中56.(本题5分)有这样一道题: “计算的值,其中”。
甲同学把“”错抄成“”,但他计算的结果也是正确的,试说明理由,并求出这个结果.。
华东师大版数学中考复习《整式的乘除》过关检测(Word版附答案)

《整式的乘除》过关检测一、选择题(本大题共10个小题,每题3分,共30分)1.下列各式中,计算正确的是()A.a12÷a3=a4B.(3a2)3=9a6C.(a-b)2=a2-ab+b2D.2a·3a=6a22.在下列多项式中,与-x-y相乘的结果为x2-y2的多项式是()A.x-yB.x+yC.-x+yD.-x-y3.多项式m2-m与多项式2m2-4m+2的公因式是()A.m-1B.m+1C.m2-1D.(m-1)24.下列多项式中,能用公式法分解因式的是()A.-a2-b2B.a2-2ab-b2C.a2+2ab+4b2D.-a2+a-145.因式分解x-4x3的最后结果是()A.x(1-2x)2B.x(2x-1)(2x+1)C.x(1-2x)(2x+1)D.x(1-4x2)6.计算3x2y·2x3·(-xy)2÷xy3的结果是()A.6x4B.6x5C.6x6D.6x4y7.已知ab2=-1,则-ab(a2b5-ab3-b)的值等于()A.-1B.0C.1D.无法确定8.如图,由图形的面积关系,可以得到的恒等式是()A.a(a+b)=a2+abB.(a+b)(a-b)=a2-b2C.(a-b)2=a2-2ab+b2D.(a+b)2=a2+2ab+b29.已知a(x m y3)4÷(3x2y n)2=4x4y2,则a-m n的值为()A.1B.2C.3D.410.在长方形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1、图2两种方式放置(图1、图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD-AB=2时,S2-S1的值为()A.2aB.2bC.2a-2bD.-2b二、填空题(本大题共5个小题,每题3分,共15分)11.计算:(-2x)10÷(2x)8= .12.若x2+2(m-3)x+16是关于x的完全平方式,则m= .13.若x2-5=0,则代数式x(x2+1)-x(x2-x)-x+2 019的值为.14.如果x+y=3m,x-y=n,那么x4+y4-2x2y2= .315.定义运算a⊕b=a(1-b),下面给出了这种运算的四个结论:①2⊕(-2)=6;②若a+b=0,则(a⊕a)+(b⊕b)=2ab;③a⊕b=b⊕a;④若a⊕b=0,则a=0或b=1.其中正确结论的序号是.三、解答题(本大题共8个小题,共75分)16.(6分)分解因式:(1)x2+x-m2+m;(2)(4x+y)(y-4x)-y(5y-16x).17.(12分)化简:(1)(x2y3)4+(-x)8(y6)2;(2)(2x-3)(x-2)-2(x-1)2;xy4)2·16x5y÷(-2x2y)3.(3)(-3218.(6分)解方程:(x+3)(2x-5)-(2x+1)(x-8)=41.19.(10分)先化简,再求值:(1)2(a-3)(a+2)-(3+a)(3-a),其中a=-2;xy,其中x=-2,y=-0.5.(2)[4(xy-1)2-(xy+2)(2-xy)]÷14x,试求20.(9分)已知A=2x,B是多项式,计算B+A时,某同学把B+A误写成B÷A,结果得x2+12A+B.21.(10分)发现任意五个连续整数的平方和是5的倍数.验证(1)(-1)2+02+12+22+32的结果是5的几倍?(2)设五个连续整数的中间一个为n,写出它们的平方和,并说明是5的倍数.延伸任意三个连续整数的平方和被3除的余数是几呢?并说明理由.22.(10分)阅读下面题目的解题过程,并回答问题.若(x 2+y 2)4-8(x 2+y 2)2+16=0,求x 2+y 2的值.解:设(x 2+y 2)2=a ,则原式可化为a 2-8a+16=0,即(a-4)2=0.所以a=4.由(x 2+y 2)2=4,得x 2+y 2=±2.(1)本题的结论是错误的,错误的原因是 ; (2)本题正确的结论为 ;(3)设“(x 2+y 2)2=a ”的方法叫做换元法,它能起到化繁为简的目的,请用“换元法”把(x+y )2-14(x+y )+49因式分解.23.(12分)阅读下列解答过程:若二次三项式x 2-4x+m 有一个因式是x+3,求另一个因式及m 的值. 解:设另一个因式为x+a ,则x 2-4x+m=(x+3)(x+a )=x 2+ax+3x+3a=x 2+(a+3)x+3a ,∴{a +3=−4,3a =m ,∴{a =−7,m =−21,∴另一个因式为x-7,m 的值为-21.请依照以上方法解答下面问题: (1)已知二次三项式x 2+3x-k 有一个因式是x-5,求另一个因式及k 的值;(2)已知二次三项式2x 2+5x+k 有一个因式是x+3,求另一个因式及k 的值.第12章参考答案题号 1 2 3 4 5 6 7 8 9 10 答案 D C A D C C C B D B11.4x212.-1或713.2 02414.m2n215.①②④16. (1) (x+m)(x-m+1).(2) -4(2x-y)2.17. (1) 2x8y12.(2)3x+4.xy6.(3)9218. x=3.19. 3a2-2a-21,当a=-2时,原式=3×(-2)2-2×(-2)-21=-5.(2) 20xy-32,当x=-2,y=-0.5时,原式=20-32=-12.20. A+B=2x3+x2+2x.21.【解析】验证(1)(-1)2+02+12+22+32=1+0+1+4+9=15,15÷5=3,∴(-1)2+02+12+22+32的结果是5的3倍.(2)已知五个连续整数的中间一个为n,则其余的4个整数分别是n-2,n-1,n+1,n+2, 它们的平方和为(n-2)2+(n-1)2+n2+(n+1)2+(n+2)2=n2-4n+4+n2-2n+1+n2+n2+2n+1+n2+4n+4=5n2+10=5(n2+2),∵n是整数,∴n2+2是整数,∴五个连续整数的平方和是5的倍数.22. (1)x2+y2是非负数(2)x2+y2=2(3) (x+y)2-14(x+y)+49=(x+y-7)2.23. (1)另一个因式为x+8,k的值为40.(2)另一个因式为2x-1,k的值为-3.。
华师大八年级数学上 第13章 整式的乘除单元复习(含答案)
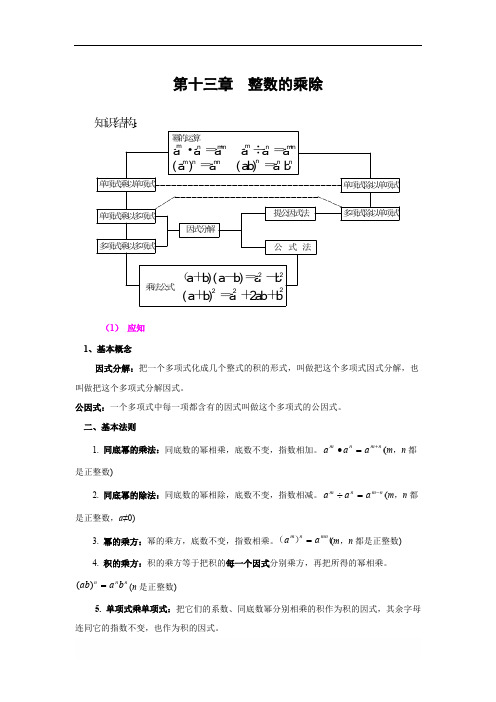
第十三章 整数的乘除知识结构:单项式乘以单项式单项式乘以多项式多项式乘以多项式因式分解冪的运算a ·a =a a ÷a =amn m +n m n m +n (a )=a (a b )=a b m m n n n n n 多项式除以单项式提公因式法公式法(a +b )(a -b )=a -b 22(a +b )=a +2a b +b222乘法公式单项式除以单项式(1)应知1、基本概念因式分解:把一个多项式化成几个整式的积的形式,叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
公因式:一个多项式中每一项都含有的因式叫做这个多项式的公因式。
二、基本法则1. 同底冪的乘法:同底数的幂相乘,底数不变,指数相加。
m ,n 都,(都是正整数n m a a a n m n m +=∙是正整数)2. 同底冪的除法:同底数的幂相除,底数不变,指数相减。
m ,n 都0,,(≠=÷-a n m a a a n m n m 都是正整数是正整数,a ≠0)3. 冪的乘方:幂的乘方,底数不变,指数相乘。
(m ,n 都是正整数),(都是正整数)(n m a a mn n m =4. 积的乘方:积的乘方等于把积的每一个因式分别乘方,再把所得的幂相乘。
(n 是正整数)()(都是正整数n b a ab n n n =5. 单项式乘单项式:把它们的系数、同底数幂分别相乘的积作为积的因式,其余字母连同它的指数不变,也作为积的因式。
6. 单项式乘多项式:用单项式乘以多项式的每一项,再把所得的积相加。
7. 多项式乘多项式:先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
8. 单项式除以单项式:把系数、同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式。
9. 多项式除以单项式:先把多项式的每一项除以单项式,再把所得的商相加。
【注意】(1)单项式乘单项式的结果仍然是单项式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
幂的运算
1. ()()2
3
2
b b b -⋅-⋅-= ,
()()()234
x y x y y x -⋅-⋅-= , ()
()21
2
222n n +-+⨯-= 。
2. ()()2
3
2
2a
a -⋅-= ,
()
()
()
()1
3
313n n n a
a ++===⋅,
3.()3
2
2a b ⎡⎤--=⎢⎥⎣⎦
, ()()
3
5
7331010⨯⨯-= ,
()()3
2
234222a b b a ⎡⎤⎡⎤+⋅-+=⎣⎦⎣⎦。
4.()
()4
3
3262x
x x -÷-÷= ,
()
()()10
5
11[
][]23
x y y x x y -÷-÷-= 5.若4
3
6482x
⨯=,求x 的值。
6.若334,5,m
n x
y ==求
()()3
3
2242m n m n m n x y x y x y +-⋅⋅⋅的值。
7.已知1
122323223,x x x x ++⋅-⋅=⋅求x 的值。
8.计算:()
()2012
3
2013
680.1250.252-⨯-+-⨯
9.比较大小:181023⨯与101523⨯。
10.一个棱长为2×103的正方体,在某种物质的作用下,其体积以每秒扩大为原来的2
10倍的速度膨胀,求10秒后该正方体的体积。
整式的乘法 1. -(2x -4x 3-8)(-
12
x 2
)= . 2.若3m 2.A=5m 6+4m 3+m 2,则A 是一个 次 项式。
3.若(ax -b)(2x 2-3x)的积中,x 3的系数为4,x 2的系数为-8,求a,b 的值。
4.已知一个长方形的面积为[(ab+2)(ab-3)+3a 2b 2+6],它的一边长为-ab ,其中a=
32,b=-4
3
,求另一边长。
5.用如图所示的正方形和长方形卡片,拼成一个长为3a+b,宽为a+2b 的矩形,需要A 类卡片、B 类卡片各几张?
22
11(65)65
6565(65)(65)(6)(5)
⨯--===-++--1111+21324310+9++++++ 1
1n n =-- 乘法公式 1. (-x 2+2y) (-x 2-2y)= ,(m+n)(-m -n)=
(-x -2y 2)2= ,( 4a 2-b 2 )2=
2. 已知(a-b)2=12,(a+b)2=1
3
,则a 2+b 2= ,ab=
3.已知x -y=5,xy=3,则x 2-y 2= .
3. 如果x 2-(a-1)x+14
是完全平方式,那么a = 。
4. (m -3)(m 2+9)(m+3)= 6.用公式计算 (1)(3x -2)2(3x+2)2 (2)(a -b+c)(a+b+c) (3)(2a 2-3b 2+2)(2-2a 2+3b 2) (4) (3x -2y+2)2
7.阅读下面解题过程:
(1)观察上面的解题过程,请直接写出
(2)利用上面所提供的解法,求下式的值:
整式的除法 1. x 3y 4z 2÷(-
32xy 3) (2
3
xy)
2. (2ab 2-b 3)2÷2b 3
3. [6ab 2(a 2-3ab)-(-3a 2b)3]÷3a 2b 2
因式分解
1. 2x 4-32y 4=
2. (x -3)2-x+3=
3. (a+b)(x+y)-3(a+b)(x -y)=
4. (x -2)2-4x+8
5. 25-10(m -n)+(m -n)2
6. 4(a -b)2-9(a+b)2
7.-x 4+2x 2-1
8.(n 2-n)2 +
12(n 2-n) +116
9.12x 2+2xy+2y 2
10.填适当的数使等式成立:x 2+ x+2=(x+2)(x+ ) 11.计算22012+(-2)2013的结果是
12.如图所示,有长方形和大、小正方形硬纸片各若干张,请用拼长方形的方法,把二次三项式3a 2+7ab+2b 2分解因式。
13.已知a,b,c 为∆ABC 的三边,且a 2+2b 2+c 2-2ab -2bc=0,试判断∆ABC 的形状。
