2020上海市华二附中高三下数学4月月考试卷(图片版,有答案)
2024-2025学年上海华二附中高三上学期数学月考试卷及答案(2024.09)

1华二附中2024学年第一学期高三年级数学月考2024.09一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分) 1.已知i 为虚数单位,复数12iz i+=,则z 的实部为________. 2.若函数()133x xf x a =⋅+为偶函数,则实a =________. 3.若事件A 、B 发生的概率分别为1()2P A =,2()3P B =,且相互独立,则()P A B =________.4.已知集合(){}2|log 1A y y x ==−,{}3|27B x x =≤,则A B =________.5.设{}n a 是等比数列,且13a =,2318a a +=,则n a =________.6.现有一球形气球,在吹气球时,气球的体积V 与直径d 的关系式为36d V π=,当2d =时,气球体积的瞬时变化率为________. 7.已知随机变量X 的分布为123111236⎛⎫⎪ ⎪ ⎪⎝⎭,且3Y aX =+,若[]2E Y =−,则实数a =________. 8.记函数()()()cos 0,0f x x =ω+ϕω><ϕ<π的最小正周期为T ,若()f T =,9x π=为()f x 的零点,则ω的最小值为________.9.若6(0)b ⎛> ⎝的展开式中含x 项的系数为60,则2a b +的最小值为________.10.顶点为S 的圆锥的母线长为60cm ,底面半径为25cm ,A ,B 是底面圆周上的两点,O 为底面中心,且35AOB π∠=,则在圆锥侧面上由点A 到点B 的最短路线长为____cm .(精确到0.1cm )11.已知△ABC 中,22AB BC ==,AB 边上的高与AC 边上的中线相等,则tan B =2________.12.给定公差为d 的无穷等差数列{}n a ,若存在无穷数列{}n b 满足: ①对任意正整数n ,都有1n n b a −≤②在21b b −,32b b −,…,20252024b b −中至少有1012个为正数,则d 的取值范围是________. 二、单选题(本大题共4小题,共18.0分.在每小题列出的选项中,选出符合题目的一项) 13.“1a b +>”是“33a b >”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件14.如果两种证券在一段时间内收益数据的相关系数为正数,那么表明( ) A .两种证券的收益之间存在完全同向的联动关系,即同时涨或同时跌 B .两种证券的收益之间存在完全反向的联动关系,即涨或跌是相反的 C .两种证券的收益有同向变动的倾向 D .两种证券的收益有反向变动的倾向15.设0k >,若向量a 、b 、c 满足::1::3a b c k =,且2()b a c b −=−,则满足条件的k 的取值可以是( )A .1B .2C .3D .416.设1A ,1B ,1C ,1D 分别是四棱锥P ABCD −侧棱PA ,PB ,PC ,PD 上的点.给出以下两个命题,①若ABCD 是平行四边形,但不是菱形,则1111A B C D 可能是菱形;②若ABCD 不是平行四边形,则1111A B C D 可能是平行四边形.( ) A .①真②真 B .①真②假 C .①假②真 D .①假②假三、解答题(本大题共5小题,共78.0分.)17.(本小题14.0分)如图,在圆柱中,底面直径AB等于母线AD,点E在底面的圆周⊥,F是垂足.(1)求证:AF DB⊥;(2)若圆柱与三棱锥D ABE−的体积的比等于3π,求直线DE与平面ABD所成角的大小.3418.(本小题14.0分)李先生是一名上班旋,为了比较上下班的通勤时间,记录了20天个工作日内,家里到单位的上班时间以及同路线返程的下班时间(单位:分钟),如下茎叶图显示两类时间的共40个记录:(1)求出这40个通勤记录的中们数M ,并完成下列22⨯列联表:(2)根据列联表中的数据,请问上下班的通勤时间是否有显著差异?并说明理由. 附:()()()()()22n ad bc a b c d a c b d −χ=++++,()2 3.8410.05P χ≥≈.519.(本小题14.0分)如图,某城市小区有一个矩形休闲广场,20AB =米,广场的一角是半径为16米的扇形BCE 绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN (宽度不计),点M 在线段AD 上,并且与曲线CE 相切;另一排为单人弧形椅沿曲线CN (宽度不计)摆放,已知双人靠背直排椅的造价每米为2a 元,单人弧形椅的造价每米为a 元,记锐角NBE ∠=θ,总造价为W 元。
2020届上海市华二附中高三下学期4月月考数学试题(解析版)

2020届上海市华二附中高三下学期4月月考数学试题一、单选题1.设,x y R ∈,“1x y +>”的一个充分条件是( ) A .1x ≥B .1x y +≥C .2y ≤-D .12x ≥且12y ≥【答案】C【解析】举例说明ABD 推不出1x y +>,再证明C 推出1x y +>. 【详解】1,0x y ==时,满足1x ≥,但1x y +=,所以A 错;1,0x y ==时,满足1x y +≥,但1x y +=,所以B 错;11,22x y ==时,满足12x ≥且12y ≥,但1x y +=,所以D 错;2y ≤-时,21y x y ≥∴+>故选:C 【点睛】本题充分条件判断,考查基本分析判断能力,属基础题. 2.图中曲线的方程可以是( )A .()()22110x y x y +-⋅+-=B ()22110x y x y +-+-= C .()22110x y x y +-+-= D 22110x y x y +-+-=【答案】C【解析】由图像可知曲线的方程是221x y +=或()22101x y x y +-=+≥,即可得出结论. 【详解】由图像可知曲线的方程是221x y +=或()22101x y x y +-=+≥,故选:C . 【点睛】本题考查了根据图像求曲线的方程,解题关键是掌握圆的标准方程和直线方程,考查了分析能力,属于基础题.3.已知非空集合M 满足:对任意x M ∈,总有2x M ∉M ,若{}0,1,2,3,4,5M ⊆,则满足条件的M 的个数是( )A .11B .12C .15D .16【答案】A【解析】可得集合M 是集合{}2,3,4,5的非空子集,且2,4不同时出现,即可得到结论. 【详解】由题意,可得集合M 是集合{}2,3,4,5的非空子集,共有42115-=个, 且2,4不能同时出现,同时出现共有4个, 所以满足题意的集合M 的个数为11个,故选A. 【点睛】本题主要考查了元素与集合的关系,以及集合的子集个数的判定及应用,着重考查了分析问题和解答问题的能力,属于中档试题.4.已知抛物线22y px =(0p >)与双曲线22221x y a b-=(0a >,0b >)有相同的焦点F ,点A 是两条曲线的一个交点,且AF x ⊥轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )A .06π⎛⎫⎪⎝⎭,B .32ππ⎛⎫⎪⎝⎭,C .43ππ⎛⎫ ⎪⎝⎭,D .64ππ⎛⎫ ⎪⎝⎭,【答案】B 【解析】【详解】分析:因为抛物线与双曲线有相同的焦点,所以可得p 与c 之间的关系, 因为AF x ⊥轴,则点A 的坐标可以由抛物线求出,将其代入双曲线方程,再由a 、b 、c 之间的关系,可求出离心率,由离心率公式可得ba,即斜率的值,由斜率求出倾斜角的范围.详解:因为抛物线与双曲线焦点相同,所以2p c =,因为AF 与x 轴垂直,所以可求得点A 的坐标为,2p p ⎛⎫ ⎪⎝⎭,将其代入双曲线方程可得:222214p p a b-=,因为222b c a =-,代入上式可得:2222241c c a c a--=, 化简得:422460c c a a -+=,两边同时除以4a 得:42610e e -+=,解得23e =+3-,设渐近线斜率为k ,由22222211c b e k a a==+=+,解得223k =+>,所以倾斜角应大于60,所以区间可能是,32ππ⎛⎫⎪⎝⎭, 故选B.点睛:本题主要考查抛物线与双曲线的几何性质,由焦点与公共点建立系数之间的联系,渐近线斜率与离心率有关,所以由系数求出离心率并求得斜率,与特殊倾斜角的斜率作对比,求出倾斜角取值范围.二、填空题5.若关于x ,y 的二元一次方程组的增广矩阵为32111m ⎛⎫⎪⎝⎭,若5x D =,则实数m =___________.【答案】2-【解析】根据增广矩阵相关概念列式,解得结果. 【详解】因为5x D =,所以1211252323211m mm -==∴=-- 故答案为:2- 【点睛】本题考查增广矩阵相关概念,考查基本分析求解能力,属基础题.6.若()2nx +的二项展开式中,所有二项式的系数和为256,则正整数n =____. 【答案】8【解析】根据二项式的系数和计算公式:2n ,可得:2256n =,即可求得答案. 【详解】根据二项式的系数和计算公式:2n∴ 题意可得:2256n =解得8n =. 故答案为:8. 【点睛】本题考查了二项式的系数和,掌握二项式的系数和计算公式是解题关键,考查了计算能力,属于基础题.7.已知球的半径为R ,A 、B 为球面上的两点.若A 、B 之间的球面距离是4Rπ,则这两点间的距离等于___________.【解析】设球心为O ,先根据A 、B 之间的球面距离得AOB ∠,再根据余弦定理求结果. 【详解】设球心为O ,因为A 、B 之间的球面距离是4R π,所以44RAOB R ππ∠==,因此22222||2cos (2||4AB R R R R AB π=+-=∴=【点睛】本题考查球面距离、余弦定理,考查基本分析求解能力,属基础题.8.设()lg f x x =,若(1)()0f a f a -->,则实数a 的取值范围为________. 【答案】1(0,)2【解析】首先判断函数的定义域和单调性,不等式等价于()()1f a f a ->,利用函数性质解不等式. 【详解】函数()f x 的定义域是()0,∞+ ,并且函数是单调递增函数,()()()()101f a f a f a f a -->⇒-> 1001a a a a->⎧⎪∴>⎨⎪->⎩,解得:102a <<.故答案为10,2⎛⎫⎪⎝⎭.【点睛】本题考查根据函数的性质解抽象不等式,意在考查函数基本性质简单应用,解抽象不等式时,需注意函数的定义域.9.已知复数11z =+,22z =,12z z 是正实数,则复数2z =______________.【答案】1【解析】设复数2()z a bi a b R =+∈,,求出12z z ,再根据已知条件列出方程组,即可求得答案. 【详解】设复数2()z a bi a b R =+∈,,12(1)()()()z z a bi a b i =++=++,22z =,12z z 是正实数,∴20,0b a =+=>⎪⎩,解得:1a b =⎧⎪⎨=⎪⎩.则复数21z = 故答案为:1 【点睛】本题考查了复数的乘法运算和求复数模,掌握复数基础知识是解题关键,考查了计算能力,属于基础题.10.设k 为常数,且cos 4k πα⎛⎫-= ⎪⎝⎭,则用k 表示sin 2α的式子为sin 2α=____.【答案】221k -【解析】利用两角差的余弦函数公式化简已知等式,进而两边平方利用二倍角的正弦函数公式,同角三角函数基本关系式即可求解.cos4k πα⎛⎫-=⎪⎝⎭,∴()cos sin 2k αα+=,可得:cos sin αα+=, ∴两边平方可得:222cos sin 2cos sin 2k αααα++=,可得:21sin 22k α+=,∴ 2sin 221k α=-.故答案为:2sin 221k α=-. 【点睛】本题考查了两角差的余弦函数公式和同角三角函数基本关系式,掌握三角函数基本知识是解本题关键,考查了分析能力和计算能力,属于基础题.11.从集合11,,2,323⎧⎫⎨⎬⎩⎭中任取一个数记作a ,从集合{}-2-1,1,2,中任取一个数记作b ,则函数xy a b =+的图象经过第三象限的概率是______ . 【答案】38【解析】先求出基本事件(,)a b 的个数4416n =⨯=,再利用列举法求出函数x y a b =+的图象经过第三象限的情况,由此能求出函数x y a b =+的图象经过第三象限的概率. 【详解】解:从集合11,,2,323⎧⎫⎨⎬⎩⎭中任取一个数记做a ,从集合{}21,1,2--,中任取一个数记做b ,基本事件(,)a b 的个数4416n =⨯=, 函数xy a b =+的图象经过第三象限有:①当3a =、1b =-时,②当3a =、2b =-时,③当2a =、1b =-时,④当2a =、2b =-时,⑤当13a =,2b =- 时,⑥当12a =,2b =- 时,共6种情况,∴函数x y a b =+的图象经过第三象限的概率是63168P ==.故答案为:38.本题考查概率的求法,解题时要认真审题,注意列举法的合理运用,属于基础题. 12.设等比数列{}n a 的通项公式为()1*n n a q n N -=∈,前n 项和为n S ,若1lim 2nn n S a →∞+=,则q =__________. 【答案】32【解析】根据公比分类求n S ,再求极限,即得结果. 【详解】当1q =时,1n S na =∴111lim lim lim 21n n n n n S naa a n q →∞→∞→∞+≠∴=≠= 当1,0q q ≠≠时,1(1)1nn a q S q -=∴-111(1)111lim lim lim 1n n n n n n nn a q S a q q q q a →∞→∞→∞+---==- 因此当||1q >时,113lim 212n n n S q a q →∞+-==∴=- 当||1,0q q <≠时,1lim nn n S a →∞+不存在, 综上,32q =故答案为:32【点睛】本题考查数列极限、等比数列求和,考查基本分析求解能力,属基础题. 13.设()1fx -为()cos 488f x x x ππ=-+,[]0,x π∈的反函数,则()()1y f x f x -=+的最大值为_________. 【答案】54π【解析】由函数()f x 是[]0,π上的递增函数,得到()1fx -的单调性相同,得出()()1y f x f x -=+的定义域为0,2π⎡⎤⎢⎥⎣⎦,进而可得()()1y f x f x -=+的最大值,即可求解. 【详解】由题意,函数()cos 488f x x x ππ=-+是[]0,π上的单调递增函数, 且()1f x -为()cos 488f x x x ππ=-+,[]0,x π∈的反函数,所以函数()f x 与()1fx -的单调性相同,当x π=时,函数()f x 取得最大值()cos 4882f ππππππ=-+=,当0x =时, co (s 0)0088f ππ=-+=,当2x π=时, 1cos 4884()222f ππππππ=⨯-+=,所以函数()()1y f x f x -=+的定义域为0,2π⎡⎤⎢⎥⎣⎦,且当2x π=时,1()2fππ-=,所以()()1y f x f x -=+的最大值为15()()2244f f πππππ-+=+=, 故答案为:54π. 【点睛】本题主要考查了反函数的基本性质,函数的定义域与值域,着重考查分析问题和解答问题的能力,属于中档试题.14.已知ABC ∆的面积为360,点P 是三角形所在平面内一点,且1144AP AB AC =+,则PAB ∆的面积为__. 【答案】90【解析】画出其几何图形,取AB 的中点D ,AC 的中点E ,则P 为DE 的中点,利用相似比,可得结论. 【详解】 画出其几何图形:取AB 的中点D ,AC 的中点E , 1144AP AB AC =+ ∴ P 为DE 的中点,ABC ∆的面积为360,根据几何关系可得:PDB PDA PAE S S S ∆∆∆==∴ AD PAB E S S ∆∆=ADEABC ∆∆,相似比为:1:2∴ PAB S ∆113609044ABC S ∆=⨯=⨯=. 故答案为:90. 【点睛】本题考查平面向量基本定理,掌握向量的基本知识是解题关键,考查了分析能力和计算能力,属于基础题.15.已知函数21,0()2,0x a x x f x x ax x ⎧++->=⎨-+≤⎩的最小值为1a +,则实数a 的取值范围为__________.【答案】{2[1,1]--⋃-【解析】对参数a 进行分类讨论,结合二次函数的最值,由已知条件,求得不同情况下对应的参数范围,再求并集即可. 【详解】分情况进行讨论:当0a ≥时,21,0()2,0x a x x f x x ax x ⎧++->=⎨-+≤⎩, 0x >时()f x 在[,1]a -取得最小值1a +,0x ≤时在0x =时取得最小值2,故12a +≤,解得1a ≤,又因为此时0a ≥,所以01a ≤≤。
上海市华东师范大学第二附属中学2023-2024学年高三下学期3月月考化学试卷(原卷版)
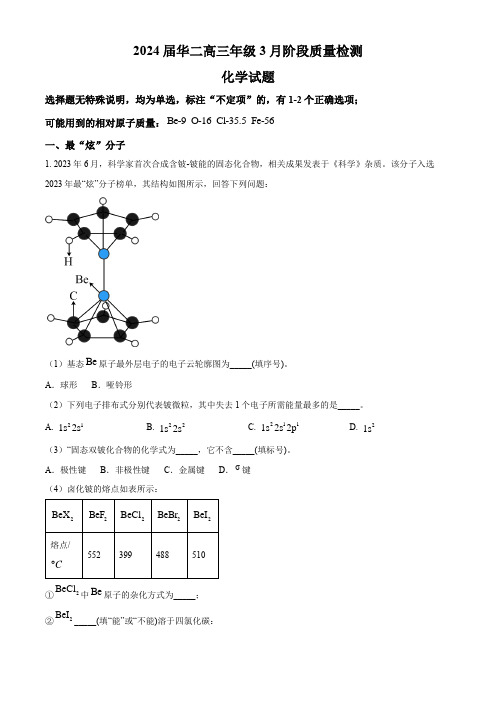
化学试题
选择题无特殊说明,均为单选,标注“不定项”的,有1-2个正确选项;
可能用到的相对原子质量:
一、最“炫”分子
1.2023年6月,科学家首次合成含铍-铍能的固态化合物,相关成果发表于《科学》杂质。该分子入选2023年最“炫”分子榜单,其结构如图所示,回答下列问题:
(3)工业生产对催化剂进行选择的时候,除了要考虑催化剂的效宰以外,催化剂的稳定性也是很重要的参考条件,一般工业生产所用催化剂更换间隔为半年到一年,请根据下图信息,选出最适合的催化剂_____。
A. B. C. D.
(4)在恒温( )密闭容器中,往容器中注入一定量 和 发生以上反应, _____;若反应达到平衡时 和 浓度相等,则平衡时 的浓度 _____ 。
A.碱性B.中性C.酸性
Ⅱ.热分解法脱硫
在密闭容器中模拟工业热分解法脱硫,发生反应 。其他条件不变时, 的平衡转化率随温度和压强的变化如图。
(4) ,反应中 _____(填“是”或“不是")气态,理由是_____。
(5)实际反应在高温下进行的原因可能是_____(答出2条即可)。
四、阳宗海治理的“功臣”——
熔点/
552
399
488
510
① 中 原子的杂化方式为_____;
② _____(填“能”或“不能)溶于四氯化碳:
③ 、 、 的熔点依次升高的原因是_____。
(5) 易形成配离子 ,其中心阳离子的配位数为_____,配体是_____(填化学符号),配离子的空间构型为_____。
(6)离子晶体中稳定配位多面体的理论半径比如表所示:
(5)通常用碘量法测定 的质量分数:称取 无水 样品,溶于稀盐酸,配制成 溶液;取出 溶液,加入稍过量的 溶液,充分反应后,滴入几滴淀粉溶液,并用 标准液滴定,消耗 标准液 (已知: )。
2019-2020学年上海市华东师范大学第二附属中学高一下学期4月月考数学试题(解析版)

故答案为 .
【点睛】
本题考查三角函数的单调性,解题时需把函数化为一个角一个三角函数形式,然后结合正弦函数的单调性求解.
8.已知函数 的图象的一条对称轴是 ,若 表示一个简谐运动,则其初相是________.
【答案】
【解析】由对称性先求出 ,再利用辅助角公式即可得到答案.
【详解】
所以 ,所以 ;
(2)将函数 的图像向左平移 个单位长度后,
得到 的图像,
再将所得图像上所有点的横坐标伸长到原来的 倍(纵坐标不变),
得到 的图像,故 ,
因为 ,
时,函数 取最小值, ;
当 ,函数 取最大值, ,
故 .
函数 在区间 上存在零点,
所以 有解,
所以实数k的取值范围为 .
【点睛】
本题考查三角函数解析式以及三角函数的值域的求法,考查三角恒等变换以及三角函数图像的变化,考查化归与转化思想,属于简单题目..
18.已知 满足 ,若其图像向左平移 个单位后得到的函数为奇函数.
(1)求 的解析式;
(2)在锐角 中,角A、B、C的对边分别为a、b、c,且满足 ,求 的取值范围.
【答案】(1) ;(2) .
【解析】(1)根据周期求出 ,利用图象变换求出 ,即可求 的解析式;
(2)由正弦定理得: ,进而求出 ,用 表示出 ,代入已知的等式,利用诱导公式及两角和的正弦函数公式化为一个角的正弦函数,根据 的范围求出这个角的范围,由正弦函数的值域即可得到所求式子的取值范围.
2019-2020学年上海市华东师范大学第二附属中学高一下学期4月月考数学试题
一、单选题
1.函数 在 上是减函数,则 的取值范围是( )
A. B.
上海华东师大附属中学2020-2021学年高三数学文月考试卷含解析

上海华东师大附属中学2020-2021学年高三数学文月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. N为圆x2+y2=1上的一个动点,平面内动点M(x0,y0)满足|y0|≥1且∠OMN=30°(O为坐标原点),则动点M运动的区域面积为()A.﹣2B.﹣C. +D. +参考答案:A【考点】J3:轨迹方程.【分析】由题意,过M作⊙O切线交⊙O于T,可得∠OMT≥30°.由此可得|OM|≤2.得到动点M运动的区域满足(|y0|≥1).画出图形,利用扇形面积减去三角形面积求得动点M运动的区域面积.【解答】解:如图,过M作⊙O切线交⊙O于T,根据圆的切线性质,有∠OMT≥∠OMN=30°.反过来,如果∠OMT≥30°,则⊙O上存在一点N使得∠OMN=30°.∴若圆C上存在点N,使∠OMN=30°,则∠OMT≥30°.∵|OT|=1,∴|OM|≤2.即(|y0|≥1).把y0=1代入,求得A(),B(),∴,∴动点M运动的区域面积为2×()=.故选:A.2. 设的内角所对的边为;则下列命题正确的是①若;则②若;则③若;则④若;则A.②③④B.①②③C.①②④D. ①③④参考答案:B3. “x>2“是“x2+2x﹣8>0“成立的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件参考答案:B【考点】必要条件、充分条件与充要条件的判断.【分析】由x2+2x﹣8>0解得x>2,或x<﹣4.即可判断出结论.【解答】解:由x2+2x﹣8>0解得x>2,或x<﹣4.∴“x>2“是“x2+2x﹣8>0“成立的充分不必要条件.故选:B.4. △ABC的内角A,B,C的对边分别为a,b,c成等比数列,且,则cos B等于()A. B. C. D.参考答案:B【分析】成等比数列,可得,又,可得,利用余弦定理即可得出.【详解】解:成等比数列,,又,,则故选:B。
2020-2021上海华二附中高一下学期期末数学试题及答案

2020-2021学年上海市浦东新区华东师大二附中高一(下)期末数学试卷一、填空题(共10小题).1.与2023°终边重合的最小正角是.2.已知向量=(2,﹣3),=(3,λ),若与共线,则实数λ=.3.已知α、β∈(0,),sinα=,cosβ=,则cos(α﹣β)=.4.|(3﹣4i)4|=.5.已知tan x=﹣2,则sin2x=.6.函数f(x)=a sin2x+b tan x+3满足f(﹣2)=1,则f(2﹣π)=.7.空间中两两平行的3条直线最多可确定的平面的个数是.8.已知关于x的方程sin x+cos x=a在区间[0,]上有解,则实数a的取值范围是.9.将y=f(x)的图象向左平移个单位,再向上平移1个单位之后,可得y=sin2x的图象,则f()=.10.已知k+2个两两互不相等的复数z1、z2、…、z k、w1、w2,满足﹣=,且|w j﹣z a|∈{1,3}(其中j=1、2;a=0、1、2、…、k),则k的最大值为.二、选择题11.设a=arcsin,b=arccos,c=arctan,则()A.a<b<c B.a<c<b C.c<a<b D.b<c<a12.已知复数z=(a2﹣a﹣2)+(a2+3a+2)i(i为虚数单位)为纯虚数,则实数a=()A.2B.﹣1C.﹣1或2D.﹣213.P是△ABC所在平面内一点,=λ+,则P点一定在()A.△ABC内部B.在直线AC上C.在直线AB上D.在直线BC上14.空间中5个平面可以把空间最多分成的部分的个数为()A.26B.28C.30D.32三、解答题15.在△ABC中,已知BC=a,CA=2,A=.(1)若C=,求a的值;.(2)若a=3,求S△ABC16.已知m∈R,α、β是关于x的方程x2+2x+m=0的两根.(1)若|α﹣β|=2,求m的值;(2)用m表示|α|+|β|.17.已知ω>0,函数f(x)=sin2ωx﹣sinωx cosωx的最小值为m,且y=f(x)图象的两条相邻对称轴之间的距离是.(1)求m的值;(2)求y=f(x)在[0,π]上的单调减区间;(3)求使得f(x)≥1成立的x的取值范围.18.已知θ∈[0,π),向量=(cosθ,sinθ),=(1,0),P1、P2、P3是坐标平面上的三点,使得=2[﹣(•)],=2[﹣(•)].(1)若θ=,P1的坐标为(20,21),求;(2)若θ=,||=6,求||的最大值;(3)若存在α∈[0,π),使得当=(cosα,sinα)时,△P1P2P3为等边三角形,求θ的所有可能值.参考答案一、填空题1.与2023°终边重合的最小正角是223°.解:因为2023°=5×360°+223°,所以与2023°终边重合的最小正角是223°.故答案为:223°.2.已知向量=(2,﹣3),=(3,λ),若与共线,则实数λ=﹣.解:∵向量=(2,﹣3),=(3,λ),若与共线,∴2λ﹣(﹣3)×3=0,解得:λ=﹣.3.已知α、β∈(0,),sinα=,cosβ=,则cos(α﹣β)=.解:α、β∈(0,),sinα=,cosβ=,∴cosα==,sinβ==,则cos(α﹣β)=cosαcosβ+sinαsinβ=×+×=,故答案为:,4.|(3﹣4i)4|=625.解:由|(3﹣4i)4|=(|3﹣4i|)4=.故答案为:625.5.已知tan x=﹣2,则sin2x=﹣.解:因为tan x=﹣2,所以sin2x====﹣.故答案为:﹣.6.函数f(x)=a sin2x+b tan x+3满足f(﹣2)=1,则f(2﹣π)=5.解:函数f(x)=a sin2x+b tan x+3满足f(﹣2)=1,∴f(﹣2)=a sin(﹣4)+b tan(﹣2)+3=﹣a sin4﹣b tan2+3=1,∴a sin4+b tan2=2,则f(2﹣π)=a sin(4﹣2π)+b tan(2﹣π)=a sin4+b tan2+3=2+3=5.故答案为:5.7.空间中两两平行的3条直线最多可确定的平面的个数是3.解:若三条直线在同一故平面内,则此时三条直线只能确定一个平面,若三条直线不在同一故平面内,则此时三条直线能确定三个平面,故三条两两平行的直线可以确定平面的个数为1个或3个,故答案为:3.8.已知关于x的方程sin x+cos x=a在区间[0,]上有解,则实数a的取值范围是[0,2].解:sin x+cos x=a化为:sin x+cos x=,∴sin(x+)=,∵x∈[0,],∴(x+)∈[,π],∴sin(x+)∈[0,1],∵关于x的方程sin x+cos x=a在区间[0,]上有解,∴0≤≤1,解得0≤a≤2.则实数a的取值范围是[0,2],故答案为:[0,2],9.将y=f(x)的图象向左平移个单位,再向上平移1个单位之后,可得y=sin2x的图象,则f()=﹣.解:函数y=sin2x的图象向下平移1个单位后,得到y=sin2x﹣1的图象,再向右平移个单位,得到f(x)=sin(2x﹣)﹣1的图象,所以f()=sin()﹣1=,故答案为:.10.已知k+2个两两互不相等的复数z1、z2、…、z k、w1、w2,满足﹣=,且|w j﹣z a|∈{1,3}(其中j=1、2;a=0、1、2、…、k),则k的最大值为5.解:设w1=a+bi,w2=c+di(a,b,c,d∈R),∵﹣=,∴(﹣)•(w1﹣w2)=4,即((a﹣b)﹣(c﹣d)i)((a﹣b)+(c﹣d)i)=4,即(a﹣b)2+(c﹣d)2=4,故w1、w2对应平面内距离为2的点,如图F、G,∵|w j﹣z a|∈{1,3},∴z a与w1、w2对应的点的距离为1或3,构成了点A、B、C、D、E共5个点,故k的最大值为5,故答案为:5.二、选择题11.设a=arcsin,b=arccos,c=arctan,则()A.a<b<c B.a<c<b C.c<a<b D.b<c<a解:根据反三角函数的定义a=arcsin,整理得sin a=,由于a,所以a=,由于b=arccos,所以cos b=,由于b∈(0,π),所以b=,由于c=arctan,所以tan c=,由于c,由于,所以c.故b>a>c.故选:C.12.已知复数z=(a2﹣a﹣2)+(a2+3a+2)i(i为虚数单位)为纯虚数,则实数a=()A.2B.﹣1C.﹣1或2D.﹣2解:∵z=(a2﹣a﹣2)+(a2+3a+2)i(i为虚数单位)为纯虚数,∴,∴a=2,故选:A.13.P是△ABC所在平面内一点,=λ+,则P点一定在()A.△ABC内部B.在直线AC上C.在直线AB上D.在直线BC上解:∵,=λ+,∴=λ+,∴﹣=λ,∴∥,即与共线,∴P点一定在AC边所在直线上,故选:B.14.空间中5个平面可以把空间最多分成的部分的个数为()A.26B.28C.30D.32解:根据题意,空间中1个平面可以将空间分为2部分,有1+1=2;空间中有2个平面时,最多可以把空间分为4部分,有1+1+2=4;空间中有3个平面时,最多可以把空间分为8部分,有1+1+2+4=8;空间中有4个平面时,新增的一个平面最多和已知的3个平面有3条交线,这3条交线会把新增的这个新平面最多分成7部分,从而多出7个部分,最多可以把空间分为7部分,故总共有1+1+2+4+7=15;空间中有5个平面时,新增的一个平面最多和已知的4个平面有4条交线,这4条交线会把新增的这个新平面最多分成11部分,从而多出11个部分,故总共有1+1+2+4+7+11=26部分,故选:A.三、解答题15.在△ABC中,已知BC=a,CA=2,A=.(1)若C=,求a的值;.(2)若a=3,求S△ABC解:(1)△ABC中,已知BC=a,CA=2,A=.若C=,所以,解得a=2.(2)在△ABC中,设AB=x,利用余弦定理:,解得,当x=3+时,=当x=3时,=.16.已知m∈R,α、β是关于x的方程x2+2x+m=0的两根.(1)若|α﹣β|=2,求m的值;(2)用m表示|α|+|β|.解:(1)∵α、β是关于x的方程x2+2x+m=0的两根.∴α+β=﹣2,αβ=m,若α,β为实数,则2=|α﹣β|==,化为:m=﹣1.若α,β为一对共轭复数,则2=|α﹣β|==|i|,化为:m=3.综上可得:m=﹣1或3.(2)x2+2x+m=0,不妨设α≤β.△=4﹣4m≥0,即m≤1时,方程有两个实数根.α+β=﹣2,αβ=m,0≤m≤1时,|α|+|β|=|α+β|=2.m<0时,α与β必然一正一负,则|α|+|β|=﹣α+β==2.△=4﹣4m<0,即m>1时,方程有一对共轭虚根.|α|+|β|=2|α|=2=2综上可得:|α|+|β|=.17.已知ω>0,函数f(x)=sin2ωx﹣sinωx cosωx的最小值为m,且y=f(x)图象的两条相邻对称轴之间的距离是.(1)求m的值;(2)求y=f(x)在[0,π]上的单调减区间;(3)求使得f(x)≥1成立的x的取值范围.解:(1)f(x)=sin2ωx﹣sinωx cos=﹣sin2ωx=sin(2ωx+),由题意可得T=2×=π,故2ω=,即ω=1,∴,当时,,∴m=.(2)令,即,k∈Z,当k=0时,,当k=1时,,又∵x∈[0,π],∴y=f(x)在[0,π]上的单调减区间为.(3)∵f(x)≥1,∴,即,∴,k∈Z,∴,k∈Z,∴f(x)≥1成立的x的取值范围为.18.已知θ∈[0,π),向量=(cosθ,sinθ),=(1,0),P1、P2、P3是坐标平面上的三点,使得=2[﹣(•)],=2[﹣(•)].(1)若θ=,P 1的坐标为(20,21),求;(2)若θ=,||=6,求||的最大值;(3)若存在α∈[0,π),使得当=(cos α,sin α)时,△P 1P 2P 3为等边三角形,求θ的所有可能值.解:(1)若θ=,则=(cos,sin)=(0,1),则=2[﹣(•)]=2{(20,21)﹣[(0,1)•(20,21)](0,1)}=2[(20,21)﹣(0,21)]=(40,0),所以=2[﹣(•)]=2{(40,0)﹣[(1,0)•(40,0)](1,0)}=(0,0);(2)因为||=6,不妨设=6(cos α,sin α),由向量=(cos θ,sin θ),得=2[﹣(•)]=2[6(cos α,sin α)﹣6cos (α﹣θ)(cos θ,sin θ)]=12(sin θsin (θ﹣α),cos θsin (α﹣θ))所以=2[﹣(•)]=2[12(sin θsin (θ﹣α),cos θsin (α﹣θ))﹣12sin θsin (θ﹣α)(1,0)]=24(0,cos θsin (α﹣θ)),若θ=,则cos θ=﹣,sin θ=,则||=12|sin (α﹣)|=12|sin (α+)|,所以,当|sin (α+)|=1时,||取最大值12;(3)=2[﹣(•)]=2[(cos α,sin α)﹣(cos αcos θ+sin αsin θ)(cos θ,sin θ)]=2(sin θsin (θ﹣α),cos θsin (α﹣θ)),=2[﹣(•)]=2[2(sin θsin (θ﹣α),cos θsin (α﹣θ))﹣2sin θsin (θ﹣α)(1,0)]=4(0,cos θsin (α﹣θ)),所以=(2sinθsin(θ﹣α)﹣cosα,2cosθsin(α﹣θ)﹣sinα),=(2sinθsin(α﹣θ),2cosθsin(α﹣θ)),因为△P1P2P3为等边三角形,所以||=||=2|sin(α﹣θ)|=1,cos<,>==﹣,所以|sin(α﹣θ)|=,2sinθsin(α﹣θ)[2sinθsin(θ﹣α)﹣cosα]+2cosθsin(α﹣θ)[2cosθsin(α﹣θ)﹣sinα]=﹣,即﹣4sin²θsin²(α﹣θ)﹣2sinθcosαsin(α﹣θ)+4cos²θsin²(α﹣θ)﹣2cosθsinαsin(α﹣θ)=﹣,即4sin²(α﹣θ)(cos²θ﹣sin²θ)﹣2sinθcosαsinαcosθ+2sinθcosαcosαsinθ﹣2cosθsinαsinαcosθ+2cosθsinαcosαsinθ=﹣,即cos²θ﹣sin²θ+2sin²θcos²α﹣2cos²θsin²α=﹣,即cos²θ﹣sin²θ+2sin²θcos²α﹣2sin²α(1﹣sin²θ)=﹣,即cos²θ﹣sin²θ+2sin²θcos²α﹣2sin²α+2sin²αsin²θ=﹣,即cos²θ﹣sin²θ+2sin²θ﹣2sin²α=﹣,即cos²θ+sin²θ﹣2sin²α=﹣,即1﹣2sin²α=﹣,即cos2α=﹣,且2α∈[0,2π),所以α=或,当α=时,由|sin(α﹣θ)|=可得θ=或,当α=时,由|sin(α﹣θ)|=可得θ=或,所以θ的所有可能值为、、.。
2021届上海市华东师范大学第二附属中学高三下学期4月月考数学试题及答案

绝密★启用前2020-2021学年上海市华师大二附中高三下4月月考数学卷注意事项:1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上一、填空题1.已知2021(2)i z i +=(i 为虚数单位),则||z =2.若一个圆锥的轴截面是面积为433.若点(2021,)P t 在抛物线24y x =上,点F 为该抛物线的焦点,则||PF 的值为4.圆1cos :sin x C y θθ=+⎧⎨=⎩(θ为参数)的圆心到直线223:13x tl y t⎧=-⎪⎨=-⎪⎩的距离为5.12nx x ⎛⎫ ⎪⎝⎭展开式的二项式系数之和为32,则展开式中x 的系数为 (用数字填写答案)6.北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和,例如:正四面体在每个顶点有3个面角,每个面角是,所以正四面体在各顶点的曲率为233πππ-⨯=,故其总曲率为4π,则四棱锥的总曲率为 7.在数列{}n a 中,若对一切n N *∈都有13n n a a +=-且()24629lim 2n n a a a a ∞→++++=,则1a 的值为8.已知函数cos ,[,]y a x x ωππ=+∈-(其中,a ω为常数,且0ω>)有且仅有3个零点,则ω的最小值为9.关于x 的不等式|2||3|4x k x k k -+-<共有2021个整数解,则k 的取值范围为10.荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示,假设现在青蛙在A 叶上,则跳四次之后停在A 叶上的概率为11.已知ABC △的外接圆圆心为,||6,||8,(,)O AB AC AO AB AC R αβαβ===+∈, 若21sin 2A t αβ⎛⎫⋅+-⎪⎝⎭(t 为实数)有最小值,则参数t 的取值范围为 12.关于x 的方程22cos sin 0x x a -+=在区间70,6π⎡⎤⎢⎥⎣⎦上恰好有两个不等实根,则实数a 的取值范围为 二、选择题13.已知全集U ,集合,M N 是U 的非空子集,且U C M N ⊇,则必有()A.U M C N ⊆B.U M C N ⊇C.U M C N =D.M N ⊆14.“2m =”是“直线210x my ++=与直线210mx y +-=平行”的()A.充分不必要条件B.必要不充分条件C.既不充分也不必要条件D.充要条件 15.已知()1a xf x x a -=--的反函数图像的对称中心为(1,3)-,则a 的值为()2 B.233 16.设04,0b a b m <<<>,若三个数22,2a ba b ab m ab ++-边长,则实数m 的取值范围为() A.135,124⎤-⎥⎣⎦B.3)C.135,224⎤-⎢⎥⎣⎦D.3,2)三、解答题17.如图在三棱锥ABC P -中,棱AB 、AC 、AP 两两垂直,3===AP AC AB ,点M 在AP 上,且1=AM .(1)求异面直线BM 和PC 所成的角的大小; (2)求三棱锥BMC P -的体积.18.若函数()y f x =对定义域内的每一个值1x ,在其定义域内都存在唯一的2x ,使()()121f x f x =成立,则该函数为“依附函数”.(1)判断函数()sin g x x =是否为“依附函数”,并说明理由;(2)若函数()12x f x -=在定义域[](),0m n m >上“依附函数”,求mn 的取值范围. 19.由于2020年1月份国内疫情爆发,经济活动大范围停顿,餐饮业受到重大影响.3月份复工复产工作逐步推进,居民生活逐步恢复正常.李克强总理在6月1日考察山东烟台一处老旧小区时提到,地摊经济、小店经济是就业岗位的重要来源,是人间的烟火,和“高大上”一样,是中国的生机.某商场经营者陈某准备在商场门前“摆地摊”,经营冷饮生意.已知该商场门前是一块角形区域,如图所示,其中120APB ∠=,且在该区域内点R 处有一个路灯,经测量点R 到区域边界PA 、PB 的距离分别为4m RS =,6m RT =,(m 为长度单位).陈某准备过点R 修建一条长椅MN (点M ,N 分别落在PA ,PB 上,长椅的宽度及路灯的粗细忽略不计),以供购买冷饮的人休息.(1)求点P 到点R 的距离;(2)为优化经营面积,当PM 等于多少时,该三角形PMN 区域面积最小?并求出面积最小值.20.已知0a b >>,如图,曲线Γ由曲线1C :22221(0)x y y a b +=≤和曲线2C :22221(0)x y y a b-=>组成,其中点12,F F 为曲线1C 所在圆锥曲线的焦点,点34,F F 为曲线2C 所在圆锥曲线的焦点.(1)若23(2,0),(6,0)F F -,求曲线Γ的方程;(2)如图,作斜率为正数的直线l 平行于曲线2C 的渐近线,交曲线1C 于点,A B ,求弦AB 的中点M 的轨迹方程;(3)对于(1)中的曲线Γ,若直线1l 过点4F 交曲线1C 于点,C D ,求1CDF ∆面积的最大值.21.已知无穷数列{}n a 满足:10a =,21n n a a c +=+(*n ∈N ,c ∈R ).对任意正整数2n ≥,记{|{1,2,3,,|}, |2}n i M c i n a =∈≤对任意,*{|2},||i M c i a =∈≤N 对任意.(1)写出2M ,3M ;(2)当14c >时,求证:数列{}n a 是递增数列,且存在正整数k ,使得k c M ∈/;(3)求集合M .2020-2021年上海市华师大二附中高三下4月月考 数学卷答案一、填空题1.已知2021(2)i z i +=(i 为虚数单位),则||z =【解析】因为41i =,所以2021ii =,所以2i z i=+,所以||2i z i ==+.2.若一个圆锥的轴截面是面积为43 【解析】设等边三角形的边长为a ,则23434=4a =, 所以圆锥的底面半径2r =,母线4l =,所以该圆锥的表面积为22 22412S S S r rl πππππ=+=⋅+=⨯+⨯⨯=侧底.3.若点(2021,)P t 在抛物线24y x =上,点F 为该抛物线的焦点,则||PF 的值为 【解析】由抛物线的定义,||2021120222P pPF x =+=+=. 4.圆1cos :sin x C y θθ=+⎧⎨=⎩(θ为参数)的圆心到直线223:13x tl y t ⎧=-⎪⎨=-⎪⎩的距离为【解析】圆心(1,0)C 到直线2:210l x y ++=的距离|10221|22d ++-==.5.12nx x ⎛⎫ ⎪⎝⎭展开式的二项式系数之和为32,则展开式中x 的系数为 (用数字填写答案)【解析】由题意得232n=,所以5n =,所以展开式的通项为535521551(2)2rr rrr r r T C x C x x ---+⎛⎫== ⎪⎝⎭,令5312r-=,得1r =, 所以展开式中x 的系数为1515280C -=.6.北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和,例如:正四面体在每个顶点有3个面角,每个面角是,所以正四面体在各顶点的曲率为233πππ-⨯=,故其总曲率为4π,则四棱锥的总曲率为【解析】因为四棱锥有5个顶点,5个面,其中4个三角形,1个四边形,所以面角和为426πππ+=,总曲率为5264πππ⨯-=.7.在数列{}n a 中,若对一切n N *∈都有13n n a a +=-且()24629lim 2n n a a a a ∞→++++=,则1a 的值为【解析】因为13n n a a +=-,所以数列{}n a 是公比为13-的等比数列,所以()121246222193lim 111219n n a a a q a a a a q q ∞→-++++====---,解得112a =-.8.已知函数cos ,[,]y a x x ωππ=+∈-(其中,a ω为常数,且0ω>)有且仅有3个零点,则ω的最小值为【解析】因为函数cos ,[,]y a x x ωππ=+∈-为偶函数,又有且仅有3个零点,故必有1个零点为0,所以cos00a +=,所以1a =-,故1cos ,[,]y x x ωππ=-+∈-,由0y =得2x k ωπ=,所以2,k x k Z πω=∈,而[,]x ππ∈-,所以24,ππππωω≤>,所以ω的最小值为2.9.关于x 的不等式|2||3|4x k x k k -+-<共有2021个整数解,则k 的取值范围为 【解析】显然0k >,由|2||3|4x k x k k -+-<解得1922k x k <<, 因为共有2021个整数解,所以912020202222k k <-≤,解得15055052k <≤, 所以113252252224k <≤,故这2021个整数解只能为253,254,,2273, 所以9227322742k <≤,解得1150550593k <≤.10.荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示,假设现在青蛙在A 叶上,则跳四次之后停在A 叶上的概率为【解析】因为逆时针方向跳的概率是顺时针方向跳的概率的两倍, 所以逆时针方向跳的概率是23,顺时针方向跳的概率是13, 若青蛙在A 叶上,则跳四次之后停在A 叶上,则满足四次跳跃中有2次是顺时针方向跳,有2次是逆时针跳,若先按逆时针开始从A→B,则剩余3次中有1次是按照逆时针,其余2次按顺时针跳,则对应的概率为2132214=33327C ⎛⎫⨯⨯⨯ ⎪⎝⎭;若先按顺时针开始从A→C,则剩余3次中有1次是按照顺时针,其余2次按逆时针跳,则对应的概率为2131124=33327C ⎛⎫⨯⨯⨯ ⎪⎝⎭;故跳四次之后停在A 叶上的概率为448272727+=. 11.已知ABC △的外接圆圆心为,||6,||8,(,)O AB AC AO AB AC R αβαβ===+∈,若21sin 2A t αβ⎛⎫⋅+- ⎪⎝⎭(t 为实数)有最小值,则参数t 的取值范围为【解析】因为211||||cos ,||||||1822AO AB AB AO AO AB AB AB AB ⋅=⋅⋅<=⋅==>, 211||||cos ,||||||3222AO AC AC AO AO AC AC AC AC ⋅=⋅⋅<=⋅==>,又(,)AO AB AC R αβαβ=+∈,所以221832AO AB AB AB AC AO AC AC AB AC αββα⎧⋅=+⋅=⎪⎨⎪⋅=+⋅=⎩,即43cos 268cos 3A A βααβ+=⎧⎨+=⎩, 解得2234cos 6sin 43cos 8sin A A AA αβ-⎧=⎪⎪⎨-⎪=⎪⎩,代入21sin 2A t αβ⎛⎫⋅+- ⎪⎝⎭,化简得2123cos cos 2382tA t A ⎛⎫-++⎪⎝⎭,因为1cos 1A -<<且有最小值, 所以233811122t ⎛⎫-+ ⎪⎝⎭-<-<⨯,解得33151616t -<<,所以参数t 的取值范围为3315,1616⎛⎫-⎪⎝⎭.12.关于x 的方程22cos sin 0x x a -+=在区间70,6π⎡⎤⎢⎥⎣⎦上恰好有两个不等实根,则实数a的取值范围为【解析】222cos sin 022sin sin x x a a x x -+=⇔+=+,令2211()2sin sin 2sin 48f x x x x ⎛⎫=+=+- ⎪⎝⎭,由复合函数的单调性得()f x 在0,2π⎛⎫⎪⎝⎭上递增,在1,arcsin 24ππ⎛⎫+ ⎪⎝⎭上递减, 在17arcsin ,46ππ⎛⎫+ ⎪⎝⎭上递增, 又113,arcsin 248f f ππ⎛⎫⎛⎫=+=-⎪ ⎪⎝⎭⎝⎭, 故12,0(0,3)8a ⎛⎫+∈- ⎪⎝⎭,故实数a 的取值范围为17,2(2,1)8⎛⎫--- ⎪⎝⎭. 二、选择题13.已知全集U ,集合,M N 是U 的非空子集,且U C M N ⊇,则必有(A )A.U M C N ⊆B.U M C N ⊇C.U M C N =D.M N ⊆【解析】作出韦恩图易得A.14.“2m =”是“直线210x my ++=与直线210mx y +-=平行”的(D ) A.充分不必要条件B.必要不充分条件C.既不充分也不必要条件D.充要条件【解析】若直线210x my ++=与直线210mx y +-=平行,则2220m ⨯-=且2(1)0m ⨯--≠,即2m =,故为充要条件,故选D.15.已知()1a xf x x a -=--的反函数图像的对称中心为(1,3)-,则a 的值为(B )2 B.233 【解析】(1)11()1111a x x a f x x a x a x a -----===--------,故()f x 的对称中心为(1,1)a +-,因为()f x 的反函数图像的对称中心为(1,3)-,所以()f x 的对称中心为(3,1)-, 所以13a +=,所以2a =,故选B.16.设04,0b a b m <<<>,若三个数2a b+边长,则实数m 的取值范围为(C )A.5,14⎤-⎥⎣⎦B.C.5,24⎤⎥⎣⎦D.【解析】因为04,0b a b m <<<>,令,2a bx y z +===,则22223()024a b x y a b +⎛⎫-==--< ⎪⎝⎭,所以x y <, 因为,,x y z 能组成一个三角形的三条边长,所以y x z x y -<<+,22a b a b++<<, 因为04,0b a b m <<<>,所以令(14)at t b=<<,2m <<即2m+<<,因为14≥+=,当且仅当1t =时取等号,但是取不到,所以4>, 所以24m ≤,所以2m ≤;令52,2k ⎛⎫= ⎪⎝⎭,则k =,可用求导或其他方法得出k 在52,2k ⎛⎫∈ ⎪⎝⎭上单调递增,所以5522k <=,所以522m ≥,所以54m ≥-,综上,13524m -≤≤,故选C. 三、解答题17.如图在三棱锥ABC P -中,棱AB 、AC 、AP 两两垂直,3===AP AC AB ,点M 在AP 上,且1=AM .(1)求异面直线BM 和PC 所成的角的大小; (2)求三棱锥BMC P -的体积.【解析】法一:(1)如图,取线段1=AN ,连结MN 、BN .因为MN ∥PC ,所以BMN ∠的大小等于异面直线BM 和PC 所成的角或补角的大小.…………3分23122=+=AC PA MN ,10132=+==BN BM 105102221cos ===∠BM MN BMN ,105arccos =∠BMN ……6分所以异面直线BM 和PC 所成的角的大小等于105arccos.………………7分(2)因为AB 、AC 、AP 两两垂直,3==AC AB ,3=AP ,1=AM .所以29333213131=⨯⨯⨯⨯=⋅=∆-PA S V ABC ABC P .…………9分 23133213131=⨯⨯⨯⨯=⋅=∆-MA S V ABC ABC M .…………11分32329=-=-=---ABC M ABC P BMC P V V V . 所以三棱锥BMC P -的体积大小等于3(立方单位).……………14分法二:(1)因为棱,,AB AC AP 两两垂直,如图建系,则(3,0,0),(0,3,0),(0,0,3),(0,0,1)B C P M ,所以(3,0,1),(0,3,3)BM PC =-=-, 设BM 和PC 所成角为θ,则||cos 10||||10BM PC θBM PC ⋅===⋅, 所以θ=(2)11||||23322PBM S PM BA ∆=⋅=⨯⨯=, 又,CA BA CA PA ⊥⊥,且,BA PA 相交于点P , 所以CA ⊥平面PBA , 则11||33333P BMC C PBM PBM V V S CA --∆==⋅=⨯⨯=. 18.若函数()y f x =对定义域内的每一个值1x ,在其定义域内都存在唯一的2x ,使()()121f x f x =成立,则该函数为“依附函数”.(1)判断函数()sin g x x =是否为“依附函数”,并说明理由; (2)若函数()12x f x -=在定义域[](),0m n m >上“依附函数”,求mn 的取值范围. 【解析】(1)对于函数()sin g x x =的定义域R 内存在16x π=,则()22sin 2g x x ==,无解. 故()sin g x x =不是“依附函数”;(2)首先证明:当()f x 在定义域上[,]m n 上单调递增,且为“依赖函数”时,有()()1f m f n =。
上海市华东师范大学第二附属中学2024-2025学年高三上学期10月月考数学试题(含解析)

2025届华二附中高三10月月考数学试卷一、填空题1.若集合,则__________.2.已知复数,则__________.3.展开式中的系数为60,则实数__________.4.己知是单调递增的等比数列,,则公比q 的值是__________.5.已知,则_________.6.已知函数,若在定义域内为增函数,则实数p 的最小值为__________.7.己知双曲线,左,右焦点分别为,关于C 的一条渐近线的对称点为P .若,则的面积为__________.8.己知,则的最小值为__________.9.已知函数是上的奇函数,则__________.10.对平面直角坐标系中两个点和,记,称,为点与点之间的“距离”,其中表示p ,q 中较大者.设是平面中一定点,.我们把平面上到点的“距离”为r 的所有点构成的集合叫做以点为圆心,以r 为半径的“圆”.以原点O 为圆心,以为半径的“圆”的面积为__________.11.长江流域水库群的修建和联合调度,极大地降低了洪涝灾害风险,发挥了重要的防洪减灾效益.每年洪水来临之际,为保证防洪需要、降低防洪风险,水利部门需要在原有蓄水量的基础上联合调度,统一蓄水,用蓄满指数(蓄满指数)来衡量每座水库的水位情况.假设某次联合调度要求如下:{23},{(4)(2)0}A xx B x x x =<<=+->∣∣A B = 1i z =+|2i |z -=5a x x ⎛⎫+ ⎪⎝⎭3x a ={}n a 453824,128a a a a +==π3sin 35α⎛⎫+= ⎪⎝⎭πsin 26α⎛⎫+= ⎪⎝⎭()2ln p f x px x x=--()f x 2222:1(0,0)x y C a b a b-=>>12F F 2F 12PF =12PF F △0,0,23x y x y >>+=23x y xy+tan tan()()12tan()x f x x θθθ-+=-+ππ,20242024⎡⎤-⎢⎥⎣⎦tan θ=()111,P x y ()222,P x y 1212121212max ,11x x y y PP x x y y ⎧⎫--⎪⎪=⎨⎬+-+-⎪⎪⎩⎭12PP 1P 2P t -max{,}p q ()000,P x y 0r >0P t -0P t -12t -100=⨯水库实际蓄水里水库总蓄水里(i )调度后每座水库的蓄满指数仍属于区间;(ii )调度后每座水库的蓄满指数都不能降低;(iii )调度前后,各水库之间的蓄满指数排名不变记x 为调度前某水库的蓄满指数,y 为调度后该水库的蓄满指数,给出下面四个y 关于x 的函数解析式:①;②;③;④.则满足此次联合调度要求的函数解析式的序号是__________.12.将棱长为1的正方体的上底面绕着其中心旋转得到一个十面体(如图),则该十面体的体积为__________.二、单选题13.“”是“对任意的正整数x ,均有的( )A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件14.己知随机变量服从正态分布,且,则等于( )A .0.8B .0.6C .0.4D .0.315.已知函数不是常数函数,且满足对于任意的,,则( )A .B .一定为周期函数C .不可能为奇函数D .存在16.如图,将线段AB ,CD 用一条连续不间断的曲线连接在一起,需满足要求:曲线经过点B ,C ,并且在点B ,C 处的切线分别为直线AB ,CD ,那么下列说法正确的是( )命题甲:存在曲线满足要求命题乙:若曲线和满足要求,则对任意实数,当时,曲线满足要求[0,100]21620y x x =-+y =5010x y =π100sin 200y x =1111ABCD A B C D -1111A B C D 45︒ABCD EFGH -1a =2a x x+≥ξ()22,N σ(0)0.2P ξ≤=(24)P ξ<≤()f x ,R a b ∈()()2()()f a b f a b f a f b ++-=(0)0f =()f x ()f x ()00R,2x f x ∈=-()y f x =()y f x =sin cos (,,)2ax bx y c a b c +=+∈R 1()y f x =2()y f x =,λμ1λμ+=12()()y f x f x λμ=+A .甲命题正确,乙命题正确B .甲命题错误,乙命题正确C .甲命题正确,乙命题错误D .甲命题错误,乙命题错误三、解答题17.如图,在正三棱柱中,分别是的中点,的边长为2.(1)求证:平面;(2)若三棱柱的高为1,求二面角的正弦值.18.放行准点率是衡量机场运行效率和服务质量的重要指标之一.己知2023年该机场飞往A 地,B 地及其他地区(不包含A ,B 两地)航班放行准点率的估计值分别为和、2023年该机场飞往A 地,B 地及其他地区的航班比例分别为0.2,0.2和0.6试解决一下问题:(1)现在从2023年在该机场起飞的航班中随机抽取一个,求该航班准点放行的概率;(2)若2023年某航班在该机场准点放行,判断该航班飞往A 地、B 地、其他地区等三种情况中的哪种情况的可能性最大,说明你的理由.19.在中,,内有一点M ,且.(1)若,求的面积;(2)若,求BM 的长.20.己知圆,直线过点且与圆交于点B ,C ,BC 中点为D ,过中点E 且平行于的直线交于点P ,记P 的轨迹为(1)当到直线时,求直线方程;(2)求的方程;(3)坐标原点O 关于的对称点分别为,点关于直线的对称点分别为,过的直线与交于点M ,N ,直线相交于点Q ,求的面积.111ABC A B C -1,,D D F 1111,,BC B C A B 4,BC BE ABC = △EF ∥11ADD A 1B EF C --84%80%,75%84%,ABC △π10,3BC ABC =∠=ABC △2,π3BM CM AMB ⊥∠=BM =ABC △14AC =221:(1)16A x y ++=1l 2(1,0)A 1A 2A C 1A D 1AC Γ1A 1l 1l Γ12,A A 12,B B 12,A A y x =12,C C 1A 2l Γ12,B M B N 12QC C △21.对于函数,定义域R ,为若存在实数,使,其中,则称为“倒数函数”,为“的倒数点”.己知.(1)如果对成立.求证:为周期函数;(2为“关于倒数点”,且只有两个不同的解,求函数m 的值;(3)设,若函数恰有3个“可移1倒数点”,求a 的取值范围.()f x 0x ()()001f x f x λ+=0λ≠()f x 0x ()f x λ()e ,()(0)x g x h x x a a ==+>()(1)1f x f x +=x R ∈()h x 2-2()()m h x g x =(),0()1,0()g x x x x h x ω>⎧⎪=⎨<⎪⎩()x ω2025届华二附中高三10月月考数学试卷参考答案一、填空题1.【答案】2.3.【答案】12【解析】展开式的通项为,令,则,所以展开式中的系数为,解得.4.【答案】2【解析】由等比数列性质知,联立,解得或,因为是单调递增的等比数列,所以,即.5.【答案】6.【答案】1【解析】函数.要使在定义域内为增函数,只需在上恒成立即可,即在上恒成立,即在上恒成立.,当且仅当,即时等号成立,,即实数p 的最小值为1.7.【答案】4{23}xx <<∣5a x x ⎛⎫+ ⎪⎝⎭552155C C kk k k k k k a T x a x x --+⎛⎫== ⎪⎝⎭523k -=1k =5ax x ⎛⎫+ ⎪⎝⎭3x 15C 60a =12a =3645a a a a =454524128a a a a +=⎧⎨=⎩45816a a =⎧⎨=⎩45168a a =⎧⎨=⎩{}n a 45816a a =⎧⎨=⎩542a q a ==725- 22222()2ln ,(0,),()p p px x p f x px x x f x p x x x x-+'=--∈+∞=+-=()f x (0,)+∞()0f x '≥(0,)+∞220px x p -+≥(0,)+∞221x p x ≥+(0,)+∞222111x x x x =≤=++ 1x x =1x =1p ∴≥【解析】设与渐近线交于M ,则,所以,由O ,M 分别与的中点,知且,即,由,所以.8.【答案】【解析】9.【答案】【解析】2PF b y x a=222,tan ,sin b b F M OM MOF MOF a c⊥∠=∠=222sin ,F M OF MOF b OM a =⋅∠===12F F 2PF 1OM PF ∥1112OM PF ==1a =e =2c b ==1221442142PF F OMF S S ==⨯⨯⨯=△△1+223(2)211x y x x y y x y xy xy y x+++==++≥+2-tan tan()()12tan()x f x x θθθ-+=-+tan tan tan 1tan tan tan tan 121tan tan x x x x θθθθθ+--=+-⨯-tan (1tan tan )(tan tan )1tan tan 2(tan tan )x x x x θθθθθ--+=--+()2tan 1tan 12tan (tan 2)tan xxθθθ-+=--+上的奇函数,又上的奇函数.10.【答案】4【解析】设是以原点O为圆心,以为半径的圆上任一点,则.若,则;若,则有.由此可知,以原点O 为圆心,以为半径的“圆”的图形如下所示:则“圆”的面积为.11.【答案】②④【解析】①,该函数在时函数值为180,超过了范围,不合题意;②为严格增函数,且,则,符合题意;③,当时,不合题意④,当时,,故该函数在上严格递增,又ππ(),20242024f x ⎡⎤-⎢⎥⎣⎦()2tan 1tan y x θ=-+⋅tan 20,tan 2θθ∴+=∴=-(,)P x y 12t -||||1max ,1||1||2x y x y ⎧⎫=⎨⎬++⎩⎭||||11||1||2y x y x ≤=++||1||1x y =⎧⎨≤⎩||||11||1||2x y x y ≤=++||1||1y x =⎧⎨≤⎩12t -t -224⨯=()2221116120(60)180202020y x x x x x =-+=--=--+60x =y =[0,100],[0,100]x y ∈∈10≤x ≤5010xy =50x =50101050x=<π100sin 200y x =[0,100]x ∈ππ0,2002x ⎡⎤∈⎢⎥⎣⎦[0,100]π100sin[0,100]200y x =∈设即即,易知在上为严格减函数令,则存在,有当;当;故在严格递增,在严格递减.故上即上,故④符合题意12.【解析】如图作出原正方体,与HE ,EF 的交点分别为M ,N ,HE 与的交点为P ,上底面非重叠部分是8个全等的等腰直角三角形,设每个等腰直角三角形的边长为a ,则,所以,π()100sin ,[0,100]200g x x xx =-∈ππ()100cos 1,[0,100]200200g x x x '=⋅⋅-∈ππ()cos 12200g x x '=⋅-ππ()cos 12200g x x =⋅-[0,100]()0g x '=0[0,100]x ∈()0g x '=[]00,,()0x x g x '∈>[]0,100,()0x x g x '∈<()g x []00,x []0,100x (0)0,(100)0g g ==[0,100]()0g x ≥[0,100]π100sin 200x x ≥1111ABCD A B C D -11A B 11A D 21a =a =所以,设该十面体的体积为V ,二、单选题13.【答案】A【解析】对任意的正整数x ,均有,所以,当时,取最大值1,所以.因为时,一定成立;时,不一定成立.所以“”是“对任意的正整数x ,均有”的充分不必要条件.14.【答案】B【解析】因为服从正态分布,且,所以,所以15.【答案】C【解析】由题意,函数满足对于任意的,令,解得或.若,令,则,故,与题设不为常数函数矛盾,所以A 错误;所以,此时令,得,即,所以必然为偶函数,所以C 正确;||1MN ==-1111144ABCD A B D A MP E ABNMC V V V V --=-+11111144||332A MP ABNM S A A S MN =-⨯⨯⨯+⨯⨯⨯△四边形211114141323=-⨯⨯⨯⨯+⨯⨯⨯=2a x x +≥222,2x a x a x x +≥∴≥-+1x =22x x -+1a ≥1a =1a ≥1a ≥1a =1a =2a x x +≥ξ()22,N σ(0)0.2P ξ≤=(4)0.2P ξ>=11(24)[12(0)](120.2)0.322P P ξξ<≤=-≤=⨯-⨯=()f x ,R,()()2()()a b f a b f a b f a f b ∈++-=0a b ==(0)0f =(0)1f =(0)0f =,0a x b ==()()0f x f x +=R,()0x f x ∀∈=(0)1f =0,a b x ==()()2()f x f x f x +-=()()f x f x -=()f x再令,则,所以D 错误;例如,函数符合题意,此时函数在上严格递增,且不为周期函数,所以B 错误.故选:C .16.【答案】B【解析】由图知点,所以直线AB 的方程为,直线CD 的方程为,所以,对于命题甲:曲线的导函数为,当时,,当时,,代入得,即,又由,得,方程组中a ,b 不可解,故命题甲不正确;对于命题乙:当时,有,即,故当时,曲线满足要求,故命题乙正确,综上,故选B三、解答题17.【答案】(1)见解析;(2)2x a b ==2()2112x f x f ⎛⎫=-≥- ⎪⎝⎭e e ()2x xf x -+=()f x (0,)+∞(0,4),(1,3),(2,1),(4,0)A B C D 4y x =-+122y x =-+11,2AB CD k k =-=-sin cos (,,)2ax bx y c a b c +=+∈R 1(cos sin )2y a ax b bx '=-1x =1y =-2x =12y =-1(cos sin )2y a ax b bx '=-1( c o s s i n )1211( c o s 2 s i n 2)22a ab b a a b b ⎧-=-⎪⎪⎨⎪-=-⎪⎩cos sin 2cos 2sin 21a a b b a a b b -=-⎧⎨-=-⎩sin cos 32sin 2cos 212a b c a b c +⎧+=⎪⎪⎨+⎪+=⎪⎩(sin cos )(sin 2cos 2)4a b a b +-+=1λμ+=121122(1)(1)()11111(2)(2)()2222x x y f f y f f λμλμλμλμλμλμ=='''⎧=+=--=-+=-⎪⎨'''=+=--=-+=-⎪⎩12112x x y y =='⎧=-⎪⎨'=-⎪⎩1λμ+=12()()y f x f x λμ=+25【解析】(1)证明:取的中点G ,连接FG ,DG ,根据题意可得,且,由三棱柱得性质知,所以,则四边形DGEF 是平行四边形,所以,因为面,面,所以面.(2)因为是等边三角形,且边长为2,所以,因为三棱柱的高为1,以D 为坐标原点,的方向分别为x 轴,y 轴,z 轴建立空间直角坐标系:所以,所以,设平面BEF的法向量11A D 11FG B D ∥1111,22FG B D DE BD ==11BD B D ∥FG BD ∥EF DG ∥EF ⊄11ADD A DG ⊂11ADD A EF ∥11ADD A ABC △AD BC ⊥1,,DB AD DD111,0,0,,,(1,0,0),(1,0,1)22E F B C ⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎝⎭113,0,0,0,,,0,122BE EF EC ⎛⎫⎛⎫⎛⎫=-==- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()111,,m x y z =则,令,所以,设平面的一个法向量为,所以,令,则,所以,设二面角为,所以,所以,所以二面角的正弦值为.18.【解析】(1)设"该航班飞往A 地", "该航班飞往B 地", "该航班飞往其他地区","该航班准点放行",则,由全概率公式得,,所以该航班准点放行的概率为0.778(2)(2),11111110020x m BE x z y m EF y z ⎧=⋅=-=⎧⎪⎪⎪⇒⎨⎨=⎪⎪⋅=+=⎩⎪⎩ 1y =113,02z x ==32m ⎛⎫= ⎪⎝⎭1C EF ()222,,n x y z =122222222330220n EC x z z x n EF y z z y ⎧⎧⋅=-+==⎪⎪⎪⎪⇒⎨⎨⎪⎪⋅=+==⎪⎪⎩⎩22y =22x z ==n = 1B EF C --([0,π])θθ∈|||cos |||||m n m n θ⋅= 2sin 5θ==1B EF C --251A =2A =3A =C =()()()1230.2,0.2,0.6P A P A P A ===()()()1230.84,0.8,0.75P C A P C A P C A ===∣∣∣()()()()()()112232()P C P A P C A P A P C A P A P C A =++∣∣∣0.840.20.80.20.750.60.778=⨯+⨯+⨯=()()()()11110.20.84()()0.778P A P C A P A C P A C P C P C ⨯===∣∣因为,所以可判断该航班飞往其他地区的可能性最大.19.【答案】(1;(2【解析】(1)在直角中,,可得,因为,则在中,,则,所以,解得,则(2)在中,,即,即,解得或(舍去),设,则,()()()()22220.20.8()()0.778P A P C A P A C P A C P C P C ⨯===∣∣()()()()33330.60.75()()0.778P A P C A P A C P A C P C P C ⨯===∣∣0.60.750.20.840.20.8⨯>⨯>⨯BMC △BM =ππ,63MBC BCM ∠=∠=10BC =BM =ABM △π2π,63ABM AMB ∠=∠=π6BAM ∠=2ππsin sin 36AB BM ==15AB =11sin 151022ABC S AB BC ABC =⋅∠=⨯⨯=△ABC △222π2cos 3AC AB BC AB BC =+-⋅211961002102AB AB =+-⋅⨯210960AB AB --=16AB =6AB =-CBM θ∠=π2ππ,π333ABM BAM θθθ⎛⎫∠=-∠=---= ⎪⎝⎭在中,可得,可得,即,则,则20.【答案】(1);(2);(3)见解析【解析】(1)(2)由题意得,.因为D 为BC 中点,所以,即,又,所以,又E 为的中点,所以,所以,所以点P 的轨迹是以为焦点的椭圆(左、右顶点除外).设,其中.则故.(3)思路一:由题意得,,且直线的斜率不为0,ABM △10cos 2πsin sin sin 3AB BM θθθ==10cos sin θθ=16sin θθ=tan θ=cos θ==cos BM BC θ=⋅=1)y x =-22:1(2)43x y x Γ+=≠±1)y x =-12(1,0),(1,0)A A -1A D BC ⊥12A D A C ⊥1PE A D ∥2PE A C ⊥2A C 2||PA PC =121112||4PA PA PA PC AC A A +=+==>Γ12,A A 2222:1()x y x a a bΓ+=≠±2220,a b a b c >>-=24,2,1,a a c b =====22:1(2)43x y x Γ+=≠±1212(2,0),(2,0),(0,1),(0,1)B B C C --2l可设直线,且.由,得,所以,所以.直线的方程为:,直线的方程为:,由,得,,解得.故点Q 在直线,所以Q 到的距离,因此的面积是定值,为.思路二:由题意得,,且直线的斜率不为0,可设直线,且.由,得,所以,()()21122:1,,,,l x my M x y N x y =-122,2x x ≠±≠±221431x y x my ⎧+=⎪⎨⎪=-⎩()2234690m y my +--=12122269,3434m y y y y m m -+==++()121223my y y y =-+1B M 11(2)2y y x x =++2B N 22(2)2y y x x =--1122(2)2(2)2y y x x y y x x ⎧=+⎪+⎪⎨⎪=-⎪-⎩()()21122222y x x x y x ++=--()()()()12212211221212112112331112223933333222y y y y y y my my y y y my my y y y y y y y -++--++=====---+---4x =-4x =-12C C 4d =12QC C △121124422C C d ⋅=⨯⨯=1212(2,0),(2,0),(0,1),(0,1)B B C C --2l ()()21122:1,,,,l x my M x y N x y =-122,2x x ≠±≠±221431x y x my ⎧+=⎪⎨⎪=-⎩()2234690m y my +--=12122269,3434m y y y y m m -+==++所以.直线的方程为:,直线的方程为:,由,得,故点Q 在直线,所以Q 到的距离,因此的面积是定值,为.思路三:由题意得,,且直线的斜率不为0.()121223my y y y =-+1B M 11(2)2y y x x =++2B N 22(2)2y y x x =--1122(2)2(2)2y y x x y y x x ⎧=+⎪+⎪⎨⎪=-⎪-⎩()()()()2112211222222y x y x x y x y x ⎡⎤++-=⎢⎥+--⎣⎦()()()()21121221211221132322133y my y my my y y y y my y my y y ⎡⎤++-⎛⎫+-==⎢⎥ ⎪+--+⎝⎭⎣⎦()()121221212323243my y y y y y y y ++-+⎡⎤==-⎢⎥+⎣⎦4x =-12C C 4d =12QC C △121124422C C d ⋅=⨯⨯=1212(2,0),(2,0),(0,1),(0,1)B B C C --2l(i )当直线垂直于x 轴时,,由得或.不妨设,则直线的方程为:,直线的方程为:,由,得,所以,故Q 到的距离,此时的面积是.(ii )当直线不垂直于x 轴时,设直线,且.由,得,所以.直线的方程为:,直线的方程为:,由,得.下证:.即证,即证,2l 2:1l x =-221431x y x ⎧+=⎪⎨⎪=-⎩132x y =-⎧⎪⎨=-⎪⎩132x y =-⎧⎪⎨=⎪⎩331,,1,22M N ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭1B M 3(2)2y x =+2B N 1(2)2y x =-3(2)21(2)2y x y x ⎧=+⎪⎪⎨⎪=-⎪⎩43x y =-⎧⎨=-⎩(4,3)Q --12C C 4d =12QC C △121124422C C d ⋅=⨯⨯=2l ()()21122:(1),,,,l y k x M x y N x y =+122,2x x ≠±≠±22143(1)x y y k x ⎧+=⎪⎨⎪=+⎩()()22224384120k x k x k +++-=221212228412,4343k k x x x x k k --+==++1MB 11(2)2y y x x =++2MB 22(2)2y y x x =--1122(2)2(2)2y y x x y y x x ⎧=+⎪+⎪⎨⎪=-⎪-⎩()()()()2112211222222y x y x x y x y x ⎡⎤++-=⎢⎥+--⎣⎦()()()()()()()()2112121221121212124262121234k x x k x x x x x x k x x k x x x x ⎡⎤++++--+==⎢⎥++-+-++⎣⎦121212426434x x x x x x -+=-++()121212426434x x x x x x -+=-++()121241016x x x x =-+-即证,即证,上式显然成立,故点Q 在直线,所以Q 到的距离,此时的面积是定值,为.由(i )(ii )可知,的面积为定值.思路四:由题意得,,且直线的斜率不为0,可设直线,且.由,得,所以.直线的方程为:,直线的方程为:,因为,所以,故直线的方程为:22224128410164343k k k k ⎛⎫⎛⎫--=-- ⎪ ⎪++⎝⎭⎝⎭()()()22244121081643k k k -=---+4x =-12C C 4d =12QC C △121124422C C d ⋅=⨯⨯=12QC C △1212(2,0),(2,0),(0,1),(0,1)B B C C --2l ()()21122:1,,,,x my M x y N x l y =-122,2x x ≠±≠±221431x y x my ⎧+=⎪⎨⎪=-⎩()2234690m y my +--=12122269,3434m y y y y m m -+==++1B M 11(2)2y y x x =++2B N 22(2)2y y x x =--2222143x y +=22222324y x x y ⎛⎫+=- ⎪-⎝⎭2B N 2223(2)4x y x y ⎛⎫+=-- ⎪⎝⎭由,得,解得.故点Q 在直线,所以Q 到的距离,因此的面积是定值,为.21.【答案】(1)递增区间为,递减区间为;(2);(3).【解析】(1)对成立,得,所以2为函数的周期.(2为"关于倒数点",得,即,即,得,设的定义域为R,求导得,当时,严格递增;时,严格递减;时,严格递增,所以的单调递增区间为,递减区间为,成立,(舍)(3)依题意,,1122(2)223(2)4y y x x x y x y ⎧=+⎪+⎪⎨⎛⎫+⎪=-- ⎪⎪⎝⎭⎩()()1212422322y y x x x x -=-+++()()()()12122222121212444933113139634y y y y mx my m y y m y y m m m ⎡⎤⎡⎤-⎢⎥=-=-=-=⎢⎥+++++-+++⎢⎥⎣⎦⎣⎦4x =-4x =-12C C 4d =12QC C △121124422C C d ⋅=⨯⨯=(,3),(1,)-∞--+∞(3,1)--34e -(2,e)()(1)1f x f x +=x R ∈1()(2)(1)f x f x f x ==++()f x ()h x 2-2)1h h =22)1,2)10a a a a ++=+-+-=(1)(1)0a a +--=1a =2()e (1)x x x ϕ=+2()e (1)2e (1)e (1)(3)x x x x x x x x ϕ'=+++=++(,3)x ∈-∞-()0,()x x ϕϕ'>(3,1)x ∈--()0,()x x ϕϕ'<(1,)x ∈-+∞()0,()x x ϕϕ'>()x ϕ(,3),(1,)-∞--+∞3(3,1).(3)4m e ϕ---=-=(1)0m ϕ=-=e ,0()1,0x x x x x a ω⎧>⎪=⎨<⎪+⎩由恰有3个“可移1倒数点”,得方程恰有3个不等实数根,①当时,,方程可化为,解得,这与不符,因此在内没有实数根;②当时,,方程可化为,该方程又可化为.设,则,因为当时,,所以在内严格递增,又因为,所以当时,,因此,当时,方程在内恰有一个实数根;当时,方程在内没有实数根.③当时,没有意义,所以不是的实数根.④当时,,方程可化为,化为,于是此方程在内恰有两个实数根,则有,解得因此当时,方程在内恰有两个实数根,当在内至多有一个实数根,综上,a 的取值范围为.()x ϕ()(1)1x x ωω+=0x >10x +>()(1)1x x ωω+=21e 1x +=12x =-0x >(0,)+∞()(1)0x x ωω+=10x -<<10x +>()(1)1x x ωω+=11x e x a+=+1ex a x +=-1()e x k x x +=-1()e 1x k x +'=-(1,0)x ∈-()0k x '>()k x (1,0)-(1)2,(0)e k k -==(1,0)x ∈-()(2,e)k x ∈(2,e)a ∈()(1)1x x ωω+=(1,0)-(0,2][e,)a ∈+∞ ()(1)1x x ωω+=(1,0)-1x =-10,(1)x x ω+=+1x =-()(1)1x x ωω+=1x <-10x +<()(1)1x x ωω+=1111x a x a ⋅=+++22(21)10x a x a a ++++-=(,1)-∞-()222(21)41021121(21)10a a a a a a a ⎧+-+->⎪+⎪-<-⎨⎪-+++->⎪⎩a >a >()(1)1x x ωω+=(,1)-∞-0a <≤()(1)1x x ωω+=(,1)-∞-(2,e)(2,e)⎫+∞=⎪⎪⎭。
