第八讲 齿轮系及其设计 齿轮精讲
齿轮传动设计培训讲解课件.ppt

轮的基圆为定圆,在其同一方向的内公
切线只有一条。所以无论两齿廓在任何
位置接触,过接触点所作两齿廓的公法
线为一固定直线,它与连心线O1O2的交 点C必是一定点。因此渐开线齿廓满足
定角速比要求。
13
上午9时0分
图d 渐开线齿廓满足定角速比证明
14
上午9时0分
由图d知,两轮的传动比为
i12
1 2
O2C O1C
36
Δy—齿顶高变动系数
上午9时0分
二、齿轮设计基础知识 1、齿轮机构及其设计 —变位齿轮传动
齿轮变位的意义:
➢ 避免根切。
➢ 改善小齿轮的寿命(传动比较大时,使小齿轮齿厚 增大,大齿轮齿厚减小,使一对齿轮的寿命相当) ➢ 凑中心距以满足实际应用要求
37
上午9时0分
二、齿轮设计基础知识 1、齿轮机构及其设计 —平行轴斜齿轮圆柱齿轮传动
3)发生线与基圆的切点N即为渐开线上
K点的曲率中心,线段为K点的曲率半径。
随着K点离基圆愈远,相应的曲率
10
上午9时0分
半径愈大;而K点离基圆愈近,相应的 曲率半径愈小。
4)渐开线的形状取决于基圆的大小。如 图c所示,基圆半径愈小,渐开线愈弯曲;
基圆半径愈大,渐开线愈趋平直。当基
圆半径趋于无穷大时,渐开线便成为直
➢分度圆螺旋角β
法面参数为标准参数
斜齿轮的基本尺寸也是以其分度圆柱为基准圆来进行计算的。斜齿轮 分度圆柱上的螺旋线的切线与其轴线所夹锐角称为分度圆螺旋角(简称螺 旋角)。
螺旋角β是斜齿轮的重要的基本参数之一,由于轮齿倾斜了β角,使斜
齿轮传动时产生了轴向力,β越大,轴向力越大。
39
上午9时0分
第八讲 齿轮系及其设计
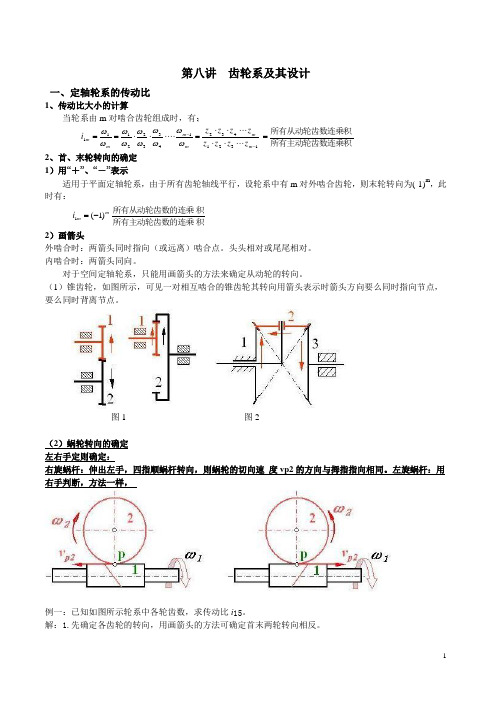
第八讲 齿轮系及其设计一、定轴轮系的传动比1、传动比大小的计算当轮系由m 对啮合齿轮组成时,有:1321432143322111--⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅==m m m m m m z z z z z z z z i ωωωωωωωωωω所有主动轮齿数连乘积所有从动轮齿数连乘积=2、首、末轮转向的确定1)用“+”、“-”表示适用于平面定轴轮系,由于所有齿轮轴线平行,设轮系中有m 对外啮合齿轮,则末轮转向为(-1)m,此时有:积所有主动轮齿数的连乘积所有从动轮齿数的连乘mm i )1(1-=2)画箭头外啮合时:两箭头同时指向(或远离)啮合点。
头头相对或尾尾相对。
内啮合时:两箭头同向。
对于空间定轴轮系,只能用画箭头的方法来确定从动轮的转向。
(1)锥齿轮,如图所示,可见一对相互啮合的锥齿轮其转向用箭头表示时箭头方向要么同时指向节点,要么同时背离节点。
图1 图2(2)蜗轮转向的确定 左右手定则确定:右旋蜗杆:伸出左手,四指顺蜗杆转向,则蜗轮的切向速 度vp2的方向与拇指指向相同。
左旋蜗杆:用右手判断,方法一样,例一:已知如图所示轮系中各轮齿数,求传动比i 15。
解:1.先确定各齿轮的转向,用画箭头的方法可确定首末两轮转向相反。
2. 计算传动比'4'31543'4'32154325115Z Z Z Z Z Z Z Z Z Z Z Z Z Z i -=-==ω其中齿轮2对传动比没有影响,但能改变从动轮的转向,称其为过轮或中介轮。
图二、 周转轮系的传动比周转轮系的分类除按自由度以外,还可根据其基本构件的不同来加以分类,如图所示,设轮系中的太阳轮以K 表示,系杆以H 表示,则图6所示为2K —H 型轮系;图7为3K 型轮系,因其基本构件为3个中心轮,而系杆只起支撑行星轮的作用。
在实际机构中常用2K —H 型轮系。
图5 图7反转原理:给周转轮系施以附加的公共转动-H ω后,不改变轮系中各构件之间的相对运动, 但原轮系将转化成为一新的定轴轮系,可按定轴轮系的公式计算该新轮系的传动比。
第八章机械原理设计齿轮系详解演示文稿

Z5 Z 3
(三)
3 H
3 5
H
35
2
2' 4
1
3'
H为输出件
(四)联立 i1H 31
n1 1450r / min
nH
n1 i1H
1450 46.77r / min 31
第25页,共43页。
§8—4 齿轮系的功用
1、传递相距较远的两轴之间的运动和动力;
第26页,共43页。
2、获得大的传动比:一对外啮合圆柱齿轮传动,其传动比一般可为i<=57。但是行星轮系传动比可达i=1000,而且结构紧凑。
1、平面定轴轮系
第8页,共43页。
推广: 设首轮A的转速为n1,末轮K的转速为nK,m为圆柱齿轮外啮
合的对数,则平面定轴轮系的传动比可写为:
i1k
1 k
n1 nk
(1) m
所有从动轮齿数的乘积 所有主动轮齿数的乘积
箭头法判断方向:
第9页,共43页。
2、空间定轴轮系
大小仍用公式计算,但首末两轮的转向关系只能在图上画箭头得到.(若首 末两轮轴线平行,在大小数值前加正负号)
3、找出轮系之间的运动关系
1 3
1 3
3'
2
2' 4
13
H
输出
1'
4、联立求解:
i1H
1 H
Hale Waihona Puke Z1Z3 Z11 Z1Z2Z3
Z2Z3
第23页,共43页。
例图示的电动机卷扬机减速器中,已知各轮的齿数 Z1=18,Z2=39,Z'2=35,Z3=130,Z'3=18,Z4=30,Z5=78。求传动比i15。
机械的设计教学培训讲座学习课件PPT齿轮系及其的设计共74页文档

齿数,求传动比 i15 。
解:1.先确定各齿轮的转向
2. 计算传动比
i15 = ω1 /ω5
过轮
=
z2 z3 z4 z5 z1 z2 z’3 z’4
z3 z4 z5 = z1 z’3 z’4
Z2 Z’3
Z1 作者:潘存云教授 Z4
Z’4 Z3
Z5
齿轮1、5 转向相反
齿轮2对传动比没有影响,但能改变从动轮的转向,
一对齿轮: i12 =ω1 /ω2 =z2 /z1 可直接得出
轮系传动比定义——轮系中首、末两构件的角速度 (或转速)之比。 轮系传动比计算的内容
首、末两构件角速度比的大小计算 首、末两构件转向关系的确定。
一、传动比大小的计算 已知轮系中主动齿轮1为首轮,从动齿轮5为末轮,则该
轮系的总传动比为
i15
2 H
1 3
2
H
作者:潘存云教授
1 3
转化后: 系杆机架, 周转轮系定轴轮系 可直接套用定轴轮系传动比的计算公式。
i1H3
H 1
H 3
1 H 3 H
z2z3 z3
z1z2
z1
上式“-”说明在转化轮系中ωH1 与ωH3 方向相反。 通用表达式:
周转轮系传动比的一般关系式:设周转轮系中的两个
i
H mn
n
H m
n
H n
nm nH nn nH源自计算周转轮系传动比时应注意的问题
1.转化机构的传动比表达式中,含有原周转轮系的各轮绝对 角速度,可从中找出待求值。
2.齿数比前的“+”、“”号按转化轮系的判别方法确定。
3. m,n均,为H代数值。
4.
imHn imn
齿轮系及其设计主要知识点

齿轮系及其设计主要知识点导言:齿轮系是一种广泛应用于机械系统中的传动装置,通过齿轮之间的啮合来传递力量和运动。
本文将介绍齿轮系的基本概念、设计要点以及相关的知识点,为读者提供深入了解和应用齿轮系的指导。
一、齿轮系概述齿轮系是由两个或多个齿轮组成的传动装置,常用于变速、传递运动和转矩的应用。
它可以改变输入轴和输出轴的转速和转矩大小,且具有高效、平稳和可靠的特点。
二、齿轮系的设计要点1. 齿轮的几何参数:包括齿轮的模数、齿轮的齿数、齿轮的压力角等。
这些参数直接影响着齿轮的传动性能和工作寿命,设计时需要根据具体的传动要求进行合理选择。
2. 齿轮啮合条件:齿轮的啮合要求是齿轮几何参数的匹配,包括齿数比、齿廓曲线等。
保证齿轮啮合的紧密度和平稳性,是齿轮系设计中的重要环节。
3. 齿轮的材料选择:由于齿轮在工作中承受较大的载荷和摩擦,材料的选择直接影响着齿轮系统的耐磨性和寿命。
常见的齿轮材料有钢、铸铁、铜合金等,需要根据具体的工作条件和需求来进行选择。
4. 齿轮的润滑与冷却:为了减小齿轮系统的摩擦和磨损,以及散热问题,必须对齿轮进行润滑和冷却,常见的方式有油润滑、气体润滑、水冷却等。
5. 齿轮的传动误差和噪声控制:由于制造误差和运动不平衡等因素,齿轮系统会产生传动误差和噪声。
设计时需要考虑减小误差和噪声的方法,如精密加工、动平衡等。
三、齿轮系的常见结构类型1. 平行轴齿轮系:由两个平行轴上的齿轮组成,常用于平行轴传动和同方向或反方向传动的场合。
2. 交叉轴齿轮系:由两个相交轴上的齿轮组成,常用于传递转矩和变速的应用。
3. 斜齿轮系:由两个斜齿轮组成,可实现非平行轴传动,常用于交叉轴传动和变速箱等应用。
4. 锥齿轮系:由两个锥齿轮组成,常用于轴线交叉和转动方向变换的场合。
四、齿轮系的设计流程1. 确定传动比和传动方式:根据输入轴和输出轴的转速和转矩要求,确定传动比和传动方式,选择合适的齿轮组合方式。
2. 计算齿轮参数:根据传动比和齿轮设计要点,计算齿轮的几何参数,包括齿数、模数、压力角等。
机械原理3D版课件-第8章 齿轮机构及其设计

齿顶高系数ha* :正常齿制ha*= 1,短齿制ha*= 0.8 。 顶隙系数c*:正常齿制c*= 0.25,短齿制c*= 0.3。
ha ham
hf (ha c )m
h ha hf (2ha c )m
§8-4 渐开线标准齿轮的基本参数和几何尺寸
三、几何尺寸 表8-4渐开线标准直齿圆柱齿轮几何尺寸公式
啮合终止点B1 —— 啮合线N1N2 与主动轮齿顶圆的交点。
线段B1B2 ——实际啮合线段。 啮合线N1N2 —— 理论啮合线段。 N1、N2 —— 啮合极限点。
图8-14齿轮重合度
§8-5 渐开线直齿圆柱齿轮的啮合传动
重合度——实际啮合线段与法向齿距的比值,用εa 表示。
a
B1B2 pb
连续传动条件—— 重合度大于或等于 1
重合度的计算
a
1 2π
z1tan a1
tan
z2 tan a2
tan
影响重合度的因素:
a) ε与模数m无关;
b) 齿数z越多,ε 越大; c) z趋于∞时,εmax=1.981; d) 啮合角α‘ 越小,ε越大;
e) 齿顶高系数ha*越大,ε越大。
图8-14齿轮重合度
图8-15 齿轮重合 度与齿轮啮合区段
图8-2渐开线的形成
二、 渐开线的特性
1. 发生线沿基圆滚过的长度,等于基圆上被 滚过的圆弧长。
2. 渐开线上任意点的法线恒与其基圆相切。发生 线与基圆的切点B就是渐开线在K 点的曲率中心,
线段KB是渐开线在K点的曲率半径。
3. 基圆内无渐开线。 4. 渐开线的形状取决于基圆的大小。
§8-3 渐开线齿廓及其啮合特性
《机械设计基础》第8章 齿轮系

48 24 4 48 18 3
250 H 4 100 H 3
H 2
2
1
2‘ H
3
3H
3
1
H 1
H 50
周转轮系传动比计算方法小结:
定轴齿轮系
平面定轴齿轮系 空间定轴齿轮系
二.行星齿轮系
1. 定义
在齿轮系运转时,若至少有一个齿轮的几何轴线 绕另一齿轮固定几何轴线转动,则该齿轮系称为行星 齿轮系(如图8-3)。它主要由行星齿轮、行星架(系 杆)、和中心轮所组成。
2. 基本构件
行星齿轮系中由于一般都以中心轮和行星架作 为运动的输入或输出构件,故称它们为行星齿轮系 的基本构件
上角标 H
周转轮系
-w
H
正负号问题
转化机构:假想的定轴轮系
i1H n 1 n H i1n
计算转化机构的传动比 计算周转轮系传动比
1H z 2 z n i H z1 z n1 n
H 1n
i1 n 1
n
例题8-2 :
一差动齿轮系如图 所示,已知个轮齿数为: z1 16, z 2 24, z3 64, 当轮1和轮3的转速为:
式中:G为主动轮,K为从动轮,中间各轮的主 从地位也应按此假定判定。m为齿轮G至K间外啮合 的次数。
求行星齿轮系传动比时,必须注意以下几点:
(1) nG , K ,nH 必须是轴线平行或重合的相应齿轮的 n 转速。 (2)将nG,nK,nH 的已知值代入公式时必须带正 号或负号。
H (3) i GK i GK。 i GK为转化机构中轮G与K的转速之 比,其大小与正负号应按定轴齿轮系传动比的计算 方法确定。
齿轮机构及其设计

5.齿轮与齿条啮合传动
特点 啮合线切于齿轮基圆并垂直于齿条齿廓 标准安装或非标准安装 d = d =
分度圆、节圆、压力角、啮合角
分度圆与节线相切
连续传动条件
重合度 分析:1) =1 表示在啮合过程中,始终只有一对齿工作; 1 2 表示在啮合过程中,有时是一对齿啮合, 有时是两对齿同时啮合。 重合度传动平稳性承载能力。
21 25
26 34
35 54
55 134
135
每把刀的刀刃形状,按它加工范围的最少齿数齿轮的齿形来设计。
§6 渐开线齿廓的切制原理、根切和最少齿数
2.范成法
1
切削 (沿轮坯轴向) 进刀和让刀 (沿轮坯径向) 范成运动 (模拟齿轮啮合传动)
2
刀具与轮坯以i12=1/2=Z2 /Z1回转
3
用同一把刀具,通过调节i12 ,就可以加工相同模数、相同压力角 ,不同齿数的齿轮。
渐开线方程:{
rK = ———
rb
cosaK
inv aK = tg aK - aK .
aK
aK
qK
K
rK
rb
O
N
A
四、渐开线齿廓的啮合特点
1.啮合线为一直线
啮合线—
啮合点 (在固定平面上) 的轨迹线.
两齿廓所有接触点的公法线均重合, 传动时啮合点沿两基圆的内公切线移动。
3. 侧隙为零的中心距
无侧隙啮合条件:
S1' = e2' ; e1' = S2'
S1= e2 = e1= S2
标准齿轮: S = e = m/2
▲当两标准齿轮按分度圆相切来安装, 则满足传动条件。 正确安装
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八讲 齿轮系及其设计一、定轴轮系的传动比1、传动比大小的计算当轮系由m 对啮合齿轮组成时,有:1321432143322111--⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅==m m m m m m z z z z z z z z i ωωωωωωωωωω所有主动轮齿数连乘积所有从动轮齿数连乘积=2、首、末轮转向的确定1)用“+”、“-”表示适用于平面定轴轮系,由于所有齿轮轴线平行,设轮系中有m 对外啮合齿轮,则末轮转向为(-1)m,此时有:积所有主动轮齿数的连乘积所有从动轮齿数的连乘mm i )1(1-=2)画箭头外啮合时:两箭头同时指向(或远离)啮合点。
头头相对或尾尾相对。
内啮合时:两箭头同向。
对于空间定轴轮系,只能用画箭头的方法来确定从动轮的转向。
(1)锥齿轮,如图所示,可见一对相互啮合的锥齿轮其转向用箭头表示时箭头方向要么同时指向节点,要么同时背离节点。
图1 图2(2)蜗轮转向的确定 左右手定则确定:右旋蜗杆:伸出左手,四指顺蜗杆转向,则蜗轮的切向速 度vp2的方向与拇指指向相同。
左旋蜗杆:用右手判断,方法一样,例一:已知如图所示轮系中各轮齿数,求传动比i 15。
解:1.先确定各齿轮的转向,用画箭头的方法可确定首末两轮转向相反。
2. 计算传动比'4'31543'4'32154325115Z Z Z Z Z Z Z Z Z Z Z Z Z Z i -=-==ωω其中齿轮2对传动比没有影响,但能改变从动轮的转向,称其为过轮或中介轮。
图二、 周转轮系的传动比周转轮系的分类除按自由度以外,还可根据其基本构件的不同来加以分类,如图所示,设轮系中的太阳轮以K 表示,系杆以H 表示,则图6所示为2K —H 型轮系;图7为3K 型轮系,因其基本构件为3个中心轮,而系杆只起支撑行星轮的作用。
在实际机构中常用2K —H 型轮系。
图5 图7反转原理:给周转轮系施以附加的公共转动-H ω后,不改变轮系中各构件之间的相对运动, 但原轮系将转化成为一新的定轴轮系,可按定轴轮系的公式计算该新轮系的传动比。
转化后所得的定轴轮系称为原周转轮系轮系的“转化轮系”。
将整个轮系机构按-ω反转后,各构件的角速度的变化如下:由角速度变化可知机构转化后,系杆角速度为0,既系杆变成了机架,周转轮系演变成定轴轮系,因此可直接套用定轴轮系传动比的计算公式。
132132313113Z Z Z Z Z Z iH HH H H -=-=--==ωωωωωω上式“-”说明在转化轮系中ωH 1与ωH 3方向相反。
通用表达式:Hn H m H n H m H mniωωωωωω--==所有主动轮齿数连乘积至转化轮系中由所有从动轮齿数连乘积至转化轮系中由n m n m ±=)(Z f = 特别注意:1、齿轮m 、n 的轴线必须平行。
2、计算公式中的±不能去掉,它不仅表明转化轮系中两个3、太阳轮m 、n 之间的转向关系,而且影响到ωm 、ωn 、ωH 的计算结果。
如果周转轮系是行星轮系,则ωm 、ωn 中必有一个为0(不妨设ωn =0),此时上述通式可改写如下:HmH H m H nH m Hmni i+=--==1ωωωωω 即: )(11Z f i i Hm n H m -=-=以上公式中的ωi 可用转速n i 代替:用转速表示有:)(z f n n n n n n iHn Hm H nH m H mn=--==图9例:如图9所示2K -H 轮系中,Z 1=Z 2=20,Z 3=60,轮3固定。
求:1)i 1H 。
2)n 1=1, n 3=-1,求n H 及i 1H 的值。
3)n 1=1, n 3=1,求n H 及i 1H 的值。
10)111313113+-=--=--===H H H H H H H H i iωωωωωωωωω解32060132132-=-=-=-=z z z z z z ∴ i 1H =4 , 齿轮1和系杆转向相同。
-311)2313113=---=--==HHH HH HHn n n n n n n n i2/1-=H n得: i 1H = n 1 / n H =-2,两者转向相反。
ii i n ωππω3060)2(==311)3313113-=--=--==HHH H H HH n n n n n n n n i1=H nn 1=1, n 3=1,得: i 1H = n 1 / n H =1,两者转向相同。
结论:1、轮1转4圈,系杆H 同向转1圈。
2、轮1逆时针转1圈,轮3顺时针转1圈,则系杆顺时针转2圈。
3、轮1轮3各逆时针转1圈,则系杆逆时针转1圈。
特别强调:1、i 13≠ i H 132、i 13≠- z 3/z 1例3:如图8—15示圆锥齿轮组成的轮系中,已知:z 1=33,z 2=12,z 2’=33,求i 3H解:判别转向:齿轮1、3方向相反11031331331-=-=+-=--=--=z z i i H H H H H Hωωωωωωωi 3H =2特别注意:转化轮系中两齿轮轴线不平行时,不能直接计算! 三、复合轮系的传动比 复合轮系的解题步骤:1、找出所有的基本轮系。
关键是找出周转轮系!2、求各基本轮系的传动比。
3、根据各基本轮系之间的连接条件,联立基本轮系的传动比方程组求解。
复合轮系的常见类型:1.一个或多个定轴轮系和行星轮系的复合轮系例 在图示的轮系中,已知各轮齿数为2425z z ==,220z '=,各轮的模数相同,4n =1000r/min 。
试求行星架的转速H n 的大小和方向。
例11-6图解:(1)求其余各轮齿数:因为1242r r r =+ 所以124275z z z =+=,2423z z z z '+=+,330z =,且13z z ''=(2)求4H i :3113311z n i n z ''''==-=- 2344334232HH H z gz n n i n n z gz '-===- 4141143HH H n n z i n n z -==-=-- (3)求各转速: 由上面三式得13n n =-433()()2H H n n n n -=-413()H H n n n n -=--所以33H n n =- 代入上两式得4332H H H n n n n -=--所以45H i =- (4)求H n :441000r/min 200r/min 5H H n n i ===-- H n 的方向与4n 相反。
2、3k-H型的轮系(即有三个2K-H型周转轮系组成)和多个周转轮系3、有蜗杆传动的复合轮系,蜗杆传动一定是定轴轮系。
4、含有差动轮系的复合轮系(已知两个主动件)例7 在图示轮系中,已知各轮齿数为201=z ,362=z ,182='z ,603=z ,703='z ,284=z ,145=z ,n A =60r/min ,n B =300r/min ,方向如图示。
试求轮5的转速n C 的大小和方向。
例11-7图解:(1)7014355 35 3-=-=--=''z z n n n n i H H H (2)6201836601 223 31 13-=⨯⨯-=-==''z z z z n n i(3)300 ,1066061 3-==-=-=-='B H n n n n 701430030010 355-=-=++-'z z n-=14245005n n 51750=-表示n 5和n 1反向。
5.有多个周转轮系和定轴轮系组成的复合轮系(东南大学2009)例题精解:例11-1 在图示轮系中,已知:蜗杆为单头且右旋,转速n 11440= r /min, 转动方向如图示,其余各轮齿数为:40 2=z ,20 2='z ,303=z ,183='z ,54 4=z ,试:(1)说明轮系属于何种类型; (2)计算齿轮4的转速4n ; (3)在图中标出齿轮4的转动方向。
解: 例11-1图(1)该轮系为定轴轮系(2)81440543040182014321 3 214=⨯⨯⨯⨯⨯=⋅⋅⋅⋅⋅=''z z z n z z z n r/min(3)蜗杆传动可用左右手定则判断蜗轮转向↓。
然后用画箭头方法判定出n 4转向。
n 4方向←。
例11-2 在图示轮系中,设已知双头右旋蜗杆的转速1900n =r/min ,260z =,225z '=,320z =,325z '=,420z =,430z '=,535z =,528z '=,6135z =,求6n 的大小和方向。
例11-2图解:该轮系为定轴轮系。
(1)2345611661234560202035135108225253028z z z z z n i n z z z z z ''''⨯⨯⨯⨯⨯⨯⨯⨯====⨯⨯⨯⨯⨯⨯⨯⨯ (2)16169008.33108n n i ===(r/min )转向如图所示例11-3 图示轮系中,各轮模数和压力角均相同,都是标准齿轮,各轮齿数为z 123=,z z z z z z n 23344515192404017331500=======,,,,,,'' r /min ,转向如图示。
试求齿轮2'的齿数z 2'及n A 的大小和方向。
例11-3图解:(1)齿轮1,2啮合的中心距等于齿轮2',3啮合的中心距,所以得z z z z 1232+=-'z z z z 231292235118'=--=--=(2))(3)22(1A --'--组成差动轮系,)(5)44(3A --'--'组成行星轮系i n n n n z z z z H H H 1313231251922318343=--=-=-⨯⨯=-' i n n n n i z z z z H H H H333354534111403340175017''''===-=+=+⨯⨯= n n n n H HH 15017343--=-33661n n n H H -=-(3)6331n n H =-n n n A H ==-=-=-1211500217143.r/min (4)负号表明n H 转向与n 1相反。
例11-4 图示轮系,已知各轮齿数:322=z ,343=z ,364=z ,645=z ,327=z ,178=z ,z 924=。
