第31届中国数学奥林匹克
奥数半世兴与废

奥数半世兴与废作者:陈宁来源:《神州·校长》2012年第10期从1956年被引入至今,奥数在中国经历了半个多世纪的兴衰。
2012年8月21日,北京市教委召开发布会宣布,将坚决治理“奥数”成绩与升学挂钩。
这是北京市政府部门第三次向“奥数热”发出警告。
回溯奥数半世的兴与废,令人深省。
1956年,高中毕业不久的裘宗沪应邀参加宁波市数学竞赛的阅卷工作,这个年轻人被邀请的理由,是会做很多“乱七八糟”的数学题。
这次数学竞赛,是华罗庚将奥数引入中国的第一次尝试。
而裘宗沪,就是日后的中国数学奥林匹克委员会常务副主席。
由兴至盛1956:初入中国60年前,华罗庚考察了苏联的“数学奥林匹克”后,兴奋异常,他认为,这是中国正需要的。
1950年代,新中国百废待举,进入全面学习苏联的年代。
1956年,在华罗庚和苏步青等人倡导下,北京、上海、天津、武汉、宁波等城市分别举办了中学生数学竞赛,这是奥数在中国最早的阶段。
1962年,北京、上海、成都等五个省市开始举办数学竞赛,参加竞赛的学生回忆,当时复赛有道试题讲的是“任意剪六个圆形纸片放在桌面上,使得没有一个纸片的中心落在另一纸片之上或被另一纸片盖住。
然后用一枚针去扎这些纸片,证明:不论针尖落在哪一点,总是不能一次把六个纸片都扎中。
”此后的1963年、1964年,北京又连续举办两届数学竞赛。
1965年到1977年,我国的数学竞赛在特殊时期中断了13年。
1978:北京恢复数学竞赛1978年夏天,在华罗庚的组织下,教育部、中国科协、团中央共同举办了首届全国八省市中学数学竞赛,由北京、上海、安徽等八个省市组织代表队参与。
考场上,当时教育部的一位副部长前来视察。
他说,中国刚接到了罗马尼亚主办的IMO (国际数学奥林匹克竞赛)的邀请,询问他们能否带队参赛。
中国并没能参赛,原因很简单,时间上来不及。
对于中国奥数来说,1979年是个充满了“第一次”的年份。
这一年,八省市数学竞赛扩展为全国数学竞赛。
喜报1高三·1班白雪杨同学在第31届全国化学奥林匹克决赛中获得

喜报1.高三·1班白雪杨同学在第31届全国化学奥林匹克决赛中获得银牌,并获得清华大学降至一本线录取的资格。
向白雪杨同学和他的辅导老师表示祝贺!2.在俄罗斯举行的“亚太地区天文奥林匹克竞赛”刚刚结束,我校初三徐舶洋同学喜获“银牌”。
3.八十中机器人社团在全国选拔赛中获得全国冠军2017年11月2日至5日,2017年第八届亚洲机器人锦标赛中国选拔赛在广东珠海中国国际航空航天展览中心举行,参加本次大赛的有来自全国26个省、市、自治区、直辖市500多支队伍,将近3000人参赛。
北京市第八十中学机器人社团22名学生在张朋、李孟尧老师的带领下,学生们克服种种困难,学生经过3天激烈紧张的比赛,最终获得VEX EDR机器人技能挑战赛全国冠军,VEX EDR机器人工程挑战赛一等奖14人,VEX IQ机器人工程挑战赛二等奖2人,三等奖6人的优异成绩。
4. 2017年11月1日至11月5日,第69届纽伦堡国际发明展(简称IENA)在德国纽伦堡市展览中心举行,吸引了来自40个国家和地区的900多项发明创新作品参展。
此次,北京市第八十中学共有八项发明作品被推荐参加此次发明展,经过紧张激烈的展示讲解和答辩,最终获得2金4银2铜的好成绩,获奖名单如下。
项目名称获奖学生姓名班级辅导教师获奖等级李念朴、冯禹赫1 控温限位膝关节康复装置刘永红金奖高二7班、高二6班5.我校国际部辩论队在全国“百汇杯”第二届国际学校中文辩论赛中荣获高中组冠军 最佳辩手:张政阳(10A3)冠军队成员:张政阳(10A3)辛子毅(10A1)李奕辰(10B )优秀辩手:张浩博(11A3)辛子毅(10A1)张政阳(10A3)6.八十中学生奥林匹克学科竞赛屡创佳绩在刚刚结束的全国奥林匹克化学和数学竞赛中,北京市第八十中学生均取得优异成绩。
首先,在第31届全国化学奥林匹克竞赛(初赛)中,全北京市一等奖66名,八十中学有2名;其中白雪杨同学进入北京队,将参加全国决赛。
奥数简介

奥数简介“奥数”是奥林匹克数学竞赛的简称。
1934年—1935年,前苏联开始在列宁格勒和莫斯科举办中学数学竞赛,并冠以数学奥林匹克竞赛的名称,1959年在布加勒斯特举办第一届国际数学奥林匹克竞赛。
国际数学奥林匹克作为一项国际性赛事,由国际数学教育专家命题,出题范围超出了所有国家的义务教育水平,难度大大超过大学入学考试。
有关专家认为,只有5%的智力超常儿童适合学奥林匹克数学,而能一路过关斩将冲到国际数学奥林匹克顶峰的人更是凤毛麟角。
1934年和1935年苏联开始在列宁格勒和莫斯科举办中学数学竞赛,并冠以数学奥林匹克的名称。
1959年罗马尼亚数学物理学会邀请东欧国家中学生参加,在布加勒斯特举办了第一届国际数学奥林匹克竞赛,从此每年举办一次,至今已举办了43届。
近年来中国代表在数学奥林匹克上的成绩就像中国健儿在奥运会的成绩一样,突飞猛进,从40届到第43届,中国代表队连续四年总分第一。
奥数分类为:浓度问题、分数比大小问题、行程问题、分数巧算、逻辑推理、工程问题、牛顿问题、数字的巧算问题。
奥数与一般数学有一定的区别:奥数相对比较深.小学数学奥林匹克活动的蓬勃发展,极大地激发了广大少年儿童学习数学的兴趣,成为引导少年积极向上,主动探索,健康成长的一项有益活动.国际奥林匹克数学竞赛奖项名称: 国际奥林匹克数学竞赛其他名称: International Mathematics Olympiad创办时间: 1959年主办单位: 由参赛国轮流主办奖项介绍:国际奥林匹克数学竞赛是国际中学生数学大赛,在世界上影响非常之大。
国际奥林匹克竞赛的目的是:发现鼓励世界上具有数学天份的青少年,为各国进行科学教育交流创造条件,增进各国师生间的友好关系。
这一竞赛1959年由东欧国家发起,得到联合国教科文组织的资助。
第一届竞赛由罗马尼亚主办,1959年7月22日至30日在布加勒斯特举行,保加利亚、捷克斯洛伐克、匈牙利、波兰、罗马尼亚和苏联共7个国家参加竞赛。
2.奥林匹克竞赛资料
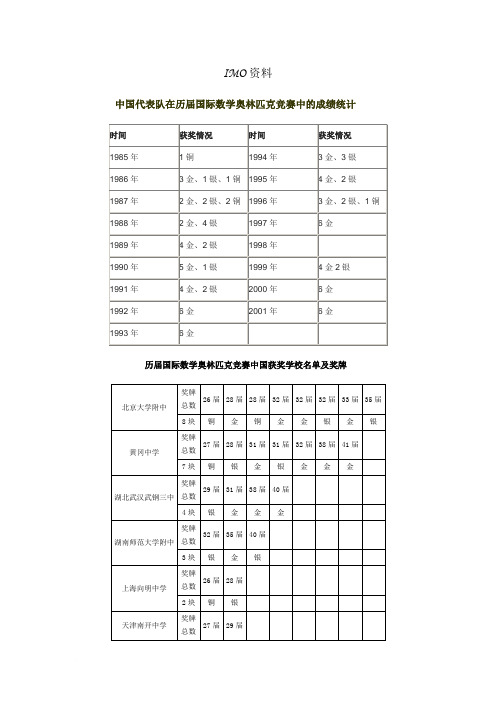
IMO资料中国代表队在历届国际数学奥林匹克竞赛中的成绩统计历届国际数学奥林匹克竞赛中国获奖学校名单及奖牌历届国际数学奥林匹克竞赛中国获奖学生名单中国也曾先后主办过三届国际奥林匹克学科竞赛:1990年的第31届国际数学奥林匹克竞赛,1994年的第25届国际物理奥林匹克竞赛和1995年的第27届国际化学奥林匹克竞赛。
在世纪之交的2000年,我国将主办第12届国际信息学奥林匹克竞赛。
中国青少年在历届国际奥林匹克学科竞赛的获奖情况第41届国际数学奥林匹克于2000年7月13日至25日在韩国大田举行。
参加本次国际数学奥林匹克的共有82支参赛队的461名选手。
中国队六名队员全部获得金牌,并以218分的总成绩一举获得团体总分第一。
今年中国队的主教练是北京大学数学系张筑生教授,领队是北京大学数学系王杰教授,副领队是南京师范大学数学系陈永高教授。
六名队员及其得分是:恽之玮(江苏常州高级中学),42分,金牌;李鑫(广东华南师大附中),38分,金牌;袁新意(湖北黄冈中学),32分,金牌;朱琪慧(广东华南师大附中),36分,金牌;吴忠涛(上海中学),31分,金牌;刘志鹏(湖南长沙一中),39分,金牌。
总分金牌数银牌数铜牌数1 中国218 6 0 02 俄罗斯215 5 1 03 美国184 3 3 04 韩国172 3 3 0注:每个选手满分为42分。
本次竞赛的金牌分数线为30分;银牌分数线为21分;铜牌分数线为11分。
最终共有39名选手获得金牌、71名选手获得银牌、119名选手获得铜牌2001年第42届国际数学奥林匹克竞赛是在美国华盛顿市郊乔治·梅森大学举行的。
参加本次奥赛的选手共有473人,分别来自83个国家和地区。
比赛包括6道题,每题7分,答题时间一共是9小时。
比赛结果,有39名学生获得金牌,81人获得银牌,122人获得铜牌。
中国代表队的学生是:北京人大附中的肖梁,长沙市第一中学的张志强,湖南师大附中的余君,湖北武钢三中的郑晖,江苏启东中学的陈建鑫和东北育才学校的瞿枫。
2018年全国青少年信息学奥林匹克联赛级赛区一.pdf

报名审核通过考生名单姓名中学备注白蒙中央民族大学附属中学符合《同济大学2019年自主招生简章》报名条件6柏荷琳四川省南充高级中学符合《同济大学2019年自主招生简章》报名条件6包青云福建省长汀县第一中学2018年全国中学生生物学联赛(省级赛区)一等奖包赟珺上海市曹杨第二中学符合《同济大学2019年自主招生简章》报名条件6薄仁轩西北师范大学附属中学第34届中国数学奥林匹克三等奖鲍奕凡上海市西南位育中学2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖毕嘉文东北育才学校2018年全国高中数学联赛(省级赛区)一等奖;2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖毕启智郑州外国语新枫杨学校第35届全国中学生物理竞赛复赛(省级赛区)一等奖边靖元天津市静海县第一中学2018年全国中学生生物学联赛(省级赛区)一等奖蔡顾佳上海市奉贤中学符合《同济大学2019年自主招生简章》报名条件6蔡坷呈江苏省扬中高级中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖蔡淼森广州市第二中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖蔡旭昀福建省厦门第一中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖;2016年全国青少年信息学奥林匹克联赛(省级赛区)一等奖蔡彦成西北工业大学附属中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖;第34届全国中学生物理竞赛复赛(省级赛区)一等奖蔡增昕四川省绵阳中学2018年全国中学生生物学联赛(省级赛区)一等奖曹冰长沙麓山国际实验学校2018年全国中学生生物学联赛(省级赛区)一等奖曹佳瑞乌鲁木齐市第一中学2018年全国高中数学联赛(省级赛区)一等奖曹津志四川省成都市石室中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖曹云舒长郡梅溪湖中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖;2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖曾富楠南宁市第三中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖曾延华上海市向明中学符合《同济大学2019年自主招生简章》报名条件6曾奕铭长沙市雅礼中学第32届中国化学奥林匹克(初赛)一等奖曾子沐长沙市雅礼中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖曾子雨福建省厦门第一中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖常可旎邯郸市第一中学2018年全国中学生生物学联赛(省级赛区)一等奖常凌云山西大学附属中学校符合《同济大学2019年自主招生简章》报名条件6常郅坤西安交通大学附属中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖车明远西安市铁一中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖陈贝宁江苏省海门中学2017年全国高中数学联赛(省级赛区)一等奖;2016年全国高中数学联赛(省级赛区)一等奖陈博航福建省厦门第一中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖陈东来大连经济技术开发区第一中学2018年全国中学生生物学联赛(省级赛区)一等奖;第26届全国中学生生物学联赛(省级赛区)一等奖陈飞阳东北师范大学附属中学符合《同济大学2019年自主招生简章》报名条件6陈涵福建省福州第三中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖陈瀚霄成都七中嘉祥外国语学校2018年全国中学生生物学联赛(省级赛区)一等奖陈虹冰大连市第二十四中学第31届中国化学奥林匹克(初赛)(省级赛区)一等奖陈季威莆田第一中学第32届中国化学奥林匹克(初赛)一等奖陈劲鸿福建师范大学附属中学2016年全国青少年信息学奥林匹克联赛(省级赛区)一等奖陈俊宇上海市向明中学符合《同济大学2019年自主招生简章》报名条件6陈楷文上海市松江二中2018年全国中学生生物学联赛(省级赛区)一等奖陈磊上饶中学第32届中国化学奥林匹克(初赛)一等奖陈礼鹏南宁市第二中学符合《同济大学2019年自主招生简章》报名条件6陈龙宇江苏省泰州中学2018年全国高中数学联赛(省级赛区)一等奖陈沛伦同济大学第二附属中学符合《同济大学2019年自主招生简章》报名条件6陈乾安徽省淮南第二中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖陈清扬武汉市第二中学2018年全国中学生生物学联赛(省级赛区)一等奖陈秋泓福建省福州第一中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖陈睿扬福建省福州第一中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖陈申洋长乐第一中学2016年全国青少年信息学奥林匹克联赛(省级赛区)一等奖;2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖陈世年上海市嘉定区第一中学符合《同济大学2019年自主招生简章》报名条件6陈煦阳上海市晋元高级中学符合《同济大学2019年自主招生简章》报名条件6陈宣宇海南中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖;第35届全国中学生物理竞赛决赛三等奖陈依娜绍兴市第一中学2018年全国中学生生物学联赛(省级赛区)一等奖陈奕霖吉林市第一中学校2018年全国高中数学联赛(省级赛区)一等奖陈羿帆延边第二高级中学2018年全国中学生生物学联赛(省级赛区)一等奖;第32届中国化学奥林匹克(初赛)一等奖陈逸凡东北师范大学附属中学第34届全国中学生物理竞赛复赛(省级赛区)一等奖陈音含合肥市第一中学2016年全国青少年信息学奥林匹克联赛(省级赛区)一等奖陈映宣西安高新唐南中学第32届中国化学奥林匹克(初赛)一等奖陈宇轩长沙市雅礼中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖陈昱龙大同市第一中学校2018年全国高中数学联赛(省级赛区)一等奖陈远翔四川省成都市树德中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖陈泽安广州大学附属中学大学城校区第35届全国中学生物理竞赛复赛(省级赛区)一等奖陈振宇海南中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖陈之毅上海市晋元高级中学符合《同济大学2019年自主招生简章》报名条件6陈致远南宁市第二中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖陈洲亮江西省广丰中学2018年全国高中数学联赛(省级赛区)一等奖陈梓柠江西省吉安市第一中学第32届中国化学奥林匹克(初赛)一等奖谌希玥成都市第七中学2018年全国中学生生物学联赛(省级赛区)一等奖成就长郡中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖成以恒上海市行知中学符合《同济大学2019年自主招生简章》报名条件6程泓涛福建省惠安第一中学2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖程琪瑞安徽省利辛县第一中学2018年全国中学生生物学联赛(省级赛区)一等奖程文韬华南师范大学附属中学第32届中国化学奥林匹克(初赛)一等奖程宇轩江西省吉安市白鹭洲中学第32届中国化学奥林匹克(初赛)一等奖池路昊石家庄市第二中学2018年全国中学生生物学联赛(省级赛区)一等奖储继盛大庆市实验中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖褚浩云复旦大学附属中学第32届中国化学奥林匹克(初赛)一等奖褚有骋合肥市第六中学2018年全国中学生生物学联赛(省级赛区)一等奖崔昊然石家庄市第二中学第32届中国化学奥林匹克(初赛)一等奖崔家健西北工业大学附属中学第32届中国化学奥林匹克(初赛)一等奖崔凯天津市新华中学第32届中国化学奥林匹克(初赛)一等奖崔天豪河南省开封高级中学2018年全国高中数学联赛(省级赛区)一等奖崔玉坤佳木斯市第一中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖崔仲杰武汉市第二中学2017年全国高中数学联赛(省级赛区)一等奖崔卓宇山西省实验中学2017年全国高中数学联赛(省级赛区)一等奖;2018年全国高中数学联赛(省级赛区)一等奖代戟锐重庆市第一中学校第35届全国中学生物理竞赛复赛(省级赛区)一等奖代佳雨东莞市东华高级中学第32届中国化学奥林匹克(初赛)一等奖戴力涵福建省泉州第五中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖戴瑞成江苏省海安高级中学符合《同济大学2019年自主招生简章》报名条件6但林涛重庆市第八中学校2018年全国中学生生物学联赛(省级赛区)一等奖邓孟尧重庆市育才中学校2018年全国高中数学联赛(省级赛区)一等奖邓世越长春东师附中青华学校符合《同济大学2019年自主招生简章》报名条件6邓翔益曲靖市第一中学2018年全国高中数学联赛(省级赛区)一等奖邓政东长郡中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖狄一卓山西大学附属中学校2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖丁晨江苏省启东中学第32届中国化学奥林匹克(初赛)一等奖丁帆江西科技学院附属中学第31届中国化学奥林匹克(初赛)(省级赛区)一等奖;第32届中国化学奥林匹克(初赛)一等奖丁豪杰同济大学第二附属中学符合《同济大学2019年自主招生简章》报名条件6丁心如江西省景德镇一中2018年全国高中数学联赛(省级赛区)一等奖董楚阳柳州高级中学2018年全国中学生生物学联赛(省级赛区)一等奖董金宇大连市育明高级中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖董秋霖贵阳市观山湖区第一高级中学第27届全国中学生生物学竞赛三等奖董喆嘉峪关市酒钢三中2018年全国高中数学联赛(省级赛区)一等奖堵瀚文南京师范大学附属中学第32届中国化学奥林匹克(初赛)一等奖杜诚宇江西省宜春市樟树市樟树中学2018年全国高中数学联赛(省级赛区)一等奖杜广昊大庆实验中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖;2018年全国中学生生物学联赛(省级赛区)一等奖杜海阔河南省实验中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖杜皓东营市第一中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖;2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖杜显龙东北师范大学附属中学第32届中国化学奥林匹克(初赛)一等奖杜依頔上海交通大学附属中学嘉定分校2018年全国中学生生物学联赛(省级赛区)一等奖杜雨桐绵阳东辰国际学校符合《同济大学2019年自主招生简章》报名条件6杜哲航成都七中嘉祥外国语学校2017年全国高中数学联赛(省级赛区)一等奖段智允长沙市南雅中学第32届中国化学奥林匹克(初赛)一等奖樊思劼四川省成都市石室中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖范碧珂庆阳市第一中学2018年全国中学生生物学联赛(省级赛区)一等奖范炳煌贵港市高级中学2017年全国高中数学联赛(省级赛区)一等奖范红阳寿光现代中学2018年全国中学生生物学联赛(省级赛区)一等奖范文萱江苏省靖江高级中学符合《同济大学2019年自主招生简章》报名条件6方搏浙江省萧山中学2018年全国中学生生物学联赛(省级赛区)一等奖方若愚成都市第七中学2018年全国高中数学联赛(省级赛区)一等奖方彦皓广州市第六中学2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖;2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖;2016年全国青少年信息学奥林匹克联赛(省级赛区)一等奖封钰震江苏省泰兴中学2018年全国中学生生物学联赛(省级赛区)一等奖冯闰博临汾市第一中学校2018年全国高中数学联赛(省级赛区)一等奖冯思远铜陵市第一中学第32届中国化学奥林匹克(初赛)一等奖冯天昊天津市南大奥宇学校第33届全国中学生物理竞赛复赛(省级赛区)一等奖冯骁四川省成都市树德中学符合《同济大学2019年自主招生简章》报名条件6冯张驰海南中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖;2018年全国高中数学联赛(省级赛区)一等奖冯子卿上海市曹杨中学符合《同济大学2019年自主招生简章》报名条件6符昕芃海南中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖付心雅石河子第一中学2018年全国中学生生物学联赛(省级赛区)一等奖;第27届全国中学生生物学竞赛三等奖傅莲婷浙江省萧山中学2018年全国中学生生物学联赛(省级赛区)一等奖傅子豪福建省厦门双十中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖;2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖甘润霖重庆市巴蜀中学校2018年全国中学生生物学联赛(省级赛区)一等奖高炳元格尔木市第二中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖;第35届全国中学生物理竞赛决赛三等奖高策衡水志臻中学2018年全国中学生生物学联赛(省级赛区)一等奖高继元大连市第八中学第32届中国化学奥林匹克(初赛)一等奖高嘉树西工大附中分校2018年全国中学生生物学联赛(省级赛区)一等奖高铭凯山西大学附属中学校符合《同济大学2019年自主招生简章》报名条件6高天宸山东省淄博第一中学2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖葛定邦福建省龙岩第一中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖龚浏权上海市七宝中学符合《同济大学2019年自主招生简章》报名条件6龚亦飞上海市曹杨第二中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖古进铜陵市第一中学第32届中国化学奥林匹克(初赛)一等奖古亚青郑州外国语学校第35届全国中学生物理竞赛复赛(省级赛区)一等奖古源楷成都市第七中学高新校区2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖谷乙鑫四平市第一高级中学第32届中国化学奥林匹克(初赛)一等奖顾培炎江西省九江第一中学2016年全国青少年信息学奥林匹克联赛(省级赛区)一等奖;第35届全国中学生物理竞赛复赛(省级赛区)一等奖顾一夫江苏省盐城中学第32届中国化学奥林匹克(初赛)一等奖顾钰淇上海市吴淞中学2018年全国中学生生物学联赛(省级赛区)一等奖管弘毅太原市五育中学2018年全国中学生生物学联赛(省级赛区)一等奖郭付育本溪市高级中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖郭健汕头市潮阳实验学校第32届中国化学奥林匹克(初赛)一等奖郭进尧山东省聊城第一中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖郭启源天津英华国际学校第35届全国中学生物理竞赛复赛(省级赛区)一等奖郭雯赣州市第三中学2018年全国高中数学联赛(省级赛区)一等奖郭禹恒上海交通大学附属中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖郭玥昕郑州外国语学校第32届中国化学奥林匹克(初赛)一等奖郭肇洋山西大学附属中学校符合《同济大学2019年自主招生简章》报名条件6韩滨竹乌鲁木齐市第一中学2018年全国高中数学联赛(省级赛区)一等奖韩晨希山西大学附属中学校符合《同济大学2019年自主招生简章》报名条件6韩础均南京师范大学附属中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖韩嘉恒上海市建平中学2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖韩艺林安徽省宿城第一中学第32届中国化学奥林匹克(初赛)一等奖韩易轩大庆实验中学第32届中国化学奥林匹克(初赛)一等奖韩颖湖州市第二中学符合《同济大学2019年自主招生简章》报名条件6郝子腾江苏省昆山中学2018年全国中学生生物学联赛(省级赛区)一等奖何东阳成都市第七中学第32届中国化学奥林匹克(初赛)一等奖何汝欣长郡中学2018年全国中学生生物学联赛(省级赛区)一等奖何奕旸上海市实验学校2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖何益超同济大学第二附属中学符合《同济大学2019年自主招生简章》报名条件6何逸芃南京师范大学附属中学第32届中国化学奥林匹克(初赛)一等奖何泽奇东北师范大学附属中学符合《同济大学2019年自主招生简章》报名条件6何哲君浙江省诸暨中学2018年全国中学生生物学联赛(省级赛区)一等奖何志凌西南大学附属中学校2016年全国青少年信息学奥林匹克联赛(省级赛区)一等奖何梓溶上海交通大学附属中学第32届中国化学奥林匹克(初赛)一等奖贺冰甜鄂尔多斯市第一中学2018年全国中学生生物学联赛(省级赛区)一等奖贺子仪华东师范大学第二附属中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖洪昭洋山西大学附属中学校符合《同济大学2019年自主招生简章》报名条件6侯淳耀山西省实验中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖侯雅玥青海湟川中学2018年全国高中数学联赛(省级赛区)一等奖;第34届中国数学奥林匹克三等奖胡聪睿东北师范大学附属中学符合《同济大学2019年自主招生简章》报名条件6胡国梁江西省九江第一中学2016年全国青少年信息学奥林匹克联赛(省级赛区)一等奖胡倪萍郑州市第一中学2018年全国中学生生物学联赛(省级赛区)一等奖胡圣旸上海市曹杨中学符合《同济大学2019年自主招生简章》报名条件6胡嵩乔江西省高安中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖胡文韬湖北省荆州中学第32届中国化学奥林匹克(初赛)一等奖胡旭林湖南省长沙市第一中学2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖胡玥上海市奉贤中学符合《同济大学2019年自主招生简章》报名条件6花鹏祥安徽省淮北市第一中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖黄澄熙成都树德中学(光华校区)2018年全国青少年信息学奥林匹克联赛(省级赛区)一等奖黄凡珂南宁市第三中学2018年全国中学生生物学联赛(省级赛区)一等奖黄复之上海市控江中学第32届中国化学奥林匹克(初赛)一等奖黄锆闽长沙市明德中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖黄海韵绵阳东辰国际学校符合《同济大学2019年自主招生简章》报名条件6黄宏霖福建省漳平第一中学第32届中国化学奥林匹克(初赛)一等奖黄佳龙江西省宜春市樟树市樟树中学第32届中国化学奥林匹克(初赛)一等奖黄佳兴东北育才学校第32届中国化学奥林匹克(初赛)一等奖黄俊超江苏省启东中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖黄咪瑕贵港市高级中学2018年全国中学生生物学联赛(省级赛区)一等奖黄鹏瑜江西科技学院附属中学2018年全国高中数学联赛(省级赛区)一等奖黄思达唐山市第一中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖黄文浩常州市第一中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖黄忆铭长郡中学2018年全国中学生生物学联赛(省级赛区)一等奖黄友韬江苏省靖江高级中学符合《同济大学2019年自主招生简章》报名条件6黄赵越遵义市第四中学2018年全国高中数学联赛(省级赛区)一等奖黄滋宇四川大学附属中学符合《同济大学2019年自主招生简章》报名条件6纪家灏广州市第二中学2018年全国中学生生物学联赛(省级赛区)一等奖纪然江苏省海安高级中学符合《同济大学2019年自主招生简章》报名条件6季嘉舟江苏省如东高级中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖季萱烨芜湖市第一中学2018年全国中学生生物学联赛(省级赛区)一等奖冀伟河北衡水中学2018年全国高中数学联赛(省级赛区)一等奖贾宇飞长治学院附属太行中学第31届中国化学奥林匹克(初赛)(省级赛区)一等奖;第32届中国化学奥林匹克(初赛)一等奖贾紫仪乌鲁木齐市第一中学2018年全国高中数学联赛(省级赛区)一等奖简文渊江西省宜春市樟树市樟树中学第32届中国化学奥林匹克(初赛)一等奖江海峰四川省绵阳中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖江禹辰南京师范大学附属中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖姜文渊江苏省泰州中学第32届中国化学奥林匹克(初赛)一等奖姜星宇江苏省淮阴中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖姜悦成郑州市第一中学第32届中国化学奥林匹克(初赛)一等奖蒋昌健佳木斯市第一中学2017年全国高中数学联赛(省级赛区)一等奖蒋铭阳成都七中嘉祥外国语学校第35届全国中学生物理竞赛复赛(省级赛区)一等奖蒋婷中央民族大学附属中学符合《同济大学2019年自主招生简章》报名条件6蒋义挥江苏省靖江高级中学符合《同济大学2019年自主招生简章》报名条件6焦芃程哈尔滨市第三中学校群力校区2018年全国中学生生物学联赛(省级赛区)一等奖解晋川山西大学附属中学校符合《同济大学2019年自主招生简章》报名条件6金琨越成都外国语学校2018年全国中学生生物学联赛(省级赛区)一等奖;第27届全国中学生生物学竞赛三等奖金悦越长沙市雅礼中学第32届中国化学奥林匹克(初赛)一等奖金哲思上海市曹杨中学符合《同济大学2019年自主招生简章》报名条件6金正昊常州市第一中学2018年全国中学生生物学联赛(省级赛区)一等奖靳开翔长春东师附中青华学校符合《同济大学2019年自主招生简章》报名条件6康彬广西师范大学附属外国语学校2018年全国中学生生物学联赛(省级赛区)一等奖康洵重庆市第一中学校第32届中国化学奥林匹克(初赛)一等奖柯艾琪上海市曹杨第二中学符合《同济大学2019年自主招生简章》报名条件6孔令涛山东省实验中学第35届全国中学生物理竞赛复赛(省级赛区)一等奖孔子阳江西省鹰潭市第一中学第32届中国化学奥林匹克(初赛)一等奖;第32届中国化学奥林匹克(决赛)三等奖赖佳宏福建省龙岩第一中学2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖赖昱行西南大学附属中学校2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖兰鸿博本溪市高级中学2018年全国高中数学联赛(省级赛区)一等奖兰一川四川省成都市石室中学第34届全国中学生物理竞赛复赛(省级赛区)一等奖;第35届全国中学生物理竞赛复赛(省级赛区)一等奖。
第31届中国数学奥林匹克获奖名单及集训队名单

名次省、姓名性别学校1上海张盛桐男上海市上海中学2吉林于翔宇男吉大附中3安徽孟培坤男马鞍山二中3广东黄峄凡男广东广雅中学3湖北王逸轩男武钢三中6河北杨 远男石家庄二中6江苏韩 啸男南师附中6上海于奕清男华东师范大学第二附属中学6上海鲁一逍男上海市上海中学10湖北段明阳男华中师大一附中11北京赵浩宇男人大附中12广西唐珑珂男南宁市第二中学12北京贾泽宇男人大附中14北京孙 谦男人大附中14湖北傅颢硕男华中师大一附中16北京林一衡男人大附中16重庆郑 洋男重庆巴蜀中学16河北高瑞奇男石家庄二中16河南熊泽都男河南省实验中学16湖南江 朗男长沙市雅礼中学16上海黄小雨男上海市上海中学16四川卢维潇男成都七中16浙江李永亮男乐成寄宿中学24河南朱宇轩男郑州外国语学校24湖北严子恒男武钢三中24浙江吴雨航男宁波市镇海中学27辽宁梁宇辰男东北育才学校27四川方一杰男成都七中嘉祥外国语学校29北京尚正元男人大附中29广东吴天昊男深圳中学29湖北王云崧男黄冈中学第 31 届中国数学奥林匹克获奖名单一等奖(112 人)29湖北郑云汉男襄阳市四中29辽宁孟 响男大连第二十四中29陕西武江铮男西工大附中29天津赵川喆男天津一中36河北解 说女衡水中学36湖北叶胥达男黄冈中学36湖北张嘉琦女华中师大一附中36湖北冯多多男华中师大一附中36辽宁王 瑞男大连育明高中36四川叶 添男成都七中嘉祥外国语学校36浙江滕丁维男乐成寄宿中学43重庆罗子茗男重庆南开中学43福建吴林桐男厦门双十中学43广东曾 琳女华南师范大学附属中学43广东唐山茖男华南师范大学附属中学43贵州卜辰璟男贵阳一中43湖南宋政钦男湖南师大附属中学43湖南左都云男湖南师大附属中学43吉林张博渊男东北师大附中43江苏丁力煌男南京外国语学校43辽宁邓佳蕊女东北育才学校43辽宁孔繁浩男东北育才学校43辽宁苏海舰男辽宁省实验中学43山东贝泰睿男泰安一中43上海梅灵捷男复旦大学附属中学43上海高皓天男上海市上海中学43上海蒋诗琪女上海市上海中学43浙江张劲松男宁波市镇海中学43浙江俞志远男宁波市镇海中学61北京欧阳铭晖男人大附中61广东何天成男华南师范大学附属中学61河北张 祺男衡水中学61湖南邱 添男长沙市雅礼中学61吉林曲梓安男吉大附中61吉林孙伟舰男东北师大附中61上海庄子杰男上海市上海中学61上海顾思远男上海市上海中学61浙江贝思捷女宁波市镇海中学61浙江骆思腾男温州中学71广东郑含之女深圳中学71浙江周俊英男浙江省诸暨中学71浙江蔡天乐男杭州二中74海南郭义销男海南中学74湖南周文杰男湖南师大附属中学74湖南刘其灵男湖南师大附属中学74江苏李煦恒男江苏省扬州中学74山东刘 坤女山东临沂第一中学74上海李欣哲男华东师范大学第二附属中学74上海范峻昊男上海市上海中学74新疆李通宇男乌鲁木齐市第一中学82安徽潘文初男合肥一中82北京邱厚德男人大附中82湖南王文瑞男长沙市雅礼中学82四川陈绪高男成都七中82浙江林 可男温州中学87广东胡颀轩男深圳中学87海南林道哲男海南中学87黑龙江秦家琰男哈三中87黑龙江姜 岩男哈师大附中87吉林李政铎男东北师大附中87吉林郭 鹏男东北师大附中87江苏纪一博男南师附中87江西曾 奕男临川二中87辽宁梁子昂男大连第二十四中87四川彭 淏男成都七中87天津尹嘉晖男天津市耀华中学87浙江徐士奥男乐成寄宿中学87浙江朱峰谷男乐成寄宿中学87浙江黄贤凯男乐成寄宿中学101安徽张淞源男合肥一中101安徽张文昌男合肥一中101福建林 挺男福建师范大学附属中学101广东王迩东男华南师范大学附属中学101河北杨帅杰男石家庄二中101河北张 苏男衡水中学101湖南吴 茁男长沙市雅礼中学101湖南刘恺睿男长沙市雅礼中学101江西黄国正男鹰潭市第一中学101四川罗月桐男成都七中101天津袁弘睿男天津市耀华中学101浙江蔡湘泽男乐成寄宿中学二等奖(124 人)113安徽胡 杨男合肥一中113北京刘 睿男北师大实验中学113广东张心捷男华南师范大学附属中学113河南古家旗男郑州市第一中学113湖北刘鹏飞男武汉二中113湖南谭华为男长沙市长郡中学113湖南刘宇峰男长沙市雅礼中学113吉林王皞琪男东北师范大学附属中学113辽宁李笑东男大连第二十四中113陕西陈嘉昊男西安高新第一中学113陕西陈 煜女西安交大附中113浙江何陶然男杭州二中125北京李冬煜男十一学校125北京黄 巍男北师大实验中学125广东沈城烽男华南师范大学附属中学125广西叶展宏男柳州高级中学125湖南仝方舟男长沙市长郡中学125湖南陈裕丰男长沙市长郡中学125江苏侯霁开男江苏省天一中学125山东倪中一男青岛二中125浙江洪俊伟男温州育英国际实验学校134安徽方晗兵男安徽池州市东至二中134北京彭俊尧男人大附中134北京薛彦钊男人大附中134河北刘天乐男石家庄二中134黑龙江迟舒乘男哈三中134湖北叶文昊男华中师大一附中134湖北崔锦成男华中师大一附中134湖南李文斌男长沙市长郡中学134江西章宇哲男吉安一中134山东常静楠女聊城一中134山西钱晨亮男山西大学附属中学134陕西刘溪恒男西安高新第一中学134陕西侯明荣女西安高新第一中学134上海崔琦文男华东师范大学第二附属中学134四川刘俊松男四川省绵阳中学134天津崔圣宇男天津市南开中学150甘肃胡明源男西北师大附中150河北霍明佳女衡水中学150湖南李师铨男长沙市雅礼中学150吉林于子越男吉大附中150江苏朱煜晨男南京外国语学校150江苏严淳译男江苏省启东中学150江西陈峻松男吉安一中150山东赵俊焱男胜利一中150上海赵轶凡男华东师范大学第二附属中学150上海乐兆颖女华东师范大学第二附属中学150上海贡安琦女上海市上海中学150云南陈致远男云南师大附中150浙江朱民哲男宁波市镇海蛟川书院163安徽王恒屹男安庆一中163北京王啸辰男清华附中163福建叶子逸男厦门双十中学163广东童家宝男中山纪念中学163广东程佳文男深圳中学163湖南肖新宇男长沙市雅礼中学163江西余扬昊男江西师大附中163上海朱昦曈女上海市市北初级中学163新疆张泽安男乌鲁木齐市第一中学163浙江金理泽男杭州学军中学173北京王雪莹女人大附中173重庆王杰文男重庆南开中学173重庆瞿国一男重庆育才中学173福建李 昱男泉州第五中学173福建王明璋男晋江市养正中学173河北杨宇轩男邯郸一中173河南李元泽男郑州市第一中学173湖北范 威男武汉二中173吉林卢旭洋男吉大附中173吉林初炜康男吉大附中173江苏高轶寒女南京外国语学校173江苏杨志强男江苏省姜堰中学173江西卢 健男鹰潭市第一中学173山东李兆林男山东章丘四中173上海冷 涛男华东师范大学第二附属中学173四川刘鹏达男成都外国语学校173浙江肖逸南男杭州二中190北京许鹤凡男北京四中190福建王靖涛男厦门第一中学190甘肃宋德英女西北师大附中190河北李高瞻男石家庄二中190河北李冀维男石家庄二中190黑龙江黄 桢男哈三中190湖北宋英剑男襄阳市四中190四川钟梓源男成都七中198北京孙榕泽男人大附中198北京彭宇辰男北师大实验中学198重庆冯欣宇男重庆巴蜀中学198福建林虹灏男福州第一中学198广东卢瑞彬男华南师范大学附属中学198河南冯润康男郑州外国语学校198江西祝奇文男余江县第一中学198辽宁刘松昆男大连育明高中198辽宁任一诺男大连第二十四中198山东胡家琦男山东省莱芜市第一中学198四川向雍立男成都七中198天津李杰宇男天津南开中学198浙江罗 昊男宁波市镇海中学211福建陈宇凡男厦门双十中学211福建张雨荷女厦门双十中学211广东李 振男深圳外国语学校211广西莫家熙男南宁市第三中学211河南夏 燚男郑州市第一中学211河南黄珮伦男郑州市第一中学211湖北曾御柏男武汉二中211湖北赵乐祺女武钢三中211湖南易晓冬男长沙市第一中学211吉林张湛唯男东北师大附中211江苏吴 昊男江苏省常州高级中学211江苏李正辉男江苏省平潮高级中学211山西屈开儒女运城市康杰中学211陕西宋彦轲男西工大附中211陕西淮泽宇女西安交大附中211四川李为远女成都七中211天津穆禧龙男天津市南开中学211云南高敏博男云南师大附中211浙江苑之宇男杭州二中230北京周展平男人大附中230河南夏萌霏男郑州外国语学校230湖北孙上雯女武钢三中230江苏徐蔡博男江苏省启东中学230上海朱 峰男上海市上海中学230四川冯一倡男成都七中230四川陈奕宏男四川省南充高中三等奖(109 人)237广东齐文轩男深圳中学237贵州王崇宇男遵义市第一高级中学237河南李子健男安阳市第一中学237湖北郑建昊男黄冈中学237江西杨 铖男吉安一中237辽宁毕梦达男辽宁省实验中学237山西张天远男运城市康杰中学237陕西陈百良男西安铁一中237上海沈梓暘男复旦大学附属中学237四川邓心砚男成都七中247安徽于越韬男安徽淮北一中247河北倪行健男石家庄二中247江西蒋瑞辰男九江一中247江西彭 帆男吉安一中247辽宁梁玮达男大连第二十四中247上海徐可涵女上海市上海中学247四川宣涵潇男成都七中247天津李宇轩男天津市耀华中学247天津晏 妮女天津市耀华中学247天津王一然男天津市实验中学247云南徐 恺男云南师大附中258广东叶浩宇女深圳中学258河南梁嘉豪男郑州外国语学校258河南陈徐行男郑州市第一中学258湖北白宇川男华中师大一附中258湖南段剑儒男长沙市雅礼中学258吉林曲江明男东北师大附中258吉林陈 阳男吉大附中258内蒙古高 乾男呼和浩特市第二中学258宁夏寇金润男银川一中258宁夏王卓凡男银川一中258陕西唐家璇男西安高新第一中学258上海吴嘉诚男复旦大学附属中学258上海韩 笑男上海市市北初级中学273北京董 玥女清华附中273福建赖嘉琪女泉州第五中学273甘肃贺智桐男甘肃省兰州第一中学273广东刘 盼女华南师范大学附属中学273黑龙江李无为男大庆一中273湖北涂博威男华中师大一附中273湖南罗文林男湖南师大附属中学273辽宁李沛桐男东北育才学校273宁夏张兴昊男银川二中273四川杨鸿铭男成都七中273四川李奇颗男四川省南充高中273北京夏晨曦男北师大二附中273重庆龙利男重庆巴蜀中学273重庆覃移杭男重庆巴蜀中学273广西奉明璇男柳州高级中学273黑龙江王浩程男哈三中273黑龙江韩昊辰男哈师大附中273黑龙江史宇辰男哈师大附中273黑龙江毛宇鹏男大庆一中273吉林张天昊男吉大附中273吉林于 卓男东北师范大学附属中学273吉林于钟博男吉大附中273江西彭奕涛男南昌二中273江西彭逸凡男江西省景德镇一中273山东张浩哲男山东省实验中学273山西潘 杰男太原五中273陕西侯谷庾男西安高新第一中学273陕西吉宇轩男西安高新第一中学273陕西王一涵男西工大附中273四川马润杰男四川省绵阳中学273四川周 洋男四川省绵阳中学273天津李峪林男天津市耀华中学273天津于蕴晨女天津一中273西藏王一琪女西藏民大附中273新疆石宜民男乌鲁木齐市第七十中学273云南李筱航男云南师大附中309安徽王海涵男安徽淮北一中309北京卢丹葳女北师大实验中学309重庆宋金峰男重庆巴蜀中学309重庆廖铁犁男重庆南开中学309重庆席子涵男重庆南开中学309重庆曾俊齐男重庆南开中学309重庆孙鸿蕊女重庆南开中学309重庆邓嵎木男西南大学附属中学309重庆马辛宇男重庆一中309甘肃付泽邦男西北师大附中309甘肃王镜权男甘肃省兰州第一中学309广东邓海航男深圳市高级中学309贵州刘赞辉男贵阳一中309贵州武洪锐男贵阳一中309海南陈太毅男海南中学309海南冯思钦男海南中学309河北张俊豪男衡水中学309黑龙江滕 飞男大庆外国语学校309江苏马行宇男江苏省淮阴中学309内蒙古吴 涛男鄂尔多斯市一中309内蒙古于心蕊女赤峰四中309内蒙古丁 力男赤峰二中309宁夏石文江男固原一中309青海吴俊辰男青海湟川中学309青海王悦翔男青海湟川中学309青海桑宇晨男青海油田一中309青海肖睿轩男青海湟川中学309山东韩增瑞男山东省泰安第一中学309山西贾泽军男山西大学附属中学309山西高凯龙男长治二中309陕西王乙成男西安交大附中309上海周毅皓男华东师范大学第二附属中学309西藏李 瑜女林芝市第一中学309西藏魏林巍男林芝市第一中学309西藏王雪蕾女林芝市第一中学309新疆蔡敬斌男乌鲁木齐市第一中学309新疆李佳玉女乌鲁木齐市第一中学。
2019年自主招生初审通过名单公示
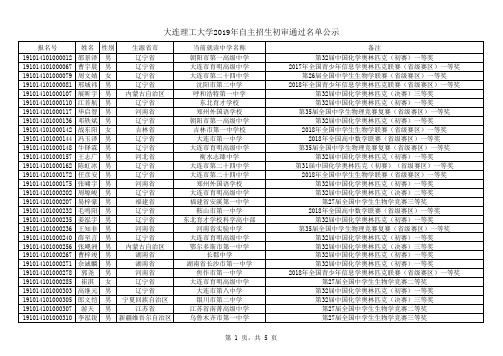
东北育才学校 郑州外国语学校 朝阳市第一高级中学 吉林市第一中学校 大连市第一中学 大连市育明高级中学 衡水志臻中学 大连市第二十四中学 大连市第二十四中学 郑州外国语学校 大连市育明高级中学 福建省安溪第一中学 鞍山市第一中学 东北育才学校科学高中部 河南省实验中学 大连市育明高级中学 鄂尔多斯市第一中学
191014101000110 江首航 男
辽宁省
191014101000117 毕启智 男
河南省
191014101000136 邓轶斌 男
辽宁省
191014101000142 战东阳 女
吉林省
191014101000144 冯玉泽 男
辽宁省
191014101000148 牛铎霖 男
辽宁省
191014101000157 王志广 男
河北省
191014101000162 陈虹冰 男
辽宁省
191014101000172 任彦安 男
辽宁省
191014101000175 张啸宇 男
河南省
191014101000202 周塬峻 男
辽宁省
191014101000207 易梓豪 男
福Байду номын сангаас省
191014101000232 毛鸣阳 男
辽宁省
191014101000235 姜泓宇 男
第32届中国化学奥林匹克(初赛)一等奖 2018年全国中学生生物学联赛(省级赛区)一等奖 2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖 2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖
第27届全国中学生生物学竞赛三等奖 2017年全国青少年信息学奥林匹克联赛(省级赛区)一等奖
历届女子数学奥林匹克试题

目录2002年女子数学奥林匹克 (1)2003年女子数学奥林匹克 (3)2004年女子数学奥林匹克 (5)2005年女子数学奥林匹克 (7)2006年女子数学奥林匹克 (9)2007年女子数学奥林匹克 (11)2008年女子数学奥林匹克 (13)2009年女子数学奥林匹克 (16)2010年女子数学奥林匹克 (19)2011年女子数学奥林匹克 (21)2012年女子数学奥林匹克 (24)2002年女子数学奥林匹克1.求出所有的正整数n,使得20n+2能整除2003n+2002.2.夏令营有3n(n是正整数)位女同学参加,每天都有3位女同学担任执勤工作.夏令营结束时,发现这3n位女同学中的任何两位,在同一天担任执勤工作恰好是一次.(1)问:当n=3时,是否存在满足题意的安排?证明你的结论;(2)求证:n是奇数.3.试求出所有的正整数k,使得对任意满足不等式k(aa+ab+ba)>5(a2+a2+b2)4.⊙O1和⊙O2相交于B、C两点,且BC是⊙O1的直径.过点C作⊙O1的切线,交⊙O2于另一点A,连结AB,交⊙O1于另一点E,连结CE并延长,交⊙O2于点F.设点H为线段AF内的任意一点,连结HE并延长,交⊙O1于点G,连结BG并延长,与AC的延长线交于点D.求证:AA AH=AA AC.5.设P1,P2,⋯,P n(n≥2)是1,2,⋯,n的任意一个排列.求证:1P1+P2+1P2+P3+⋯+1P n−2+P n−1+1P n−1+P n>n−1n+2.6.求所有的正整数对(x,y),满足x y=y x−y.7.锐角△ABC的三条高分别为AD、BE、CF.求证:△DEF的周长不超过△ABC周长的一半.8.设A1,A2,⋯,A8是平面上任意取定的8个点,对平面上任意取定的一条有向直线l,设A1,A2,⋯,A8在该直线上的摄影分别是P1,P2,⋯,P8.如果这8个射影两两不重合,以直线l的方向依次排列为P i1,P i2,⋯,P i8,这样,就得到了1,2,…,8的一个排列i1,i2,⋯,i8(在图1中,此排列为2,1,8,3,7,4,6,5).设这8个点对平面上所有有向直线作射影后,得到的不同排列的个数为N8=N(A1,A2,⋯88的最大值.图12003年女子数学奥林匹克1. 已知D 是△ABC 的边AB 上的任意一点,E 是边AC 上的任意一点,连结DE ,F 是线段DE 上的任意一点.设AC AA =x ,AA AA =y ,CH CA =z .证明: (1) S △ACH =(1−x )yzS △AAA ,S △AAH =x (1−y )(1−z )S △AAA ;(2) �S △ACH 3+�S △AAH 3≤�S △AAA 3.2. 某班有47个学生,所用教室有6排,每排有8个座位,用(i ,j )表示位于第i 排第j 列的座位.新学期准备调整座位,设某学生原来的座位为(i ,j ),如果调整后的座位为(m ,n ),则称该生作了移动[a ,a ]=[i −m ,j −n ],并称a +b 为该生的位置数.所有学生的位置数之和记为S .求S 的最大可能值与最小可能值之差.3. 如图1,ABCD 是圆内接四边形,AC 是圆的直径,BB ⊥AA ,AC 与BD 的交点为E ,F 在DA 的延长线上.连结BF ,G 在BA 的延长线上,使得BD ∥BB ,H 在GF 的延长线上,AC ⊥DB .证明:B 、E 、F 、H 四点共圆.图14.(1)证明:存在和为1的5个非负实数a、b、c、d、e,使得将它们任意放置在一个圆周上,总有两个相邻数的乘积不小于19;(2)证明:对于和为1的任意玩个非负实数a、b、c、d、e,总可以将它们适当放置在一个圆周上,且任意相邻两数的乘积均不大于19.5.数列{a n}定义如下:a1=2,a n+1=a n2−a n+1,n=1,2,⋯.证明:1−120032003<1a1+1a2+⋯+1a2003<1.6.给定正整数n(n≥2).求最大的实数λ,使得不等式a n2≥λ(a1+a2+⋯+a n−1)+2a n对任意满足a1<a2⋯<a n的正整数a1,a2,⋯,a n均成立.7.设△ABC的三边长分别为AB=b、BA=a、AA=a,a、b、c互不相等,AD、BE、CF分别为△ABC的三条内角平分线,且DE=DF.证明:(1)a b+c=b c+a+c a+b;(2)∠BAA>90°.8.对于任意正整数n,记n的所有正约数组成的集合为S n.证明:S n中至多有一半元素的个位数为3.2004年女子数学奥林匹克1.如果存在1,2,⋯,n的一个排列a1,a2,⋯,a n,使得k+a k(k=1,2,⋯,n)都是完全平方数,则称n为“好数”.问:在集合{11,13,15,17,19}中,哪些是“好数”,哪些不是“好数”?说明理由.(苏淳供题)2.设a、b、c为正实数.求a+3c a+2b+c+4b a+b+2c−8c a+b+3c的最小值.(李胜宏供题)3.已知钝角△ABC的外接圆半径为1.证明:存在一个斜边长为√2+1的等腰直角三角形覆盖△ABC.(冷岗松供题)4.一副三色纸牌,共有32张,其中红黄蓝每种颜色的牌各10张,编号分别是1,2,⋯,10;另有大小王牌各一张,编号均为0.从这副牌中任取若干张牌,然后按如下规则计算分值:每张编号为k的牌记为2k分.若它们的分值之和为2004,则称这些牌为一个“好牌组”.试求“好牌组”的个数.(陶平生供题)5.设u、v、w为正实数,满足条件u√vv+v√vu+v√uv≥1.试求u+v+v的最小值. (陈永高供题)6.给定锐角△ABC,点O为其外心,直线AO交边BC于点D.动点E、F分别位于边AB、AC上,使得A、E、D、F四点共圆.求证:线段EF在边BC上的投影的长度为定值.(熊斌供题)7.已知p、q为互质的正整数,n为非负整数.问:有多少个不同的整数可以表示为ii+jj的形式,其中i,j为非负整数,且i+j≤n.(李伟固供题)8.将一个3×3的正方形的四个角上各去掉一个单位正方形所得到的图形称为“十字形”.在一个10×11的棋盘上,最多可以放置多少个互不重叠的“十字形”(每个“十字形”恰好盖住棋盘上的5个小方格)?(冯祖明供题)2005年女子数学奥林匹克1.如图1,点P在△ABC的外接圆上,直线CP、AB相交于点E,直线BP、AC相交于点F,边AC的垂直平分线与边AB相交于点J,边AB的垂直平分线与边AC相交于点K.求证:AA2AH=AA⋅AA AA⋅AH.图1(叶中豪供题)2.求方程组�5�x+1x�=12�y+1y�=13(z+1z)xy+yz+zx=1,的所有实数解.(朱华伟供题)3.是否存在这样的凸多面体,它共有8个顶点、12条棱和6个面,并且其中有4个面,每两个面都有公共棱?(苏淳供题)4.求出所有的正实数a,使得存在正整数n及n个互不相交的无限整数集合A1,A2,⋯,A n满足A1∪A2∪⋯∪A n=Z,而且对于每个A i中的任意两数b>c,都有a−b≥a i.(袁汉辉供题)5.设正实数x、y满足x3+y3=x−y.求证:x2+4y2<1. (熊斌供题)6.设正整数n(n≥3).如果在平面上有n个格点P1,P2,⋯,P n满足:当�P i P j�为有理数时,存在P k,使得|P i P k|和�P j P k�均为无理数;当�P i P j�为无理数时,存在P k,使得|P i P k|和�P j P k�均为有理数,那么,称n是“好数”.(1)求最小的好数;(2)问:2005是否为好数(冯祖明供题)7.设m、n是整数,m>n≥2,S=�1,2,⋯,m�,T=�a1,a2,⋯,a n�是S的一个子集.已知T中的任两个数都不能同时整除S中的任何一个数.求证:1a1+1a2+⋯+1a n<m+n m. (张同君供题)8.给定实数a、b(a>a>0),将长为a、宽为b的矩形放入一个正方形内(包含边界).问正方形的边至少为多长?(陈永高供题)2006年女子数学奥林匹克1.设a>0,函数f:(0,+∞)→R满足f(a)=1.如果对任意正实数x、y,有f(x)f(y)+f�a x�f�a y�=2f(xy),求证:f(x)为常数.(朱华伟供题)2.设凸四边形ABCD的对角线交于点O.△OAD、△OBC的外接圆交于点O、M,直线OM分别交△OAB、△OCD的外接圆于点T、S.求证:M是线段TS的中点.(叶中豪供题)3.求证:对i=1,2,3,均有无穷多个正整数n,使得n,n+2,n+28中恰有i个可表示为三个正整数的立方和.(袁汉辉供题)4.8个人参加一次聚会.(1)如果其中任何5个人中都有3个人两两认识,求证:可以从中找出4个人两两认识;(2)试问:如果其中任何6个人中都有3个人两两认识,那么是否一定可以找出4个人两两认识?(苏淳供题)5.平面上整点集S=�(a,a)�1≤a,a≤5(a、a∈Z)�,T为平面上一整点集,对S中任一点P,总存在T中不同于P的一点Q,使得线段PQ上除点P、Q外无其它的整点.问T的元素个数最少为多少?(陈永高供题)6.设集合M={1,2,⋯,19},A={a1,a2,⋯,a k}⊆M.求最小的k,使得对任意的a∈M,存在a i、a j∈A,满足a=a i或a=a i±a j(a i、a j 可以相同).(李胜宏供题)7.设x i>0(i=1,2,⋯,n),k≥1.求证:∑11+x i n i=1⋅∑x i n i=1≤∑x i k+11+x i n i=1⋅∑1x i k n i=1. (陈伟固供题)8.设p为大于3的质数,求证:存在若干个整数a1,a2,⋯,a t满足条件−p2<a1<a2<⋯<a t<p2,使得乘积p−a1|a1|⋅p−a2|a2|⋅⋯⋅p−a t|a t|是3的某个正整数次幂.(纪春岗供题)2007年女子数学奥林匹克1.设m为正整数,如果存在某个正整数n,使得m可以表示为n和n的正约数个数(包括1和自身)的商,则称m是“好数”.求证:(1)1,2,⋯,17都是好数;(2)18不是好数.(李胜宏供题)2.设△ABC是锐角三角形,点D、E、F分别在边BC、CA、AB上,线段AD、BE、CF经过△ABC的外心O.已知以下六个比值AC CA、AA AA、AH HA、AH HA、AA AA、AC CA中至少有两个是整数.求证:△ABC是等腰三角形.(冯祖明供题)3.设整数n(n>3),非负实数a1,a2,⋯,a n满足a1+a2+⋯+a n=2.求a1a22+1+a2a32+1+⋯+a n a12+1的最小值.(朱华伟供题)4.平面内n(n≥3)个点组成集合S,P是此平面内m条直线组成的集合,满足S关于P中每一条直线对称.求证:m≤n,并问等号何时成立?(边红平供题)5.设D是△ABC内的一点,满足∠BAA=∠BAA=30°,∠BBA=60°,E是边BC的中点,F是边AC的三等分点,满足AF=2FC.求证:BD⊥DB.(叶中豪供题)6.已知a、a、b≥0,a+a+b=1.求证:�a+14(a−b)2+√a+√b≤√3(李伟固供题)7.给定绝对值都不大于10的整数a、b、c,三次多项式f(x)=x3+ ax2+ax+b满足条件�f(2+√3)�<0.0001.问:2+√3是否一定是这个多项式的根?(张景中供题)8.n个棋手参加象棋比赛,每两个棋手比赛一局.规定:胜者得1分,负者得0分,平局得0.5分.如果赛后发现任何m个棋手中都有一个棋手胜了其余m-1个棋手,也有一个棋手输给了其余m-1个棋手,就称此赛况具有性质P(m).对给定的m(m≥4),求n的最小值f(m),使得对具有性质P(m)的任何赛况,都有所有n名棋手的得分各不相同.(王建伟供题)2008年女子数学奥林匹克1.(1)问能否将集合�1,2,⋯,96�表示为它的32个三元子集的并集,且每个三元子集的元素之和都相等;(2)问能否将集合�1,2,⋯,99�表示为它的33个三元子集的并集,且每个三元子集的元素之和都相等.(刘诗雄供题)2.已知式系数多项式ϕ(x)=ax3+ax2+bx+d有三个正根,且ϕ(0)<0.求证:2a3+9a2d−7aab≤0. (朱华伟供题)3.求最小常数a(a>1),使得对正方形ABCD内部任一点P,都存在△P AB、△PBC、△PCD、△PDA中的某两个三角形,其面积之比属于区间�a−1,a�.(李伟固供题)4.在凸四边形ABCD的外部分别作正△ABQ、△BCR、△CDS、△DAP,记四边形ABCD的对角线的和为x,四边形PQRS的对角线中点连线的和为y.求y x的最大值.(熊斌供题)5.如图1,已知凸四边形ABCD满足AB=BC,AD=DA,E、F分别是线段AB、AD上一点,满足B、E、F、D四点共圆,作△DPE顺向相似于△ADC,作△BQF顺向相似于△ABC.求证:A、P、Q三点共线.图1 注:两个三角形顺向相似是指它们的对应顶点同按顺时针方向或同按逆时针方向排列.(叶中豪 供题)6. 设正数列x 1,x 2,⋯,x n ,⋯满足(8x 2−7x 1)x 17=8及x k+1x k−1−x k 2=x k−18−x k 8(x k x k−1)7(k ≥2).求正实数a ,使得当x 1>a 时,有单调性x 1>x 2>⋯>x n >⋯,当0<x 1<a 时,不具有单调性. (李胜宏 供题)7. 给定一个2008×2008的棋盘,棋盘上每个小方格的颜色均不相同.在棋盘的每一个小方格中填入C 、G 、M 、O 这4个字母中的一个,若棋盘中每一个2×2的小棋盘中都有C 、G 、M 、O 这4个字母,则称这个棋盘为“和谐棋盘”,问有多少种不同的和谐棋盘?(冯祖明 供题)8. 对于正整数n ,令f n =�2n √2008�+[2n √2009].求证:数列f 1,f 2,⋯中有无穷多个奇数和无穷多个偶数([x ]表示不超过实数x 的最大整数).(冯祖明 供题)B2009年女子数学奥林匹克1. 求证:方程aab =2009(a +a +b )只有有限组正整数解(a,b,c).(梁应德 供题)2. 如图1,在△ABC 中,∠BAA =90°,点E 在△ABC 的外接圆圆Γ的弧BC (不含点A )内,AE >EC .连结EC 并延长至点F ,使得∠DAA =∠AAB ,连结BF 交圆Γ于点D ,连结ED ,记△DEF 的外心为O .求证:A 、C 、O 三点共线.图1 (边红平 供题)3. 在平面直角坐标系中,设点集�P 1,P 2,⋯,P 4n+1�=�(x ,y )�x 、y 为整数,|x |≤n ,|y |≤n ,xy =0�,其中,n ∈N +.求(P 1P 2)2+(P 2P 3)2+⋯+(P 4n P 4n+1)2+(P 4n+1P 1)2的最小值.(王新茂 供题)4. 设平面上有n (n ≥4)个点V 1,V 2,⋯,V n ,任意三点不共线,某些点之间连有线段.把标号分别为1,2,⋯,n 的n 枚棋子放置在这n 个点处,每个点处恰有一枚棋子.现对这n 枚棋子进行如下操作:每B次选取若干枚棋子,将它们分别移动到与自己所在点有线段相连的另一个点处;操作后每点处仍恰有一枚棋子,并且没有两枚棋子在操作前后交换位置.若一种连线段的方式使得无论开始时如何放置这n 枚棋子,总能经过有限次操作后,使每个标号为k (k =1,2,⋯,n )的棋子在点V k 处,则称这种连线段的方式为“和谐的”.求在所有和谐的连线段的方式中,线段数目的最小值. (付云皓 供题)5. 设实数xyz 大于或等于1.求证:(x 2−2x +2)(y 2−2y +2)(z 2−2z +2)≤(xyz )2−2xyz +2 (熊 斌 供题)6. 如图2,圆Γ1、Γ2内切于点S ,圆Γ2的弦AB 与圆Γ1切于点C ,M 是弧AB (不含点S )的中点,过点M 作MN ⊥AB ,垂足为N .记圆Γ1的半径为r .求证:AA ⋅AB =2rMN .图2 (叶中豪 供题)7. 在一个10×10的方格表中有一个有4n 个1×1的小方格组成的图形,它既可被n 个“”型的图形覆盖,也可被n 个“”或“”型(可以旋转)的图形覆盖.求正整数n的最小值.(朱华伟供题)8.设a n=n√5−�n√5�.求数列a1,a2,⋯,a2009中的最大项和最小项,其中,[x]表示不超过实数x的最大整数.(王志雄供题)2010年女子数学奥林匹克1. 给定整数n (n ≥3),设A 1,A 2,⋯,A 2n 是集合�1,2,⋯,n�的两两不同的非空子集,记A 2n+1=A 1.求∑|A i ∩A i+1||A i |⋅|A i+1|2n i=1的最大值.(梁应德 供题)2. 如图1,在△ABC 中,AB =AA ,D 是边BC 的中点,E 是在△ABC 外一点,满足AD ⊥AB ,BD =BB .过线段BE 的中点M 作直线MB ⊥BD ,交△ABD 的外接圆的劣弧AD 于点F .求证:DB ⊥BB .图1 (郑焕 供题)3. 求证:对于每个正整数n ,都存在满足下面三个条件的质数p 和整数m :(1)i ≡5(mmd 6);(2)i ∤n ;(3)n ≡m 3(mmd i ).(付云皓 供题) 4. 设实数x 1,x 2,⋯,x n 满足∑x i 2=1(n ≥2)n i=1.求证:∑(1−k ∑ix i 2n i=1)2x k 2k n k=1≤(n−1n+1)2∑x k 2k n k=1,并确定等号成立的条件.(李胜宏供题)5.已知f(x)、g(x)都是定义在R上递增的一次函数,f(x)为整数当且仅当g(x)为整数.证明:对一切x∈R,f(x)−g(x)为整数.(刘诗雄供题)6.如图2,在锐角△ABC中,AB>AA,M为边BC的中点,∠BAA的外角平分线交直线BC于点P.点K、F在直线P A上,使得MB⊥BA,MM⊥PA.求证:BC2图2(边红平供题)7.给定正整数n(n≥3).对于1,2,⋯,n的任意一个排列P=(x1,x2,⋯,x n),若i<j<k,则称x j介于x i和x k之间(如在排列(1,3,2,4)中,3介于1和4之间,4不介于1和2之间).设集合S={P1,P2,⋯,P m}的每个元素P i(1≤i≤m)中都不介于另外两个数之间.求m的最大值.(冯祖鸣供题)8.试求满足下列条件的大于5的最小奇数a:存在正整数m1、n1、m2、n2,使得a=m12+n12,a2=m22+n22,且m1−n1=m2−n2.(朱华伟供题)2011年女子数学奥林匹克1.求出所有的正整数n,使得关于x,y的方程1x+1y=1n恰有2011组满足x≤y的正整数解(x,y) .(熊斌供题)2.如图1,在四边形ABCD的对角线AC与BD相交于点E,边AB、CD的中垂线相交于点F,点M、N分别为边AB、CD的中点,直线EF分别与边BC、AD相交于点P、Q,若MB⋅AB=NB⋅AB, BQ⋅BP=AQ⋅AP,求证:PQ垂直于BC.图1(郑焕供题)3.设正数a,a,b,d满足aabd=1,求证:1+1+1+1+9≥25(朱华伟供题)4.有n(n≥3)名乒乓球选手参加循环赛,每两名选手之间恰好比赛一次(比赛无平局).赛后发现,可以将这些选手排成一圈,使得对于任意三名选手A,B,C,若A,B在圈上相邻,则A,B中至少有一人战胜了C,求n的所有可能值.(付云皓供题)5.给定非负实数a,求最小实数f=f(a),使得对任意复数,Z1,Z2和实数x(0≤x≤1),若|Z1|≤a|Z1−Z2|,则|Z1−xZ2|≤f|Z1−Z2|.(李胜宏供题)6.是否存在正整数m,n,使得m20+11n是完全平方数?请予以证明.(袁汉辉供题)7.从左到右编号为B1,B2,⋯,B n的n个盒子共装有n个小球,每次可以选择一个盒子B k,进行如下操作:若k=1且B1中至少有1个小球,则可从B1中移1个小球至B2中;若k=n,且B n中至少有1个小球,则可从B n中移1个小球至B n-1中,若2≤k≤n-1且B k中至少有2个小球,则可从B k中分别移1个小球至B k-1和B k+1中,求证:无论初始时这些小球如何放置,总能经过有限次操作使得每个盒子中恰有1个小球.(王新茂供题)8. 如图2,已知⊙O 为△ABC 中BC 边上的旁切圆,点D 、E 分别在线段AB 、AC 上,使得BD ∥BA .⊙O 1为△ADE 的内切圆,O 1B 交DO 于点F ,O 1C 交EO 于点G .⊙O 切BC 于点M .⊙O 1切DE 于点N .求证:MN 平分线段FG .图2 (边红平 供题)A2012年女子数学奥林匹克1.设a1,a2,⋯,a n为非负实数,求证:11+a1+a1(1+a1)(1+a2)+⋯+ a1a2⋯a n−1(1+a1)(1+a2)⋯(1+a n)≤1.2.如图1所示,圆O1和O2外切于点T,点A、E在圆O1上,AB切圆O2于点B,ED切圆O2于点D,直线BD、AE交于点P.(1)求证:AB⋅DT=AT⋅DB;(2)求证:∠ATP+∠DTP=180°Array图13.求所有整数对(a,b),使得存在整数d>1,对任意的正整数n,都有d|a n+a n+1.4.在正十三边形的13个顶点上各摆放一枚黑子或者白子,一次操作是指将两枚棋子的位置交换.求证:无论开始时棋子是如何摆放的,总可以至多操作一次,使得各个棋子的颜色关于正十三边形的某一条对称轴是对称的.5.如图2所示,在△ABC中,I为内切圆圆心,D、E分别为AB、AC边上的切点,O为△BIC的外心,求证:∠OBB=∠ODA.图26. 某个国家有n (n ≥3)个城市,每两个城市间都有一条双向航线.这个国家有两个航空公司,每条航线由一家公司经营.一个女数学家从某个城市出发,经过至少两个其它城市,回到出发地.如果无论怎样选择出发城市和路径,都无法只乘坐一家公司的航班,求n 的最大值.7. 有一个无穷项的正整数数列a 1≤a 2≤a 3≤⋯.已知存在正整数k和r ,使得r a r =k +1,求证:存在正整数s ,使得s a s =k .8. 集合{0,1,2,⋯,2012}中有多少个元素k ,使得A 2012k 是2012的倍数.B。
