第十五单元线性回归
高一数学必修线性回归分析知识点

⾼⼀数学必修线性回归分析知识点 分析按照⾃变量和因变量之间的关系类型,可分为线性回归分析和⾮线性回归分析。
下⾯是店铺给⼤家带来的⾼⼀数学必修线性回归分析知识点,希望对你有帮助。
⾼⼀数学线性回归分析知识点总结(⼀) 重点难点讲解: 1.回归分析: 就是对具有相关关系的两个变量之间的关系形式进⾏测定,确定⼀个相关的数学表达式,以便进⾏估计预测的统计分析⽅法。
根据回归分析⽅法得出的数学表达式称为回归⽅程,它可能是直线,也可能是曲线。
2.线性回归⽅程 设x与y是具有相关关系的两个变量,且相应于n组观测值的n个点(xi, yi)(i=1,......,n)⼤致分布在⼀条直线的附近,则回归直线的⽅程为。
其中 。
3.线性相关性检验 线性相关性检验是⼀种假设检验,它给出了⼀个具体检验y与x之间线性相关与否的办法。
①在课本附表3中查出与显著性⽔平0.05与⾃由度n-2(n为观测值组数)相应的相关系数临界值r0.05。
②由公式,计算r的值。
③检验所得结果 如果|r|≤r0.05,可以认为y与x之间的线性相关关系不显著,接受统计假设。
如果|r|>r0.05,可以认为y与x之间不具有线性相关关系的假设是不成⽴的,即y与x之间具有线性相关关系。
典型例题讲解: 例1.从某班50名学⽣中随机抽取10名,测得其数学考试成绩与物理考试成绩资料如表:序号12345678910数学成绩54666876788285879094,物理成绩61806286847685828896试建⽴该10名学⽣的物理成绩对数学成绩的线性回归模型。
解:设数学成绩为x,物理成绩为,则可设所求线性回归模型为, 计算,代⼊公式得 ∴所求线性回归模型为=0.74x+22.28。
说明:将⾃变量x的值分别代⼊上述回归模型中,即可得到相应的因变量的估计值,由回归模型知:数学成绩每增加1分,物理成绩平均增加0.74分。
⼤家可以在⽼师的帮助下对⾃⼰班的数学、化学成绩进⾏分析。
《线性回归》PPT课件_OK

7
8
读取数据
• 在R环境下将数据读入系统并显示,使用如下语句:
9
数据的概括性度量
• R语句:
10
变量间相关性分析
• R语句:
11
• R语句: plot(a1$ROEt,a1$ROE)
12
模型的建立
模型、假设和参数估计
13
模型形式及假设
• 线性回归模型
y • i模 型假0 设 1 x i1 2 x i2 p x i pi
异方差性、非正态性、异常值
24
同方差性检验
25
同方差性检验
26
同方差性检验
27
同方差性检验
28
正态性检验
• 若t ~N(,2), 并且
• 则有 Pt q
Ptq
29
正态性检验
• 进一步可以得到
• 以及
q
z,
q z. • 所以在正态性假设下,残差 与 应该成线性关系。
t z
30
正态性检验
Ttnp1,1/2
21
22
显著性检验的结论
• 从F检验的结果看,模型的线性关系是显著的。 • 从T检验的结果看,ROEt和LEV两个变量通过了检验,GROWTH变量在
显著性水平降至0.1时也可以通过检验,因此这三个变量与因变量的线性 关系较为显著。
• 注意,这不说明应该删除其它变量!
23
模型的诊断
反映公司利润状况
• GROWTH: 主营业务增长率(sales growth rate)
反映公司已实现的当年增长率
• INV: 存货/资产总计(inventory to asset ratio)
反映公司的存货状况
线性回归计算方法及公式课件

• adjR2最大: adjR2=1-MS误差/ MS总
• Cp值最小 Cp=(n-p-1)(MS误差.p/MS误差.全部-1)+(p+1)
线性回归计算方法及公式
14
选择变量的方法
• 最优子集回归分析法: p个变量有2p-1个方程
• 逐步回归分析 向前引入法(forward selection) 向后剔除法(backward selection) 逐步引入-剔除法(stepwise selection) H0:K个自变 量为好 H1:K+1个自变量为好
线性回归计算方法及公式
9
回归分析中的若干问题
• 资料要求:总体服从多元正态分布。但实际工 作中分类变量也做分析。
• n足够大,至少应是自变量个数的5倍 • 分类变量在回归分析中的处理方法
有序分类: 治疗效果:x=0(无效 ) x=1(有效) x=2(控制) 无序分类:
有k类,则用k-1变量(伪变量)
线性回归计算方法及公式
25
一般地,设某事件D发生(D=1)的概率P依 赖于多个自变量(x1,x2, …,xp),且
P(D=1)=e Bo+B1X1+…+BpXp /(1+e Bo+B1X1+…+BpXp )
或
Logit(P) = Bo+B1X1+…+Bp X p
则称该事件发生的概率与变量间关系符合多元 Logistic回归或对数优势线性回归。
线性回归计算方法及公式
27
Logistic回归的参数估计
• Logistic回归模型的参数估计常用最大似然法,最大似然法的基本思想是先 建立似然函数或对数似然函数,似然函数或对数似然函数达到极大时参数的 取值,即为参数的最大似然估计值。其步骤为对对数似然函数中的待估参数 分别求一阶偏导数,令其为0得一方程组,然后求解。由于似然函数的偏导 数为非线性函数,参数估计需用非线性方程组的数值法求解。常用的数值法 为Newton-Raphson法。不同研究的设计方案不同,其似然函数的构造略有 差别,故Logistic回归有非条件Logistic回归与条件Logistic回归两种。
线性回归分析的基本步骤
线性回归分析的基本步骤步骤一、建立模型知识点:1、总体回归模型、总体回归方程、样本回归模型、样本回归方程 ①总体回归模型:研究总体之中自变量和因变量之间某种非确定依赖关系的计量模型。
Y X U β=+特点:由于随机误差项U 的存在,使得Y 和X 不在一条直线/平面上。
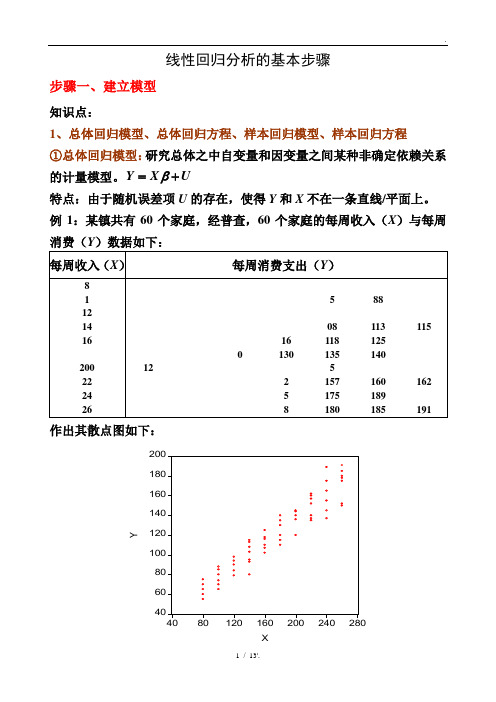
例1:某镇共有60个家庭,经普查,60个家庭的每周收入(X )与每周消费(Y )数据如下:作出其散点图如下:②总体回归方程(线):由于假定0EU =,因此因变量的均值与自变量总处于一条直线上,这条直线()|E Y X X β=就称为总体回归线(方程)。
总体回归方程的求法:以例1的数据为例 由于01|i i i E Y X X ββ=+,因此任意带入两个X i 和其对应的E (Y |X i )值,即可求出01ββ和,并进而得到总体回归方程。
如将()()222777100,|77200,|137X E Y X X E Y X ====和代入()01|i i i E Y X X ββ=+可得:01001177100171372000.6ββββββ=+=⎧⎧⇒⎨⎨=+=⎩⎩以上求出01ββ和反映了E (Y |X i )和X i 之间的真实关系,即所求的总体回归方程为:()|170.6i i i E Y X X =+,其图形为:③样本回归模型:总体通常难以得到,因此只能通过抽样得到样本数据。
如在例1中,通过抽样考察,我们得到了20个家庭的样本数据:那么描述样本数据中因变量Y 和自变量X 之间非确定依赖关系的模型ˆY X e β=+就称为样本回归模型。
④样本回归方程(线):通过样本数据估计出ˆβ,得到样本观测值的拟合值与解释变量之间的关系方程ˆˆY X β=称为样本回归方程。
如下图所示:⑤四者之间的关系:ⅰ:总体回归模型建立在总体数据之上,它描述的是因变量Y 和自变量X 之间的真实的非确定型依赖关系;样本回归模型建立在抽样数据基础之上,它描述的是因变量Y 和自变量X 之间的近似于真实的非确定型依赖关系。
线性回归PPT优秀课件

1.正方形面积S与边长x之间的关系: 确定关系 正方形边长x 面积S x 2 2.一块农田的水稻产量与施肥量之间的关系: 气候情况 施肥量 不确定关系 水稻产量
浇水
除虫
与函数关系不同,相关关系是一种非确定
性关系.对具有相关关系的两个变量进行统
计分析的方法叫做回归分析. 在现实生活中存在着大量的相关关系.人 的身高与年龄、产品的成本与生产数量、商品
的销售额与广告费、家庭的支出与收入等都是
相关关系.
问题1:正方形的面积y与正方形的边长x之间
的函数关系是 y = x2 确定性关系 问题2:某水田水稻产量y与施肥量x之间是 否有一个确定性的关系? (不确定关系) 例如:在7块并排、形状大小相同的试验田上进行 施肥量对水稻产量影响的试验,得到如下所示的一 组数据:
为了书写方便,我们先引进一个符号 “ ”.这个符号表示若干个数相加.
n
例如,可将x1+x2+……+xn记作 x i
i1
,即
表示从x1加到xn的和.这样,n个数的平均
1 n 数的公式可以写作 x x i .上面的③ n i 1 n 2 式可以写作Q= ( yi bxi a) .
因此所求的回归直线方程是 yˆ =4.75x+257. 根据这个回归直线方程,可以求出相应于x 的估计值.例如当x=28(kg)时,y的估计
值是
yˆ
= 4.75×28+257=390(kg).
例1.一个工厂在某年里每月产品的总成本y
(万元)与该月产量x(万件)之间有如下一组
数据:
(l)画出散点图; (2)求月总成本y与月产量x之间的回归直线方
i 1
这个式子展开后,是一个关于a,b的二 次多项式.利用配方法,可以导出使Q取得 最小值的a,b的求值公式(详细推导过程 请见本小节后的阅读材料.P43页).
线性回归分析与应用例题和知识点总结

线性回归分析与应用例题和知识点总结在统计学和数据分析的领域中,线性回归分析是一种非常重要和常用的方法。
它可以帮助我们理解变量之间的线性关系,并进行预测和推断。
接下来,让我们一起深入探讨线性回归分析的知识点,并通过一些具体的例题来加深理解。
一、线性回归的基本概念线性回归是一种用于建立两个或多个变量之间线性关系的统计方法。
简单线性回归涉及两个变量,一个是自变量(通常用 x 表示),另一个是因变量(通常用 y 表示)。
其基本形式可以表示为:y = b₀+b₁x,其中 b₀是截距,b₁是斜率。
二、线性回归的假设条件在进行线性回归分析时,有几个重要的假设条件需要满足:1、线性关系:自变量和因变量之间存在线性关系。
2、独立性:观测值之间相互独立。
3、正态性:残差(实际值与预测值之间的差异)服从正态分布。
4、同方差性:残差的方差在不同的自变量取值上是相同的。
三、最小二乘法为了确定线性回归方程中的参数 b₀和 b₁,我们通常使用最小二乘法。
其基本思想是使残差平方和最小,即找到一组 b₀和 b₁的值,使得观测值与预测值之间的差异最小化。
四、决定系数(R²)决定系数用于衡量回归模型对数据的拟合程度。
R²的取值范围在 0 到 1 之间,越接近 1 表示模型拟合得越好。
五、例题分析假设我们想研究一个城市中房屋面积(自变量 x)与房屋价格(因变量 y)之间的关系。
我们收集了以下 10 组数据:|房屋面积(平方米)|房屋价格(万元)|||||80|120||90|135||100|150||110|165||120|180||130|195||140|210||150|225||160|240||170|255|首先,计算这组数据的均值:x 的均值=(80 + 90 + 100 + 110 + 120 + 130 + 140 + 150 +160 + 170)/ 10 = 125 平方米y 的均值=(120 + 135 + 150 + 165 + 180 + 195 + 210 + 225 + 240 + 255)/ 10 = 180 万元然后,计算斜率 b₁:\\begin{align}b_1&=\frac{\sum_{i=1}^{n}(x_i \bar{x})(y_i \bar{y})}{\sum_{i=1}^{n}(x_i \bar{x})^2}\\&=\frac{(80 125)(120 180) +(90 125)(135 180) +\cdots +(170 125)(255 180)}{(80 125)^2 +(90 125)^2 +\cdots +(170 125)^2}\\&=15\end{align}\截距 b₀= y 的均值 b₁ x 的均值= 180 15 125 =-75所以,线性回归方程为 y =-75 + 15x接下来,我们可以用这个方程进行预测。
线性回归模型PPT课件

(2)
Var(u
i
)
σ
2 u
i 1,2,,n
等方差性
(3)Cov(ui,u j ) 0 (4) Cov(ui,X i ) 0
i j,i,j 1,2,,n i 1,2,,n
无序列相关
进一步假定
u~N(
0,σ
2 u
)
6
1 回归模型的一般描述
五、回归分析预测的一般步骤
1. 以预测对象为因变量建立回归模型; 2. 利用样本数据对模型的参数进行估计; 3. 对参数的估计值及回归方程进行显著性检验; 4. 利用通过检验的方程进行预测。
σ 2(e0 )
σ u2 [1
1 n
(x0 (xi
x)2 -x)2
]
3. 给定置信水平1 ,置信区间为 ( yˆ tα σˆ(e ),yˆ tα σˆ(e, ))其中, 是自t由α 度为年n-2的t分布临界值,
ˆ (e0 ) ˆu
1 1 n
解:使用Excel实现回归
b
(yi
y)(xi (xi x)
x)
.
b y βˆx .
于是所求的方程为 yˆi 138.3480 6.9712 xi
这说明,该厂电的供应量每增加一 万度,年产值增加6.9712万元。
产值(万元)Y 213 242 286 305 306 342 351 373 379 377 384 395 387 402 418
1. 定义:假定Y与X的回归方程为 yˆi bo bxi ,对于给定的 自变量 X x,0 求得 yˆ0 bo bx0 ,称这种预测为点预测。
高三数学_线性回归分析

五、如下图是一组观测值的散点图:
任给出一组数据能 否由此求出它的线 形回归方程? Y • • • •• • • • •• • • • • • • • O X
按照上述方法,同样可
以就这组数据求得一 个回归直线方程,这 显然毫无意义。
想一想?
所求得的回归直线方程,在什么情况
下才能对相应的一组数据观测值具有代表
pi 的符号有正有负,相加会相互抵消。
pi 的和不能代表n个点与相应直线在
整体上的接近程度。
(3)各偏差的平方和:
Q ( y1 bx1 a) ( y2 bx2 a)
2
2
( yn bxn a)
n
即:
2
Q ( yi bxi a)
i 1
2
用Q来表示n个点与相应直线在整体上 的接近程度。
2.散点图: (1)定义:表示具有相关关系的两个变量的 一组数据的图形。 (2)作用:形象反映各对数据的密切程度。
Y
这样的直线 可以画多少 条呢?
哪一条最能代表变量X与Y 之间的关系呢?
O
X
3、观察散点图的特征
发现各点大致分布在一条直线的附近。
4、一般地,设x与y是具有相关关系的两个
变量,且相应于n个观测值的n个点大致分布 在一条直线的附近,我们来求在整体上与这 n个点最接近的一条直线。
a y bx 399.3 4.75 30 257.
因此所求回归直线方程是:
ˆ y 4.75 x 257
(5)回归直线方程的用途:
可以利用它求出相应于x的估计值。
例如:当x=28kg时,y的估计值是多少呢?
ˆ y 4.75x 257 ˆ y 4.75 28 257 390(kg ).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十五單元線性迴歸(一)
梁文敏副教授葉懿諄統計分析師
簡單線性迴歸分析與前一單元所介紹的相關係數分析,兩者有許多相似之處,兩者均可用於探討兩個連續變數(continuous variable)的線性關係,但在相關係數分析中,兩個變數的角色是對等的,也就是可互換的;而在簡單線性迴歸分析中,兩者之間的關係以一個線性方程式(linear equation;或稱線性模式linear model)來連結,使我們能從其中看到兩個變數之間的互動關係,在模式中兩個變數的角色一個為依變數(dependent variable;反應變數response variable;或稱結果變數outcome variable,一般以y表示),另一個為自變數(independent variable;或稱解釋變數explanatory variable,一般以x表示),兩者互換後所得到的模式不同。
在迴歸中的自變數可為連續變數(SPSS稱之為Covariate(s)共變量)或類別變數(SPSS稱之為Fixed Factor(s)固定因子)。
在SPSS中有很多模組可以用來進行線性迴歸分析,在本單元中我們介紹兩個操作步驟:進入「Regression迴歸」的操作,或進入「General Linear Model一般線性模式」的操作。
15.1簡單線性迴歸
【範例1】年齡是否會影響睡眠小時?
範例資料:
id age sleepHR1
1 30.1
2 8.5
2 38.72 7.3
3 32.06 7
… … …
50 29.25 7.3
使用方法:
在本範例中欲探討年齡對於睡眠小時的影響,可以利用線性迴歸來進行分析,在此迴歸式中,年齡為自變數(X),而睡眠小時為依變數(Y)。
軟體操作步驟-1
【SPSS步驟】
步驟一:選擇功能【Analyze分析】→進入【Regression迴歸】→進入【Linear...
線性】。
步驟二:在Dependent variable依變數框格中(選入變數:sleepHR1)→在Independent(s)自變數框格中(選入變數:age)。
步驟三:選擇OK確定。
結果表格
上表為迴歸模式的模式評估,R square(R2)稱為迴歸分析的決定係數(Coefficient of Determinantion)。
本分析只有一個自變數且y與x之間皆為連續變數,所以R值會與兩個變數之間的皮爾森相關係數(r)一樣,但r主要表示與y之間的線性相關程度,其值介於-1與1之間;而R2主要用以探討y的總變異中能夠被x解釋的比例,其值介於0與1之間。
在本分析中,x(年齡)能夠解釋y(睡眠小時)總變異的75.1%。
上表為此迴歸模式的變異數分析表。
在Sum of Square(平方和)欄位中分別列出Regression 的平方和(為迴歸所能解釋y 的變異量=48.504),Residual 的平方和(為迴歸無法解釋y 的變異量=16.116),及Total 的平方和(為y 的總變異量=64.620)。
註:48.504+16.116=64.620。
※ Sig.表示p 值
上表的註標顯示依變數為sleepHR1。
根據上表可以得到此迴歸模式:
age sleepHR *123.07.11ˆ1-=μ
,1ˆsleepHR μ表示平均睡眠小時的估計值,截距項為11.7,表示年齡等於0 (age=0)的平均睡眠小時為11.7小時,且有統計上顯著的差異
(Sig.=0.000,表示p<0.001),但許多時候截距項為”0”,並沒有實際應用上的意義,故較少解釋截距項所代表的意義。
年齡(age)的係數估計值為-0.123表示年齡每增加1歲,平均睡眠小時減少0.123小時,且有統計上顯著的意義(Sig.=0.000,表示p<0.001)。
2R 值要多大才理想呢?
R 2用以表示迴歸所可以解釋的變異比例,故可作為以x 預測y 之準確度的指標。
例如用年齡(x)來預測睡眠小時(y),R 2=0.76表示睡眠小時總變異的76%能被年齡所解釋,但是另外還有24%(1- R 2)的變異是無法被年齡所解釋的。
通常,2R 愈大表示準確度越高。
但是2R 值的大小並不能決定該迴歸模式是否為一個有用的模式,2R 為1表示所有的觀察值均等於其預測值(或稱估計值),但在實務上這種情狀發生的可能性很小,例如以父親的身高預測兒子的身高,我們可以想見這結果可能還會受到許多其他因素如母親身高、種族、飲食習慣、及許多個人因素的影響,因此2R 是不可能高的。
此處我們聚焦的重點應該只是在看,平均而言,在控制了其他變數後,兒子的身高與父親的身高之間是否有顯著的線性關係存在(主要由迴歸係數之檢定,0:0=βH 0:1≠βH 結果來判別),因此即便2R 不到20%,也不影響我們的結果。
但在有些研究中,2R 值的標準就必需訂得非常高,例如針對等待心臟移植的病患,必需要等到一個”適當”的心臟(即心臟大小要相當)才能確保手術的成功,此時我們的重點應該是要精確地估計出待移植者心臟體積的大小,因此即便2R 高達95%可能都不夠呢!總而言之,2R 要多大才理想,需視情況而定。
軟體操作步驟-2
【SPSS
步驟】
步驟一:選擇功能【Analyze 分析】→進入【General Linear Model 一般線性模式】
→進入【Univariate 單變量】。
步驟二:在Dependent variable 依變數框格中(選入變數:sleepHR1)→在Covariate(s)
共變量框格中(選入變數:age)。
步驟三:選擇進入:Model 模式→勾選:Custom 自訂→選入變數:age(C)→Continue
繼續。
步驟四:選擇進入:Options 選項→勾選: (1)Descriptive statistics 敘述統計 (2)Parameter estimates 參數估計值 →Continue 繼續。
步驟五:選擇OK 確定。
※Univariate Linear Regression 表示只有一個依變數(y)。
結果表格
上表為現在睡眠小時(sleepHR1)的描述性統計。
上表為此迴歸模式的變異數分析表。
此迴歸模式為age sleepHR *123.07.11ˆ1-=μ
,1ˆsleepHR μ表示平均睡眠小時的估計值,年齡(age)的係數估計值為-0.123,表示年齡每增加1歲,平均睡眠小時減少0.123小
時且有統計上顯著的意義(p<0.001)。
註:此部分與前面用「Regression 迴歸」分析所得結果相同。
