02-4.3 平面力对点的矩和平面力偶(课件)
合集下载
平面力系和平面力偶系课件

弹性力学问题的能量方程
应变能
物体在外力作用下产生变形时,内部 储存的能量称为应变能,单位是焦耳 (J)。
应力
胡克定律
在弹性范围内,应力与应变之间成正 比,即σ=Eε。
物体内部单位截面积上所受的力称为 应力,单位是帕斯卡(Pa)。
典型例题解析
06
固定端约束反力的计算例题
总结词
该例题主要展示了如何利用固定端约束反力的计算方法。
力的性质
力具有物质性、相互性和矢量性。力不能离开物体单独存在, 有施力物体和受力物体;两个物体之间的作用总是相互的, 存在作用力和反作用力;力用矢量表示,可以计量大小和方向。
平面力系的分类和性质
平面力系的分类
平面力系可以分为平面汇交力系、平面平行力系和任意平面力系。
平面力系的性质
平面力系中,力的合成和平衡具有特定的性质。例如,平面汇交力系合成后合力为零,即力系平衡;平面平行力 系合成后合力与原力系等效,即力系平衡;对于任意平面力系,合成后如存在合力,则合力与原力系等效,即力 系平衡。
详细描述
杠杆是一种简单机械,它可以通过放大或缩 小力臂来改变力的作用效果。在杠杆的平衡 条件中,我们需要考虑物体的质量、重力以 及支点的位置。通过计算,我们可以得到支 点的反作用力以及杠杆的平衡条件。进一步
求解可以得到物体的平衡状态。
弹性力学问题的能量方程例题
要点一
总结词
要点二
详细描述
该例题介绍了弹性力学中能量方程的建立与应用。
课程目的和内容
内容 平面力系的定义、性质和计算方法
平面力偶系的定义、性质和计算方法
课程目的和内容
平面力系和力偶系的合成与平衡 典型例题的讲解和练习
平面力系的基本概念
平面汇交力系与平面力偶系精品PPT课件

四块相同的均质板,各重P,长2b,叠放如图示。 在板I右端点A挂着重物B,其重2P。欲使各板都平衡, 求每块板可伸出的最大距离。
3P
P
N3
4P
P
N4
P 2P
求图示结构AB杆与AC杆所受的力,已知F力位于AD 的中点E且垂直AD。
FA FAB
A FA
FAC
45 o 45 o
F
FA
FD
450
F
B
C
D
W3
F
W2
W1
塔吊及所受荷载如图。自重P=200kN,中心 通过塔基中心。起重量W=25kN,距右轨B为 15m.平衡物重Q,距左轨A为6m,在不考虑风 荷载时, 求: (1)满载时,为了保证塔
身不至于倾覆,Q至 少应多大? (2)空载时,Q又应该不 超过多大,才不至于 使塔身向另一侧倾覆?
如图示,一钢筋混凝土梁BC置于砖墙上,挑出1.5m, 顶端C作用一集中力P=1kN,梁自重q=1.2kN/m,取 抗倾覆安全系数κ=1.5,试求BA段的长度a。
的力矩。
抗倾覆力矩(Mk):抵抗结构或构件倾覆
的力矩。
K=抗倾覆安全系数
K MK Mq
规范规定:钢筋砼构件的抗倾覆安全系数 K≥1.5
带有雨蓬的钢筋混凝土门顶过梁,尺寸如图示,梁 和板的长度均为4m。设在此梁上的砖砌至3m高时, 便欲将雨篷下的木支撑拆除。试验算此时雨蓬会不 会绕A点倾覆。已知钢筋混凝土容重为25kN/m3 , 砖砌体容重为19kN/m3 ,验算时应考虑雨蓬最外边 缘B上作用有施工荷载F=1kN。
3 如果力F通过矩心O,则mo(F)=0,此时力对物体
的作用效应为移动。
4 互成平衡的二力对同一点之矩的代数和等于零。
14平面力系--平面力对点之矩 力偶系

FA
FB
FA FB
M 0
FB
60 300N FA FB 300 N 0.2
FB 0.2 m1 m2 m3 m4 0
例2-6 图示机构不计自重。圆轮上的销子在摇杆BC的光滑导 槽内可自由滑动;圆轮上作用一力偶,其力偶矩 M 1 2kN m, 30 ),系统平衡。 OA r 0.5m 。在图示位置( OA⊥OB, 求作用在摇杆BC上力偶的矩M2 及铰链O、B处的约束力。
合力矩的解析表达式:
y
O
Fx
x
x
MO (FR ) MO (Fi )
( xi Fiy yi Fix )
例2 4图示直杆长为l,力F与x轴夹角为。求力F对插入端O之矩。
y
O o 方法一:利用定义
h
l
Fy
F
Fx
x
M O ( F ) F h F l sin
合力矩定理:平面汇交力系的合力对于平面内任一点之矩等于所有 各分力对于该点之矩的代数和.
三、力矩与合力矩的解析表达式 力矩的解析表达式:
y
MO (F ) M O ( Fx ) M O ( Fy )
F
Fy
A
x Fy y Fx
x F sin y F cos
F
' F
2、力偶矩
力偶作用面: 力偶臂:
— 代数量 力偶中两力所在的平面
d1 O O
1
力偶中两力作用线间的垂直距离 ' ' M O1 ( F , F ) M O1 ( F ) M O1 ( F ) 力偶可以看作 ' F ( d d ) F d1 1 不能合成的两 Fd 个力
理论力学L平面力矩PPT课件
第2页/共4页
2. 汇交力系合力 矩定 理
设则汇:交M力Or(系FR()FFi 1r~FF(nRr)的F合i ) 力为FRFR
,FR
Fi r
O
MO(Fi )
汇交力系合力矩定理:
汇交力系的合力对任意一点的矩矢量,等于力
系中各分力对同一点力矩矢量的矢量和。
对于平面力矩:
MO( FR ) MO( Fi )
取代数和。
第3页/共4页
感谢您的观看!
第4页/共4页
Байду номын сангаас
§2-3 平面力对点的矩
研究平面上力对点的矩有两个目的。
首先,该内容有实际的工程应用背景;
其次,是为研究更一般的力系作准备。
力对点的矩是力使物体产生绕某点转动效应
的度量。
该点称为力矩的矩心。
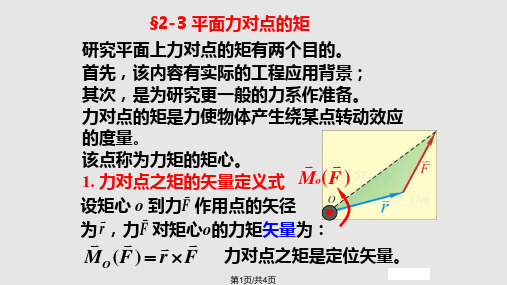
1. 力对点之矩的 矢量定义式 Mo(F )
设矩 心 o到力F 作用点的矢径
为MrO,(F力 )F对r矩 F心 o的力力对矩点矢之量矩为是:定位矢量。
第1页/共4页
MO(F) r F
1.力矩 矢量的大小(模):
r
F
是矢量
Fr、 Fr
sin F d
之间的正向夹角。
d 称为力臂。
2. 方向:平面力矩仅顺/逆时针两个转动方向,
所以,平面力矩只需正、负两个符号即可区分 其转动方向。 MO(F) F d
规定逆时针转动方向为+。
所以,平面力对点的力矩是代数量。
《工程力学》教学课件第二章平面力系和平面力偶系

M(F,F′)=±2S△ABC
力偶的性质:
❖ 性质1:力偶在任何坐标轴上的投影等于零。 ❖ 性质2:力偶不能合成为一个力,或者说力偶没有合力。 ❖ 性质3:平面力偶等效定理。
力偶等效条件:
❖ (1)力偶可以在其作用面内任意移动,而不影响它对刚体 的作用效应。
❖ (2)只要保持力偶矩大小和转向不变,可以任意改变力偶 中力的大小和相应力偶臂的长短,而不改变它对刚体的作用 效应。
M O (FR) M O (F )
第六节 平面任意力系的平衡方程及应用
物体在力系作用下,保持平衡的充分必要条件是:力系
的主矢与对任一点的主矩均为零 ,即:
X 0 , Y 0 , M O F 0
上式称为平衡方程一矩式,二矩式和三矩式分别为:
X 0M MBA或 FFY00 0
M M M
MO(F)Fsihn
M O(Q)Qh
(2)应用合力矩定理,得
M O(F)F xhF yhc tg Fsin hFco shctg Fsh in
M O(Q)Qh
二、力偶
1、力偶及其性质 力偶:两力大小相等、作用线不重合的反向平行力叫力偶。
力偶使物体转动效应一般通过力偶 矩来衡量,力偶矩的大小为Fd, 方向由右手法则确定,平面力偶矩 也为代数量,用M(F,F′)来表 示,即
第一节力在坐标轴上的投影第二节平面汇交力系的合成与平衡第三节力矩平面力偶系的合成与平衡第四节力线的平移定理第五节平面任意力系的简化第六节平面任意力系的平衡方程及应用第七节静定与静不定问题及物系的平衡企业文化就是传统氛围构成的公司文化它意味着公司的价值观诸如进取守势或是灵活这些价值观构成公司员工活力意见和行为的规范
X=Fx=F cos=F sin Y=Fy=F cos = F sin
力偶的性质:
❖ 性质1:力偶在任何坐标轴上的投影等于零。 ❖ 性质2:力偶不能合成为一个力,或者说力偶没有合力。 ❖ 性质3:平面力偶等效定理。
力偶等效条件:
❖ (1)力偶可以在其作用面内任意移动,而不影响它对刚体 的作用效应。
❖ (2)只要保持力偶矩大小和转向不变,可以任意改变力偶 中力的大小和相应力偶臂的长短,而不改变它对刚体的作用 效应。
M O (FR) M O (F )
第六节 平面任意力系的平衡方程及应用
物体在力系作用下,保持平衡的充分必要条件是:力系
的主矢与对任一点的主矩均为零 ,即:
X 0 , Y 0 , M O F 0
上式称为平衡方程一矩式,二矩式和三矩式分别为:
X 0M MBA或 FFY00 0
M M M
MO(F)Fsihn
M O(Q)Qh
(2)应用合力矩定理,得
M O(F)F xhF yhc tg Fsin hFco shctg Fsh in
M O(Q)Qh
二、力偶
1、力偶及其性质 力偶:两力大小相等、作用线不重合的反向平行力叫力偶。
力偶使物体转动效应一般通过力偶 矩来衡量,力偶矩的大小为Fd, 方向由右手法则确定,平面力偶矩 也为代数量,用M(F,F′)来表 示,即
第一节力在坐标轴上的投影第二节平面汇交力系的合成与平衡第三节力矩平面力偶系的合成与平衡第四节力线的平移定理第五节平面任意力系的简化第六节平面任意力系的平衡方程及应用第七节静定与静不定问题及物系的平衡企业文化就是传统氛围构成的公司文化它意味着公司的价值观诸如进取守势或是灵活这些价值观构成公司员工活力意见和行为的规范
X=Fx=F cos=F sin Y=Fy=F cos = F sin
力矩与平面力偶系 PPT课件

F1 d A F 1 B A F2 D ABD , M ( P , P ) 2 S ABC S ABD S ABC M ( F , F ) M ( P , P ) M ( P , P ) M ( P1 , P1) M ( F , F ) M ( P1 , P1)
F′ F
F2 F O F1
o 图 3-2 (b)
图 3-2 (c)
2. 合力矩定理 表达式: M O ( FR ) M O ( F ) 证明:由图得 y
M O ( F ) F d F r sin( ) F r (sin cos sin cos ) F r sin cos
图 3-4
图3-5
(2) 力偶的性质 (a) 力偶在任何坐标轴上的投影等于零; (b)力偶不能合成为一力,或者说力偶没有合力, 即它不能与一个力等效,因而也不能被一个力平 衡; (c) 力偶对物体不产生移动效应,只产生转动效 应,即它可以也只能改变物体的转动状态。
F d F′ 力偶作用面 力偶臂
图3-6
而
O x r Fy F
A
y Fx x
F r sin cos
F cos Fx , F sin Fy r cos x A , r sin y A
d
M
图 3-3
则
MO (F) xA Fy yA Fx
(a)
MO (F) xA Fy yA Fx
谁曾经想过用杠杆来移动地球? 古希腊科学家阿基米德曾说过“如果给我一个支点,我就能
撬起地球”。这句名言从理论上讲是完全正确的,
因为杠杆能使力变大,只要杠杆足够长,就 能产生足够大的力来“搬动”地球。
F′ F
F2 F O F1
o 图 3-2 (b)
图 3-2 (c)
2. 合力矩定理 表达式: M O ( FR ) M O ( F ) 证明:由图得 y
M O ( F ) F d F r sin( ) F r (sin cos sin cos ) F r sin cos
图 3-4
图3-5
(2) 力偶的性质 (a) 力偶在任何坐标轴上的投影等于零; (b)力偶不能合成为一力,或者说力偶没有合力, 即它不能与一个力等效,因而也不能被一个力平 衡; (c) 力偶对物体不产生移动效应,只产生转动效 应,即它可以也只能改变物体的转动状态。
F d F′ 力偶作用面 力偶臂
图3-6
而
O x r Fy F
A
y Fx x
F r sin cos
F cos Fx , F sin Fy r cos x A , r sin y A
d
M
图 3-3
则
MO (F) xA Fy yA Fx
(a)
MO (F) xA Fy yA Fx
谁曾经想过用杠杆来移动地球? 古希腊科学家阿基米德曾说过“如果给我一个支点,我就能
撬起地球”。这句名言从理论上讲是完全正确的,
因为杠杆能使力变大,只要杠杆足够长,就 能产生足够大的力来“搬动”地球。
第三章_力对点的矩_平面力偶系

力对点的矩
如图所示,当用扳手拧紧螺母时, 如图所示,当用扳手拧紧螺母时,力F对螺母拧紧的转 动效应不仅与力F的大小有关,而且还与转动中心O至力F 动效应不仅与力F的大小有关,而且还与转动中心O至力F 的垂直距离有关。 的垂直距离有关。 因此,可用两者的乘积Fd来度量力使物体绕点O Fd来度量力使物体绕点 因此,可用两者的乘积Fd来度量力使物体绕点O的转动 力矩, MO(F)表示 效应,称为力F对点O之矩,简称力矩 以符号MO(F) 效应,称为力F对点O之矩,简称力矩,以符号MO(F)表示 ,即 MO(F)=± MO(F)=±Fd 矩心, 称为力臂 力矩是一个代数量。 力臂。 式中, 称为矩心 式中,点O称为矩心,d称为力臂。力矩是一个代数量。
M = Fd
= F (d + x1 ) F x1 = Fd
M O1 (F , F ′) = M O1 (F ) + M O1 (F ′)
M O2 (F , F ′) = F ′ (d + x2 ) F x2 = F ' d = Fd
推论
1、力偶可以在其作用面内任意移动和转动,而不 、力偶可以在其作用面内任意移动和转动, 改变它对物体的效应。 改变它对物体的效应。
1、根据力矩定义求
2、根据合力矩定义求
2
力偶与力偶矩
力偶的定义
由两个等值、反向、 由两个等值、反向、不共线的的平行力组成 的力系称为力偶, 表示。 的力系称为力偶,用 ( F , F ′) 表示。
力偶矩的定义
力偶臂:力偶中两个力的作用线之间的垂直距离 力偶臂:力偶中两个力的作用线之间的垂直距离h 称为该力偶的力偶臂。 称为该力偶的力偶臂。 力偶的作用面:力偶所在的平面称为力偶的作用面。 力偶的作用面:力偶所在的平面称为力偶的作用面。 力偶矩:力偶中一个力的大小与力偶臂的乘积, 力偶矩:力偶中一个力的大小与力偶臂的乘积,并 取以正负号,称为该力偶的力偶矩。 取以正负号,称为该力偶的力偶矩。 表示为: 表示为: M F , F ′ = ± Fh, M = ± Fh
工程力学——平面力偶系PPT课件

F
F/
a bc d
F
ab
完整编辑ppt
21
性质2
力偶对其所在平面内任一点
的矩恒等于力偶矩,而 与矩心的
位置无关,因此力偶对刚体的效
应用力偶 矩度量。
F
B Ad
x
O
F'
m O (F ) m O (F ') F (x d ) F 'xFd
完整编辑ppt
22
性质3:平面力偶等效定理 作用在同一平面内的两个力偶,只要它的力偶矩的大小相
dA
A
dC
F
F=100N, 30 求 F对A、B、C三点之矩。
C D 解:由定义
B
m A (F ) F A d F As D i 3n 0 25 N 2 m
m C (F ) F C d F CsD i 3n 0 7 5 N m
由合力矩定理 m B (F ) F xA F B yA D F c3 o 0 A s F B s3 i n 0 A D 4.4 8 N 8 m
解:
图(a): 图(b):
MA = - 8×2 = -16 kN ·m MB = 8×2 = 16 kN ·m
MA = - 4×2×1 = -8 kN · m 完整编M辑Bppt= 4×2×1 = 8 kN ·m 8
[例3] 已知:如图 F、Q、l, 求:mO (F ) 和 mo (Q )
解:①用力对点的矩法
在一钻床上水平放置工件在一钻床上水平放置工件在工件上同时钻四个等直径在工件上同时钻四个等直径的孔每个钻头的力偶矩为每个钻头的力偶矩为求工件的总切削力偶矩和求工件的总切削力偶矩和abb端水平反力端水平反力
§2–3 平面力偶系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
(1)平面力对点的矩
3、平面力对点的矩和平面力偶
• O称为矩心 • O与力矢量的首尾确定的平
面称为力矩作用面
• O到力的作用线的垂直距 离 h称为力臂
•力F 使物体绕O点的转动效果,完全 由两个要素决定: a. 大小:力F与力臂h的乘积 F·h b. 转向:使物体绕O点转动方向
b. 转向:作用面内的转动方向
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
(5)同平面内力偶的等效定理
定理:在同一平面内的两个力偶,如果力偶矩相等,则两力偶彼此相等。 推论(1):力偶可在其作用面内任意移转,而不改变它对刚体的作用。力偶对 刚体的作用与力偶在其作用面内的位置无关。 推论(2):只要保持力偶矩的大小和力偶的转向不变,可以同时改变力偶中力 的大小与力偶臂的长短,对刚体的作用效果不变。
力偶矩是平面力偶作用的唯一度量
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
该结论适用于任何存在合力的力系!
y
力矩的解析表达式:
MO(F) MO(Fy ) MO(Fx ) x F sin θ y F cos θ xFy yFx
Fy
θ
y
A
Ox
F
Fx x
如果有多个汇交力,则:
MO FR MO Fi
M O FR xi Fiy yi Fix
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
(3)力偶
3、平面力对点的矩和平面力偶
由两个大小相等(等值)、方向相反(反向)、不共线的(平行)力组成的
力系称为力偶,记作 臂
a. 力偶是力系但不是平衡力系。 b. 力偶没有合力,不能用一个力来等效替换,也不能用一个力来平衡。 c. 力偶和力一样,是力学中的一个基本要素。
平面汇交力系和平面力偶系
(4)力偶矩
力偶矩是对力偶使物体转动效果的度量。
平面力偶矩是一个代数量,其绝对值等于力的大小与力偶臂的乘积,正 负号表示力偶的转向:一般以逆时针转向为正,顺时针转向为负。单位 N·m,大小也可以用三角形(平行四边形)的面积表示。
M F d 2 AABC
两个要素 a. 大小:力与力偶臂乘积
用数学式子来表示:
MO (F ) F h
F
O
h
平面力对点之矩是一个代数量, 它的绝对值等于力的大小与力臂 的乘积,它的正负:力使物体绕 矩心逆时针转向时为正,反之为 负.常用单位N.m或kN.m
平面汇交力系和平面力偶系
(2)合力矩定理与力矩的解析表达式
MO(FR ) MO (Fi )
合力矩定理:平面汇交力系的合力对平面内任一点的矩等于各分力对该点 的矩的代数和。
平面汇交力系和平面力偶系
(1)平面力对点的矩
3、平面力对点的矩和平面力偶
• O称为矩心 • O与力矢量的首尾确定的平
面称为力矩作用面
• O到力的作用线的垂直距 离 h称为力臂
•力F 使物体绕O点的转动效果,完全 由两个要素决定: a. 大小:力F与力臂h的乘积 F·h b. 转向:使物体绕O点转动方向
b. 转向:作用面内的转动方向
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
(5)同平面内力偶的等效定理
定理:在同一平面内的两个力偶,如果力偶矩相等,则两力偶彼此相等。 推论(1):力偶可在其作用面内任意移转,而不改变它对刚体的作用。力偶对 刚体的作用与力偶在其作用面内的位置无关。 推论(2):只要保持力偶矩的大小和力偶的转向不变,可以同时改变力偶中力 的大小与力偶臂的长短,对刚体的作用效果不变。
力偶矩是平面力偶作用的唯一度量
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
该结论适用于任何存在合力的力系!
y
力矩的解析表达式:
MO(F) MO(Fy ) MO(Fx ) x F sin θ y F cos θ xFy yFx
Fy
θ
y
A
Ox
F
Fx x
如果有多个汇交力,则:
MO FR MO Fi
M O FR xi Fiy yi Fix
3、平面力对点的矩和平面力偶
平面汇交力系和平面力偶系
(3)力偶
3、平面力对点的矩和平面力偶
由两个大小相等(等值)、方向相反(反向)、不共线的(平行)力组成的
力系称为力偶,记作 臂
a. 力偶是力系但不是平衡力系。 b. 力偶没有合力,不能用一个力来等效替换,也不能用一个力来平衡。 c. 力偶和力一样,是力学中的一个基本要素。
平面汇交力系和平面力偶系
(4)力偶矩
力偶矩是对力偶使物体转动效果的度量。
平面力偶矩是一个代数量,其绝对值等于力的大小与力偶臂的乘积,正 负号表示力偶的转向:一般以逆时针转向为正,顺时针转向为负。单位 N·m,大小也可以用三角形(平行四边形)的面积表示。
M F d 2 AABC
两个要素 a. 大小:力与力偶臂乘积
用数学式子来表示:
MO (F ) F h
F
O
h
平面力对点之矩是一个代数量, 它的绝对值等于力的大小与力臂 的乘积,它的正负:力使物体绕 矩心逆时针转向时为正,反之为 负.常用单位N.m或kN.m
平面汇交力系和平面力偶系
(2)合力矩定理与力矩的解析表达式
MO(FR ) MO (Fi )
合力矩定理:平面汇交力系的合力对平面内任一点的矩等于各分力对该点 的矩的代数和。
