2016年第25届希望杯九年级第一试(Word版)
2014 第25届希望杯高一级全国获奖名单

云南省水富县云天化中学 高一 二等奖 马浩瀚 高台县第一中学 高一 二等奖 王宏宇 林嵘灏 漳州市厦门大学附属实验中学 高一 二等奖 阜阳市第三中学 高一 二等奖 杨晓天 阜阳市第三中学 高一 二等奖 朱洪彬 鲁泽逸 河北省唐山市曹妃甸区第一中学 高一 二等奖 河北省青县一中 高一 二等奖 陈桐阳 嘉善高级中学 高一 二等奖 龚庭楠 嘉善高级中学 高一 二等奖 陶佳豪 海宁市高级中学 高一 二等奖 陈寅 嘉兴市一中 高一 二等奖 金哲一 嘉兴市一中 高一 二等奖 陈瑜阳 嘉兴市一中 高一 二等奖 傅辰佶 桐乡市高级中学 高一 二等奖 高顺成 桐乡市高级中学 高一 二等奖 胡雨慧 桐乡市高级中学 高一 二等奖 章申琰 桐乡市高级中学 高一 二等奖 戈立威 桐乡市高级中学 高一 二等奖 范可扬 嘉兴市元济高级中学 高一 二等奖 陈晓冬 嘉兴市元济高级中学 高一 二等奖 赵思博 嘉兴市元济高级中学 高一 二等奖 沈雨欣 嘉兴市元济高级中学 高一 二等奖 葛诗佳 嘉兴市元济高级中学 高一 二等奖 朱家琦 嘉兴市元济高级中学 高一 二等奖 王琦 嘉兴市元济高级中学 高一 二等奖 俞骆遥 嘉兴市平湖中学 高一 二等奖 张齐心 嘉兴市平湖中学 高一 二等奖 屠俊杰 嘉兴市平湖中学 高一 二等奖 沈婷 茂名市一中 高一 二等奖 古文鑫 茂名市第一中学 高一 二等奖 何松儒 茂名市信宜中学 高一 二等奖 黎浩良 茂名市信宜中学 高一 二等奖 曾景辉 茂名市信宜中学 高一 二等奖 刘春楠 茂名市高州中学 高一 二等奖 李绍基 化州市第一中学 高一 二等奖 庞进林 化州市第一中学 高一 二等奖 庞业展 化州市第一中学 高一 二等奖 黄梓林 化州市第一中学 高一 二等奖 李宇振 福清市西山学校高中部 高一 二等奖 张江建 福建省师大附中 高一 二等奖 陈思哲 福清市华侨中学 高一 二等奖 刘晋榕 福州市三中 高一 二等奖 孙宋源 深圳市杰英培训中心 高一 二等奖 欧婷婷 深圳市深华教育 高一 二等奖 许哲豪 龙岩市武平一中 高一 二等奖 曾恬静 龙岩市长汀一中 高一 二等奖 李杰
希望杯第1-10届五年级数学试题及答案(WORD版)
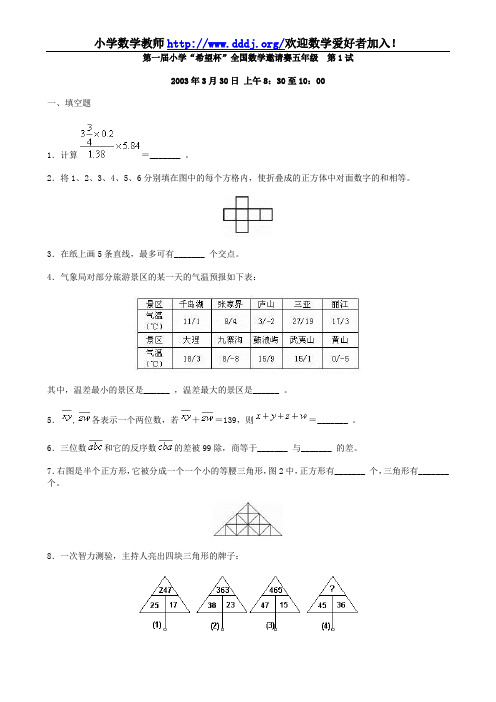
2003年3月30日上午8:30至10:00一、填空题1.计算=_______ 。
2.将1、2、3、4、5、6分别填在图中的每个方格内,使折叠成的正方体中对面数字的和相等。
3.在纸上画5条直线,最多可有_______ 个交点。
4.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是______ ,温差最大的景区是______ 。
5.,各表示一个两位数,若+=139,则=_______ 。
6.三位数和它的反序数的差被99除,商等于_______ 与_______ 的差。
7.右图是半个正方形,它被分成一个一个小的等腰三角形,图2中,正方形有_______ 个,三角形有_______ 个。
8.一次智力测验,主持人亮出四块三角形的牌子:9.正方形的一条对角线长13厘米,这个正方形的面积是平方厘米。
10.六位自然数1082□□能被12整除,末两位数有种情况。
11.右边的除法算式中,商数是。
12.比大,比小的分数有无穷多个,请写出三个:。
13.A、B、C、D、E五位同学进行乒乓球循环赛(即每2人赛一场),比赛进行了一段时间后,A赛了4场,B赛了3场,C赛了2场,D赛了1场,这时,E赛了场。
14.观察5*2=5+55=60,7*4=7+77+777+7777=8638,推知9*5的值是。
15.警察查找一辆肇事汽车的车牌号(四位数),一位目击者对数字很敏感,他提供情况说:“第一位数字最小,最后两位数是最大的两位偶数,前两位数字的乘积的4倍刚好比后两位数少2”。
警察由此判断该车牌号可能是。
16.一个小方木块的六个面上分别写有数字2,3,5,6,7,9。
小光,小亮二人随意往桌上扔放这个木块。
规定:当小光扔时,如果朝上的一面写的是偶数,得1分。
当小亮扔时,如果朝上的一面写的是奇数,得1分。
每人扔100次,得分高的可能性最大。
17.从1,2,3,4,5,6,7,8,9。
中随意取出两个数字,一个作分子,一个作分母,组成一个分数,所有分数中,最大的是,循环小数有个。
希望杯第1-8届五年级数学试题及答案(WORD版)

第一届小学“希望杯”全国数学邀请赛五年级第1试一、填空题1.计算=_______ .2.将1、2、3、4、5、6分别填在图中的每个方格内,使折叠成的正方体中对面数字的和相等。
3.在纸上画5条直线,最多可有_______ 个交点.4.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是______ ,温差最大的景区是______ 。
5.,各表示一个两位数,若+=139,则=_______ 。
6.三位数和它的反序数的差被99除,商等于_______ 与_______ 的差。
7.右图是半个正方形,它被分成一个一个小的等腰三角形,图2中,正方形有_______ 个,三角形有_______ 个。
8.一次智力测验,主持人亮出四块三角形的牌子:在第(4)块牌子中,?表示的数是_______ 。
9.正方形的一条对角线长13厘米,这个正方形的面积是平方厘米。
10.六位自然数1082□□能被12整除,末两位数有种情况。
11.右边的除法算式中,商数是。
12.比大,比小的分数有无穷多个,请写出三个:。
13.A、B、C、D、E五位同学进行乒乓球循环赛(即每2人赛一场),比赛进行了一段时间后,A赛了4场,B赛了3场,C赛了2场,D赛了1场,这时,E 赛了场.14.观察5*2=5+55=60,7*4=7+77+777+7777=8638,推知9*5的值是。
15.警察查找一辆肇事汽车的车牌号(四位数),一位目击者对数字很敏感,他提供情况说:“第一位数字最小,最后两位数是最大的两位偶数,前两位数字的乘积的4倍刚好比后两位数少2”。
警察由此判断该车牌号可能是。
16.一个小方木块的六个面上分别写有数字2,3,5,6,7,9。
小光,小亮二人随意往桌上扔放这个木块。
规定:当小光扔时,如果朝上的一面写的是偶数,得1分。
当小亮扔时,如果朝上的一面写的是奇数,得1分。
每人扔100次,得分高的可能性最大。
17.从1,2,3,4,5,6,7,8,9。
第19讲 一元二次方程的解法

第六章 一元二次方程第19讲 一元二次方程的解法【思维入门】1.若关于x 的一元二次方程的两根为x 1=1,x 2=2,则这个方程是 ( B )A .x 2+3x -2=0B .x 2-3x +2=0C .x 2-2x +3=0D .x 2+3x +2=02.用配方法解一元二次方程ax 2+bx +c =0(a ≠0),此方程可变形为 ( A )A.⎝ ⎛⎭⎪⎫x +b 2a 2=b 2-4ac 4a 2 B.⎝ ⎛⎭⎪⎫x +b 2a 2=4ac -b 24a 2 C.⎝ ⎛⎭⎪⎫x -b 2a 2=b 2-4ac 4a 2 D.⎝ ⎛⎭⎪⎫x -b 2a 2=4ac -b 24a 2 3.一元二次方程2x 2-3x +1=0的解为__x 1=1,x 2=12__.4.已知关于x 的一元二次方程2x 2-3kx +4=0的一个根是1,则k =__2__.5.一元二次方程(a +1)x 2-ax +a 2-1=0的一个根为0,则a =__1__.【解析】 ∵一元二次方程(a +1)x 2-ax +a 2-1=0的一个根为0,∴a +1≠0且a 2-1=0,∴a =1.6. 先化简,再求值:(x -1)÷⎝ ⎛⎭⎪⎫2x +1-1,其中x 为方程x 2+3x +2=0的根. 解:原式=(x -1)÷⎝ ⎛⎭⎪⎪⎫2-x -1x +1=(x -1)·x +1-x +1=-x -1. 由x 2+3x +2=0,得x 1=-1,x 2=-2.当x 1=-1时,原式无意义,所以x 1=-1舍去.当x 2=-2时,原式=1.【思维拓展】7.若关于x 的方程m (x +h )2+k =0(m ,h ,k 均为常数,m ≠0)的解是x 1=-3,x 2=2,则方程m (x +h -3)2+k =0的解为( B ) A .x 1=-6,x 2=-1B .x 1=0,x 2=5C .x 1=-3,x 2=5D .x 1=-6,x 2=28.定义运算“★”:对于任意实数a ,b ,都有a ★b =a 2-3a +b ,如:3★5=32-3×3+5.若x ★2=6,则实数x 的值是__-1或4__.9.关于x 的一元二次方程为(m -1)x 2-2mx +m +1=0.(1)求出方程的根;(2)m 为何整数时,此方程的两个根都为正整数?解:(1)根据题意得m ≠1,Δ=(-2m )2-4(m -1)(m +1)=4,∴x 1=2m +22()m -1=m +1m -1, x 2=2m -22()m -1=1.(2)由(1)知x 1=m +1m -1=1+2m -1,∵方程的两个根都是正整数,∴2m -1是正整数, ∴m -1=1或2.∴m =2或3.10.某文献对分式方程验根的归纳如下:“解分式方程时,去分母后所得整式方程的解有可能使原分式的分母为0,因此应如下检验:将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.”请你根据对这段话的理解,解决下面问题:已知关于x的方程m-1x-1-xx-1=0无解,方程x2+kx+6=0的一个根是m.(1)求m和k的值;(2)求方程x2+kx+6=0的另一个根.解:(1)∵将分式方程m-1x-1-xx-1=0去分母化成整式方程得(m-1)-x=0,解得x=m-1.又∵关于x的方程无解,∴x=m-1是增根.∴m-1-1=0,解得m=2.∵方程x2+kx+6=0的一个根是m,即x=2.∴22+2k+6=0.解得k=-5.(2)x2-5x+6=0,解得x1=2,x2=3.【思维升华】11.[2014·第25届“希望杯”初三第1试]若关于x的一元二次方程(m-2)x2+3x +m2-5m+6=0的常数项为0,则m的值是(B) A.2 B.3C.2或3 D.012.[2014·第25届“希望杯”初二第2试]若n(n≠0)是关于x的方程x2+mx+3n =0的根,则m+n的值是__-3__.13.[2014·全国联赛初二]已知n为正整数,且n4+2n3+6n2+12n+25为完全平方数,则n=__8__.【解析】易知n=1,n=2均不符合题意,所以n≥3,此时一定有(n2+n+2)2=n4+2n3+5n2+4n+4<n4+2n3+6n2+12n+25,(n2+n+4)2=n4+2n3+9n2+8n+16≥n4+2n3+6n2+12n+25,而n4+2n3+6n2+12n+25为完全平方数,所以一定有n4+2n3+6n2+12n+25=(n2+n+3)2,整理得n2-6n-16=0,解得n=8(负根n=-2舍去).2x-1-4=0,则满足该方程的所有根之14.[2013·全国竞赛九年级预赛]若x2-||和为.15.若x=-1是关于x的方程a2x2+2 015ax-2 016=0的一个根,则a的值为__2__016或-1__.【解析】∵x=-1是关于x的方程a2x2+2 015ax-2 016=0的一个根,∴将x=-1代入方程得a2-2 015a-2 016=0,因式分解得(a-2 016)(a+1)=0,可化为a-2 016=0或a+1=0,解得a1=2 016,a2=-1,则a的值为2 016或-1.。
(完整word)一元一次不等式(组)与二元一次方程(组)结合培优资料

一元一次不等式(组)与方程(组)的结合培优资料考点·方法·破译1.进一步熟悉二元一次方程组的解法,以及一元二次不等式组的解法.2.综合运用一元一次不等式组和二元一次方程组解决一些典型的实际问题.经典·考题·赏析【例1】求方程3x +27=17的正整数解.【解法指导】一般地,一个二元一次方程有无数个解,但它的特殊解是有限个,如一个二元一次方程的正整数解,非负整数解都是有限个.求不定方程的正(非负)整数解时,往往借助不等式,整数的奇偶性等相关知识来帮助求解.解:将方程变形为2y =17-3x 即2317x y -= ∵y >0 ∴2317x ->0 ∴x <317即x <325 又∵y 为正整数(即2317x -为整数) ∴17-3x 为偶数∴x 必为奇数∴x =1,3,5当x =1时,7213172317=⨯-=-=x y 当x =3时,4233172317=⨯-=-=x y 当x =5时,1253172317=⨯-=-=x y故原方程的正整数解为错误! 或错误! 或错误!【变式题组】01.求下列各方程的正整数解:⑴2x +y =10(2) 3x +4y =2102.有10个苹果,要分给两个女孩和一个男孩,要求苹果不得切开,且两个女孩所得的苹果数相等,每个孩子都有苹果吃,问有哪几种分法?【例2】足球联赛得分规定如下:胜1场得3分,平1场得1分,负1场得0分•某队在足球联赛的4场比赛中得6分,这个队胜了几场,平了几场,负了几场?【解法指导】本题中,所有的等量关系只有两个,而未知量有三个•因而所列方程的个数少于未知数的个数,即为不定方程组,但每个未知数量的数目必为非负整数•因此,此题的实质就是滶不定方程的非负整数解的问题.此方程组有两个方和,三个未知数,解法仍然是消元,即消去某一个未知数后,变为二元一次方程,再仿照例1的解法施行.解:设该队胜了x场,平了y场 ,负了z场,依题意可得:错误!②-①得:2x-z=2 ③变形得:z=2x-2∵0≤z≤2∴0≤2x-2≤2即1≤x≤2又x为正整数∴x=1,2相应地,y=3,0 z=0,2答:这个队胜了1场,平了3场,或胜了2,负了2场.【变式题组】01.(佳木斯)为了奖励进步较大的学生,某班决定购买甲、乙、丙三种钢笔作为奖品,其单价分别为4元、5元、6元,购买这些钢笔需要花60元;经过协商,每种钢笔单价下降1元,结果只花了48元,那么可能购买甲种笔().A.11支B.9支C.7支D.5支02.一旅游团50人到一旅舍住宿,旅舍的客户有三人间、二人间、单人间三种•其中三人间的客房每人每晚20元,二人间的客房每人每晚30元,单人间的客房每人每晚50元.(1)若旅游团共住满了20间客房,问三种客房各住了几间?怎样住消费最低?(2)若该旅游团中,夫妻住二人间,单身住三人间,小孩随父母住在一起,现已知有小孩4人(每对夫妻最多只带1个小孩),单身30人,其中男性17人,有两名单身心脏病患者要求住单人间,问这一行人共需多少间客房?【例3】已知:关于x、y的方程组错误!若x>y,求a的取值范围.【解法指导】解本题的指导思想就是构建以a为未知数的不等式•解之即得a的取值范围,构建不等式的依据就是x>y,而解方程组即可用a的代数式分别表示x和y,进而可得不等式.解:解方程组错误!得错误!∵x>y∴2a+1>a-2 解得a>-3故a的取值范围是a>-3.【变式题组】01.已知:关于x的方程3x-(2a-3) =5x+(3a+6)的解是负数,则a的取值范围是_____.02.已知:关于x、y的方程组错误!的解为非负数.(1)求a的取值范围;(2)化简|4a+5|-|a-4|.03.当m 为何值时,关于x 的方程2153166--=--m x m x 的解大于1?4.已知方程组错误! 的解x 、y 都是正数,且x 的值小于y 的值,求m 的取值范围.【例4】(凉州)若不等式{x -a >2,b -2x >0 的解集是-1<x <1,求(a +b )2009的值. 【解法指导】解此不等式组得a +2<x <2b ,而依题意,该不等式的解集又是-1<x <1,而解集是唯一的,因此两解集的边界点分别“吻合”,从而得两等式即得方程组,解之可得a 、b 之值.解:解不等式组错误! 得a +2<x <2b 又∵此不等式组的解集是-1<x <1∴ 错误! 解设错误!∴(a +b )2009=(-1)2009=-1【变式题组】 01.若错误! 的解集为-1<x <2,则a =___________,b =_____________.02.已知:关于x 的不等式组错误!的解集为3≤x <5,则a b 的值为( ) A .-2 B .21- C .-4 D . 41- 03.若关于x 的不等式组错误! 的解集为x <2,则a 的取值范围是___________.04.已知:不等式组错误! 的解庥为-1<x <2,求(a +b )2008的值.【例5】(永春)商场正在销售“福娃"玩具和徽章两种奥运商品,已知购买1盒“福娃”玩具和2盒徽章共需145元;购买2盒“福娃”玩具和3盒徽章共需280元•(1)一盒“福娃"玩具和一盒徽章的价格各是多少元?(2)某公司准备购买这两种奥运商品共20盒送给幼儿园(要求每种商品都要购买),且购买金额不能超过450元,请你帮该公司设计购买方案•【解法指导】本题属材料选择类的方程与不等式结合的实际应用题,但方程组与不等式组是分开的•分析可知:第(1)问只需依照题目主干所提供的两个等量关系即可列出二元一次方程组•第(2)问由题目所给不等关系“购买金额不能超过450元”及第(1)问所求出的数据列出不等式,从而求解•解:(1)设一盒“福娃"玩具和一盒徽章的价格分别为x元和y元.依题意,得错误!解得错误!答:一盒“福娃”玩具和一盒徽章的价格分别是125元和10元.(2)设购买“福娃”玩具m盒,则购买徽章(20-m)盒.由题意,得125m+10(20-m)≤450,解得m≤2。
二十五届希望杯初三二试有答案

第二十五届 希望杯 全国数学邀请赛初三㊀第2试试题一㊁选择题(每小题4分,共40分.)1.I fb o t h a a n d c a r e r e a l n u m b e r s ,2a n d 3a r e t h e t w o s o l u t i o n s o f t h e e qu a t i o n a x 2-10x +c =0f o r x ,t h e n t h e v a l u e o f a +c i s ()(A )10.(B )12.(C )14.(D )16.图12.如图1,在әA B C 中,B C >C A >A B ,D ㊁E ㊁F 分别是A B ㊁B C ㊁C A 边上的点,D E ʊA C ,F D ʊC B ,若A D ʒD B =1ʒ2,则图中的相似三角形有()对.(A )3.(B )4.(C )5.(D )6.3.若a -b =4,a b +c 2+4=0,则a 的值是()(A )2.(B )3.(C )4.(D )5.4.将抛物线y =x 2先向左平移1个单位,再向下平移2个单位,则所得的抛物线的解析式是()(A )y =x 2-2x +1.(B )y =x 2+2x -1.(C )y =x 2+4x +3.(D )y =x 2-2x -1.5.若3x 2-x =1,则9x 4+12x 3-2x 2-7x +2014的值是()(A )2013.(B )2014.(C )2015.(D )2016.6.半径分别是1,2的☉O 1和☉O 2相外切,若半径是3的☉O 3和它们都相切,则满足条件的☉O 3的个数是()(A )6.(B )3.(C )4.(D )5.7.给如图2所示的无水游泳池注水,如果进水速度是均匀的,那么,泳池内水的高度h 随时间t 变化的图象可能是()图28.三角形内的一点和三角形三个顶点的连线将三角形分成三部分,若这三部分的面积比是1ʒ2ʒ3,则这样的点的个数是()(A )1.(B )3.(C )6.(D )9.9.G i v e n p o s i t i v e i n t e g e r m w h i c h i s n o l a r g e r t h a n 10,a n d m 2014+2014mc a nb ed i v i de db y5,t h e n t h en u m b e r o f s u c h m i s()图3(A )2.(B )3.(C )4.(D )5.10.如图3,在平面直角坐标系x O y 中,点A (2,0),M (0,33),N (5,23),N B ʅx 轴于点B ,P 为MN 上一动点,则P A +P B 的最小值为()(A )33.(B )23.(C )323.(D )343.二㊁填空题(每小题4分,共40分.)11.若y =a x 2+b x +c (a ʂ0)的图象如图4所示,则a b c 的值是(填: 正数 ㊁ 负数 或 0 ).12.若关于x 的方程x 2+p x +q =0有两个负根,则直线y =p x +q 不经过第象限.(填: 一 ㊁ 二 ㊁ 三 或 四 )13.已知{x +x y +y =6,x 2+y 2=12,则x 3+y 3的值是.14.在әA B C 中,A C =8,B C =6,øA C B =90ʎ,C D ʅA B 于点D ,若әA B C ㊁әA C D ㊁әB C D的内切圆的半径分别是r 1,r 2,r 3,则r 1+r 2+r 3的值是.15.若关于x 的方程x 2-(m +5)|x |+4=m 恰有3个实数解,则实数m =.16.在平面直角坐标系x O y 中,若直线x =-1,x =3,y =3,y =kx -2围成的四边形的面积是16,则k =.图4F i g .5图6图717.A ss h o w ni n F i g .5,t h e r ea r e3s q u a r e s i nt h er i g h tt r i a n gl e .T h es i d e so ft h et w o s m a l l e r s q u a r e s a r e a a n d4.T h e s i d eo f t h e s qu a r e i n t h em i d d l e i s x ,t h e n x =(i n t e r m s o f a ).18.如图6,在边长为2的正方形A B C D 内有等边三角形C D E ,A C 交D E 于点F ,则S әC F E =.19.如图7,将长为4,宽为2的长方形A B C D 绕顶点A 顺时针旋转90ʎ到达A B ᶄC ᶄD ᶄ,图中的两段弧线分别是顶点C ㊁D 经过的路径,则阴影部分的面积为.(π取3)20.长与宽的比是2ʒ1的长方形称为 特征长方形 .用宽分别为a 1,a 2,a 3,a 4,a 5(a 1<a 2<a 3<a 4<a 5)的5个 特征长方形 拼成的大长方形,记为(a 1,a 2,a 3,a 4,a 5),则大长方形(1,2,a 3,a 4,a 5)的面积最大是.三、解答题.21.(本题满分10分)如图8,在边长为1的正方形A B C D 中,以A 为圆心㊁A B 为半径的弧与以D C 为直径的半圆交于点E ,连结D E 并延长交B C 于F ,连结B E 并延长交D C 于G .(1)求D G ʒG C 的值;(2)求四边形E F C G 的面积.图8图9图1022.(本题满分15分)如图9,排球场总长18m ,设球网高为2m ,运动员站在离网3m 的线上(图中虚线所示)正对网前跳起将球水平击出.以击球点为原点,建立如图10的直角坐标系,球运动的轨迹方程是y =5x 2v2(x ,y 单位:m ),其中v 是球被击出时的速度(单位:m /s ).(1)设击球点在3m 线的正上方,高度为2.5m ,求使球既不触网也不出界的击球速度的范围;(2)若击球点在3m 线的正上方,当高度小于h (单位:m )时,无论水平击球的速度多大,球不是触网就是越界,求h .23.(本题满分15分)如图11,有一束光线,从中心为O 的圆环的A 点射入,在圆环内经过两次反射后从A 点射出;如图12,从A 点射入的光线经过三次反射后从A 点射出.图11图12图13图14(1)如图13,若从A 点射入的光线经过五次反射后从A 点射出,求从A 点射入的光线和圆环半径O A 的夹角α的度数;(2)如图14,若从A 点射入的光线和圆环半径O A 的夹角是50ʎ,则经过几次反射后光线从A 点射出?初三第2试答案21.(1)=2DG GC.(2)760CGEF S =.22.(1)击球速度的范围是v <<;(2)若击球点在3m 线的正上方3215m 处,则无论水平击球的速度多大,球不是触网就是越界.23.(1)60α=︒.(2)经过8次反射后,从A 点出来.。
第25届希望杯初二一试试题解答
一选择题
1化简 (n是自然数)
答案为:
解答:化简得 关键讨论 的值是正1还是负1
即 是偶数还是奇数, 为连续2个整数的乘积,必为偶数;或者分奇数和偶数2种情况分类讨论也可以。
2、分式 的值为0,则b的值为()
答案为b=1
由 =0,b=1或-1,但b=-1时, ,分式无意义,舍去。
3、已知 y是不大于x的最大整数,则 的值是()
答案:
解答: ,即 ,y=2
=
4.反比例函数 的图像上有三个点(x1,y1),(x2,y2),(x2,y2),其中x1<x2<0<x3,则y1,y2,y3的大小关系是(y2<y1<0<y3)
解答:特殊值法,根据x1<x2<0<x3,分别取-2<-1<0<1代入即可。
所以
可得,b=3,或b=4,故解析式为y=-x+3或y=-2x+4
24、如图,正方形OCBA的顶点B和正方形AFED的顶点E都在函数 (x>0)的图像上,则点E到X轴的距离是_______,到y轴的距离是________.
答案:
解答:如图
点E(1+x,x),(1+x)x=1,由求根公式得。
25.如图,Rt⊿ABC中,∠C=900,CB=3,AC=4,且CB在直线l上,将⊿ABC绕点B顺时针旋转到位置(1),可得到点P1,此时CP1=_____,将位置(1)⊿ABC绕点P1顺时针旋转到位置(2)可得到P2,将位置(2)⊿ABC绕点P2顺时针旋转到位置(3)可得到P3,…,按此规律继续旋转,直到点P2014为止,则CP2014=________。
小学四年级希望杯历年数学竞赛试题和答案解析1_14届[最新[全套](完整版)]
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
第16届“希望杯”全国数学邀请赛试题 初中一年级 第1试:参考答案
第16届“希望杯”全国数学邀请赛试题初中一年级第1试:
参考答案
佚名
【期刊名称】《数理天地:初中版》
【年(卷),期】2017(000)006
【总页数】5页(P36-40)
【正文语种】中文
【中图分类】G4
【相关文献】
1.建模思想在小学数学教学中的渗透——一个“希望杯”全国数学邀请赛试题的启示
2.认识问题本质,追求自然解法——一道"希望杯"全国初中数学邀请赛试题的解
法及变式探究3.第五届"创新杯"全国数学邀请赛(复试)初中一年级试题4.《第十四
届“希望杯”全国数学邀请赛》(初一第1试)答案/9月份《数学竞赛训练题》参考答案5.第一届小学“希望杯”全国数学邀请赛试题答案(四年级第1试)
因版权原因,仅展示原文概要,查看原文内容请购买。
历届(1-23)希望杯数学竞赛初一七年级真题及答案(最新整理WORD版)
“希望杯”全国数学竞赛(第1-23届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题............................................. 003-0052.希望杯第一届(1990年)初中一年级第二试试题............................................. 010-0123.希望杯第二届(1991年)初中一年级第一试试题............................................. 016-0204.希望杯第二届(1991年)初中一年级第二试试题............................................. 022-0265.希望杯第三届(1992年)初中一年级第一试试题............................................. 029-0326.希望杯第三届(1992年)初中一年级第二试试题............................................. 034-0407.希望杯第四届(1993年)初中一年级第一试试题............................................. 043-0508.希望杯第四届(1993年)初中一年级第二试试题............................................. 050-0589.希望杯第五届(1994年)初中一年级第一试试题............................................. 057-06610.希望杯第五届(1994年)初中一年级第二试试题 .......................................... 063-07311.希望杯第六届(1995年)初中一年级第一试试题 ........................................... 070-080 12希望杯第六届(1995年)初中一年级第二试试题........................................... 077-08713.希望杯第七届(1996年)初中一年级第一试试题........................................... 086-09814.希望杯第七届(1996年)初中一年级第二试试题............................................. 91-10515.希望杯第八届(1997年)初中一年级第一试试题............................................. 99-11316.希望杯第八届(1997年)初中一年级第二试试题........................................... 106-12017.希望杯第九届(1998年)初中一年级第一试试题........................................... 114-12918.希望杯第九届(1998年)初中一年级第二试试题........................................... 123-13819.希望杯第十届(1999年)初中一年级第二试试题........................................... 130-14720.希望杯第十届(1999年)初中一年级第一试试题........................................... 148-15121.希望杯第十一届(2000年)初中一年级第一试试题....................................... 143-16122.希望杯第十一届(2000年)初中一年级第二试试题....................................... 150-16923.希望杯第十二届(2001年)初中一年级第一试试题....................................... 154-17424.希望杯第十二届(2001年)初中一年级第二试试题....................................... 158-17825.希望杯第十三届(2002年)初中一年级第一试试题....................................... 164-18426.希望杯第十三届(2001年)初中一年级第二试试题....................................... 168-18927.希望杯第十四届(2003年)初中一年级第一试试题....................................... 175-19628.希望杯第十四届(2003年)初中一年级第二试试题....................................... 179-20029.希望杯第十五届(2004年)初中一年级第一试试题 (183)30.希望杯第十五届(2004年)初中一年级第二试试题 (184)31.希望杯第十六届(2005年)初中一年级第一试试题....................................... 213-21832.希望杯第十六届(2005年)初中一年级第二试试题 (184)33.希望杯第十七届(2006年)初中一年级第一试试题....................................... 228-23334.希望杯第十七届(2006年)初中一年级第二试试题....................................... 234-23835.希望杯第十八届(2007年)初中一年级第一试试题....................................... 242-246 26.希望杯第十八届(2007年)初中一年级第二试试题....................................... 248-25137.希望杯第十九届(2008年)初中一年级第一试试题....................................... 252-25638.希望杯第十九届(2008年)初中一年级第二试试题....................................... 257-26239.希望杯第二十届(2009年)初中一年级第一试试题....................................... 263-26620.希望杯第二十届(2009年)初中一年级第二试试题....................................... 267-27121.希望杯第二十一届(2010年)初中一年级第一试试题 ................................... 274-27622.希望杯第二十二届(2011年)初中一年级第二试试题 ................................... 285-28823.希望杯第二十三届(2012年)初中一年级第二试试题 ................................... 288-301希望杯第一届(1990年)初中一年级第1试试题一、选择题(每题1分,共10分)1.如果a ,b 都代表有理数,并且a +b=0,那么 ( )A .a ,b 都是0.B .a ,b 之一是0.C .a ,b 互为相反数.D .a ,b 互为倒数.2.下面的说法中正确的是 ( )A .单项式与单项式的和是单项式.B .单项式与单项式的和是多项式.C .多项式与多项式的和是多项式.D .整式与整式的和是整式.3.下面说法中不正确的是 ( )A. 有最小的自然数. B .没有最小的正有理数.C .没有最大的负整数.D .没有最大的非负数.4.如果a ,b 代表有理数,并且a +b 的值大于a -b 的值,那么( ) A .a ,b 同号. B .a ,b 异号.C .a >0. D .b >0.5.大于-π并且不是自然数的整数有( ) A .2个. B .3个.C .4个. D .无数个.6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身.这四种说法中,不正确的说法的个数是 ( )A .0个.B .1个.C .2个.D .3个.7.a 代表有理数,那么,a 和-a 的大小关系是 ( )A .a 大于-a .B .a 小于-a .C .a 大于-a 或a 小于-a .D .a 不一定大于-a .8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( )A .乘以同一个数.B .乘以同一个整式.C .加上同一个代数式.D .都加上1.9.杯子中有大半杯水,第二天较第一天减少了10%,第三天又较第二天增加了10%,那么,第三天杯中的水量与第一天杯中的水量相比的结果是( )A .一样多.B .多了.C .少了.D .多少都可能.10.轮船往返于一条河的两码头之间,如果船本身在静水中的速度是固定的,那么,当这条河的水流速度增大时,船往返一次所用的时间将( )A .增多.B .减少.C .不变.D .增多、减少都有可能.二、填空题(每题1分,共10分)1. 21115160.01253(87.5)(2)4571615⨯-⨯-÷⨯+--= ______. 2.198919902-198919892=______.3.2481632(21)(21)(21)(21)(21)21+++++-=________. 4. 关于x 的方程12148x x +--=的解是_________. 5.1-2+3-4+5-6+7-8+…+4999-5000=______.6.当x=-24125时,代数式(3x 3-5x 2+6x -1)-(x 3-2x 2+x -2)+(-2x 3+3x 2+1)的值是____. 7.当a=-0.2,b=0.04时,代数式272711()(0.16)()73724a b b a a b --++-+的值是______. 8.含盐30%的盐水有60千克,放在秤上蒸发,当盐水变为含盐40%时,秤得盐水的重是______克.9.制造一批零件,按计划18天可以完成它的13.如果工作4天后,工作效率提高了15,那么完成这批零件的一半,一共需要______天.10.现在4点5分,再过______分钟,分针和时针第一次重合.答案与提示一、选择题1.C 2.D 3.C 4.D 5.C 6.B 7.D 8.D 9.C 10.A提示:1.令a=2,b=-2,满足2+(-2)=0,由此2.x2,2x2,x3都是单项式.两个单项式x3,x2之和为x3+x2是多项式,排除A.两个单项式x2,2x2之和为3x2是单项式,排除B.两个多项式x3+x2与x3-x2之和为2x3是个单项式,排除C,因此选D.3.1是最小的自然数,A正确.可以找到正所以C“没有最大的负整数”的说法不正确.写出扩大自然数列,0,1,2,3,…,n,…,易知无最大非负数,D正确.所以不正确的说法应选C.5.在数轴上容易看出:在-π右边0的左边(包括0在内)的整数只有-3,-2,-1,0共4个.选C.6.由12=1,13=1可知甲、乙两种说法是正确的.由(-1)3=-1,可知丁也是正确的说法.而负数的平方均为正数,即负数的平方一定大于它本身,所以“负数平方不一定大于它本身”的说法不正确.即丙不正确.在甲、乙、丙、丁四个说法中,只有丙1个说法不正确.所以选B.7.令a=0,马上可以排除A、B、C,应选D.8.对方程同解变形,要求方程两边同乘不等于0的数.所以排除A.我们考察方程x-2=0,易知其根为x=2.若该方程两边同乘以一个整式x-1,得(x-1)(x -2)=0,其根为x=1及x=2,不与原方程同解,排除B.若在方程x-2=0两边加上同一个代数式去了原方程x=2的根.所以应排除C.事实上方程两边同时加上一个常数,新方程与原方程同解,对D,这里所加常数为1,因此选D.9.设杯中原有水量为a,依题意可得,第二天杯中水量为a×(1-10%)=0.9a;第三天杯中水量为(0.9a)×(1+10%)=0.9×1.1×a;第三天杯中水量与第一天杯中水量之比为所以第三天杯中水量比第一天杯中水量少了,选C.10.设两码头之间距离为s,船在静水中速度为a,水速为v0,则往返一次所用时间为设河水速度增大后为v,(v>v0)则往返一次所用时间为由于v-v0>0,a+v0>a-v0,a+v>a-v所以(a+v0)(a+v)>(a-v0)(a-v)∴t0-t<0,即t0<t.因此河水速增大所用时间将增多,选A.二、填空题提示:2.198919902-198919892=(19891990+19891989)×(19891990-19891989)=(19891990+19891989)×1=39783979.3.由于(2+1)(22+1)(24+1)(28+1)(216+1)=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)=(22-1)(22+1)(24+1)(28+1)(216+1)=(24-1)(24+1)(28+1)(216+1)=(28-1)(28+1)(216+1)=(216-1)(216+1)=232-1.2(1+x)-(x-2)=8,2+2x-x+2=8解得;x=45.1-2+3-4+5-6+7-8+…+4999-5000=(1-2)+(3-4)+(5-6)+(7-8)+…+(4999-5000)=-2500.6.(3x3-5x2+6x-1)-(x3-2x2+x-2)+(-2x3+3x2+1)=5x+27.注意到:当a=-0.2,b=0.04时,a2-b=(-0.2)2-0.04=0,b+a+0.16=0.04-0.2+0.16=0.8.食盐30%的盐水60千克中含盐60×30%(千克)设蒸发变成含盐为40%的水重x克,即0.001x千克,此时,60×30%=(0.001x)×40%解得:x=45000(克).10.在4时整,时针与分针针夹角为120°即希望杯第一届(1990年)初中一年级第2试试题一、选择题(每题1分,共5分)以下每个题目里给出的A,B,C,D四个结论中有且仅有一个是正确的.请你在括号填上你认为是正确的那个结论的英文字母代号.1.某工厂去年的生产总值比前年增长a%,则前年比去年少的百分数是( )A.a%.B.(1+a)%. C.1100aa+D.100aa+2.甲杯中盛有2m毫升红墨水,乙杯中盛有m毫升蓝墨水,从甲杯倒出a毫升到乙杯里, 0<a<m,搅匀后,又从乙杯倒出a毫升到甲杯里,则这时( )A.甲杯中混入的蓝墨水比乙杯中混入的红墨水少.B.甲杯中混入的蓝墨水比乙杯中混入的红墨水多.C.甲杯中混入的蓝墨水和乙杯中混入的红墨水相同.D.甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定.3.已知数x=100,则( )A.x是完全平方数.B.(x-50)是完全平方数.C.(x-25)是完全平方数.D.(x+50)是完全平方数.4.观察图1中的数轴:用字母a,b,c依次表示点A,B,C对应的数,则111,,ab b a c-的大小关系是( )A.111ab b a c<<-; B.1b a-<1ab<1c; C.1c<1b a-<1ab; D.1c<1ab<1b a-.5.x=9,y=-4是二元二次方程2x2+5xy+3y2=30的一组整数解,这个方程的不同的整数解共有( )A.2组.B.6组.C.12组.D.16组.二、填空题(每题1分,共5分)1.方程|1990x-1990|=1990的根是______.2.对于任意有理数x,y,定义一种运算*,规定x*y=ax+by-cxy,其中的a,b,c表示已知数,等式右边是通常的加、减、乘运算.又知道1*2=3,2*3=4,x*m=x(m≠0),则m 的数值是______.3.新上任的宿舍管理员拿到20把钥匙去开20个房间的门,他知道每把钥匙只能开其中的一个门,但不知道每把钥匙是开哪一个门的钥匙,现在要打开所有关闭着的20个房间,他最多要试开______次.4.当m=______时,二元二次六项式6x2+mxy-4y2-x+17y-15可以分解为两个关于x,y 的二元一次三项式的乘积.5.三个连续自然数的平方和(填“是”或“不是”或“可能是”)______某个自然数的平方.三、解答题(写出推理、运算的过程及最后结果.每题5分,共15分)1.两辆汽车从同一地点同时出发,沿同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆车前进60公里,两车都必须返回出发地点,但是可以不同时返回,两车相互可借用对方的油.为了使其中一辆车尽可能地远离出发地点,另一辆车应当在离出发地点多少公里的地方返回?离出发地点最远的那辆车一共行驶了多少公里?2.如图2,纸上画了四个大小一样的圆,圆心分别是A,B,C,D,直线m通过A,B,直线n通过C,D,用S表示一个圆的面积,如果四个圆在纸上盖住的总面积是5(S-1),直线m,n之间被圆盖住的面积是8,阴影部分的面积S1,S2,S3满足关系式S3=13S1=13S2,求S.3.求方程11156x y z++=的正整数解.答案与提示一、选择题1.D 2.C 3.C 4.C 5.D提示:1.设前年的生产总值是m,则去年的生产总值是前年比去年少这个产值差占去年的应选D.2.从甲杯倒出a毫升红墨水到乙杯中以后:再从乙杯倒出a毫升混合墨水到甲杯中以后:乙杯中含有的红墨水的数量是①乙杯中减少的蓝墨水的数量是②∵①=②∴选C.∴x-25=(10n+2+5)2可知应当选C.4.由所给出的数轴表示(如图3):可以看出∴①<②<③,∴选C.5.方程2x2+5xy+3y2=30可以变形为(2x+3y)(x+y)=1·2·3·5∵x,y是整数,∴2x+3y,x+y也是整数.由下面的表可以知道共有16个二元一次方程组,每组的解都是整数,所以有16组整数组,应选D.二、填空题提示:1.原方程可以变形为|x-1|=1,即x-1=1或-1,∴x=2或0.2.由题设的等式x*y=ax+by-cxy及x*m=x(m≠0)得a·0+bm-c·0·m=0,∴bm=0.∵m≠0,∴b=0.∴等式改为x*y=ax-cxy.∵1*2=3,2*3=4,解得a=5,c=1.∴题设的等式即x*y=5x-xy.在这个等式中,令x=1,y=m,得5-m=1,∴m=4.3.∵打开所有关闭着的20个房间,∴最多要试开4.利用“十字相乘法”分解二次三项式的知识,可以判定给出的二元二次六项式6x2+mxy-4y2-x+17y-15中划波浪线的三项应当这样分解:3x -52x +3现在要考虑y,只须先改写作然后根据-4y2,17y这两项式,即可断定是:由于(3x+4y-5)(2x-y+3)=6x2+5xy-4y2-x+17y-15就是原六项式,所以m=5.5.设三个连续自然数是a-1,a,a+1,则它们的平方和是(a-1)2+a2+(a+1)2=3a2+2,显然,这个和被3除时必得余数2.另一方面,自然数被3除时,余数只能是0或1或2,于是它们可以表示成3b,3b+1,3b+2(b是自然数)中的一个,但是它们的平方(3b)2=9b2(3b+1)2=9b2+6b+1,(3b+2)2=9b2+12b+4=(9b2+12b+3)+1被3除时,余数要么是0,要么是1,不能是2,所以三个连续自然数平方和不是某个自然数的平方.三、解答题1.设两辆汽车一为甲一为乙,并且甲用了x升汽油时即回返,留下返程需的x桶汽油,将多余的(24-2x)桶汽油给乙.让乙继续前行,这时,乙有(24-2x)+(24-x)=48-3x桶汽油,依题意,应当有48-3x≤24,∴x≥8.甲、乙分手后,乙继续前行的路程是这个结果中的代数式30(48-4x)表明,当x的值愈小时,代数式的值愈大,因为x≥8,所以当x=8时,得最大值30(48-4·8)=480(公里),因此,乙车行驶的路程一共是2(60·8+480)=1920(公里).2.由题设可得即2S-5S3=8……②∴x,y,z都>1,因此,当1<x≤y≤z时,解(x,y,z)共(2,4,12),(2,6,6),(3,3,6),(3,4,4)四组.由于x,y,z在方程中地位平等.所以可得如下表所列的15组解.希望杯第二届(1991年)初中一年级第1试试题一、选择题(每题1分,共15分)以下每个题目的A,B,C,D四个结论中,仅有一个是正确的,请在括号内填上正确的那个结论的英文字母代号.1.数1是( )A.最小整数.B.最小正数.C.最小自然数.D.最小有理数.2.若a>b,则( )A.11a b; B.-a<-b.C.|a|>|b|.D.a2>b2.3.a为有理数,则一定成立的关系式是( )A.7a>a.B.7+a>a.C.7+a>7.D.|a|≥7.4.图中表示阴影部分面积的代数式是( )A.ad+bc.B.c(b-d)+d(a-c).C.ad+c(b-d).D.ab-cd.5.以下的运算的结果中,最大的一个数是( )A.(-13579)+0.2468; B.(-13579)+1 2468;C.(-13579)×12468; D.(-13579)÷124686.3.1416×7.5944+3.1416×(-5.5944)的值是( ) A.6.1632. B.6.2832.C.6.5132.D.5.3692.7.如果四个数的和的14是8,其中三个数分别是-6,11,12,则笫四个数是( )A.16. B.15. C.14. D.13.8.下列分数中,大于-13且小于-14的是( )A.-1120; B.-413; C.-316; D.-617.9.方程甲:34(x-4)=3x与方程乙:x-4=4x同解,其根据是( )A.甲方程的两边都加上了同一个整式x.B.甲方程的两边都乘以43x;C. 甲方程的两边都乘以43; D. 甲方程的两边都乘以34.10.如图: ,数轴上标出了有理数a,b,c的位置,其中O是原点,则111,,a b c的大小关系是( ) A.111a b c>>; B.1b >1c >1a ; C. 1b >1a >1c ; D. 1c >1a >1b .11.方程522.2 3.7x =的根是( ) A .27. B .28. C .29. D .30. 12.当x=12,y=-2时,代数式42x y xy -的值是( )A .-6.B .-2.C .2.D .6.13.在-4,-1,-2.5,-0.01与-15这五个数中,最大的数与绝对值最大的那个数的乘积是( )A .225.B .0.15.C .0.0001.D .1.14.不等式124816x x x xx ++++>的解集是( ) A .x <16. B .x >16.C .x <1. D.x>-116. 15.浓度为p%的盐水m 公斤与浓度为q%的盐水n 公斤混合后的溶液浓度是 ( ) A.%2p q +; B.()%mp nq +; C.()%mp nq p q ++;D.()%mp nq m n++.二、填空题(每题1分,共15分)1. 计算:(-1)+(-1)-(-1)×(-1)÷(-1)=______. 2. 计算:-32÷6×16=_______. 3. 计算:(63)36162-⨯=__________.4. 求值:(-1991)-|3-|-31||=______. 5. 计算:1111112612203042-----=_________. 6.n 为正整数,1990n -1991的末四位数字由千位、百位、十位、个位、依次排列组成的四位数是8009.则n 的最小值等于______.7. 计算:19191919199191919191⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=_______.8. 计算:15[(-1989)+(-1990)+(-1991)+(-1992)+(-1993)]=________.9.在(-2)5,(-3)5,512⎛⎫-⎪⎝⎭,513⎛⎫-⎪⎝⎭中,最大的那个数是________.10.不超过(-1.7)2的最大整数是______.11.解方程21101211,_____. 3124x x xx-++-=-=12.求值:355355113113355113⎛⎫---⎪⎝⎭⎛⎫- ⎪⎝⎭=_________.13.一个质数是两位数,它的个位数字与十位数字的差是7,则这个质数是______.14.一个数的相反数的负倒数是119,则这个数是_______.15.如图11,a,b,c,d,e,f均为有理数.图中各行,各列、两条对角线上三个数之和都相等,则ab cd efa b c d e f+++++++=____.答案与提示一、选择题1.C 2.B 3.B 4.C 5.C 6.B 7.B 8.B 9.C 10.B 11.D 12.A 13.B 1 4.A 15.D提示:1.整数无最小数,排除A;正数无最小数,排除B;有理数无最小数,排除D.1是最小自然数.选C.有|2|<|-3|,排除C;若2>-3有22<(-3)2,排除D;事实上,a>b必有-a<-b.选B.3.若a=0,7×0=0排除A;7+0=7排除C|0|<7排除D,事实上因为7>0,必有7+a>0+a=a.选B.4.把图形补成一个大矩形,则阴影部分面积等于ab-(a-c)(b-d)=ab-[ab-ad-c(b-d)]=ab-ab+ad+c(b-d)=ad+c(b-d).选C.5.运算结果对负数来说绝对值越小其值越大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第25届希望杯九年级第一试
一、选择题
1. 以下三角形中与图1中的三角形相似的是( )
2. 某商品原价200元,先降价a %,又提价a %,售价是182元,则下列关系式中正确的是( )
A .200(1-a %)÷(1+a %)=182
B .182(1-a %)÷(1+a %)=200
C .200(1+a %)÷(1-a %)=182
D .182÷(1-a %)÷(1+a %)=200
3. 一个几何体的三视图如图2所示,则该几何体可能是下列四个选项中的( )
4. 若关于x 的一元二次方程(m -2)x 2+3x +m 2
-5m +6=0的常数项为0,则m 的值是( )
A .2
B .3
C .2或3
D .0
5. 方程|x -2014|=2014-x 的正整数解有( )
A .2013个
B .2014个
C .2015个
D .无穷多个
6. 在△ABC 中,若AC BC =AB △ABC 的面积为( )
A .10
B .23
C .11
D .6
7. Given equation
ofx ,then the number of solutions for this equation is ( ) A .0 B .1 C .2 D .countless
8. 若6x x +=,则x =( )
A .2
B .-2
C .±2
D .12
± 9. 如图3,AB =AC ,AD =DE =EC =BC ,则∠ABC 的度数为( )
A .30°
B .40°
C .45°
D .60°
10. 如图4,设AB 是⊙O 的弦,CD 是⊙O 直径,且CD 与AB 相交,若m =|S △CAB -S △DAB |,n =S △OAB ,则( )
A .m >2n
B .m =2n
C .m <2n
D .m 与2n 的大小不确定
11.若y2+4y+2=0,则
2
42
24
y
y y
-+
=.
12.如图5,矩形ABCD中,AB=60,BD=BC+2
3
CD,则BC==.
13.In△ABC as shown in Fig.6,∠ABC=40°,∠BAC=60°.Both BD and CD are the interior angle bisectors of△ABC
which intersect at point D,BE and CE are exterior angle bisectors of△ABC which intersect at point E,then∠BDC -∠BEC=°.
14.有1g,2g,5g,10g的砝码各2个,从中任取2个放在已经平衡的天平的两端,则天平仍然保持平衡的概率
P=.
15.如图7,将等边△ABC的外接圆对折,使点A与弧BC的中点F重合,折痕与边AB、AC分别交于点D、E.若
BC=3,则△ADE的面积是.
16.如图8,Rt△ABC中,∠C=90°,AC=2,BC=1.若以C为圆心,CB为半径的圆交AB于点D,则AD
DB
=.
17.在平面直角坐标系中,抛物线C经过点A(3,8),B(7,8),且与x轴恰有1个交点,则抛物线C上纵坐标为
32的两个点的距离为.
18.如图9等边△AFG被线段BC、DE分割成周长相等的三部分:等边三角形ACB、梯形BCED、梯形DEGF,
其面积分别为S1,S2,S3,若S2=63,则S1-S3=.
19.如图10,四边形ABCD中,∠ABC=∠CDA=90°,AD=DC=5,AB=7,BC=1,则BD=.
20.正方体骰子的每个面内都写了一个正整数.随意地投掷这样的两个骰子,若朝上的两个面内的数的和为偶数
的概率最小是P,则P=.
21.若关于x的方程(x-2)(x-4)=(p-2)(p-4)的两个实数根x1,x2是某直角三角形的两条直角边的长,则此直角三
角形的面积最大是,此时p=.
22.If x,y,and z satisfy the equation x y z
=++,then x+y+z=,and xyz=.23.若△ABC的三条边长a,b,c满足b+c=10,bc=a2-12a+61,则△ABC的周长等于,面积等于.
24.如图11,在平面直角坐标系xOy中,反比例函数
k
y
x
=(x>0)的图象交矩形OBCD的边BC于点E,交CD于
F点,且DF=1
4
CD.若四边形OECF的面积为24,则k=,S△OEF=.
25.在直角坐标系xOy中,抛物线y=ax2+bx+c(a,b,c是正整数)与x轴有两个不同的交点A(x1,0),B(x2,0).若
|x1|和|x2|都大于1,则abc的最小值是,此时a+b+c=.。
