3-8四节点矩形单元讲解
第四讲 矩形单元

a1 ~ a8
代换为节点位移分量:
u N k uk Nl ul N mum N nun Niui
v N k vk Nl vl N mvm N nvn Ni vi
写成矩阵形式为:
u e N v
•
由应力~应变关系得到:
DB S
e
e
•
对于矩形单元,其单元上应力、应变不再是常数,而 是一定程度上呈线性变化,即:x方向正应变、正应 力随y坐标线性变化;y方向正应变和正应力随x坐标 线性变化。因此,在一定条件下,精度会高一阶。
0 b y 0 b y 0 b y 0 b y B 1 0 a x 0 a x 0 a x 0 ax 4ab a x b y a x b y a x b y a x b y
N
为形函数矩阵。
Nk N 0
0 Nk
Nl 0
0 Nl
Nm 0
0 Nm
Nn 0
0 Nn
•
各形函数为:
1 x y (1 )(1 ) 4 a b 1 x y N l (1 )(1 ) 4 a b 1 x y N m (1 )(1 ) 4 a b 1 x y N n (1 )(1 ) 4 a b Nk
5 矩形单元
• 三节点三角形单元精度低,在单元内不能反映应力
应变的变化。这一切是因为该单元只有3个节点,
单元自由度少,单元位移模式只能是线性的,描述 单元内位移变化的能力差。
•
解决这个问题的一个办法是采用具有更多节点数的高
单元类型

LINK1可承受单轴拉压的单元,不能承受弯矩作用LINK8三维杆(或桁架)单元,用来模拟:桁架、缆索、连杆、弹簧等等,是杆轴方向的拉压单元,每个节点具有三个自由度:沿节点坐标系X、Y、Z方向的平动LINK32二维热传导杆单元,应用在二维(板或轴对称)稳态或瞬态热分析PLANE2 2维6节点三角形实体结构单元,可用作平面单元 (平面应力或平面应变),也可以用作轴对称单元Beam3可承受拉、压、弯作用的单轴单元,每个节点有三个自由度,即沿x,y 方向的线位移及绕Z轴的角位移Beam4承受拉、压、弯、扭的单轴受力单元,每个节点上有六个自由度:x、y、z三个方向的线位移和绕x,y,z三个轴的角位移SOLID5三维耦合场体单元,8个节点,每个节点最多有6个自由度PLANE13 2 维耦合场实体单元,有 4 个节点,每个节点最多有 4 个自由度PLANE25 4 节点轴对称谐波结构单元,用于承受非轴对称载荷2 维轴对称结构的建模PLANE35 2 维 6 节点三角形热实体单元,用作平面单元或轴对称单元PLANE42 2 维实体结构单元,作平面单元 (平面应力或平面应变),也可以用作轴对称单元。
本单元有 4 个节点,每个节点有 2 个自由度,分别为 x 和 y 方向的平移Shell43 4 节点塑性大应变单元,适合模拟线性、弯曲及适当厚度的壳体结构。
单元中每个节点具有六个自由度:沿x、y和z 方向的平动自由度以及绕x、y和z 轴的转动自由度PLANE53 2 维 8 节点磁实体单元,用于 2 维 (平面和轴对称) 磁场问题的建模PLANE55 2 维 4 节点热实体单元,作为平面单元或轴对称环单元,用于 2 维热传导分析。
本单元有 4 个节点,每个节点只有一个自由度–温度Shell63弹性壳单元,具有弯曲能力和又具有膜力,可以承受平面内荷载和法向荷载。
本单元每个节点具有6个自由度:沿节点坐标系X、Y、Z方向的平动和沿节点坐标系X、Y、Z轴的转动SOLID64 3-D 各向异性结构实体单元,用于各向异性实体结构的3D建模。
第七章 平面问题的有限单元法(Q4)

8
4节点四边形单元
y, v
u1 v 1 u2 u de 2 u3 u3 u4 u 4 displacements at node 1 displacements at node 2 displacements at node 3 displacements at node 4
x 1 2 3 4 N1 x1 N 2 x2 N 3 x3 N 4 x4 y 1 2 3 4 N1 y1 N 2 y2 N 3 y3 N 4 y4
1 N (1 )(1 ) 1 4 N 1 (1 )(1 ) 2 4 1 N (1 )(1 ) 3 4 N 1 (1 )(1 ) 4 4
1 4
Nj 1 4 (1 j )(1 j )
4 ( 1, +1) ( u4, v4)
1
N3 1 4 (1 )(1 ) N4 1 4 (1 )(1 )
N 3 at node 1 1 4 (1 )(1 ) 1 0 N 3 at node 2 1 4 (1 )(1 ) 1 0
同理:
1 1 1 1 1 y1 2 1 1 1 1 1 y2 1 1 1 1 4 3 y3 1 1 1 1 y4 4
K e B DBtd
e
T
11
等参单元
对于一般的四边形单元,在总体坐标系下构造 位移插值函数,则计算形状函数矩阵、单元刚 度矩阵及等效节点载荷列阵时十分冗繁;而对 于矩形单元,相应的计算要简单的多。 矩形单元明显的缺点是不能很好的符合曲线边 界,因此可以采用矩形单元和三角形单元混合 使用(网格划分困难)。更为一般的方法是通 过等参变换将局部自然坐标系内的规格化矩形 单元变换为总体坐标系内的任意四边形单元( 包括高次曲边四边形单元)。 等参单元的提出为有限元法成为现代工程实
第九讲 有限元
x 0 y 1 2 xy 2(1 )
平面应变问题弹性矩阵D
6. 单元刚度矩阵
[ K e ] [ B]T [ D][B]d (vol)
V
a b
a b
[ B]T [ D][B]tdxdy t——厚度
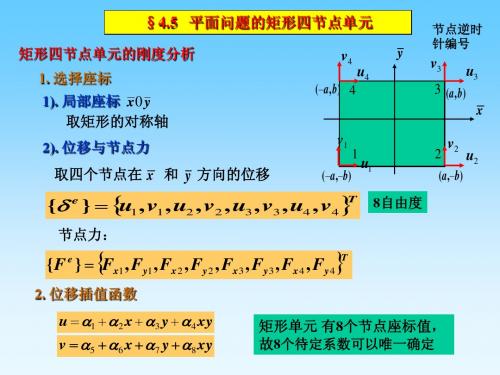
§4.5 平面问题的矩形四节点单元
矩形四节点单元的刚度分析 1. 选择座标 1). 局部座标 x0 y 取矩形的对称轴 2). 位移与节点力
v4
( a , b ) 4
y
节点逆时 针编号
u4
v3
3 (a , b)
u3
x
v1
(a,b)
1
T
取四个节点在 x 和 y 方向的位移
e
u1
8自由度
2
v2
u2
v 5 6 x 7 y 8 xy
矩形单元 有8个节点座标值, 故8个待定系数可以唯一确定
u 1 2 x 3 y 4 xy
v 5 6 x 7 y 8 xy
1 2 3 u 1 x y xy 0 0 0 0 4 0 0 0 0 1 x y xy 5 v 6 7 8
e E T T A
Fx1 N1 F 0 y1 N Fx 2 2 F t 0 y2 N3 Fx 3 0 F y3
E
0 0 N1q y N1 0 0 0 dxdy t N q dxdy N 2 q y 2 y 0 0 N 3q y N3
[B]——矩形4节点单元几何矩阵 简写成:
ansys单元类型介绍

LINK1可承受单轴拉压的单元,不能承受弯矩作用PLANE22维6节点三角形实体结构单元,可用作平面单元(平面应力或平面应变),也可以用作轴对称单元Beam3可承受拉、压、弯作用的单轴单元,每个节点有三个自由度,即沿x,y 方向的线位移及绕Z轴的角位移Beam4承受拉、压、弯、扭的单轴受力单元,每个节点上有六个自由度:x、y、z三个方向的线位移和绕x,y,z三个轴的角位移SOLID5三维耦合场体单元,8个节点,每个节点最多有6个自由度LINK8三维杆(或桁架)单元,用来模拟:桁架、缆索、连杆、弹簧等等,是杆轴方向的拉压单元,每个节点具有三个自由度:沿节点坐标系X、Y、Z方向的平动PLANE13 2 维耦合场实体单元,有 4 个节点,每个节点最多有 4 个自由度PLANE25 4 节点轴对称谐波结构单元,用于承受非轴对称载荷2 维轴对称结构的建模LINK32二维热传导杆单元,应用在二维(板或轴对称)稳态或瞬态热分析PLANE35 2 维 6 节点三角形热实体单元,用作平面单元或轴对称单元PLANE42 2 维实体结构单元,作平面单元(平面应力或平面应变),也可以用作轴对称单元。
本单元有 4 个节点,每个节点有 2 个自由度,分别为 x 和y 方向的平移Shell43 4 节点塑性大应变单元,适合模拟线性、弯曲及适当厚度的壳体结构。
单元中每个节点具有六个自由度:沿x、y和z 方向的平动自由度以及绕x、y和z 轴的转动自由度PLANE53 2 维 8 节点磁实体单元,用于 2 维 (平面和轴对称) 磁场问题的建模PLANE55 2 维 4 节点热实体单元,作为平面单元或轴对称环单元,用于 2 维热传导分析。
本单元有 4 个节点,每个节点只有一个自由度 – 温度Shell63弹性壳单元,具有弯曲能力和又具有膜力,可以承受平面内荷载和法向荷载。
本单元每个节点具有6个自由度:沿节点坐标系X、Y、Z方向的平动和沿节点坐标系X、Y、Z轴的转动SOLID64 3-D 各向异性结构实体单元,用于各向异性实体结构的3D建模。
四节点矩形单元有限元分析

e
1 0
0 0 1 2
(b y ) (a x ) (b y ) (a x ) (b y ) (a x ) (b y ) (a x ) E (b y ) S (a x ) (b y ) (a x ) (b y ) (a x ) (b y ) (a x ) 2 4ab(1 ) 1 1 1 1 1 1 1 1 (a x ) (b y ) (a x ) (b y ) (a x ) (b y ) (a x ) ( b y ) 2 2 2 2 2 2 2 2
Tianjin University
四节点矩形单元有限元分析过程
六、物理方程求解应力
由平面问题物理方程可得:
D D B
其中:
1 E D 2 (1 ) 0 因此,应力矩阵 S 为:
e
S
三节点三角形单元精度低,收敛慢,由于单元内应力 和应变均为常量,故在单元内不能很好地反映应力和 应变的变化。 该单元只有三个节点,单元自由度少,单元位移插值
函数(位移模式)只能是线性函数,描述单元内位移
变化的能力差。
Tianjin University
分析提高有限元求解精度的途径
二、提高有限元求解精度的途径
Tianjin University
四节点矩形单元有限元分析过程
其中,形函数为:
1 x y N k (1 )(1 ) 4 a b 1 x y N l (1 )(1 ) 4 a b 1 x y N m (1 )(1 ) 4 a b 1 x y N n (1 )(1 ) 4 a b
ANSYS中单元类型的选择

实际选用单元类型的时候,到底是选择第一类还是选择第二类呢?也就是到底是选用六面体还是带中 间节点的四面体呢? 如果所分析的结构比较简单,可以很方便的全部划分为六面体单元,或者绝大部分是六面体,只含有少 量四面体和棱柱体,此时,应该选用第一类单元,也就是选用六面体单元;如果所分析的结构比较复杂, 难以划分出六面体,应该选用第二类单元,也就是带中间节点的四面体单元。 新手最容易犯的一个错误就是选用了第一类单元类型(六面体单元),但是,在划分网格的时候,由于结 构比较复杂,六面体划分不出来,单元全部被划分成了四面体,也就是退化的六面体单元,这种情况,
Beam44 3 维弹性锥形不对称梁。单轴元素,具有拉压扭和弯曲能力。该元素每个节点有 6 个自由度:x,y,z 和绕 x,y,z 方向。该元素允许每个端点具有不均匀几何特性,并且允许端 点与梁的中性轴偏移。若不需要这些特性,可采用 beam4。该元素的 2 维形式是 beam54。该 元素也提供剪应变选项。还提供了输出作用于单元上的与单元同方向的力的选项。具有应力 强化和大变形能力。
3.实体单元的选择
实体单元类型也比较多,实体单元也是实际工程中使用最多的单元类型。常用的实体单元类型有 solid45, solid92,solid185,solid187 这几种。其中把 solid45,solid185 可以归为第一类,他们都是 六面体单元,都可以退化为四面体和棱柱体,单元的主要功能基本相同,(SOLID185 还可以用于不可压缩 超弹性材料)。Solid92, solid187 可以归为第二类,他们都是带中间节点的四面体单元,单元的主要功 能基本相同。
3-8 四节点矩形单元

(3-51)
若将单元刚度矩阵写成分块形式
k 11 k 21 k k 31 k 41
T
k 12 k 22 k 32 k 42
k 13 k 23 k 33 k 43
其中每一个子矩阵为
e
k 14 k 24 k 34 k 44
(3-52)
Kij Bi D Bj tdxdy
e
N
p tdxdy
R1x R 1y R2 x R2 y R3 x R3 y R4 x R4 y
e
F 2 n1 R F0
e
R
e
{F0} 表示作用在各节点上的集中力
(i=1,2,3,4)
(3-49)
由虎克定律我们可以得出用节点位移表示的单元应力,即
D S1
S2
S3
S4
e
(3-50)
返回
式中
Si D Bi
E
(i=1,2,3,4)
(h)
对于平面应力问题
Si
4ab 1 2
a i 1 0 b i 1 0 b 1 a i 1 0 i 0 1 1 a i 1 0 b i 1 0 2 2
Kij tab1 1 Bi S j d d
矩形单元的等效节点力计算
由集中力引起的等效节点力
G N
e
T
g
T
由表面力引起的等效节点力 Qe N T q tds
由体积力引起的等效节点力 P
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3-48)
其中 (xi , yi)是节点i的整体坐标,i =1,2,3,4。
返回
在局部坐标系中,节点i的坐标是(i , i ),其值分别 为±1。取位移模式
u 1 2 3 4 v 5 6 7 8
(a)
该函数称为双线性函数。将节点的局部坐标值代入上 式,可列出四个节点处的位移分量,即两组四元联立方程 ,由此可求得位移模式中的8个未知参数1,2,…,8,
x x0 a
y y0 b
式中
x0 ( x1 x2 ) / 2 ( x3 x4 ) / 2 y0 ( y2 y3 ) / 2 ( y1 y4 ) / 2 a ( x2 x1 ) / 2 ( x3 x4 ) / 2 b ( y3 y2 ) / 2 ( y4 y1 ) / 2
返回
求出α1, α2, α3, α4;α 5, α 6 , α7 , α8
u1 u2 u3 u4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 2 1 3 4 1 1 1 1 4
(3-51)
(i=1,2,3,4)
(3-49)
由虎克定律我们可以得出用节点位移表示的单元应力,即
D S1
S2
S3
S4
e
(3-50)
返回
式中
Si D Bi
E
(i=1,2,3,4)
(h)
对于平面应力问题
Si
4ab 1 2
a i 1 0 b i 1 0 b 1 a i 1 0 i 0 1 1 a i 1 0 b i 1 0 2 2
1 u1 u 1 1 2 1 1 u3 1 1 u4 1
ห้องสมุดไป่ตู้
5 1 1 1 1 1 6 7 4 1 1 1 1 8
1 v1 v 1 1 2 1 1 v3 1 1 v4 1
(f)
返回
将(b)式代入,得
B1 B2
式中
N i b 1 Bi ab 0 N a i
B3
B4
e
(g)
0 b i 1 0 0 N 1 a i 0 a 1 i 0 4ab a i 1 0 b i 1 0 N i b
v
式中
N i N i I ,
1 0 I 0 1 ,
i i
u vi
(i 1,2 ,3,4)
(e)
由几何方程可以求得单元的应变
u 1 u u b a x x 1 v 1 v v y a b y ab u v xy u v 1 u 1 v a b y x b a
y
u4 ( U 4) 2b
v4 (V4)
4
v3 (V3)
o
3
u3 ( U 3 )
2
1
u2 ( U 2 ) v2 (V2)
u1 ( U 1)
2a v1 (V1)
o
x
图3-9 矩形单元1234
返回
在图3-9中,取矩形单元的形心为局部坐标系的原点, 和轴分别与整体坐标轴x和y平行,两坐标系存在有以下的 坐标变换关系
再把这些参数代回(a)式中,便可得到用节点位移表示的位移模式 4
u N i ui
i 1 4
v N i vi
i 1
(b)
式中 N i (1 0 )(1 0 ) / 4 ,0 =i ,0 =i ,i =1,2,3,4 。若写成与前面一致的形式,有 u f N i i (d)
有限元法做为一个有效的数值分析工具,在许 多科学领域当中有成功的应用。 本门课程主要有 以下的目的: 1)了解什么是有限元法。 2)了解当前有限元软件的发展水平,学会用有限 元软件如何来分析一些工程问题。 3)学习有限元法的原理,主要结合弹性力学问题 来介绍有限元法的基本方法,包括单元分析,整 体分析,载荷与约束处理,等参单元的概念等。 有限元法作为一种数值方法,有限元法的起源正 好是在力学领域,因此要涉及一些力学知识,但 不把重点放在力学上。
第六节
矩形单元
矩形单元也是一种常用的单元, 它采用了比常应变三角形单元次数更 高的位移模式,因而可以更好地反映 弹性体中的位移状态和应力状态。 矩形单元 1234 如图 3-9 所示,其边 长分别为 2 a 和 2 b ,两边分别平行于 x 、 y 轴。若取该矩形的四个角点为节 点,因每个节点位移有两个分量,所 以矩形单元共有8个自由度。采用 § 3-2 节中的方法,同样可以完成对 这种单元的力学特性分析。然而,如 果我们引入一个局部坐标系、,那 么就可以推出比较简洁的结果。
