2019新考研高等数学模拟题库(含答案)
2019新版考研高数模拟测试试题(含参考答案)

2019最新考研数学模拟试题(含答案)学校:__________ 考号:__________一、解答题1.用定积分的几何意义求下列积分值:10(1)2 d x x ⎰; 解:由几何意义可知,该定积分的值等于由x 轴、直线x =1、y =2x 所围成的三角形的面积,故原式=1.0(2)(0)x R >⎰ . 解:由几何意义可知,该定积分的值等于以原点为圆心,半径为R 的圆在第一象限内的面积,故原式=21π4R .2.设()()(),,,,,,w f x y z u g x z v h x y ===,求,,w w w x y z∂∂∂∂∂∂. 解:,w w w v w w u w v w w u x x v x y u y v x z u z∂∂∂∂∂∂∂∂∂∂∂∂=+=+=∂∂∂∂∂∂∂∂∂∂∂∂,3. 试求曲线e x y -=在点(0,1)及点(-1,0)处的切线方程和法线方程.解:231e e (1)3x x y x ---'=-⋅+ 012. 3x x y y ==-''=-=∞故在点(0,1)处的切线方程为:21(0)3y x -=--,即2330x y +-= 法线方程为:21(0)3y x -=-,即3220x y -+= 在点(-1,0)处的切线方程为:1x =-法线方程为:0y =4.在括号内填入适当的函数,使等式成立:⑴ d( )cos d t t =; ⑵ d( )sin d x x ω=;⑶ 1d( )d 1x x =+; ⑷ 2d( )e d x x -=; ⑸ d( )x=; ⑹ 2d( )sec 3d x x =; ⑺ 1d( )ln d x xx =; ⑻ d( )x =. 解:⑴ (sint)cos t '=d(sin )cos d t C t t ∴+=.⑵ 11(cos )(sin )sin x x x ωωωωω'-=-⋅-=1d(cos )sin d x C x x ωωω∴-+=.⑶ 1[ln(1)]1x x'+=+ 1d[ln(1)]d 1x C x x ∴++=+. ⑷ 22211(e )(2)e =e 22x x x ---'-=-⋅- 221d(e )e d 2x x C x --∴-+=. ⑸ (2)2x '=)C x∴=. ⑹ 2211(tan3)sec 33sec 333x x x '=⋅⋅= 21d(tan3)sec 3d 3x C x x ∴+=. ⑺ 21111(ln )2ln ln 22x x x x x'=⋅⋅= 211d(ln )ln d 2x C x x x∴+=. ⑻ 2(1(2)x x '--=-=d()C x ∴=.5.求由下列方程确定的隐函数()y y x =的微分d y :。
2019新考研高数模拟训练题目(含参考答案)

2019最新考研数学模拟试题(含答案) 学校:__________ 考号:__________一、解答题1.设a 为非零常数,b 为正常数,求y =ax 2+bx 在以0和b a 为端点的闭区间上的最大值和最小值.解:20y ax b '=+=得2b x a =-不可能属于以0和b a为端点的闭区间上, 而 22(0)0,b b y y a a ⎛⎫== ⎪⎝⎭, 故当a >0时,函数的最大值为22b b y a a ⎛⎫= ⎪⎝⎭,最小值为(0)0y =; 当a <0时,函数的最大值为(0)0y =,最小值为22b b y a a ⎛⎫= ⎪⎝⎭.2.计算下列向量场A 的散度与旋度:(1)()222222,,y z z x x y =+++A ;解:()0,2,,y z z x x y ---(2)()222,,x yz x y z x yz =A ;解:()()()()2222226,,,xy x z y y x z z y x ---(3),,y x z yz z x x y ⎛⎫= ⎪⎝⎭A . 解:111yz zx xy ++,2222221,,y y z z x x xyz z y x z y x ⎛⎫--- ⎪⎝⎭3.求下列函数的高阶导数:⑴ e sin ,x y x =⋅求(4)y; ⑵ 22e ,x y x =⋅求(6)y ; ⑶ 2sin ,y x x =⋅求(80)y .解:⑴e sin e cos e (sin cos )x x xy x x x x '=⋅+⋅=+(4)e (sin cos )e (cos sin )2cos e 2e (cos sin )2e (cos sin )2e (sin cos )=4e sin x x x x x x x y x x x x x y x x y x x x x x ''=++-=⋅'''=-=-+---⑵ 6(6)2(6)260(e )()i x i i i y C x -==∑22(6)22(5)22(4)622524222(e )6()(e )15()(e )2e 622e 1522e 32e (21215)x x x x x xx x x x x x x x '''=++=+⋅⋅+⋅⋅=++⑶ 80(80)2()(80)800()(sin )i i i i y C x x -==∑2(80)(79)(78)22(sin )802(sin )31602(sin )πππsin(80)+160sin (79)6320sin (78)222sin 160cos 6320sin .x x x x x x x x x x x x x x x =+⋅⋅+⋅⋅=⋅+⋅⋅+⋅++⋅=--4.已知()f x ''存在,求22d d y x: ⑴ 2()y f x =; ⑵ ln ()y f x =.解:⑴ 22()y xf x ''= 222222()22()2()4()y f x x xf x f x x f x '''''=+⋅'''=+ ⑵ ()()f x y f x ''= 22()()[()]()f x f x f x y f x '''-''=5.在括号内填入适当的函数,使等式成立:⑴ d( )cos d t t =; ⑵ d( )sin d x x ω=;⑶ 1d( )d 1x x =+; ⑷ 2d( )e d x x -=; ⑸d( )x =; ⑹ 2d( )sec 3d x x =; ⑺ 1d( )ln d x x x =; ⑻d( )x =. 解:⑴ (sint)cos t '=。
2019新考研高数模拟测试考题(含参考答案)

(2)
(3) ;(4) ;
(5) ;(6) .
解:(1)∵
而 收敛,由比较审敛法知 收敛.
(2)∵
而 发散,由比较审敛法知,原级数发散.
(3)∵
而 收敛,故 也收敛.
(4)∵
而 收敛,故 收敛.
(5)当a>1时, ,而 收敛,故 也收敛.
当a=1时, ,级数发散.
当0<a<1时, ,级数发散.
当t>1或t<-1时, ,曲线是凹的,
当0<t<1或-1<t<0时, ,曲线是凸的,
故曲线有两个拐点(1,4),(1,-4).
(2)x=2acotθ,y=2asin2θ.
解:
令 ,得 或 ,
不妨设a>0,不失一般性,当 时,即 时, ,
当 或 时,即 或 时, ,
故当参数 或 时,都是y的拐点,且拐点为 及 .
2019最新考研数学模拟试题(含答案)
学校:__________姓名:__________班级:__________考号:__________
题号
一
总分
得分
一、解答题
1.已知 ,求 .
解:原式=
2.求下各微分方程的通解:
;
解:
得相应齐次方程的通解为
令特解为 ,代入原方程得
,
解得 ,故 ,
故原方程通解为 .
10.问a,b为何值时,点(1,3)为曲线y=ax3+bx2的拐点?
解:y′=3ax2+2bx,y″=6ax+2b
依题意有
解得 .
11.设 具有二阶连续导数,且 ,试证:
可导,且导函数连续.
2019新考研高数模拟训练考题(含答案)

2019最新考研数学模拟试题(含答案) 学校:__________ 考号:__________一、解答题1.利用函数的图形的凹凸性,证明下列不等式:()1(1) (0,0,,1)22nn n x y x y x y n x y +⎛⎫>>>≠>+ ⎪⎝⎭; 证明:令 ()n f x x = 12(),()(1)0n n f x nx f x n n x --'''==-> ,则曲线y =f (x )是凹的,因此,x y R +∀∈, ()()22f x f y x y f ++⎛⎫< ⎪⎝⎭, 即 1()22nn n x y x y +⎛⎫<+ ⎪⎝⎭. 2e e (2)e ()2x y x yx y ++>≠ ; 证明:令f (x )=e x()e ,()e 0x x f x f x '''==> .则曲线y =f (x )是凹的,,,x y R x y ∀∈≠则 ()()22f x f y x y f ++⎛⎫< ⎪⎝⎭即 2e e e 2x yx y ++<. (3) ln ln ()ln (0,0,)2x y x x y y x y x y x y ++>+>>≠ 证明:令 f (x )=x ln x (x >0) 1()ln 1,()0(0)f x x f x x x '''=+=>> 则曲线()y f x =是凹的,,x y R +∀∈,x ≠y ,有 ()()22f x f y x y f ++⎛⎫< ⎪⎝⎭即 1ln (ln ln )222x y x y x x y y ++<+, 即 ln ln ()ln2x y x x y y x y ++>+.2.求下列欧拉方程的通解:2(1)0x y xy y '''+-=解:作变换e t x =,即t =ln x ,原方程变为 (1)0D D y Dy y -+-=即 22d 0d y y t-= 特征方程为 210r -=121,1r r =-=故 12121e e t t y c c c c x x-=+=+. 23(2)4x y xy y x '''+-=.解:设e t x =,则原方程化为3(1)4e t D D y Dy y -+-=232d 4e d t y y t-= ① 特征方程为 240r -=122,2r r =-=故①所对应齐次方程的通解为2212e e t t y c c -=+又设*3e ty A =为①的特解,代入①化简得 941A A -=15A =, *31e 5t y = 故 223223121211e e e .55t t t y c c c x c x x --=++=++3.求n 次多项式1101n n n n y a x a xa x a --=++++的n 阶导数. 解: 1()()1()()()()0100()()()()=()=!n n n n n n n n n n n y a x a x a x a a x a n --=++++⋅4.设函数()f x 在[,]a b 上连续,在(,)a b 内可导,且lim (),x a f x A +→'=试证: ()f a A +'=.。
2019新版考研高等数学模拟考试考题(含答案解析)
若 则 都是方程 的根,
若 ,则 ,由零点定理知,至少 ,使 ,
即 ,即 是方程 的根,
综上所述,方程 在 内至少有一根.
15.设星形线的参数方程为x=acos3t,y=asin3t,a>0求
d)星形线所围面积;
e)绕x轴旋转所得旋转体的体积;
f)星形线的全长.
(3)函数在x=(2n+1)π (n∈z)处间断,在间断点处,级数收敛于0,当x≠(2n+1)π时,由f(x)为奇函数,有an=0,(n=0,1,2,…)
所以
(x≠(2n+1)π,n∈z)
(4)因为 作为以2π为周期的函数时,处处连续,故其傅里叶级数收敛于f(x),注意到f(x)为偶函数,有bn=0(n=1,2,…),
2019最新考研数学模拟试题(含答案)
学校:__________姓名:__________班级:__________考号:__________
题号
一
总分
得分
一、解答题
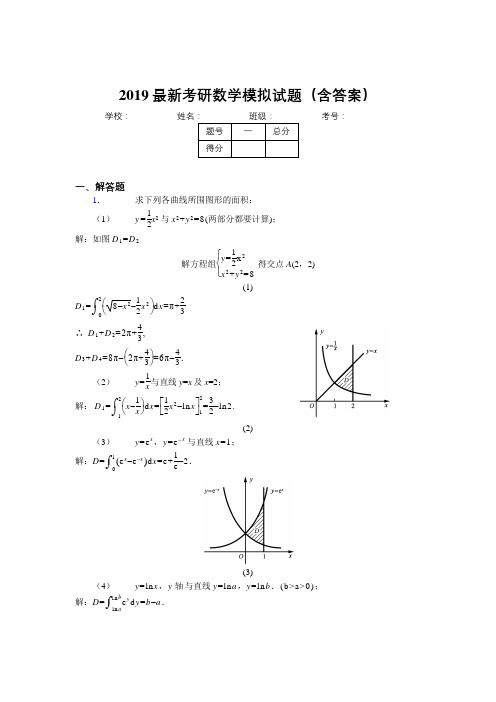
1.求下列各曲线所围图形的面积:
(1)与x2+y2=8(两部分都要计算);
解:如图D1=D2
解方程组得交点A(2,2)
(1)
∴,
.
(2)与直线y=x及x=2;
(9)极坐标曲线ρ=asin3φ;
解:
.
(9)
(10)ρ=2acosφ;
解:
.
(10)
2.设 ,求 .
解:
3.设 ,其中a为常数, 为连续函数,讨论 在 处的可导性.
解:
.
故当 时, 在 处可导,且
当 时, 在 处不可导.
4.试求过点(3,8)且与曲线 相切的直线方程.
2019新版考研高数模拟训练考题(含答案解析)

2019最新考研数学模拟试题(含答案)学校:__________ 考号:__________一、解答题1.求下列函数的最大值、最小值:254(1) (), (,0)f x x x x=-∈-∞; 解:y 的定义域为(,0)-∞,322(27)0x y x +'==,得唯一驻点x =-3 且当(,3]x ∈-∞-时,0y '<,y 单调递减;当[3,0)x ∈-时,0y '>,y 单调递增, 因此x =-3为y 的最小值点,最小值为f (-3)=27. 又lim ()x f x →-∞=+∞,故f (x )无最大值.(2) () [5,1]f x x x =+∈-;解:10y '==,在(5,1)-上得唯一驻点34x =,又 53,(1)1,(5)544y y y ⎛⎫==-= ⎪⎝⎭ ,故函数()f x 在[-5,1]上的最大值为545. 42(3) 82, 13y x x x =-+-≤≤.解:函数在(-1,3)中仅有两个驻点x =0及x =2,而 y (-1)=-5, y (0)=2, y (2)=-14, y (3)=11,故在[-1,3]上,函数的最大值是11,最小值为-14.2.设()y f x =是由方程组2323,e sin 1,y x t t y t ⎧=++⎪⎨=+⎪⎩ 所确定的隐函数,求202d d t y x =.解:分别对已知方程组的两边关于x 求导,得:d d 162,d d d d de sin e cos ,d d d y yt t t x x y y tt t x x x ⎧=⋅+⎪⎪⎨⎪=+⎪⎩再对x 求一次导,得2222222222d dd 06()62,d d d d d dyd d d (e )sin 2e cos e sin ()e cos ,d d d d d d y y y y x t t tt x x x y y tt tt t t t x x x x x x ⎧=++⎪⎪⎨⎪'=+⋅⋅-+⋅⎪⎩ 将00,1t t y ===代入上述各式,得002022202d 1d e, ,d 2d 2d 3, d 4d e 3e.d 24t t t t tyx x t x y x =======-=-3.设函数()f x 在[,]a b 上连续,在(,)a b 内可导,且lim(),x a f x A +→'=试证:()f a A +'=. 证明:()()()lim x a f x f a f a x a ++→-'=-()lim lim ()1x a x a f x f x A ++→→''===.4.求由下列方程确定的隐函数()y y x =的微分d y : ⑴ 1e y y x =+; ⑵ 22221x y a b +=;⑶ 1sin 2y x y =+; ⑷ 2arccos y x y -=.解:⑴ 对等式两端微分,得d e d d(e )y y y x x =+即d e d e d y y y x x y =+ 于是e d d .1e yy y x x =-⑵ 对等式两端微分,得22112d 2d 0x x y y a b ⋅+⋅= 得22d d .b xy x a y =-⑶ 对等式两端微分,得。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019最新考研数学模拟试题(含答案)学校:__________ 考号:__________一、解答题1.试决定22(3)y k x =-中的k 的值,使曲线的拐点处的法线通过原点.解:224(3),12(1)y kx x y k x '''=-=- 令0y ''=,解得x =±1,代入原曲线方程得y =4k , 只要k ≠0,可验证(1,4k ),(-1,4k )是曲线的拐点.18x k y =±'=±,那么拐点处的法线斜率等于18k ,法线方程为18y x k=. 由于(1,4k ),(-1,4k )在此法线上,因此148k k=±, 得22321, 321k k ==-(舍去)故8k ==±2.求下列线性微分方程满足所给初始条件的特解:πd 11(1)sin ,1d x y y x y x x x=+== ; 解: 11d d 11sin e sin d [cos ]e d x x x x x y x x c c x x c x x x -⎡⎤⎰⎰⎡⎤==+=-+⎢⎥⎣⎦⎣⎦⎰⎰ 以π,1x y ==代入上式得π1c =-, 故所求特解为 1(π1cos )y x x=--. 2311(2)(23)1,0x y x y y x='+-== . 解:22323d 3ln x x x x c x--=--+⎰ 22223323d 23+3ln d 3ln ee e d e d x xx x x x x xxxy x c x c -------⎰⎡⎤⎰⎡⎤∴==++⎢⎥⎣⎦⎣⎦⎰⎰ 2223311e .e e 22x x x x x c c ----⎛⎫⎛⎫=⋅=++ ⎪ ⎪⎝⎭⎝⎭以x =1,y =0代入上式,得12ec =-. 故所求特解为 2311e 22e x y x -⎛⎫=-⎪⎝⎭.3.一点沿曲线2cos r a ϕ=运动,它的极径以角速度ω旋转,求这动点的横坐标与纵坐标的变化率.解: 22cos 2cos sin sin 2x a y a a ϕϕϕϕ⎧=⎨==⎩d d d 22cos (sin )2sin 2,d d d d d d 2cos 22cos .d d d x x a a t ty y a a t tϕϕϕωωϕϕϕϕωωϕϕ=⋅=⋅⋅-⋅=-=⋅=⋅=4.求曲线y =ln(sec x )在点(x ,y )处的曲率及曲率半径. 解:2tan ,sec y x y x '''==故 223/223/2sec cos (1)(1tan )y x k x y x ''==='++ 1sec R x k==.5.一飞机沿抛物线路径210000x y =( y 轴铅直向上,单位为m )做俯冲飞行,在坐标原点O处飞机速度v =200 m ·s -1,飞行员体重G =70kg ,求飞机俯冲至最低点即原点O 处时,座椅对飞行员的反力. 解:0010,5000x x y y =='''==, 23/2(1)5000y R y'+==''飞行员在飞机俯冲时受到的向心力22702005605000mv F R ⋅=== (牛顿)故座椅对飞行员的反力560709.81246F =+⨯= (牛顿).6.设总收入和总成本分别由以下两式给出:2()50.003,()300 1.1R q q q C q q =-=+其中q 为产量,0≤q ≤1000,求:(1)边际成本;(2)获得最大利润时的产量;(3)怎样的生产量能使盈亏平衡? 解:(1) 边际成本为:()(300 1.1) 1.1.C q q ''=+=(2) 利润函数为2()()() 3.90.003300() 3.90.006L q R q C q q q L q q=-=--'=-令()0L q '=,得650q = 即为获得最大利润时的产量. (3) 盈亏平衡时: R (q )=C (q ) 即 3.9q -0.003q 2-300=0 q 2-1300q +100000=0 解得q =1218(舍去),q =82.7.求下列初等函数的边际函数、弹性和增长率: (1) y =ax +b ;(其中a ,b ∈R ,a ≠0) 解:y ′=a 即为边际函数. 弹性为:1Ey axa x Ex axb ax b=⋅⋅=++, 增长率为: y aax bγ=+. (2) y =a e bx ;解:边际函数为:y ′=ab e bx 弹性为:1e ebx bx Ey ab x bx Ex a =⋅⋅=, 增长率为: e e bxy bxab b a γ==. (3) y =x a解:边际函数为:y ′=ax a -1.弹性为:11a a Ey ax x a Ex x-=⋅⋅=, 增长率为: 1.a y a ax ax xγ-==8.验证:拉格朗日定理对函数3()2f x x x =+在区间[0,1]上的正确性.验证:因为()f x 在[0,1]上连续,在(0,1)内可导,满足拉格朗日定理的条件. 由(1)(0)()(10)f f f ξ'-=-得2322ξ=+解得ξ=,即存在ξ=使得拉格朗日定理的结论成立.9.证明恒等式:222arctan arcsinπ (1).1xx x x +=≥+ 证明:令22()2arctan arcsin 1xf x x x =++,22222222(1)22()1(1)2211x x xf x x x x x +-⋅'=++=-=++ 故()f x C ≡,又因(1)πf =,所以()πf x =,即222arctan arcsinπ.1xx x +=+10.设()f x 在[,]a b 上有(1)n -阶连续导数,在(,)a b 内有n 阶导数,且(1)()()()()0.n f b f a f a f a -'=====试证:在(,)a b 内至少存在一点ξ,使()()0n f ξ=.证明:首先,对()f x 在[,]a b 上应用罗尔定理,有1(,)a a b ∈,即1a a b <<,使得1()0f a '=;其次,对()f x '在[,]a b 上应用罗尔定理,有21(,)a a b ∈,即12a a a b <<<, 使得2()0; ,f a ''=一般地,设在(,)a b 内已找到1n -个点121,,,,n a a a -其中121,n a a a a b-<<<<<使得(1)1()0n n f a --=,则对(1)()0n f x -=在1[,]n a b -上应用罗尔定理有1(,)(,),n a b a b ξ-∈⊂使得()()0n fξ=.11.求下列极限问题中,能使用洛必达法则的有( ).⑴ 201sinlimsin x x x x →; ⑵ lim (1)x x k x→+∞+; ⑶ sin lim sin x x xx x→∞-+; ⑷ e e lim .e e x x xx x --→+∞-+ 解:⑴ ∵200111sin2sin coslimlim sin cos x x x x x x x x x→→-=不存在,(因1sin x ,1cos x 为有界函数) 又2001sin1limlim sin 0sin x x x x x x x→→==, 故不能使用洛必达法则.⑶ ∵sin 1cos limlimsin 1cos x x x x xx x x→∞→∞--=++不存在, 而sin 1sin lim lim 1.sin sin 1x x x x x x xx x x→∞→∞--==++故不能使用洛必达法则.⑷ ∵e e e e e e lim lim lim e e e e e ex x x x x xxx x x x x x x x ------→+∞→+∞→+∞-+-==+-+ 利用洛必达法则无法求得其极限.而22e e 1e lim lim 1e e 1e x x xxx xx x ----→+∞→+∞--==++. 故答案选(2).12.求函数()e xf x x =的n 阶麦克劳林公式.解: 21e 1e 2!(1)!!n n xx x x x x n n θ-=+++++- 312()e e (01)2!(1)!!n n xx x x x f x x x x n n θθ+∴==+++++<<-13.求下列曲线的拐点:23(1) ,3;x t y t t ==+解:22223d 33d 3(1),d 2d 4y t y t x t x t +-== 令22d 0d yx=,得t =1或t =-1 则x =1,y =4或x =1,y =-4当t >1或t <-1时,22d 0d yx >,曲线是凹的,当0<t <1或-1<t <0时,22d 0d yx<,曲线是凸的,故曲线有两个拐点(1,4),(1,-4). (2) x =2a cot θ, y =2a sin 2θ. 解:32d 22sin cos 2sin cos d 2(csc )y a x a θθθθθ⋅⋅==-⋅- 222442222d 11(6sin cos 2sin )sin cos (3tan )d 2(csc )y x a aθθθθθθ=-+⋅=⋅--令22d 0d y x =,得π3θ=或π3θ=-, 不妨设a >0tan θ>>时,即ππ33θ-<<时,22d 0d y x >,当tan θ>tan θ<π3θ<-或π3θ>时,22d 0d y x <,故当参数π3θ=或π3θ=-时,都是y的拐点,且拐点为3,32a a ⎛⎫ ⎪⎝⎭及3,32a a ⎛⎫- ⎪⎝⎭.14.利用一阶微分形式的不变性,求下列函数的微分,其中f 和ϕ均为可微函数: ⑴ 34(())y f x x ϕ=+; ⑵ (12)3sin ()y f x f x =-+. 解:⑴ 3434d [()]d[()]y f x x x x ϕϕ'=++34234=[()][34()]d f x x x x x x ϕϕ''++⑵ d d (12)3dsin ()y f x f x =-+=(12)d(12)3cos ()d ()(12)(2)d 3cos ()()d [2(12)3cos ()()]d .f x x f x f x f x x f x f x x f x f x f x x '--+''=--+''=--+15.(略).16.求下列不定积分:221(1)d (1)(1)x x x x ++-⎰;解:原式=2111111d ln ln 1122122(1)(1)(1)x c x x x x x x ⎛⎫ ⎪-=++++-++ ⎪+++-⎝⎭⎰ 211ln .112c x x =++-+ 33d (2)1x x +⎰;解:原式=22211112d ln ln d 1122111x x x x x x x x x x x -+⎛⎫=-+++-+⎪-++-+⎝⎭⎰⎰c =+. 5438(3)d x x x x x+--⎰;解:原式=2843d 111x x x x x x ⎛⎫+++-- ⎪+-⎝⎭⎰ 32118ln 4ln 3ln .1132x x x c x x x =+++--++- 26(4)d 1x x x +⎰;解:原式=33321d()1arctan .31()3x x c x =++⎰ sin (5)d 1sin xx x+⎰;解:原式=222sin 1d tan d (sec 1)d sec tan .cos cos x x x x x x x x x c x x -=--=-++⎰⎰⎰ cot (6)d sin cos 1xx x x ++⎰;解:原式22tan 222222212d 1111111d d d 22(1)22211111x t t t t t t t t t t t t t t t t t t =-⋅-++==-+⎛⎫-++⎪+++⎝⎭⎰⎰⎰⎰令1111ln ln tan .tan 222222x x t c c t =-+=-+(7)x ;解:原式=2.c =+(8)x ;解:原式=2d 2ln 21x x x x x ⎛=+-+ ⎝⎰ 又2x2221d 44d 11t t t t t t =+--⎰⎰142ln1t t c c t -''=++=++故原式=1)x c -+.17.证明:无穷积分敛散性的比较判别法的极限形式,即节第六节定理2. 证明:如果|()|lim0()x f x g x ρ→+∞=≠,那么对于ε(使0ρε->),存在x 0,当0x x ≥时|()|0()f xg x ρερε<-<<+ 即 ()()|()|()()g x f x g x ρερε-<<+ 成立,显然()d ag x x +∞⎰与|()|d af x x +∞⎰同进收敛或发散.如果0ρ=,则有|()|()f x g x ε<, 显然()d ag x x +∞⎰收敛, 则|()|d af x x +∞⎰亦收敛.如果ρ=+∞,则有|()|()()f x g x ρε>-,显然()d ag x x +∞⎰发散,则|()|d af x x +∞⎰亦发散.习题五18.已知曲线f (x )=x -x 2与g (x )=ax 围成的图形面积等于92,求常数a .解:如图13,解方程组⎩⎨⎧f (x )=x -x2g (x )=ax得交点坐标为(0,0),(1-a ,a (1-a )) ∴D =⎠⎛01-a ()x -x 2-ax d x=⎣⎡⎦⎤12()1-a ·x 2-13x 31-a=16()1-a 3 依题意得 16()1-a 3=92得a =-2.(13)19.某父母打算连续存钱为孩子攒学费,设建行连续复利为5%(每年),若打算10年后攒够5万元,问每年应以均匀流方式存入多少钱? 解:设每年以均匀流方式存入x 万元,则 5=10(10)0.050e d t x t -⎰即 5=20x (e 0.5-1)0.514(e1)x =-≈0.385386万元=3853.86元.习题六20.用比较审敛法判别下列级数的敛散性. (1)()()111465735n n ++++⋅⋅++;(2)22212131112131nn+++++++++++ (3)1πsin 3n n ∞=∑;(4)1n ∞=;(5)()1101nn a a∞=>+∑;(6)()1121nn ∞=-∑.解:(1)∵ ()()21135n U nn n =<++而211n n ∞=∑收敛,由比较审敛法知1n n U ∞=∑收敛. (2)∵221111n n n U n n n n++=≥=++ 而11n n ∞=∑发散,由比较审敛法知,原级数发散. (3)∵ππsinsin 33lim lim ππ1π33n nn n n n→∞→∞=⋅=而1π3n n ∞=∑收敛,故1πsin 3n n ∞=∑也收敛.(4)∵321n Un=<=而3121n n∞=∑收敛,故1n ∞=收敛.(5)当a >1时,111n n n U a a =<+,而11n n a ∞=∑收敛,故111nn a ∞=+∑也收敛. 当a =1时,11lim lim022n n n U →∞→∞==≠,级数发散. 当0<a <1时,1lim lim101n nn n U a →∞→∞==≠+,级数发散.综上所述,当a >1时,原级数收敛,当0<a ≤1时,原级数发散.(6)由021lim ln 2x x x →-=知121lim ln 211nx n→∞-=<而11n n ∞=∑发散,由比较审敛法知()1121n n ∞=-∑发散.21.用根值判别法判别下列级数的敛散性:(1) 1531nn n n ∞=⎛⎫ ⎪+⎝⎭∑; (2)()[]11ln 1nn n ∞=+∑;(3) 21131n n n n -∞=⎛⎫ ⎪-⎝⎭∑;(4) 1nn n b a ∞=⎛⎫⎪⎝⎭∑,其中a n →a (n →∞),a n ,b ,a 均为正数.解:(1)55lim1313n n n n →∞==>+,故原级数发散.(2) ()1lim01ln 1n n n →∞==<+,故原级数收敛.(3)121lim 1931nn n n n -→∞⎛⎫==<⎪-⎝⎭, 故原级数收敛.(4) lim limn n nb b a a →∞==, 当b <a 时,b a <1,原级数收敛;当b >a 时,b a >1,原级数发散;当b =a 时,ba=1,无法判定其敛散性.22.若2lim n n n U →∞存在,证明:级数1nn U∞=∑收敛.证:∵2lim n n n U →∞存在,∴∃M >0,使|n 2U n |≤M ,即n 2|U n |≤M ,|U n |≤2Mn 而21n Mn ∞=∑收敛,故1n n U ∞=∑绝对收敛.23.求下列级数的和函数:(1)()211121n n n x n ∞-=--∑; (2)21021n n x n +∞=+∑; (3)()11!1n n nxn ∞-=-∑; (4)()11nn x n n ∞=+∑.解:(1)可求得原级数的收敛半径R =1,且当|x |=1时,级数()111121n n n ∞-=--∑是收敛的交错级数,故收敛域为[-1,1] 记()()()()22111111112121n n n n n n x x S x xS x x n n -∞∞--=====----∑∑ 则S 1(0)=0,()()122121111n n n S x x x∞--='==-+∑ 所以()()11201d arctan 01xS S x x x x -==+⎰即S 1(x )=arctan x ,所以S (x )=x arctan x ,x ∈[-1,1].(2)可求得原级数的收敛半径R =1,且当|x |=1时,原级数发散.记()2121n n x S x n +∞==+∑则()2211n n S x x x ∞='==-∑ ()200111d d ln 121xxx S x x x x x +'==--⎰⎰,即()()11ln 021xS S x x+-=-,S (0)=0 所以()11ln 21xS x x+=-,(|x |<1)(3)由()11!limlim 0!1n nn n n a n n a n +→∞→∞+==-知收敛域为(-∞,+∞).记()()11!1n n n S x x n ∞-==-∑则()()()111d e !!11nn xx n n x x S x x x x n n -∞∞=====--∑∑⎰,所以()()()e 1e x x S x x x '==+,(-∞<x <+∞)(4)由()()()112lim 111n n n n n →∞++=+知收敛半径R =1,当x =1时,级数变为()111n n n ∞=+∑,由()2111n n n <+知级数收敛,当x =-1时,级数变为()()111n n n n ∞=-+∑是收敛的交错级数,故收敛域为[-1,1].记()()11nn x S x n n ∞==+∑则S (0)=0,()()111n n x xS x n n +∞==+∑,()[]1111n n x xS x x ∞-=''==-∑ (x ≠1) 所以()[]()0d ln 1xxS x x x ''=--⎰即()[]()ln 1xS x x '=--()[]()()()00d ln 1d 1ln 1xxxS x x x x x x x '=--=--+⎰⎰ 即()()()1ln 1xS x x x x =--+ 当x ≠0时,()()111ln 1S x x x ⎛⎫=+-- ⎪⎝⎭,又当x =1时,可求得S (1)=1 (∵()1lim lim 111n n S x n →∞→∞⎛⎫=-= ⎪+⎝⎭) 综上所述()()[)()0,01,1111ln 1,1,00,1x S x x x x x =⎧⎪==⎪⎨⎛⎫⎪+--∈- ⎪⎪⎝⎭⎩24.设f (x ) = x +1(0≤x ≤π),试分别将f (x )展开为正弦级数和余弦级数. 解:将f (x )作奇延拓,则有a n =0 (n =0,1,2,…)()()()()ππ0022sin d 1sin d ππ111π2πn nb f x nx x x nx x n==+--+=⋅⎰⎰从而()()()1111π2sin πnn f x nx n∞=--+=∑ (0<x <π)若将f (x )作偶延拓,则有b n =0 (n =1,2,…)()()ππ00222cos d 1cos d ππ0,2,4,64,1,3,5,πn a f x nx x x nx x n n n ==+=⎧⎪=-⎨=⎪⎩⎰⎰ ()()ππ0π012d 1d π2ππa f x x x x -==+=+⎰⎰从而()()()21cos 21π242π21n n xf x n ∞=-+=--∑ (0≤x ≤π)25.确定下列函数的单调区间:(1) 3226187y x x x =---;解:所给函数在定义域(,)-∞+∞内连续、可导,且2612186(1)(3)y x x x x '=--=+-可得函数的两个驻点:121,3x x =-=,在(,1),(1,3),(3,)-∞--+∞内,y '分别取+,–,+号,故知函数在(,1],[3,)-∞-+∞内单调增加,在[1,3]-内单调减少. (2) 82 (0)y x x x=+>; 解: 函数有一个间断点0x =在定义域外,在定义域内处处可导,且282y x '=-,则函数有驻点2x =,在部分区间(0,2]内,0y '<;在[2,)+∞内y '>0,故知函数在[2,)+∞内单调增加,而在(0,2]内单调减少.(3) ln(y x =; 解: 函数定义域为(,)-∞+∞,0y '=>,故函数在(,)-∞+∞上单调增加.(4) 3(1)(1)y x x =-+;解: 函数定义域为(,)-∞+∞,22(1)(21)y x x '=+-,则函数有驻点: 11,2x x =-=,在1(,]2-∞内, 0y '<,函数单调减少;在1[,)2+∞内, 0y '>,函数单调增加.(5) e (0,0)n xy x n x -=>≥; 解: 函数定义域为[0,)+∞,11e e e ()n xn x x n y nxx x n x -----'=-=-函数的驻点为0,x x n ==,在[0,]n 上0y '>,函数单调增加;在[,]n +∞上0y '<,函数单调减少.(6) sin 2y x x =+; 解: 函数定义域为(,)-∞+∞,πsin 2, [π,π], ,2πsin 2, [π,π], .2x x x n n n y x x x n n n ⎧+∈+∈⎪⎪=⎨⎪-∈-∈⎪⎩Z Z1) 当π[π,π]2x n n ∈+时, 12cos 2y x '=+,则1π0cos 2[π,π]23y x x n n '≥⇔≥-⇔∈+; πππ0cos 2[π,π]232y x x n n '≤⇔≤-⇔∈++. 2) 当π[π,π]2x n n ∈-时, 12cos 2y x '=-,则 1ππ0cos 2[π,π]226y x x n n '≥⇔≤⇔∈-- 1π0cos 2[π,π]26y x x n n '≤⇔≥⇔∈-.综上所述,函数单调增加区间为πππ[,] ()223k k k z +∈,函数单调减少区间为ππππ[,] ()2322k k k z ++∈. (7) 54(2)(21)y x x =-+. 解: 函数定义域为(,)-∞+∞.4453345(2)(21)4(2)(21)2(21)(1811)(2)y x x x x x x x '=-++-+⋅=+--函数驻点为123111,,2218x x x =-==, 在1(,]2+∞-内, 0y '>,函数单调增加, 在111[,]218-上, 0y '<,函数单调减少, 在11[,2]18上, 0y '>,函数单调增加, 在[2,)+∞内, 0y '>,函数单调增加.故函数的单调区间为: 1(,]2-∞-,111[,]218-,11[,)18+∞.26.求下列函数的定义域211(1)arctan ;(2);lg(1)(3); (4)arccos(2sin ).1y y x x xy y x x ==-==-解: (1)要使函数有意义,必须400x x -≥⎧⎨≠⎩ 即 4x x ≤⎧⎨≠⎩所以函数的定义域是(,0)(0,4]-∞.(2)要使函数有意义,必须30lg(1)010x x x +≥⎧⎪-≠⎨⎪->⎩ 即 301x x x ≥-⎧⎪≠⎨⎪<⎩所以函数的定义域是[-3,0)∪(0,1). (3)要使函数有意义,必须210x -≠ 即 1x ≠±所以函数的定义域是(,1)(1,1)(1,)-∞--+∞.(4)要使函数有意义,必须12sin 1x -≤≤ 即 11sin 22x -≤≤即ππ2π2π66k x k -+≤≤+或5π7π2π2π66k x k +≤≤+,(k 为整数).也即ππππ66k x k -+≤≤+ (k 为整数).所以函数的定义域是ππ[π,π]66k k -++, k 为整数.27.把△ABC 的BC 边分成五等份,设分点依次为D 1,D 2,D 3,D 4,再把各分点与A 连接,试以AB =c ,BC =a 表示向量1D A ,2D A ,3D A 和4D A . 解:1115D A BA BD =-=--c a 2225D A BA BD =-=--c a3335D A BA BD =-=--c a444.5D A BA BD =-=--c a28.解:设{,,}x y z a a a a =则有cos(1,1)3x a i a a i a i π⋅====⋅求得12x a =. 设a 在xoy 面上的投影向量为b 则有{,,0}x y b a a =则222cos 42a ba b π⋅=⇒=⋅则214y a =求得12y a =± 又1,a =则2221x y z a a a ++= 从而求得11{,,}222a =±或11{,,}222-±29.指出下列各平面的特殊位置,并画出其图形: (1) y =0; (2) 3x -1=0; (3) 2x -3y -6=0; (4) x – y =0; (5) 2x -3y +4z =0.解:(1) y =0表示xOz 坐标面(如图7-2) (2) 3x -1=0表示垂直于x 轴的平面.(如图7-3)图7-2 图7-3(3) 2x -3y -6=0表示平行于z 轴且在x 轴及y 轴上的截距分别为x =3和y =-2的平面.(如图7-4)(4) x –y =0表示过z 轴的平面(如图7-5) (5) 2x -3y +4z =0表示过原点的平面(如图7-6).图7-4 图7-5 图7-630.试定出下列各题中直线与平面间的位置关系: (1)34273x y z++==--和4x -2y -2z =3; (2)327x y z ==-和3x -2y +7z =8; (3)223314x y z -+-==-和x +y +z =3.解:平行而不包含. 因为直线的方向向量为s ={-2,-7,3} 平面的法向量n ={4,-2,-2},所以(2)4(7)(2)3(2)0⋅=-⨯+-⨯-+⨯-=s n于是直线与平面平行.又因为直线上的点M 0(-3,-4,0)代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量,故直线垂直于平面.(3) 直线在平面上,因为3111(4)10⨯+⨯+-⨯=,而直线上的点(2,-2,3)在平面上.31.求下列各极限:1y x y →→ 22001(2)lim;x y x y →→+00x y →→x y →→00sin (5)lim ;x y xy x →→2222221cos()(6)lim.()ex y x y x y x y +→→-++解:(1)原式0ln 2.=(2)原式=+∞. (3)原式=01.4x y →→=-(4)原式=002.x y →→=(5)原式=00sin lim100.x y xyy xy →→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2e x y x y x x y y x y x y x y ++→→→→++==+32.计算下列二次积分:10112111224sin (1)d d ;(2)d e d d e d .yy y xxyxy x xy x y x +⎰⎰⎰⎰解:(1)因为sin d xx x ⎰求不出来,故应改变积分次序。
