适应值引导下的粒子群算法群体特性分析
粒子群优化算法ppt

联合优化
粒子群优化算法可以用于联合优化神经网络的参数和结构,进一步提高神经网络的性能。
粒子群优化算法在神经网络训练中的应用
粒子群优化算法可以用于优化控制系统的控制器参数,以提高控制系统的性能和稳定性。
控制器参数优化
鲁棒性优化
联合优化
粒子群优化算法可以用于提高控制系统的鲁棒性,以应对系统中的不确定性和干扰。
粒子群优化算法可以用于联合优化控制系统的参数和结构,进一步提高控制系统的性能和稳定性。
03
粒子群优化算法在控制系统中的应用
02
01
06
总结与展望
粒子群优化算法是一种高效的全局优化算法,具有速度快、简单易行、易于并行化等优点。它利用群体智慧,通过粒子间的协作与信息共享,可以快速找到全局最优解。
优点
PSO算法的特点包括:简单易懂、易实现、能够处理高维问题、对初始值不敏感、能够处理非线性问题等。
定义与特点
粒子群优化算法的起源与发展
PSO算法的起源可以追溯到1995年,由 Kennedy 和 Eberhart博士提出,受到鸟群觅食行为的启发。
最初的PSO算法主要应用于函数优化问题,后来逐渐发展应用到神经网络训练、模式识别、图像处理、控制等领域。
边界条件的处理
通过对粒子速度进行限制,可以避免粒子在搜索空间中过度震荡,从而更好地逼近最优解。
粒子速度的限制
实例一
针对函数优化问题,通过对粒子速度和位置进行更新时加入随机扰动,可以增加粒子的探索能力,从而寻找到更好的最优解。
实例二
针对多峰函数优化问题,将粒子的个体最佳位置更新策略改为基于聚类的方法,可以使得粒子更好地逼近问题的全局最优解。
粒子的适应度函数用于评估其位置的好坏。
灰狼算法和粒子群算法

灰狼算法和粒子群算法灰狼算法和粒子群算法是两种常用的进化计算算法,它们在优化问题中具有广泛的应用。
本文将分别介绍灰狼算法和粒子群算法的原理和特点,并通过比较它们的优缺点,探讨其适用的场景。
1. 灰狼算法灰狼算法是由灰狼群体的行为和特性启发而来的一种群体智能算法。
灰狼群体中的每只狼都有一个适应度值,适应度值越高表示狼的位置越好。
算法的核心思想是模拟灰狼群体中的寻食行为,通过迭代更新每只狼的位置,最终找到最优解。
灰狼算法的具体步骤如下:1)初始化灰狼群体的位置和适应度值;2)通过适应度值的大小确定群体中的Alpha狼、Beta狼和Delta 狼;3)根据Alpha狼的位置和其他狼的位置,更新每只狼的位置;4)更新每只狼的适应度值;5)重复步骤3和4,直到满足停止条件。
灰狼算法的优点是简单易实现,收敛速度快,适用于解决复杂的非线性优化问题。
然而,灰狼算法在处理高维优化问题时,容易陷入局部最优解。
2. 粒子群算法粒子群算法是一种模拟鸟群觅食行为的群体智能算法。
算法中的每个粒子都有一个位置和速度,通过更新粒子的速度和位置,最终找到最优解。
粒子群算法的核心思想是通过个体和群体的交互合作来搜索最优解。
粒子群算法的具体步骤如下:1)初始化粒子群体的位置和速度;2)根据粒子的适应度值,更新局部最优解;3)根据局部最优解和全局最优解,更新粒子的速度和位置;4)更新粒子的适应度值;5)重复步骤2、3和4,直到满足停止条件。
粒子群算法的优点是容易实现,具有较好的全局搜索能力,适用于解决多峰优化问题。
然而,粒子群算法在处理高维优化问题时,易陷入局部最优解。
3. 算法比较与适用场景灰狼算法和粒子群算法都是基于群体智能的优化算法,它们在某些方面具有相似之处,但也存在一些差异。
灰狼算法与粒子群算法相比,优点是收敛速度快,适用于解决复杂的非线性优化问题;缺点是在处理高维优化问题时,容易陷入局部最优解。
粒子群算法与灰狼算法相比,优点是具有较好的全局搜索能力,适用于解决多峰优化问题;缺点是在处理高维优化问题时,易陷入局部最优解。
基于群体适应度方差的粒子群优化算法

摘要 : 由于粒子群算法在进化后期存在搜索速度较慢 , 容易陷入局部最优点 以及搜索到解的时间较长且精度不 高的缺点 , 所
以对算法进行改进的研究 就成为一个必要的课题 。通过利用混沌 的遍历性和随机性的特点, 引入基于 T n 映射的混沌理论 et
es d ei i es no ogeai e e , u hr oe t m k eio s hte t hv ho pr i s ayt j g s s ri r nrgt nd g e fr e r, o aedcs n e r o aecasoeao ou td p o c o r t m i w h tn
机制 , 使算法在进化后期 一旦陷入局部最优点就可以跳出局 部最优点的位置 , 并且通 过群体适应度方差 的计算来 判断 当前 群体 的离散程度或聚集程度 , 进而判断是 否需要 以一定的概率选择微粒个体去进行 混沌更新 。几个测试 函数的仿真实验结
果也表 明了该算法在搜索时间上 、 解的精度上都 要远远优于标 准的粒 子群算法 , 是一种 可行 的优 化工具 , 有一定 的应用前
a c r i gt e an i dv d a r b b l y h i ltd e p rme t e u t s o h t ti p o t d d P O c od n oc r i ii u p a i t .T e s t n l o i muae x e i n a r s l h w t a r rt sa a S i l s i s i o n r n t e s a c i d s l t n ’p e iin h e h t r me a o ui s rc s .Alo i p v s t a t sa r a o a l p i z d to n s p o sn . n o o s t r e h t e s n be o t o ii mi o l d i r mii g e a KEYW ORDS: a so t z t n ag r h ; e ma pn ; a t l w r p i z t n; oo y f n s a a c Ch o p i ai o t m T m p i g P ri e s a l o t mi o l i c n mi i C ln t e s v r n e ao i i
粒子群适应值

粒子群适应值
粒子群优化算法是一种基于群体智能的优化算法,它模拟了鸟群或鱼群在搜索食物或逃避危险的过程中的行为规律。
粒子群算法中的每个个体被称为粒子,它们通过不断地搜索和学习来逐渐优化自己的适应值,从而找到最优解。
粒子群适应值是指在问题求解过程中,粒子所对应的解的性能评价值。
在粒子群算法中,适应值是一个重要的概念,它用于描述粒子的优劣程度。
适应值越高的粒子,越有可能成为下一次搜索的基础,从而找到更优的解。
粒子的适应值可以根据问题的不同而有所差异。
例如,在求解函数最小化问题时,适应值可以定义为函数值的相反数,这样适应值越高的粒子就表示函数值越小的解。
在求解路径规划问题时,适应值可以定义为路径长度的倒数,这样适应值越高的粒子就表示路径长度越短的解。
在粒子群算法中,适应值的计算是一个重要的过程。
通常情况下,适应值的计算需要根据问题的特点进行设计,以便更好地评价粒子的性能,从而加速算法的收敛速度和提高求解效率。
- 1 -。
举例说明粒子群算法的特点

举例说明粒子群算法的特点粒子群算法(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,最早由Eberhart和Kennedy在1995年提出。
粒子群算法模拟了鸟群或鱼群等生物集体行为,通过在解空间中不断搜索和迭代,寻找最优解。
本文将从几个方面具体举例说明粒子群算法的特点。
首先,粒子群算法具有全局寻优的特点。
在粒子群算法中,每个粒子都代表着一个潜在的解,并通过更新自己的位置和速度与其他粒子进行信息交换,以寻找更好的解。
这种信息交换使得粒子能够在解空间中向全局最优解的方向移动。
例如,在解决旅行商问题时,可以使用粒子群算法来寻找最短路径。
每个粒子表示一条路径,通过不断更新位置和速度,粒子群逐渐收敛于全局最优解,找到了旅行商要访问的最短路径。
其次,粒子群算法具有自适应搜索能力。
粒子群算法中的每个粒子都具有自己的速度和位置,通过不断地与其他粒子交换信息,粒子能够根据群体中最优解的位置调整自己的运动方向和速度。
这种自适应搜索能力使得粒子群算法能够有效地避免陷入局部最优解,并在解空间中进行全局搜索。
例如,在解决函数优化问题时,可以利用粒子群算法来求解函数的最小值。
通过不断更新粒子的位置和速度,粒子群能够逐渐收敛于全局最优解,并找到函数的最小值点。
此外,粒子群算法具有快速收敛速度的特点。
粒子群算法中的每个粒子都会根据自己和群体中最优解的位置调整自己的运动方向和速度,使得粒子能够迅速向全局最优解的方向移动。
这种快速收敛的特点使得粒子群算法能够在较短的时间内找到较好的解。
例如,在解决神经网络训练问题时,可以使用粒子群算法来优化网络的权重和偏置,通过不断调整粒子的位置和速度,粒子群能够较快地找到网络的最优参数设置,提高网络的分类或回归性能。
最后,粒子群算法具有较好的鲁棒性和适用性。
粒子群算法通过模拟生物集体行为,在解空间中搜索最优解。
这种全局搜索的机制使得粒子群算法能够较好地适用于不同的优化问题,并具有较好的鲁棒性。
粒子群算法粒子群算法简介
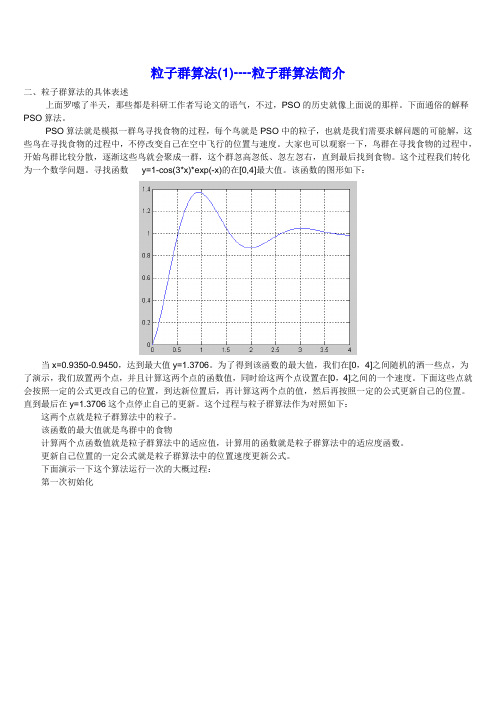
粒子群算法(1)----粒子群算法简介二、粒子群算法的具体表述上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO的历史就像上面说的那样。
下面通俗的解释PSO算法。
PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0,4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0,4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群算法(2)----标准的粒子群算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
直观理解粒子群算法

直观理解粒子群算法1.引言1.1 概述粒子群算法是一种模拟自然界群体行为的优化算法。
它最早由Eberhart和Kennedy于1995年提出,受到了鸟群觅食和鱼群游动行为的启发。
粒子群算法模拟了一个由许多粒子组成的群体,每个粒子代表一个潜在的解,并通过不断地调整自身的位置和速度来寻找最优解。
粒子群算法的基本原理是通过粒子之间的合作与竞争来达到全局最优解。
在算法开始时,每个粒子都会随机地在问题的解空间内选择一个初始位置和速度。
然后,根据粒子的当前位置和速度以及历史最优解的信息,每个粒子会更新自己的速度和位置。
更新的过程中,粒子会根据个体历史最优解和群体历史最优解两方面的信息进行权衡,从而平衡个体探索和群体协作的需求。
通过不断地迭代更新,粒子群算法能够逐渐收敛到全局最优解。
粒子群算法被广泛应用于优化问题的求解。
它在函数优化、组合优化、神经网络训练等领域取得了显著的成果。
由于其简单而直观的思想,粒子群算法易于理解和实现,同时具有较快的收敛速度和较好的全局搜索能力。
与其他优化算法相比,粒子群算法在处理高维、非线性、多模态等复杂问题时具有一定的优势。
综上所述,粒子群算法是一种基于群体行为的优化算法,通过模拟粒子之间的合作与竞争来寻找最优解。
它具有简单直观、易于实现和较好的全局搜索能力等优势。
在实际应用中,粒子群算法已经取得了一些显著的成果,并且有着较大的发展潜力。
文章结构部分的内容如下:文章结构部分旨在介绍本文的组织框架和内容安排,让读者能够清晰地了解整篇文章的结构和逻辑顺序。
本文分为三个主要部分:引言、正文和结论。
接下来将对每个部分的内容进行简要介绍。
首先是引言部分(Section 1),它主要用于引入本文的主题和背景。
在引言的第一部分(1.1 概述),我们将简要概括粒子群算法的基本概念和特点,为读者提供一个整体的认识。
接着,在第二部分(1.2 文章结构),我们将详细说明本文的组织结构和每个部分的内容安排,以便读者能够清晰地了解整个文章的构成。
粒子群算法基本流程

粒子群算法基本流程粒子群算法(Particle Swarm Optimization, PSO)是一种基于自然界群体智能现象的优化算法,常用于解决各种优化问题,如函数优化、组合优化、机器学习等。
本文将详细介绍粒子群算法的基本流程,包括初始化、适应度评价、移动、更新等环节,希望能对读者理解该算法提供一定的帮助。
一、算法介绍粒子群算法最初由Kennedy和Eberhart于1995年提出 [1],其基本思想来源于鸟群觅食行为。
在野外觅食时,鸟群中的鸟会根据所找到的食物数量来确定自己下一步的移动方向。
PSO算法中的“粒子”类似于鸟群中的鸟,它们以个体和群体为导向,通过速度和位置的调整来进行优化搜索。
PSO算法的目标是寻找最优解,通常是最小化或最大化一个函数的值,可表示为:f(x)=\sum_{i=1}^n{f_i(x)}x 是 n 维实数向量,f_i(x) 表示第 i 个函数。
寻找最优解的目标就是在 x 的搜索空间中寻找函数 f(x) 的全局最优解或局部最优解。
二、基本流程粒子群算法的基本流程如下:1. 初始化:随机生成一群粒子,每个粒子的位置和速度都是随机的。
2. 适应度评价:计算每个粒子的适应度值,也就是函数 f(x) 所对应的值,用来表示该粒子所处的位置的优劣程度。
3. 移动:根据当前位置和速度,移动粒子到新的位置。
4. 更新:根据历史上最好的粒子位置和当前最好的粒子位置,更新每个粒子的历史最好位置和当前最好位置,并更新全局最优位置。
5. 终止:当满足一定的终止条件时,停止迭代,并输出最终的粒子位置和最优解。
下文将分别对各环节进行详细介绍。
三、初始化在PSO算法中,粒子的位置和速度都是随机的。
对于每个粒子,需要随机生成一个 n 维实数向量表示其位置,一个同维度的实数向量表示其速度。
可以采用如下方法进行初始化:1. 对于每一个维度,随机生成一个实数范围内的数值,表示该维度上的位置和速度。
2. 在满足约束条件的前提下,生成一个可行解,作为初始化的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ci
=
Hi
1 2
ki
(ki
− 1)
=
2Hi ki (ki − 1)
(4)
( ) Pi = ( pi1, pi2,..., piD ) 和邻域内历史最优位置 Pig = ( pig1, pig2,..., pigD ) 其中,Hi 是与节点 i 直接关联的边的数量; ki ki −1 / 2
= ( pig1, pig2,..., pigD ) 调整自己的飞行状态,可以得出算法的搜索公式:
搜索,其搜索的轨迹由自身的状态和飞行中学习其它优秀粒 子的结果共同决定 [4]。假设规模为 N 的粒子群体在 D 维空
的所有节点之间的关联度,即所有与某节点直接相连的节点 中实际的连接边数占全连接情况下边数的比例。具体定义为:
间中飞行,每个粒子的当前位置为 X i = (xi1, xi2,..., xiD ) ,当 前速度为 Vi = (vi1,vi2,...,viD ) 。粒子根据自身的历史最优位置
是最多可能存在的边的数量。由此可以得出整个网络的聚集
vid
(t
)
=
vωidv(idt)+=cω1rvaind d+()c(1rpaidn(dt)()−( + c2Ran+dc()2(Rpaigndd(t())(−pxigidd
pxiidd ((tt)))− ((tt)))− xid
xid (t (t))
响;第三部分是粒子所在邻域内其它粒子对其飞行轨迹的影
粒子群群体随着算法的搜索,按照适应值的优劣同步完
响。显然,群体的规模大小和连接方式能够影响邻域的范围, 成群体网络的自适应生长。初始化群体为随机网络模型,当
进而影响粒子的寻优轨迹。当邻域为整个群体时群体结构为 搜索陷入停滞状态或者多次震荡性搜索时,根据适应值大小
大大减少。为了避免出现孤立节点,因而给断边后的节点选
择学习对象的机会。增加边的概率定义如下:
∑ Pzi =
Ranki (t) N Rank j (t)
(7)
j =1
除和添加边的概率大小,进而达到调整群体进化速度和结构 特性的效果,因而对不同的 θ 取值对于群体结构和算法性能 的影响,取 θ = 1,θ = 5,θ = 10,θ = 20 进行对比实验,结果如 图 1 和图 2 所示。
加突出。由于复杂网络的自适应形成过程和特点与粒子群算 学习经验最少要经历的边数的平均值,它是用来衡量群体内
法的搜索的驱动力之间具有许多相似之处,本文就适应性引 粒子之间信息传播速度的重要性能指标,其定义为:
导下的粒子群算法群体特性进行研究,探索提高粒子群算法 性能的方法。
1 粒子群算法模型
∑ L( p)
软件开发
适应值引导下的粒子群算法群体特性分析
穆华平 (鹤壁技术学院公共基础教研部,河南鹤壁,458030)
基金项目:河南省高等学校重点科研项目(项目编号:18B520023)。 摘要:模拟现实中复杂网络的自组织生长过程,使粒子群算法在寻优的同时,以适应值为引导动态演化群体结构,以适应值相关的概率增 加或删除粒子之间的连接,适应值好的粒子获得更多的连接机会,适应值差的粒子则以更大的概率断开与其他粒子的关联。通过仿真实验 研究探讨算法搜索过程中群体结构的特性,以此为切入点进行群体结构与算法搜索性能相关性的研究。 关键词:适应值;粒子群算法;群体特性
响因子,来调节粒子间的排名差距。删除边的概率定义如下:
Psi (t)
=
Ranki (t) − RankXworst (t) RankXbest (t) − RankXworst (t)
(6)
对于粒子 i 和 j 之间的边 (i, j) ,删除边的概率根据适应
值较差的粒子确定。经过多次的删边操作,群体间的连接会
=
2 N (N + 1)
n i, j
d ( p)i, j
(3)
其中, d ( p)i, j 表示进化概率为 P 时粒子 i 和 j 之间的最
少边数。
粒子群算法是将优化问题的潜在解看作一个个没有质
(2)平均聚集系数
量、没有体积的“粒子”,以一定的初速度在解空间中飞行
节点的聚集系数描述的是群体网络中与某节点直接关联
图 1 平均最短路径长度变化情况
■■3.2 算法流程 适应值引导下的粒子群算法(Particle Swarm Optim
完全连接,邻域内最优位置即为整个群体的历史最优位置; 增加或者删除连接,促进算法搜索的同时演化群体结构。
当邻域只包含自身时群体结构完全离散,邻域内最优位置与 ■■3.1 增删边策略
自身历史最优位置相同。
为了使算法跳出局部最优,获得更佳的优化性能,应当
56 | 电子制作 2019 年 09 月
中对于搜索经验的借鉴而相互作用形成的关系网络,根据复 杂网络的相关理论 [5],同时结合图论的基本概念,抽取能够 描述群体网络特点的特征属性来进行研究。
然而随着应用领域的扩展和深入,早熟收敛的问题日渐突
(1)平均最短路径长度
出,尤其对于大规模、复杂的多维优化问题,这种弊端就更
平均最短路径长度是指群体网络中任意两个粒子之间
软件开发
让适应值好的粒子比适应值差的粒子获得更多的连接。因
此,算法在进入搜索停滞状态时,要将群体内的所有粒子按
照适应值的优劣进行排名,适应值差的粒子在前,适应值好
的在后。
定义:第 t 代时粒子 i 的排名为: Ranki (t) = Indexθ ( Xi (t)) ,
其中 Index(Xi (t ) 为粒子适应值排名后的粒子的编号, θ 为影
))
xid (t + 1)xi=d (txi+d (1t)) =+ vxiidd ((tt)) + vid (t)
(1) (2)
系数为:
∑ C
=
1 N
N
Ci
i =1的第一部分是粒子自身的速度惯性对飞行轨迹
的影响;第二部分是粒子的历史最优位置对其飞行轨迹的影 3 以适应值为驱动的群体演化机制
0 引言
2 群体网络特征属性
粒子群算法 [1](PSO)是一种具有适应性的搜索算法,
粒子群算法的群体模型实质上是通过粒子在寻优过程
由美国的 Kennedy 和 Eberhart 教授于 1995 年共同研究提 出。由于该算法模型简单、收敛速度快并且收敛的精度较其 他智能算法要高,因而得到了领域内诸多学者的关注 。 [2-3]
