小升初奥数等积变形
小升初奥赛几何五大模型
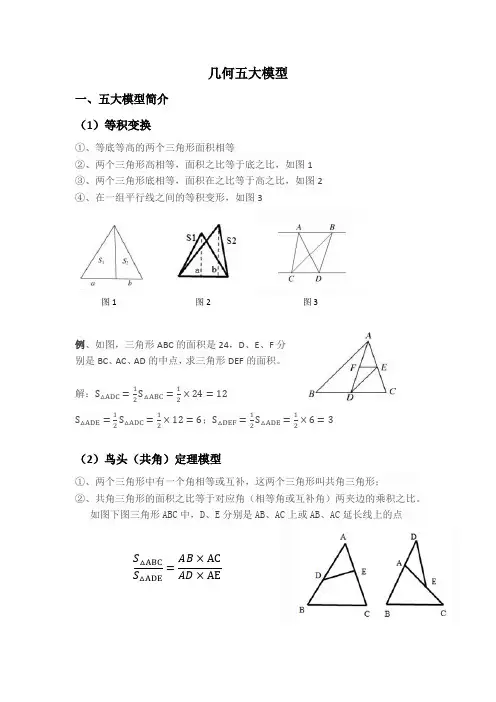
几何五大模型一、五大模型简介（1）等积变换①、等底等高的两个三角形面积相等②、两个三角形高相等，面积之比等于底之比，如图1③、两个三角形底相等，面积在之比等于高之比，如图2④、在一组平行线之间的等积变形，如图3图1 图2 图3例、如图，三角形ABC的面积是24，D、E、F分别是BC、AC、AD的中点，求三角形DEF的面积。
解：S△ADC=12S△ABC=12×24=12S△ADE=12S△ADC=12×12=6；S△DEF=12S△ADE=12×6=3（2）鸟头（共角）定理模型①、两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；②、共角三角形的面积之比等于对应角（相等角或互补角）两夹边的乘积之比。
如图下图三角形ABC中，D、E分别是AB、AC上或AB、AC延长线上的点S△ABC S△ADE =AB×AC AD×AE例、如图在ΔABC中，D在BA的延长线上，E在AC上，且AB：AD=5:2，AE：EC=3:2，△ADE的面积为12平方厘米，求ΔABC 的面积。
解：由题意知：S△ABCS△ADE =AB×ACAD×AE=52×53=256∴S△ABC=256×S△ADE=256×12=50(平方厘米)（3）蝴蝶模型1、梯形中比例关系(“梯形蝴蝶定理”)①S2=S4(梯形两翼相等)②S1:S3:S2:S4=a2:b2:ab:ab③梯形S对应的分数为（a+b)2例、如图，梯形ABCD，AB与CD平行，对角线AC、BD交于点O，已知△AOB、△BOC的面积分别为25平方厘米、35平方厘米，求梯形ABCD的面积。
解：S△AOB:S△BOC=25:35=5:7S△AOB:S△DOC=AB2:DC2=52:72=25：49∴S△DOC=49又S△AOD=S△BOC=35∴S ABCD=25+35+35+49=144(平方厘米)2、任意四边形中的比例关系(“蝴蝶定理”)：①S1:S2=S4:S3或S1×S3=S2×S4②AO:OC=S1:S4=S2:S3=(S1+S2):(S4+S3)例、如图，四边形ABCD的对角线AC、BD交于点O，如果三角形ABD的面积等于三角形BCD面积的1/3，且AO=2，求OC解：AO:OC=S△ABD:S△BCD=1:3OC=2×3=6（4）相似模型1、相似三角形：形状相同,大小不相等的两个三角形相似；2、寻找相似模型的大前提是平行线：平行于三角形一边的直线和其他两边或两边延长线相交，所构成的三角形与原三角形相似。
小学四年级奥数竞赛班作业第43讲：等积变形(一)
O
P
B
C
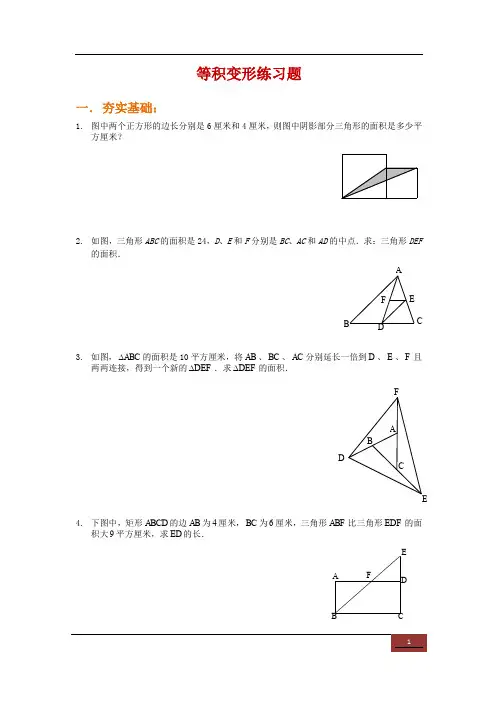
12. 如下图，过平行四边形 ABCD 内的一点 P 作边的平行线 EF 、 GH ，若 PBD 的面积为 8 平方分米，求平行四边形 PHCF 的面积比平行四边形 PGAE 的面积大多少平方分米？
AG
D
EP F
BH
C
13. 如图，长方形 ABCD 的面积是 56 平方厘米，点 E 、 F 、 G 分别是长方形 ABCD 边上的 中点， H 为 AD 边上的任意一点，求阴影部分的面积．
6. 因为阴影部分比三角形 EFG 的面积大10 平方厘米，都加上梯形 FGCB 后，根据差不变 性质，所得的两个新图形的面积差不变，即平行四边形 ABCD 比直角三角形 ECB 的面 积大10 平方厘米,所以平行四边形 ABCD 的面积等于108 2 10 50 平方厘米．
7. 题目中出现了两个三角形面积之差 16，若将 AOD 作为公共部分分别加给这两个三角形 后，根据差不变原理可知， AED 的面积比 BAD 的面积小16 平方厘米,而 BAD 正好 是正方形面积的一半即 88 2 32 (平方厘米)，从而 AED 的面积为 32 16 16 （平 方厘米）．作为梯形的另一部分， EBD 的面积与 BAD 面积相等（同底等高）． 可见，梯形的面积=16 32 48 (平方厘米).
3. 根据题意可知， SADF 2SABC ，同理可知 SBDE SCEF 2SABC ， 于是 SDEF (1 2 3)S ABC 7S ABC 7 10 70 平方厘米．
4. (4 6 9) 6 2 4 1 （厘米）
5. 连结 CB ．三角形 DCB 的面积为 4 4 2 2 6（平方厘米），CD 6 4 2 3（厘米）．
六年级下册小升初等积变形人教版人教版
则满足条件的三角形有：
重要 例6：如图，ABFE和CDEF都是长方形，AB的长是4厘米，BC的长是3厘米。
角形的底是另一个三角形的几倍，那么，这个三角形 (1)等底等高的三角形面积相等。
结论 (2)等高看底：若两个三角形的高相等，其中一个三角形的底是另一个三角形的几倍，那么，这个三角形的面积也是另一个三角形面积的几倍。
例5：如图，在直角三角形ABC中，D、E分别是AB、AC的中点，如果△AED的面积是30平方厘米，求△ABC的面积？
S△ACD=S△BCD
S△ABD=S△ACD+S△ABC=b+ b= b
那么图中阴影部分的面积是多少平方厘米？
例3：（平行线间的等积变形）如下图，△ACD和△BCD夹在一组平行线之间，且有公共底边，那么△ACD和△BCD的面积关系是怎样的？为什么？
例5：如图，在直角三角形ABC中，D、E分别是AB、AC的中点，如果△AED的面积是30平方厘米，求△ABC的面积？
S△ABD=S△ACD=25-15=10 S△DFC=2S△DEF=2×24=48(cm2)
的面积也是另一个三角形面积的几倍。
等积变形的几个重要结论：
(3)等底看高：若两个三角形的底相等，其中一个三 同学们，你们能想出什么办法把这块土地分成面积相等的两个三角形吗？开动你们的脑筋吧！
思 例4：如图，在梯形ABCD中共有8个三角形，其中面
维 积相等的三角形有哪几对？
探
索 根据结论：同底等高的三角形面积相等 A
D
则满足条件的三角形有：
0
△ABD和△ACD
B
C
△ABC和△DBC
小升初数学思维拓展几何图形专项训练专题4-等积变形(位移、割补)
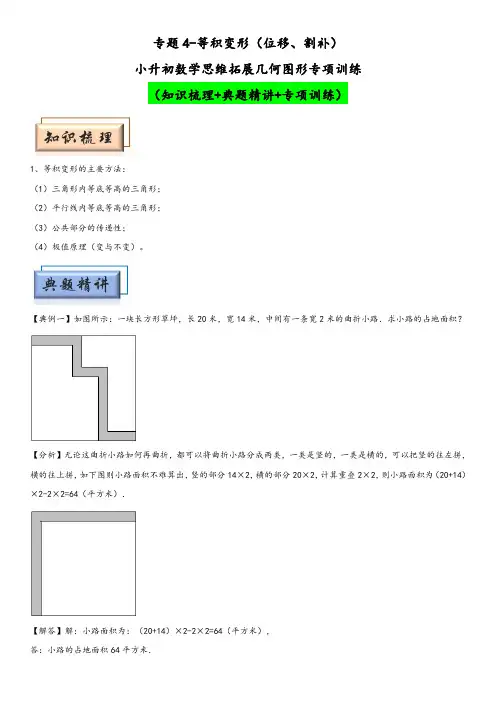
专题4-等积变形（位移、割补）小升初数学思维拓展几何图形专项训练（知识梳理+典题精讲+专项训练）1、等积变形的主要方法：（1）三角形内等底等高的三角形；（2）平行线内等底等高的三角形；（3）公共部分的传递性；（4）极值原理（变与不变）。
【典例一】如图所示：一块长方形草坪，长20米，宽14米，中间有一条宽2米的曲折小路．求小路的占地面积？【分析】无论这曲折小路如何再曲折，都可以将曲折小路分成两类，一类是竖的，一类是横的，可以把竖的往左拼，横的往上拼，如下图则小路面积不难算出，竖的部分14×2，横的部分20×2，计算重叠2×2，则小路面积为（20+14）×2-2×2=64（平方米）．【解答】解：小路面积为：（20+14）×2-2×2=64（平方米），答：小路的占地面积64平方米．【点评】利用等积变形、平移知识把曲折的小路拉直，就变成规则的图形包括三部分竖的长方形，横的长方形和重叠的小正方形，进而解答．【典例二】如图，五边形ABCDE是一片荒地的示意图，陈家承包后想将其中的小路E M N---改成直路EG，然后在直路EG，然后在直路EG两旁分别种植不同的蔬菜，并使改道前后路两旁的面积，保持不变，请你左图中画出这条直路．（图中体现画法1)【分析】利用尺规作图做//EN MG，如图根据两条平行线之间的垂线段相等和同底等高的三角形的面积相等，可得S ENG S EMN∆=∆，由此作图即可．【解答】解：画法如图所示，连接EN，过点M作//MG EN，交CB于点G，连接EG，EG即为所求直路的位置．【点评】此题利用两条平行线之间的垂线段相等和同底等高的三角形的面积相等的知识作图．【典例三】A和B都是高度为12厘米的圆柱形容器，底面半径分别是1厘米和2厘米，一水龙头单独向A注水，一分钟可注满．现将两容器在它们的高度的一半出用一根细管连通（连通管的容积忽略不计），仍用该水龙头向A 注水，求（1）2分钟容器A中的水有多高？（2）3分钟时容器A中的水有多高．【分析】已知B容器的底面半径是A容器的2倍，高相等，B容器的容积就是A容器的4倍；因此，单独注满B容器需要4分钟，要把两个容器都注满一共需要145+=（分钟），已知现在两个容器在它们高度一半处用一个细管连通，2分钟后A中的水位是容器高的一半，即1226÷=（厘米）（其余的水流到B容器了）；由此可知，用2.5分钟的时间两个容器中的水的高度相等，都是6厘米；以后的时间两个容器中的水位同时上升，用3 2.50.5-=（分钟）分钟注入两个容器的高度加上6厘米即是3分钟后的高度．【解答】解：（1）A 容器的容积是：23.141 3.141 3.14⨯=⨯=（立方厘米），B 容器的容积是：23.142 3.14412.56⨯=⨯=（立方厘米），12.56 3.144÷=，即B 容器的容积是A 容器容积的4倍，因为一水龙头单独向A 注水，一分钟可注满，所以要注满B 容器需要4分钟，因此注满A 、B 两个容器需要145+=（分钟），已知现在两个容器在它们高度一半处用一个细管连通，2分钟后A 中的水位是容器高的一半，即1226÷=（厘米）；（2）因为注满A 、B 两个容器需要145+=（分钟），所以52 2.5÷=（分钟）时，A 、B 容器中的水位都是容器高的一半，即6厘米，2.5分钟后两容器中的水位是同时上升的，3分钟后，实际上3 2.50.5-=（分钟）水位是同时上升的，10.5510÷=，112 1.210⨯=（厘米），6 1.27.2+=（厘米）；答：2分钟时，容器A 中的高度是6厘米，3分钟时，容器A 中水的高度是7.2厘米．【点评】此题主要考查圆柱的体积（容积）的计算，解答关键是理解现在两个容器在它们高度一半处用一个细管连通，当A 中的水高是容器高的一半时，其余的水流到B 容器了；以后的时间两个容器中的水位同时上升，即注满两容器时间的110乘容器高就是0.5分钟上升的水的高度．一．选择题（共4小题）1．我国古代数学家刘徽利用“出入相补”原理计算平面图形的面积，其原理是：把一个图形分割、移补，而面积保持不变。
小升初平面几何常考五大模型
一、等积变换模型1、等底等高的两个三角形面积相等。
2、两个三角形高相等，面积比等于它们的底之比。
3、两个三角形底相等，面积比等于它的的高之比。
二、共角定理模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角（相等角或互补角）两夹边的乘积之比。
三、蝴蝶定理模型（说明：任意四边形与四边形、长方形、梯形，连接对角线所成四部的比例关系是一样的。
）四、相似三角形模型相似三角形：是形状相同，但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示，点G在线段DK上，正方形BEFG的边长为4，则△DEK的面积为由题知DC/GP=GC/PK，即DC/(DC-4)=(4+PK)/PK，令DC=a，PK=c，则a=4+c，则S△DEK=a^2+16+c*(4-c)/2+c^2-ac-a(4+a)/2=a^2/2+c^2/2-ac-2a+2c+16=(c+4)^2/2+c^2/2-c( c+4)-2(c+4)+2c+16=16。
1、图17是一个正方形地板砖示意图，在大正方形ABCD中AA1=AA2=BB1=BB2=CC1=CC2=DD1=D D2，中间小正方形 EFGH的面积是16平方厘米，四块蓝色的三角形的面积总和是72平方厘米，那么大正方形ABCD的面积是多少平方厘米？分析与解连AC和BD两条大正方形的对角线，它们相交于O，然后将三角形AOB放在D PC处（如图18和图19）。
已知小正方形EFGH的面积是16平方厘米，所以小正方形EFGH的边长是4厘米。
又知道四个蓝色的三角形的面积总和是72平方厘米，所以两个蓝色三角形的面积是72÷2=36平方厘米，即图19的正方形OCPD中的小正方形的面积是36平方厘米，那么这个正方形的边长就是6厘米。
小升初分班奥数平面图形面积
小升初奥数几何部分辅导讲义讲义编号：学员编号: 年 级：小六 课时数：3 学员姓名: 辅导科目：奥数 学科教师： 课 题 平面图形面积问题授课时间： 备课时间：教学目标1. 掌握五大模型的特征，会从复杂图形中找出基本模型.2. 灵活运用五大模型求直线型图形的面积和线段长度.教学内容【专题知识点概述】一、等积变换模型①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比；baS 2S 1 DC BA如左图12::S S a b =③夹在一组平行线之间的等积变形，如右上图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD ． ④正方形的面积等于对角线长度平方的一半；⑤三角形面积等于与它等底等高的平行四边形面积的一半；二、鸟头定理（共角定理）模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形． 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比如图在ABC △中，,D E 分别是,AB AC 上的点如图 ⑴（或D 在BA 的延长线上，E 在AC 上），则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵推理过程连接BE ，再利用等积变换模型即可三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)：S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．梯形中比例关系(“梯形蝴蝶定理”)：A BCDOba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =； ③梯形S 的对应份数为()2a b +．四、相似模型相似三角形性质：GF E ABCD （金字塔模型）AB CDEF G（沙漏模型）①AD AE DE AFAB AC BC AG===； ②22:ADE ABC S S AF AG =△△：．所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方；五、燕尾定理模型 S △ABG :S △AGC =S △BGE :S △EGC =BE :EC ；S △BGA :S △BGC =S △AGF :S △FGC =AF :FC ； S △AGC :S △BCG =S △ADG :S △DGB =AD :DB ； 【习题精讲】【例1】（难度等级 ※※）用四种不同的方法，把任意一个三角形分成四个面积相等的三角形．【例2】（难度等级 ※※）如右图，已知在△ABC 中，BE=3AE ，CD=2AD ．若△ADE 的面积为1平方厘米．求三角形ABC 的面积．【例3】（难度等级 ※※）如图，长方形ABCD 的面积是56平方厘米，点E 、F 、G 分别是长方形ABCD 边上的中点，H 为AD 边上的任意一点，求阴影部分的面积．G F E DC B AHGFE D CBA【例4】（难度等级 ※※）如图，在三角形ABC 中，，D 为BC 的中点，E 为AB 上的一点，且BE=13AB,已知四边形EDCA 的面积是35，求三角形ABC 的面积.【例5】（难度等级 ※※）(2008年四中考题)如右图，AD DB =，AE EF FC ==，已知阴影部分面积为5平方厘米，ABC ∆的面积是 平方厘米．FE DCBA【举一反三】（难度等级 ※※）如右图，在平行四边形ABCD 中，E 、F 分别是AC 、BC 的三等分点，且SABCD=54平方厘米，求S △BEF ．【例6】（难度等级 ※※※）图30-10是一个正方形，其中所标数值的单位是厘米．问：阴影部分的面积是多少平方厘米?【例7】（难度等级 ※※）如图在ABC △中，,D E 分别是,AB AC 上的点，且:2:5AD AB =，:4:7AE AC =，16ADE S =△平方厘米，求ABC △的面积．EDCBA【举一反三】（难度等级 ※※）如图，三角形ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，如果三角形ADE 的面积等于1，那么三角形ABC 的面积是多少？EDCBA【例8】（难度等级 ※※）如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =，:3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积．EDCBA【例9】（难度等级 ※※）如图所示，在平行四边形ABCD 中，E 为AB 的中点，2AF CF =，三角形AFE (图中阴影部分)的面积为8平方厘米．平行四边形的面积是多少平方厘米？EFD CBA【例10】（难度等级 ※※※）已知DEF △的面积为7平方厘米，,2,3BE CE AD BD CF AF ===，求ABC △的面积．FED CBA【例11】（难度等级 ※※※）(2007年”走美”五年级初赛试题)如图所示，正方形ABCD 边长为6厘米，13AE AC =，13CF BC =．三角形DEF 的面积为_______平方厘米．FEDC BA【例12】（难度等级 ※※※）如图，在ABC △中，延长AB 至D ，使BD AB =，延长BC 至E ，使12CE BC =，F 是AC 的中点，若ABC △的面积是2，则DEF △的面积是多少？A BCDEF【例13】（难度等级 ※※※）如图所示，已知 1.,2.ABCSAE ED BD DC ===求图中阴影部分的面积.【举一反三】（难度等级 ※※※）下图中阴影部分甲的面积与阴影部分乙的面积哪个大？【例14】（难度等级※※※）右图是一块长方形耕地，它由四个小长方形拼合而成，其中三个小长方形的面积分别为15、18、30公顷，问图中阴影部分的面积是多少？【例15】（难度等级※※※）梯形ABCD的上底长为3厘米，下底长为9厘米，而三角形ABO的面积为12平方厘米。
小学奥数~三角形等积变形
小学奥数~三角形等积变形
如图一，正方形ABCD和正方形ECGF并排放置，BF与CD相交于点H，连接BD、GD、GH、。
已知AB＝4厘米，则阴影部分的面积是多少平方厘米？
题目解析：
连接DF、FC；
因为BD、CF分别为正方形ABCD和正方形ECGF对角线，所以BD//CF；
根据等高模型；
又因为三角形DHG与三角形DHF为同底等高三角形，所以面积相等；
同理，因为BD//CF；三角形BDF与三角形BDC为同底等高三角形，所以面积相等；
所以阴影面积为4×4÷2=8平方厘米。
知识点——三角形等积变形
三角形面积公式：底×高÷2
对于两个三角形，如果它们对应的底和高相等（如同底等高、等底等高），那么它们的面积也相等。
方法：三角形钉住其中两点，构造底边平行线，沿平行线移动另外一点，所得三角形面积相等。
（必要时可构造平行线)。
再战
如下图，有三个正方形并排安置，并且它们的顶点D、G、K三点恰好在同一条直线上，其中正方形GFEB边长是8厘米，那么阴影部分的面积为多少平方厘米？。
小升初数学专题训练 15.等积变形
第15讲 等积变形第一部分：知识介绍我们已经知道三角形面积的计算公式：三角形面积=底⨯高2÷从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积。
如果三角形的底不变，高越大（小），三角形面积也就越大（小）； 如果三角形的高不变，底越大（小），三角形面积也就越大（小）；这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化。
但是，当三 角形的底和高同时发生变化时，三角形的面积不一定变化。
比如当高变为原来的3倍，底变为原来的13，则三角形面积与原来的一样。
这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化。
同时也告诉我们：面积相同三角形有无数多个不同的形状。
在实际问题的研究中，我们还会常常用到以下结论： ①等底等高的两个三角形面积相等。
②若两个三角形的高相等，其中一个三角形的底是另一个三角形的几倍，那么这个三角形的面积也是另一个三角形面积的几倍。
若两个三角形的底相等，其中一个三角形的高是另一个三角形的几倍，那么这个三角形的面积也是另一个三角形面积的几倍。
③夹在一组平行线之间的等积变形，如下图，ACD ∆和BCD ∆夹在一组平行线之间，且有公共底边CD 那么ACDBCD S S ∆∆=；反之，如果ACD BCD S S ∆∆=，则可知直线AB 平行于CD 。
在小学的学习中几何是一个很重要的部分，每一个几何图形都非常美妙，几何图形的美妙不仅来源于它的外形，更重要的是在几何模型上出现的那些美妙的规律，下面我们就一起来看看几个美妙的几何模型模型一：任意四边形中的比例关系(“蝴蝶定理”)： ①1243::S S S S =或者1324S S S S ⨯=⨯ ②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系． 模型二：梯形中比例关系(“梯形蝴蝶定理”)： ①2213::S S a b =；②221324::::::S S S S a b ab ab =； ③ABCD S 的对应份数为()2a b +．梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道，通过构造模型，直接应用结论，往往在题目中有事半功倍的效果． 模型三：鸟头定理：两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形． 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．如图在ABC △中，,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上，E 在AC 上)，则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A在ABC ∆中，点E 是AB 上的n 等分点，AE AB n =÷；点F 是AC 上的m 等分点， AF AC m =÷，那么ABCAEFABCS SSn m n m=÷÷=⨯。
小学奥数几何六大模型及例题
AO : OC S1 : S4 S2 : S3 (S1 S2 ) : (S4 S3)
梯形中蝴蝶模型
燕尾模型 从三角形一个顶点向对边上任意一点画线段，在线段上
任取一点组成的图形面积也会有如下关系：
闯关目标
平面几何之直线图形
六大模型
等积变形 一半模型 鸟头模型 蝴蝶模型 燕尾模型 相似模型
赛前热身
平面几何是小升初考试的必考内容，而且常常以大题的
形式出现，重点中学选拔考试中几何题目分值较高，并且 难度有逐步增加的趋势，虽然几何题形式多样，但通过总 结归纳，掌握基本的几何模型，有助于解决更多几何新题， 难题。
例题7 如图1，△ABC中，BD=2DA，CE=2EB，AF=2FC，那么 △ABC的面积是阴影三角形面积的 倍。
例题9 如图1，对角线BD将长方形ABCD分割为两个三角形，AE 和CF分别是两个三角形上的高，长度都等于6cm，EF的长 度为5cm，求长方形ABCD的面积。
例题1 （2008年第一届“陈省身杯”六年级2试） 如图，BC=45，AC=21，△ABC被分成9个面积相等的小三 角形，那么DI+FK为多少？
例题2 如图1，并排放有三个正方形，其中正方形GBEF的边长为 10厘米，连接GK，交EF于O，连接DE，交BG于Q，连接 DG，求阴影部分的面积。
例题3 如图1，梯形ABCD，下底BC上有一点E，梯形空白处的面 积比阴影△ADE得到面积多200平方厘米，又知梯形下底 BC比上底AD长20厘米。求这个梯形的高是多少？
例题4 将长16厘米，宽9厘米的长方形的长和宽都分成三等份， 长方形内任意一点O与分点及顶点连接，如图，则阴影部 分的面积是 平方厘米。
热点：关于立体图形的等积变形问题-2024年小升初数学(解析版)
热点：关于立体图形的等积变形问题一、填空题。
1在一个长20分米、宽9分米、高7分米的长方体容器内注入3.6分米深的水，然后放入一个棱长为6分米的正方体铁块，则水位上升了()分米。
【答案】0.9【分析】水的水位只有3.6分米，则可以将水看成一个长20分米、宽9分米、高3.6分米的长方体，则水的体积是=长×宽×高。
放入正方体方块虽然水位上升了，但是水的体积没有发生改变。
但是底面积发生可改变。
现在水的高度=水的体积÷底面积。
注意：求的是水位上升的高度。
水位上升的高度=现在水的高度-开始水的高度。
【详解】20×9×3.6=648(立方分米)20×9-6×6=180-36=144(平方分米)648÷144=4.5(分米)4.5-3.6=0.9(分米)则水位上升了0.9米。
2把一个底面是半径4分米、高是6分米的圆柱体铁块，熔铸成一个底面半径是3分米的圆锥体，这个圆锥体的高是()分米，体积是()立方分米。
【答案】32301.44【分析】根据题意可知，把一个圆柱体铁块熔铸成一个圆锥体，铁块的形状变了，但体积不变；先根据圆柱的体积公式V=πr2h，求出这个铁块的体积，也就是圆锥的体积；再根据圆锥的高h=3V÷S，求出这个圆锥体的高。
【详解】铁块的体积：3.14×42×6=3.14×16×6=50.24×6=301.44(立方分米)圆锥的底面积：3.14×32=3.14×9=28.26(平方分米)圆锥的高：301.44×3÷28.26=904.32÷28.26=32(分米)这个圆锥体的高是32分米，体积是301.44立方分米。
3一个密闭的长方体容器，它的长、宽、高分别是10cm、10cm、20cm，容器如图1放置时，容器内水的高度是10cm。
第三讲 等积变形
根据蝶形定理， ，故 ，
所以 (平方厘米)．
2.右图中 是梯形， 是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是平方厘米．
答案：连接 ．由于 与 是平行的，所以 也是梯形，那么 ．
∵在正方形 中， 边上的高，
∴ (三角形面积等于与它等底等高的平行四边形面积的一半)
同理， ．
∴正方形 与长方形 面积相等． 长方形的宽 (厘米)．
2.在边长为6厘米的正方形 内任取一点 ，将正方形的一组对边二等分，另一组对边三等分，分别与 点连接,求阴影部分面积．
答案；（法1）特殊点法．由于 是正方形内部任意一点，可采用特殊点法，假设 点与 点重合，则阴影部分变为如上中图所示，图中的两个阴影三角形的面积分别占正方形面积的 和 ，所以阴影部分的面积为 平方厘米．
答案；连接 ．
∵ ，
∴ ，
又∵ ，
∴ ，∴ ， ．
B
6.如图，以正方形的边 为斜边在正方形内作直角三角形 ， ， 、 交于 ．已知 、 的长分别为 、 ，求三角形 的面积．
答案；如图，连接 ，以 点为中心，将 顺时针旋转 到 的位置．
那么 ，而 也是 ，所以四边形 是直角梯形，且 ，
所以梯形 的面积为：
根据面积比例模型， 的面积为 ．
A
1.如图所示，正方形 的边长为 厘米，长方形 的长 为 厘米，那么长方形的宽为几厘米？
答案；本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)．三角形面积等于与它等底等高的平行四边形面积的一半．
证明：连接 ．(我们通过 把这两个长方形和正方形联系在一起)．
等积变形题目五年级
等积变形题目五年级等积变形是指图形在形状发生改变的过程中，其面积大小保持不变的一种变形。
例如，一个四边形可以变成正方形、长方形、梯形或不规则的其他几边形，只要其面积大小保持不变，就是等积变形。
1.问题：有一个长方体，它的长、宽、高分别是a、b、c（a＞b＞c），现在进行等积变形，把长方体的长变成d，宽和高保持不变。
请问变形后的长方体与原长方体的体积相比，是变大还是变小？解析：因为等积变形不改变物体的体积，所以原长方体和变形后的长方体的体积是相等的。
2.问题：有一个正方体，边长为a，现在进行等积变形，把正方体的边长变成d，请问变形后的正方体与原正方体的体积相比，是变大还是变小？解析：因为等积变形不改变物体的体积，所以原正方体和变形后的正方体的体积是相等的。
3.问题：有一个三角形，它的底边为a，高为h，现在进行等积变形，把三角形的底边变成d，高保持不变。
请问变形后的三角形与原三角形的面积相比，是变大还是变小？解析：因为等积变形不改变三角形的面积，所以原三角形和变形后的三角形的面积是相等的。
4.问题：有一个正方形，边长为a，现在进行等积变形，把正方形的边长变成d，请问变形后的正方形与原正方形的面积相比，是变大还是变小？解析：因为等积变形不改变正方形的面积，所以原正方形和变形后的正方形的面积是相等的。
5.问题：有一个长方形，长为a，宽为b，现在进行等积变形，把长方形的长变成d，宽保持不变。
请问变形后的长方形与原长方形的面积相比，是变大还是变小？解析：因为等积变形不改变长方形的面积，所以原长方形和变形后的长方形的面积是相等的。
小学奥数等积变形2
奥数拓展：等积变形2【例1】重叠面积中的等积变形1.如图是有两个相同的直角梯形重叠而成（单位：厘米），阴影部分的面积是（）平方厘米．2.如图，两个完全一样的直角三角形重叠一部分，图中阴影部分面积是（）平方厘米．A．90 B．75 C．52 D．30【例2】等积变形的灵活运用1.如图，长方形ABCD的面积是56平方厘米，点E、F、G分别是长方形ABCD边上的中点，H为AD边上的任意一点，求阴影部分的面积．2.将三角形ABC的BA边延长1倍到D；CB边延长2倍到E，AC边延长3倍到F，如果三角形ABC的面积等于2，那么三角形DEF的面积是_____。
备用图1 备用图23.如图直角三角形中的空白部分是正方形，正方形的一个顶点将这个直角三角形的斜边分成两部分，阴影部分的面积是6 平方厘米，DB长厘米．EBA三．出门考1. 一个等腰三角形的两条边长分别是51米和21米，这个三角形的周长是（ ）米。
2. 如下图，ABCD 为平行四边形，E 、F 分别为AD 、DC 的中点，如果△BFC 的面积为4平方厘米，则△AEB 的面积是（ ）平方厘米．3. 如图是由两个相同的直角梯形重叠而成的，图中只标出三个数据（单位：厘米），图中阴影部分的面积是多少平方厘米？4*.如图，两个正方形摆放在一起，其中大正方形边长为12，那么阴影部分面积是多少？(圆周率取3.14)四．课后作业1. 计算，能简算的要简算。
435177-- 4847157+- 74512712⎛⎫-- ⎪⎝⎭ 4357910910+++ 41327373-+-2. 一根长2米的绳子，先用去41米，又用去21米，这根绳子短了多少米？3. 光明小学拥有一块公顷的菜地，其中青菜占菜地的，黄瓜占菜地的．剩下的种西红柿，西红柿占菜地的几分之几？4. 光明小学拥有一块公顷的菜地，其中种青菜的有公顷，种黄瓜的有公顷．剩下的种西红柿，西红柿有多少公顷？5. 如图将△ABC 的AB 边延长到D ，BC 边延长到E ，CA 边延长到F ，使DB=AB ，EC=2BC ，FA=2AC ，如果三角形ABC 的面积是5平方厘米，那么三角形DEF 的面积是平方厘米．6. 探索规律并计算=-4131 =-5131 =-6151 =-8151 =+4131 =+5131 =+6151 =+8151 我发现每日一练第一天：周天（5月20日）1. 三根电线共长87米，第一根和第二根共长43米，第二根和第三根共长31米。
盘点平面几何常考五大模型
盘点平面几何常考五大模型（一）等积变换模型性质与应用简介导读：平面几何问题，是历年小升初的必考题目，也在各大杯赛中占有很大比例，这些题目都是以等积变形为主导思想，结合五大模型的变化应用交织而成的，这一期我们讲解了解一下五大模型第一块——等积变换模型。
等积变换模型例题讲解与课后练习题（一）例题讲解与分析【例1】：如右图，在△ABC中，BE=3AE，CD=2AD．若△ADE的面积是1平方厘米，那么三角形ABC的面积是多少【解答】连接BD,S△ABD和S△ AED同高，面积比等于底边比，所以三角形ABD的面积是4，S△ABD和S△ABC同高面积比等于底边比，三角形ABC的面积是ABD的3倍，是12.【总结】要找准那两个三角形的高相同。
【例2】：如图，四边形ABCD中，AC和BD相交于O点，三角形ADO的面积=5，三角形DOC的面积=4，三角形AOB的面积=15，求三角形BOC的面积是多少【解答】S△ADO=5,S△DOC=4根据结论2，△ADO与△DOC同高所以面积比等于底的比,即AO/OC=5:4同理S△AOB/S△BOC=AO/OC=5:4,因为S△AOB=15所以S△BOC=12。
【总结】从这个题目我们可以发现，题目的条件和结论都是三角形的面积比，我们在解题过程中借助结论2，先把面积比转化成线段比，再把线段比用结论2转化成面积比，解决了问题。
事实上，这2次转化的过程就相当于在条件和结论中搭了一座“桥梁”，请同学们体会一下。
（二）课后练习题讲解与分析（二）鸟头定理（共角定理）模型导语：平面几何问题，是历年小升初的必考题目，也在各大杯赛中占有很大比例，这些题目都是以等积变形为主导思想，结合五大模型的变化应用交织而成的，第二期我们讲解了解一下五大模型第二块——鸟头定理（共角定理）模型。
o（三）蝴蝶定理模型导读：平面几何问题，是历年小升初的必考题目，也在各大杯赛中占有很大比例，这些题目都是以等积变形为主导思想，结合五大模型的变化应用交织而成的，这一期我们讲解了解一下五大模型第三块——蝴蝶定理模型。
小升初-数学-几何-等积变换
精心整理
第五节 等积变换
【知识要点】
1．等积形： 面积相等的两个图形称为等积形． 2．三角形的等积变换：
三角形的等积变换指的是使三角形面积相等的变换．
例
例是例平方厘米，求阴影部分的面积．
例4 已知△ABC 面积为8cm 2，2BD=AB ，BE=CE ，
D
D
求△DBE 的面积？
例5 ABC ∆中，D 、E 为BC 边的三等分点，M 、N 分别为 AE 、AC 的中点．若224cm S ABC =∆，则=∆MCN S ？
例6
2形的面积是原三角形面积的多少倍？
练习
1． 2
3求△ 4
5面积是
6求三角形DBE 的面积．
7．如图中：如果△ABC 中的BD ＝DE ＝EC ，△EDF 的面积是1个面积单位，△ABC 作业 B
D
E
b
1．图中CD＝3BD，ABD
∆的面积为2cm2，求ABC
∆的面积是多少？
2．如图所示，在△ABC中，D、E、F分别是AB、BC、AE 的中点，图中与△ADE等积的三角形有哪几个？
3
CE=EB
4
三角形
5
为2
6
7
BD=3BC
面积与三角形的面积相等．
B B
D。
【小升初专项训练】04 等积变形
第5讲等积变形第一关三角形的等积变形【例1】如图，在等腰直角三角形ABC中，已知AB的长是7厘米，那么这个直角三角形的面积为 平方厘米。
【答案】12.25【例2】如图，E、F分别是梯形ABCD两腰上的中点，已知阴影部分的面积是43c㎡，那么梯形ABCD 的面积是多少？【答案】172【例3】如图：三条直线互相平行，l1与l3之间的距离是7厘米，l2上AB=4厘米．求阴影部分三角形的面积是多少平方厘米？ 【答案】14【例4】你能看出下面两个阴影部分A与B面积的大小关系吗？（两个长方形面积相等）【答案】A与B的面积相等【例5】如图，在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB，留下两个阴影部分直角三角形AED和DFC．若AD=8cm，CD=12cm，则阴影部分面积为多少？给出答案并说明你的计算依据．【答案】48【例6】如图，在直角三角形中有一个正方形，已知BD=10厘米，DC=7厘米，阴影部分的面积是多少？【答案】35平方厘米【例7】如图，梯形ABCD的面积是36，下底长是上底长的2倍，阴影三角形的面积是多少？【答案】16【例8】下图中阴影部分甲的面积与阴影部分乙的面积哪个大？【答案】图中甲乙的面积相等【例9】如图，在三角形ABC中，D是BC上靠近C的三等分点，E是AD中点，已知三角形ABC的面积为1，那么图中两个阴影三角形面积之和是多少？【答案】0.4【例10】已知△ABC面积为5，且BD=2DC，AE=ED，求阴影部分面积．要求写出关键的解题推理过程．【答案】2【例11】如图，将一个梯形分成四个三角形，其中两个三角形的面积分别为10与12．已知梯形的上底长度是下底的．请问：阴影部分的总面积是多少？【答案】23【例12】如图，已知梯形ABCD中，CD=10，梯形ABCD的高是4，那么阴影部分的面积是多少。
【答案】20【例13】（1）如图1，阴影部分的面积是多少？（2）如图2，一个长方形长4厘米，宽3厘米．A为长方形内的任意一点，阴影部分的面积是多少？【答案】（1）100；（2）6【例14】如图，在图中△ABE、ADF和四边形AECF面积相等．阴影部分的面积是多少？【答案】15【例15】如图，两个正方形（单位：厘米）中阴影部分的面积是多少平方厘米？【答案】8【例16】由面积为1，2，3，4的矩形拼成如图的长方形，图中阴影部分的面积为多少？【答案】【例17】如图所示，正方形ABCD的对角线BD长20厘米，BDFE是长方形．那么，五边形ABEFD的面积是多少平方厘米。
小升初数学思维拓展几何图形专项训练专题10-体积的等积变形
专题10-体积的等积变形小升初数学思维拓展几何图形专项训练（知识梳理+典题精讲+专项训练）1、体积的等积变形主要是用排水法，主要有以下几种情形：（1）当物体浸没于容器中时，要根据物体的体积等于容器内下降（升高）部分水的体积这一隐含条件来解题；（2）当物体仍有部分露于水面时，要根据水的体积未变，只是底面积变了，且体积=底面积×高这一隐含条件来解题；（3）要使得高相等，要记得把物质的体积看做一个整体，然后根据总体积未变，只是底面积变了，且体积=底面积×高这一隐含条件来解题。
350cm，【典例一】有一块长方体木料，锯成相等的3段，可以得到3个完全一样的正方体．已知原木料的表面积是2 cm？那么原木料的体积是多少3【分析】根据题意，小正方体一个面的面积是350(634)25÷⨯-=（平方厘米），因为2555=⨯，所以小正方体的棱长是5厘米，那么长方体体积为：5553375⨯⨯⨯=（立方厘米），解决问题．【解答】解：小正方体一个面的面积是：÷⨯-，350(634)=÷，3501425=（平方厘米）；小正方体的棱长：因为2555=⨯，所以小正方体的棱长是5厘米；长方体体积为：⨯⨯⨯=（立方厘米）；5553375答：原木料的体积是375立方厘米．【点评】此题解答的关键是先求出小正方体一个面的面积，进而求出小正方体的棱长，从而解决问题．【典例二】将底面积是3.14平方分米，高4分米的圆柱形铁块熔铸成一个圆锥．已知圆锥铁块的底面半径是2分米，那么它的高是多少分米？【分析】由题意可知：圆锥铁块的体积应该和圆柱形铁块的体积相等，先据条件求出圆柱的体积，也就等于知道了圆锥的体积，由圆锥的体积公式可得“圆锥的高=圆锥的体积3⨯÷底面积”，圆锥的底面半径已知，从而可以求出底面积，进而求出圆锥的高．【解答】解：23.1443(3.142)⨯⨯÷⨯，12.563(3.144)=⨯÷⨯，12.56312.56=⨯÷，3=（分米）；答：圆锥的高是3分米．【点评】此题主要考查圆柱与圆锥的体积的计算方法，关键是利用体积不变．【典例三】有一个棱长4分米的正方体铁块熔铸成宽2.5分米，高1.6分米的长方体铁块，长方体铁块的长是多少分米？【分析】根据题干可得，这个棱长为4分米的正方体的体积为：44464⨯⨯=立方分米，就是熔铸后的长方体铁块的体积，根据长方体的体积公式可得：长方体的长=体积÷宽÷高，由此代入数据即可计算得出正确答案．【解答】解：44464⨯⨯=（立方分米），64 2.5 1.616÷÷=（分米）；答：长方体铁块的长是16分米．【点评】此类题目要抓住熔铸前后的体积大小没有变化这一关键，利用正方体和长方体的体积公式即可解决问题．一．选择题（共4小题）1．把一个高为24cm 的圆锥形容器装满水，将这些水全部倒入等底的圆柱形容器里，水的高度是()A．72cm B．24cm C．16cm D．8cm 2．如图，甲（底面直径8厘米），乙（底面直径10厘米），两个圆柱形容量中的水深都是6厘米，分别往两个容器中放入一个体积相同的铁球（全部淹没，水没有溢出）后，甲乙两个容器水面高度是()A．甲高B．乙高C．一样高D．无法判断3．把一个长方体木块，截成两段完全一样的正方体，这两个正方体的棱长之和比原长方体增加40厘米，每个正方体的体积是()立方厘米．A．240B．1000C．125D．4004．如图1是三个直立于水平面上的形状完全相同的几何体（下底面为圆面，单位：)cm ．将它们拼成如图2的新几何体，则该新几何体的体积用π表示，应为()A．364cm πB．360cm πC．356cm πD．340cm π二．填空题（共8小题）5．用一块橡皮泥，先捏成一个正方体，再捏成一个圆柱体，两个物体的一样大．6．一个长方体水箱，高15分米，里面水深6分米，把一个圆柱体铁块完全浸没在水中后，这时水面高度是9.6分米，接着又把一个圆锥体铁块完全浸没在水中．已知圆柱体铁块与圆锥体铁块底面半径的比是3:2，高的比是2:3，现在水面的高度是分米．7．甲、乙两个容器内盛有相同体积的水；已知甲容器长是10厘米．宽是10厘米．高12厘米．容器内原来水面高是9厘米．放入一个圆锥体完全浸没后．水面高度与容器高度相等（且没有溢出）：乙容器的棱长是15厘米．放入一个同样大小的圆锥体和一个圆柱体完全浸没后．水面高度距离容器口8厘米．那么圆锥的体积与圆柱体积的比是．8．一个密封的长方体玻璃箱，里面装水，从里面量，长30厘米，宽10厘米，高15厘米，水深5厘米．如果把箱子的左侧面作为底面放在桌面上，那么水深厘米．9．小悦用一块体积为216立方厘米的橡皮泥，捏塑成等底等高的一个圆柱和一个圆锥，圆柱的体积是立方厘米，圆锥的体积是立方厘米．10．一个圆锥钢坯，体积是18.84立方厘米，高是4.5厘米，把2个这样的钢坯改铸成一个圆柱形钢坯，如果底面积不变，改铸后的圆柱形钢坯的高应是．11．一个棱长是6dm 的正方体容器装满了水后，倒入一个底面积是218dm 的圆锥形容器正好装满，这个圆锥的高是．12．把一个长方体木块，截成两段完全一样的正方体，这两个正方体的棱长之和比原长方体增加40厘米，每个正方体的体积是立方厘米．三．解答题13．一个长方体容器，长5cm，宽4cm，高3cm，装满水后将水全部倒入一个高5cm的圆锥形的容器内刚好装满，这个圆锥形容器的底面积是多少平方厘米？14．明明想用一个圆柱形容器测量一个玻璃球的体积，他做了以下实验：①给容器中注入一定量的水，接着把一个棱长6厘米的正方体完全浸没在水中，当把正方体从水中取出后，水面下降了9厘米。
等积变形问题
等积变形问题引言等积变形问题是数学中的一个重要概念，涉及到几何图形的形状变化和面积的关系。
在这个问题中，我们考虑一个固定面积的图形，在保持面积不变的情况下，改变图形的形状。
这个问题有着广泛的应用背景，例如在工程设计、物理学和经济学中都能找到对等积变形问题的研究。
等积变形问题的定义等积变形问题是指在保持图形面积不变的前提下，通过改变图形的尺寸或者形状，使得其它属性发生相应的改变。
通常情况下，我们会固定一个属性（例如周长、直径等），然后通过调整另外一个属性（例如宽度、长度等）来实现对图形进行等积变形。
等积变形问题的解法1. 基于比例关系的解法在等积变形问题中，最常见且直观的解法就是基于比例关系。
假设我们有一个矩形，并且知道其面积为A。
如果我们要将这个矩形进行等积变换，并且保持其宽度不变，那么我们可以通过调整其长度来实现。
根据矩形的面积公式，我们可以得到长度与宽度之间的比例关系：长度/宽度 = A/宽度。
通过这个比例关系，我们可以计算出新的长度。
同样地，如果我们要保持矩形的长度不变，而调整其宽度来实现等积变换，我们也可以利用比例关系进行计算。
这种基于比例关系的解法适用于各种图形，包括矩形、圆形、三角形等。
2. 基于微积分的解法除了基于比例关系的解法外，我们还可以使用微积分方法来解决等积变形问题。
这种方法通常需要使用到函数的导数和积分等概念。
考虑一个简单的例子：一个圆形区域的面积为A。
现在我们要将这个圆形区域进行等积变换，并且保持其半径不变。
我们可以通过求解一个方程来找到新的半径。
设原始圆的半径为r，新圆的半径为R。
根据圆的面积公式，我们有πr^2 = πR2，即r2 = R^2。
由此可得R = ±r。
根据几何意义可知，R不能取负值，因此新圆的半径为r。
这意味着，在保持圆的半径不变的情况下，进行等积变换得到的仍然是一个圆形。
3. 基于几何变换的解法除了基于比例关系和微积分方法的解法外，我们还可以使用几何变换来解决等积变形问题。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、学奥数到底有什么用
对目前绝大部分学奥数的孩子和他们的家长来说，那就是通过各种杯赛获奖得到一个上
重点中学试验班的机会，因为现在的升学制度决定了奥数已经成为升学的一个重要手段。
其实我们目前学的某些内容，比如抽屉原理等，可能以后在初中甚至高中的课本里我们都根本
不可能接触到的，但是我们学习的其实是一些思想方法，更具体的说，是培养一种解决问题的能力。
能把小学奥数学好的同学，我相信学习中学的知识的时候，至少在理科方面，那绝对是游刃有余的。
二、怎样学好奥数
学奥数最佳的起步时间应该是三年级，这个时间启蒙教育特别重要，能不能尽快入门，
或者说“开窍“，这是一个很重要的时期。
五年级的时候最好就应该把六年级的内容学的差不
多了.
下面具体谈一下奥数的学习方法学奥数有诀窍吗？根据我学习奥数的经验，答案是没
有。
但如果非要我说一个的话，那就是“做题”。
那么这里就有两个问题了，一是我该做哪些题呢？二是我该做多少，应该怎么做呢？
我们先说一下做哪些题，现在市面上的奥数书种类繁多。
我觉推荐《华罗庚学校数
学课本》，这本书内容不难，适合入门学习。
《华罗庚思维训练导引》是一本分类习
题集，每个专题15个题目，虽然有的题目偏难，但这本书选题都非常有代表性，值
得一做（做三星题目为主）。
除了专题训练外，大量的综合练习也是必不可少的，《小学数学ABC》《小学数学奥林匹克试题详解》和刘京友编写的《题库》这3本书非常好。
通过做综合练习找出自己问题所在，再集中的有针对性的加强这方面的练习，达到差漏补缺的目的。
这就要求我们每次做完题，不会的或者做错的一定要弄明白为
止。
有的同学可能一天做好几套题目，做完了对对答案，每套错的都不多，自我感
觉也不错，做了半天也累了就把书扔下不管了。
这样的学习是没有效果的，因为你
原先会的还是会，不会的那些呢？还是不会！
因此题目不在于你做了多少，关键是你遇到的每一道题目无论你当时是否会做，事后你是否都真正理解了，再遇到类似的题目还会不会做。
如果我真正能做到做一
套题就把里面所有的题目吃透，那么我学习的效果要比刚才提到的一天做好几套但
不注意总结的同学好的多。
其实你好好把题目总结一下花不了太多时间，而且对自己的帮助真的很大。
希望同学们也能做到这点，至少，对于做错的题目一定要引起重视。
每天学习完或者做
完题，自己都问问自己，我今天学到了什么新的方法，我哪个题目思路上有问题以
后要注意的。
总结不光在笔头上，思想上也要经常总结，不能学了半天连自己学会
了什么还有哪些该掌握的没掌握都不清楚。
三角形的等积变形
我们已经掌握了三角形面积的计算公式：
三角形面积=底×高÷2
这个公式告诉我们：三角形面积的大小，取决于三角形底和高的乘积．如果三
角形的底不变，高越大（小），三角形面积也就越大（小）．同样若三角形的高不
变，底越大（小），三角形面积也就越大（小）．这说明；当三角形的面积变化时，
它的底和高之中至少有一个要发生变化．但是，当三角形的底和高同时发生变化时，
三角形的面积不一定变化．比如当高变为原来
角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化．同
时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状．本讲即研究面积相同的三角形的各种形状以及它们之间的关系．
为便于实际问题的研究，我们还会常常用到以下结论：
①等底等高的两个三角形面积相等．
②底在同一条直线上并且相等，该底所对的角的顶点是同一个点或在与底平行
的直线上，这两个三角形面积相等．
③若两个三角形的高（或底）相等，其中一个三角形的底（或高）是另一个三
角形的几倍，那么这个三角形的面积也是另一个三角形面积的几倍．
，它们所对的顶点同为A点，（也就是它们的高相等）那么这两个三角形的面积相
等．
同时也可以知道△ABC的面积是△ABD或△AEC面积的3倍．
例如在右图中，△ABC与△DBC的底相同（它们的底都是BC），它所对的两个
顶点A、D在与底BC平行的直线上，（也就是它们的高相等），那么这两个三角形
的面积相等．
例如右图中，△ABC与△DBC的底相同（它们的底都是BC），△ABC的高是△DBC 高的2倍（D是AB中点，AB=2BD，有AH=2DE），则△ABC的面积是△DBC面积的2倍．
上述结论，是我们研究三角形等积变形的重要依据．
例1 用三种不同的方法，把任意一个三角形分成四个面积相等的三角形．
方法2：如右图，先将BC二等分，分点D、连结AD，得到两个等积三角形，即
△ABD与△ADC等积．然后取AC、AB中点E、F，并连结DE、DF．以而得到四个等积
三角形，即△ADF、△BDF、△DCE、△ADE等积．。