曲线正矢计算公式的理论局限
曲线正矢的现场量测方法及读数注意事项
曲线正矢的现场量测方法及读数注意事项随着技术的不断发展，曲线正矢已经成为了电力系统中重要的指标之一。
然而，在进行曲线正矢的现场量测时，需要注意很多细节才能确保测量的准确性和可靠性。
首先，现场量测时需要使用准确度高的电能表和电流互感器，以确保测量结果的准确性。
其次，量测时需要注意电能表的安装位置，应该避免将电能表安装在电流变化较大的地方，否则会影响测量结果。
另外，还需要注意曲线正矢的计算公式。
在进行计算时，应该根据实际情况选择合适的公式，并注意单位的换算。
最后，需要注意数据的记录和保存。
量测结束后应及时将数据记录下来，并保存在安全可靠的位置，以备后续分析和使用。
综上所述，曲线正矢的现场量测不仅需要注意技术细节，还需要有严谨的操作和数据管理。
只有这样才能保证测量结果的准确性和可靠性。
- 1 -。
铁路线路工技能鉴定中级工
第二部分中级工一、选择题1.( D )不属于我国铁路采用的到发线有效长度。
(A)1250m (B)1050m (C)850m (D)600m2.( C )不属于线路标志。
(A)公里标(B)曲线标(C)警冲标(D)管界标3.路基侧沟的深度和宽度均不应小于( B )。
(A)0.3m (B)0.4m (C)0.6m (D)0.8m4.当350m＞曲线半径≥300m 时，其轨距加宽值为( B )。
(A)0mm (B)5mm (C)10mm (D)15mm5.铁路轨距变化应和缓平顺，允许速度大于120km/h 线路的轨距变化率不得大于( A )。
(A)1‰ (B)2‰ (C)3‰ (D)4‰6.直线线路上轨向以10m 弦在轨头内侧顶面下( C )处量取最大矢度。
(A)10mm (B)15mm (C)16mm (D)20mm7.轨底坡设置是否正确，可以从钢轨顶面上的光带位置判定。
下列关于光带和轨底坡的说法中正确是( C )。
(A)如果光带偏向内侧，说明轨底坡合适(B)如果光带偏向外侧，则说明轨底坡不足(C)如果光带居中，说明轨底坡合适(D)如果光带偏向内侧，说明轨底坡过大8.( C )不属于钢轨主要参数。
(A)钢轨的头部顶面宽(B)钢轨的轨腰厚(C)钢轨的长度(D)钢轨的轨底宽9.在60kg/m 钢轨上钻螺栓孔上夹板时，轨端距第一孔中心距为( B )。
(A)96mm (B)76mm (C)66mm (D)56mm10.在50kg/m 钢轨上钻螺栓孔上夹板时，第一孔至第二孔中心距为( C )。
(A)220mm (B)140mm (C)150mm (D)110mm11.在75kg/m 钢轨上钻螺栓孔上夹板时，第二孔至第三孔中心距为( D )。
(A)160mm (B)150mm (C)140mm (D)130mm12.60kg/m 钢轨轨头宽度为( C )。
(A)70mm (B)72mm (C)73mm (D)75mm13.50kg/m 钢轨轨底宽度为( B )。
铁路曲线正矢合计闭合差分析与处理探讨(1)
铁 道 建 筑Railway EngineeringMarch ,2006文章编号:100321995(2006)0320076202铁路曲线正矢合计闭合差分析与处理探讨邓昌大(湖南交通工程职业技术学院交通工程系,湖南衡阳 421001)摘要:通过对计划正矢编制和正矢测量误差分析,剖析了曲线正矢合计闭合差产生的原因,提出了曲线正矢合计闭合差的限值标准,介绍正矢合计闭合差的正确处理方法和绳正法的使用要点。
关键词:计划正矢 实测正矢 等精度双观测 误差 正矢合计闭合差 绳正法中图分类号:U41212 文献标识码:B0 前言在日常养护维修中,铁路曲线的拨正,一般采用绳正法。
绳正法拨道计算的方法是科学的,但在实际使用过程中,真正能够正确掌握该方法的人不多,往往是计算者自认为计算好象并没有出错,可就是无法往后继续做下去,只好中途放弃。
如出现拨量达到几百个mm ,按计算出的拨量去拨道,曲线的方向反到拨得更加不圆顺;某些测点拨得实测正矢与计划正矢相符时,目视曲线方向却反而不圆顺。
诸如此类问题,一直困扰绳正法的正确使用,下面通过对正矢合计闭合差的分析,阐述如何正确使用绳正法来拨道。
设曲线计划正矢合计与实测正矢合计的差值称为正矢合计闭合差:Δ∑f =∑f 计-∑f 测,式中的Δ∑f为正矢合计闭合差;∑f 计为计划正矢合计;∑f 测为实测正矢合计。
拨量计算原则之一要求保证曲线整正前后两端的切线方向不变,也就是要求∑f 计=∑f 测,即Δ∑f =∑f 计-∑f 测=0,否则就不能继续计算。
在实际计算中,正矢合计闭合差Δ∑f 往往不可能为零。
产生正矢合计闭合差Δ∑f ≠0,可分别在计划正矢与实测正矢两个方面找原因。
1 计划正矢方面的原因分析实测正矢存在误差,大家好理解,却很少有人去怀疑计划正矢有问题,事实上笔者调查发现编制的计划正矢的确存在不少问题。
111 计划正矢及合计的计算计划正矢是根据竣工的曲线要素资料计算出的正矢,也就是曲线处于理论圆顺状态对应的正矢。
曲线正矢作业验收容许偏差 表3
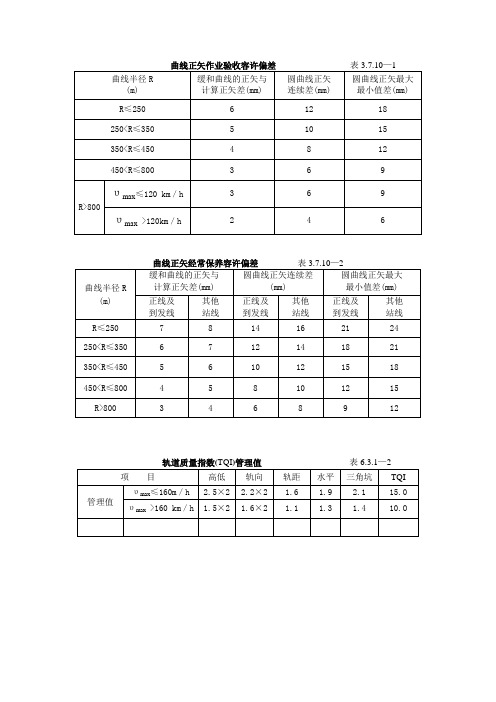
②轨向偏差和高低偏差为10m弦测量的最大矢度值；
③三角坑偏差不含曲线超高顺坡造成的扭曲量，检查三角坑时基长为 6.25m，但在延长18m的距离内
无超过表列的三角坑；
④专用线按其他站线办理。
②导曲线下股高于上股的限值：作业验收为0，经常保养为2mm，临时补惨为3 mm；
③三角坑偏差不含曲线超高顺坡造成的扭曲量，检查三角坑时基长为 6.25m。
但在延长18。
的距离内无超过表列的三角坑；
④尖轨尖处轨距的作业验收的容许偏差管理值为±1 mm；
⑤专用线道岔按其他站线道岔办理。
②高低、轨向不平顺按实际值评定；
③水平限值不含曲线上按规定设置的超高值及超高顺坡量；
④三角坑限值包含缓和曲线超高展坡造成的扭曲量；
⑤固定型辙叉的有害空间部分不检查轨距、轨向。
其他检查项目及检查标准与线路相同。
曲线计划正矢的计算
曲线计划正矢的计算一、计算方法1、圆曲线计划正矢的计算f c=L2/8R式中：L----弦长，一般为20m，当曲线状态不良为确保曲线圆顺，增加正矢点时，为10m；f c----圆曲线正矢（mm）；R----曲线半径（m）。
当L=20m时，f c=L2/8R=20*20/8R=50000/R；当L=10m时，f c=L2/8R=10*10/8R=12500/R；2、缓和曲线计划正矢的计算（1）缓和曲线正矢递增率f s= f c/n式中：f c----圆曲线正矢（mm）；n----缓和曲线的分段数，其值为l0/ , 其中l0为缓曲长， 为测点间的距离，一般为10m。
（2）缓和曲线各点的计划正矢缓和曲线始点0点（ZH）点的正矢f0=f s/6缓和曲线第1点的正失f1=f s缓和曲线第2点的正失f2=2f s缓和曲线第3点的正失f3=3f s。
缓和曲线终点(HY)的正矢f hy=f c- f03、测点不在曲线始、终点时计划正矢的计算前述缓和曲线和圆曲线的长度都假定是10m的整数倍，但在实际工作中，缓和曲线的长度一般都设置成10m的整数倍，而圆曲线的长度一般都不是10m的整数倍，因此第二缓和曲线的始、终点就不可能恰好落在测点上。
这样缓和曲线始、终点左右相邻测点的计划正矢，都要作为一种特殊情况另行计算。
（1）第二缓和曲线始点（HZ）左右邻点计划正矢的计算HZ不在测点上，位于缓和曲线上的n点和直线上的n+1点之间，n点距HZ点的距离为b，n+1距HZ点的距离为a，相应的正矢分别为f n和f n+1， 为测点间的距离，等于弦长的一半，a+b= ，则：f n=1/6 f s[（1+b/ ）3-2（b/ ）3]f n+1=1/6 f s（b/ ）3（2）第二缓和曲线终点（YH）左右邻点计划正矢的计算第二缓和曲线终点（YH）不在测点上，位于圆曲线上的n点和缓和曲线上的n+1点之间，n点距YH点的距离为a，n+1点距YH点的距离为b,相应的正矢分别为f n和f ，则：n+1f n = f c－1/6 f s（b/ ）3f n+1= f c－1/6 f s[（1+b/ ）3-2（b/ ）3]（3）第二缓和曲线上其他各点计划正矢的计算第二缓和曲线上其他各点计划正矢，可根据各点正矢与其距终点HZ距离成直线比例的关系，按下式求取：f i= f c/ l0*l i式中：f i----缓和曲线上距HZ点为l i的测点正矢；二、算例1、圆曲线长度为10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m，两端缓和曲线长l0=50m，求曲线各测点的计划正矢解：（1）圆曲线计划正矢：f c=L2/8R=20*20/8R=50000/R=50000/600=83.3mm，取84mm（2）缓和曲线正矢递增率：f s= f c/n=84/5=16.8mm（3）直缓（缓直）点正矢：f0=f s/6=16.8/6=2.8mm，取3mm（4）缓和曲线中间各点的正矢：缓和曲线第1点的正失f1=f s=16.8mm，取17mm缓和曲线第2点的正失f2=2f s=2*16.8=33.6mm，取34mm缓和曲线第3点的正失f3=3f s=3*16.8=50.4mm，取50mm缓和曲线第4点的正失f4=4f s=4*16.8=67.2mm，取67mm（5）缓圆（圆缓）点正矢：f hy=f c- f0=84-3=81mm2、圆曲线长度不是10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m，两端缓和曲线l0=50m，圆曲线长304m,求各测点的计划正矢解：（1）第一缓和曲线和圆曲线的计划正矢算法同上；（2）第二缓和曲线各点计划正矢的计算：①第二缓和曲线始（HZ）点相邻测点的计划正矢因为圆曲线长L=304m，故第二缓和曲线始（HZ）点距缓和曲线和直线上相邻点（40点、41点）的距离分别为b≈4m，a≈6m， 为测点间的距离，等于弦长的一半，a+b= 则f40=1/6 f s[（1+b/ ）3-2（b/ ）3]=1/6*16.8*[（1+4/10）3-2*（4/10）3]=7.32mm，取7mmf41=1/6 f s（b/ ）3=1/6*16.8*（4/10）3=0.18mm，取0mm②第二缓和曲线终点（YH）相邻测点的计划正矢第二缓和曲线终点（YH）距圆曲线和缓和曲线上相邻点（35点、36点）的距离分别为a≈4m，b≈6m， 为测点间的距离，等于弦长的一半，a+b=则f35 = f c－1/6 f s（b/ ）3=84－1/6*16.8*（6/10）3=84－0.6=83.4mm，取84mmf36= f c－1/6 f s[（1+b/ ）3-2（b/ ）3]=84－1/6*16.8*[（1+6/10）3-2*（6/10）3]=73.74mm，取74mm③第二缓和曲线上其他各点计划正矢的计算其他各点计划正矢，可根据各点正矢与其距终点（HZ）距离成直线比例的关系，按下式求取：f i=f c/l0*l i则第37点、38点、39点的计划正矢分别为：f37=f c/l0*l37=84/50*34=57.12mm，取57mmf38=f c/l0*l38=84/50*24=40.32mm，取40mmf39=f c/l0*l39=84/50*14=23.52mm，取24mm3、辅助点计划正矢的计算辅助点计划正矢的计算按圆曲线长度不是10m整数倍时缓和曲线的算法计算（1）圆曲线长度为10m整数倍时辅助点计划正矢的计算已知某曲线半径R=600m，两端缓和曲线长l0=50m，求缓和曲线辅助点的计划正矢解：辅助点与测点相距5m，即a=b=5m，①缓和曲线上与始点（ZH、HZ）相邻辅助点计划正矢为：f=1/6 f s[（1+b/ ）3-2（b/ ）3]=1/6*16.8*[（1+5/10）3-2*（5/10）3]=8.75mm，取9mm②缓和曲线上与终点（YH、HY）相邻辅助点计划正矢为：f= f c－1/6 f s[（1+b/ ）3-2（b/ ）3]=84－1/6*16.8*[（1+5/10）3-2*（5/10）3]=75.25mm，取75mm③缓和曲线其他各中间辅助点的计划正矢：分别取l i=15、25、35，按f i=f c/l0*l i算得辅助点计划正矢分别为：25mm、42mm、59mm（2）圆曲线长度不是10m整数倍时辅助点计划正矢的计算曲线半径R=600m，缓和曲线长l0=50m，圆曲线长304m,求缓和曲线辅助点的计划正矢解：第一个缓和曲线辅助点的算法同上，第二个缓和曲线上辅助点计划正矢的计算按B=b±5计算，即：①缓和曲线上与始点（ZH、HZ）相邻辅助点计划正矢为（B=4+5=9）：f=1/6 f s[（1+B/ ）3-2（B/ ）3]=1/6*16.8*[（1+9/10）3-2*（9/10）3]=15.12mm，取15mm②缓和曲线上与终点（YH、HY）相邻辅助点计划正矢为（B=6-5=1）：f= f c－1/6 f s[（1+B/ ）3-2（B/ ）3]=84－1/6*16.8*[（1+1/10）3-2*（1/10）3]=80.3mm，取80mm③缓和曲线其他各中间辅助点的计划正矢：分别取l i=19、29、39，按f i=f c/l0*l i算得辅助点计划正矢分别为：32mm、49mm、66mm。
曲线正矢计算公式(二)
曲线正矢计算公式(二)
曲线正矢计算公式
1. 什么是曲线正矢？
曲线正矢是计算电路中电流和电压之间的相位差的一种方法。
在交流电路中，电流和电压可能存在相位差，曲线正矢则用于描述这个相位差。
2. 曲线正矢的计算公式
曲线正矢由正弦波电压和电流的相位差决定，可以用下列公式来计算：
功率因数PF = cos(θ)
其中，θ为电流和电压的相位差角度。
3. 曲线正矢的意义
曲线正矢用于衡量电路中有功功率的有效性和功率因数。
功率因数是指实际有功功率与视在功率的比值，通过计算曲线正矢可以得出功率因数的数值。
4. 曲线正矢计算公式的例子
假设有一个电路，电源电压为220V，电路中的电流和电压相位差为30度。
我们可以使用曲线正矢计算公式来计算功率因数：
θ = 30
功率因数PF = cos(30) ≈
通过计算可得，该电路的功率因数约为。
5. 其他曲线正矢计算公式的应用
曲线正矢计算公式还可以用于计算交流电路中的视在功率和无功功率。
常见的计算公式如下：
•视在功率：
视在功率S = 电压U × 电流I
•无功功率：
无功功率Q = 视在功率S × sin(θ)
其中，θ为电压和电流的相位差角度。
6. 总结
曲线正矢计算公式是描述交流电路中电流和电压相位差的一种方法。
通过计算功率因数，可以得出电路中有功功率的有效性。
此外，曲线正矢计算公式还具有计算视在功率和无功功率的应用。
以上是曲线正矢计算公式的相关内容。
曲线正矢、负矢的计算
曲线正矢、负矢的计算
曲线的正矢和负矢可以用以下方式计算：
1. 首先，确定曲线上某一点的切线方向。
可以通过求导函数得到曲线在该点的斜率，然后求出与曲线切线垂直的斜率。
2. 然后，确定该点的切线方向的正方向和负方向。
可以通过选取曲线上该点两侧的点，然后比较切线的斜率方向来确定。
3. 最后，计算该点的正矢和负矢。
正矢是曲线在该点沿切线方向的长度，而负矢是曲线在该点沿切线相反方向的长度。
可以通过测量切线上该点两侧的弧长来计算。
需要注意的是，以上计算方法仅适用于光学曲线（如球面、抛物线等），对于非光学曲线（如螺旋线、心形曲线等），正矢和负矢的定义可能会有所不同。
铁路曲线正矢计算公式例题
铁路曲线正矢计算公式例题铁路曲线正矢计算公式例题在铁路设计中，曲线是一个重要的设计元素，目的是为了确保行车安全和行车速度。
曲线的设计参数包括半径、曲线长度和曲线正矢等。
本文将详细讨论曲线正矢的计算公式和应用例题。
1. 曲线正矢的定义曲线正矢是曲线的一个参数，是曲线下一条直线的长度，该直线与曲线的切线平行，在曲线上方。
曲线正矢是铁路曲线设计的重要指标之一，影响着铁路行车的安全和速度。
2. 曲线正矢的计算公式曲线正矢的计算公式可以根据铁路设计标准或手册给出，常用的计算公式有以下两种：（1）C=V²/127R式中，C为曲线正矢，单位为米（m）；V为轨道线速度，单位为千米/小时（km/h）；R为曲线半径，单位为米（m）。
该公式适用于直线轨道和大半径曲线，曲线半径大于1500米时，误差较小。
（2）C=137V²/(127R+9C)式中，C为曲线正矢，单位为米（m）；V为轨道线速度，单位为千米/小时（km/h）；R为曲线半径，单位为米（m）。
该公式适用于一般曲线和小半径曲线，曲线半径小于1500米时，误差较小。
3. 曲线正矢的应用例题下面举例说明曲线正矢的应用。
例题：一条半径为800米的曲线，设计速度为100km/h，求曲线正矢。
解：根据第一种计算公式，代入数据得：C=V²/127R=（100×100）/（127×800）=0.0982≈0.1(m)根据第二种计算公式，代入数据得：C=137V²/(127R+9C)=137×（100×100）/（127×800+9C）移项整理得：23C=127×800C=348.7≈350(m)因此，曲线正矢为0.1m和350m。
根据实际情况，如果曲线正矢过大，会影响行车速度；如果曲线正矢过小，则会影响行车安全。
因此，在设计曲线时，必须根据行车安全、行车速度和经济效益等因素进行合理的参数设计。
曲线计划正矢的计算
曲线计划正矢的计算一、计算方法1、圆曲线计划正矢的计算f c=L2/8R式中：L----弦长，一般为20m，当曲线状态不良为确保曲线圆顺，增加正矢点时，为10m；f c----圆曲线正矢（mm）；R----曲线半径（m）。
当L=20m时，f c=L2/8R=20*20/8R=50000/R；当L=10m时，f c=L2/8R=10*10/8R=12500/R；2、缓和曲线计划正矢的计算（1）缓和曲线正矢递增率f s= f c/n式中：f c----圆曲线正矢（mm）；n----缓和曲线的分段数，其值为l0/ , 其中l0为缓曲长， 为测点间的距离，一般为10m。
（2）缓和曲线各点的计划正矢缓和曲线始点0点（ZH）点的正矢f0=f s/6缓和曲线第1点的正失f1=f s缓和曲线第2点的正失f2=2f s缓和曲线第3点的正失f3=3f s。
缓和曲线终点(HY)的正矢f hy=f c- f03、测点不在曲线始、终点时计划正矢的计算前述缓和曲线和圆曲线的长度都假定是10m的整数倍，但在实际工作中，缓和曲线的长度一般都设置成10m的整数倍，而圆曲线的长度一般都不是10m的整数倍，因此第二缓和曲线的始、终点就不可能恰好落在测点上。
这样缓和曲线始、终点左右相邻测点的计划正矢，都要作为一种特殊情况另行计算。
（1）第二缓和曲线始点（HZ）左右邻点计划正矢的计算HZ不在测点上，位于缓和曲线上的n点和直线上的n+1点之间，n点距HZ点的距离为b，n+1距HZ点的距离为a，相应的正矢分别为f n和f n+1， 为测点间的距离，等于弦长的一半，a+b= ，则：f n=1/6 f s[（1+b/ ）3-2（b/ ）3]f n+1=1/6 f s（b/ ）3（2）第二缓和曲线终点（YH）左右邻点计划正矢的计算第二缓和曲线终点（YH）不在测点上，位于圆曲线上的n点和缓和曲线上的n+1点之间，n点距YH点的距离为a，n+1点距YH点的距离为b,相应的正矢分别为f n和f ，则：n+1f n = f c－1/6 f s（b/ ）3f n+1= f c－1/6 f s[（1+b/ ）3-2（b/ ）3]（3）第二缓和曲线上其他各点计划正矢的计算第二缓和曲线上其他各点计划正矢，可根据各点正矢与其距终点HZ距离成直线比例的关系，按下式求取：f i= f c/ l0*l i式中：f i----缓和曲线上距HZ点为l i的测点正矢；二、算例1、圆曲线长度为10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m，两端缓和曲线长l0=50m，求曲线各测点的计划正矢解：（1）圆曲线计划正矢：f c=L2/8R=20*20/8R=50000/R=50000/600=83.3mm，取84mm（2）缓和曲线正矢递增率：f s= f c/n=84/5=16.8mm（3）直缓（缓直）点正矢：f0=f s/6=16.8/6=2.8mm，取3mm（4）缓和曲线中间各点的正矢：缓和曲线第1点的正失f1=f s=16.8mm，取17mm缓和曲线第2点的正失f2=2f s=2*16.8=33.6mm，取34mm缓和曲线第3点的正失f3=3f s=3*16.8=50.4mm，取50mm缓和曲线第4点的正失f4=4f s=4*16.8=67.2mm，取67mm（5）缓圆（圆缓）点正矢：f hy=f c- f0=84-3=81mm2、圆曲线长度不是10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m，两端缓和曲线l0=50m，圆曲线长304m,求各测点的计划正矢解：（1）第一缓和曲线和圆曲线的计划正矢算法同上；（2）第二缓和曲线各点计划正矢的计算：①第二缓和曲线始（HZ）点相邻测点的计划正矢因为圆曲线长L=304m，故第二缓和曲线始（HZ）点距缓和曲线和直线上相邻点（40点、41点）的距离分别为b≈4m，a≈6m， 为测点间的距离，等于弦长的一半，a+b= 则f40=1/6 f s[（1+b/ ）3-2（b/ ）3]=1/6*16.8*[（1+4/10）3-2*（4/10）3]=7.32mm，取7mmf41=1/6 f s（b/ ）3=1/6*16.8*（4/10）3=0.18mm，取0mm②第二缓和曲线终点（YH）相邻测点的计划正矢第二缓和曲线终点（YH）距圆曲线和缓和曲线上相邻点（35点、36点）的距离分别为a≈4m，b≈6m， 为测点间的距离，等于弦长的一半，a+b=则f35 = f c－1/6 f s（b/ ）3=84－1/6*16.8*（6/10）3=84－0.6=83.4mm，取84mmf36= f c－1/6 f s[（1+b/ ）3-2（b/ ）3]=84－1/6*16.8*[（1+6/10）3-2*（6/10）3]=73.74mm，取74mm③第二缓和曲线上其他各点计划正矢的计算其他各点计划正矢，可根据各点正矢与其距终点（HZ）距离成直线比例的关系，按下式求取：f i=f c/l0*l i则第37点、38点、39点的计划正矢分别为：f37=f c/l0*l37=84/50*34=57.12mm，取57mmf38=f c/l0*l38=84/50*24=40.32mm，取40mmf39=f c/l0*l39=84/50*14=23.52mm，取24mm3、辅助点计划正矢的计算辅助点计划正矢的计算按圆曲线长度不是10m整数倍时缓和曲线的算法计算（1）圆曲线长度为10m整数倍时辅助点计划正矢的计算已知某曲线半径R=600m，两端缓和曲线长l0=50m，求缓和曲线辅助点的计划正矢解：辅助点与测点相距5m，即a=b=5m，①缓和曲线上与始点（ZH、HZ）相邻辅助点计划正矢为：f=1/6 f s[（1+b/ ）3-2（b/ ）3]=1/6*16.8*[（1+5/10）3-2*（5/10）3]=8.75mm，取9mm②缓和曲线上与终点（YH、HY）相邻辅助点计划正矢为：f= f c－1/6 f s[（1+b/ ）3-2（b/ ）3]=84－1/6*16.8*[（1+5/10）3-2*（5/10）3]=75.25mm，取75mm③缓和曲线其他各中间辅助点的计划正矢：分别取l i=15、25、35，按f i=f c/l0*l i算得辅助点计划正矢分别为：25mm、42mm、59mm（2）圆曲线长度不是10m整数倍时辅助点计划正矢的计算曲线半径R=600m，缓和曲线长l0=50m，圆曲线长304m,求缓和曲线辅助点的计划正矢解：第一个缓和曲线辅助点的算法同上，第二个缓和曲线上辅助点计划正矢的计算按B=b±5计算，即：①缓和曲线上与始点（ZH、HZ）相邻辅助点计划正矢为（B=4+5=9）：f=1/6 f s[（1+B/ ）3-2（B/ ）3]=1/6*16.8*[（1+9/10）3-2*（9/10）3]=15.12mm，取15mm②缓和曲线上与终点（YH、HY）相邻辅助点计划正矢为（B=6-5=1）：f= f c－1/6 f s[（1+B/ ）3-2（B/ ）3]=84－1/6*16.8*[（1+1/10）3-2*（1/10）3]=80.3mm，取80mm③缓和曲线其他各中间辅助点的计划正矢：分别取l i=19、29、39，按f i=f c/l0*l i算得辅助点计划正矢分别为：32mm、49mm、66mm。
曲线正矢、付矢、超高、加宽的计算方法
一、曲线（有缓）正矢、付矢、超高、加宽计算方法（例）：例：已知某曲线R＝310m，α＝26°38′09″，l1＝70m，l2＝70m，H ＝125mm，S＝5mm，V max＝70km / h，求该曲线L全，L外，内距D，外距C，内距B，外距A，F Y及曲线各点F，f，H，S？解：L全＝π×α×R/ 180＋l1 / 2＋l2 / 2 ＝214.114L外＝π×α×R外/ 180＋l1 / 2＋l2 / 2＝214.447内距D＝(π×α×R外/ 180＋l1 / 2－l2 / 2)－INT((π×α×R外/ 180＋l1 / 2－l2 / 2)/10) ×10＝4.447 外距C＝10－D＝5.553内距B＝L外－INT(L外/ 10)×10 ＝4.447外距A＝10－B＝5.553外距系数a＝A/10＝0.5553，内距系数b＝B/10＝0.4447外距系数c＝C/10＝0.5553，内距系数d＝D/10＝0.4447F Y＝λ2/2 R外＝50000/（R＋0.7175）＝160.918，取161F d1＝F Y /（l1/λ）＝22.988F d2＝F Y /（l2/λ）＝22.988因 H d1＝H /l1＝1.786＞H d＝1/（9×V max）＝1.587H d2＝H /l2＝1.786＞H d＝1/（9×V max）＝1.587故始端、终端超高顺坡各向直线延伸9m，则 H d1＝H /（l1＋9）＝1.582≤H dH d2＝H /（l2＋9）＝1.582≤H dS d1＝S /l1＝0.071S d2＝S /l2＝0.071★始端正矢计算：(整桩)F ZH＝F0＝F d1/6＝3.831，取4因 F n＝n d×F d1＝（D n / 10）×F d1故 F1＝23、F2＝46、F3＝69、F4＝92、F5＝115、F6＝138F HY＝F7＝F Y－F d1/6＝157.086，取157★始端付矢计算：因 f n＝0.75×F n＋0.125×F d1故 f1＝20、f2＝37、f3＝55、f4＝72、f5＝89、f6＝106★始端超高、加宽计算：（略）H n＝D n ×H d1S n＝D n×S d1★终端正矢计算：(破桩)F D＝F14＝F Y－c3 /6×F d2＝160.262，取160＝F Y－C3/(12×R外×l2)F C＝F15＝F Y－(c+d3 /6)×F d2＝147.816，取148＝F Y－（600C＋D3）/(12×R外×l2)因 F n＝n d×F d2＝（D n / 10）×F d2＝（50×D n ）/(R外×l2)故 F16＝125、F17＝102、F18＝79、F19＝56、F20＝33F B＝F21＝（b+a3 /6）×F d2＝10.879，取11＝（600B＋A3）/(12×R外×l2)F A＝F22＝b3 /6×F d2＝0.337，取0＝B2/(12×R外×l2)★终端付矢计算：因 C＞5m，故 f YH＝f15即 f15＝(300×(l2＋D)－(D3＋2500))/(8×R外×l2)=113因 f n＝0.75×F n＋0.125×F d2故 f16＝97、f17＝80、f18＝62、f19＝45、f20＝28f HZ＝f21＝（2500＋600B＋30B2－B3）/(24×R外×l2)=11★终端超高、轨距计算：（略）H n＝D n ×H d2S n＝D n ×S d2二、曲线（无缓）正矢计算方法：曲线全长 L全＝π×α×R/ 180曲线外长 L外＝π×α×R外/ 180内距 B＝L外－INT(L外/ 10)×10外距 A＝10－B圆曲线正矢 F Y＝λ2/2 R外＝50000/（R＋0.7175）始端正矢：(整桩) F ZY＝1/2×F Y终端正矢：(破桩) F A＝1/2×B2/2 R外F B＝1/2×(λ+B)2/2 R外－B2/2 R外＝F Y－1/2×A 2/2 R外三、曲线（附带）正矢计算方法：曲线全长 L全＝π×α×R/ 180（α为辙叉角）曲线外长 L外＝π×α×R外/ 180内距 B＝L外－INT(L外/ 5)×5外距 A＝5－B圆曲线正矢 F Y＝λ2/2 R外＝12500/（R＋0.7175）始端正矢：(整桩) F ZY＝1/2×F Y终端正矢：(破桩) F A＝1/2×B2/2 R外F B＝1/2×(λ+B)2/2 R外－B2/2 R外＝F Y－1/2×A 2/2 R外四、曲线（有缓）正矢、付矢、超高、加宽（自动）计算表：五、曲线（无缓）正矢（自动）计算表：六、常用附带曲线正矢（自动计算）表：。
铁路轨道曲线正矢计算(修正)
第一讲：曲线正矢计算一、曲线的分类：目前我段主要曲线类型有：1、由两端缓和曲线和圆曲线组成的曲线，如正线曲线。
容许行车速度高。
2、由圆曲线构成的曲线。
如道岔导曲线、附带曲线。
二、圆曲线正矢的计算1、曲线头尾正好位于起终点桩上F C=L2/8RL=20M时，F C=50000/RF ZY=F YZ= F C/22、曲线头尾不在起终点桩上ZY前点：Fμ=（FC/2）*（δ/10）2ZY后点：Fη=FC-{（FC/2）*（τ/10）2}FC：圆曲线正矢δ：ZY点到后点的距离τ：ZY点到前点的距离三、缓和曲线上整点正矢的计算（起始点正好是测点）（1）缓和曲线头尾的计算：F0=F1/6（缓和曲线起点）F终= F C-F0（缓和曲线终点）（2）缓和曲线中间点正矢的计算：F1=F S= F C/N （N=L0/B：缓和曲线分段数）F2=2 F1 F3=3F1 F I=IF1（I为中间任意点）四、半点（5米桩）正矢的计算：a)ZH点后半点正矢的计算：F后=25/48*F1因为ZH点正矢f0=f1/6,很小一般为1~2MM，其前半点很小（小于1MM）因此不作计算。
b)H Y（YH）点前半点计划正矢的计算F前=1/2{[L03+（L0-15）3]/6R L0+[5L0+25]/2R}-（L0-5）3/6R L0c)HY（YH）点后半点计划正矢的计算F后=1/2{[ （L0-5）3 -L03]/6R L0+[5L0+175]/2R}d)中间点（5米桩）正矢的计算F中=（F前+F后）/2五、测点不在曲线始终点时缓和曲线计划正矢的计算a)缓和曲线始点(ZH点)处相邻测点的计划正矢Fμ=αυF S(直缓点外点) αυ=1/6(δ/B)3Fη=αηF S(直缓点内点) αη=1/6[(1+δ/B)3-(δ/B)3](2) 缓圆点处相邻测点的计划正矢Fφ=F C-αυF S (缓圆点外点，缓和曲线之外)Fθ= F C-αηF S (缓圆点内点，缓和曲线之内)(αυ、αη查纵距率表《曲线设备与曲线整正》附表二)(3)缓和曲线中间点各点计划正矢的计算F I=(F C/L0)L I（I为中间任意点）说明：B：半弦长δ：缓和曲线内点到ZH、HY（YH）距离L0：缓和曲线长F C：圆曲线正矢第二讲：曲线拨道一、绳正法基本原理1、基本假定：（1）假定拨道前后两端切线方向不变，或起始点位置不变，即曲线终点拨量为零。
曲线正矢总和与偏角及测点距之间的几何关系应用分析
检修运用上海铁道增刊2020年第2期119曲线正矢忌刷与臑南艮测烏距之间的n悃天系脰用只肮俞友强中国铁路上海局集团有限公司金温铁路有限责任公司摘要通过建立圆曲线正矢总和(2f)、偏角（a)和测点 距(i)三者之间的关系，举例说明其在解决线路维修中曲 线正矢总和、偏角计算及既有曲线复核等方面的具体应 用〇关键词曲线；正矢总和；几何关系；应用各类教材、规范对曲线计划正矢的计算过程进行了叙 述，但未提及正矢总和、偏角和测点距三者之间的几何关系 计算，给曲线正矢及拨道量计算造成一定困惑。
通过建立曲 线正矢总和(S f)、偏角（a)和测点距(i)三者之间的几何关系，并结合现场进行检验，在金温货线武义站、芝溪站曲线维修 中实际应用，取得较好的效果。
1曲线正矢总和的计算1.1曲线正矢总和公式弦上任一点到曲线上的垂直距离叫做矢距，在中央点的 矢距叫做正矢。
如图1所示。
图1正矢、半径、测点示意图根据射影定理可得:AD=f=iCD=AC-AD=2R-f BD= L即弦长的一半 BD=孑L由于f与2R相比较，其值甚微，在(2R-f)项中,f可忽略,._(L/2)2~ (L/2)2不计，上式可近似地写成：2i?_f2RBD2=AD x DC AB2=AD x AC bp：(L/2 )fx(2R-f) Ni2- fx2R j由于半弦长与测点距长度近似相等，因此上述关系式转 换为:r=b图2曲线全长与偏角、半径关系示意图如图2所示，曲线全长与偏角、半径的关系为T n a〇L c=R x------7T180将曲线全长平均等分成n段（n>2)，每段长度为i，则Lcn=—2R180Z f=n •f则 E f=nx_L x1〇〇〇=2RS fa=-----------…八..8.7266 i1.2曲线正矢总和与其它参数的关系由公式（1)可得，曲线正矢总和与曲线半径、曲线全长无 关，与测点距、偏角成正比关系。
Lc ^f=—X—X1000*Lcxi 1R-ixl〇〇〇=8.7266 a° i(公式1<1000-Rx1802曲线正矢总和计算与应用120曲线正矢总和与偏角及测点距之间的几何关系应用分析检修运用2.1道岔岔后曲线正矢总和计算(1)道岔岔后曲线正矢计算公式图3岔后连接曲线示意图如图3所示，道岔岔后连接曲线(特别是附带曲线）正矢 点一般按5 m设置，按公式（1)计算Sf=8.7266x5a°=43.633a。
曲线正矢布设方法
曲线分中法计划正矢计算及布设方法此文已由洛阳工务段在《郑铁工务通讯》发表铁路曲线的缓和曲线一般为10m 的整倍数，但圆曲线一般不是10m 的整倍数，为了提高养护曲线的精度，便于计算以及方便现场对曲线拉绳测量，曲线正矢点按照曲线全长向上规整为10米的整倍数对曲线的正矢点进行分中布设，对于缓和曲线不等长的曲线，应先对圆曲线正矢点进行分中布设，确保曲中位置正确。
例如：曲线理论全长为531.135米，长度规整为540米。
本方法适用于单曲线，需要根据曲线半径、偏角、缓长等曲线要素对曲线全长重新进行检算以确保数据的精确，利用微软的Excel 电子表格函数功能可以提高计算效率，具体的曲线分中法正矢计算及布设方法如下：一、通过测量正矢确定曲中及头尾位置1．在测量现场曲线正矢前，应先将曲线前后直线拨直，把一切不正常弯曲（鹅头）拨入曲线范围以内。
2．在曲线外轨每隔10米用钢尺排好测点，测点应伸入曲线两端直线范围内，将各测点顺序编号。
3．在风力较小的条件下，用20米弦绳，在钢轨顶面作用边下16mm 处，拉绳测每个测点正矢，拉弦要用力均匀，读数要眼、线、尺三者成垂线，读弦线靠钢轨一边的读数。
4．曲中点：用测点分段数来表示的曲线中央位置为现场正矢倒累计合计除以现场正矢合计（缓和曲线不等长应抛去缓和曲线检算）。
即：曲中点＝现场正矢倒累计合计÷现场正矢合计（曲中点位置应按拉正矢始点方向算起，小数点后单位为米）5．曲中分中布设正矢方法：如果规整后的曲线全长减去两端缓长的长度为整10米倍数的偶数，用对桩分中法（由曲中点向两边每10米布点）。
如果规整后的曲线全长减去两端缓长的长度为整10米倍数的奇数，用10米分中法（先由曲中点分别向两边量取5米布点，然后再向两边每10米布点），如下图：二、正矢计算公式：1．圆曲线正矢：f 圆=R50000 2．正矢递减率：f 递=/10f 缓长圆 3．曲线全长：L=l 180πR α 式中α为度°，曲线偏角一般为六十进制的度°分′秒″，计算时应转化为十进制的度，l 为缓和曲线长度，如曲线两头缓和曲线不等长，应取两缓和曲线长度的平均长度。
(全新)轨道交通线路工知识理论题库(含答案)
A、施工灵活、简单、易行 B、封锁时间较长 C、用工较多 D、质量易保证 答案：D 6.尖轨顶面()mm 范围内,是车辆往返于尖轨与基本轨之间的过渡段,尖轨与基本 轨的高差降低了行车的平稳性。 A、20~30 B、20~40 C、20~50 D、30~60 答案：C 7.根据 h=11.8v² 平/R 计算出的超高值,未被平衡欠超高一般不大于()mm A、50 B、75 C、90 D、125 答案：B 8.预铺移设法更换道岔时,滑道轨一端固定在平台上,另一端伸入既有道岔的枕 木盒内,使其保持()左右的坡度,便于移设。 A、1% B、2% C、3% D、4% 答案：B 9.波形磨耗常发生在地铁整体道床() A、小半径曲线上股 B、小半径曲线下股 C、直线左股
（全新）轨道交通线路工知识理论题库（含答案）
一、单选题 1.设计无缝线路时,一般规定最低轨温()最低气温。 A、等于 B、大于 C、小于 D、大于或等于 答案：A 2.下列关于道床的作用,错误的是() A、保护路基 B、保持轨道几何形位 C、排水 D、抗腐蚀 答案：D 3.人工换轨时,通常先把新换入轨连接成一定长度的轨组,长度一般为()m A、200 B、150 C、80 D、100 答案：D 4.道岔导曲线部分钢轨接头为()布置,增加了车轮通过时的单股撞击,使列车摇 晃加剧,增加了对轨道的破坏。 A、对接 B、错接 C、交叉 D、不均匀 答案：B 5.现地更换法不需要机械和特殊工具,()不属于其特点。吊车更换法更换道岔时,应根据车辆和线路的具体情况,将预铺新道岔成组 或分段放在()上。 A、空地 B、滑轨 C、平板车 D、组装平台 答案：C 11.无缝线路钢轨温度在锁定轨温以下时,钢轨内部产生() A、拉应力 B、压应力 C、剪应力 D、拉应力与压应力 答案：A 12.对于大于()的下坡制动地段,正线轨道应增加轨枕数量。 A、15‰ B、20‰ C、12‰ D、8‰ 答案：C 13.两端缓和曲线等长时,曲线总缩短量计算公式为() A、1500³(圆曲线长+一端缓和曲线长)/半径 B、1500³(圆曲线长-一端缓和曲线长)/半径 C、(1500³一端缓和曲线全长)/(半径³2) D、(1500³一端缓和曲线全长)/(半径³2³一端缓和曲线长) 答案：A 14.困难地段,曲线半径为 80m 时,按 3‰的变坡率设过渡段,其长度不短于()m A、1
铁路轨道曲线正矢计算新方法研究
铁路轨道曲线正矢计算新方法研究马文静【摘要】曲线正矢管理是铁路运营维修过程中的关键环节，对列车曲线动态平稳运行具有重要作用。
针对传统的曲线正矢管理与轨道坐标测量法不相适应的现状，提出了一种基于轨道坐标计算曲线正矢的新方法，并通过仿真计算进行了验证。
研究结果表明，该方法具有很高的数值计算精度及数值计算稳定性，对于实现任意弦长的曲线正矢自动化计算具有重要的参考价值。
【期刊名称】《铁道勘察》【年(卷),期】2012(038)006【总页数】4页(P1-3,17)【关键词】铁路;曲线正矢;弦长;坐标【作者】马文静【作者单位】中铁工程设计咨询集团有限公司,北京100055【正文语种】中文【中图分类】U212.332.21 概述列车行车对铁路曲线的圆顺性有着较高的要求，特别是行车速度较快时，不圆顺的铁路曲线将造成行车质量下滑，降低乘坐舒适性，增加轮轨磨耗等一系列问题，严重的还会影响到行车安全。
因此，铁路曲线的圆顺性管理从来都是铁路运营管理的一项重要内容。
曲线正矢是评价曲线是否圆顺的量化指标，在实际工作场合被广泛应用，针对不同的曲线半径有着非常细致的具体规定［1］。
传统的铁路曲线正矢管理常以渐伸线原理为计算基础，以10m或20m弦长测量为实施手段，具有计算比较简单，易于手工计算的优点［2－3］。
然而，随着铁路轨道测量方法的进步，偏角法、矢距法等传统曲线测量方法让位于轨道坐标测量法，因此需要一种基于轨道坐标、稳定可靠且能计算任意弦长的曲线正矢计算方法，实现轨道测量的内外业一体化。
2 曲线正矢计算的严密模型铁路线路的线形由直线、缓和曲线、圆曲线三种要素构成，当计算正矢的弦线的两端都处于同一种线形时，则分析起来较为简单:直线上的正矢为零;圆曲线上的正矢为一常数，且正矢值是圆曲线半径及弦长的函数;缓和曲线上的正矢为渐变量，其值跟弦线在缓和曲线上所处的位置有关，且也存在以渐伸线原理为基础的简单公式用于计算。
但是当弦线两端跨越不同的线形时，情况则较为复杂。
中级线路工理论知识复习题(含答案)
中级线路工理论知识复习题（含答案）1、正线上缓和曲线与道岔间的直线段长度困难条件下不小于（）υA、0.8B、0.6C、1D、0.5答案：D2、曲线轨道轨距加宽递减，复曲线应在正失递减范围内从较大轨距加宽向较小轨距加宽（）递减A、平均B、均匀C、正常D、缓和答案：B3、铁路职业道德中，职工遵循的廉洁自律、秉公办事是指在职业活动中存在的职业方便和( )而言的A、自我约束B、职务行为C、工种特性D、行业特权答案：D4、胀轨跑道处理时，轨温明显下降后，方可拨回线路，回填道砟，整正线路，夯拍道床，按（） km/h放行列车A、10B、5C、15D、20答案：B5、轨道动态质量容许偏差规定vmax≤120km/h正线，水平Ⅲ级分管理值为（）A、12B、16C、20D、18答案：D6、曲线半径R≤250，缓和曲线的圆曲线正失连续差作业验收标准（）mmA、15B、12C、10D、8答案：B7、临时处理插入的短轨，不宜在线路上长时间保留，应在不超过（）的时间内采取焊接短轨的方法进行永久处理A、一个月B、一天C、半个月D、一周答案：A8、辙叉心宽50mm及以后处所，一条垂直裂纹长度（）以下时，应注意检查观测及时修理A、45mmB、60mmC、50mmD、65mm答案：C9、在断缝处上好夹板或臌包夹板，用急救器固定，在断缝前后各（）m拧紧扣件，并派人看守A、60B、80C、50D、40答案：C10、提速200km/h-250km/h规定曲线正失允许偏差圆曲线作业验收标准实测正失与计算正失差（）mmA、5B、2C、4D、3答案：D11、长钢轨折断临时处理时，沿断缝两侧对称切除伤损部分，锯口距断缝不得小于（）mA、1B、2C、3D、5答案：A12、平过道指在车站、货场、专用线内，专为（）使用，不直接贯通道路的平面交叉A、汽车过往B、学生上学C、内部作业D、村民行走答案：C13、曲线上各点正失之和为一（）A、单数B、双数C、常数D、整数答案：C14、Ⅱ级铁路线路一般地段速度120km/h，最小曲线半径（）mA、1300B、1000C、1200D、1500答案：C15、道口铺面宽度应与道路路面的宽度相同，且不应小于（）mA、3B、5C、2.5D、3.5答案：C16、曲线半径250＜R≤350，缓和曲线的圆曲线正失最大最小差正线到发线经常保养标准（）mmA、15C、10D、18答案：D17、道德评价有社会评价和( )两种类型A、自我评判B、自我评价C、自我评议D、自我批评答案：B18、曲线半径350＜R≤450，缓和曲线的圆曲线正失最大最小差作业验收标准（）mmA、10B、15C、12D、18答案：C19、P60钢轨每米钢轨质量为（）A、60.64B、60.46C、60D、61答案：A20、正线、到发线线路和道岔钢轨探伤周期年通过总重量8-25,50kg/m年探伤遍数（）A、7B、8C、10D、15答案：A21、道岔护轨平直部分轮缘槽宽主的容许误差为（）A、+4 -4mmB、+3 -2mmC、+3 -1mmD、+6 -2mm22、曲线半径R≤250，缓和曲线的圆曲线正失连续差其他站线经常保养标准（）mmA、16B、10C、8D、14答案：A23、曲线半径R≤350，12.5m钢轨安装轨撑（）对A、14B、10C、12D、7答案：D24、P50以下-43钢轨重伤标准，Vmax≤120 km/h正线及到发线钢轨头部总磨耗超过（）mmA、11B、9C、10D、12答案：B25、有人看守的道口发生故障时，必须按照先（）后处理的原则办理A、处理B、报告C、防护D、加固答案：C26、曲线半径800m行车速度100km/h，缓和曲线长度困难地段（）mA、60B、80C、50D、70答案：D27、路基横断面是指垂直于线路（）线截取的断面A、中心D、中央答案：A28、轨道动态质量容许偏差规定vmax≤120km/h正线，三角坑II级分管理值为（）A、10B、6C、8D、4答案：A29、P75钢轨每米钢轨质量为（）A、74.414B、75.414C、74D、75答案：A30、道口铺面应与钢轨顶面同水平为防止因钢轨及车轮磨耗而导致路面与车轮接触而发生危险，钢轨外侧路面距钢轨外侧（）mm范围内，应较钢轨面低5mmA、80B、40C、60D、50答案：D31、艰苦奋斗、（）是人民铁路的光荣传统，是推动铁路事业发展的精神动力A、乐于奉献B、无私奉献C、勇于奉献D、勇于拼搏答案：C32、时速300 - 350 km区段的基床表层厚度，无砟轨道为0.4m，有砟轨道为（）m、基床底层厚度为2. 3rnA、1.5D、0 .7答案：D33、曲线半径250＜R≤350，缓和曲线的圆曲线正失最大最小差作业验收标准（）mmA、12B、10C、18D、15答案：D34、曲线半径R≤250，缓和曲线的圆曲线正失最大最小差正线到发线经常保养标准（）mmA、15B、20C、18D、21答案：D35、P75钢轨轨端至1孔中心距为（）A、96B、56C、76D、66答案：A36、正线、到发线线路和道岔钢轨探伤周期年通过总重量50-80,50kg/m年探伤遍数（）A、10B、15C、8D、5答案：A37、接头螺栓扭矩扳手和扣件扭矩扳手，容许误差不得大于（）大修单位的扭矩扳手，应在附近工务段检定A、4%B、2%答案：A38、P75钢轨轨底宽度为（）A、150B、152C、120D、132答案：A39、P60以下-50钢轨轻伤标准，Vmax≤120 km/h正线及到发线钢轨头部总磨耗超过（）mmA、16B、10C、14D、12答案：D40、道口宜设置在线路充许速度不大于120km/h时应能看到两侧各（）m （双线各500m）A、500B、300C、200D、400答案：D41、曲线半径450m行车速度80km/h，缓和曲线长度困难地段（）mA、70B、60C、80D、90答案：A42、曲线半径450＜R≤800，缓和曲线的圆曲线正失最大最小差其他站线经常保养标准（）mmA、10B、9C、12D、1543、轨道动态质量容许偏差规定vmax≤120km/h正线，高低II级分管理值为（）A、6B、10C、8D、12答案：D44、道口标志应设在通向道口，距道口最外股钢轨不少于20m处的道路（），预告前方有铁路道口A、后方B、右侧C、左侧D、前方答案：B45、轨道动态质量容许偏差规定vmax≤120km/h正线，垂直加速度Ⅳ级分管理值为（）A、0.20B、0.16C、0.18D、0.25答案：D46、需要确定头尾标桩的曲线计划正矢计算公式的规定是（）A、圆缓点（YH）=曲线尾（YZ）-缓和曲线长分段数/2B、缓圆点（HY）=曲线头（ZY）+缓和曲线长分段数/2C、直缓点（ZH）=曲线头（ZY）-缓和曲线长分段数/2D、曲线头尾（ZY/YZ）=曲线中央点±曲线长分段数/2E、缓直点（HZ）=曲线尾（YZ）+缓和曲线长分段数/2答案：ABCDE47、以下关于I型混凝土枕的承载能力说法正确的是（）A、适用于中型、轻型轨道B、轴重23tC、最高速度85km/hD、铺设密度1840根/kmE、适用于重型轨道答案：ABCD48、影响轨温的因素有（）A、日照程度B、测量部位和测量条件C、气温、风力D、地形E、线路方向答案：ABCDE49、以下关于曲线正矢作业验收允许偏差管理值速度vmax≤2-00km/h正线及到发线圆曲线正矢最大、最小值差正确的是（）A、R≤25018mmB、350≤R≤45012mmC、R≧8-009MMD、250≤R≤35014mmE、450≤R≤8-0010mm答案：ABC50、预防整治导曲线轨距扩大的措施有（）A、扣件达到足够扭力矩B、在导曲线外侧设置轨撑C、更换腐朽岔枕D、在导曲线外股接头处安装桥型垫板E、整治轨撑离缝消除假轨距答案：ABCDE51、线路上插入个别短轨的规定是（）A、正线上不得短于6mB、站线上不得短于45mC、不得连续插入两根及以上D、个别插入短轨线路的允许速度不得大于160km/hE、在曲线上不得插入短轨答案：ABCDE52、影响道床纵向阻力的因素是（）A、脏污程度、轨道框架重量B、道床断面C、道砟材质D、颗粒大小E、捣固质量答案：ABCDE53、55kg钢轨Ⅰ型弹条轨距扣件及挡板座号码右股钢轨的配置是（）A、轨距1437mmB、外侧挡板10#C、内侧挡板18#D、外侧挡板座4#E、内侧挡板座4#答案：AE54、电气化铁路维修作业标准包括A、起道机不能放在曲线里股B、起道高度单股不超过30mmC、一侧拨道量年度累计不得大于120mmD、绝缘接头是薄弱部位，应加强捣固E、禁止在同一地点将两股钢轨同时拆下答案：BCDE55、50kg钢轨Ⅰ型弹条轨距扣件及挡板座号码左股钢轨的配置是（）A、内侧挡板座2#B、内侧挡板18#C、轨距1445mmD、外侧挡板14#E、外侧挡板座3#答案：CDE56、温度应力式无缝线路缓冲区不应设置在道口或不作单独设计的桥上。
铁路曲线中正矢点位设置的探讨
铁路曲线中正矢点位设置的探讨金能龙;张庆海【摘要】曲线正矢点在现场设置中会存在设置点位不正确的现象,曲线外股钢轨与曲线中心线之间会存在缩短量,该缩短量会对曲线正矢点设置造成一定的影响.主要通过具体案例计算分析了缩短量对正矢点布置的影响,得出了两种布置正矢点相对精确方法,提出了一些布置正矢点的注意事项,给铁路养护维修提供一定指导与借鉴.【期刊名称】《广东土木与建筑》【年(卷),期】2018(025)010【总页数】3页(P63-65)【关键词】正矢布置;计算正矢;缩短量;曲线养护【作者】金能龙;张庆海【作者单位】湖南高速铁路职业技术学院湖南衡阳421002;湖南高速铁路职业技术学院湖南衡阳421002【正文语种】中文【中图分类】U216.42按照《铁路线路修理规则》（下称《修规》）规定，铁路线路正线上在外股钢轨上用钢尺丈量，每10 m设置1个测点（曲线头尾是否在测点上不限），根据10 m 设置一个测点，采用20 m弦线进行测量。
常见的正矢点布置方法如下：⑴以QZ 点对称布置（QZ不布置测点），如图1所示；⑵以QZ点对称布置（QZ布置测点）；⑶以ZH或HZ点为起点进行布置，如图2所示，还可以采用其他的布点方式，只要满足《修规》规定即可。
图1 以QZ点对称布置正矢点（QZ不布置测点）示意图Fig．1 Schematic Diagram of Versine Points Arranged Symmetrically with QZ Point（QZ Not Measured）图2 以ZH或HZ点为起点布置正矢点示意图Fig．2 Schematic Diagram of Versine Start With ZH or HZ Point1 正矢的计算方法我们将理论计算出的正矢称为计算正矢（或计划正矢、理论正矢），将现场中量测的正矢称为实际正矢（或现场正矢）。
正矢在计算过程中，一般采用曲线资料进行计算，曲线资料包括：曲线半径R、曲线长L、缓和曲线长l0等，曲线资料是对线路中心线位置的准确描述。
铁路轨道曲线正矢计算(修正)
第一讲：曲线正矢计算一、曲线的分类：目前我段主要曲线类型有：1、由两端缓和曲线和圆曲线组成的曲线，如正线曲线。
容许行车速度高。
2、由圆曲线构成的曲线。
如道岔导曲线、附带曲线。
二、圆曲线正矢的计算1、曲线头尾正好位于起终点桩上F C=L2/8RL=20M时，F C=50000/RF ZY=F YZ= F C/22、曲线头尾不在起终点桩上ZY前点：Fμ=（FC/2）*（δ/10）2ZY后点：Fη=FC-{（FC/2）*（τ/10）2}FC：圆曲线正矢δ：ZY点到后点的距离τ：ZY点到前点的距离三、缓和曲线上整点正矢的计算（起始点正好是测点）（1）缓和曲线头尾的计算：F0=F1/6（缓和曲线起点）F终= F C-F0（缓和曲线终点）（2）缓和曲线中间点正矢的计算：F1=F S= F C/N （N=L0/B：缓和曲线分段数）F2=2 F1 F3=3F1 F I=IF1（I为中间任意点）四、半点（5米桩）正矢的计算：a)ZH点后半点正矢的计算：F后=25/48*F1因为ZH点正矢f0=f1/6,很小一般为1~2MM，其前半点很小（小于1MM）因此不作计算。
b)HY（YH）点前半点计划正矢的计算F前=1/2{[L03+（L0-15）3]/6R L0+[5L0+25]/2R}-（L0-5）3/6R L0c)HY（YH）点后半点计划正矢的计算F后=1/2{[ （L0-5）3 -L03]/6R L0+[5L0+175]/2R}d)中间点（5米桩）正矢的计算F中=（F前+F后）/2五、测点不在曲线始终点时缓和曲线计划正矢的计算a)缓和曲线始点(ZH点)处相邻测点的计划正矢Fμ=αυF S(直缓点外点) αυ=1/6(δ/B)3Fη=αηF S(直缓点内点) αη=1/6[(1+δ/B)3-(δ/B)3](2) 缓圆点处相邻测点的计划正矢Fφ=F C-αυF S (缓圆点外点，缓和曲线之外)Fθ= F C-αηF S (缓圆点内点，缓和曲线之内)(αυ、αη查纵距率表《曲线设备与曲线整正》附表二)(3)缓和曲线中间点各点计划正矢的计算F I=(F C/L0)L I（I为中间任意点）说明：B：半弦长δ：缓和曲线内点到ZH、HY（YH）距离L0：缓和曲线长F C：圆曲线正矢第二讲：曲线拨道一、绳正法基本原理1、基本假定：（1）假定拨道前后两端切线方向不变，或起始点位置不变，即曲线终点拨量为零。
教案(曲线整正)
郑州铁路局职工培训教师课堂教学教案首页，共6页任课老师签名：任会民教育科长审阅签名：曲线整正一、教学目标及要求：通过本节教学，希望大家能了解一个概念、记住一个标准，掌握一个方法：•1、了解曲线整正的概念；•2、掌握曲线圆顺度标准;•3、掌握用绳正法进行曲线整正的方法及步骤;二、教学重点：•1、衡量曲线圆顺度的标准;（一个标准）•2、用绳正法进行曲线整正的方法及步骤。
（一个方法）三、教学难点：•1、用流水法计算拨量。
四、教学方法：•结合算例进行理论讲解导语：大家知道◆曲线是铁路轨道的薄弱环节、更是线路养护的关键；◆曲线方向的整正-又是曲线养护的难点；◆曲线整正中最难的就是拨道量的计算，这也就是我们这节课要解决的难点。
讲新课之前，让我们先回顾一下曲线轨道的特点：•1、列车在曲线上运行时，由于轨道平面迫使车体转向，使机车车辆对轨道水平推力大于直线，再加上未被平衡超高的影响，使得曲线轨道的受力状态比直线复杂，方向变化快,而不良的曲线方向又会加剧列车的摇摆，增大列车对轨道的破坏力，形成恶性循环。
就拿我们段年6月份的轨检车情况来说吧，二级超限总共50处，其中曲率变化率42处，在曲线地段的二级超限占24处，比例高达57%，远大与曲线与直线长度之比。
因此，对曲线方向要定期检查，及时进行整正。
•所谓曲线整正就是对方向变化超过标准的曲线轨道进行整治，使其恢复到原设计位置。
•那么，曲线方向变化达到什么标准时需要进行整正？如何整正？是这节课要解决的两个主要问题。
一、曲线方向变化达到啥标准时需要整正？换句话说，就是曲线圆顺度的标准是什么？我们知道：“直线要直、曲线要圆顺”，曲线轨道的好坏，是以它的圆顺度表示的，二衡量曲线圆顺度标准有哪些哪？一般来说：衡量曲线圆顺度的标准包括三项内容：1、缓和曲线上各点正矢与计算正矢差；2、圆曲线上各点正矢连续差；3、圆曲线上各点正矢最大最小差。
曲线正矢的偏差又是如何规定的？《修轨》规定不超过表1标准，即我们平常所说的“三、六、九”表1：曲线正矢的偏差管理值我段为进一步提高设备质量，制定了更为严格曲线验收标准。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
曲线全长L＝R×α（弧度）＝22.21114m
曲线在直股上的投影长度为0点到n点间距离＝T＋T×cosα＝
距离(直股投影）
支距(近似）
距离（曲线距离）
5000－R（1－cosα）
0
5000
0
5000
1
1
2
2
3
3
4
4
以上两种算法之差为：
利用近似公式计算附带曲线起点支距如下：
曲线起点支距
Y起＝E－L2/2R外＝5000－2/=3776
利用道岔后长、夹直线长与夹角、起点支距关系计算如下：
曲线起点支距
Y起＝（道岔后长＋夹直线长）×sinα＝（＋）×sinα＝3772
注：表中支距点间距离均按5米，包括按直股投影距离计算和按曲线距离计算
表中计算结果显示，近似计算与实际位置之间存在将近m的偏差，其间的偏差将随着曲线长度的增加而增加，这个偏差通过直股支距法整正附带曲线后，再利用绳正法测量时表现为正矢过大，有难以消除的“鹅头”存在。
第二个推导公式是计算道岔附带曲线支距的公式
附带曲线的整正一般常用的整正方法有长弦矢距法和直股支距法两种。
长弦矢距法是在保证曲线首尾位置正确的情况下整正曲线的一种办法，而它本身并不能保证首尾位置正确，并且它采用的公式也是曲线正矢计算公式，即：ｆ＝L2/8R，然后按不同的弦长计算对应测量点的矢距。
而直股支距法的优点在于，它可以从岔后直曲两股钢轨及道岔的位置来综合考虑，即能保证道岔与其后线路的相对位置正确，又可保证曲线的圆顺。但它在计算直股支距时所用的公式也是从曲线正矢的计算公式演化而来的，具体计算公式如下：
而精确的的正矢数值应当为：f＝R（1－cos(α/2)）
假定有一曲线，半径R＝500米，用近似公式求得的正矢为：
f＝50000/R＝50000/500＝100mm
精确的正矢值为：
f＝R（1－cos(α/2)）＝500×（1－cos(10/500)）=99.99666mm
二者相差不到0.1mm，所以利用简便公式不影响计算结果，该公式完全可以在日常生产中使用。
如图二示，由尖轨跟端（导曲线起点）处作两条辅助线，一线与基本轨平行，一线为尖轨的延长线。显然，各点支距都被截为三段，ｙ０、A、Ｂ。用化简法将各点的ｙ０、A、Ｂ计算相加，即是其各点的支距。
计算公式为：Yｉ＝ｙ0+Aｉ+Bｉ
Aｉ＝ｕ×2000÷ｌ尖×ｉ
Bｉ＝（2×支距点横距）2/(8R)=(2×2000×ｉ)2/(8R)=20002/(2R外)×ｉ2
第二章 曲线正矢计算公式的理论局限
由图中可知：AD＝f，即曲线正矢；BD＝L/2，即弦长的一半。
正矢计算公式为：f＝（L/2）2/（2R－f）＝L2/4（2R－f）。
在（2R－f）中，由于f与2R相比甚小，可忽略不计，
则公式可近似写成为：f＝L2/8R
弦长L现场一般取为20m,当L＝20m时，有f＝50000/R
7
144
1011
144
1201
ｙ终＝S－Ksinα＝1435－2115×sin6°20′25″＝
ｙ终≈S－K/ N＝1435－2115÷9＝1435－235＝1200
ｙ终的近似计算结果与实际值之间相差1.434mm
从以上支距计算对照表(表一)可以看出，随着曲线长度的增加，利用近似计算法所得结果的误差也随着增大，当我们利用近似法计算所有2米点间的支距，而在辙叉前的导曲线终点却用另一个公式计算，这样便导致导曲线终点与其相邻点之间的圆顺程度相差3mm。《铁路线路修理规则》中对导曲线支距标准是：作业验收标准2mm，经常保养标准3mm，临时补修标准4mm。不分行车速度与线路级别，统一使用以上标准。如果采用近似算法，即便把现场平面状态处理得和计算结果一致，而实际的线型也超出了正常情况下列车运行所应满足的经常保养容许偏差管理值，所以这种近似的算法在这种情况下是不适用的。
Yｉ＝E－（ｉ×5000）2/（2R外）＝E－ｉ2×50002/（2R外）
Yｉ———中间某点的支距；
ｉ———某支距点的点号；
E———线间距
ｌ———岔后夹直线长
如图三所示，为一9号道岔，线间距E＝5米，岔后附带曲线半径为200米。
切线长T＝R×tan(α/2)=200×tan3°10′″＝11.077m
另外，直股支距法也存在现场操作上的不便，在现场作业时，按要求自曲线尾部开始以5米间距确定支距测量点位置，自每点向曲线方向测量距离，可是垂直于直股的方向在现场难以确定，当直股一端测量点固定后，曲线方向的测量点因两线不是平行的，确定起来比较困难，并且越到曲线始点将越难确定。如果在曲线上确定测量点，然后自曲线上的点向直股方向测量支距，将很容易找到对应的支距点，因为一点到另一线的距离，垂直方向最短。
但以简便公式为基础推导出的公式是否也适用便值得商榷了，以一个近似的公式推导出的公式可能会使误差扩大，以致于影响到计算结果的正确，下面就我们常用的两个推导公式进行试算，以观察其结果的差异。
第一个推导公式是计算道岔导曲线支距的公式
以50kg/m型9号道岔为例： 自导曲线起点至终点全长15.793米，K＝2115mm，尖轨长6.25米，导曲线半径R＝180717.5mm。
导曲线起点ｙ０＝ｕ
导曲线终点ｙ终＝S－Ksinα≈S－K/ N
S———轨距
N———道岔号数
K———导曲线终点到辙叉心轨理论尖端的直线段长度
导曲线支距计算对照表表一
点号
Y0
Ai
Bi
Yi
设计支距
差值
144
0
0
144
144
0
1
144
201
2
144
281
3
144
382
4
144
506
5
144
652
6
144
821