伯努利方程伯努利Bernoulli
伯努利流体方程

伯努利流体方程
伯努利方程(Bernoulli's equation)是流体力学基本方程之一,常用于描述静止流体或运动流体在流经不同位置时,压力、速度、高度等物理量的变化关系。
伯努利方程最早由瑞士数学家和物理学家伯努利(Daniel Bernoulli)在1738年提出,被称
为伯努利定理,也称作伯努利方程或伯努利流体方程。
伯努利方程的数学形式为:
P + 1/2ρv^2 + ρgh = constant
其中,P表示流体的压力,ρ表示流体的密度,v表示流体的
速度,g表示重力加速度,h表示流体的高度,constant表示一个常数。
伯努利方程可以表达出一个流体在液体静压力、动能和势能三者之间的平衡状态。
在一个理想的流体中,如果流体穿过一段水管,那么在这段水管的任何位置,液体静压力、动能和势能总和相等。
应用伯努利方程,可以计算液体在不同位置的压力、速度和高度等物理量的变化。
伯努利方程可以应用在气体、液体等不同介质的流体力学问题中,如风力发电机、水压机等。
9.2.4 伯努里方程

x=e
ln cos y
[∫ sin 2 y ⋅ e
− ln cos y
dy + C
]
2 sin y cos y dy + C = cos y ∫ cos y
= cos y[C − 2 cos y ].
小 结:一阶微分方程的解法 可分离变量
dy = g ( x ) ⋅ h( y ) dx
=e
y2 − 2
y2 − y 3 e y2 dy + C −2 = Ce − y 2 + 2 ∫
2
用适当的变量代换解微分方程: 用适当的变量代换解微分方程:
例3 求方程 y' 的通解. + 2 x arctan y = 4 x 3 的通解. 2 1+ y
du 1 dy = , 原方程可化为 2 dx 1 + y dx du + 2 xu = 4 x 3 dx
将 u = x + y 代回, 所求通解为
y − ln( x + y + 1) = C ,
或 x = C 1e y − y − 1
dx 另解 方 变 为 = x + y. 程 形 dy
小结
y 1.齐次方程 y ′ = f ( ) 齐次方程 x
2.线性非齐次方程 2.线性非齐次方程 3.伯努利方程 伯努利方程
−1
将 z = xy 代回,
所求通解为 2 xy − sin( 2 xy ) = 4 x + C .
dy 1 3. ; = dx x + y
dy du 解 令x + y = u, 则 = − 1, dx dx du 1 −1= , 代入原式 dx u 分离变量法得 u − ln( u + 1) = x + C ,
伯努利方程伯努利Bernoulli
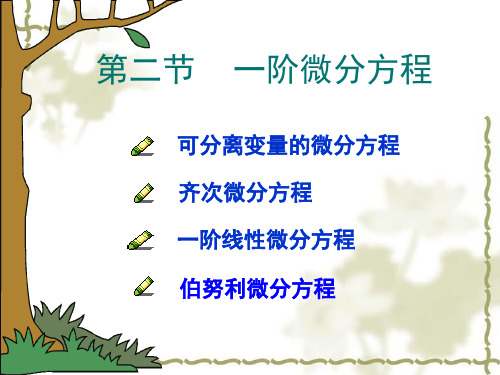
则 dz (1 n) yn dy ,
dx
dx
代入上式 dz (1 n)P( x)z (1 n)Q( x), dx
求出通解后,将 z y1n 代入即得
y1n z
e ( (1n)P( x)dx Q( x)(1 n)e (1n)P( x)dxdx C ).
例 10
解 两端除以 y,得 1 dy 4 y x2 , y dx x
即 du f (u) u .
dx
x
可分离变量的方程
当
f (u) u
0时,
得
du f (u) u
ln C1 x ,
即 x Ce(u) ,
( (u) du )
f (u) u
将 u y 代入, x
得通解
x
(
Ce
y) x
,
当 u0 , 使 f (u0 ) u0 0, 则 u u0是新方程的解,
所求曲线为 y 3(2ex x2 2x 2).
思考题1
求微分方程
y
cos
y
cos sin 2 y
y
x
sin
y
的通解.
思考题解答
dx cos y sin 2 y x sin y sin 2 y x tan y,
dy
cos y
dx tan y x sin 2 y,
dy
x elncos y sin2 y e lncos ydy C
积分得 一阶线性非齐次微分方程的通解为:
对应齐次 方程通解
非齐次方程特解
例8
解 P( x) 1 , Q( x) sin x ,
x
x
y
e
1 x
dx
伯努利方程

伯努利方程伯努利方程是描述理想流动的基本方程之一,它是在瑞士数学家伯努利(James Bernoulli)在1738年发表的一篇论文中提出的。
该方程对于理解流体力学以及飞行、水力、空气动力学等领域具有重要的应用。
伯努利方程是基于质量守恒定律、动量守恒定律和能量守恒定律推导而来的方程。
该方程表达式为:P + ½ρv² + ρgh = 常数其中,P为流体的压力,ρ为流体的密度,v为流体的速度,h为流体的高度,g为重力加速度。
伯努利方程是在假设部分没有粘性损失的情况下成立的,也就是无黏性流动。
在实际的情况下,流体会存在一定的粘性损失,因此伯努利方程只适用于无粘流体,但在低速流动下,伯努利方程可近似地应用于粘性流体。
对于伯努利方程,我们可以从以下角度来解释其中的每个项:① P:压力项,它表示了流体在流动过程中所受到的压力。
当流体速度增加时,压力往往会降低,例如在突缩管中,当管道的截面积变小时,流体的速度会增加,而压力会降低。
②½ρv²:动能项,它表示了流体的动能。
在流体的流动过程中,当速度增加时,动能也会增加,例如在水力发电站中,当水流的速度增加时,水的动能也会增加,从而推动水轮发电。
③ρgh:势能项,它表示了流体的势能。
当流体在重力作用下流动时,流体会从高处向低处移动,势能也随之降低。
例如当我们用pump把水从低处抽到高处时,水的势能就会增加。
由于伯努利方程中的常数在同一条流线上保持不变,因此可以利用伯努利方程来分析流体在不同位置的流速、压力和高度之间的关系。
这在飞行、水利及空气动力学等领域的设计和应用中具有重要的作用。
伯努利方程的应用十分广泛。
例如在空气动力学领域中,伯努利方程被用来解释飞机起飞、飞行、着陆过程中的颤振等现象。
在水利工程领域中,伯努利方程被用来计算水流在不同地方的速度、压力和高度等因素,对于设计水坝、水龙头、流量计等工程设施具有重要的作用。
总之,伯努利方程作为理解流体力学基本方程之一,不仅在理论研究中具有广泛的应用,也在实际的设计和应用中具有十分重要的意义。
流体力学-04-2 伯努利方程的应用

伯努利方程的应用伯努利方程对于流动体系除了掌握体系的对于流动体系,除了掌握体系的物料衡算关系以外,还必须找出体系各种形式能量之间的转换关系系各种形式能量之间的转换关系。
伯努利(Bernoulli)方程:描述了流体流动过程中各种形式能量之间的转换关系,是流体在定常流动情。
是热力学第一Daniel Bernoulli ,1700-1782况下的能量衡算式是热力学第定律对流体流动过程的具体描述。
流动系统的能量流动系统的能量:流动系统的能量流动系统的能量:(3) 动能:流体以一定的速度运动时便具有一定的动能,大时所需要的功小等于流体从静止加速到流速v时所需要的功。
(4) 静压能:流体进入划定体积时需要对抗压力所做的功。
流体进入划定体积时需要对抗压力所做的功若质量为m的流体体积为,某截面处的静压强为p,截面面积为A,则将质量为m的流体压入划定体积的功为:则将质量为的流体压入划定体积的功为质量为能量还可以通过其他外界条件与流动系统进行交换,包括::流体通过换热器吸热或放热Q e吸热时为正,放热时为负。
:泵等流体输送机械向系统做功W em 的流体交换热量=m Q e流体接受外功为正流体对外作功为负作功为负的流体所接受的功= mW e以截面两边同除以m单位质量流体稳定流动过程的总能量衡算式力学第一定律表达式系统内能变化是单位质量流体从截面1-1到截面系统内能变化:是单位质量流体从截面1-1到截面2-2(1)流体通过环境直接获得的热量流体通过环境直接获得的热量,Q e 流体流动时需克服阻力做功,因而消耗机械能转化为热量,若流体等温流动,这部分热量则散失到系统外部。
设单位流体因克服阻力而损失的则,则不可压缩流体ρ=const=0无外加功W e=0理想流体,Σhf伯努力方程努力方程的有关伯努力方程的讨论(1)伯努力方程的适用条件:不可压缩的理想流体做定常流动而无外功输入的情况,选取截面符合缓变流条件。
单位质量流体在任一截面上所具有的势能、动能和静压能之和是常数是一常数。
总流伯努利方程中各项意义

总流伯努利方程中各项意义流体力学中的伯努利方程是描述流体在相对稳定流动时能量守恒的一个重要方程。
该方程以瑞士科学家丹尼尔·伯努利(Daniel Bernoulli)的名字命名,他在18世纪中期首次引入了这个方程。
伯努利方程在流体力学、空气动力学和水力学等领域具有广泛的应用,被用来解决气体或液体在流动过程中的问题。
伯努利方程可以用来描述不可压缩流体在没有粘性损失、无外力力场和恒温条件下沿流线流动时,单位质量的流体所具有的总机械能(动能和势能)保持不变。
方程的一般形式如下:P + ρgh + ½ρv² = constant其中,P表示流体的压力,ρ表示流体的密度,g表示重力加速度,h表示高度(流体从参考位置的垂直距离),v表示流体的速度。
伯努利方程中各项的意义如下:1.压力(P):压力项表示单位面积上的力对流体施加的作用,从而改变流体的动能。
压力越高,单位质量流体的机械能就越高。
2. 重力势能(ρgh):重力势能项表示流体的高度能对流体施加的作用。
流体在上升时,势能增加;流体在下降时,势能减小。
流体在垂直方向上的运动会通过重力势能的变化来转换其动能。
3.动能(½ρv²):动能项表示流体的运动能对流体施加的作用。
当流体速度增加时,单位质量的动能就增加了。
4.总机械能:伯努利方程描述的是单位质量的流体所具有的总机械能保持不变。
这意味着如果没有能量的输入或损失,流体在不同位置的总机械能是相等的。
在稳态流动中,沿流线的压力、高度和速度的变化相互关联,通过这个方程可以求解流体的流速、压力和高度的变化。
伯努利方程的应用非常广泛,常被用来分析流体经过管道、喷嘴、扩散器、收缩器等装置时的流动情况。
通过使用伯努利方程,可以计算出流体在不同位置的速度和压力,并用于解决实际工程问题。
需要注意的是,伯努利方程是针对不可压缩流体和理想条件下的描述。
在实际流动中,流体的粘性和不可压缩性往往会引入能量损失,因此在涉及到高速、密度变化大或粘性流体的问题中,伯努利方程的应用需要结合其他流体力学原理进行修正和分析。
伯努利方程积分推导

伯努利方程积分推导伯努利方程(Bernoulli's equation)是流体力学中的一个重要方程,描述了沿着流体的流动方向,流体质点在流动过程中总能量守恒的情况。
下面将对伯努利方程进行推导。
设流体在运动中的某一点的物理量为P、ρ、v和h,分别代表流体的压强、密度、速度和高度。
根据流体力学基本原理,伯努利方程可表示为:P + 1/2 ρv^2 + ρgh = 常数其中,P + 1/2 ρv^2 是动压项,ρgh 是静压项。
为了推导伯努利方程,我们先从流体力学的基本公式出发——欧拉方程开始。
欧拉方程是描述流体运动的基本方程之一,其数学形式为:∂v/∂t + (v · ∇)v = - 1/ρ ∇P + g其中,∂v/∂t 是速度随时间的变化率,(v ·∇)v 是速度随空间的变化率,∇P 是压力随空间的变化率,g 是重力加速度。
将欧拉方程中的各项乘以ρ,并利用连续性方程(∇·v = 0),可以得到:ρ∂v/∂t + ρ(v · ∇)v = - ∇P + ρg这样,方程就变成了一个由速度、时间、压力和重力加速度构成的方程。
接下来,我们考虑无粘流体在等压情况下的流动。
在等压情况下,压力沿着流体的流动方向不变,即∇P = 0。
再考虑自由面,自由面上的压强为大气压,即 P = P0。
这时,欧拉方程可以简化为:ρ∂v/∂t + ρ(v · ∇)v + ρg = 0同时,假设流体为定常流动,即流体的速度与时间无关∂v/∂t = 0。
这样,方程可以进一步简化为:ρ(v · ∇)v + ρg = 0对于无粘流体,在速度的梯度值极小的条件下,可以利用链式法则将∇v进行展开,即∇v ≈ (∂v/∂x,∂v/∂y, ∂v/∂z)。
这样,方程可以进一步简化为:(v ·∇)v ≈ v · (∂v/∂x, ∂v/∂y, ∂v/∂z) ≈ (v ∂v/∂x, v ∂v/∂y, v ∂v/∂z)由于流体是连续的,在稳定流动中,速度大小在不同位置上是相等的,即 v = |v|。
伯努利方程推导
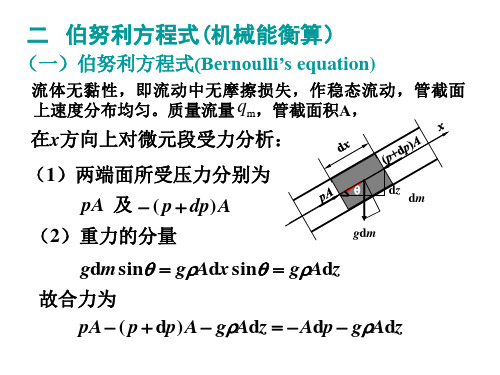
zg 1 u2 p Const. (1) 2 ——伯努利方程式
适用于不可压缩非黏性流体,无摩擦损失,理 想流体伯努利方程式
对于气体,管路两截面间压力差很小,密度变化很小, 此式适用。
(二)伯努利方程式的物理意义
zg ——单位质量流体所具有的位能,J/kg;
kg
m s2
m
N .m
二 伯努利方程式(机械能衡算)
(一)伯努利方程式(Bernoulli’s equation)
流体无黏性,即流动中无摩擦损失,作稳态流动,管截面
上速度分布均匀。质量流量 qm,管截面积A,
在x方向上对微元段受力分析:
(1)两端面所受压力分别为 pA 及 ( p dp)A
(2)重力的分量
dz dm
gdmgBiblioteka msin gAdx sin gAdz 故合力为
pA ( p dp)A gAdz Adp gAdz
动量变化率 动量原理
qmdu Audu
Audu Adp gAdz
gdz dp udu 0
不可压缩性流体, Const.
J
p
kg
kg kg
——单位质量流体所具有的静压能,J/kg ;
N / m 2 N.m J
kg / m3
kg
kg
1 u2 ——单位质量流体所具有的动能,J/kg。
2
kg
m2 s2
N.m
J
kg
kg kg
(1)是单位质量流体能量守恒方程式
将(1)式各项同除重力加速度g :
z 1 u2 p Const.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 xdx,
ln y x2 C1
y Ce x2为所求通解.
二、齐次方程
1.定义 形如 dy f ( y ) 的微分方程称为齐次方程. dx x
2.解法 作变量代换 u y , 即 y xu, x
dy u x du ,
dx
dx
代入原式
u x du f (u), dx
g( y)dy f ( x)dx
分离变量法
设函数G( y)和F ( x)是依次为g( y) 和 f ( x) 的原函
数, G( y) F ( x) C 为微分方程的解.
例1 求解微分方程 dy 2xy 的通解. dx
解 分离变量 dy 2xdx, y
两端积分
dy y
u
xu
2u2 1 u
u u2
,
[1 ( 1 1) 2 1 ]du பைடு நூலகம் dx ,
2 u2 u u2 u1
x
ln(u 1) 3 ln(u 2) 1 ln u ln x lnC,
2
2
u 1 3 Cx. u(u 2)2
微分方程的解为 ( y x)2 Cy( y 2x)3 .
Q(
x
)e
P
(
x
)dx
dx
对应齐次
非齐次方程特解
方程通解
例8 求方程 y 1 y sin x 的通解. xx
解 P( x) 1 , Q( x) sin x ,
x
x
y
e
1 x
dx
sin x
x
e
1 x
dx
dx
C
e
ln
x
sin x
x
eln
代回原方程 , 得齐次方程的解 y u0 x.
例 5 求解微分方程
( x y cos y)dx x cos y dy 0.
x
x
解 令u y, 则 dy xdu udx, x
( x ux cos u)dx x cos u(udx xdu) 0,
cos udu dx , sin u ln x C, x
dx
dt
yy 2xy 3, y cos y 1, 非线性的.
一阶线性微分方程的解法
1.
线性齐次方程
dy dx
P( x) y
0.
(使用分离变量法)
dy P( x)dx, y
dy y
P
(
x)dx,
ln y P( x)dx lnC,
齐次方程的通解为 y Ce P( x)dx .
利用变量代换求微分方程的解
例7 求 dy ( x y)2的通解. dx
解 令 x y u, dy du 1 代入原方程 dx dx
du 1 u2 解得 arctanu x C, dx
代回 u x y,得 arctan( x y) x C,
2.
线性非齐次方程
dy dx
P( x) y
Q( x).
讨论
dy y
Q( x) y
P(
x)dx,
两边积分
ln
y
Q( x)dx y
P( x)dx,
设
Q( x)dx为v( y
x
),
ln y v( x) P( x)dx,
即 y e e v( x) P( x)dx . 非齐次方程通解形式
与齐次方程通解相比: C u( x)
常数变易法 把齐次方程通解中的常数变易为待定函数的方法. 新未知函数 u( x) 原未知函数 y( x),
作变换 y u( x)e P( x)dx
y u( x)e P( x)dx u( x)[P( x)]e P( x)dx ,
0
y
x ydx x3 y, 0
y x3
Q
两边求导得 y y 3x2 ,
y f (x) P
解此微分方程
o
xx
y y 3x2
将y和y代入原方程得 u( x)e P( x)dx Q( x),
积分得 u( x) Q( x)e P( x)dxdx C ,
一阶线性非齐次微分方程的通解为:
y [ Q( x)e P( x)dxdx C ]e P( x)dx
Ce P( x)dx e P( x)dx
微分方程的解为 sin y ln x C . x
例6
求解微分方程
x2
dx xy
y2
dy 2y2
. xy
解
dy dx
2y2 x2 xy
xy y2
2 1
y 2
x
y x
y
y
2
,
x x
令u y , 则 dy xdu udx, x
即 du f (u) u .
dx
x
可分离变量的方程
当
f (u) u
0时,
得
du f (u) u
ln C1 x ,
即 x Ce(u) ,
( (u) du )
f (u) u
将 u y 代入, x
得通解
x
(
Ce
y) x
,
当 u0 , 使 f (u0 ) u0 0, 则 u u0是新方程的解,
xdx
C
1 x
si
n
xdx
C
1 cos x C .
x
例9 如图所示,平行与 y 轴的动直线被曲
线 y f ( x)与 y x3 ( x 0)截下的线段PQ之
长数值上等于阴影部分的面积, 求曲线 f ( x).
解
x
f ( x)dx
[ x3 f ( x)]2 ,
西华大学应用数学系朱雯
第二节 一阶微分方程
可分离变量的微分方程 齐次微分方程 一阶线性微分方程 伯努利微分方程
一、可分离变量的微分方程
g( y)dy f ( x)dx 可分离变量的微分方程.
例如 dy
4
2x2 y5
4
y 5dy
2 x2dx,
dx
解法 设函数g( y)和 f ( x)是连续的,
原方程的通解为 y tan( x C) x.
三、线性方程
一阶线性微分方程的标准形式:
dy P( x) y Q( x) dx
当Q( x) 0, 上方程称为齐次的.
当Q( x) 0, 上方程称为非齐次的.
例如 dy y x2 , dx x sin t t 2 , 线性的;
