邱关源《电路》笔记和课后习题(含考研真题)详解-第十六章至第十八章【圣才出品】
邱关源《电路》配套题库-课后习题(三相电路)【圣才出品】

图 12-8 解: (1)开关 S 打开时,为对称的三相电路,令 如图 12-9(a)所示。
,电流方向
(a)
(b)
图 12-9
(2)开关 S 闭合时,用二瓦计测量电源端的三线功率的接线图如图 12-9(b)所示。
,
此时功率表上的读数为:
8.图 12-8 所示电路中,对称三相电源端的线电压 U1=380 V,Z=(50+j50)Ω, Z1=(100+j100)Ω,ZA 为 R、L、C 串联组成,R=50 Ω,XL=314 Ω,XC=-264 Ω。 试求:
7 / 16
圣才电子书 十万种考研考证电子书、题库视频学习平台
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 12 章 三相电路
1.已知对称三相电路的星形负载阻抗 Z=(165+j84)Ω,端线阻抗 Z1=(2+j1)Ω,
中性线阻抗 ZN=(1+i1)Ω,线电压 U1=380 V。求负载端的电流和线电压,并作电路的
相量图。
吸收的功率为原来的 /2 倍。
(5)如果加接零阻抗中性线,那么对于(3),电流表的读数为 317.2A,电压表的读
数为 660V;对于(4),电流表上的读数为 0,电压表上的读数为 1191.41V。
6.图 12-6 所示对称三相电路中, =380 V,三相电动机吸收的功率为 1.4 kW, 其功率因数 λ=0.866(滞后),Z1=-j55Ω。求 和电源端的功率因数 。
5.图 12-5 所示对称 Y-Y 三相电路中,电压表的读数为 1143.16V,Z=(15+j15 ) Ω,Z1=(1+j2)Ω。求:
邱关源《电路》配套题库-课后习题(含有耦合电感的电路)【圣才出品】
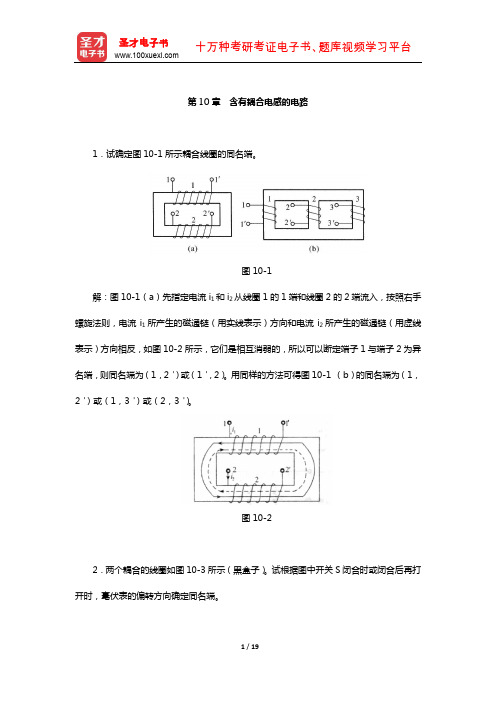
第10章含有耦合电感的电路1.试确定图10-1所示耦合线圈的同名端。
图10-1解:图10-1(a)先指定电流i1和i2从线圈1的1端和线圈2的2端流入,按照右手螺旋法则,电流i1所产生的磁通链(用实线表示)方向和电流i2所产生的磁通链(用虚线表示)方向相反,如图10-2所示,它们是相互消弱的,所以可以断定端子1与端子2为异名端,则同名端为(1,2')或(1',2)。
用同样的方法可得图10-1 (b)的同名端为(1,2')或(1,3')或(2,3')。
图10-22.两个耦合的线圈如图10-3所示(黑盒子)。
试根据图中开关S闭合时或闭合后再打开时,毫伏表的偏转方向确定同名端。
图10-3解:根据右手螺旋法可知,线圈的同名端为(1,2)。
当开关S闭合时,线圈1中随时间增大的电流i从电源正极流入线圈端子1,这时毫伏表的高电位与端子1为同名端;当开关S闭合后再打开时,电流i减小,毫伏表的低电位端与端子1为同名端。
3.若有电流i1=2+5cos(10t+30°)A,i2=10A,各从图10-4(a)所示线圈的1端和2端流入,并设线圈1的电感=6H,线圈2的电感=3H,互感为M=4H。
试求:(1)各线圈的磁通链;(2)端电压和;(3)耦合因数k。
解:(1)(1,2)为异名端,两个线圈的磁通是相互消弱的,所以(2)根据电压和磁通的关系得:(3)耦合因数为:k==0.943。
4.如图10-5所示电路中(1)=8H,=2H,M=2H;(2)=8H,=2H,M=4H;(3)==M=4H。
试求以上三种情况从端子1-1′看进去的等效电感。
图10-5解:(a)=M+(L1-M)//(L2-M)当L1=8H,L2=2H,M=2H时,=2H;当L1=8H,L2=2H,M=4H时,=0H;当L1=L2=M=4H时,=4H。
(b)=-M+(L1+M)//(L2+M)当L1=8H,L2=2H,M=2H时,=0.857H;当L1=8H,L2=2H,M=4H时,=0H;当L1=L2=M=4H时,=0H。
邱关源第五版电路习题解答(全)

2t -210-3(4-103t)
0 t 2 ms 2 t 4 ms
0
4 t ms
1-10
(题目略)
解:
Circuii1t
+
6exercaise
+
5
10V
_
i
_ uS
0.9i1
b (a)
5 a 20 c
2A + u1 _ _
i
3V
+
0.05u1
b (b)
图(a): 电流i为: i 10 2A
a
2
2
1 2
2
b (f)
a
R2’ b
R1’
R1 R2
R3
2
R3’
(f’)
(f):图中(1,1,2)和(2,2,1)构成两个Y形连接,分
别将两个Y形转换成形连接,如图f’ 所示。设(1,1,2)转
换后的电阻为R1、R2、R3, (2,2,1)转换后的电阻为R1’、
22i 88i 10
解得: i 0.091A
则: u 88i 880.091V 8V
在图(b)中设电流 i1、i2、i3,
a结点的KCL方程为: i1 i2 i3 8 KVL方程: i1 3i3 2, i1 2i2
注:列KVL方程时应 尽量选取没有电流源
103t 0 t 2 ms 4 -103t 2 t 4 ms
0
4 t
(1) 求电流:根据u、i的微分关系:
it C dut
dt
得电流表达式:
0
it 2106 dut
dt
210-3 -210-3
邱关源《电路》笔记和课后习题(含考研真题)详解-第十四章至第十五章【圣才出品】

第14章线性动态电路的复频域分析14.1复习笔记一、拉氏变换及其基本性质对定义在[0,∞)上的函数f(t),其拉氏变换与拉氏反变换分别为()()0e d st F s f t t -∞-=⎰()()j j 1e d 2πj c st c f t F s s +∞-∞=⎰式中,s=σ+jω为复数,称为复频率。
其主要性质如下:(1)线性性质L[A 1f 1(t)+A 2f 2(t)]=A 1L[f 1(t)]+A 2L[f 2(t)]=A 1F 1(s)+A 2F 2(s)(2)微分性质若L[f(t)]=F(s),d ()()d f t f t t'=则L[f′(t)]=sF(s)-f(0-)。
(3)积分性质若L[f(t)]=F(s),则01()d ()t L f F s sξξ-⎡⎤=⎢⎥⎣⎦⎰(4)延迟性质若L[f(t)]=F(s),则()()()000e st L f t t t t F s ε-⎡⎤--=⎣⎦(5)拉氏变换的卷积定理设f 1(t)和f 2(t)的象函数分别为F 1(s)和F 2(s),则有()()()()()()1212012*d t L f t f t L f t f F s F s ξξξ⎡⎤=-⎡⎤⎣⎦⎢⎥⎣⎦=⎰二、拉氏反变换的部分分式展开法1.部分分式展开法概述通常用两个实系数的s 的多项式之比来表示电路响应的象函数,有()()()()101101m m m n n n N s a s a s a F s m n D s b s b s b --+++==≤+++ 且均为正整数将有理分式F(s)用部分分式展开时,首先要把F(s)化为真分式,若n>m,则F (s)为真分式;若n=m,则将F(s)化为F(s)=A+N 0(s)/D(s)。
求反变换时,分情况讨论,如表14-1-1所示。
表14-1-12.部分分式展开法求拉氏反变换的步骤(1)n=m时,将F(s)化成真分式和多项式之和;(2)求真分式分母的根,确定分解单元;(3)将真分式展开成部分分式,求各部分分式的系数;(4)对每个部分分式和多项式逐项求拉氏反变换。
电路原理第五版邱关源罗先觉第五版最全包括所有章节及习题解答-资料

进一步计算支路电压和进行其它分析。
支路电流法的特点:
支路法列写的是 KCL和KVL方程,所以方程列 写方便、直观,但方程数较多,宜于在支路数不多 的情况下使用。
例1. 求各支路电流及电压源各自发出的功率。
I1 7
+ 70V
–
a
I2
1 11
+
6V
2
–
b
解:(1) n–1=1个KCL方程:
I3
节点a:–I1–I2+I3=0
7
(2) b–( n–1)=2个KVL方程:
7I1–11I2=70-6=64
11I2+7I3= 6
I112182036A I24062032A
P 70670420W
I3I1I2624A
P62612W
例2.
I1 7
+ 70V
–
解2.
结论:
n个结点、b条支路的电路, 独 立的KCL和KVL方程数为:
(n1 )b(n1 )b
三、支路电流法 (branch current
method )
以各支路电流为未知量列写电路方程分析电路的方法
对于有n个节点、b条支路的电路,要求解 支路电流,未知量共有b个。只要列出b个独立 的电路方程,便可以求解这b个变量。
(1) 先将受控源看作独立源列方程;
(2) 将控制量用未知量表示,并代入(1)中所列的方程,消去 中间变量。
四、网孔电流法(mesh current method)
以网孔电流为未知量列写电路方程分析电路的方法
基本思想
为减少未知量(方程)的个数,假想每个网孔中
《电路》邱关源第五版课后习题答案解析

题 10】: 3;-3。
题 11】: -5;-13。
题 12】: 4(吸收);25。
题 13】: 0.4。
题 14】: 3I +12=3; I = A 。
3题 15】: I =3A ; I = -3A ; I = -1A ; I = -4A 。
题 16】: I =-7A ;U =-35V ;X 元件吸收的功率为 P =-IU =-245W 。
题 17】:由图可得U =4V ;流过 2电阻的电流I =2A ;由回路 ADEBCA 列 KVL 得=2-3I ;又由节点 D 列 KCL 得 I =4-I ;由回路 CDEC 列 KVL 解得; I =3;代入上式,得 U =-7V 。
P 1 = 2I 12 = 2 ;故I 12 =I 22;I 1=I 2;P2 I23 8 8⑴ KCL : 4- I = I ; I = A ; U =2I -1I = V 或 1.6 V ;或 I =-I 。
3⑵ KCL :4-I =- I ;I = -8 A ;U =-24 V 。
电路答案——本资料由张纪光编辑整理(C2-241 内部专用)第一章 电路模型和电路定律题 1 】: 题 2 】:题 3 】:题 4 】:题 5 】:题 6 】:题 7 】:题 8 】: 题 9 】:由U =5V 可得: I = -2.5 A :U =0:U =12.5V 。
D 。
300;-100。
D 。
(a ) i =i -i ;(b ) u =u -u ;(c ) u =u S -(i -i S )R S; ( d ) i =i S- 1(u -u S)。
1 2 1 2R S3;-5;-8。
D 。
P US1 =50 W ; P US 2=-6 W ; P US3 =0; P IS1=-15 W ; P IS2=-14 W ;P IS3=-15 W 。
C 。
题 18】:第二章电阻电路的等效变换题 1 】:[解答]I= A=0.5 A;U ab =9I+4=8.5V;I1=U ab -6=1.25 A;P =6 1.25 W=7.5 W;吸收12功率7.5W。
《电路》邱关源第五版课后习题答案解析

电路答案——本资料由张纪光编辑整理(C2-241 内部专用)第一章电路模型和电路定律【题 1】:由UAB 5 V可得: I AC 2.5A: U DB0 : U S12.5V。
【题 2】: D。
【题 3】: 300; -100 。
【题 4】: D。
【题5】:a i i1i 2;b u u1u2;c u u S i i S R S;d i i S 1R Su u S。
【题 6】: 3;-5 ; -8。
【题 7】: D。
【题 8】:P US150 W ;P US26W;P US30 ; P IS115 W ; P IS214W ;P IS315W。
【题 9】: C。
【题 10】:3; -3 。
【题 11】:-5 ; -13 。
【题 12】:4(吸收); 25。
【题 13】:0.4 。
【题 14】:31I 2 3; I 1A 。
3【题 15】:I43A; I23A; I31A; I5 4 A。
【题 16】:I7A;U35 V;X元件吸收的功率为 P UI245W。
【题 17】:由图可得U EB 4 V;流过 2电阻的电流 I EB 2 A;由回路ADEBCA列KVL得U AC 2 3I ;又由节点D列KCL得 I CD 4I ;由回路CDEC列KVL解得;I 3 ;代入上式,得 U AC7 V。
【题 18】:P122 I12;故 I 22; I 1I 2;P2I 221I 2⑴ KCL:4I 13I 1;I 18;U S 2I1 1 I 18V或16.V;或I I。
2 5 A512⑵ KCL:4I 13I1;I18A;U S。
224 V第二章电阻电路的等效变换【题 1】:[解答 ]94A = 0.5 A ;U ab9I 4 8.5 V;I73U ab66 125. W = 7.5 W ;吸收I 12 1.25 A;P功率 7.5W。
【题 2】:[解答 ]【题 3】:[解答]C 。
【题 4】: [ 解答 ]等效电路如图所示,I 005. A。
邱关源《电路》笔记和课后习题(含考研真题)详解-第八章至第九章【圣才出品】

(2)有效值相量:U=U∠φu,复值常数的模表示有效值,由此可知
U U u u t = 2U ct i )
(3)正弦量的相量表示法:分为有效值相量和最大值相量。
例如,正弦量
i 10 2 cos(314t 50)A
▪
其有效值相量I=10∠50°A。
图 8-1-5
8.2 课后习题详解
8-1 将下列复数化为极坐标形式: (1)F1=-5-j5; (2)F2=-4+j3; (3)F3=20+j40; (4)F4=j10; (5)F5=-3; (6)F6=2.78-j9.20。 解:复数 F 的坐标表示:F=a+jb=|F|∠θ,其中θ=arctan(b/a),
其对应的最大值相量
Im 10 250A
三、电路定律的相量形式
(1)KCL、KVL 定律的相量形式
▪
∑I=0
▪
∑U=0
(2)电路元件 VCR 的相量形式
4 / 108
圣才电子书
▪
▪
①电阻元件:U=RI。
十万种考研考证电子书、题库视频学习平台
即电阻上的电压和电流同相位,相量图如图 8-1-3 所示。
(2)乘法运算
图 8-1-2 复数的加减运算
2 / 108
圣才电子书 十万种考研考证电子书、题库视频学习平台
F1F2 F1 e jθ1 F2 e jθ2 F1 F2 e j(θ1θ2 )
所以
|F1F2|=|F1||F2|
arg(F1F2)=arg(F1)+arg(F2)
(3)除法运算
F1 F2
F1 θ1 F2 θ2
F1 F2
(θ1 θ2 )
所以
F1 F1 F2 F2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图 16-1-2
给定二端口的 Y 参数,可确定二端口的等效π形电路,如图 16-1-3 所示。此时
Y=Y11+Y12 Y2=-Y12=-Y21 Y3=Y22+Y21
3 / 90
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 16-1-3 三、二端口网络的连接 1.串联 如图 16-1-4(a)所示,为二端口网络的串联,此时有 Z=ZA+ZB。
Y21
I2 U1
, Y12
U2 0
I1 U2
称为转移导纳; U1 0
H11=1/Y11,H22=1/Z22,
H 21
I2 I1
U2 0
2 / 90
圣才电子书 十万种考研考证电子书、题库视频学习平台
H12
U1 U2
I1 0
A=-Y22/Y21,B=-1/Y21,C=Y12-Y11Y22/Y21,D=-Y11/Y21。
二、二端口网络的等效电路 3 个阻抗(或导纳)组成的二端口形式:T 形电路和π形电路。若两个二端口网络的参 数全部相同,则称这两个二端口网络对端口而言,互为等效网络。 给定二端口的 Z 参数,能确定二端口的等效 T 形电路,如图 16-1-2 所示。此时 Z1=Z11-Z12 Z2=Z12 Z3=Z22-Z12
j
1 L
U
1
j
1 L
U
2
I
2
j
1 L
U
1
U
2
jC U 2
j
1 L
U
1
Hale Waihona Puke j C1 LU
2
10 / 90
圣才电子书 十万种考研考证电子书、题库视频学习平台
U 1
jL
I1
1 jC
I1
I2
jL
1 C
I
1
1 jC
I2
U 2
1 jC
I
1
I
2
1 jC
I1
1 jC
i1 i2
gu2 gu1
或
i1 i2
0 g
g u1
0
u2
uu12
ri2 ri1
或
u1 u2
0 r
r i1
0
i2
式中,g=1/r,g 和 r 均为回转常数。
7 / 90
圣才电子书
十万种考研考证电子书、题库视频学习平台
图 16-1-5
回转器具有阻抗逆变换功能,如图 16-1-6 所示,即有
图 16-1-4(e) 四、二端口的转移函数 二端口的电压转移函数:U2(s)/U1(s)=Z21(s)/Z11(s)=-Y21(s)/Y22(s), I2(s)=0。 二端口的电流转移函数:I2(s)/I1(s)=-Z21(s)/Z22(s)=Y21(s)/Y11(s), U2(s)=0。
6 / 90
I2
U 1
jL I1 U 2
①
I
1
jC U 2
I2
②
将式②代入式①得
▪
▪
▪
▪
▪
▪
U1=jωL(jωCU2-I2)+U2=(1-ω2LC)U2-jωLI2
U
1
I1
K 0
0 1
U2
I2
图 16-1-7
图 16-1-8 负阻抗变换器具有阻抗负变换作用,如图 16-1-8 所示。其中,Zo=-ZL/K 或 Zo=- KZL。
16.2 课后习题详解
16-1 求图 16-2-1 所示二端口的 Y 参数、Z 参数和 T 参数矩阵。
9 / 90
图 16-1-4(c) 4.串并联 如图 16-1-4(d)所示,为二端口网络的串并联,此时有 H=H1+H2。
5 / 90
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 16-1-4(d) 5.并串联 如图 16-1-4(e)所示,为二端口网络的并串联,此时有 G=G1+G2。
圣才电子书 十万种考研考证电子书、题库视频学习平台
Z UI 其中, 11
Z U 1
, 22
I 1 I2 0
2
称为开路输入阻抗;
2 I1 0
Z21
U2 I1
, Z12
I2 0
U1 I2
称为开路转移阻抗; I1 0
Y11
I1 U1
, Y22
U2 0
I2 U2
称为输入导纳; U1 0
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 16-2-1 解:(1)图 16-2-1(a),两端口电压和电流参考方向,如图 16-2-2(a)所示。
图 16-2-2(a)
根据各元件的特性及电路的 KVL 和 KCL 定理,可得
I 1
1 j L
U
1
U
2
图 16-1-1 二端口的端口特性由关于端口四个变量(U1,I1,U2,I2)的两个方程来描述,在上述 四个端口变量中任取两个为自变量,另外两个为因变量构成的两个方程,是二端口网络的一 组端口特性方程。 常用的参数方程为 Z、Y、H、T 四种参数方程,如表 16-1-1 所示。
表 16-1-1
1 / 90
Zo=1/(g2ZL)=r2/ZL
图 16-1-6
2.负阻抗变换器
负阻抗变换器的电路符号如图 16-1-7 所示,其端口伏安关系为
U 1
U
2
I
1
K
I2
或
U 1 I1
1 0
0 K
U2
I 2
U 1
K
U
2
I
1
I
2
8 / 90
圣才电子书
或
十万种考研考证电子书、题库视频学习平台
圣才电子书 十万种考研考证电子书、题库视频学习平台
二端口的转移导纳函数:I2(s)/U1(s)=Y21(s),U2(s)=0。 二端口的转移阻抗函数:U2(s)/I1(s)=Z21(s),I2(s)=0。
五、回转器和负阻抗变换器
1.回转器
回转器的电路符号如图 16-1-5 所示,其端口伏安关系为
图 16-1-4(a) 2.并联 如图 16-1-4(b)所示,为二端口网络的并联,此时有 Y=YA+YB。
4 / 90
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 16-1-4(b) 3.级联 如图 16-1-4(c)所示,为二端口网络的级联,此时有 T=TA×TB。
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 16 章 二端口网络
16.1 复习笔记
一、二端口特性方程 端口:满足从一个端子进入网络的电流等于从另一端子流出的电流的这样一对端子即为 一个端口。 含有 m 个端口的网络为 m 端口网络。如图 16-1-1 所示为二端口网络,简称二端口。
