长安大学2014真题
长安大学往年城市公交试卷答案综合

一、名词解释:1.线路重复系数:线路重复系数=运营线路总长度/运营线网长度,重复系数不可能等于1,因为一个城市的公共交通线路绝对没有重复是不可能的。
2.城市公共交通规划:根据城市发展规模、用地布局和道路网规划,在客流预测的基础上,确定公共交通车辆数、线路网络、换乘枢纽和场站设施用地等、使公共交通客运能力满足客流高峰的需求。
3.线网密度:有公交线路的街道长度与城市建成区面积之比,单位为m/m24.非直线系数:首末站之间的实际距离与首末站之间的空间直线距离之比。
5.出行:一次出行是以某种交通方式(包括步行)由一个地方到另一个地方的有目的的行程。
6.公交首战:首站是指一条线路主要功能聚集的地方,包括车队、停车场地、职工食堂、调度室、票务室、检修室、司乘人员休息室等。
末站与首站相比,无论从占地面积、建筑面积、停车功能等方面来讲,规模都小一些。
7.公交末站:公交线路两端的起止点,根据功能不同,一般称为首末站。
8.平均运距:平均运距是指乘客乘坐1次的平均距离。
9.平均乘距:平均乘距是乘客1次出行全程的平均乘车距离,其计算公式为:乘车距离=完成1次出行的乘车次数*平均运距.10.运营线路总长度:城市公共交通全部固定运营线路的长度之和。
11.换乘枢纽:一种及以上对外交通方式和两种及以上城市交通方式的交汇点,是具有运输组织与管理、中转换乘、信息流通和辅助服务等功能的综合性设施,是城市内外交通的衔接点,是实现不同交通方式之间和同种交通方式内部转换、交通性质变换的场所。
12.城市公交交通系统:城市中供公众使用的经济方便的各种客运交通方式的总称。
狭义的公共交通是指在规定的路线上,按规定的时刻表,以公开的费率为城市公众提供短途客运服务的系统,广义的公共交通指所有供公众使用的交通方式。
13.O-D调查:交通起止点调查,为了调查各种交通(车、人、货物)出行的起点和终点,在一定区域内所进行的调查工作。
14.二、简答题:1.城市公共交通规划的几种类型?答:城市公共交通规划为:城市(道路)交通规划中的公共交通规划。
长安大学《线性代数》历年期末考试真题及答案解析

目录长安大学2018-2019第一学期线性代数期末试题 (1)长安大学2018-2019第一学期线性代数期末试题解析 (4)长安大学2019-2020第一学期线性代数期末试题 (12)长安大学2019-2020第一学期线性代数期末试题解析 (14)长安大学2019-2020第二学期线性代数期末试题A (21)长安大学2019-2020第二学期线性代数期末试题A解析 (23)长安大学2019-2020第二学期线性代数期末试题B (29)长安大学2019-2020第二学期线性代数期末试题B解析 (32)长安大学2020-2021第一学期线性代数期末试题 (41)长安大学2020-2021第一学期线性代数期末试题解析 (43)长安大学2018-2019第一学期线性代数期末试题长安大学2018-2019第一学期线性代数期末试题解析长安大学2019-2020第一学期线性代数期末试题长安大学2019-2020第一学期线性代数期末试题解析长安大学2019-2020第二学期线性代数期末试题长安大学2019-2020第二学期线性代数期末试题解析长安大学2019-2020第二学期线性代数期末试题一、选择题。
(每小题4分,共16分)1.,有()无解有无穷多组解有非零解可能有无穷多组解2.设则()。
3.设向量组的秩为,则()必定向量组中任意小于个向量的部分组无关向量组中任意个向量线性无关个向量组线性相关4.()二、填空题(每小题4分,共16分)1.设齐次线性方程组为,若它有非零解,则应满足2.设矩阵是4阶方阵,矩阵是5则3.若可由,线性表示,则=4.设。
三、计算或证明下列各题(每小题8分,共16分)1.计算行列式2.设矩阵,求四、计算下列各题(每小题8分,共16分)1.写成二次型并判别其正定性。
2.设,证明是向量组的一个极大线性无关组,并把分别用该极大线性无关组线性表示。
五、(本题12分)设有方程组,问为何值时,方程组有唯一解?无解?有无穷多解?并在有无穷多解时,求出通解。
长安大学846软件工程2014年(回忆版)考研专业课真题试卷

2014年硕士研究生入学考试试题试题代码:846试题名称:软件工程第1页共3页一、选择题(每小题2分,共20分)1、软件测试人员应具备的素质()A、表达能力B、移情能力C、操作能力D、适应能力2、软件测试方法中的()属于静态测试方法。
A、黑盒法B、路径覆盖C、错误推测D、人工检测3、如果想制作学生网上报名系统,应该使用哪种模型()A、瀑布模型B、快速原型模型C、增量模型D、形式化方法模型4、下列关于UML叙述不正确的是()A、UML是一种高级编程语言,且是可视化的B、UML是一种可用于详细描述的语言C、UML是一种构造语言D、UML是一种文档化语言5、软件工程将()有机地结合在一起。
A、人员、技术、组织与管理B、程序、作者、理论与实践C、程序、理论、哲学与实践D、理论、作者、思想与实践6、网站系统是一个典型的()A、胖客户机/服务器结构B、仓库体系结构C、瘦客户机/服务器结构D、以上选项都不是7、对于开发面向数据库应用的软件,应当选择的程序设计语言是()A、CB、PASCALC、SQLD、JAVA8、逆向工程通常用在软件生命周期的()阶段,它是从源代码或目标代码中提取设计信息的。
A、需求分析B、软件设计C、软件测试D、软件维护9、在软件实现的这一软件工程的活动中哪一项不是其产生的主要过程制品()A、源程序B、目标代码C、软件体系结构D、可执行构件10、()是系统测试中最基本的测试,它不管软件内部的实现逻辑,主要根据软件需求规格说明和测试需求列表进行测试。
A、功能测试B、确认测试C、系统测试D、验收测试。
长安大学616马克思主义哲学2004-2007.2012-2014年(2012-2014回忆版)考研专业课历年真题汇编

2013年长安大学616马克思主义哲学考研试题(回忆版)
一、名词解释 1.质变 2.度 3.矛盾 4.意识形态 5.经济基础
二、辨析题 1.人民群众就是所有人2.逻辑证明能代替实践标准来检验真理
2014年长安大学616马克思主义哲学考研试题(回 忆版)
一、名词解释 5×8 分=40 分 1、物质 2、意识 3、认识 4、价值 5、忘记了
二、简答 (一个 10 分,共 40 分) 1、简述社会形态更替的相关知识 2、简述唯物辩证法的基本内容 3、如何看待社会发展中个人的作用 4、简述社会实践中主客体之间的关系
三、浅析题 1.社会存在和社会意识的关系 2.如何理解社会矛盾是推动社会发展的基本动力 3.生产关系必须适合生产状况的规律及意义
四、论述题 试述群众观点和群众路线及其意义
2012年长安大学马克思主义哲学考研试题(回忆版)
一、概念解释(6 个*10 分) 1、物质 2、绝对真理相对真理 3、经济基础上层建筑 4、意识形态 5、异化劳动 6、辨证法在本质上是批判的革命的
答案必须写在答题纸上,写在试题或草稿纸上不给分。
二、论述题(4 选三 30 分一个) 1、人的本质是一切社会关系的总和 2、感性认识理性认识辩证关系 3、马克思是怎样在批判旧哲学基础上创立新哲学的 4、历史规律与人的活动的关系
2007 年硕士研究生入学考试试题(A 卷)
试题代码:314 试题名称:马克思主义哲学
第1页共1页
一、名词解释(共 10 小题,每题 3 分,共 30 分) 1、 哲学基本问题 2、 物质 3、 矛盾 4、 规律 5、 生产力 6、 人民群众 7、 社会形态 8、 相对静止 9、 形而上学 10、道德 二、辨析题(判断正误并说明理由,共 6 小题,每题 5 分,共 30 分) 11、有人脑就会产生意识。 12、否定是事物发展的决定性环节。 13、绝对真理和相对真理是两个不同的真理。 14、唯心主义哲学是生长在人类认识之树上的一朵不结果实的花。 15、人民群众的创造作用不受历史条件的限制。 16、社会历史观的基本问题是生产力和生产关系的矛盾问题。 三、简答题(共 5 小题,每题 8 分,共 40 分) 17、为什么说马克思主义哲学的产生是哲学史上的伟大变革? 18、为什么说静止是运动的一种特殊状态? 19、什么是真理?为什么只有实践才是检验真理的惟一标准? 20、简述辩证的否定观。 21、简述社会意识的相对独立性。 四、论述题(共 2 小题,每题 15 分,共 30 分) 22、试论述矛盾同一性和斗争性的辩证关系原理及其对正确处理稳定和发展关 系的指导意义。 23、试述马克思主义哲学关于生产力的理论 五、分析题(1 题,20 分) 24、歌德有一句名言:你若喜欢你自己的价值,你就得给世界创造价值。试评 述这一论断。
15.2014年普通高等学校招生全国统一考试(陕西卷)(答案版)
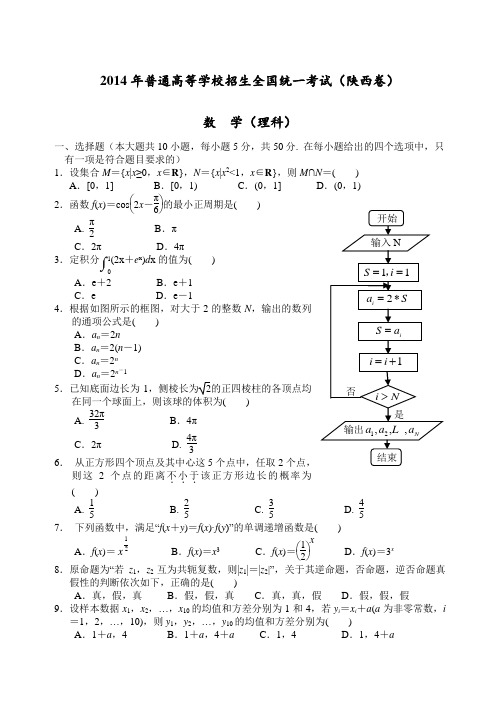
2014年普通高等学校招生全国统一考试(陕西卷)数 学(理科)一、选择题(本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合M ={x |x ≥0,x ∈R },N ={x |x 2<1,x ∈R },则M ∩N =( ) A .[0,1] B .[0,1) C .(0,1] D .(0,1)2.函数f (x )=cos ⎝⎛⎭⎫2x -π6的最小正周期是( ) A. π2B .πC .2πD .4π3.定积分⎠⎛01(2x +e x )d x 的值为( )A .e +2B .e +1C .eD .e -1 4.根据如图所示的框图,对大于2的整数N ,输出的数列的通项公式是( )A .a n =2nB .a n =2(n -1)C .a n =2nD .a n =2n -15.已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )A. 32π3 B .4πC .2π D. 4π36. 从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于...该正方形边长的概率为 ( )A. 15B. 25C. 35D. 457. 下列函数中,满足“f (x +y )=f (x )·f (y )”的单调递增函数是( )A .f (x )=21x B .f (x )=x 3 C .f (x )=⎝⎛⎭⎫12x D .f (x )=3x8.原命题为“若z 1,z 2互为共轭复数,则|z 1|=|z 2|”,关于其逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )A .真,假,真B .假,假,真C .真,真,假D .假,假,假9.设样本数据x 1,x 2,…,x 10的均值和方差分别为1和4,若y i =x i +a (a 为非零常数,i =1,2,…,10),则y 1,y 2,…,y 10的均值和方差分别为( )A .1+a ,4B .1+a ,4+aC .1,4D .1,4+a10. 如图,某飞行器在4千米高空水平飞行,从距着陆点A 的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图像的一部分,则该函数的解析式为 ( )A .y =1125x 3-35xB .y =2125x 3-45xC .y =3125x 3-xD .y =-3125x 3+15x二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上) 11.已知4a =2,lg x =a ,则x =________.12.若圆C 的半径为1,其圆心与点(1,0)关于直线y =x 对称,则圆C 的标准方程为 ___________________________.13.设0<θ<π2,向量a =(sin 2θ,cos θ),b =(cos θ,1),若a ∥b ,则tan θ=________.14.15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)A .(不等式选做题)设a ,b ,m ,n ∈R ,且a 2+b 2=5,ma +nb =5,则m 2+n 2的最小值为________.B .(几何证明选做题)如图1-3,△ABC 中,BC =6,以BC 为直径的半圆分 别交AB ,AC 于点E ,F ,若AC =2AE ,则EF =________. C .(坐标系与参数方程选做题)在极坐标系中,点⎝⎛⎭⎫2,π6到直线ρsin ⎝⎛⎭⎫θ-π6=1的距离是________. 三、解答题(本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤) 16.(本小题满分12分)△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .(1) 若a ,b ,c 成等差数列,证明:sin A +sin C =2sin(A +C ); (2) 若a ,b ,c 成等比数列,求cos B 的最小值.四面体ABCD 及其三视图如图所示,过棱AB 的中点E 作平行于AD ,BC 的平面分别交四面体的棱BD ,DC ,CA 于点F ,G ,H .(1) 证明:四边形EFGH 是矩形;(2) 求直线AB 与平面EFGH 夹角θ的正弦值.18.(本小题满分12分)在直角坐标系xOy 中,已知点A (1,1),B (2,3),C (3,2),点P (x ,y )在△ABC 三边围成的区域(含边界)上.(1) 若P A →+PB →+PC →=0,求|OP →|;(2) 设OP →=mAB →+nAC →(m ,n ∈R ),用x ,y 表示m -n ,并求m -n 的最大值.在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:(1) 设X(2) 若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于...2000元的概率.20.(本小题满分13分)如图所示,曲线C由上半椭圆C1:y2a2+x2b2=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为3 2.(1) 求a,b的值;(2) 过点B的直线l与C1,C2分别交于点P,Q(均异于点A,B),若AP⊥AQ,求直线l的方程.设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数.(1) 令g1(x)=g(x),g n+1(x)=g(g n(x)),n∈N+,求g n(x)的表达式;(2) 若f(x)≥ag(x) 恒成立,求实数a的取值范围;(3) 设n∈N+,比较g(1)+g(2)+…+g(n)与n-f(n)的大小,并加以证明.参考答案一、选择题1—10 B B C C D C D B A A1.[解析] 由M ={x |x ≥0,x ∈R },N ={x |x 2<1,x ∈R }={x |-1<x <1,x ∈R },得 M ∩N =[0,1).2.[解析] 已知函数y =A cos(ωx +φ)(A >0,ω>0)的周期为T =2πω,故函数f (x )的最小正周期T =2π2=π.3.[解析] ⎠⎛01(2x +e x )d x =(x 2+e x )10=(12+e 1)-(02+e 0)=e . 4.[解析] 阅读题中所给的程序框图可知,对大于2的整数N ,输出数列:2,22=22,222=23,223=24,…,22N -1=2N ,故其通项公式为a n =2n .5.[解析] 设该球的半径为R ,根据正四棱柱的外接球的直径长为正四棱柱的体对角线长,可得(2R )2=(2)2+12+12,解得R =1,所以该球的体积为V =43πR 3=43π.6.[解析] 利用古典概型的特点可知从5个点中选取2个点的全部情况有C 25=10(种),选取的2个点的距离不小于该正方形边长的情况有:选取的2个点的连线为正方形的4条边长和2条对角线长,共有6种.故所求概率P =610=35.7.[解析] 由于f (x +y )=f (x )f (y ),故排除选项A ,C.又f (x )=⎝⎛⎭⎫12x 为单调递减函数,所以排除选项B.8.[解析] 设z 1=a +b i ,z 2=a -b i ,且a ,b ∈R ,则|z 1|=|z 2|=a 2+b 2,故原命题为真,所以其否命题为假,逆否命题为真.当z 1=2+i ,z 2=-2+i 时,满足|z 1|=|z 2|,此时z 1,z 2不是共轭复数,故原命题的逆命题为假.9.[解析] 由题意可知x 1+x 2+x 3+…+x 1010=1,故y -=(x 1+x 2+x 3+…+x 10)+10a10=1+a .数据x 1,x 2,…,x 10同时增加一个定值,方差不变.故选A.10.[解析] 设该三次函数的解析式为y =ax 3+bx 2+cx +d .因为函数的图像经过点(0,0),所以d =0,所以y =ax 3+bx 2+cx .又函数过点(-5,2),(5,-2),则该函数是奇函数,故b =0,所以y =ax 3+cx ,代入点(-5,2)得-125a -5c =2.又由该函数的图像在点(-5,2)处的切线平行于x 轴,y ′=3ax 2+c ,得当x =-5时,y ′=75a +c =0.联立⎩⎪⎨⎪⎧-125a -5c =2,75a +c =0,解得⎩⎨⎧a =1125,c =-35.故该三次函数的解析式为y =1125x 3-35x .二、填空题11. 10 12.x 2+(y -1)2=1 13. 1214.F +V -E =215.A. 5 B .3 C .111. [解析] 由4a =2,得a =12,代入lg x =a ,得lg x =12,那么x =1012=10.12.[解析] 由圆C 的圆心与点(1,0)关于直线y =x 对称,得圆C 的圆心为(0,1).又因为圆C 的半径为1,所以圆C 的标准方程为x 2+(y -1)2=1.13. [解析] 因为向量a ∥b ,所以sin 2θ-cos θ·cos θ=0,又cos θ≠0,所以2sin θ=cos θ,故tan θ=12.14.[解析] 由题中所给的三组数据,可得5+6-9=2,6+6-10=2,6+8-12=2,由此可以猜想出一般凸多面体的顶点数V 、面数F 及棱数E 所满足的等式是F +V -E =2.15. [解析] A .由柯西不等式可知(a 2+b 2)(m 2+n 2)≥(ma +nb )2,代入数据,得m 2+n 2≥5,当且仅当an =bm 时,等号成立,故m 2+n 2 的最小值为 5.B .由题意,可知∠AEF =∠ACB ,又∠A =∠A ,所以△AEF ∽ACB ,所以AEAC=EFBC.因为AC =2AE ,BC =6,所以EF =3. C .点⎝⎛⎭⎫2,π6的极坐标可化为x =ρcos θ=2cos π6=3,y =ρsin θ=2sin π6=1,即点⎝⎛⎭⎫2,π6在平面直角坐标系中的坐标为(3,1).直线ρsin ⎝⎛⎭⎫θ-π6=ρsin θcos π6-ρcos θsin π6=1,即该直线在直角坐标系中的方程为x -3y +2=0,由点到直线的距离公式得所求距离为d =|3-3+2|12+(-3)2=1.三、解答题16.解:(1)∵a ,b ,c 成等差数列,∴a +c =2b .由正弦定理得sin A +sin C =2sin B . ∵sin B =sin[π-(A +C )]=sin(A +C ), ∴sin A +sin C =2sin(A +C ).(2)∵a ,b ,c 成等比数列,∴b 2=ac . 由余弦定理得cos B =a 2+c 2-b 22ac =a 2+c 2-ac 2ac ≥2ac -ac 2ac =12,当且仅当a =c 时等号成立,∴cos B 的最小值为12.17.解:(1)证明:由该四面体的三视图可知,BD ⊥DC ,BD ⊥AD ,AD ⊥DC ,BD =DC =2,AD =1.由题设,BC ∥平面EFGH ,平面EFGH ∩平面BDC =FG , 平面EFGH ∩平面ABC =EH ,∴BC ∥FG ,BC ∥EH ,∴FG ∥EH . 同理EF ∥AD ,HG ∥AD ,∴EF ∥HG . ∴四边形EFGH 是平行四边形.又∵AD ⊥DC ,AD ⊥BD ,∴AD ⊥平面BDC ,∴AD ⊥BC ,∴EF ⊥FG , ∴四边形EFGH 是矩形.(2)方法一:如图,以D D (0,0,0),A (0,0,1),B (2,0,0),C (0,2,0),DA =(0,0,1),BC =(-2,2,0),BA =(-2,0,1). 设平面EFGH 的法向量n =(x ,y ,z ), ∵EF ∥AD ,FG ∥BC ,∴n ·DA =0,n ·BC =0, 得⎩⎪⎨⎪⎧z =0,-2x +2y =0,取n =(1,1,0), ∴sin θ=|cos 〈BA →,n 〉|=⎪⎪⎪⎪BA ·n |BA ||n |=25×2=105.方法二:如图,以D 为坐标原点建立空间直角坐标系, 则D (0,0,0),A (0,0,1),B (2,0,0),C (0,2,0),∵E 是AB 的中点,∴F ,G 分别为BD ,DC 的中点,得E ⎝⎛⎭⎫1,0,12,F (1,0,0),G (0,1,0).∴FE →=⎝⎛⎭⎫0,0,12,FG =(-1,1,0), BA =(-2,0,1).设平面EFGH 的法向量n =(x ,y ,z ), 则n ·FE =0,n ·FG =0,得⎩⎪⎨⎪⎧12z =0,-x +y =0,取n =(1,1,0),∴sin θ=|cos 〈BA →,n 〉|=⎪⎪⎪⎪⎪⎪BA ·n |BA →||n |=25×2=105.18.解:(1)方法一:∵P A →+PB →+PC →=0,又P A →+PB →+PC →=(1-x ,1-y )+(2-x ,3-y )+(3-x ,2-y )=(6-3x ,6-3y ), ∴⎩⎪⎨⎪⎧6-3x =0,6-3y =0,解得⎩⎪⎨⎪⎧x =2,y =2, 即OP →=(2,2),故|OP →|=2 2.方法二:∵P A →+PB →+PC →=0, 则(OA →-OP →)+(OB →-OP →)+(OC →-OP →)=0,∴OP →=13(OA →+OB →+OC →)=(2,2),∴|OP →|=2 2.(2)∵OP →=mAB →+nAC →,∴(x ,y )=(m +2n ,2m +n ), ∴⎩⎪⎨⎪⎧x =m +2n ,y =2m +n ,两式相减得,m -n =y -x ,令y -x =t ,由图知,当直线y =x +t 过点B (2,3)时,t 取得最大值1,故m -n 的最大值为1.19.解:(1)设A 表示事件“作物产量为300 kg”,B 表示事件“作物市场价格为6元/kg”,由题设知P (A )=0.5,P (B )=0.4, ∵利润=产量市场价格-成本, ∴X 所有可能的取值为50010-1000=4000,5006-1000=2000, 30010-1000=2000,3006-1000=800.P (X =4000)=P (A )P (B )=(1-0.5)(1-0.4)=0.3,P (X =2000)=P (A )P (B )+P (A )P (B )=(1-0.5)0.4+0.5(1-0.4)=0.5, P (X =800)=P (A )P (B )=0.50.4=0.2, 所以X 的分布列为(2) 设C i 表示事件“第i 3), 由题意知C 1,C 2,C 3相互独立,由(1)知,P (C i )=P (X =4000)+P (X =2000)=0.3+0.5=0.8(i =1,2,3), 3季的利润均不少于2000元的概率为P (C 1C 2C 3)=P (C 1)P (C 2)P (C 3)=0.83=0.512; 3季中有2季利润不少于2000元的概率为P (C 1C 2C 3)+P (C 1C 2C 3)+P (C 1C 2C 3)=30.820.2=0.384,所以,这3季中至少有2季的利润不少于2000元的概率为0.512+0.384=0.896. 20.解:(1)在C 1,C 2的方程中,令y =0,可得b =1,且A (-1,0),B (1,0)是上半椭圆C 1的左、右顶点.设C 1的半焦距为c ,由c a =32及a 2-c 2=b 2=1得a =2,∴a =2,b =1.(2)方法一:由(1)知,上半椭圆C 1的方程为y 24+x 2=1(y ≥0).易知,直线l 与x 轴不重合也不垂直,设其方程为y =k (x -1)(k ≠0), 代入C 1的方程,整理得(k 2+4)x 2-2k 2x +k 2-4=0.(*) 设点P 的坐标为(x P ,y P ),∵直线l 过点B ,∴x =1是方程(*)的一个根.由求根公式,得x P =k 2-4k 2+4,从而y P =-8kk 2+4,∴点P 的坐标为⎝ ⎛⎭⎪⎫k 2-4k 2+4,-8k k 2+4.同理,由⎩⎪⎨⎪⎧y =k (x -1)(k ≠0),y =-x 2+1(y ≤0), 得点Q 的坐标为(-k -1,-k 2-2k ).∴AP →=2k k 2+4(k ,-4),AQ →=-k (1,k +2).∵AP ⊥AQ ,∴AP ·AQ =0,即-2k 2k 2+4[k -4(k +2)]=0,∵k ≠0,∴k -4(k +2)=0,解得k =-83. 经检验,k =-83符合题意,故直线l 的方程为y =-83(x -1).方法二:若设直线l 的方程为x =my +1(m ≠0),比照方法一给分.21.解:由题设得,g (x )=x1+x (x ≥0).(1)由已知,g 1(x )=x1+x ,g 2(x )=g (g 1(x ))=x 1+x 1+x 1+x=x1+2x ,g 3(x )=x 1+3x ,…,可得g n (x )=x1+nx .下面用数学归纳法证明.①当n =1时,g 1(x )=x1+x,结论成立.②假设n =k 时结论成立,即g k (x )=x1+kx.那么,当n =k +1时,g k +1(x )=g (g k (x ))=g k (x )1+g k (x )=x 1+kx 1+x 1+kx=x1+(k +1)x ,即结论成立.由①②可知,结论对n ∈N +成立.(2)已知f (x )≥ag (x )恒成立,即ln(1+x )≥ax1+x恒成立.设φ(x )=ln(1+x )-ax1+x(x ≥0),则φ′(x )=11+x -a(1+x )2=x +1-a (1+x )2,当a ≤1时,φ′(x )≥0(仅当x =0,a =1时等号成立), ∴φ(x )在[0,+∞)上单调递增,又φ(0)=0, ∴φ(x )≥0在[0,+∞)上恒成立,∴a ≤1时,ln(1+x )≥ax1+x恒成立(仅当x =0时等号成立).当a >1时,对x ∈(0,a -1]有φ′(x )<0,∴φ(x )在(0,a -1]上单调递减,∴φ(a -1)<φ(0)=0.即a >1时,存在x >0,使φ(x )<0,故知ln(1+x )≥ax 1+x不恒成立. 综上可知,a 的取值范围是(-∞,1].(3)由题设知g (1)+g (2)+…+g (n )=12+23+…+n n +1, 比较结果为g (1)+g (2)+…+g (n )>n -ln(n +1).证明如下:方法一:上述不等式等价于12+13+…+1n +1<ln(n +1), 在(2)中取a =1,可得ln(1+x )>x 1+x,x >0. 令x =1n ,n ∈N +,则1n +1<ln n +1n . 下面用数学归纳法证明.①当n =1时,12<ln 2,结论成立. ②假设当n =k 时结论成立,即12+13+…+1k +1<ln(k +1). 那么,当n =k +1时,12+13+…+1k +1+1k +2<ln(k +1)+1k +2<ln(k +1)+ln k +2k +1=ln(k +2),即结论成立.由①②可知,结论对n ∈N +成立.方法二:上述不等式等价于12+13+…+1n +1<ln(n +1), 在(2)中取a =1,可得ln(1+x )>x 1+x,x >0. 令x =1n ,n ∈N +,则ln n +1n >1n +1.故有ln 2-ln 1>12, ln 3-ln 2>13, ……ln(n +1)-ln n >1n +1, 上述各式相加可得ln(n +1)>12+13+…+1n +1, 结论得证.方法三:如图,⎠⎛0n x x +1d x 是由曲线y =x x +1,x =n 及x 轴所围成的曲边梯形的面积,而12+23+…+n n +1是图中所示各矩形的面积和,∴12+23+…+n n +1>⎠⎛0n x x +1d x = ⎠⎛0n⎝⎛⎭⎫1-1x +1d x =n -ln (n +1), 结论得证.。
长安大学公路学院路基路面工程(复试)历年考研真题汇编含部分答案【圣才出品】

2014年长安大学公路学院路基路面工程(复试)考研真题
一、试述公路路基设计的基本要求,什么是一般路基和特殊路基?请列举常见的特殊路基。
二、试分析自然因素(温度和湿度)对公路路基的影响,在路基设计中采取哪些相应对策?
三、试述表征土基承载能力的参数指数及其概念,以及我国现行沥青路面设计规范中采用的指标及确定
方法。
四、重力式挡土墙的构造,设计时的验算内容及增加稳定性的措施。
五、简述路面结构分层的原因,分别为哪些层次,以及各层的作用及对材料的基本要求。
六、试分析环境温度对沥青路面结构和水泥混凝土路面结构的影响,以及在两种路面结构设计时如何考
虑这种影响?
七、试述无机结合料稳定材料的主要用途,分类及主要物理力学特性。
八、试述水稳定性的破环过程,作用机理,评价方法及提高水稳定性的技术措施。
九、试分析沥青路面和水泥混凝土路面结构设计中如何考虑荷载的疲劳作用。
十、试解释下列名词
1.刚性基层
2.路基工作区
3.压实度
4.SMA
5.连续配筋混凝土路面
2013年长安大学公路学院路基路面工程(复试)考研真题
2011年长安大学公路学院路基路面工程(复试)考研真题A卷
2011年长安大学公路学院路基路面工程(复试)考研真题A卷参考答案。
长安大学机械设计历年真题

长安大学机械设计历年真题2005年2006长安大学2007年硕士研究生入学考试试题(A卷)试题名称:机械设计第 1 页共3页一、选择填空题(每小题2分,共计20分)1、影响零件疲劳强度的综合影响系数Kσ与等因素有关。
A、零件的应力集中、过载、高温B、零件的应力循环特性、应力集中、加载状态C、零件的表面状态、绝对尺寸、应力集中D、零件的材料、热处理方法、绝对尺寸2、采用螺纹联接时,若被联接件总厚度较大,且材料较软,强度较低,但不需要经常拆装的情况下,一般宜采用。
A、螺栓联接B、双头螺柱联接C、螺钉联接D、紧定螺钉联接3、设计普通平键联接的几项主要内容是:a、按轮毂的长度选择键的长度;b、按使用要求选择键的适当类型;c、按轴的直径选择键的剖面尺寸;d、对联接进行必要的强度校核。
在具体设计时一般顺序是。
A、b→a→c→dB、b→c→a→dC、a→c→b→dD、c→d→b→a4、在V带传动打滑一般发生在。
A、主动带轮B、从动带轮C、小带轮D、大带轮5、在设计链传动时,为使传动结构紧凑、寿命长,应尽量选取。
A、小节距的单排链B、大节距的单排链C、小节距的多排链D、大节距的多排链6、对于齿面硬度HBS≤350的闭式齿轮传动,主要的失效形式是。
A、齿轮疲劳折断B、齿面点蚀C、齿面磨损D、齿面胶合7、对于一般传递动力的闭式蜗杆传动,其选择蜗轮材料的主要依据是()。
A、配对蜗杆的齿面硬度B、蜗杆传动的效率C、蜗杆传动的载荷D、蜗轮齿面的滑动速度8、一对齿轮作单向传动时,轮齿的弯曲应力可看成。
A、静应力B、对称循环变应力C、脉动循环变应力D、随机变化的应力9、所谓滚动轴承的基本额定动载荷,就是使轴承的寿命为106转时,轴承所能承受的载荷值,用字母C代表。
A、基本额定B、预期计算C、实际D、相对答案必须写在答题纸上,写在试题或草稿纸上不给分;答题纸上写明考试科目。
试题名称:机械设计第 2 页共3页10、联轴器的主要作用是。
长安大学2004~2014结构工程结构力学学硕考研真题

3、 (20 分)用力矩分配法计算图示刚架。绘弯矩图, 并求 C 支座的反力。
题3图 4、 (18 分)连续梁的支座 A 和 B 均发生了支座位移如图。试列出力法方程, 求出方程中的系数和常数项。 (注意:不解方程) 题4图
(于) 5、 (20 分)用位移法计算图示刚架。绘出弯矩图。
6
EI 0=
6、 (18 分)做图示梁 A 截面的弯矩 MA、剪力 FQA 及 k 截面的弯矩 Mk 影响线;已知可任意分布均布荷载集度 q=10kN/m,计算 FQA 的最大值,并 注出相应的最不利荷载位置。
8
(于) 2007 年硕士研究生入学考试试题 (于 P65)对称性
8
3、(22 分)结构在图示荷载作用下,并在 A 支座发生角位移 ,试建立图示 结构的力法方程,求出方程中的系数和常数项。已知 A 求解方程; )
I 。 (注意:不需 10
4、(22 分)用位移法计算图示在荷载作用下的刚架,作出弯矩 M 图。已知各 杆 EI=常数。
E F
4m
B
C
4m
G 5kN 4m H 4m
A 4m
D
J
2.计算图示荷载作用下的静定刚架,绘出弯矩图、剪力图。(18 分)
20kNm
5 k N /m
3m
C B A 4m
F
3m
D 4m
E
题2图 3.已知,图(a)所示三跨连续梁,中间的两个支座分别发生竖向沉陷 a、b, 并且 a>b;图(b)所示单跨超静定梁,上下两侧分别温度改变了 t1 、 t 2 ,并且
9. (1)求图示体系的自振频率 ;(2)设简谐荷载频率 . ,求体系质点 的最大动位移 y max 以及竖杆底端 A 截面的最大动弯矩 M A 。已知:竖杆的抗 弯刚度 EI=常数,杆 BC 的抗弯刚度无穷大,杆 CD 轴向刚度 EA=EI/20。(18
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长安大学2014年材料科学基础考研真题
一.名词解释(共30分)
1.共价晶晶带轴定律
2.浓度三角形共轭三角形
3.细晶强化形变强化
4.包晶反应包晶偏析
5.全位错不全位错
二.简答(共70分)
1.纯金属、合金可能采取的强化措施10分
2.简述扩散机制种类,比较不同扩散机制的激活能大小。
15分
3.凝固过程中形核长大与再结晶过程中形核长大的区别是什么。
15分
4.用位错理论解释细晶强化和加工硬化。
15分
5.比较变形金属在不同温度下的回复机制。
15分
三.计算题(任选一道题目作答)25分
1.面心立方(111)面上单位位错b=a/2【-110】。
在(111)面上分解为两个
肖克莱不全位错。
写出位错反应,并证明扩展为错宽度为d≈Gb2/24πr。
2.当锌向铜内扩散(假设为稳态扩散)时,已知在x点处锌的含量为2.5×
1017个锌原子/cm3,300℃时每分钟每mm2再扩散60个锌原子(已知锌在
铜内的扩散体系中D
=0.34×10-14m2/s Q=1.85×104J/mol)
(1)推导菲克第二定律。
(2)求与x点相距2mm处锌原子浓度。
四.分析题(任选一道题目作答)25分
1. 铁碳相图题(25分)
(1)画出Fe—Fe3C相图。
(5分)
(2)画出含碳量0.6%时的室温下的平衡组织。
(5分)
(3)求Fe3C
ⅡFe
3
C
Ⅲ
最大可能含量。
(5分)
(4)含碳量为3%的亚稳定系冷却到室温时,组织中的珠光体,二次渗碳体和莱氏体含量。
(10分)
2. 烧结过程是怎样产生的,各烧结阶段特征是什么?(25分)。
