动刚度阻尼加速度计算
结构动力学基础
m l/ 5
m l/ 5
m l/ 5
m l/ 5
0
1
2
3
4
5
l/5
0
l/5
1y = 1 1 φ1(x) 2
l/5
3
l/5
4
l/5
5
0
2 θ1 = 1 1 φ (x) 2
3
4
5
如图10-9a中，梁分为5个单元，取结点位移参数（挠度y 和转角θ）作为 广义坐标。在图10-9a中取中间四个结点的八个位移参数 y1、θ1，y2、θ2，y3、 θ3，y4、θ4 作广义坐标。
T
sin t
(10 3)
(10 4)
0 -y y T
t
y cos t
v v
y A
0
t
v
sin t
T t
0
A sin t
-A
3、结构的自振周期
由式
A
y (t ) A sin(t ) 及图，可见位移方程是一个周期函数。 2 y T 周 期： T
⑶ 是结构动力特性的重要数量标志。
泛美大厦，60层 钢结构，南北方向 的基本固有周期为 2.90秒，
大坝，400英尺高的混凝土重力坝的基 本固有周期由强迫振动试验测得在蓄水 为310英尺和345英尺十分别为0.288秒 和0.306秒，
金门大桥，金门大桥桥墩跨距1280.2米全桥总 长2737.4米的悬索桥，其横向振动的基本基本固 有周期为18.20秒，竖向振动的基本基本固有周期 为10.90秒，纵向振动的基本基本固有周期为3.81 秒，扭转振动的基本基本固有周期为4.43秒
ABAQUS+计算+动刚度+详细说明
F(ω)=F0×sin(ωt) 输入激励力当使用abaqus-steady-state daynmics modal，其中20-1000即为激励力的最低频率和最高频率。
开始模态和结束模态要覆盖上图所示的激励力的最低频率和最高频率，选择直接阻尼，即每阶模态的临界阻尼比3%，（典型的取值范围在1%-10%）Ma+cv+kx= F0×sin(ωt)其中F0是固定的数值（简谐力的幅值），且频率由20Hz 变化到1000Hz 。
f ••=πω2位移阻抗（动刚度）：()()()ωωωx F K =()()t F F ωωsin 0•= 为输入激励力，是一个谐波输入。
()()θωω+•=t x x sin 0 为输出稳态位移响应，根据振动理论，稳态位移响应的频率与输入激励力的频率相同，振幅 0x 和相位角θ均取决与系统本身的物理性质（质量，弹簧刚度，阻尼）和激振力的性质（频率与振幅），而与初始条件无关，初始条件仅影响系统的瞬态响应的振幅和初始相位角。
()ωK ，表示，在某频率下，产生单位位移振幅所需要的激振力幅值。
实际情况下，频率不同，刚度也不同。
假设()ωK =10N/m ，及动刚度在任意频率都是固定的，不随频率的变化而变化（理想情况），即在任意频率激振下，产生1m 单位位移振幅所需要的激振力幅值为10N 。
假设()ωF 的幅值为1 ，()ωK =10N/m()ωx 的幅值x=()()ωωK F =101特点：位移响应的幅值与频率没有关系，且是固定值。
由于在abaqus 中可方便的输出某个点的位移，速度，加速度。
所以通常以某个点的位移，速度，加速度来表征动刚度的大小。
速度阻抗：()()()ωωω•=x F Z 如何将速度阻抗：()()()ωωω•=x F Z 与位移阻抗（动刚度）：()()()ωωωx F K =联系起来？用速度表示： ()ω•x = ()ωx 的导数=()θω+•t x sin 0的导数=()'sin 0θωω+••t x =()ωωx •（我们只要幅值，忽略相位角）响应速度与响应位移幅值相差ω，相位角不同，频率相同。
matlab油膜动态刚度和阻尼的程序代码
matlab油膜动态刚度和阻尼的程序代码文章标题：探索Matlab中油膜动态刚度和阻尼的程序代码一、引言在工程领域中，油膜动态刚度和阻尼是润滑系统中重要的参数之一。
它们是描述油膜在润滑油的作用下对载荷的支撑能力和阻尼效果的重要指标，对于机械设备的设计和性能分析有着重要的意义。
本文将以Matlab程序为工具，探索油膜动态刚度和阻尼的计算方法及其程序代码实现。
二、理论基础油膜动态刚度和阻尼的计算是基于流体力学和弹性力学理论的。
动态刚度是描述油膜对外力变化的敏感程度，而阻尼则是描述油膜对振动的消耗能力。
其计算涉及到流体动力学的压力分布计算和弹性体的变形分析。
在Matlab中，我们可以通过数值计算和模拟方法来实现其程序代码。
三、油膜动态刚度的程序代码实现1. 定义油膜几何参数和载荷条件我们需要定义油膜的几何参数，如厚度、长度和宽度，以及外载荷的大小和方向。
这些参数将作为程序计算的输入条件。
2. 计算油膜压力分布根据流体动力学的理论，油膜的压力分布是动态刚度计算的关键。
我们可以利用Matlab中的数值求解方法，如有限差分或有限元法，来计算油膜中的压力分布，并将其作为后续计算的基础数据。
3. 计算油膜动态刚度根据油膜压力分布和外载荷条件，利用弹性力学中的刚度计算公式，我们可以编写Matlab程序来求解油膜的动态刚度，并得到相应的计算结果。
四、油膜阻尼的程序代码实现1. 计算油膜振动频率油膜的阻尼特性与其振动频率密切相关。
在Matlab中，我们可以利用数值模拟方法来计算油膜的振动频率，包括油膜的自由振动频率和受迫振动频率，从而为阻尼的计算打下基础。
2. 计算油膜阻尼比根据振动频率和油膜的阻尼特性公式，我们可以编写Matlab程序来计算油膜的阻尼比，并得到相应的计算结果。
五、个人观点和理解通过对Matlab程序代码的探索和实现，我对油膜动态刚度和阻尼的计算方法有了更深入的理解。
Matlab作为强大的数值计算工具，为工程技术人员提供了便利和高效的计算手段，能够有效地简化复杂的工程计算过程，提高工作效率。
车身模态及接附点动刚度分析
后ꎬ共有 ３ １０４ ４２９ 个单元、２ ７１７ ０２９ 个节点ꎬ三角
形单元占比为 ５ ３％ ꎮ
表 １ 车身材料参数
Ｔａｂｌｅ １ Ｂｏｄｙ ｍａｔｅｒｉａｌ ｐａｒａｍｅｔｅｒｓ
材料
弹性模量 / ＭＰａ
泊松比
钢
２ １ × １０ ５
ｔｈｅ ｒｅｓｅａｒｃｈ ｏｂｊｅｃｔꎬｉｔｓ ｆｉｎｉｔｅ ｅｌｅｍｅｎｔ ｍｏｄｅｌ ｉｓ ｅｓｔａｂｌｉｓｈｅｄꎬｔｈｅ ｆｒｅｅ ｍｏｄｅ ｏｆ ｔｈｅ ｖｅｈｉｃｌｅ ｂｏｄｙ ｗｉｔｈｉｎ
０ ~ １００ Ｈｚ ａｎｄ ｔｈｅ ｄｙｎａｍｉｃ ｓｔｉｆｆｎｅｓｓ ｏｆ １６ ａｔｔａｃｈｍｅｎｔ ｐｏｉｎｔｓ ｉｓ ｏｂｔａｉｎｅｄꎬｔｈｅ ｌｅｆｔ ｆｒｏｎｔ ａｎｄ ｒｉｇｈｔ
格比例较大ꎬ网格主要由四边形单元和少量三角
形单元混合而成ꎬ采用三角形单元是为了获得更
高质 量 的 整 体 网 格ꎬ 其 数 量 不 超 过 单 元 总 数 的
１０％ ꎮ 组件进行连接时ꎬ主要使用螺栓、点焊和粘
胶三种方式ꎬ车身相关材料参数如表 １ 所示ꎮ 车
身厚度约 ０ ７ ~ ３ ２ ｍｍꎬ有限元模型中厚度设置
下的动刚度特性较差ꎬ此时进行模态分析ꎬ通过分
析车 身 模 态 频 率 与 振 型 来 判 断 产 生 峰 值 的 原
因 [１３] ꎮ ＩＰＩ 计算公式为
ＩＰＩ ＝
－ ｗ２ ｘ０ ｅ ｊｗｔ － ｗ２
ｘ̈
－ ｗ２
＝
＝
＝
ｊｗｔ
Ｆ
Ｋｄ
Ｆ０ ｅ
ｋ ห้องสมุดไป่ตู้ ｗ２ ｍ ＋ ｊｗｃ
(９)
沈 阳 理 工 大 学 学 报
起重机的动刚度及其测试方法
3 起重机动刚度的测试方法
如前所述 ,起重机动刚度的测试 ,实际上就是测 试起重机在规定方向上的自振频率 。对于不同类型 的起重机 ,在不同方向上动刚度的大小 ,相应的标准
— 26 —
图 4 贴应变片法测试与分析框图 《起重运输机械》 1999 (4)
的动刚度 。这一方法的测试精度高于光线示波器 法 ;而采用动态数据采集分析系统则可直接对信号 进行采集和频谱或功率谱分析 ,实时地得到所测的 动刚度 ,具有速度快 、精度高的特点 。 3. 2 压电加速度计法
图 1 受简谐激振力的单自由度系统 图 2 单自由度系统的动刚度曲线
4 结束语
该微机监控系统在建设部长沙机械研究院设计 的 Q TZ2800 型塔式起重机上作了现场试验 ,结果证 明该微机电控系统工作稳定 、可靠 ,抗干扰能力强 , 功能强大 ,司机可以通过液晶屏随时掌握塔式起重 机的工作参数 ,起吊重物的自动就位误差小于 10cm ,各项功能达到了设计要求 。
λ= ω/ ωn ω ———简谐激振力角频率
动刚度的幅值为
| KD| = K (1 - λ2) 2 + (2ξλ) 2
(2)
可见 ,动刚度并非是一个常数 ,而是随频率的改
变而变化 ,是频率的函数 (见图 2) 。
1 动刚度的基本概念
在机械振动学中 ,动刚度的定义为起重机结构
产生单位振幅所需要的动态力 。对于受简谐激振力
的单自由度系统 (如图 1 所示) ,其动刚度 KD 可以 表示为 :
KD = K〔(1 - λ2) + 2 ξi λ〕
(1)
式中 K ———系统的静刚度
ξ———阻尼比
ξ= C/ (2 mωn) C ———阻尼系数
m ———系统质量 ωn ———系统固有频率 ωn = K/ m = 2πf n
原点动刚度
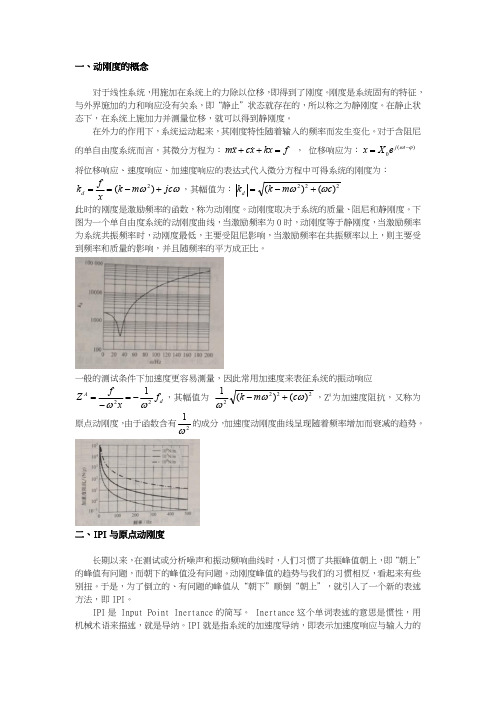
一、动刚度的概念对于线性系统，用施加在系统上的力除以位移，即得到了刚度。
刚度是系统固有的特征，与外界施加的力和响应没有关系，即“静止”状态就存在的，所以称之为静刚度。
在静止状态下，在系统上施加力并测量位移，就可以得到静刚度。
在外力的作用下，系统运动起来，其刚度特性随着输入的频率而发生变化。
对于含阻尼的单自由度系统而言，其微分方程为：f kx x c xm =++ ，位移响应为：)(0ϕω-=t j e X x 将位移响应、速度响应、加速度响应的表达式代入微分方程中可得系统的刚度为：ωωjc m k xf k d +-==)(2，其幅值为：222)()(c m k k d ωω+-=此时的刚度是激励频率的函数，称为动刚度。
动刚度取决于系统的质量、阻尼和静刚度。
下图为一个单自由度系统的动刚度曲线，当激励频率为0时，动刚度等于静刚度，当激励频率为系统共振频率时，动刚度最低，主要受阻尼影响，当激励频率在共振频率以上，则主要受到频率和质量的影响，并且随频率的平方成正比。
一般的测试条件下加速度更容易测量，因此常用加速度来表征系统的振动响应d A f x fZ 221ωω-=-=，其幅值为2222)()(1ωωωc m k +-，Z A 为加速度阻抗，又称为原点动刚度，由于函数含有21ω的成分，加速度动刚度曲线呈现随着频率增加而衰减的趋势。
二、IPI 与原点动刚度长期以来，在测试或分析噪声和振动频响曲线时，人们习惯了共振峰值朝上，即“朝上”的峰值有问题，而朝下的峰值没有问题。
动刚度峰值的趋势与我们的习惯相反，看起来有些别扭。
于是，为了倒立的、有问题的峰值从“朝下”顺倒“朝上”，就引入了一个新的表述方法，即IPI。
IPI 是Input Point Inertance 的简写。
Inertance 这个单词表述的意思是惯性，用机械术语来描述，就是导纳。
IPI 就是指系统的加速度导纳，即表示加速度响应与输入力的传递函数。
动刚度
动刚度试验系统
在橡胶制品的动态特性中，其动刚度、损耗因子有着及其重要的地位，本文基于ＡＮＳＹＳ提出了利用瞬态动力学分析方法来求解简谐载荷下的响应，进而获得橡胶制品的迟滞回线来计算橡胶制品的动刚度、损耗因子的方法。
通过利用该方法对某型橡胶金属环进行了动态特性分析，计算了其动刚度、损耗因子，从计算结果与试验结果对比表明，该方法是行之有效，可以用于橡胶制品的动态特性分析．
一、用途
动刚度试验系统，主要用于弹性体、橡胶弹性体、减振器等进行动静刚度、阻尼系数、阻尼角等参数的测试和耐疲劳性能试验。
本系统能在正弦波、三角波、方波、梯形波、斜波、用户自定义波形下进行多种试验。
二、设备主要技术指标
1、最大动态试验力：5kN；1kN；15kN
2、动态负荷值波动度：
平均负荷波动度：±0.5%，力传感器准确度： 0.5%
负荷振幅波动度: ±2%
3、位移测量范围：±0.01——50mm；分辨率：0.1%；准确度：0.001mm
4、试验频率：0.01—200Hz
5、作动器行程：±50mm
6、试验波形：正弦波、三角波、方波、斜波、锯齿波及各种组合波，外输入采集波等波形
7、试验软件：适应于WINDOWS98/2000/XP系统平台的试验控制软件，计算机实时显示试验过程中静态负荷、动态负荷、试验频率、疲劳次数。
8、具有智能型超载、断裂、位移保护等安全措施。
9、具有设定多个模块疲劳试验管理功能。
三、使用环境和使用范围
1、使用环境：
用于室内环境温度：室温—40℃
2、使用范围
依用户试样尺寸设计试验夹具，满足橡胶弹性体疲劳试验的要求。
阻尼器阻尼比计算公式
阻尼器阻尼比计算公式全文共四篇示例，供读者参考第一篇示例：阻尼器是一种用来减少系统振动幅度并使系统达到稳定状态的装置。
在工程领域中，阻尼器广泛应用于减振和减震系统中，起到了至关重要的作用。
在设计阻尼器时，阻尼比是一个非常重要的参数，它能够影响系统的振动特性和稳定性。
本文将介绍阻尼器阻尼比的计算公式，帮助读者更好地理解并设计阻尼器。
阻尼比通常用ζ来表示，它是一个无量纲的参数，反映了实际阻尼器的阻尼效果相对于临界阻尼效果的大小。
阻尼比越大，阻尼效果越强，系统的振动幅度会更快地减小，系统也会更快地达到稳定状态。
而阻尼比越小，系统的振动幅度会越大，系统达到稳定状态的时间也会更长。
对于线性阻尼器，阻尼比可以通过以下公式进行计算：ζ = c / (2 * √(mk))ζ表示阻尼比，c表示阻尼器的阻尼系数，m表示系统的质量，k 表示系统的刚度。
这个公式描述了阻尼比和阻尼器的特性、系统的质量和刚度之间的关系。
在实际设计中，需要根据实际工程需求和系统参数来确定阻尼比的大小，以确保系统具有良好的稳定性和减振效果。
值得注意的是，阻尼比并不是越大越好，也不是越小越好。
在设计阻尼器时，需要根据系统的振动特性和工作环境来确定合适的阻尼比。
过大的阻尼比可能导致系统反应迟钝，振动幅度较小，但系统稳定性差；而过小的阻尼比可能导致系统振动幅度过大，在系统达到稳定状态前会经历长时间的振荡。
在实际的工程设计中，经常需要通过试验和模拟来确定阻尼比的大小。
通过对系统进行振动分析和实验测试，可以获得系统的振动特性，从而确定合适的阻尼比。
工程师需要综合考虑系统的质量、刚度、工作环境等因素，来确定阻尼比的大小，以实现系统的稳定和减振效果。
阻尼器阻尼比的计算公式为ζ = c / (2 * √(mk))，其中阻尼比反映了阻尼器的阻尼效果相对于临界阻尼效果的大小。
在设计阻尼器时，需要根据系统的振动特性和工作环境来确定合适的阻尼比，以实现系统的稳定和减振效果。
阻尼器的阻尼和刚度计算
阻尼器的阻尼和刚度计算
阻尼器是一种用于减震和减振的装置，主要通过消耗振动能量来减小结构物的振幅和振动。
阻尼器的阻尼和刚度计算是设计阻尼器时需要考虑的重要问题。
一、阻尼计算
阻尼器的阻尼计算需要考虑结构物的质量、刚度和自然频率等因素。
一般来说，阻尼器的阻尼系数越大，阻尼效果越好。
阻尼系数的计算可以采用以下公式：
D = c * M
其中，D表示阻尼系数，c表示阻尼器的阻尼比，M表示结构物的质量。
阻尼比是指阻尼器的阻尼力与结构物动力学响应的比值，通常取值在0.1~0.5之间。
二、刚度计算
阻尼器的刚度计算需要考虑结构物的刚度和自然频率等因素。
一般来说，阻尼器的刚度越小，阻尼效果越好。
刚度的计算可以采用以下公式：
K = (2 * π* f)^2 * M
其中，K表示阻尼器的刚度，f表示结构物的自然频率，M表示结构物的质量。
自然频率是指结构物在没有外力作用下自由振动的频率，通常在设计时需要控制在一定范围内。
总之，阻尼器的阻尼和刚度计算需要综合考虑结构物的质量、刚度和自然频率等因素，以达到减震和减振的目的。
动力学分析中的阻尼(!需要更新一下,图片没有了!)
ANSYS结构动力学分析中的阻尼ANSYS动力学分析中提供了各种的阻尼形式，这些阻尼在分析中是如何计算，并对分析有什么影响呢？本文将就此做一些说明何介绍.一．首先要清楚，在完全方法和模态叠加法中定义的阻尼是不同。
因为前者使用节点坐标，而后者使用总体坐标.1．在完全的模态分析、谐相应分析和瞬态分析中，振动方程为：阻尼矩阵为下面的各阻尼形式之和：α为常值质量阻尼（α阻尼）（ALPHAD命令）β为常值刚度阻尼（β阻尼）（BETA命令）ξ为常值阻尼比，f为当前的频率（DMPRAT命令）βj为第j种材料的常值刚度矩阵系数（MP,DAMP命令）[C]为单元阻尼矩阵（支持该形式阻尼的单元）2．对模态叠加方法进行的谐相应分析、瞬态分析何谱分析，动力学求解方程为：每个模态产生有效阻尼比ξid而不是创建阻尼矩阵α为常值质量阻尼β为常值刚度阻尼ξ为常值阻尼比ξmi为第i个模态的常值阻尼比ξj为第j个材料的阻尼系数Ejs为第j个材料的应变能，ANSYS由{f}T[K]{f}计算得到。
二．对谱分析，阻尼仅仅包含在模态组合里，而在计算模态系数的时候并没有考虑。
当使用模态叠加法时，材料阻尼被添加到扩展的模态中，因此，用户必须在进行模态分析之前，就包括材料阻尼（MP,DAMP）并进行单元应力的计算（MXPAND命令）。
三．模态叠加法支持使用QR阻尼，但是用户必须知道尽管是模态组合方法，阻尼在模态分析中已包含了，所以应该使用上面的完全阻尼矩阵[C]来计算阻尼。
如果使用QR阻尼的的模态提取方法（MOPT,QRDAMP），并且在前处理或模态分析中指定了任何形式的阻尼，那么ANSYS将在进行模态叠加时忽略阻尼。
四．了解MP,DAMP在不同的情况下有不同的作用非常重要。
在完全分析中，材料阻尼代表了该材料的一个刚度矩阵乘子，与粘性阻尼（与频率成线性关系，但针对所有的材料）类似。
因此，在这种情况下，对单自由度结构，材料阻尼值等于ξ/πf或c/k。
ABAQUS 计算 动刚度 详细说明
F(ω)=F0×sin(ωt) 输入激励力当使用abaqus-steady-state daynmics modal，其中20-1000即为激励力的最低频率和最高频率。
开始模态和结束模态要覆盖上图所示的激励力的最低频率和最高频率，选择直接阻尼，即每阶模态的临界阻尼比3%，（典型的取值范围在1%-10%）Ma+cv+kx= F0×sin(ωt)其中F0是固定的数值（简谐力的幅值），且频率由20Hz 变化到1000Hz 。
f ••=πω2位移阻抗（动刚度）：()()()ωωωx F K =()()t F F ωωsin 0•= 为输入激励力，是一个谐波输入。
()()θωω+•=t x x sin 0 为输出稳态位移响应，根据振动理论，稳态位移响应的频率与输入激励力的频率相同，振幅 0x 和相位角θ均取决与系统本身的物理性质（质量，弹簧刚度，阻尼）和激振力的性质（频率与振幅），而与初始条件无关，初始条件仅影响系统的瞬态响应的振幅和初始相位角。
()ωK ，表示，在某频率下，产生单位位移振幅所需要的激振力幅值。
实际情况下，频率不同，刚度也不同。
假设()ωK =10N/m ，及动刚度在任意频率都是固定的，不随频率的变化而变化（理想情况），即在任意频率激振下，产生1m 单位位移振幅所需要的激振力幅值为10N 。
假设()ωF 的幅值为1 ，()ωK =10N/m()ωx 的幅值x=()()ωωK F =101特点：位移响应的幅值与频率没有关系，且是固定值。
由于在abaqus 中可方便的输出某个点的位移，速度，加速度。
所以通常以某个点的位移，速度，加速度来表征动刚度的大小。
速度阻抗：()()()ωωω•=x F Z 如何将速度阻抗：()()()ωωω•=x F Z 与位移阻抗（动刚度）：()()()ωωωx F K =联系起来？用速度表示： ()ω•x = ()ωx 的导数=()θω+•t x sin 0的导数=()'sin 0θωω+••t x =()ωωx •（我们只要幅值，忽略相位角）响应速度与响应位移幅值相差ω，相位角不同，频率相同。
什么是动刚度
什么是动刚度在NVH领域，经常计算或测试动刚度，像悬置动刚度、支架动刚度、车身接附点动刚度等等。
那什么是动刚度，动刚度的大小对结构有什么影响本文主要内容包括：1.??? 静刚度；2.??? 单自由度动刚度；3.??? 多自由度动刚度；4.??? 原点动刚度；5.??? 悬置动刚度；6.??? 支架动刚度；7.??? 怎么测量动刚度；?刚度是指结构或材料抵抗变形的能力。
由于结构或材料所受荷载的不同，可能受到静载荷或动载荷，因此，刚度又分为静刚度和动刚度。
当结构或材料受到静载荷时，抵抗静载荷下的变形能力称为静刚度；当受到动载荷时，抵抗动载荷下的变形能力称为动刚度。
故，结构或材料既有静刚度又有动刚度。
?相对而言，在NVH领域，结构或材料受到动载荷的概率远大于静载荷，因此，更普遍关心动刚度。
在之前文章《什么是频响函数FRF》中也提到用加速度与力之比的频响函数和用力与位移之比的动刚度应用更为广泛。
1.静刚度在讲述动刚度之前，有必要先了解静刚度。
静刚度用单值即可表示，不随频率变化。
由于静载荷引起的变形又分为弯曲或扭转等，因此，刚度又分为抗弯刚度和抗扭刚度，材料的刚度计算可参考材料力学教科书。
?在这以弹簧为例说明静刚度，当弹簧受到静力F时，其静态伸长量为X，此时F=kX，k为弹簧的静刚度。
单位为N/mm，表示每增加1mm需要的拉力大小。
?弹簧静刚度常数跟材料的杨氏模量、线径、中径和有效圈数有关。
当拉力越来越大时，弹簧的伸长量也增大，如下图所示，但二者满足线性关系。
红色曲线表示的斜率即为弹簧静刚度。
注：以下所说到的刚度，如没有特殊说明，都是指的动刚度。
2. 单自由度动刚度在文章《什么是频率函数FRF》中，我们已经明白了频响函数可以用位移/力表示，当用力/位移时，表示的是动刚度。
对于单自由度系统，如下图所示，我们再回顾一下用位移表征的FRF表达式而动刚度为力与位移之比，则从上式可以看出动刚度：1）??????? 复值函数；2）??????? 随频率变化；3）??????? 与系统的质量、阻尼和静刚度有关；4）??????? 当频率等于0时，动刚度等于静刚度；?让我们再回想一下单自由度系统的FRF区域及性质同理，单自由度系统的动刚度曲线也有类似性质在低频段，动刚度接近静刚度，幅值是k，表明共振频率以下的频率段主要用占主导地位的刚度项来描述。
滑动轴承刚度和阻尼计算的fluent udf
滑动轴承刚度和阻尼计算的fluent udf序滑动轴承在工程领域中扮演着重要的角色，它们常常被用于支撑旋转机械设备，并承受高速旋转下的摩擦和载荷。
而对于滑动轴承的设计和优化，则需要了解其刚度和阻尼等重要参数。
本文将探讨在使用Fluent UDF进行滑动轴承刚度和阻尼计算的过程，希望能为工程师们提供一些有价值的指导。
一、滑动轴承的作用和重要性1. 滑动轴承的定义和原理在工程应用中，滑动轴承是一种通过壁压力维持摩擦阻力的设备，用于支撑和定位旋转机械部件。
其基本原理是通过摩擦力和表面压力来支撑和限制轴的运动，从而减少磨损和能量损失。
2. 滑动轴承的重要性滑动轴承作为机械设备中的关键部件，其性能对于整个机械系统的安全性和稳定性有着重要的影响。
了解滑动轴承的刚度和阻尼等参数，对于提高机械设备的运行效率和使用寿命具有重要意义。
二、使用Fluent UDF进行滑动轴承刚度和阻尼计算的步骤1. Fluent UDF的介绍Fluent UDF是用于Fluent软件的用户定义函数，它可以通过编程的方式对流体流动、传热和化学反应等进行定制化处理。
在滑动轴承的刚度和阻尼计算中，可以通过编写Fluent UDF来实现定制化的计算和分析。
2. 刚度和阻尼的定义在进行滑动轴承刚度和阻尼的计算之前，首先需要了解其定义。
滑动轴承的刚度可以理解为其在受力作用下的变形能力，而阻尼则是指其在受到外界振动或冲击时的能量消耗能力。
3. Fluent UDF的编写在使用Fluent UDF进行滑动轴承刚度和阻尼计算时，需要编写相应的函数来描述滑动轴承在不同工况下的力学特性。
这包括了材料特性、载荷情况、流体力学等方面的计算和分析。
4. 数据采集和分析通过编写好的Fluent UDF，可以对滑动轴承在不同工况下的刚度和阻尼进行计算和分析。
这需要对液压力、位移变形等参数进行实时监测和数据采集，然后进行相应的分析和处理。
三、对滑动轴承刚度和阻尼计算的个人观点和理解1. 刚度和阻尼对于滑动轴承的重要性在滑动轴承的设计和优化过程中，刚度和阻尼是需要重点考虑的参数。
多层质量-弹簧-阻尼结构刚度计算
多层质量-弹簧-阻尼结构刚度计算下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。
文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!多层质量弹簧阻尼结构刚度计算1. 引言在工程领域中，多层质量弹簧阻尼结构是一种常见的振动控制系统。
一般多层钢结构抗震计算的阻尼比
一般多层钢结构抗震计算的阻尼比大家好，我今天要和大家聊一聊关于一般多层钢结构抗震计算的阻尼比的问题。
我们要明白什么是阻尼比，它在钢结构抗震计算中起到了什么作用。
阻尼比是衡量结构在地震作用下抵抗振动的能力的一个重要参数。
简单来说，阻尼比越大，结构在地震中的振动越小，越能保证结构的安全性。
那么，如何计算阻尼比呢？接下来，我将从三个方面来详细介绍。
一、阻尼比的计算方法1.1 基本原理阻尼比的计算方法主要有两种：一种是基于结构的动力响应分析，另一种是基于结构的静力性能分析。
这两种方法各有优缺点，但都可以得到相对准确的阻尼比结果。
在这里，我们主要介绍基于动力响应分析的方法。
1.2 动力响应分析法动力响应分析法主要是通过对结构在地震作用下的动力响应进行分析，得到阻尼比。
具体步骤如下：(1)建立结构动力学模型，包括结构的几何形状、质量分布、刚度矩阵等。
(2)输入地震作用下的激励信号，如地震波。
(3)计算结构的动力响应，如加速度、位移等。
(4)根据动力响应结果，采用适当的数学模型(如双线性模型、多体动力学模型等)计算阻尼比。
二、阻尼比的影响因素2.1 结构参数结构参数对阻尼比的影响主要体现在两个方面：一是刚度，刚度越大，结构在地震中的振动越小，阻尼比越大；二是质量分布，质量分布不均匀会导致结构在地震中的振动增大，阻尼比减小。
因此，在计算阻尼比时，需要充分考虑结构参数的影响。
2.2 地震动特性地震动特性是指地震动的幅值、频率等特性。
不同的地震动特性会对结构的阻尼比产生不同的影响。
例如，当地震动的幅值较大时，结构的振动也会较大，阻尼比会减小；反之，当地震动的幅值较小时，结构的振动也会较小，阻尼比会增大。
因此，在计算阻尼比时，需要考虑地震动特性的影响。
三、阻尼比的应用与优化3.1 应用阻尼比在钢结构抗震设计中有广泛的应用，如在建筑结构、桥梁结构等的设计中都需要考虑阻尼比的问题。
通过合理的阻尼比设计，可以提高结构的抗震性能，降低地震灾害的风险。
什么是动刚度
什么是动刚度同理，单自由度系统的动刚度曲线也有类似性质在低频段，动刚度接近静刚度，幅值是k，表明共振频率以下的频率段主要用占主导地位的刚度项来描述。
如果作用在系统的外力变化很慢，即外力变化的频率远小于结构的固有频率时，可以认为动刚度和静刚度基本相同。
在高频段，动刚度的幅值为ω2m，表明共振频率以上的频率段主要用占主导地位的质量项来描述，这是因为质量在高频振动中，产生很大的惯性阻力。
当外力的频率远大于结构的固有频率时，结构则不容易变形，即变形较小，此时结构的动刚度相对较大，也就是抵抗变形的能力强。
在共振频率处动刚度的幅值下降明显，其幅值为ωc，表明在共振频率处主要受阻尼控制。
而在共振频率处，我们知道，结构很容易被外界激励起来，结构的变形最大，因而结构抵抗变形的能力最小，也就是动刚度最小。
3. 多自由度动刚度单自由度系统是基础，但现实世界中的系统大多数都是多自由度系统，因此，我们测量出来的动刚度也是多自由度的动刚度。
下图为多自由度系统的同一位置的加速度频响函数（加速度导纳）和该点的动刚度曲线。
多自由度系统的驱动点FRF存在多个共振峰和反共振峰，在共振峰处，对结构施加很小的激励能量，结构就会产生非常大的振动（变形），因而在共振峰处，结构很容易被激励起来，结构的变形大，抵抗变形的能力弱，也就是动刚度小。
在反共振峰所对应的频率处进行激励，即使激励能量再大，结构也没有响应或者响应很微弱，也就是说在反共振峰所对应的频率处，结构很难被激励起来，结构的变形小，抵抗变形的能力强，因此，动刚度大。
从上图可以看出，频响函数共振峰对应的是动刚度曲线的极小值，也就是说频响函数幅值大的频率处，动刚度小。
在反共振峰处，动刚度大，二者刚好相反。
4. 原点动刚度原点动刚度IPI（Input Point Inertance，IPI）：概念上类似原点（或称作驱动点）频响函数，指的是同一位置、同一方向上的激励力与位移之比，主要测量与车身接附点处的原点动刚度，比如车身与发动机悬置、副车架、悬架连接处、排气挂钩处等位置的局部动刚度，考虑的是在所关注的频率范围内该接附点局部区域的刚度水平，过低必须引起更大的噪声，因此，该性能指标对整车的NVH性能有较大的影响。
起重机的动刚度及其测试方法
的单自由度系统 (如图 1 所示) ,其动刚度 KD 可以 表示为 :
KD = K〔(1 - λ2) + 2 ξi λ〕
(1)
式中 K ———系统的静刚度
ξ———阻尼比
ξ= C/ (2 mωn) C ———阻尼系数
m ———系统质量 ωn ———系统固有频率 ωn = K/ m = 2πf n
f n ———结构的自振频率 λ———频率比
实测时 ,为了快速 、准确地得到起重机动刚度 , 主要采用以下两种方法 :
起重机在起吊 、卸载以及突然起制动过程中 ,均 会引起冲击动载 ,使其产生一定振幅和一定时间的 衰减振动 。起重机对动刚度的要求主要是为了控制
由于冲击动载所引起的振幅和振动的衰减时间 。由
于起重机结构 、材质等因素的不同 ,阻尼比在一个较 大范围内进行变化 ,而且难以进行理论估计 ,这就给 直接计算动刚度带来了困难 。
参 考 文 献 1 起重机设计手册 1 北京 :机械工业出版社 ,19801 2 张阿舟 1 振动控制工程 1 宇航出版社 ,19891 3 机械工程手册 1 北京 :机械工业出版社 ,19781 4 500t/ 300t/ 40t 双向门式起重机测试报告 1 太原重型机
械研究所 ,19891
图 1 受简谐激振力的单自由度系统 图 2 单自由度系统的动刚度曲线
4 结束语
该微机监控系统在建设部长沙机械研究院设计 的 Q TZ2800 型塔式起重机上作了现场试验 ,结果证 明该微机电控系统工作稳定 、可靠 ,抗干扰能力强 , 功能强大 ,司机可以通过液晶屏随时掌握塔式起重 机的工作参数 ,起吊重物的自动就位误差小于 10cm ,各项功能达到了设计要求 。
由于 k = mω2n ,ωn = 2πf n ,则式 (4) 可变为