多尺度耦合系统的簇发振荡机制及控制
多尺度耦合理论

何国威、白以龙中国科学院力学研究所,非线性力学国家重点实验室多尺度力学是当代科学技术发展的需求和前沿。
在生物科学,材料科学,化学科学和流体力学中,许多重要问题的本质都表现为多尺度,它们涉及从分子尺度到连续介质尺度上不同物理机制的耦合和关联。
例如,在生物和化学科学里,在分子尺度上的不同性态产生了生物体尺度上的复杂现象;在固体破坏中,不同尺度的微损伤相互作用产生更大尺度上的裂纹导致材料破坏;在流体力学中,不同时空尺度的涡相互作用构成复杂的流动图案。
这些问题的共同特点是不同尺度上物理机制的耦合和关联。
只考虑单个尺度上某个物理机制,不可能描述整个系统的复杂现象。
因此,多尺度力学的核心问题是多过程耦合和跨尺度关联。
多尺度力学是传统的针对多尺度问题研究的发展,但有着本质的不同。
它们都研究不能通过解耦进行求解的多尺度耦合问题。
但是,传统的多尺度问题具有相似性或弱耦合,即:不同尺度上的物理过程具有相似性,因此我们可以求相似解;或者,不同尺度上的物理过程具有弱耦合,因此我们可以采用平均法求解。
然而,多尺度力学的研究对象具有多样性和强耦合,即:不同尺度上的物理过程既不具有相似性,耦合也不再是弱的了。
因此,传统的相似解和平均法对多尺度力学的问题都不适用。
动力系统理论和统计力学为多尺度现象的研究提供了基本方法。
在一个给定尺度上的物理过程可以用动力学方程描述,而动力学方程的建立主要依赖于经典力学和量子力学。
问题的关键在于不同尺度上物理过程的相互耦合。
如果可以忽略耦合,单个尺度上的物理过程完全可以由经典力学或量子力学描述,剩下的就是类似于解方程那样的认识过程,原则上并不是什么困难的事情。
在平衡态统计物理里,不同尺度之间物理过程耦合的基本假设是基于等概率原理的统计平均。
但是,大多数多尺度问题涉及统计力学中非平衡态的非线性演化过程,不同的尺度之间存在强耦合或敏感耦合,不能简单地采用绝热近似、统计平均以及微扰等方法处理,而必须将不同尺度耦合求解。
余维三fold-fold-Hopf分岔下簇发振荡及其分类

A b s t r a c t T h e d y n a m i c a l s y s t e m s w i t h the c o u p l i n g o f different scales o b s e r v e d w i d l y in e n g i n e e r i n g p r o b l e m s o f , - ten b e h a v e in t he b u r s t i n g oscilltions c h a r a c t e r i z e d b y th e alternations b e t w e e n l a r g e - a m p l i t u d e oscilltations a n d s m a l l , a m p l i t u d e oscillations t h e g e n e r a t i o n m e c h a n i s m o f w h i c h h a s b e e n o n e o f th e h o t topi c s in n o n l i n e a r s c i e n c e at h o m e . a n d a b r o a d T h e traditional g e o m e t r i c p e r t u b a t i o n m e t h o d c a n b e e m p l o y e d to e x p l o r e t h e m e c h a n i s m o f the oscillations , o n l y in the s y s t e m s w i t h t w o s c ales in t i m e d o m a i n w h i c h c a n n o t b e directly u s e d to investigate t he interaction b e t w e e n
【国家自然科学基金】_routh-hurwitz判据_基金支持热词逐年推荐_【万方软件创新助手】_20140802

科研热词 阈值 竞争系统 渐近稳定性 数学模型 传染病
推荐指数 1 1 1 1 1
2009年 序号
科研热词 1 连续接种免疫 2 稳定性 3 seir模型
推荐指数 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
科研热词 虚拟阻抗 稳定性 直接电流控制 滤波器 并网逆变器 routh-hurwitz判据 频率捕获 谣言传播 自同步运动 系统稳定性 系统动力学 混沌控制 改良的线性反馈法 振动机 振动同步传动 可调半径的极限环 分数阶耦合发电机系统 routh数列 lyapunov函数
科研热词 稳定性分析 阻尼系数 速度自适应律 自适应全阶观测器 线性负反馈法控制 直接输出电流控制 病虫害 生态流行病模型 混沌 浮环轴承 森林 标准传染率 极限环 无速度传感器 接口 强身型 异步电机 并网逆变器 局部渐近稳定 发电状态 刚度系数 全局稳定 全局渐近稳定 供油压力 仿真 临界阈值 临界质量 lcl
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
2011年 科研热词 稳定性 hopf分岔 时滞反馈控制 washout滤波器 耦合系统 罗斯-霍维兹判据 缩阶反同步 窗口更新周期 特殊矩阵构造 改进的主动控制 控制器 惯性神经网络 广义投影同步 参数选择 单模激光lorenz系统 三次非线性 r(o)ssler系统 normalform normal form duffing系统 推荐指数 3 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
双频激励下Filippov系统的非光滑簇发振荡机理

双频激励下Filippov系统的非光滑簇发振荡机理曲子芳;张正娣;彭淼;毕勤胜【摘要】旨在揭示含双频周期激励的不同尺度Filippov系统的非光滑簇发振荡模式及分岔机制.以Duffing和Van der Pol耦合振子作为动力系统模型,引入周期变化的双频激励项,当两激励频率与固有频率存在量级差时,将两周期激励项表示为可以作为一慢变参数的单一周期激励项的代数表达式,给出了当保持外部激励频率不变,改变参数激励频率的情况下,快子系统随慢变参数变化的平衡曲线及因系统出现的fold分岔或Hopf分岔导致的系统分岔行为的演化机制.结合转换相图和由Hopf分岔产生稳定极限环的演化过程,得到了由慢变参数确定的同宿分岔、多滑分岔的临界情形及因慢变参数改变而出现的混合振荡模式,并详细阐述了系统的簇发振荡机制和非光滑动力学行为特性.通过对比两种不同情形下的平衡曲线及分岔图,指出虽然系统有相似的平衡曲线结构,却因参数激励频率取值的不同,致使平衡曲线发生了更多的曲折,对应的极值点的个数也有所改变,并通过数值模拟,对结果进行了验证.【期刊名称】《力学学报》【年(卷),期】2018(050)005【总页数】11页(P1145-1155)【关键词】多频激励;Filippov系统;簇发振荡;多滑分岔【作者】曲子芳;张正娣;彭淼;毕勤胜【作者单位】江苏大学理学院,江苏镇江212013;山东工商学院数学与信息科学学院,山东烟台264005;江苏大学理学院,江苏镇江212013;江苏大学理学院,江苏镇江212013;江苏大学土木工程与力学学院,江苏镇江212013【正文语种】中文【中图分类】O322引言非光滑动力系统因其在模拟各种物理和工程技术系统方面表现出强大的功能而备受关注.带有摩擦的机械系统、步行机器人系统、基因调控网络系统、电子变换器系统等皆因非光滑因素的存在而表现出不同的动力学行为[1-3].通常,系统相空间可被划分为若干个与系统向量场的不同功能形式相关联的区域.当系统的部分轨线在相空间的不同区域之间的边界相切时,系统的轨迹会发生一系列奇特的变化[4].由于轨线与分界面接触点的不同特性和系统向量场的特点,当系统参数变化时轨线可能发生的滑动、转迁、穿越、黏滞等多种非线性现象会频繁出现[5-9].在分段光滑系统中同样有非光滑特性体现,如系统在转换边界平衡点发生的分岔行为,极限环经历的擦边和滑动分岔等[10]及线性碰振系统周期解的擦边分岔[11].在自然科学和工程实践中,非线性系统的动力学行为不仅仅是各子系统行为的简单叠加,而是一定数量的子系统耦合而成,即由子系统层面的动力学行为到整个系统层面的动力学行为的演变,于是多尺度耦合现象应运而生[12-15].通常所讲的两尺度耦合,指的是由于含不同时间尺度的对象,导致在无量纲数学模型中,状态变量或其不同形式的组合可以分为两个不同的组,而各组之间随时间变化的速率存在着明显量级上的差异[16-20].在对两个或多个单向的或双向振荡器的耦合现象的研究基础上,可深入地了解系统中的相互同步、准周期振荡、混沌等现象的产生机制[21-24].目前,针对多尺度耦合系统的研究,国内外学者大都遵循着耦合系统的模型分析、近似求解、数值模拟和实验分析等环节进行[25-27],研究方法缺乏针对性,而直到Izhikevich[28]快慢分析法的提出,才使研究方法得以丰富,并能深入地分析各种动力学行为的演化机制,其主旨是将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理.虽然含一个慢变周期参数的系统的周期簇发振荡分析已有诸多成果[29-30],但由于实际系统中往往存在着多种激励共存的现象,因此含多频激励的系统的动力学行为分析也激起了学者们浓厚的兴趣,特别是含参数激励和外部激励共同作用的系统表现出了更为丰富和神奇的周期簇发振荡等动力学行为[31].尽管分别关于非光滑系统,多尺度耦合系统,含多频激励的系统都有各自针对性的研究成果,但对于含两个慢变周期参数的非光滑耦合系统的簇发振荡分析却仍有进一步的研究空间.本文以Duffing和VanderPol耦合振子为例,研究了含两慢变激励的具有非光滑向量场的Filippov系统的簇发振荡模式及非光滑行为演化机制.给出了平衡曲线和分岔图及在非光滑边界产生非光滑行为的演化行为分析;结合转换相图,得到了在外部激励频率不变的情况下,参数激励频率改变引起的系统簇发振荡模式及非光滑演化行为机理;通过数值模拟,分析了平衡曲线在不同参数激励频率下发生的曲折变化情况.1 计算模型以Duffing和Van der Pol耦合振子为例,引入一个双边二极管作为调和开关,考虑含双频激励的具非光滑向量场的Filippov系统,无量纲化后的数学模型为其中w1=A1cos(Ω1τ)为外部激励项,w2=A2cos(Ω2τ)为参数激励项,A1,A2表示振幅,Ω1,Ω2表示频率,α1,α2,α3,µ是常系数,ξ代表两子系统的耦合强度.以δsgnx1定义的非光滑分界面Σ={(x1,y1,x2,y2)|x1=0}按照两个非自治光滑子系统F+和F−将向量场分为两个光滑区域,分别以D+和D−表示在应用快慢分析法分析含双频激励的系统的簇发振荡时,考虑各激励间并非相互独立,往往以一个激励项作为慢变参数,其他激励项表示为该慢变参数的函数表达式的方法进行分析讨论.这里保持Ω1=0.0005不变,改变Ω2的值,其他参数取常规量,此时两激励频率与系统的固有频率之间存在了量级差,于是产生了尺度效应,即不同频域尺度之间的耦合,导致簇发等特殊的振荡模式.2 分岔分析系统(1)中各状态变量振荡行为主要由系统的固有频率ω决定,然而,ω同时又受到外部激励项w1和参数激励项w2的调制.就外部激励项w1而言,对一任意周期TN,定义TN=2π/ω,有t∈[t0,t0+TN],外部激励项w1将在wA=Acos(Ωt0)和wB=Acos(Ωt0+2πΩ/ω)之间变化.而Ω1≪ϖ意味着0<Ω1/ω=1,因此有wA≈wB.这意味着在一相应周期内,外部激励项几乎为一常数.同理可得:参数激励项也几乎为一常数.根据上述分析,相对于状态变量而言,由于整个外部激励项w1和参数激励项w2在更慢的时间尺度上变化,因此可以视w1和w2为慢变参数,而又因为外激频率Ω1和参激频率Ω2存在共振关系,这里假设W=cos(Ω1τ)=cos(0.0005τ),外部激励可表示为w1=A1cos(Ω1τ)=A1W,参数激励表示为w2=A2cos(Ω2τ)=A2fi(W)(i=1,2). 于是实际上可以将W看作一个慢变参数,此时这里的w1和w2仅是普通参数,而不再具有w1=A1cos(Ω1τ)和w2=A2cos(Ω2τ)的形式.此时称含慢变参数W 的系统(1)为广义自治系统.即整个系统(1)可视为快慢两个系统的耦合.快子系统为其中,当Ω1=0.0005,Ω2=0.002时,当Ω1=0.0005,Ω2=0.003时,慢子系统为W=cos(0.0005τ).为揭示快慢耦合系统复杂行为的产生机制,首先分析快子系统(2)的分岔行为.由于系统(1)为广义自治系统,其中的参数w1和w2此时已是普通参数,于是可以看作是一个自治系统[30].根据快慢分析法[28],系统(1)由快子系统(2)和慢子系统耦合而成,所以系统(2)也是一个自治系统.于是可以求出平衡点为:当x0>0时,平衡点可表示为其中x0满足当x0<0时,平衡点为其中x0满足平衡点的稳定性可通过其特征方程表征,表示为其中当参数满足时,平衡点EQ±是稳定的.当参数满足a4=0(a1>0,a1a2−a3>0,a3>0),即系统可能会发生fold分岔,导致不同平衡点之间的跳跃现象.根据系统可能会发生Hopf分岔的判定条件,具体到系统(2),三个判定条件列举如下: (I)分岔条件(II)非退化条件快子系统(2)可以改写为1=Jx+F(x),x∈R4,其中,J是雅可比矩阵,可以表示为其中,JT是雅可比矩阵 J 的转置矩阵,⟨·,·⟨是 R4中的标准内积.F(x)=O(∥x∥2)是一个光滑函数,在x=0附近,其Taylor展开为式中B(x,y)和C(x,y,z)是多重线性函数,在坐标下的分量为通过matcont软件可以验证其中(III)横截性条件讨论当Ω1=0.0005,Ω2=0.002时的情形,当Ω1=0.0005,Ω2=0.003时可类似讨论. 对特征方程(7)两边关于W求偏导,得将代入式(9)并令λ=iω,得整理式(10)并分离的实部,得将参数赋值后可以判定得出证明系统会出现Hopf分岔,平衡点可能会因Hopf分岔而失稳.3 数值模拟固定参数α1=8,α2=1,α3=1,ξ=0.7,µ=0.2,δ=−1,讨论当双频激励振幅及外激频率不变,参激频率改变的情况下,系统出现的不同周期簇发振荡模式和轨线与非光滑分界面接触后发生的特殊非光滑动力学行为.主要阐述:(1)Ω1=0.0005,Ω2=0.002;(2)Ω1=0.0005,Ω2=0.003.两种情形下系统周期簇发振荡的产生机制与非光滑行为演化分析.3.1 Ω1=0.0005,Ω2=0.002时簇发振荡机理分析固定振幅 A1=7,A2=3,取Ω1=0.0005,Ω2=0.002.通过数值模拟研究系统所可能发生的各种簇发振荡模式和非光滑演变行为.图1和图2分别给出了系统在(x1,y1)平面上的相图和x1的时间历程图.图1 Ω1=0.0005,Ω2=0.002时(x1,y1)平面上相图Fig.1 Phase portrait onthe(x1,y1)plane for Ω1=0.0005,Ω2=0.002图2 Ω1=0.0005,Ω2=0.002时 x1的时间历程图Fig.2 Time history of x1forΩ1=0.0005,Ω2=0.002如图1所示,根据非光滑分界面Σ,系统向量场被划分为两个光滑的子区域D+和D−,轨线在分界面Σ和子区域D+,D−中都表现出了丰富的非光滑动力学行为.轨线或在分界面发生滑动,或穿过分界面在两子区域D+和D−间来回往返,表现为大幅振荡和微幅振荡的交替出现,即系统在沉寂态和激发态之间来回转化,呈现为簇发振荡.为揭示系统周期簇发振荡的演化机制,我们给出了系统随慢变参数W变化的平衡曲线及分岔图,如图3所示.如平衡曲线及分岔图3中所示,系统的平衡曲线被4个超临界Hopf分岔点HB±1(W,x1)=(±1.0686,±0.4282),HB±2(W,x1)=(±0.2529,±0.4270)及曲线与分界面的2个交点N1(W,x1)=(−0.1467,0)和N2(W,x1)=(−0.1467,0)分成7部分.实线代表稳定的平衡曲线,虚线代表不稳定的平衡曲线.运用微分包含理论,引入辅助参数q,以F表示系统(1),于是系统(1)可改写为其中辅助参数q可表示为式中,ys,Ws分别表示当轨线接触到非光滑分界面时状态变量y和慢变参数W的值.由于非光滑分界面的非线性动力学特性,结合微分包含理论,系统的平衡曲线中出现了一段Σ-平衡点曲线EB0,如图3所示.在(W,x1)平面上的转换相图与平衡曲线及相关分岔图的叠加能更好地诠释系统周期簇发振荡机制,如图4和图5所示.可以发现,在一个周期的簇发振荡中,轨线出现了多个激发态和沉寂态,且轨线在不同激发态之间转迁时多次接触分界面,或发生滑动行为,或进入另一子区域,如此在两子区域D+和D−中多次往返并表现出特殊的振荡模式.图3 Ω1=0.0005,Ω2=0.002时平衡曲线及分岔图Fig.3 Equilibrium branches as well as the bifurcations fo rΩ1=0.0005,Ω2=0.002图4 Ω1=0.0005,Ω2=0.002时(W,x1)平面转换相图Fig.4 Transformed phase portrait on the(W,x1)plane forΩ1=0.0005,Ω2=0.002图5 Ω1=0.0005,Ω2=0.002时转换相图与平衡曲线的叠加图Fig.5 Overlap of equilibrium branches and transformed phase portrait on the(W,x1)forΩ1=0.0005,Ω2=0.002通过转换相图与平衡曲线及相关分岔图的叠加图5阐述系统周期簇发振荡机制.不失一般性,假设轨线从子区域D−中W取最小值W=−1处出发,之后轨线几乎严格沿焦点型稳定平衡曲线EB−2运动,表现为沉寂态QS1,当轨线穿越Hopf分岔点HB−2(W,x1)=(−0.2529,−0.4270)时,Hopf分岔出现,平衡点失稳,产生稳定的极限环LC.由于极限环LC在随着慢变参数W变化的过程中会与非光滑分界面有接触,因而受到非光滑因素的影响,轨线的振荡结构会发生明显的变化.为更好地展现轨线在光滑区域的振荡形式及接触到分界面后发生的簇发振荡行为.图6∼图9给出了因Hopf分岔产生的不同慢变参数情形下的稳定极限环的演变过程.当W=−0.2529时,超临界 Hopf分岔点HB−2(W,x1)=(−0.2529,−0.4270)出现,产生了围绕位于平衡线EB−3的不稳定焦点振荡的极限环LC.图6给出了对应于慢变参数W=−0.2529的极限环,可以发现,其在围绕平衡曲线HB−3逆时针振荡的过程中完全处于光滑区域D−,并未接触非光滑分界面Σ.随着慢变参数W的增大,极限环LC的振幅在光滑区域D−内逐渐增加.当慢变参数W增大到W=−0.2476时,极限环在P1(x1,y1)=(0,0.6847)点接触到非光滑分界面,然后沿向上箭头方向在分界面上开始滑动,经过一段时间滑动到点P2(x1,y1)=(0,0.9857)后,又沿向下箭头方向运动到点P3(x1,y1)=(0,1.6601),之后离开分界面Σ,即表现为从光滑区域D−进入分界面滑动一段时间之后,然后脱离分界面,后又再次返回光滑区域D−继续运行.所以,慢变参数W=−0.2476对应着Filippov型广义自治系统的同宿分岔.当慢变参数增加至W=−0.1650时,极限环LC从位于分界面上的P1(x1,y1)=(0,0.1066)点进入分界面后沿向上箭头方向滑动到P2(x1,y1)=(0,1.9943)点,之后立刻穿过分界面Σ进入光滑区域D+,然后继续在区域D+短暂运动后又于P3(x1,y1)=(0,2.1560)点返回到分界面,沿分界面按向下箭头方向继续滑动到位于分界面上的P4(x1,y1)=(0,0.5775)点,继而返回到区域D−继续运动.所以,慢变参数W=−0.1650对应着Filippov型广义自治系统的非常规分岔——多滑分岔[32].图9给出的是W=0时轨线呈现的一种对称的振荡模式.极限环仍然是在P1(x1,y1)=(0,−1.0336)点接触到分界面后沿向上箭头方向滑动到P2(x1,y1)=(0,1.0336)点,然后立刻穿过分界面Σ进入光滑区域D+,在区域D+内进行大幅振荡后于P3(x1,y1)=(0,0.6990)点再次进入分界面,继续按向下箭头方向滑动到P4(x1,y1)=(0,−0.6990)点,之后进入区域D−开始大幅振荡.在区域D+和D−内轨线表现为对称的簇发振荡.图6 W=−0.2529时的稳定极限环Fig.6 Stable limit c ycle with W=−0.2529图7 W=−0.2476时的稳定极限环Fig.7 Stable limit cycle with W=−0.2476图8 W=−0.1650时的稳定极限环Fig.8 Stable limit cycle with W=−0.1650图9 W=0时的稳定极限环Fig.9 Stable limit cycle with W=0W值随时间继续增大,轨线振荡幅值逐渐减小,当W增大到最大值W=1时,轨线收敛到平衡曲线EB+2.之后,W的值将开始逐渐减小,轨线几乎严格沿稳定的平衡曲线EB+2运动,表现为沉寂态 QS2,直到遇到Hopf分岔点HB+2(W,x1)=(0.2529,0.4270),再次出现 Hopf分岔,仍然产生稳定的极限环,呈现出与由HB−2(W,x1)=(0.2529,0.4270)产生的极限环LC在不同参数下的相似且对称的演化状态,此时轨线处于激发态.随着W值继续减小,轨线振荡幅值逐渐减小,当W减小到最小值W=−1时,轨线收敛到平衡曲线EB−2.至此,轨线完成一个周期的簇发振荡.3.2 Ω1=0.0005,Ω2=0.003时簇发振荡机理分析固定振幅A1=7,A2=3,取Ω1=0.0005,Ω2=0.003.通过数值模拟研究系统所可能发生的各种簇发振荡模式以及非光滑演变行为.图10和图11分别给出了系统在(x1,y1)平面的相图和x1的时间历程图.图10 Ω1=0.0005,Ω2=0.003时(x1,y1)平面上相图Fig.10 Phase portrait on the(x1,y1)plane for Ω1=0.0005,Ω2=0.003图11 Ω1=0.0005,Ω2=0.003时x1的时间历程图Fig.11 Time history of x1for Ω1=0.0005,Ω2=0.003为揭示系统周期簇发振荡的演化机制,我们仍然给出了系统随慢变参数W变化的平衡曲线及分岔图,在(W,x1)平面上的转换相图,在(W,x1)平面上的转换相图与平衡曲线的叠加图,如图12∼图14所示.同时图15∼图18给出了在(W,x1)平面上转换相图的局部放大图.如平衡曲线及分岔图12中所示,系统的平衡曲线被2个超临界Hopf分岔点HB±1(W,x1)=(±1.0285,±0.4282),2 个 fold 分岔点FB±1(W,x1)=(±0.1874,±0.3821)和曲线与分界面的 2个交点N1(W,x1)=(−0.1467,0)和 N2(W,x1)=(0.1467,0)分成7部分.实线代表稳定的平衡曲线,虚线代表不稳定的平衡曲线.对比Ω1:Ω2=1:4时,平衡曲线发生了多次曲折,对应极值点的个数也由2个变为6个.从(W,x1)平面上的转换相图与平衡曲线的叠加图14看出,在一个周期的簇发振荡中,轨线出现了2个激发态SP±i(i=1,2)和2个沉寂态QS±i(i=1,2).轨线在不同激发态之间转迁时会接触到分界面,沿分界面滑动之后,进入另一区域发生簇发振荡现象,并经一段时间之后又返回分界面,回到之前所在区域,如此在两子区域D+和D−中往返并表现为簇发振荡.图12 Ω1=0.0005,Ω2=0.003时平衡曲线及分岔图Fig.12 Equilibrium branches as well as the bifurcations forΩ1=0.0005,Ω2=0.003图13 Ω1=0.0005,Ω2=0.003时(W,x1)平面上转换相图Fig.13 Transformed phase portrait on the(W,x1)plane forΩ1=0.0005,Ω2=0.003图14 Ω1=0.0005,Ω2=0.003时转换相图与平衡曲线的叠加图Fig.14 Overlap of equilibrium branches and transformed phase portrait on the(W,x1)forΩ1=0.0005,Ω2=0.003图15 Ω1=0.0005,Ω2=0.003 时 (W,x1)平面上的转换相图的局部放大图1Fig.15 Locally enlarged part one of the transformed phase portrait onthe(W,x1)for Ω1=0.0005,Ω2=0.003图16 Ω1=0.0005,Ω2=0.003 时 (W,x1)平面上的转换相图的局部放大图2Fig.16 Locally enlarged part two of the transformed phase portrait onthe(W,x1)for Ω1=0.0005,Ω2=0.003不失一般性,假设轨线从子区域D−中W取最小值W=−1处出发,之后轨线几乎严格沿焦点型稳定平衡曲线EB−2运动,表现为沉寂态Q S−1,直到轨线抵达 fold分岔点FB−1(W,x1)=(0.1874,−0.3821),fold分岔出现导致轨线开始跳跃,使得轨线表现为激发态SP−1,在PS1(W,x1)=(0.1909,0)点 (如图 10)到达分界面,滑动至点PS2(W,x1)=(0.1918,0)后穿过分界面,到达区域D+后轨线继续大幅振荡,表现为激发态SP+1.随着W值的增大,振荡幅值逐渐减小,当W增大到最大值W=1时,轨线收敛到平衡曲线EB+2.随着时间的延长,W值将逐渐减小,轨线几乎严格沿稳定的平衡曲线EB+2运动,表现为沉寂态QS+1,直到轨线抵达FB+1(W,x1)=(−0.1874,0.3821),fold分岔再次发生,轨线开始跳跃,表现为激发态SP+2,在PS3(W,x1)=(−0.1909,0)点到达分界面,滑动至点PS4(W,x1)=(−0.1918,0)后穿过分界面.当轨线到达区域D−后,继续大幅振荡,表现为激发态SP−2.随着W取值的减小,振荡幅值也逐渐减小,当W减小到最小值W=−1时,轨线稳定到平衡曲线EB−2,表现为沉寂态QS−2.至此,轨线完成一个周期的非光滑簇发振荡.图17 Ω1=0.0005,Ω2=0.003 时 (W,x1)平面上的转换相图的局部放大图3Fig.17 Locally enlarged part three of the transformed phase portrait onthe(W,x1)for Ω1=0.0005,Ω2=0.003图18 Ω1=0.0005,Ω2=0.003 时 (W,x1)平面上的转换相图的局部放大图4Fig.18 Locally enlarged part four of the transformed phase portrait onthe(W,x1)for Ω1=0.0005,Ω2=0.0034 两种情形下平衡曲线的演化趋势观察两种情形下的平衡曲线图3和图12可以发现,虽然平衡曲线具有相似的结构,但随着参数激励频率的改变,平衡曲线发生曲折的次数有所增加,致使极值点个数也随之增多,相应簇发振荡的转换相图也变得复杂,而导致这一现象产生的原因是两激励的频率存在明显的量级差.以Ω1=0.0005,Ω2=0.002为例,当频率小的变量运动一个周期时,频率大的变量却已经运动了4个周期,而此两者的耦合恰好形成一个新周期.为描述平衡曲线极值点个数的变化,图19和图20给出了两种情形下极值点个数的变化趋势,其中,图19和图20中的黑色标识点分别对应图3和图12中的平衡曲线中的极值点.图19中的曲线对应的函数表达式分别为y1=32W3−16W和.图20中的曲线对应的函数表达式分别为y1=192W5−192W3+36W和图19 Ω1=0.0005,Ω2=0.002时极值点个数情况Fig.19 Variation of extreme points with Ω1=0.0005,Ω2=0.002图20 Ω1=0.0005,Ω2=0.003时极值点个数情况Fig.20 Variation of extreme points with Ω1=0.0005,Ω2=0.003如图 19和图 20所示,当Ω1=0.0005,Ω2=0.002时,平衡曲线的极值点个数为2,当Ω1=0.0005,Ω2=0.003时,极值点增加为6个.将图19和图20分别与图3和图12进行对比,发现图19和图20中黑色标识的极值点的个数分别与图3和图12所示的平衡曲线中的极值点个数相一致,并且各极值点坐标也与平衡曲线所示的相吻合.当Ω1=0.0005,Ω2=0.002时,对应极值点的W的坐标是W= ±0.7435,当Ω1=0.0005,Ω2=0.003时,对应极值点的W 的坐标是W±1=±0.1756,W±2=±0.4547.5 结论对于含双频激励的Filippov系统进行非光滑簇发振荡机理分析时,引入周期变化的双频激励项,当两激励频率之间存在共振关系,且周期激励频率远小于系统的固有频率时,将两周期激励项转换为单一周期激励项的函数表达式,并将该单一周期激励项视为慢变参数,利用快慢分析法,在固定两激励振幅的取值,保持外激频率不变,改变参激频率的情形下,得到了快子系统随慢变参数变化的平衡曲线及其分岔行为的演化机制.结合转换相图和不同慢变参数情形下的稳定极限环的演变过程,发现随着慢变参数的改变,轨线会出现同宿分岔、多滑分岔及多种复杂振荡模式,而参激频率的改变,使得系统的分岔模式增加,系统的簇发振荡机制变得复杂,从而非光滑动力学行为特性也更明显.通过对比两种不同参激频率下的平衡曲线及分岔图,发现虽然系统有相似的平衡曲线结构,却因参激频率取值的不同,致使平衡曲线发生曲折的次数增加,极值点个数也由Ω1=0.0005,Ω2=0.002时的2个变为Ω1=0.0005,Ω2=0.003时的6个,数值模拟也很好地验证了这一结果.必须指出的是,本文讨论的是保持外激频率Ω1=0.0005不变,改变参激频率Ω2的值时系统产生的簇发振荡及非光滑行为特性.若固定Ω2不变,改变Ω1的值,系统可能会有不同的非线性动力学行为,我们将另外讨论这种情形.参考文献【相关文献】1 秦志英,李群宏.一类非光滑映射的边界碰撞分岔.力学学报,2013,45(1):25-29(Qin Zhiying,Li Qunhong.Border-collision bifurcation in a kind of non-smooth maps.Chinese Journal of Theoretical and Applied Mechanics,2013,45(1):25-29(in Chinese))2 高雪,陈前,刘先斌.一类分段光滑隔振系统的非线性动力学设计方法.力学学报,2016,48(1):192-200(Gao Xue,Chen Qian,Liu Xianbin.Nonlinear dynamics design for piecewise smooth vibration isolation system.Chinese Journal of Theoretical and AppliedMechanics,2016,48(1):192-200(in Chinese))3 范新秀,王琪.车辆纵向非光滑多体动力学建模与数值算法研究.力学学报,2015,47(2):301-309(Fan Xinxiu,Wang Qi.Research on modeling and simulation of longitudinal vehicle dynamics based on non-smooth dynamics of multibody systems.Chinese Journal of Theoretical and Applied Mechanics,2015,47(2):301-309(in Chinese))4 Leine RI,Van Campen DH,Van De Vrande BL.Bifurcations in nonlinear discontinuous systems.Nonlinear Dyn,2000,23:105-1645 Kowalczyk P,Bernardo MD.Two-parameter degenerate sliding bifurcations in Filippov systems.Physica D,2005,204:204-2296 Fuhrmann G.Non-smooth saddle-node bifurcations III:Strange attractors in continuous time.J Differ Equations,2016,261:2109-21407 Bernardo MD,Nordmark A,Olivar G.Discontinuity-induced bifurcations of equilibria in piecewise-smooth and impacting dynamical systems.Physica D,2008,237:119-1368 Xiong YQ.Limit cycle bifurcations by perturbing non-smooth Hamiltonian systems with 4 switching lines via multiple parameters.Nonlinear Anal-Real,2018,41:384-4009 张舒,徐鉴.时滞耦合系统非线性动力学的研究进展.力学学报,2017,49(3):565-587(Zhang Shu,Xu Jian.Review on nonlinear dynamics in systems with coupling delays.Chinese Journal of Theoretical and Applied Mechanics,2017,49(3):565-587(in Chinese))10 Colombo A,Bernardo MD,Hogan SJ,et al.Bifurcations of piecewise smoothflows:Perspectives,methodologies and open problems.Physica D,2012,241:1845-186011 张思进,周利彪,陆启韶.线性碰振系统周期解擦边分岔的一类映射分析方法.力学学报,2007,39(1):132-136(Zhang Sijin,Zhou Libiao,Lu Qishao.A map method for grazing bifurcation in linear vibro-impact system.Chinese Journal of Theoretical and Applied Mechanics,2007,39(1):132-136(in Chinese))12 卓小翔,刘辉,楚锡华等.非均质材料动力分析的广义多尺度有限元法.力学学报,2016,48(2):378-386(Zhuo Xiaoxiang,Liu Hui,Chu Xihua,et al.A generalized multiscale finite element method for dynamic analysis of heterogeneous material.Chinese Journal of Theoretical and Applied Mechanics,2016,48(2):378-386(in Chinese))13 Zhao XJ,Sun YP,Li XM,et al.Multiscale transfer entropy:Measuring information transferon multiple time mun Nonlinear Sci Numer Simulat,2018,62:202-21214 Li QQ , Wang YH, Vasilyeva M. Multiscale model reduction for fluid infiltration simulation through dual-continuum porous media with localized uncertainties.J Comput Appl Math,2018,336:127-14615 Chinkanjanarot S,Radue MS,Gowtham S,et al.Multiscale thermal modeling of cured cycloaliphatic epoxy/carbon fiber composites.J Appl Polym Sci,2018,135(25):4637116 Lameu EL,Borges FS,Borges RR,et work and external perturbation induce burst synchronisation in cat cerebral mun Nonlinear Sci,2016,34:45-5417 张正娣,毕勤胜.自激作用下洛伦兹振子的簇发现象及其分岔机制.中国科学:物理学力学天文学,2013,43:511-517(Zhang Zhengdi,Bi Qinsheng.Bursting phenomenon as well as the bifurcation mechanism of self-excited Lorenz system.Sci Sin-Phys MechAstron,2013,43(4):511-517(in Chinese))18 Bi QS.The mechanism of bursting phenomena in Belousov Zhabotinsky(BZ)chemical reaction with multiple time scale.Sci China-Technol Sci,2010,53(1):748-76019 李向红,毕勤胜.铂族金属氧化过程中的簇发振荡及其诱发机理.物理学报,2012,61:020504(Li Xianghong,Bi Qinsheng.Bursting oscillations and the bifurcation mechanism in oxidation on platinum group metals.Acta Phys Sin,2012,61:020504(in Chinese))20 Chen XK,Li SH,Zhang ZD,et al.Relaxation oscillations induced by an order gap between exciting frequency and natural frequency.Sci China Tech Sci,2017,60:289-29821 Jensen RV.Synchronization of driven nonlinear oscillators.Am J Phys,2002,70:607-61922 Peng J,Wang L,Zhao Y,et al.Synchronization and bifurcation in limit cycle oscillators with delayed coupling.Int J Bifurcat Chaos,2011,21:3157-316923 Pereda E, De La Cruz DM, Manas S, et al. Topography of EEG complexity in human neonates:Effect of the postmenstrual age and the sleep state.NeurosciLett,2006,394(2):152-15724 Naidu DS.Analysis of non-dimensional forms of singular perturbation structures for hypersonic vehicles.Acta Astronaut,2010,66(1):577-58625 Chumakov GA,Chumakova NA,Lashina EA.Modeling the complex dynamics of heterogeneous catalytic reactions with fast,intermediate,and slow variables.Chem Eng J,2015,282:11-1926 Tsaneva-Atanasova K,Osinga HM,Riess T,et al.Full system bifurcation analysis of endocrine bursting models.J Theor Biol,2010,264:1133-114627 Alexandrov DV,Bashkirtseva IA,Ryashko LB.Excitability,mixedmode oscillations and transition to chaos in a stochastic ice ages model.Physica D,2017,343(15):28-3728 Izhikevich EM.Neural excitability,spiking and bursting.Int J BifurcatChaos,2000,10:1171-126629 Yue Y,Zhang ZD,Han XJ.Periodic or chaotic bursting dynamics via delayed pitchforkbifurcation in a slow-varying controlled mun Nonlinear Sci Numer Simulat,2018,56:380-39130 Bi QS, Chen XK, Juergen K,et al. Nonlinear behaviors as well as the mechanismin a piecewise-linear dynamical system withtwo time scales.Nonlinear Dyn,2016,85:2233-2245 31 Han XJ,Xia FB,Zhang C,et al.Origin of mixed-mode oscillations through speed escape of attractors in a Rayleigh equation with multiple-frequency excitations.NonlinearDyn,2017,88:2693-270332 Bernardo MD,Kowalczyk P,Nordmark A.Bifurcations of dynamical systems with sliding:Derivation of normal-form mappings.Physica D,2002,170:175-205。
2011年度安徽省自然科学基金结题项目清单

26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
090414272X 090413138 090414165 090414175 090414183 090411016 090411023 090411004 090411019 090411020 090411025 090411026 070411028 090411005 090411003 090411008 090411012 090411024 090416229 090416234 090416236 090414173 090414198
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
090416248 090415210 090414189 090414200 090416230 090416235 090412035 090412045 090412063 090413076 090413079 090414164 090415202 090416220 090416231 070413127 090416273X 090412071 090414172 090416225 090414201 090412057 090412069 090414151 090414149
54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81
090413145 070413103 090413265X 090413263X 090413264X 090413266X 090413267X 090413268X 090413269X 09020103001 09020103002 09020103003 09020103004 09020103008 09020103009 09020103010 09020103005 090412260X 090414190 090412062 090412055 090412067 090412044 090414158 090414167 090414180 090414185 090411007
教育部关于2011年度高等学校科学研究优秀成果奖(科学技术)奖励的决定

教育部关于2011年度高等学校科学研究优秀成果奖(科学技术)奖励的决定文章属性•【制定机关】教育部•【公布日期】2012.02.10•【文号】教技发[2012]1号•【施行日期】2012.02.10•【效力等级】部门规范性文件•【时效性】现行有效•【主题分类】高等教育,机关工作正文教育部关于2011年度高等学校科学研究优秀成果奖(科学技术)奖励的决定(教技发[2012]1号)为全面贯彻党的十七大和十七届六中全会精神,深入贯彻落实科学发展观,大力实施科教兴国战略和人才强国战略,推进科技进步和自主创新,根据《高等学校科学研究优秀成果奖(科学技术)奖励办法》的规定,我部组织开展了2011年度高等学校科学研究优秀成果奖(科学技术)评审工作。
经评审,决定授予“原发性小血管炎临床表型和发病机制”等43项成果高等学校自然科学奖一等奖,授予“恒星形成活动和恒星形成区的观测研究”等58项成果高等学校自然科学奖二等奖;授予“立体视频获取与重建技术及装置”等14项成果高等学校技术发明奖一等奖,授予“大型三维接触面试验设备系统和测试技术”等14项成果高等学校技术发明奖二等奖;授予“异基因造血干细胞移植后移植物抗宿主病早期预警与干预技术及应用”等56项成果高等学校科学技术进步奖一等奖,授予“非霍奇金淋巴瘤诊断治疗的基础和临床研究”等92项成果高等学校科学技术进步奖二等奖;授予“医学信息智能计算支撑平台与应用”等7项成果高等学校科学技术进步奖(推广类)二等奖;授予“在单晶硅片表面制备碳纳米管复合薄膜的方法”成果高等学校专利奖二等奖。
全国高等学校的科学技术工作者要向全体获奖者学习,继续发扬求真务实、勇于创新的科学精神,不畏艰险、勇攀高峰的探索精神,团结协作、淡泊名利的团队精神,报效祖国、服务社会的奉献精神,坚定不移走中国特色自主创新道路,不断提高自主创新能力,积极投身于科教兴国战略的实践中,为建设创新型国家、促进科学发展做出新的更大贡献。
2021年全国优秀博士学位论文提名论文名单

高自友
XXXX大学
微通道内气体流动换热的理论与实验研究
张田田
贾力
XXXX大学
神经网络结构动态优化设计方法及应用
韩红桂
乔俊飞
XX大学
多载波系统的联合收发算法设计研究
刘婷婷
杨晨阳
XX航空航天大学
离散双线性系统可控性与临近可控性研究—一种隐函数方法
铁林
蔡开园
XX航空航天大学
分数阶傅里叶域多抽样率滤波器组理论及应用
袁野
王国仁
XX北大学
车载网络XX访问控制与信息广播技术研究
毕远国
赵海
XX北大学
XXXX解释中的原旨主义理论研究
侯学宾
姚建宗
XX大学
XX下新型超硬材料的结构设计
李全
马琰铭
XX大学
多金属氧簇超分子复合物动态自组装研究
闫毅
吴立新
XX大学
刺激—响应聚合物复合一维光子晶体
王占华
杨柏
XX大学
聚电解质的构象行为及复杂流动研究
施章杰
XX大学
天然蜂窝和人工管束材料的力学研究
张凯
王建祥
XX大学
基于碳纳米管的无掺杂高性能器件和集成电路
丁力
彭练矛
XX大学
系统性红斑狼疮遗传背景研究
周绪杰
张宏
XX大学
议会主权下的XX违宪审查
李蕊佚
韩大园
XX民大学
唐代中书舍人与文学研究
鞠岩
傅璇琮
XX民大学
公允价值计量与资产价格波动
曾雪云
徐经长
XX民大学
王堃
孙润仓
XX林业大学
P14、P53和P73基因遗传多态性与头颈部鳞状细胞癌患者二次原发肿瘤易感性的相关性研究
江苏省2014年度普通高校研究生科研创新计划项目名单(校助)
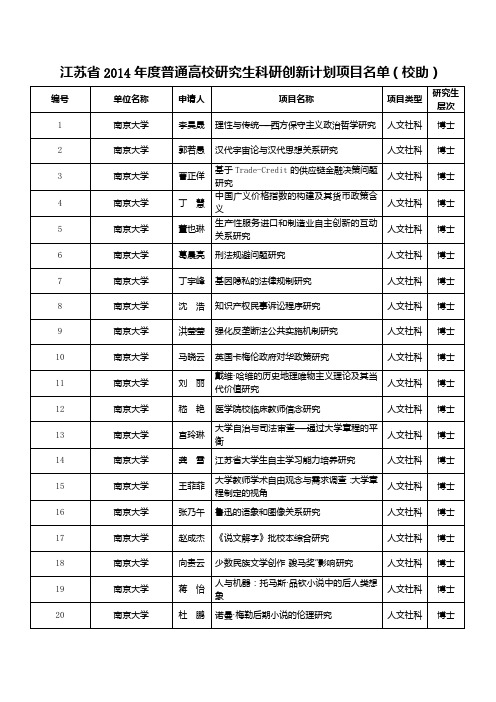
项目类型 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学 自然科学
研究生 层次 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士 博士
张淑文 王 胜
赵飞飞 李 平
黄海富 孟 明
李艳艳 郑先创 顾江江 杨 许 王 明 鑫 豪
叶丽芳 杨 阳
段勇涛 吴 王 萍 聪
刘云龙 王来国 姚峥嵘 邵振广
编号 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62
单位名称 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学
杨已彪 赵 伟
于南洋 韩永和 杨江华 李文涛 梁 潇
乔海石 潘半舟 陈卫波 杨硕菲 庄君龙 牛文举 曹启龙
编号 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83
单位名称 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 南京大学 东南大学 东南大学 东南大学 东南大学 东南大学 东南大学 东南大学 东南大学 东南大学 东南大学 东南大学 东南大学 东南大学 东南大学
王倩倩 孙晓宁 乔联宝 郭 晶
孙旭鹏 卜俊兰 谭 胡 舒 芮
赵永平 李 鹏
吴晓怡 姜 波
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多尺度耦合系统的簇发振荡机制及控制
多尺度耦合系统的簇发振荡机制及控制
摘要:本文通过对多尺度耦合系统的簇发振荡机制及控制的研究,揭示了复杂系统中的簇发现象背后的物理机制和控制方法。
多尺度耦合系统具有重要的科学和工程应用价值,在生物学、物理学、化学和社会科学等领域都有广泛的应用。
同时,簇发振荡作为一种重要的自组织现象,在电力系统控制、脑神经网络研究和城市交通流等领域也有重要作用。
本文对这一领域的研究进行了概述,总结了簇发振荡的物理机制,并介绍了控制多尺度耦合系统的方法和策略。
1. 引言
多尺度耦合系统是指由多个相互作用的子系统组成的系统,其中每个子系统的尺度和时标差异较大。
这种系统具有复杂的动力学行为,往往呈现出一种统一的特征:簇发振荡。
簇发振荡是指子系统之间的相互作用导致整个系统的集体行为,表现为周期性的快速变化和稳定的低频分量。
在物理系统、生物系统和社会系统中都能够观察到这种现象。
2. 多尺度耦合系统的簇发机制
簇发的产生是因为多尺度耦合系统中的子系统之间具有非线性相互作用。
当系统的耦合强度适当时,子系统之间的非线性耦合可以引起系统整体的相互作用。
通过数学建模和仿真实验,簇发振荡的机制可以划分为两类:同步和反应扩散。
2.1 同步机制
同步机制是指多尺度耦合系统中不同子系统之间的周期性变化趋于同步。
当耦合强度适当时,子系统之间的周期性变化可以通过耦合相互影响而达到同步。
同步机制相对简单,易于理解
和控制。
2.2 反应扩散机制
反应扩散机制是指多尺度耦合系统中子系统的周期性变化在空间上扩散。
每个子系统的周期性变化通过耦合相互作用在空间上传播,形成簇发振荡。
这种机制常常出现在空间分布较大的系统中,例如城市交通流的研究。
3. 多尺度耦合系统的控制
多尺度耦合系统的控制是指通过调节耦合强度和拓扑结构来实现对系统的稳定性和振荡特性的调控。
现实中的多尺度耦合系统通常受到外界扰动和不确定性的影响,因此控制方法需要考虑系统的鲁棒性和适应性。
3.1 控制耦合强度
通过调节耦合强度可以实现对系统的控制。
耦合强度过大或过小都会破坏簇发振荡的形成。
因此,寻找适当的耦合强度是控制多尺度耦合系统的关键。
3.2 调控拓扑结构
拓扑结构在多尺度耦合系统中起着重要的作用。
通过调节拓扑结构可以实现系统的稳定性和振荡特性的改变。
例如,通过增加或删除子系统之间的连接可以改变系统的簇发行为。
4. 结论
多尺度耦合系统的簇发振荡机制及控制是一个具有重要科学意义和工程应用价值的领域。
理解系统的簇发机制可以帮助我们对复杂系统的行为有更深入的认识,而控制方法则有助于我们在实际应用中解决各种问题。
尽管目前多尺度耦合系统的研究还存在一定的挑战,但我们相信随着技术的发展和研究的不断深入,这一领域将有更多的突破
多尺度耦合系统的簇发振荡机制和控制是一个具有重要科学意义和工程应用价值的领域。
通过研究簇发机制,我们可以更深入地了解复杂系统的行为,并为解决实际问题提供有力的指导。
控制多尺度耦合系统的方法可以通过调节耦合强度和拓扑结构来实现系统的稳定性和振荡特性的调控,但需要考虑外界扰动和不确定性对系统的影响,以确保控制方法具有鲁棒性和适应性。
虽然该领域目前仍面临一些挑战,但随着技术的发展和研究的不断深入,我们相信将会有更多的突破。
通过进一步研究和探索多尺度耦合系统的簇发机制和控制方法,我们可以为科学研究和实际应用提供更好的支持。
