2019-2020年八年级下期中考试试卷
2019-2020学年第二学期期中考试初二年级英语试题及答案

2019-2020学年第⼆学期期中考试初⼆年级英语试题及答案2019-2020学年第⼆学期期中考试⼋年级英语试题分值:120分考试时间:100分钟命题⼈:审核⼈:听⼒部分(20分)第⼀部分听对话回答问题本部分共有10道⼩题,每⼩题你将听到⼀段对话,选出你认为最合适的答案,每段对话听两遍。
1. How did the girl go to have a meeting?A B C2. Which country has Mary been to ?A B C2. What are they talking about?A. B. C.4. What does Daniel need?A B C5. Where is the woman from?A. CanadaB. AmericaC. Germany6. What kind of animals does Lisa like best?A. Monkeys.B. Dogs.C. Elephants.7. What has the man done?A. He has done some cooking.B. He has done some washing.C. He has done some cleaning.8. What’s the possible relationship between the two speakers?A. Teacher and student.B. Doctor and patient.C. Mother and son.9. When does David want to leave?A. Next Tuesday.B. Next Monday.C. Next Wednesday.10. What time is it now?A. 7:30.B. 8:00C. 8:30第⼆部分听对话和短⽂回答问题。
你将听到⼀段对话和两篇短⽂,各听两遍。
精品解析:重庆市2019-2020学年八年级下学期期中语文试题(解析版)

八年级下册期中测试卷(时间:150分钟满分:120分)一、语言知识及其运用(每小题2分,共10分)1.下列字形和加点字注音全部正确的一项是()A. 翩.然piān 褶皱戛.然而止gá消声匿迹B. 两栖.xī 羁畔流水淙.淙cóng 人情事故C. 缄.默jiān 斡旋阡陌.相通mò楔形文字D. 龟.裂guī箬篷风雪载.途zài 怡然不动【答案】C【解析】【详解】C字形和加点字注音全部正确。
A戛然而止jiá,销声匿迹。
B两栖qī,羁绊,人情世故。
D龟裂jūn,佁然不动。
2.下列句子中加点成语使用正确的一项是()A. 欧•亨利的小说情节起伏跌宕,抑扬顿挫。
.....B. 安顺市通过搭建德育教育实践平台,在潜移默化....中培养未成年人的真挚情感和高尚品质。
C. 《奔跑吧,兄弟!》热播以来,广大中小学生对该节日的热衷程度可谓迫在眉睫。
.....D. 他在政治课上答错了一道题,结果弄得面红耳赤,声名狼藉。
.....【答案】B【解析】【详解】A.使用有误,抑扬顿挫:指声音的高低起伏和停顿转折。
句中指的是小说情节,所以该成语使用不当;B.使用正确,潜移默化:指人的思想或性格不知不觉受到感染、影响而发生了变化;C.使用有误,迫在眉睫:已经逼近眉毛和眼睫毛之间。
比喻事情十分紧急;已到眼前。
句中指的是学生对该节目的热衷程度高,所以该成语使用不当;D.声名狼藉,声名:名誉,名声;狼藉:传说中狼群垫草而卧;起来时把草踏乱以消灭痕迹。
后借以形容散乱;引申为破败得不可收拾。
形容声望和名誉败坏。
用在此处是搭配不当;故选B。
3.下列句子没有语病的一项是()A. 这次会议规定每一位发言者的发言时间最多不能超过30分钟。
B. 但不知怎地,我总还时时记起他,在我所认为我师之中,他是最给我鼓励,最使我感激的一个。
C. 这位设计师出色的工作和独特的设计,已被有关单位采用。
D. 为了全面提升办学水平,英才学校决定加快创建文明校园的速度。
人教版2019-2020学年下学期八年级物理期中测试卷附答案

语文试题 第1页(共12页) 语文试题 第2页(共12页)………………○………………内………………○………………装………………○………………订………………○………………线………………○………………………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校:______________姓名:_____________班级:_______________考号:______________________绝密★启用前2019-2020学年第二学期期中试卷八年级物理(时间:90分钟,满分:100分)一、选择题(每小题3分,共36分)1.建筑工人砌墙时,常利用铅垂线来检查墙砌得是否竖直,如题4图甲。
一堵南北走向的墙上,所挂铅垂线如题4图乙所示,则这堵墙一定是( )A.向东倾斜B.向南倾斜C.向西倾斜D.向北倾斜2.人从沙滩上走过,会留下一串深深的脚印,但从草地上走过,脚印却并不明显。
同学们针对这一现象,经过讨论提出了如下四个科学问题,其中较有探究价值且易于探究的是( ) A.为什么脚印有时候深有时候浅 B.脚印的深浅与哪些因素有关 C.压力的作用效果与哪些因素有关 D.压强的大小与哪些因素有关3.下列数据最符合实际的是( )A.在菏泽用普通茶壶烧开水,沸水的温度可达100℃B.两个鸡蛋的重约为1NC.中学生双脚站立时对水平地面的压力约为6×103ND.一张课桌的高度约1.2m4.下列实例中,目的是为了减小压强的是( )A.上学出发前,将不用的书本从书包中取出B.啄木鸟的喙坚硬而细长C.把酸奶吸管的一端切成斜口D.把菜刀磨得很锋利 5.关于g =9.8N/kg 的物理意义,下列说法中正确的是:( ) A.1kg 等于9.8NB.质量为1kg 的物体所受到的重力是9.8NC.1N 等于9.8kgD.当物体所受的重力为9.8N 时,它的质量一定是1kg6.如图所示,在弹簧测力计的两侧沿水平方向各加6N 拉力并使其保持静止,此时弹簧测力计的示数为:( )A.0NB.3NC.6ND.12N 7.关于物体间的相互作用力,下列叙述错误的是:( ) A.物体间只有直接接触,才有力的作用B.力的相互作用可以发生在任何相互作用的物体之间C.彼此不接触的物体之间,力的作用也是相互的D.一个物体受到另一个物体力的作用时,同时也对另一个物体施加力的作用 8.在实验事实的基础上,通过科学想象和推理得出的物理规律是( )A.欧姆定律B.牛顿第一定律C.阿基米德原理D.光的反射定律8.竖直握在手中的瓶子不滑落下来,这是因为:( ) A.手的握力等于瓶子所受的重力 B.手的握力大于瓶子所受的重力 C.手对瓶子的静摩擦力等于瓶子所受的重力 D.手对瓶子的静摩擦力大于瓶子所受的重力10.在匀速直线行驶的火车车厢里,坐着一位乘客,他发现自己正上方顶棚上有一小水滴正要下落,这滴水将落在:( )A.此乘客的前面B.此乘客的后面C.此乘客的头上D.此乘客的左边 11.你骑自行车上学么?下列关于自行车增大摩擦或减小摩擦的说法,哪个是错误的:( ) A.轮胎上有凸凹不平的花纹是为了增大摩擦 B.刹车时用力捏闸是为了增大摩擦 C.往车轮轴承上加润滑油是为了减小摩擦 D.车轮上装有滚动轴承是为了增大摩擦12.用一水平推力推矿泉水瓶的下部,水瓶会沿桌面滑动,用同样大小的水平推力推矿泉水瓶的上部,水瓶会翻到。
湖北省2019-2020学年八年级数学下学期期中测试卷一(含答案)

湖北省2019–2020学年下学期期中测试卷八年级数学一、选择题(本大题共10小题,每小题3分,共30分)1.下列二次根式中,最简二次根式是A .8B .223C .37xD 22x y +.2.如果3,4,a 是勾股数,则a 的值是A .5B .C .或5D .73.下列各式中,计算正确的是A .1212= B .2(33)9-= C .2(21)322+=+ D .1052÷=4.如图,一个25m 长的梯子AB ,斜靠在一竖直的墙AO 上,这时的AO 距离为24m ,如果梯子的顶端A 沿墙下滑4m ,那么梯子底端B 外移A .7米B .8米C .9米D .10米5.在四边形ABCD 中,给出条件:①AB ∥CD ;②AD ∥BC ;③AB=CD ;④AD=BC ;⑤∠A=∠C ;⑥∠B=∠D .将其中的任意两个进行组合,能判定四边形ABCD 是平行四边形的有A .10组B .9组C .8组D .7组6.如图,在菱形ABCD 中,AB=5,对角线AC=6.若过点A 作AE ⊥BC ,垂足为E ,则AE 的长为( )A .4B .2.4C .4.8D .57.已知()()22m 12,n 12,7m 14m 93n 6n 7=+=-----则代数式的值为A .8B .–8C .10D .–6 8.如图,在▱ABCD 中,对角线AC 、BD 相交成的锐角α为60°,若AC=10,BD=8,则▱ABCD 的面积是A .20B .20C .30D .309.矩形ABCD 与CEFG ,如图放置,点B ,C ,E 共线,点C ,D ,G 共线,连接AF ,取AF 的中点H ,连接GH .若BC=EF=2,CD=CE=1,则GH=( )A .1B .23C .22D .5 10.如图,E 、F 分别是正方形ABCD 的边CD ,AD 上的点,且CE=DF ,AE ,BF 相交于点O ,下列结论:①AE=BF ;②AE⊥BF ;③AO=OE ;④S △AOB =S 四边形DEOF 中,正确的有A .1个B .2个C .3个D .4个二、填空题(本大题共6小题,每小题3分,共18分)112x 9-x 的取值范围是_______.12.若实数x 、y 满足y 2020x x 20202019=-+-+,()2020x-y =则_______.13.如图,点O 是矩形ABCD 的对角线AC 的中点,OM ∥AB 交AD 于点M ,若OM=3,BC=10,则OB 的长为___________.14.如图,在Rt △ABC 中,∠C =90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,当AC=4,BC=2时,则阴影部分的面积为________.15.如图,矩形ABCD 的对角线AC 与BD 交于点O ,过点O 作BD 的垂线分别交AD ,BC 于E ,F 两点.若AC=,∠AEO=120°,则FC 的长度为___________316.如图,P 是边长为4的正方形ABCD 的对角线BD 上的一动点,且点E 是边AD 的中点,求PE+PA 的最小值为___________.三、解答题(本大题共8个小题,满分72分)17.(本题满分8分,每小题4分)计算:(1)120-555(2((551515231523+. 18.(8分)先化简,再求值:3x 3x 36x xy 4x 36xy ,x y 3.y y y 2+-+==⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭其中, 19.(8分)如图,已知平行四边形ABCD 的两条对角线相交于点O ,E 是BO 的中点,过B 点作AC 的平行线,交CE 的延长线于点F ,连接BF.(1)求证:FB=AO ;(2)当平行四边形ABCD 满足什么条件时,四边形AFBO 是菱形?说明理由.20.(本题满分8分)在Y ABCD 中,点E 、F 分别在边BC 、AD 上,且BE=DF .(1)如图1,连接AE 、CF ,求证:四边形AECF 是平行四边形;(2)如图2,连接AE 、BF 交于点G ,连接DE 、CF 交于点H ,连接GH ,若E 为BC 的中点,在不添加辅助线的情况下,请直接写出以G 、H 为顶点的平行四边形.21.(本题满分8分)如图,在矩形ABCD 中,AB=4cm ,BC=8cm ,点P 从点D 出发向点A 运动,运动到点A 即停止;同时点Q 从点B 出发向点C 运动,运动到点C 即停止.点P 、Q 的速度的速度都是1cm/s ,连结PQ ,AQ ,CP ,设点P 、Q 运动的时间为t (s ).(1)当t 为何值时,四边形ABQP 是矩形?(2)当t 为何值时,四边形AQCP 是菱形?(3)分别求出(2)中菱形AQCP 的周长和面积.22.(10分)如图1,已知AD ∥BC ,AB ∥CD ,∠B=∠C .(1)求证:四边形ABCD为矩形;(2)M为AD的中点,在AB上取一点N,使∠BNC=2∠DCM.①如图2,若N为AB中点,BN=2,求CN的长;②如图2,若CM=3,CN=4,求BC的长.23(10分).如图,点D、E是Rt△ABC两直角边AB、AC上的一点,连接BE,已知点F、G、H分别是DE、BE、BC的中点.(1)求∠FGH度数(2)连CD,取CD中点M,连接GM,若BD=8,CE=6,求GM的长.24.(本题满分12分).如图所示,在平面直角坐标系中,正方形OABC的点A、C分别在x 轴和y轴的正半轴上,点B(6,6)在第一象限,AP平分∠CAB交OB于P.(1)求∠OPA的度数和OP的长;(2)点P不动,将正方形OABC绕点O逆时针旋转至图2的位置,∠COP=60°,AP交OB于点F,连接CF.求证:OF+CF=PF;(3)如图3,在(2)的条件下,正方形的边AB交x轴于点D、OE平分∠BAD,M、N是OB、OE 上的动点,求BN+MN的最小值,请在图中画出示意图并简述理由.湖北省2019–2020学年八年级数学下学期期中测试卷 (解析版) 一、选择题(本大题共10小题,每小题3分,共30分) 1.下列二次根式中,最简二次根式是A .8B .223C .37xD 22x y +. 【答案】D2.如果3,4,a 是勾股数,则a 的值是A .5B .C .或5D .7 【答案】A3.下列各式中,计算正确的是A .1212= B .2(33)9-= C .2(21)322+=+D .1052÷=【答案】C 4.如图,一个25m 长的梯子AB ,斜靠在一竖直的墙AO 上,这时的AO 距离为24m ,如果梯子的顶端A 沿墙下滑4m ,那么梯子底端B 外移A .7米B .8米C .9米D .10米【答案】B 5.在四边形ABCD 中,给出条件:①AB ∥CD ;②AD ∥BC ;③AB=CD ;④AD=BC ;⑤∠A=∠C ;⑥∠B=∠D .将其中的任意两个进行组合,能判定四边形ABCD 是平行四边形的有A .10组B .9组C .8组D .7组【答案】C6.如图,在菱形ABCD 中,AB=5,对角线AC=6.若过点A 作AE ⊥BC ,垂足为E ,则AE 的长为( )A .4B .2.4C .4.8D .5【答案】C 7.已知()()22m 12,n 12,7m 14m 93n 6n 7=+=-----则代数式的值为 A .8B .–8C .10D .–6 【答案】A8.如图,在▱ABCD 中,对角线AC 、BD 相交成的锐角α为60°,若AC=10,BD=8,则▱ABCD 的面积是A .20B .20C .30D .30 【答案】B 9.矩形ABCD 与CEFG ,如图放置,点B ,C ,E 共线,点C ,D ,G 共线,连接AF ,取AF 的中点H ,连接GH .若BC=EF=2,CD=CE=1,则GH=( )A .1B .23C .22D 5【答案】C 10.如图,E 、F 分别是正方形ABCD 的边CD ,AD 上的点,且CE=DF ,AE ,BF 相交于点O ,下列结论:①AE=BF ;②AE⊥BF ;③AO=OE ;④S △AOB =S 四边形DEOF 中,正确的有A .1个B .2个C .3个D .4个【答案】C二、填空题(本大题共6小题,每小题3分,共18分)11.若代数式2x 9x 3--在实数范围内有意义,则x 的取值范围是_______.【答案】x 3x 3>≤-或12.若实数x 、y 满足y 2020x x 20202019=-+-+,()2020x-y =则_______.【答案】1.13.如图,点O 是矩形ABCD 的对角线AC 的中点,OM ∥AB 交AD 于点M ,若OM=3,BC=10,则OB 的长为___________.【答案】3414.如图,在Rt △ABC 中,∠C =90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,当AC=4,BC=2时,则阴影部分的面积为________.【答案】4.15.如图,矩形ABCD 的对角线AC 与BD 交于点O ,过点O 作BD 的垂线分别交AD ,BC 于E ,F 两点.若AC=,∠AEO=120°,则FC 的长度为___________3 【答案】316.如图,P 是边长为4的正方形ABCD 的对角线BD 上的一动点,且点E 是边AD 的中点,求PE+PA 的最小值为___________.【答案】25三、解答题(本大题共8个小题,满分72分) 17.(本题满分8分,每小题4分)计算:(1)120-555(2((551515231523+. 【解答】(1)原式5555(2)原式=553-–12=83-18.(8分)先化简,再求值:3x 3x 3xy 36xy ,x y 3.y y y 2+-+==⎛⎛ ⎝⎝其中, 【解答】原式=2x 3xy y-() 3x ,y 3=322==-当时,原式19.(8分)如图,已知平行四边形ABCD 的两条对角线相交于点O ,E 是BO 的中点,过B 点作AC 的平行线,交CE 的延长线于点F ,连接BF.(1)求证:FB=AO ;(2)当平行四边形ABCD 满足什么条件时,四边形AFBO 是菱形?说明理由.【解答】证明:(1)如图,取BC的中点G,连接EG.∵E是BO的中点,∴EG是△BFC的中位线,∴EG=0.5BF.同理,EG=0.5OC,∴BF=OC.又∵点O是▱ABCD的对角线交点,∴AO=CO,∴BF=AO.又∵BF∥AC,即BF∥AO,∴四边形AOBF为平行四边形,∴FB=AO;(2)当平行四边形ABCD是矩形时,四边形AFBO是菱形.理由如下:∵平行四边形ABCD是矩形,∴OA=OB,∴平行四边形AFBO是菱形.20.(本题满分8分)在Y ABCD中,点E、F分别在边BC、AD上,且BE=DF.(1)如图1,连接AE、CF,求证:四边形AECF是平行四边形;(2)如图2,连接AE、BF交于点G,连接DE、CF交于点H,连接GH,若E为BC的中点,在不添加辅助线的情况下,请直接写出以G、H为顶点的平行四边形.【解答】(1)证AF平行且等于CE即可.(2)AGHF,FGHD,GEHF,GBEH,GECH.21.(本题满分8分)如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度的速度都是1cm/s,连结PQ,AQ,CP,设点P、Q运动的时间为t(s).(1)当t为何值时,四边形ABQP是矩形?(2)当t为何值时,四边形AQCP是菱形?(3)分别求出(2)中菱形AQCP的周长和面积.【解答】(1)当四边形ABQP是矩形时,BQ=AP,即:t=8﹣t,解得t=4.答:当t=4时,四边形ABQP是矩形;(2)设t秒后,四边形AQCP是菱形当AQ=CQ,即224t =8﹣t时,四边形AQCP为菱形.解得:t=3.答:当t=3时,四边形AQCP是菱形;(3)当t=3时,CQ=5,则周长为:4CQ=20cm,面积为:4×8﹣2×12×3×4=20(cm2).22.(10分)如图1,已知AD∥BC,AB∥CD,∠B=∠C.(1)求证:四边形ABCD为矩形;(2)M为AD的中点,在AB上取一点N,使∠BNC=2∠DCM.①如图2,若N为AB中点,BN=2,求CN的长;②如图2,若CM=3,CN=4,求BC的长.【解答】(1)证明:如图1中,∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形,∵AB∥CD,∴∠B+∠C=180°,∵∠B=∠C,∴∠B=∠C=90°,∴四边形ABCD是矩形.(2)①如图2中,延长CM、BA交于点E.∵AN=BN=2,∴AB=CD=4,∵AE∥DC,∴∠E=∠MCD,在△AEM和△DCM中,∠E=∠MCD,∠AME=∠CMD,AM=DM,∴△AME≌△DMC,∴AE=CD=4,∵∠BNC=2∠DCM=∠NCD,∴∠NCE=∠ECD=∠E,∴CN=EN=AE+AN=4+2=6.②如图2中由①可知,△EAM≌△CDM,EN=CN,∴EM=CM=3,EN=CN=4,设BN=x,则BC2=CN2–BN2=CE2–EB2,∴42–x2=62–(x+42,∴x=,∴BC=2222137 CN BN422⎛⎫-=-=⎪⎝⎭23(10分).如图,点D、E是Rt△ABC两直角边AB、AC上的一点,连接BE,已知点F、G、H分别是DE、BE、BC的中点.(1)求∠FGH度数(2)连CD,取CD中点M,连接GM,若BD=8,CE=6,求GM的长.【解答】(1)∵度F,G,H分别是DE,BE,BC的中点知∴FG∥AB,GH∥AC∵道AB⊥回AC∴FG⊥GH即∠FGH=90°(2)连答接HM,则HM∥BD,HM=12BD=4同理GH=12CE=3∵BD⊥CE,∴HM⊥GH由勾股定理的可得GM=524.(本题满分12分).如图所示,在平面直角坐标系中,正方形OABC的点A、C分别在x 轴和y轴的正半轴上,点B(6,6)在第一象限,AP平分∠CAB交OB于P.(1)求∠OPA的度数和OP的长;(2)点P不动,将正方形OABC绕点O逆时针旋转至图2的位置,∠COP=60°,AP交OB于点F,连接CF.求证:OF+CF=PF;(3)如图3,在(2)的条件下,正方形的边AB交x轴于点D、OE平分∠BAD,M、N是OB、OE 上的动点,求BN+MN的最小值,请在图中画出示意图并简述理由.【解答】(1)如图1,∵AC,OB是正方形OABC的对角线,∴OA=AB,∠2=∠3=∠BAC=45°,∵AP是∠BAC的角平分线,∴∠1=∠BAC=22.5°,∴∠OAP=∠3+∠1=67.5°,在△OAP中,∠OPA=180°﹣∠2﹣∠OAP=67.5°,∴∠OAP=∠OPA,∴OA=OP,∵B(6,6),∴AB=6,∴OA=AB=6,∴OP=6;(2)如图2,∵四边形OABC是正方形,∴OA=OC,∠AOC=90°,∵∠COP=60°,∴∠AOP=150°,由(1)知,OP=OA∴∠P=15°,由(1)知,∠POG=45°,∴∠AGO=∠P+∠POG=60°,∵OB是正方形的对角线,∴∠BOC=45°,∵∠COP=60°,∠POG=45°,∴∠BOG=∠COP=60°,∴△OFG是等边三角形,∴OF=FG=OG,∴△COF≌△POG(SAS),∴PG=CF,∴CF+OF=PG+FG=PF;(3)如图3,过点B作BQ⊥OE于Q,延长BQ交x轴于B',∵OE是∠DOB的平分线,∴BQ=B'Q,∴点B'与点B关于OE对称,连接B'M'交OE于N',∴BN'+M'N'=B'N'+M'N'=B'M',过点B'作B'M⊥OB于M,交OE于E,此时,BN+MN最小,∵OB是边长为6的正方形的对角线,∴OB=62由作图知,OB'=OB=62由(2)易知,∠BOH=30°,在Rt△B'OM中,B'M=OB'=3即:BN+MN的最小值为32.。
2019-2020学年广东省揭阳市八年级(下)期中数学试卷

2019-2020学年广东省揭阳市八年级(下)期中数学试卷一、选择题(本大题10小题,每小题3分,共30分)1.(3分)(2020春•揭阳期中)如果a>b,下列各式中不正确的是()A.a﹣3>b﹣3B.>C.﹣2a<﹣2b D.﹣2a>﹣2b 2.(3分)(2014•威海)已知点P(3﹣m,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是()A.B.C.D.3.(3分)(2016•碑林区校级模拟)在以下”绿色食品、响应环保、可回收物、节水“四个标志图案中,是中心对称图形的是()A.B.C.D.4.(3分)(2020春•揭阳期中)如图,已知点A(1,2)和点B(3,﹣1),把线段AB向右平移2个单位,则点B的坐标变为()A.(﹣1,5)B.(5,﹣1)C.(1,﹣1)D.(﹣1,1)5.(3分)(2020春•揭阳期中)①3>0;②4x+y≤1;③x+3=0;④y﹣7;⑤m﹣2.5>3.其中不等式有()A.1个B.2个C.3个D.4个6.(3分)(2021•宁波模拟)在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形:③有一边上的高也是这边上的中线的三角形是等边三角形:④三个外角都相等的三角形是等边三角形正确的命题有()A.4个B.3个C.2个D.1个7.(3分)(2020春•盱眙县期末)已知关于x的不等式组有解,则a的取值不可能是()A.0B.1C.2D.﹣28.(3分)(2019秋•栾城区期末)如图,将直角三角形ABC绕直角顶点C按顺时针方向旋转90°后得到三角形A′B′C,连接AA′,若∠1=25°,则∠B的度数是()A.55°B.65°C.60°D.70°9.(3分)(2020春•揭阳期中)已知实数x,y满足|x﹣6|+=0,则以x,y的值为两边的等腰三角形的周长为()A.27或36B.27C.36D.以上答案都不对10.(3分)(2020春•松北区期末)关于x的不等式(m+1)x>m+1的解集为x<1,那么m 的取值范围是()A.m<﹣1B.m>﹣1C.m>0D.m<0二、填空题:(本大题7小题,每小题4分,共28分)11.(4分)(2020春•揭阳期中)在△ABC中,AB=AC,∠A=44°,则∠B=度.12.(4分)(2013•黔西南州)如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=度.13.(4分)(2020春•揭阳期中)如图,已知∠A=90°,AC=AB=8,CD=4,BD=12.则∠ACD=度.14.(4分)(2020春•揭阳期中)如图,已知一次函数y1=k1x+b1与一次函数y2=k2x+b2的图象相交于点(1,2),则不等式k1x+b1<k2x+b2的解集是.15.(4分)(2019春•渭滨区期末)已知关于x的不等式3x﹣m+1>0的最小整数解为2,则实数m的取值范围是.16.(4分)(2013•聊城)如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为.17.(4分)(2013•资阳)如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是.三、解答题:(本大题3小题,每小题6分,共18分)18.(6分)(2019秋•北海期末)解不等式+1≥,并把它的解集在数轴上表示出来.19.(6分)(2020春•揭阳期中)如图,已知点A(﹣2,﹣1)、B(﹣5,﹣5)、C(﹣2,﹣3),点P(﹣6,0).(1)将△ABC绕点P逆时针旋转90°得△A1B1C1,画出△A1B1C1,并写出点C的对应点C1的坐标为;(2)画出△ABC关于原点成中心对称的图形△A2B2C2,并写出点A的对应点A2的坐标为.20.(6分)(2020秋•中山市期中)如图,在△ABC中,AB=AC,AB的垂直平分线交AB 于M,交AC于N.(1)若∠ABC=70°,求∠MNA的度数.(2)连接NB,若AB=8cm,△NBC的周长是14cm.求BC的长.四、解答题:(本大题3小题,每小题8分,共24分)21.(8分)(2019春•杜尔伯特县期末)如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,证明:(1)CF=EB.(2)AB=AF+2EB.22.(8分)(2020春•揭阳期中)已知关于x、y的方程组的解满足x≤0,y<0.(1)用含m的代数式分别表示x和y;(2)求m的取值范围;(3)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解为x>1?23.(8分)(2008•荆门)将两块全等的含30°角的三角尺如图(1)摆放在一起,它们的较短直角边长为3.(1)将△ECD沿直线l向左平移到图(2)的位置,使E点落在AB上,则CC′=;(2)将△ECD绕点C逆时针旋转到图(3)的位置,使点E落在AB上,则△ECD绕点C旋转的度数=;(3)将△ECD沿直线AC翻折到图(4)的位置,ED′与AB相交于点F,求证:AF=FD′.五、解答题:(本大题2小题,每小题10分,共20分)24.(10分)(2008•鄂州)为了更好治理洋澜湖水质,保护环境,市治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.A型B型价格(万元/台)a b处理污水量(吨/月)240180(1)求a,b的值;(2)经预算:市治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;(3)在(2)问的条件下,若每月要求处理洋澜湖的污水量不低于1860吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.25.(10分)(2015•裕华区模拟)如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC =α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.(1)求证:△COD是等边三角形;(2)当α=150°时,试判断△AOD的形状,并说明理由;(3)探究:当α为多少度时,△AOD是等腰三角形?2019-2020学年广东省揭阳市八年级(下)期中数学试卷参考答案与试题解析一、选择题(本大题10小题,每小题3分,共30分)1.【解答】解:A、∵a>b,∴由不等式的基本性质1可知,a﹣3>b﹣3,故本选项正确;B、∵a>b,∴由不等式的基本性质2可知,>,故本选项正确;C、∵a>b,∴由不等式的基本性质3可知,﹣2a<﹣2b,故本选项正确;D、∵a>b,∴由不等式的基本性质3可知,﹣2a<﹣2b,故本选项错误.故选:D.2.【解答】解:已知点P(3﹣m,m﹣1)在第二象限,3﹣m<0且m﹣1>0,解得m>3,m>1,故选:A.3.【解答】解:A、不是中心对称图形.故错误;B、是中心对称图形.故正确;C、不是中心对称图形.故错误;D、不是中心对称图形.故错误.故选:B.4.【解答】解:由线段AB向右平移2个单位的平移规律可知,此题规律是(x+2,y),照此规律计算可知点B的坐标变为(5,﹣1).故选:B.5.【解答】解:①是用“>”连接的式子,是不等式;②是用“≤”连接的式子,是不等式;③是等式,不是不等式;④没有不等号,不是不等式;⑤是用“>”连接的式子,是不等式;∴不等式有①②⑤共3个,故选:C.6.【解答】解:①有一个外角是120°的等腰三角形是等边三角形,说法正确;②有两个外角相等的等腰三角形是等边三角形,说法错误;③有一边上的高也是这边上的中线的三角形是等边三角形,说法错误;④三个外角都相等的三角形是等边三角形,说法正确,正确的命题有2个,故选:C.7.【解答】解:∵关于x的不等式组有解,∴a<2,∵0<2,1<2,﹣2<2,∴a的取值可能是0、1或﹣2,不可能是2.故选:C.8.【解答】解:∵将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,∴AC=A'C,∠ACA'=90°,∠BAC=∠B'A'C,∴∠AA'C=∠CAA'=45°,且∠1=25°,∴∠B'A'C=20°,∴∠BAC=20°,∴∠B=90°﹣∠BAC=70°,故选:D.9.【解答】解:∵实数x,y满足|x﹣6|+=0,∴x=6,y=15.∵6、6、15不能组成三角形,∴等腰三角形的三边长分别为6、15、15,∴等腰三角形周长为6+15+15=36.故选:C.10.【解答】解:∵不等式(m+1)x>m+1的解集为x<1,∴m+1<0,即m<﹣1,故选:A.二、填空题:(本大题7小题,每小题4分,共28分)11.【解答】解:如图:∵在△ABC中,∠A=44°,∴∠B+∠C=180°﹣∠A=136°,又∵AB=AC,∴∠B=∠C,∴∠B=68°.故答案为:68.12.【解答】解:∵△ABC是等边三角形,∴∠ACB=60°,∠ACD=120°,∵CG=CD,∴∠CDG=30°,∠FDE=150°,∵DF=DE,∴∠E=15°.故答案为:15.13.【解答】解:∵∠A=90°,AC=AB=8,∴BC=,∵CD=4,BD=12,∴CD2+BC2=16+128=144=BD2,∴△BCD是直角三角形,∴∠DCB=90°,∵AC=AB,∠A=90°,∴∠ACB=45°,∴∠ACD=45°,故答案为:4514.【解答】解:一次函数y1=k1x+b1与一次函数y2=k2x+b2的图象相交于点(1,2),所以不等式k1x+b1<k2x+b2的解集是x<1.故答案为:x<1.15.【解答】解:解不等式3x﹣m+1>0,得:x>,∵不等式有最小整数解2,∴1≤<2,解得:4≤m<7,故答案为4≤m<7.16.【解答】解:如图,∵在等边△ABC中,∠B=60°,AB=6,D是BC的中点,∴AD⊥BD,∠BAD=∠CAD=30°,∴AD=AB cos30°=6×=3.根据旋转的性质知,∠EAC=∠DAB=30°,AD=AE,∴∠DAE=∠EAC+∠CAD=60°,∴△ADE的等边三角形,∴DE=AD=3,即线段DE的长度为3.故答案为:3.17.【解答】解:∵沿AD折叠C和E重合,∴∠ACD=∠AED=90°,AC=AE,∠CAD=∠EAD,∴AD垂直平分CE,即C和E关于AD对称,CD=DE=1,∴当P和D重合时,PE+BP的值最小,即此时△BPE的周长最小,最小值是BE+PE+PB =BE+CD+DB=BC+BE,∵∠DEA=90°,∴∠DEB=90°,∵∠B=60°,DE=1,∴BE=,BD=,即BC=1+,∴△PEB的周长的最小值是BC+BE=1++=1+,故答案为:1+.三、解答题:(本大题3小题,每小题6分,共18分)18.【解答】解:去分母,得2(1+2x)+6≥3(1+x)去括号得,2+4x+6≥3+3x,再移项、合并同类项得,x≥﹣5.在数轴上表示为:.19.【解答】解:如图,(1)△A1B1C1即为所求;点C1的坐标为(﹣3,4);(2)△A2B2C2即为所求;点A2的坐标为(2,1).故答案为:(﹣3,4),(2,1).20.【解答】(1)∵AB=AC,∴∠ABC=∠ACB=70°,∴∠A=40°,∵MN是AB的垂直平分线,∴AN=BN,∴∠ABN=∠A=40°,∴∠ANB=100°,∴∠MNA=50°;(2)①∵AN=BN,∴BN+CN=AN+CN=AC,∵AB=AC=8cm,∴BN+CN=8cm,∵△NBC的周长是14cm.∴BC=14﹣8=6cm.四、解答题:(本大题3小题,每小题8分,共24分)21.【解答】证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,∴DE=DC,在Rt△CDF和Rt△EDB中,,∴Rt△CDF≌Rt△EDB(HL).∴CF=EB;(2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,∴CD=DE.在Rt△ADC与Rt△ADE中,,∴Rt△ADC≌Rt△ADE(HL),∴AC=AE,∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.22.【解答】解:(1),①+②得2x=2m﹣6,所以,x=m﹣3;①﹣②得2y=﹣4m﹣8,所以,y=﹣2m﹣4,故含m的代数式分别表示x和y为;(2)∵x≤0,y<0∴,解,得﹣2<m≤3;(3)(2m+1)x<2m+1,∵原不等式的解集是x>1,∴2m+1<0,∴,又∵﹣2<m≤3∴﹣2<m<﹣,∵m为整数,∴m=﹣1.23.【解答】(1)解:CC′=3﹣.理由如下:∵EC=3,∠A=30°,∴AC=3,∴AE=3﹣3,∴CC′=EE′=AE×tan30°=3﹣;(2)解:△ECD绕点C旋转的度数即∠ECE′的度数;∵∠ABC=60°,BC=CE′=3,AB=6,∴△E′BC是等边三角形,∴BC=E′C=E′B=3,∴AE′=E′C=3,∴∠E′AC=∠E′CA,∴∠ECE′=∠BAC=30°;(3)证明:在△AEF和△D′BF中,∵AE=AC﹣EC,D′B=D′C﹣BC,又∵AC=D′C,EC=BC,∴AE=D′B,又∵∠AEF=∠D′BF=180°﹣60°=120°,∠A=∠CD′E=30°,∴△AEF≌△D′BF,∴AF=FD′.五、解答题:(本大题2小题,每小题10分,共20分)24.【解答】解:(1)根据题意得,解得.(2)设购买污水处理设备A型设备x台,B型设备(10﹣x)台,根据题意得,12x+10(10﹣x)≤105,∴x≤2.5,∵x取非负整数,∴x=0,1,2,∴10﹣x=10,9,8,∴有三种购买方案:①A型设备0台,B型设备10台;②A型设备1台,B型设备9台;③A型设备2台,B型设备8台.(3)由题意:240x+180(10﹣x)≥1860,∴x≥1,又∵x≤2.5,∴x为1,2.当x=1时,购买资金为12×1+10×9=102(万元),当x=2时,购买资金为12×2+10×8=104(万元),∴为了节约资金,应选购A型设备1台,B型设备9台.25.【解答】(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,∴CO=CD,∠OCD=60°,∴△COD是等边三角形.(2)解:当α=150°时,△AOD是直角三角形.理由是:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,∴△BOC≌△ADC,∴∠ADC=∠BOC=150°,又∵△COD是等边三角形,∴∠ODC=60°,∴∠ADO=∠ADC﹣∠ODC=90°,∵∠α=150°,∠AOB=110°,∠COD=60°,∴∠AOD=360°﹣∠α﹣∠AOB﹣∠COD=360°﹣150°﹣110°﹣60°=40°,∴△AOD不是等腰直角三角形,即△AOD是直角三角形.(3)解:①要使AO=AD,需∠AOD=∠ADO,∵∠AOD=360°﹣110°﹣60°﹣α=190°﹣α,∠ADO=α﹣60°,∴190°﹣α=α﹣60°,∴α=125°;②要使OA=OD,需∠OAD=∠ADO.∵∠OAD=180°﹣(∠AOD+∠ADO)=180°﹣(190°﹣α+α﹣60°)=50°,∴α﹣60°=50°,∴α=110°;③要使OD=AD,需∠OAD=∠AOD.∵∠AOD=360°﹣110°﹣60°﹣α=190°﹣α,∠OAD==120°﹣,∴190°﹣α=120°﹣,解得α=140°.综上所述:当α的度数为125°或110°或140°时,△AOD是等腰三角形.。
2019-2020学年浙江省温州市八年级(下)期中数学试卷(附答案详解)
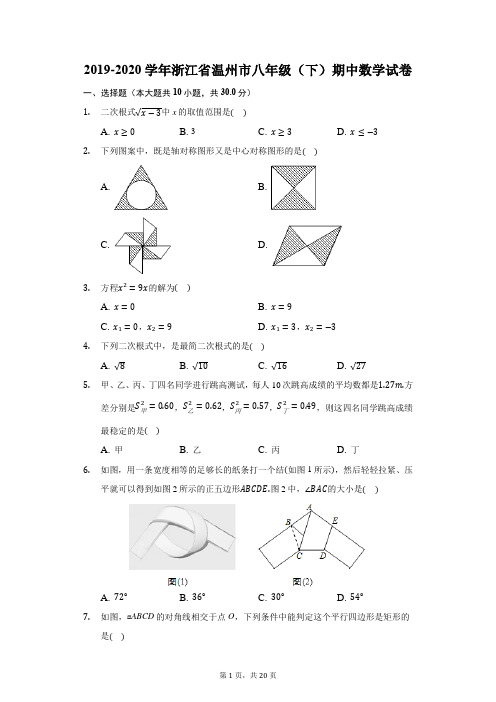
2019-2020学年浙江省温州市八年级(下)期中数学试卷一、选择题(本大题共10小题,共30.0分)1.二次根式√x−3中x的取值范围是()A. x≥0B. 3C. x≥3D. x≤−32.下列图案中,既是轴对称图形又是中心对称图形的是()A. B.C. D.3.方程x2=9x的解为()A. x=0B. x=9C. x1=0,x2=9D. x1=3,x2=−34.下列二次根式中,是最简二次根式的是()A. √8B. √10C. √16D. √275.甲、乙、丙、丁四名同学进行跳高测试,每人10次跳高成绩的平均数都是1.27m.方差分别是S甲2=0.60,S乙2=0.62,S丙2=0.57,S丁2=0.49,则这四名同学跳高成绩最稳定的是()A. 甲B. 乙C. 丙D. 丁6.如图,用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图2中,∠BAC的大小是()A. 72°B. 36°C. 30°D. 54°7.如图,▱ABCD的对角线相交于点O,下列条件中能判定这个平行四边形是矩形的是()A. AC=BDB. AB=BCC. ∠BAC=∠CADD. AC⊥BD8.用反证法证明命题“若√a2=a,则a≥0”时,第一步应假设()A. √a2≠aB. a≤0C. a<0D. a>09.受益于电子商务的发展以及法治环境的改善等多重因素,“快递业”成为我国经济的一匹“黑马”,2018年我国快递业务量为500亿件,2020年快递量预计将达到740亿件,若设快递量平均每年增长率为x,则下列方程中,正确的是()A. 500(1+x)2=740B. 500(1+2x)=740C. 500(1+x)=740D. 500(1−x)2=74010.如图,菱形ABCD的对角线相交于点O,AC=12,BD=16,点P为边BC上一点,且P不与B、C重合.过P作PE⊥AC于E,PF⊥BD于F,连结EF,则EF 的最小值为()A. 4B. 4.8C. 5D. 6二、填空题(本大题共8小题,共24.0分)11.计算:√6÷√2=______.12.已知x=1是方程x2+ax+2=0的一个根,则a的值为______ .13.在某市举办的垂钓比赛上,7名垂钓爱好者参加了比赛,比赛结束后,统计了他们各自的钓鱼条数,成绩如下:4,5,10,6,10,7,9,则这组数据的众数是______ .14.若关于x的一元二次方程kx2−5x+4=0有两个相等的实数根,则k的值为______ .15.如图,河坝横断面迎水坡AB的坡比是1:√3(坡比是斜坡AB两点之间的高度差BC与水平距离AC之比),坝高BC=2m,则坡面AB的长度是______m.16.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=7,则EF的长为______ .17.七巧板又称“智慧板”,是我们古代祖先的一项卓越创造.小华利用七巧板(如图1)拼出一个房子模型(如图2),已知图1中正方形ABCD的边长为4cm,则图2中六边形EFGHIJ的周长是______ cm.18.如图1,在菱形ABCD中,动点P从点C出发,沿C−A−D运动至终点D.设点P的运动路程为x(cm),△BCP的面积为y(cm2).若y与x的函数图象如图2所示,则图中a的值为______ .三、解答题(本大题共6小题,共46.0分)19.计算与解方程:(1)计算(4+√32)×2−8;(2)解方程x2−4x+1=0.20.如图,在所给的8×8方格纸中,点A,B均为格点,请画出符合要求的格点四边形.(1)在图1中画出一个以AB为边的矩形.(2)在图2中画出一个以AB为对角线的正方形.21.近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,某高校为了解本校学生出行使用共享单车的情况,随机调查了某天50名出行学生使用共享单车的情况,并整理成如下统计表.使用次数(012345次)人数(名)12144884(1)这50名出行学生使用共享单车次数的中位数是______ 次.(2)这50名出行学生平均每人使用共享单车多少次?(3)若该校某天有1100名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?22.在▱ABCD中,过点D作DE⊥AB于点E,点F在CD上,AE=CF,连接BF、AF.(1)求证:四边形DEBF是矩形;(2)若AF平分∠DAB,AE=3,DE=4.则AF长为______ .23.瑞安城市规划展览馆位于瑞样新区瑞祥公园内,是温州目前规模最大的城市规划展览馆.为了让参观的人方便停车,城市规划展览馆利用一块矩形空地建了一个停车场,其布局如图所示,已知停车场的长为58米,宽为22米,阴影部分为停车位,其余部分是等宽的通道,已知停车位的面积为700平方米.(1)求通道的宽是多少米?(2)该停车场共有车位70个,据调查分析,当每个车位的月租金为300元时,可全部租出:当每个车位的月租金每上涨10元,就会少租出1个车位,那么停车场的月租金收入最大为______ 元?(请直接写出答案)24.如图1,在平面直角坐标系中,正方形OABC的边OA,OC分别在x轴,y轴的正半轴上,直线y=2x−4经过线段OA的中点D,与y轴交于点G,E是射线CG上一点,作点E关于直线DG的对称点F,连接BE,BF,FG.设点E的坐标为(0,m).(1)求点B的坐标是(______ ,______ ).(2)如图2,当点F落在线段BA的延长线上时,求证:四边形BEGF为菱形.(3)在点E的整个运动过程中,①当S△BEG=58S正方形OABC时,求线段CE的长.②N为平面内任意一点,当B,E,F,N四点构成的四边形为矩形时,则m的值为______ .(请直接写出答案)答案和解析1.【答案】C【解析】解:由题意知x−3≥0,解得:x≥3,故选:C.根据二次根式的性质,被开方数大于或等于0,可以求出x的范围.本题考查的知识点为:二次根式的被开方数是非负数.2.【答案】B【解析】解:A、是轴对称图形,不是中心对称图形.故本选项错误;B、是轴对称图形,也是中心对称图形.故本选项正确;C、不是轴对称图形,是中心对称图形.故本选项错误;D、不是轴对称图形,是中心对称图形.故本选项错误.故选:B.根据轴对称图形与中心对称图形的概念求解.本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.3.【答案】C【解析】解:移项,得x2−9x=0,x(x−9)=0,即x=0或x−9=0∴x1=0,x2=9.故选:C.方程x2=9x移项,得x2−9x=0,再运用因式分解法求出方程的解,选出正确的答案.此类问题也可以根据方程的解的定义,把四个选项分别代入原方程进行检验得出正确的解.4.【答案】B【解析】解:A 、√8=√4×2=2√2,被开方数中含能开得尽方的因数,不是最简二次根式;B 、√10是最简二次根式;C 、√16=4,被开方数中含能开得尽方的因数,不是最简二次根式;D 、√27=√9×3=3√3,被开方数中含能开得尽方的因数,不是最简二次根式; 故选:B .根据最简二次根式的概念判断.本题考查的是最简二次根式的概念,被开方数不含分母、被开方数中不含能开得尽方的因数或因式的二次根式,叫做最简二次根式.5.【答案】D【解析】解:∵S 甲2=0.60,S 乙2=0.62,S 丙2=0.57,S 丁2=0.49, ∴S 丁2<S 丙2<S 甲2<S 乙2,∴这四名同学跳高成绩最稳定的是丁, 故选:D .根据方差的意义求解可得.本题主要考查方差,解题的关键是掌握方差的意义:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.6.【答案】B【解析】解:∵∠ABC =(5−2)×180°5=108°,△ABC 是等腰三角形,∴∠BAC =∠BCA =36°. 故选:B .利用多边形的内角和定理和等腰三角形的性质即可解决问题.本题主要考查了多边形的内角和定理和等腰三角形的性质.n 边形的内角和为:180°(n −2).7.【答案】A【解析】解:A、∵四边形ABCD是平行四边形,AC=BD,∴四边形ABCD是矩形;故选项A符合题意;B、∵四边形ABCD是平行四边形,AB=BC,∴平行四边形ABCD是菱形;故选项B不符合题意;C、∵四边形ABCD是平行四边形,∴AB//CD,∴∠BAC=∠ACD,∵∠BAC=∠CAD,∴∠ACD=∠CAD,∴AD=CD,∴平行四边形ABCD是菱形;故选项C不符合题意;D、∵四边形ABCD是平行四边形,AC⊥BD,∴平行四边形ABCD是菱形;故选项D不符合题意;故选:A.根据矩形的判定方法和菱形的判定方法分别对各个选项进行判断,即可得出结论.本题考查矩形的判定、菱形的判定、平行四边形的性质、等腰三角形的判定等知识;熟练掌握矩形和菱形的判定方法是解题的关键,属于中考常考题型.8.【答案】C【解析】解:用反证法证明命题“若√a2=a,则a≥0”时,第一步应假设a<0.故选:C.用反证法证明命题的真假,先假设命题的结论不成立,从这个结论出发,经过推理论证,得出矛盾;由矛盾判定假设不正确,从而肯定命题的结论正确.考查了反证法,反证法是指“证明某个命题时,先假设它的结论的否定成立,然后从这个假设出发,根据命题的条件和已知的真命题,经过推理,得出与已知事实(条件、公理、定义、定理、法则、公式等)相矛盾的结果.这样,就证明了结论的否定不成立,从而间接地肯定了原命题的结论成立.”9.【答案】A【解析】解:设快递量平均每年增长率为x,依题意,得:500(1+x)2=740.故选:A.设快递量平均每年增长率为x,根据我国2018年及2020年的快递业务量,即可得出关于x的一元二次方程,此题得解.本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.10.【答案】B【解析】解:连接OP,∵四边形ABCD是菱形,AC=12,BD=16,∴AC⊥BD,BO=12BD=8,OC=12AC=6,∴BC=√OB2+OC2=√64+36=10,∵PE⊥AC,PF⊥BD,AC⊥BD,∴四边形OEPF是矩形,∴FE=OP,∵当OP⊥BC时,OP有最小值,此时S△OBC=12OB×OC=12BC×OP,∴OP=6×810=4.8,∴EF的最小值为4.8,故选:B.由菱形的性质可得AC⊥BD,BO=12BD=8,OC=12AC=6,由勾股定理可求BC的长,可证四边形OEPF是矩形,可得EF=OP,OP⊥BC时,OP有最小值,由面积法可求解.本题考查了菱形的性质,矩形的判定和性质,勾股定理,掌握菱形的性质是本题的关键.11.【答案】√3【解析】解:√6÷√2=√6÷2=√3,故答案为:√3.根据二次根式的除法法则:√a√b =√ab(a≥0,b>0)进行计算即可.此题主要考查了二次根式的除法,关键是掌握计算法则.12.【答案】−3【解析】解:∵x=1是方程x2+ax+2=0的一个根,∴1+a+2=0,∴a=−3.故答案为:−3.把x=1代入方程得到关于a的方程,解方程即可.本题考查了一元二次方程的解的概念:使方程两边成立的未知数的值叫方程的解.13.【答案】10【解析】解:这组数据中数字10出现2次,次数最多,所以这组数据的众数是10,故答案为:10.根据众数的概念求解可得.本题主要考查众数,解题的关键是掌握众数的定义:一组数据中出现次数最多的数据叫做众数.14.【答案】2516【解析】解:根据题意得k≠0且△=(−5)2−4k×4=0,.解得k=2516.故答案为2516根据判别式的意义得到△=(−5)2−4k×4=0,本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2−4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.15.【答案】4【解析】解:∵坡AB的坡比是1:√3,坝高BC=2m,∴AC=2√3,由勾股定理得,AB=√BC2+AC2=4(m),故答案为:4.根据坡度的概念求出AC,根据勾股定理求出AB.本题考查的是解直角三角形的应用−坡度坡角问题,掌握坡度的概念是解题的关键.16.【答案】1.5【解析】解:∵DE为△ABC的中位线,BC=3.5,∴DE=12在Rt△AFB中,∠AFB=90°,D是AB的中点,∴DF=1AB=2,2∴EF=DE−DF=1.5,故答案为:1.5.根据三角形中位线定理求出DE,根据直角三角形的性质求出DF,结合图形计算,得到答案.本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.17.【答案】8√2+4.【解析】解:在图2中加上节点K:观察图1和图2可知:EK=EF=FL=HG=12BD,JI=KH=LG=12EK=14BD,EJ=IH,∵正方形ABCD的边长为4CM,∴BD=√42+42=4√2,FL=EF=HG=12×4√2=2√2,JI=KH=LG=12EK=14×4√2=√2,则EJ=IH=2,∴六边形EFGKIJ的周长为:EJ+JI+IH+HG+(LG+FL)+EF,=2+√2+2+2√2+√2+2√2+2√2,=8√2+4,故答案为:8√2+4.七巧板由正方形分割成七小块(其中:五块等腰直角三角形,一块正方形和一块平行四边形组成),再根据图形的特点,由正方形的性质和勾股定理求出各板块的边长,即可求出图2中六边形的周长.本题考查七巧板的识图以及正方形的性质和勾股定理,数形结合是解决本题的关键.18.【答案】2512【解析】解:从图2知,AC=5,AD=2a,当点P在点A时,此时,y=4a=S△BCP=S△ABC,此时,AB=BC=AD=2a,即△ABC为等腰三角形,过点B作BH⊥AC于点H,则CH=AH=12AC=52,在△ABC中,S△ABC=12AC×BH=12×5×BH=4a,解得BH=8a5,在Rt△HBC中,BC2=BH2+CH2,即(2a)2=(8a5)2+(52)2,解得a=±2512(舍去负值),故答案为2512.从图2知,AC=5,AD=2a,在△ABC中利用S△ABC=12AC×BH=12×5×BH=4a,求得BH=8a5,最后在Rt△HBC中,利用勾股定理即可求解.本题考查的是动点图象问题,涉及到三角形的面积公式、菱形和等腰三角形的性质,勾股定理的运用等,此类问题关键是:弄清楚不同时间段,图象和图形的对应关系,进而求解.19.【答案】解:(1)原式=(4+4√2)×2−8=8+8√2−8=8√2;(2)∵x2−4x=−1,∴x2−4x+4=−1+4,即(x−2)2=3,则x−2=±√3,∴x=2±√3,即x1=2+√3,x2=2−√3.【解析】(1)先化简二次根式,再计算乘法,最后计算加减可得;(2)利用配方法求解可得.本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.20.【答案】解:(1)如图,矩形ABCD即为所求.(2)如图,正方形ADBC即为所求.【解析】(1)利用数形结合的思想解决问题即可.(2)利用数形结合的思想解决问题即可.本题考查作图−应用与设计,矩形的判定和性质,正方形的判定和性质等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.21.【答案】1=1(次),【解析】解:(1)这50名出行学生使用共享单车次数的中位数是1+12故答案为:1;×(0×12+1×14+2×4+3×8+ (2)这50名出行学生平均每人使用共享单车1504×8+5×4)=1.96(次);=440(人).(3)估计这天使用共享单车次数在3次以上(含3次)的学生有1100×8+8+450(1)根据中位数的概念求解可得;(2)利用加权平均数的概念列式计算可得;(3)用总人数乘以样本中使用共享单车次数在3次以上(含3次)的学生人数占被调查人数的比例.本题考查了中位数、平均数的概念以及利用样本平均数估计总体.抓住概念进行解题,难度不大,但是中位数一定要先将所给数据按照大小顺序重新排列后再求,以免出错.22.【答案】4√5【解析】(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB//CD,∴DF//BE,∵CF=AE,∴DF=BE,∴四边形BFDE是平行四边形,∵DE⊥AB,∴∠DEB=90°,∴四边形BFDE是矩形.(2)解:∵AB//CD,∴∠BAF=∠AFD,∵AF平分∠BAD,∴∠DAF=∠AFD,∴AD=DF,在Rt△ADE中,∵AE=3,DE=4,∴AD=√32+42=5,∴DF=5,∵四边形DEBF是矩形,∴BE=DF=5,BF=DE=4,∠ABF=90°,∴AB=AE+BE=8,∴AF=√AB2+BF2=√82+42=4√5;故答案为:4√5.(1)根据有一个角是90度的平行四边形是矩形即可判定.(2)首先证明AD=DF,求出AD=5,由矩形的性质得BE=DF=5,BF=DE=4,则AB=AE+BE=8,由勾股定理即可解决问题.本题考查了平行四边形的判定和性质,矩形的判定和性质、角平分线的定义、等腰三角形的判定、勾股定理等知识,解题的关键是灵活运用所学知识解决问题.23.【答案】25000【解析】解:(1)设通道的宽为x米,根据题意得:(58−2x)(22−2x)=700,解得:x=36(舍去)或x=4,答:甬道的宽为4米;(2)设月租金上涨a元,设停车场的月租金收入为w元,根据题意得:w=(300+a)(70−110a)=−110(a−700)(a+300),∵−110<0,故w有最大值,当a=12(700−300)=200(元)时,w的最大值为25000(元),故答案为25000.(1)设通道的宽为x米,根据矩形的面积公式列出方程并解答.(2)设车位的月租金上涨a元,则租出的车位数量是(70−110a)个,根据“月租金=每个车位的月租金×车位数”列出函数表达式,进而求解.本题考查了二次函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,进而求解.24.【答案】4 4 83【解析】解:(1)对于y=2x−4,令x=0,则y=−4,令y=0,即2x−4=0,解得x=2,故点D、G的坐标分别为(2,0)、(0,−4),则点A(4,0),即正方形的边长为4,故点B(4,4),故答案为4,4;(2)如题干图2,∵点E、点F关于直线DG对称,∴BE=BF,EG=GF,而BG=BG,∴△BGE≌△BGF(SSS),∴∠EBG=∠FBG,∵BF//EG,∴∠GBF=∠EGB,∴∠EBG=∠EGB,∴BE=GE,∵BE=BF,EG=GF,∴EB=BF=FG=GE,∴四边形BEGF为菱形;(3)①∵S△BEG=58S正方形OABC,∴12×GE×BC=58×4×4,即12×|m+4|×4=10,解得m=1或−9,故CE=3或13;②如下图,当B,E,F,N四点构成的四边形为矩形时,∵BE=BF,则该矩形为正方形,则∠EBF为直角,故点F作x轴的平行线交BA的延长线于点T,∵∠CBE+∠EBA=90°,∠EBA+∠FBA=90°,∴∠CBE=∠FBA,∵∠BCE=∠BTF=90°,BE=BF,∴△BCE≌△BTF(AAS),∴CE=TF=4−m,BT=BC,故点A、T重合,则点F在x轴上,则AF=CE=4−m,故点F(8−m,0),∵GE=GF,∴(m+4)2=(8−m)2+(−4)2,解得:m=83,故答案为83.(1)对于y=2x−4,令x=0,则y=−4,令y=0,即2x−4=0,解得x=2,故点D、G的坐标分别为(2,0)、(0,−4),则点A(4,0),即可求解;(2)证明△BGE≌△BGF(SSS),则可证∠EBG=∠EGB,则BE=GE,进而求解;(3)①S△BEG=58S正方形OABC,即12×GE×BC=58×4×4,则12×|m+4|×4=10,即可求解;②当B,E,F,N四点构成的四边形为矩形时,则该矩形为正方形,然后证明△BCE≌△BGF(AAS),得到F(8−m,0),再利用GE=GF,即可求解.本题考查的是一次函数综合运用,涉及到一次函数的性质、菱形的性质、三角形全等等,其中(3)①,要注意分类求解,避免遗漏.。
山东省2019-2020学年八年级语文下学期期中测试卷二(含答案)
山东省2019-2020学年下学期期中测试卷(二)八年级语文注意事项:1.本试卷共8页,共150分。
考试时间为120分钟。
考生答题全部答在答题卡上,答在本试卷上无效。
2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上。
3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑。
如需改动,请用橡皮擦干净后,再选涂其他答案。
答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡的指定位置,在其他位置答题一律无效。
一、(20分)1.下列加点字注音全部正确的一项是()(4分)A.脑畔(..pàn)眼眶.(kuànɡ)海棠.(táng)戛.然而止(jiá)B.羁.绊(jī)登.时(dēnɡ)陨.石(yuán)天衣无缝.(fènɡ)C.凫.水(fú)怅惘.(wánɡ)山麓.(lù)豁.然开朗(huò)D.凋.零(diāo)家眷.(juàn)沼.泽(zhǎo)窈窕.淑女(zhào)2.下列词语中字书写完全正确的一项是()(4分)A.凫水棹船涌跃海枯石烂B.蹿掇皎洁疲乏草长莺飞C.争讼退色幽悄大彻大悟D.严峻震撼燎原目空一切3.下面句子中加点词语使用正确的一项是()(4分)A.在老师和同学们的帮助下,小玲对学习的重要性终于大彻大悟....。
B.随着互联网在中国的兴起与普及,网络诈骗手段花样百出,令人叹为观止....。
C.那时我不懂人情世故....,心还像素丝那样纯洁。
D.这场轰轰烈烈的活动进行到中途戛然而止....,实在让人费解。
4.下列句子没有语病的一项是()(4分)A.传统文化源远流长,其中不少优秀的文化著作,可作为青少年人格教育的读本。
B.“一带一路”国际合作高峰论坛,是一次共商合作大计、共建合作平台、共享合作成果。
2019-2020学年度八年级下册语文期中考试题(含解析)
八年级语文(下)期中测试题一、积累与运用(40分)(一)选择题(每题3分,共30分)1.(原创题)下列加点字注音完全正确的一项是(C)A.撺掇( cuān)家醅(pēi)蓦然(mò) 戛然而止(gā)B.亢奋(kàng) 羁绊(jī) 恣意(zì) 销声匿迹(lì)C.翩然(piān) 萌发(méng) 两栖(qī) 草长莺飞(yīng)D.狩猎(shòu) 瑕疵(cī) 迁徙(xǐ) 如法炮制(pào)解析:A.戛然而止(jiá);B.销声匿迹(nì);D.如法炮制(páo)。
2.(原创题)下列词语书写有错别字的一项是(C)A.一马当先顾名思义如法炮制叹为观止B.戛然而止销声匿迹周而复始目空一切C.抢词夺理挑拨离间若无其事出类拔萃D.如饥似渴理直气壮打抱不平难以置信解析:C.抢——强。
3.(2017·毕节中考)下列句子中加点成语使用恰当的一项是(D)A.中考临近,室友们都在认真复习,丁刚同学却苦心孤诣地沉迷游戏。
B.这道数学题很难,在老师的反复讲解下,同学们终于大彻大悟了。
C.她性格孤僻,常常妄自菲薄,大家都认为她是一个自负的人。
D.生活对于任何人都非易事,我们必须有坚忍不拔的精神,还要有信心。
解析:A.褒贬失当、前后矛盾;B.语义过重;C.前后矛盾;D.坚忍不拔,形容信念坚定,意志顽强,不可动摇。
使用正确。
4.下列句子没有语病的一项是A.著名媒体人“罗胖”提出这样一个概念,他认为,未来中国人必须适应“U盘化生存”,即自带信息、不装系统、随时插拔、自由协作。
B.与早餐、中餐相比,晚餐宜少吃。
长期晚餐过饱,反复刺激胰岛素大量分泌,往往造成胰岛素细胞提前衰竭而埋下糖尿病。
C.精神颜值,是衡量一个人内心善良或靓丽的数值。
精神颜值的高低代表了一个人心灵美的程度,相对外表颜值高只是一时而言,精神颜值则可以永葆青春。
2019-2020学年北京八中八年级(下)期中数学试卷
2019-2020学年北京八中八年级(下)期中数学试卷一、选择题(每题3分,共30分)1.(3分)下列二次根式中,属于最简二次根式的是()A.B.C.D.2.(3分)下列各式中,计算正确的是()A.B.=﹣2C.=3D.23.(3分)已知n是正整数,是整数,则n的值可以是()A.5B.7C.9D.104.(3分)如图,▱ABCD的对角线交点是直角坐标系的原点,BC∥x轴,若顶点C坐标是(5,3),BC=8,则顶点D的坐标是()A.(3,﹣3)B.(﹣3,3)C.(5,﹣3)D.(3,﹣5)5.(3分)如图,在▱ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为()A.3B.2.5C.2D.1.56.(3分)已知a=3,b=2,c=,将其按照从小到大的顺序排列,正确的是()A.b<c<a B.b<a<c C.a<c<b D.c<a<b 7.(3分)如图,小明将一张长为20cm,宽为15cm的长方形纸(AE >DE)剪去了一角,量得AB=3cm,CD=4cm,则剪去的直角三角形的斜边长为()A.5cm B.12cm C.16cm D.20cm 8.(3分)如图,菱形ABCD,E是对角线AC上一点,将线段DE绕点E顺时针旋转角度2α,点D恰好落在BC边上点F处,则∠DAB 的度数为()A.αB.90°﹣αC.180°﹣2αD.2α9.(3分)有公共边的两个直角三角形,称为“双生直角三角形”.下列给定的数组中,不能构成“双生直角三角形”边长的是()A.3,4,5,12,13B.,4,,3,5C.7,15,20,24,25D.5,6,8,10,510.(3分)如图,矩形ABCD中,AB=9,AD=3,点E从D向C 以每秒1个单位的速度运动,以AE为一边在AE的左上方作正方形AEFG同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当点F落在直线MN上,设运动的时间为t,则t的值为()A.1B.4C.D.二、填空题(每题3分,共30分)11.(3分)已知二次根式,写出x的范围.12.(3分)化简二次根式:=,=.13.(3分)计算:=,()2=.14.(3分)如图,在△ABC中,∠B=30°,∠BAC=105°,AB=6,则∠C=°,BC的长是.15.(3分)如图,菱形ABCD的对角线长分别为2和4,EF∥DC分别交AD,BC于点E,F,在EF上任取两点G,H,那么图中阴影部分的面积为.16.(3分)如图,已知△ABC中,∠BAC=68°,点D、E、F分别是三角形三边AB,AC,BC的中点,AM是三角形BC边上的高,连接DM,EM,EF,则∠DME=°,∠DFE=°.17.(3分)已知,如图,四边形ABCD,AC,BD交于点O,请从给定四个条件:①AB=CD;②AD∥BC;③∠BAD=∠BCD;④BO=DO中选择两个,使得构成四边形可判定为平行四边形.你的选择是.18.(3分)已知a+=7,则=,a﹣=.19.(3分)我们学完二次根式后,爱思考的小鲍和小黄提出了一个问题:我们可以算22,3﹣2的值,我们可以算,的值吗?金老师说:也是可以的,你们可以查阅资料来进行学习.他们查阅资料后,发现了这样的结论:(a≥0),例如:,=8,那请你根据以上材料,写出=,=.20.(3分)已知,如图:一张矩形纸片ABCD,AB=6,AD=8,E为AD边上一动点,将矩形沿BE折叠,要使点A落在BC上,则折痕BE的长度是;若点A落在AC上,则折痕BE与AC 的位置关系是;若翻折后A点的对应点是A'点,连接DA',则在点E运动的过程中,DA'的最小值是.三、解答题(21题12分,22题4分,23题5分,24题6分,25题6分,26题7分,共40分)21.(12分)计算(1);(2)2;(3).22.(4分)小易同学在数学学习时,遇到这样一个问题:如图,已知点P在直线l外,请用一把刻度尺(仅用于测量长度和画直线),画出过点P且平行于l的直线,并简要说明你的画图依据.小易想到一种作法:①在直线l上任取两点A、B(两点不重合);②利用刻度尺连接AP并延长到C,使PC=AP;③连接BC并量出BC中点D;④作直线PD.∴直线PD即为直线l的平行线.(1)请依据小易同学的作法,补全图形.(2)证明:∵PC=AP,∴P为AC的中点,又∵D为BC中点,∴PD∥AB().(3)你还有其他画法吗?请画出图形,并简述作法.作法:23.(5分)求代数式a+的值,其中a=﹣2020.如图是小亮和小芳的解答过程.(1)的解法是错误的;(2)错误的原因在于未能正确地运用二次根式的性质:;(3)求代数式a+2的值,其中a=﹣2019.24.(6分)如图,已知等腰△ABC,AB=AC,AD平分∠BAC,E为AD上一动点,作EF平行AB,交AC于F,在AB上取一点G,使得AG=CF,连接GF.(1)根据题意补全图形;(2)求证四边形BEFG是平行四边形;(3)若∠BAC=50°,写出一个∠ABE的度数,使得四边形BEFG 是菱形.25.(6分)如图,每个小正方形的边长都是1.A、B、C、D均在网格的格点上.(1)直接写出四边形ABCD的面积与BC、BD的长度;(2)∠BCD是直角吗?请说出你的判断理由.(3)找到一个格点E,并画出四边形ABED,使得其面积与四边形ABCD的面积相等.26.(7分)如图,在正方形ABCD中,点E在边CD上(点E与点C、D不重合),过点E作FG⊥BE,FG与边AD相交于点F,与边BC的延长线相交于点G.(1)BE与FG有什么样的数量关系?请直接写出你的结论:;(2)DF、CG、CE的数量之间具有怎样的关系?并证明你所得到的结论.(3)如果正方形的边长是1,FG=1.5,直接写出点A到直线BE 的距离.一、填空题(5分)27.(5分)如图,在矩形ABCD中,AB=6,BC=8.(1)如果E、F分别是AD、BC的中点,G是对角线AC上的点,∠EGF=90°,则AG的长为;(2)如果E、F分别是AD、BC上的点,G,H是对角线AC上的点.下列判断正确的是.①在AC上存在无数组G,H,使得四边形EGFH是平行四边形;②在AC上存在无数组G,H,使得四边形EGFH是矩形;③在AC上存在无数组G,H,使得四边形EGFH是菱形;④当AG=时,存在E、F、H,使得四边形EGFH是正方形.二、作图题(6分)28.(6分)下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.(1)根据剪拼前后图形的面积关系求出拼成的正方形的边长;(2)如图甲,把六边形ABCDEF沿EH,BG剪成①②③三部分,请在图甲中画出将②③与①拼成的正方形,然后标出②③变动后的位置,并指出②③属于旋转、平移和轴对称中的哪一种变换;(3)在图乙中画出一种与图甲不同位置的两条裁剪线,并在图乙中画出将此六边形剪拼成的正方形.三、探究题(9分)29.(9分)学完二次根式一章后,小易同学看到这样一题:“函数y =中,自变量x的取值范围是什么?”这个问题很简单,根据二次根式的性质很容易得到自变量x的取值范围.联想到一次函数,小易想进一步研究这个函数的图象和性质.以下是他的研究步骤:第一步:函数y=中,自变量x的取值范围是.第二步:根据自变量取值范围列表:x﹣101234……y=01m2……m=.第三步:描点画出函数图象.在描点的时候,遇到了,这样的点,小易同学用所学勾股定理的知识,找到了画图方法,如图所示:你能否从中得到启发,在下面的y轴上标出表示2、m、的点,并画出y=的函数图象.第四步:分析函数的性质.请写出你发现的函数的性质(至少写两条):;第五步:利用函数y=图象解含二次根式的方程和不等式.(1)请在上面坐标系中画出y=x的图象,并估算方程=x的解.(2)不等式>x的解是.2019-2020学年北京八中八年级(下)期中数学试卷参考答案与试题解析一、选择题(每题3分,共30分)1.【解答】解:A、=4,不合题意;B、=,不合题意;C、=2,不合题意;D、为最简二次根式,符合题意,故选:D.2.【解答】解:(A)与不是同类二次根式,故不能合并,故A错误.(B)原式=2,故B错误.(D)原式=6×3=18,故D错误.故选:C.3.【解答】解:A、当n=5时,==2,不是整数,故A不符合题意;B、当n=7时,=,不是整数,故B不符合题意;C、当n=9时,==2,不是整数,故C不符合题意;D、当n=10时,==7,是整数,故D符合题意.故选:D.4.【解答】解:∵平行四边形ABCD的对角线交点是直角坐标系的原点,BC∥x轴,BC=8,C(5,3),∴B(﹣3,3),B与D关于原点O对称,∴D(3,﹣3);故选:A.5.【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=5,∴∠E=∠ECD,∵CE平分∠BCD,∴∠BCE=∠ECD,∴∠E=∠BCE,∴BE=BC=5,∴AE=BE﹣AB=5﹣3=2;故选:C.6.【解答】解:∵a=3=,b=2=,c==,∴b<c<a;故选:A.7.【解答】解:延长AB、DC相交于F,则BFC构成直角三角形,运用勾股定理得:BC2=(15﹣3)2+(20﹣4)2=122+162=400,所以BC=20.则剪去的直角三角形的斜边长为20cm.故选:D.8.【解答】解:如图,连接BE,∵四边形ABCD是菱形,∴CD=BC,∠DAB=∠DCB,∠ACD=∠ACB,在△DCE和△BCE中,,∴△DCE≌△BCE(SAS),∴DE=BE,∠EDC=∠EBC,∵将线段DE绕点E顺时针旋转角度2α,∴DE=EF,∠DEF=2α,∴BE=DE=EF,∴∠EBF=∠EFB,∴∠EDC=∠EBC=∠EFB,∵∠EFB+∠EFC=180°,∴∠EDC+∠EFC=180°,∵∠EDC+∠EFC+∠DEF+∠DCF=360°,∴∠DCF=180°﹣2α=∠DAB,故选:C.9.【解答】解:A.∵32+42=52,52+122=132,∴能组成两个直角三角形,公共边的长度是5,即是“双生直角三角形”,故本选项不符合题意;B.∵32+42=52,()2+()2≠32,()2+()2≠42,()2+()2≠52,∴不能组成两个直角三角形,即不是“双生直角三角形”,故本选项符合题意;C.∵72+242=252,152+202=252,∴能组成两个直角三角形,公共边的长度是25,即是“双生直角三角形”,故本选项不符合题意;D.∵62+82=102,52+(5)2=102,∴能组成两个直角三角形,公共边的长度是10,即是“双生直角三角形”,故本选项不符合题意;故选:B.10.【解答】解:过点F作FH⊥CD,交直线CD于点H,则∠EHF =90°,如图所示:∵四边形ABCD为矩形,∴∠ADE=90°,∴∠ADE=∠EHF,∵在正方形AEFG中,∠AEF=90°,AE=EF,∴∠AED+∠HEF=90°,∵∠HEF+∠EFH=90°,∴∠AED=∠EFH,在△ADE和△EHF中,,∴△ADE≌△EHF(AAS),∴AD=EH=3,由题意得:t+2t=3+9,∴t=4,故选:B.二、填空题(每题3分,共30分)11.【解答】解:由题意得,x﹣2≥0,解得,x≥2,故答案为:x≥2.12.【解答】解:==,=.故答案为:,.13.【解答】解:(+2)(﹣2)=5﹣4=1.(1﹣2)2=1﹣4+12=13﹣4.故答案为:1,13﹣4.14.【解答】解:如图,过点A作AD⊥BC于D,∵∠B=30°,AB=6,∴AD=AB=3,∠BAD=90°﹣30°=60°,由勾股定理得,BD=,∵∠BAC=105°,∴∠CAD=105°﹣60°=45°,∴△ACD是等腰直角三角形,∴CD=AD=3,∠C=45°,∴BC=BD+CD=3+3.故答案为:45;3+3.15.【解答】解:∵四边形ABCD是菱形,对角线长分别为2和4,∴AB∥DC,AD∥BC,菱形ABCD的面积=×2×4=4,∵EF∥DC,∴EF∥DC∥AB,∴四边形ABFE和四边形CDEF是平行四边形,∴△ABH的面积=平行四边形ABFE的面积,△CDG的面积=平行四边形CDEF的面积,∴△ABH的面积+△CDG的面积=菱形ABCD的面积=2,∴图中阴影部分的面积=4﹣2=2;故答案为:2.16.【解答】解:∵∠BAC=68°,∴∠B+∠C=180°﹣68°=112°,∵AM是三角形BC边上的高,∴∠AMB=∠AMC=90°,在Rt△AMB中,D是AB的中点,∴DM=AB=DB,∴∠DMB=∠B,同理可得,∠EMC=∠C,∴∠DMB+∠EMC=∠B+∠C=112°,∴∠DME=180°﹣(∠DMB+∠EMC)=68°,∵点D、E、F分别是三角形三边AB,AC,BC的中点,∴DF、EF分别是△ABC的中位线,DF∥AC,EF∥AB,∴∠DFB=∠C,∠EFC=∠B,∴∠DFB+∠EFC=∠B+∠C=112°,∴∠DFE=180°﹣(∠DFB+∠EFC)=68°,故答案为:68;68.17.【解答】解:选择②③或②④;理由如下:选择②③时,∵AD∥BC,∴∠BAD+∠ABC=180°,∵∠BAD=∠BCD,∴∠BCD+∠ABC=180°,∴AB∥CD,∴四边形ABCD是平行四边形;选择②④时,∵AD∥BC,∴∠OAD=∠OCB,在△OAD和△OCD中,,∴△OAD≌△OCD(AAS),∴OA=OC,又∵OB=OD,∴四边形ABCD是平行四边形;故答案为:②③或②④.18.【解答】解:∵a+=7,∴====3;a﹣=±=±=±=±3.故答案为3;±3.19.【解答】解:;.故答案为:;4.20.【解答】解:若将矩形沿BE折叠,点A落在BC上,∴AB=AE=6,∴BE=6,若将矩形沿BE折叠,点A落在AC上,∴AC⊥BE,如图,连接BD,∵AB=6,AD=8,∴BD===10,若翻折后A点的对应点是A'点,∴BA=BA'=6,∴点A'在以点B为圆心,6为半径的圆上,∴当点A'在线段BD上时,DA'有最小值=10﹣6=4,故答案为:6;AC⊥BE;4.三、解答题(21题12分,22题4分,23题5分,24题6分,25题6分,26题7分,共40分)21.【解答】解:(1)原式=×4﹣3×+=2﹣+=+;(2)原式=6÷5==;(3)原式=﹣1+2﹣+2=﹣.22.【解答】解:(1)如图,(2)故答案为三角形中位线定理;(3)如图,过P点作直线MP交直线l于点Q,作∠MPN=∠PQG,则直线PN∥直线l.23.【解答】解:(1)∵a=﹣2020,∴1﹣a=1﹣(﹣2020)=2021,故小芳开方时,出现错误,故答案为:小芳;(2)错误的原因在于未能正确地运用二次根式的性质:=|a|,故答案为:=|a|;(3)a+2=a+2,∵a=﹣2019,∴a﹣3<0,∴原式=a+2(3﹣a)=a+6﹣2a=6﹣a=6﹣(﹣2019)=6+2019=2025,即代数式a+2的值是2025.24.【解答】(1)解:如图,(2)证明:∵AB=AC,AG=CF,∴AF=BG,∵AD平分∠BAC,∴∠BAD=∠CAD,∵EF∥AB,∴∠AEF=∠EAB,∴∠AEF=∠F AE,∴EF=AF,∴EF=BG,而BG∥EF,∴四边形BEFG是平行四边形;(3)解:当FG=FE时,四边形BEFG为菱形,而FE=F A,∴F A=FG,∴∠FGA=∠FAG=50°,∵GF∥BE,∴∠ABE=∠AGF=50°,即当∠ABE=50°时,四边形BEFG是菱形.25.【解答】解:(1)由题意:S四边形ABCD=5×5﹣×1×5﹣×2×5﹣×1×2﹣×1×3﹣1=.BC==,BD==4.(2)结论:∠BCD不是直角.理由:∵CD==,BC=,BD=4,∴BC2+CD2=34,BD2=32,∴BC2+CD2≠BD2,∴∠BCD不是直角.(3)如图点E或点E′即为所求.26.【解答】解:(1)过点F作FH∥DC交BC于H,∵四边形ABCD是正方形,∴∠BCD=90°,BC=CD,AD∥BC,∵FH∥DC,∴∠FHG=90°,FH=CD,∵∠BCD=90°,FG⊥BE,∴∠EBC+∠BEC=90°,∠EBC+∠G=90°,∴∠G=∠BEC,在△BEC和△FGH中,,∴△BEC≌△FGH(AAS),∴BE=FG,故答案为:BE=FG;(2)DF+CG=CE,理由如下:∵FH∥DC,AD∥BC,∠BCD=90°,∴四边形FHCD为矩形,∴DF=HC,由(1)得,△BEC≌△FGH,∴HG=CE,∵HG=HC+CG=DF+CG,∴DF+CG=CE;(3)连接AE,过点A作AP⊥BE于P,∵△BEC≌△FGH,∴BE=FG=1.5,∵正方形的边长为1,∴△ABE的面积=×1×1=,则×BE×AP=,即××AP=,解得,AP=,即点A到直线BE的距离为.一、填空题(5分)27.【解答】解:(1)如图,∵四边形ABCD是矩形,∴AD∥BC,∠B=90°,AD=BC,∴AC===10,∵AD∥BC,∴∠EAO=∠FCO,∵E、F分别是AD、BC的中点,∴AE=CF=BF=DE,∴四边形ABFE是平行四边形,∴EF=AB=6,在△AEO和△CFO中,,∴△AEO≌△CFO(AAS),∴EO=FO=3,AO=CO=5,当点G在点O上方时,∵∠EGF=90°,EO=FO,∴GO=EO=3,∴AG=AO﹣GO=5﹣3=2,当点G'在点O下方时,∵∠EG'F=90°,EO=FO,∴G'O=EO=3,∴AG'=AO+G'O=5+3=8,综上所述:AG=2或8;(2)①在AC上存在无数组G,H,使得四边形EGFH是平行四边形,故该说法正确;②在AC上存在无数组G,H,使得四边形EGFH是矩形,故该说法正确;③在AC上存在无数组G,H,使得四边形EGFH是菱形,故该说法正确;④当AG=时,存在E、F、H,使得四边形EGFH是正方形,故答案为①②③④.二、作图题(6分)28.【解答】解:(1)根据剪拼前后图形的面积相等,得出拼成的正方形的边长==4,(2)如图,②③都属于平移,(3)如图乙:或者三、探究题(9分)29.【解答】解:第一步:∵x+1≥0,∴x≥﹣1,∴x的取值范围是x≥﹣1,故答案为:x≥﹣1;第二步:当x=2时,m==,故答案为:;第三步:根据勾股定理,得=,=,=,函数图象如图所示:第四步:根据函数图象可知:该函数的两条性质(答案不唯一):性质一:当x≥﹣1时,y随x的增大而增大;性质二:函数图象只有一个点在x轴上,其余的都在x轴上方;故答案为:当x≥﹣1时,y随x的增大而增大;函数图象只有一个点在x轴上,其余的都在x轴上方;第五步:(1)函数图象如下:利用函数图象可知:根据函数的交点估算方程=x的解是:x≈1.6;(2)根据函数图象可知:不等式>x的解是﹣1≤x<1.6.故答案为:﹣1≤x<1.6。
人教版初中数学八年级下册期中试卷(2019-2020学年湖北省鄂州市
2019-2020学年湖北省鄂州市八年级(下)期中数学试卷一.选择题(本大题有10小题,每题3分,共30分)1.(3分)下列各式中,最简二次根式是()A.B.C.D.2.(3分)下列计算正确的是()A.3﹣=3B.2+=2C.=﹣2D.=23.(3分)关于特殊四边形对角线的性质,矩形具备而平行四边形不一定具备的是()A.对角线互相平分B.对角线互相垂C.对角线相等D.对角线平分一组对角4.(3分)△ABC的三边分别为a,b,c,下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b ﹣c);③a:b:c=3:4:5.其中能判断△ABC是直角三角形的条件个数有()A.0个B.1个C.2个D.3个5.(3分)如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是()A.矩形B.菱形C.正方形D.无法判断6.(3分)如图所示,数轴上点A所表示的数为a,则a的值是()A.﹣1B.﹣+1C.+1D.7.(3分)如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是()A.2B.C.D.8.(3分)如图,在菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是()A.3B.4C.5D.69.(3分)如图图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑥个图形中菱形的个数为()A.42B.43C.56D.5710.(3分)如图,在Rt△ABC中,AB=AC,∠BAC=90°,D、E为BC上两点,∠DAE =45°,F为△ABC外一点,且FB⊥BC,F A⊥AE,则下列结论:①CE=BF;②BD2+CE2=DE2;③;④CE2+BE2=2AE2,其中正确的是()A.①②③④B.①②④C.①③④D.②③二、填空题(本大题共8小题,共24分)11.(3分)如果二次根式有意义,那么x的取值.12.(3分)已知ab<0,则化简后为.13.(3分)已知直角三角形的两条边长为3和4,则第三边的长为.14.(3分)如图,一根长18cm的筷子置于底面直径为5cm.高为12cm圆柱形水杯中,露在水杯外面的长度hcm,则h的取值范围是.15.(3分)如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=10,则EF的长为.16.(3分)如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3,上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是.17.(3分)如图,在菱形ABCD中,AB=18cm,∠A=60°,点E以2cm/s的速度沿AB 边由A向B匀速运动,同时点F以4cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为.18.(3分)将五个边长都为4cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为cm2.三、解答题(共7小题,满分66分)19.(12分)解答题计算题:(1)+﹣﹣4(2)(3)已知=0,求的值.20.(8分)如图,在▱ABCD中,经过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.(1)求证:△AED≌△CFB;(2)求证:四边形AFCE是平行四边形21.(8分)如图,把一块三角形(△ABC)土地挖去一个直角三角形(∠ADC=90°)后,测得CD=6米,AD=8米,BC=24米,AB=26米.求剩余土地(图中阴影部分)的面积.22.(8分)小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E =60°,量得DE=8,试求BD的长.23.(10分)如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)判断OE与OF的大小关系?并说明理由;(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;24.(8分)如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.(1)求证:△ABG≌△AFG;(2)求BG的长.25.(12分)如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM的平分线BF相交于点F.(1)如图1,当点E在AB边得中点位置时:①通过测量DE、EF的长度,猜想DE与EF满足的数量关系是.②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是,请证明你的猜想.(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.2019-2020学年湖北省鄂州市八年级(下)期中数学试卷参考答案与试题解析一.选择题(本大题有10小题,每题3分,共30分)1.(3分)下列各式中,最简二次根式是()A.B.C.D.【分析】A、D选项的被开方数中都含有能开得尽方的因数或因式;C选项的被开方数中含有分母;因此这三个选项都不是最简二次根式.所以只有B选项符合最简二次根式的要求.【解答】解:因为:A、=3;C、=;D、=|a|;所以,这三个选项都可化简,不是最简二次根式.故选:B.【点评】在判断最简二次根式的过程中要注意:(1)在二次根式的被开方数中,只要含有分数或小数,就不是最简二次根式;(2)在二次根式的被开方数中的每一个因式(或因数),如果幂的指数大于或等于2,也不是最简二次根式.2.(3分)下列计算正确的是()A.3﹣=3B.2+=2C.=﹣2D.=2【分析】直接利用二次根式的性质分别化简计算即可.【解答】解:A、3﹣=2,故此选项错误;B、2+无法计算,故此选项错误;C、=2,故此选项错误;D、=2,正确.故选:D.【点评】此题主要考查了二次根式的hi额性质与化简,正确化简二次根式是解题关键.3.(3分)关于特殊四边形对角线的性质,矩形具备而平行四边形不一定具备的是()A.对角线互相平分B.对角线互相垂C.对角线相等D.对角线平分一组对角【分析】根据矩形、平行四边形的性质即可判断;【解答】解:矩形的对角线互相平分且相等,平行四边形的对角线互相平分,∴矩形具备而平行四边形不一定具备的是矩形的对角线相等,故选:C.【点评】本题考查矩形的性质,矩形具有平行四边形的性质,又具有自己的特性,要注意运用矩形具备而一般平行四边形不具备的性质.如,矩形的对角线相等是常考内容.4.(3分)△ABC的三边分别为a,b,c,下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b ﹣c);③a:b:c=3:4:5.其中能判断△ABC是直角三角形的条件个数有()A.0个B.1个C.2个D.3个【分析】根据三角形的内角和定理和已知求出最大角∠B的度数,即可判断①;根据已知得出a2+c2=b2,根据勾股定理的逆定理即可判断②;设a=3k,b=4k,c=5k求出a2+c2=b2,根据勾股定理的逆定理即可判断③.【解答】解:①∵∠A=∠B﹣∠C,∴∠A+∠C=∠B,∵∠A+∠B+∠C=180°,∴2∠B=180°,∴∠B=90°,∴△ABC是直角三角形,∴①正确;②a2=(b+c)(b﹣c),∴a2=b2﹣c2,∴a2+c2=b2,∴△BAC是直角三角形,∴②正确;③∵a:b:c=3:4:5,∴设a=3k,b=4k,c=5k,∵a2+b2=25k2,c2=25k2,∴a2+b2=c2,∴△ABC是直角三角形,∴③正确;故选:D.【点评】本题考查了勾股定理的逆定理和三角形的内角和定理的应用,主要考查学生的辨析能力,题目比较典型,难度适中.5.(3分)如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是()A.矩形B.菱形C.正方形D.无法判断【分析】由条件可知AB∥CD,AD∥BC,再再证明AB=BC即可解决问题.【解答】解:过点D作DE⊥AB于E,DF⊥BC于F.∵两张长方形纸条的宽度相等,∴DE=DF.又∵平行四边形ABCD的面积=AB•DE=BC•DF,∴AB=BC,∴平行四边形ABCD为菱形.故选:B.【点评】本题考查了菱形的判定,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.6.(3分)如图所示,数轴上点A所表示的数为a,则a的值是()A.﹣1B.﹣+1C.+1D.【分析】首先计算出直角三角形斜边的长,然后再确定a的值.【解答】解:∵=,∴a=﹣1,故选:A.【点评】此题主要考查了实数与数轴,关键是利用勾股定理计算出直角三角形斜边长.7.(3分)如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是()A.2B.C.D.【分析】由OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,易得△OCP是等腰三角形,∠COP=30°,又由含30°角的直角三角形的性质,即可求得PE的值,继而求得OP的长,然后由直角三角形斜边上的中线等于斜边的一半,即可求得DM的长.【解答】解:∵OP平分∠AOB,∠AOB=60°,∴∠AOP=∠COP=30°,∵CP∥OA,∴∠AOP=∠CPO,∴∠COP=∠CPO,∴OC=CP=2,∵∠PCE=∠AOB=60°,PE⊥OB,∴∠CPE=30°,∴CE=CP=1,∴PE==,∴OP=2PE=2,∵PD⊥OA,点M是OP的中点,∴DM=OP=.故选:C.【点评】此题考查了等腰三角形的性质与判定、含30°直角三角形的性质以及直角三角形斜边的中线的性质.此题难度适中,注意掌握数形结合思想的应用.8.(3分)如图,在菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是()A.3B.4C.5D.6【分析】设AC交BD于O,作E关于AC的对称点N,连接NF,交AC于P,则此时EP+FP的值最小,根据菱形的性质推出N是AD中点,P与O重合,推出PE+PF=NF =AB,根据勾股定理求出AB的长即可.【解答】解:设AC交BD于O,作E关于AC的对称点N,连接NF,交AC于P,则此时EP+FP的值最小,∴PN=PE,∵四边形ABCD是菱形,∴∠DAB=∠BCD,AD=AB=BC=CD,OA=OC,OB=OD,AD∥BC,∵E为AB的中点,∴N在AD上,且N为AD的中点,∵AD∥CB,∴∠ANP=∠CFP,∠NAP=∠FCP,∵AD=BC,N为AD中点,F为BC中点,∴AN=CF,在△ANP和△CFP中∵,∴△ANP≌△CFP(ASA),∴AP=CP,即P为AC中点,∵O为AC中点,∴P、O重合,即NF过O点,∵AN∥BF,AN=BF,∴四边形ANFB是平行四边形,∴NF=AB,∵菱形ABCD,∴AC⊥BD,OA=AC=4,BO=BD=3,由勾股定理得:AB==5,故选:C.【点评】本题考查了轴对称﹣最短路线问题,勾股定理,菱形的性质等知识点的应用,关键是理解题意确定出P的位置和求出AB=NF=EP+FP,题目比较典型,综合性比较强,主要培养学生的计算能力.9.(3分)如图图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑥个图形中菱形的个数为()A.42B.43C.56D.57【分析】设第n个图形中一共有a n个菱形(n为正整数),根据各图形中菱形个数的变化可得出变化规律“a n=n2+n+1(n为正整数)”,再代入n=6即可求出结论.【解答】解:设第n个图形中一共有a n个菱形(n为正整数),∵a1=12+2=3,a2=22+3=7,a3=32+4=13,a4=42+5=21,…,∴a n=n2+n+1(n为正整数),∴a6=62+7=43.故选:B.【点评】本题考查了规律型:图形的变化类,根据各图形中菱形个数的变化,找出变化规律“a n=n2+n+1(n为正整数)”是解题的关键.10.(3分)如图,在Rt△ABC中,AB=AC,∠BAC=90°,D、E为BC上两点,∠DAE =45°,F为△ABC外一点,且FB⊥BC,F A⊥AE,则下列结论:①CE=BF;②BD2+CE2=DE2;③;④CE2+BE2=2AE2,其中正确的是()A.①②③④B.①②④C.①③④D.②③【分析】根据等腰直角三角形的性质,判断出△AFB≌△AEC,即可得出CE=BF,根据勾股定理与等量代换可得②正确,根据在等腰三角形中,角平分线与中线为一条直线即可得出③,再根据勾股定理以及等量代换即可得出④.【解答】解:①∵∠BAC=90°,F A⊥AE,∠DAE=45°,∴∠CAE=90°﹣∠DAE﹣∠BAD=45°﹣∠BAD,∠F AB=90°﹣∠DAE﹣∠BAD=45°﹣∠BAD,∴∠F AB=∠EAC,∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵FB⊥BC,∴∠F AB=45°,∴△AFB≌△AEC,∴CE=BF,故①正确,②:由①中证明△AFB≌△AEC,∴AF=AE,∵∠DAE=45°,F A⊥AE,∴∠F AD=∠DAE=45°,∴△AFD≌△AED,连接FD,∵FB=CE,∴FB2+BD2=FD2=DE2,故②正确,③:如图,设AD与EF的交点为G,∵∠F AD=∠EAD=45°,AF=AE,∴AD⊥EF,EF=2EG,∴S△ADE=•AD•EG==,故③正确,④:∵FB2+BE2=EF2,CE=BF,∴CE2+BE2=EF2,在RT△AEF中,AF=AE,AF2+AE2=EF2,∴EF2=2AE2,∴CE2+BE2=2AE2,故④正确.故选:A.【点评】本题考查了勾股定理、全等三角形的判定定理以及等腰直角直角三角形的性质,此题涉及的知识面比较广,解题时要注意仔细分析,难度较大.二、填空题(本大题共8小题,共24分)11.(3分)如果二次根式有意义,那么x的取值x≥4.【分析】直接利用二次根式有意义的条件得出答案.【解答】解:依题意有x﹣4≥0,解得:x≥4.故答案为:x≥4.【点评】此题主要考查了二次根式有意义的条件,正确把握定义是解题关键.12.(3分)已知ab<0,则化简后为﹣a.【分析】根据ab<0和二次根式有意义的条件可分析出a<0,则b>0,然后再根据二次根式的性质进行化简即可.【解答】解:∵ab<0,∴a、b为异号,∵=,ab<0,∴a<0,∴b>0,∴==﹣a,故答案为:﹣a.【点评】此题主要考查了二次根式的性质与化简,关键是正确分析出a和b的符号.13.(3分)已知直角三角形的两条边长为3和4,则第三边的长为5或.【分析】本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,因此两条边中的较长边4既可以是直角边,也可以是斜边,所以求第三边的长必须分类讨论,即4是斜边或直角边的两种情况,然后利用勾股定理求解.【解答】解:设第三边为x,(1)若4是直角边,则第三边x是斜边,由勾股定理得:32+42=x2,∴x=5;(2)若4是斜边,则第三边x为直角边,由勾股定理得:32+x2=42,∴x=;∴第三边的长为5或.故答案为:5或.【点评】本题考查了利用勾股定理解直角三角形的能力,当已知条件中没有明确哪是斜边时,要注意讨论,一些学生往往忽略这一点,造成丢解.14.(3分)如图,一根长18cm的筷子置于底面直径为5cm.高为12cm圆柱形水杯中,露在水杯外面的长度hcm,则h的取值范围是5cm≤h≤6cm.【分析】根据杯子内筷子的长度的取值范围得出杯子外面长度的取值范围,即可得出答案.【解答】解:∵将一根长为18cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,∴在杯子中筷子最短是等于杯子的高,最长是等于杯子斜边长度,∴当杯子中筷子最短是等于杯子的高时,x=12,最长时等于杯子斜边长度是:x==13,∴h的取值范围是:(18﹣13)cm≤h≤(18﹣12)cm,即5cm≤h≤6cm.故答案为:5cm≤h≤6cm.【点评】此题主要考查了勾股定理的应用,正确得出杯子内筷子的取值范围是解决问题的关键.15.(3分)如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=10,则EF的长为3.【分析】根据三角形中位线定理求出DE,根据直角三角形的性质求出DF,计算即可.【解答】解:∵DE为△ABC的中位线,∴DE=BC=5,∵∠AFB=90°,D是AB的中点,∴DF=AB=2,∴EF=DE﹣DF=3,故答案为:3.【点评】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.16.(3分)如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3,上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是2.【分析】过A、C点作l3的垂线构造出直角三角形,根据三角形全等和勾股定理求出BC 的长,再利用勾股定理即可求出.【解答】解:作AD⊥l3于D,作CE⊥l3于E,∵∠ABC=90°,∴∠ABD+∠CBE=90°,又∵∠DAB+∠ABD=90°,∴∠BAD=∠CBE,又∵AB=BC,∠ADB=∠BEC,在△ABD与△BCE中,,∴△ABD≌△BCE(AAS),∴BE=AD=3,CE=2+3=5,在Rt△BCE中,根据勾股定理,得BC=,在Rt△ABC中,根据勾股定理,得AC==2,故答案为:2【点评】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.17.(3分)如图,在菱形ABCD中,AB=18cm,∠A=60°,点E以2cm/s的速度沿AB 边由A向B匀速运动,同时点F以4cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为3s.【分析】连接BD.易证△ADE≌△BDF,即可推出AE=BF,列出方程即可解决问题.【解答】解:连接BD.如图:∵四边形ABCD是菱形,∠A=60°,∴AD=CD=BC=AB=18,△ADB,△BDC都是等边三角形,∴AD=BD,∠ADB=∠DBF=60°,∵△DEF是等边三角形,∴∠EDF=60°,∴∠ADB=∠EDF,∴∠ADE=∠BDF,在△ADE和△BDF中,,∴△ADE≌△BDF(ASA),∴AE=BF,∴2t=18﹣4t,∴t=3,故答案为:3s.【点评】本题考查菱形的性质、等边三角形的判定和性质、全等三角形的判定与性质、一元一次方程等知识,解题的关键是利用全等三角形解决问题,属于中考常考题型.18.(3分)将五个边长都为4cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为16cm2.【分析】如图,连接AB、AF.由△ABE≌△AFG(ASA),推出S△ABE=S△AFG,推出S四=S△ABF=S正方形,推出S阴=4×S正方形=16即可解决问题.边形AEBG【解答】解:如图,连接AB、AF.∵∠EAG=∠BAF=90°,∴∠BAE=∠F AG,在△ABE和△AFG中,,∴△ABE≌△AFG(ASA),∴S△ABE=S△AFG,∴S四边形AEBG=S△ABF=S正方形,∴S阴=4×S正方形=16(cm2),故答案为:16.【点评】本题考查正方形的性质、全等三角形的判定和性质等知识,证明每一个阴影部分的面积等于正方形的面积的是解题的关键.三、解答题(共7小题,满分66分)19.(12分)解答题计算题:(1)+﹣﹣4(2)(3)已知=0,求的值.【分析】(1)先把各二次根式化简,然后合并即可;(2)先进行二次根式的除法运算,然后把各二次根式化简后合并即可;(3)根据分式为0的条件得到,解得,然后把x、y的值代入代数式,最利用分母有理化计算即可.【解答】解:(1)原式=2+3﹣﹣2=2;(2)原式=3﹣2﹣=3﹣2﹣2=﹣;(3)根据题意得,解得,所以原式===.【点评】本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.20.(8分)如图,在▱ABCD中,经过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.(1)求证:△AED≌△CFB;(2)求证:四边形AFCE是平行四边形【分析】(1)根据AAS,只要证明∠ADE=∠CBF,∠AED=∠CFB,AD=BC即可;(2)只要证明AE=CF,AE∥CF即可;【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠CBF=∠ADE,∵AE⊥BD,CF⊥BD,∴∠CFB=∠AED=90°,∴△AED≌△CFB(AAS).(2)证明:∵△AED≌△CFB,∴AE=CF,∵AE⊥BD,CF⊥BD,∴AE∥CF,∴四边形AFCE是平行四边形.【点评】本题考查平行四边形的性质和判定、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.21.(8分)如图,把一块三角形(△ABC)土地挖去一个直角三角形(∠ADC=90°)后,测得CD=6米,AD=8米,BC=24米,AB=26米.求剩余土地(图中阴影部分)的面积.【分析】先根据勾股定理求出AC的长,再根据勾股定理的逆定理判断出△ACB为直角三角形,再根据S阴影=AC×BC﹣AD×CD即可得出结论.【解答】解:在Rt△ADC中,∵CD=6米,AD=8米,BC=24米,AB=26米,∴AC2=AD2+CD2=82+62=100,∴AC=10(取正值).在△ABC中,∵AC2+BC2=102+242=676,AB2=262=676.∴AC2+BC2=AB2,∴△ACB为直角三角形,∠ACB=90°.∴S阴影=AC×BC﹣AD×CD=×10×24﹣×8×6=96(米2).答:剩余土地(图中阴影部分)的面积为:96米2.【点评】本题考查的是勾股定理在实际生活中的应用,有利于培养学生生活联系实际的能力.22.(8分)小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E =60°,量得DE=8,试求BD的长.【分析】过点F作FM⊥AD于M,利用在直角三角形中,30°角所对的直角边等于斜边的一半和平行线的性质以及等腰直角三角形的性质即可求出BD的长.【解答】解:过点F作FM⊥AD于M,∵∠EDF=90°,∠E=60°,∴∠EFD=30°,∵DE=8,∴EF=16,∴DF==8,∵EF∥AD,∴∠FDM=30°,∴FM=DF=4,∴MD==12,∵∠C=45°,∴∠MFB=∠B=45°,∴FM=BM=4,∴BD=DM﹣BM=12﹣4.【点评】本题考查了勾股定理的运用、平行线的性质以及等腰直角三角形的性质,解题的关键是作垂直构造直角三角形,利用勾股定理求出DM的长.23.(10分)如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)判断OE与OF的大小关系?并说明理由;(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;【分析】(1)利用平行线的性质得:∠OEC=∠ECB,根据角平分线的定义可知:∠ACE =∠ECB,由等量代换和等角对等边得:OE=OC,同理:OC=OF,可得结论;(2)先根据对角线互相平分证明四边形AECF是平行四边形,再由角平分线可得:∠ECF =90°,利用有一个角是直角的平行四边形可得结论;【解答】解:(1)OE=OF,理由如下:∵MN∥BC,∴∠OEC=∠ECB,∵CE平分∠ACB,∴∠ACE=∠ECB,∴∠OEC=∠ACE,∴OE=OC,同理可得:OC=OF,∴OE=OF;(2)当O为AC中点时,四边形AECF是矩形;理由如下:∵OA=OC,OE=OF(已证),∴四边形AECF是平行四边形,∵EC平分∠ACB,CF平分∠ACG,∴∠ACE=∠ACB,∠ACF=∠ACG,∴∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,即∠ECF=90°,∴四边形AECF是矩形.【点评】本题主要考查了平行四边形的判定、矩形的判定以及正方形的判定、平行线的性质、角平分线的定义,熟练掌握并区分平行四边形、矩形、正方形的判定是解题关键.24.(8分)如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.(1)求证:△ABG≌△AFG;(2)求BG的长.【分析】(1)首先证明AB=AF=AD,然后再证明∠AFG=90°,接下来,依据HL可证明△ABG≌△AFG;(2)利用勾股定理得出GE2=CG2+CE2,进而求出BG即可.【解答】解:(1)在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,∵将△ADE沿AE对折至△AFE,∴AD=AF,DE=EF,∠D=∠AFE=90°,∴AB=AF,∠B=∠AFG=90°,又∵AG=AG,在Rt△ABG和Rt△AFG中,,∴△ABG≌△AFG(HL);(2)∵△ABG≌△AFG,∴BG=FG,设BG=FG=x,则GC=6﹣x,∵E为CD的中点,∴CE=EF=DE=3,∴EG=3+x,∴在Rt△CEG中,32+(6﹣x)2=(3+x)2,解得x=2,∴BG=2.【点评】此题主要考查了勾股定理的综合应用以及翻折变换的性质,根据翻折变换的性质得出对应线段相等是解题关键.25.(12分)如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM的平分线BF相交于点F.(1)如图1,当点E在AB边得中点位置时:①通过测量DE、EF的长度,猜想DE与EF满足的数量关系是DE=EF.②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是NE=BF,请证明你的猜想.(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.【分析】(1)①根据图形可以得到DE=EF,NE=BF,②要证明这两个关系,只要证明△DNE≌△EBF即可.(2)DE=EF,连接NE,在DA边上截取DN=EB,证出△DNE≌△EBF即可得出答案.【解答】解:(1)①DE=EF;②NE=BF;理由如下:∵四边形ABCD为正方形,∴AD=AB,∠DAB=∠ABC=90°,∵N,E分别为AD,AB中点,∴AN=DN=AD,AE=EB=AB,∴DN=BE,AN=AE,∵∠DEF=90°,∴∠AED+∠FEB=90°,又∵∠ADE+∠AED=90°,∴∠FEB=∠ADE,又∵AN=AE,∴∠ANE=∠AEN,又∵∠A=90°,∴∠ANE=45°,∴∠DNE=180°﹣∠ANE=135°,又∵∠CBM=90°,BF平分∠CBM,∴∠CBF=45°,∠EBF=135°,在△DNE和△EBF中,∴△DNE≌△EBF(ASA),∴DE=EF,NE=BF.(2)DE=EF,理由如下:连接NE,在DA边上截取DN=EB,∵四边形ABCD是正方形,DN=EB,∴AN=AE,∴△AEN为等腰直角三角形,∴∠ANE=45°,∴∠DNE=180°﹣45°=135°,∵BF平分∠CBM,AN=AE,∴∠EBF=90°+45°=135°,∴∠DNE=∠EBF,∵∠NDE+∠DEA=90°,∠BEF+∠DEA=90°,∴∠NDE=∠BEF,在△DNE和△EBF中,∴△DNE≌△EBF(ASA),∴DE=EF.【点评】此题主要考查了正方形的性质以及全等三角形的判定与性质等知识,解决本题的关键就是求证△DNE≌△EBF.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年八年级下期中考试试卷卷首寄语:亲爱的同学,这学期的学习已近一半,这份试卷将记录你的自信、沉着、智慧和收获。
加油!第一部分:积累与运用(28 分)一.按课文内容或要求填空。
(11分)1.《清平乐·村居》表现老年夫妇温馨生活乐趣句子是:,2.《朝天子咏喇叭》一曲中比喻民穷财尽、家破人亡的句子是:。
3.《采薇》中烘托出士兵们因思乡之切而沉重抑郁的心境,也预示着归途艰辛的句子是:,。
4.《十五从军征》中写老兵归家所做事情的句子是:________ ____,。
5.《送别》中渲染离情别绪句子是:_______ ___________,_____________ _____。
6.请写出一句课外古代诗词中有关游子怀恋故土,思念家乡的诗句:_______________,_____________ __。
二.按要求完成第7—10题(10分)7.读叙事散文首先得抓住行文线索。
本单元的几篇散文,如《永久的悔》以______ _____ ____ 为线索,《苏珊·安东尼》以____________________________ 为线索。
(2分)8.出自《祖逖北伐》的一个成语是:,现人们常用来形容:9.根据下面一段话中的统计数字,请为这段话写一个结束语。
(不超过20个字)(2分)最近,记者考察了某市繁华的商业街,对这条商业街的商业用字进行了调查,发现整个路段的747个招牌中,含有不规范字的招牌多达118个,约占总数的16%,在这118个招牌中共有362个不规范字。
由此看来,10.一个多月来,我们在古今中外的历史长河中领略了苏珊.安东尼、抗日中一班铁骑兵、邹忌、周亚夫、祖逖、子墨子等人物的风采,请选择其中一个人物,给他(她)写一个颁奖词,字数不超过50字。
(4分)三.名著阅读(7分)11.说说《骆驼祥子》中祥子有哪些大事导致祥子“萎靡不振”?请概括出来。
(3分)答:12.优秀的文学作品,传达着人类的憧憬和理想,凝聚着人类美好的情感和灿烂的智慧。
请从下面所列的名著中选择一部,结合人物形象或者故事情节,从提高修养或者丰富情感的角度谈谈你的阅读收获。
(4分)《格列佛游记》《水浒传》《钢铁是怎样炼成的》答:第二部分:阅读能力(52分)四.阅读下面选段,完成13-17题。
(19分)[甲]于是入朝见威王,曰:“臣诚知不如徐公美。
臣之妻私臣,臣之妾畏臣,臣之客欲有求于臣,皆以美于徐公。
今齐地方千里,百二十城,宫女左右莫不私王,朝廷之臣莫不畏王,四境之内莫不有求于王:由此观之,王之蔽甚矣。
”王曰:“善。
”乃下令:“群臣吏民能面刺寡人之过者,受上赏;上书谏寡人者,受中赏;能谤讥于市朝,闻寡人之耳者,受下赏。
”令初下,群臣进谏,门庭若市;数月之后,时时而间进;朝年之后,虽欲言,无可进者。
燕、赵、韩、魏闻之,皆朝于齐。
此所谓战胜于朝廷。
(节选自《战国策•邹忌讽齐王纳谏》)[乙]晋侯复假道于虞①以伐虢②。
宫之奇谏曰“虢,虞之表也。
虢亡,虞必从之。
晋不可启③,寇不可玩④,一之为谓甚,其可再乎?谚所谓‘辅车相依,唇亡齿寒’者,其虞、虢之谓也。
”弗听,许晋使。
宫之奇以其族行⑤,曰:“虞不腊矣!在此行也,晋不更举矣。
”冬,晋灭虢。
师还,馆于虞,遂袭虞,灭之,执虞公。
(节选自《左传•宫之奇谏假道》)[注]①虞:虞国。
②虢:虢国。
③启:开头④玩:轻视。
⑤官之奇以其族行:宫之奇带全族的人离开虞国。
13.解释下列加横线的词(5分)(1)但当涉猎,见往事耳()(2)士别三日,即更刮目相看。
()(3)今齐地方千里,百二十城。
()(4)弗听,许晋使()(5)灭之,执虞公。
()14.翻译下列句子。
(4分)(1)能谤讥于市朝,闻寡人之耳者,受下赏。
翻译:(2)辅车相依,唇亡齿寒翻译:15.邹忌是怎样分析“王之蔽”的?宫之奇又是怎样分析不能从虞国借路的?(4分)答:16.探究两则材料中邹忌、宫之奇进谏方式的相同和不同之处。
(3分)相同:不同:17.两则材料中劝谏的结果截然相反,试探究其原因。
这给我们什么启示?(3分)(1)(2)(3)五.阅读下面两段文字回答(18-22)题(14分)一片槐树叶这是全世界最美的一片,最珍奇,最可宝贵的一片,而又是最使人伤心,最使人流泪的一片,薄薄的,干的,浅灰黄色的槐树叶。
忘了是在江南,江北,是在哪一个城市,哪一个园子里捡来的了,被夹在一册古老的诗集里,多年来,竟没有些微的损坏。
A、蝉翼般 | 轻轻 | 滑落的 | 槐树叶,B、细看时,还沾着 | 些故国的 | 泥土啊。
C、故国哟,啊啊,要到 | 何年 | 何月 | 何日D、才能 | 让我 | 回到 | 你的怀抱里去享受一个世界上最愉快的飘着淡淡的槐花香的季节?……18.诗的第三节ABCD四句朗读节奏和重音划分有误的一项是()(2分)19.用自己的话描绘一下诗人看到的那片槐树叶的“样子”。
(2分)答:20.结合第一节回答,诗的开头说这片槐树叶“最美、最珍奇、最可宝贵”是因为:“最使人伤心、最使人流泪,则又因为(4分)21.第二节中,诗人是真的忘记了“是在江南江北”“哪一个城市,哪一个园子”捡来的吗?说说你的理由。
(3分)答:22.谈谈你对“多年来,竟没有些微的损坏”的理解。
(3分)答:六.阅读下面文章回答(23-28)题(21分)(三)借你一个微笑(19分)①李俊是个性格内向的学生,阅完的试卷一发下,我发现他眉头又锁到一起了,他只得了58分。
②一个从来不及格的学生,自信心有多差就不用说了。
③我合上教案而无表情地走出了教室,李俊跟了上来,他喉头动了一下,然后眼泪就要掉下来了。
我站住,等他说话。
同学们也围了上来,他的脸涨得通红。
我静静地站着,希望他能开口,但他的嘴唇好像紧紧锁住了似的。
④他递过一张纸条:老师,我的物理太差,您能不能每天放学后为我补一个小时的课?⑤我可以马上答应他,但面对这样的一个学生我决定“迂回”一下。
我牵着他的手到僻静处说:“老师答应你的要求,可这两天我太忙,你等等好不好?”他有些失望,但还是点点头。
我知道他中计了,接着说,你必须先借一样东西给我!他着急起来,可还是说不出一句话。
⑥“你每天借给我一个微笑,好不好?”⑦这个要求太出乎他的意料,他很困惑地看着我。
我耐心地等待着,他终于眼噙泪花艰难地咧开嘴笑了,尽管有些情不由衷。
⑧第二天上课,我注意到李俊抬头注视我,我微笑着,但他把脸避开了,显然他还不习惯对我回应。
我让全班一起朗读例题,然后再让他重读一遍。
他没有感觉我为难他,大大方方地站起来读了。
也许想起了昨天对我的承诺,读完后,很困难地对我笑了笑。
见他这样,我心生一计,又给他设置了一道障碍。
我说,你复述一下题目的要求,这回他为难得快要哭了。
不少同学对他的无能表现得很不耐烦,七嘴八舌地争着说起来,我制止住了大家。
他终于张口了,语无伦次。
我笑着让他坐下。
⑨他开始和同学来往了,一起上厕所,回教室……这样过了好长一段时间,我都没提为他补习的事。
一天下课李俊又拦住我,我知道他要干什么,很幽默地向他摊开手。
他一愣,老师您要什么?我说,你写给我的条子呀。
他笑了:我不写条子了,您给我补补课吧。
我面带笑容:“功课你不必着急,到时我会主动找你的,但我向你借的你还没给够我。
”⑩“好的,我一定给足您。
”等他高高兴兴又蹦又跳地走出好一段路后,我才像想起来什么似的把他叫回来,递给他一张纸条,那里有我为他准备的一道题。
我告诉他,一天之内把它做出来,可以和同学讨论也可以独立完成。
我知道,他宁可“独吞”,也决不会和同学讨论的。
这正是性格内向学生的最大弱点。
下午他说还没做出来,我有点不高兴,说晚自习你还没做好,我可要收回承诺了。
自习时我见他站在一个男生边上,忸忸怩怩很不自然的样子,我得意地笑了。
就这样我先后为他写了4张纸条,题目一次比一次难。
后来,纸条一到手他就迫不及待地和同学们争论开来。
⑾期末考试李俊成绩尚可,科科及格——看来我为他补的都差不多了。
新学期刚开学,李俊休学了,因为他爸遇车祸瘫痪了,而他自小就被妈妈遗弃了——这也是他忧郁的一个原因。
我有些担心,一个连话都不大愿说的少年,能担负起养护父亲的责任吗?⑿星期天,我和几位朋友到茶室聊天。
刚坐下就被一群小孩子围上了,硬要为我们擦皮鞋。
只有一个小孩没冲进来,在外面吆喝着:擦皮鞋擦皮鞋!……离开茶室,我从那个小孩子面前走过时,发现那孩子竟是李俊!⒀“老师,让我为您擦一次皮鞋吧。
”他说,脸上没有腼腆也没有沮丧。
我答应了,伸过鞋子让他很用心地擦着。
他一边擦一边说,他虽然不缠人,生意也不错。
顾客告诉他,他的笑容很好看。
⒁我说是吗?他又笑着告诉我,不久他还会复学的。
他学会了笑,他的笑让他挣半天钱也能养活他和爸爸了。
⒂我也高兴起来,我说我一定等你回来。
可转过身,我的泪水就出来了。
李俊大声地在后面喊,老师您要笑呀,您不要哭!我点点头,反而呜咽有声了。
⒃我终于没有给他补课,是他为我补了一堂人生课。
(选自《中国微型小说精选》) 23.通读这篇小说,简述题目“借你一个微笑”的深层含义。
(3分)答:24.第⑦自然段写李俊听说“我”要向他每天借一个微笑后,始而“很困惑地看着我”,终而“眼噙泪花艰难地咧开嘴笑了,尽管有些情不由衷”。
由于受叙事方式的限制,这当中作者没有写李俊复杂的心理活动,假如你是当时的李俊,请将你的心理活动描写出来。
(不超过50字) (4分)答:25.在这篇小说中,为了让李俊每天能够借给“我”一个微笑,作为老师的“我”具体做了哪几件事?请概括作答。
(4分)答:26.作者在第⑩自然段写道:“期末考试李俊成绩尚可,科科及格——看来我为他补的都差不多了”,而在小说结尾却又说“我终于没有给他补课”,这是否矛盾?为什么?请简要作答。
(4分)答:27.在小说结尾,作者饱含深情地写道:“是他(李俊)为我补了一堂人生课”,请简要说说李俊为“我”补的这堂人生课的主要内容。
(4分)答:第三部分:写作能力(70 分)29、下面两个题目,任选一题作文。
(1)、请以“和你在一起”为题,写一篇文章,字数不少于700字(2)、“知道周迅(著名演员)的越来越多,知道鲁迅的越来越来少”,是当今中学生中的一个普遍现象,为此又引发了一次关于偶像问题的大讨论。
你有自己的偶像吗?你是怎样看待偶像问题的呢?请以“偶像”为话题,联系自己的经历、体验、见闻和认识,自定立意,自拟题目,写一篇记叙文或议论文。
字数不少于700字初二年语文期中考答案1-----10略11.祥子自己辛苦攒钱买的车子,给兵抢了。
B老婆难产死了。
C大病几场,原来强壮的身体也垮了。
12.示例:《水浒传》中的鲁智深侠肝义胆、疾恶如仇又粗中有细、豁达明理。
鲁智深在潘家酒楼听到金氏父女的遭遇后,便找上门寻借口三拳打死了“镇关西”,还一边骂他“诈死”,一边不慌不忙地离开。
