第二次作业
现企第二次作业及答案(1)

《现代企业管理方法》第二次作业一、单项选择题(每题给出4个选项,其中一个是正确的。
)1.最早给控制下定义的是( A ),他认为:在一个企业中,控制就是核实所发生的每一件事是否符合所规定的计划、所发布的指示以及所确定的原则。
A、法约尔B、泰罗C、孔茨D、韦伯2.控制的整体性特征是指(C )。
A、控制应能迅速适应外部环境的变化B、控制主要是对组织中人的控制C、控制是全体成员的工作,对象包括组织的各个方面D、控制不仅仅是监督,更重要的是指导、帮助以及员工的参与3.( D )存在的最大弊端是在实施矫正措施之前偏差已经发生了。
A、监督控制B、前馈控制C、现场控制D、反馈控制4.下列控制标准中,不属于货币控制标准的是( A )。
A、实物标准B、价值标准C、成本标准D、收益标准5.根据设计的生产能力确定机器的产出标准属于(B )。
A、统计标准B、经验标准C、定性标准D、工程标准6.科学管理之父泰罗首创的通过动作研究确定生产定额的方法是( B )的早期形式。
A、统计方法B、工业工程法C、经验估计法D、德尔非法7.在控制的过程中,( C )是控制的关键。
A、制定控制标准B、衡量工作绩效C、纠正偏差D、制定控制计划8.被许多公司称为“走动管理”的管理控制方法是(B )。
A、报告法B、现场观察法C、内部审计D、比率分析法9.在人力资源管理中,员工被认为是( D )。
A、企业重要的费用支出B、和机器一样的生产要素C、企业沉重的负担D、有价值的、难以模仿的资源10.需要工作分析人员亲自从事所要分析的工作,以获得第一手资料的工作分析法是(A )A、工作实践法B、观察法C、面谈法D、写实法11.在绘制技能管理图时,首次资料收集一般采用(C )A、实践法B、日志法C、问卷法D、观察法12.某企业预计明年的销售量会大幅增加,根据统计,以前的人均销售额为每人500件产品,年销售5000件,预计明年将达到年销售12000件,销售部门设两个管理层次,管理幅度为5人,那么销售部门总共需要( A )人员A、30B、24C、29D、2513.企业获得初级技术人员和管理人员的最重要的途径是( B )A、劳务市场招聘B、校园招聘C、猎头公司招聘D、再就业中心14.适合于挑选管理人员的甄选方法是( C )A、申请表B、工作抽样C、测评中心D、履历调查15.在开发分析能力、综合能力和评价能力时,( C )比较合适。
数理方程第二次作业参考答案

第二次作业1.化下列方程为标准形式:0=+yy xx yu u解:根据题意可得y c b a ===,0,1,则有y ac b -=-=∆2。
(1)当0=y 时,0=∆,方程为抛物型方程,标准形式为0=xx u ;(2)当0>y 时,0<∆,方程为椭圆型方程,对应的特征方程为022=+ydx dy解得两条特征线为C ix y =±2 选取变换x y ==ηξ,2,带入原方程可得01=-+ξηηξξξu u u (3)当0<y 时,0>∆,方程为双曲型方程,对应的特征方程为022=+ydx dy解得两条特征线为C x y =±--2 选取变换y x y x -+=--=2,2ηξ,带入原方程可得()()ηξξηηξu u u ---=21 2.确定下列方程的通解:023=+-yy xy xx u u u解:根据题意可得2,23,1=-==c b a ,0412>=-=∆ac b ,方程为双曲型方程,对应的特征方程为 02322=++dx dxdy dy解得两条特征线为212C x y C x y =+=+选取变换x y x y 2,+=+=ηξ,可把原方程化简为0=ξηu此方程的通解是()()ηξg f u +=其中是g f ,关于ηξ,的任意二次可微的连续函数,所以原方程的通解为()()y x g y x f u +++=2作业中出现的问题:第一题:1.有的同学以为特征线就是通解,这也太荒谬了。
2.有的同学没有讨论0=y 时候的情况。
3.作变量代换的时候有的同学设的变量很复杂,不可取。
另外化简的时候没有化到最简,方程中还包含y x ,。
此外有的同学认为书上最简形式的椭圆、双曲方程就是本题的结果,这是完全错误的。
还有计算问题也出现了很多。
第二题:1.到0=ξηu 这一步都没有什么大问题,主要是后面求这个积分出现了问题,一方面有的同学最后结果中后面还带着积分号,另一方面有很多同学都没有讨论g f ,和性质。
经济法概论第二次在线作业

经济法概论第二次在线作业经济法第二次在线作业—经济法基础一、单项选择题(每题2分,共32分)1.行政法规的制定部门是( D )。
A.省级、自治区、直辖市人民政府B.国务院直属机构C.全国人民代表大会D.国务院1、【正确答案】D【答案解析】本题考核经济法的渊源。
法规包括行政法规、地方性法规。
行政法规是由国务院制定的规范性文件。
2.下列规范性文件中,属于规章的是(D)。
A.深圳市人民代表大会制定的《深圳经济特区注册会计师条例》B.国务院制定的《中华人民共和国外汇管理条例》C.全国人民代表大会常务委员会制定的《中华人民共和国公司法》D.中国人民银行制定的《人民币银行结算账户管理办法》2、【正确答案】 D【答案解析】本题考核经济法的渊源。
本题考核规章的制定机关。
规章包括由国务院部委及具有行政管理职能的直属机构依据法律、行政法规制定的国务院部门规章,以及由省、自治区、直辖市和较大的市的人民政府根据法律、法规制定的地方政府规章,选项D属于部门规章的范围。
3.引起某一经济法律关系发生、变更或消灭的数个法律事实的总和,称为( D )。
A.法律依据B.法律后果C.法律事实D.事实构成3、【正确答案】D【答案解析】本题考核事实构成的概念。
一般而言,经济法律关系的发生、变更和消灭只需一个法律事实出现即可成立,但有的经济法律关系的发生、变更和消灭则需要两个以上的法律事实同时具备。
引起某一经济法律关系发生、变更或消灭的数个法律事实的总和,称为事实构成。
4.下列各项中,属于法律事实中事件范围的是( C )。
A.经营管理行为B.偷税行为C.洪水D.公司股票上市4、【正确答案】C【答案解析】本题考核事件的范围。
ABD选项均为行为,C选项属于绝对事件范围。
5.仲裁裁决作出后,当事人就同一纠纷,不能再申请仲裁或向法院起诉,这个体现的仲裁原则是( D )。
A.独立性原则B.自愿原则C.以事实为依据,以法律为准绳,公平合理解决纠纷原则D.一裁终局原则5、【正确答案】D【答案解析】本题考核仲裁的基本规定。
经济法概论第二次作业答案

经济法概论第二次作业第5章----第7章一、单项选择题:(每题1分,计15分) 1.对合同内容的修改、补充(D )。
A .是合同内容的变更B .是合同主体的变更C .是合同一方主体的变更D .是合同双方主体的变更我国《民法典》对要约生效的时间(B )。
A .采用发信主义B .采用到达主义C .采用投邮主义D .采用实践主义根据我国商标法规定,商标不得使用的图形是(A )。
A .我国的八一军旗B .太阳C .熊猫D .黄山迎客松我国商标法规定,注册商标的有效期为(C ),自核准之日起计算。
A .20年B .15年C .10年D .8年财政法的调整对象是(D ),其在发展过程中并不是一成不变的。
A .财政法律关系B .财政行为C .财政关系D .财政法律行为下列(A )基本原则是现代社会整个财政法的基础,在财政法体系中居于核心地位。
A .财政民主主义B .财政法定主义C .财政健全主义D .财政平等主义目前,(A )法律在我国财政法律体系中形式上居于关键地位,是调整国家基本财政分配关系的法律准则。
A .国家预算法B .财政收支划分法C .分税制财政管理体制法D .税收征管法预算草案需要经过特定的机构批准生效,才能成为正式的国家预算,并具有法律约束力,而且非经法定程序,不得变更。
根据我国《预算法》的规定,(A )机构负责审查和批准2.3.4.5.6.7.8.A .全国人民代表大会B .全国人民代表大会常务委员会C .国务院D .财政部合同履行是指(D )。
A .是债权人完成受领义务的行为B .债务人拒绝履行合同C .债权人拒绝履行合同D .债务人按照合同约定履行自己的义务的行为政府采购应采取的主要方式是(A )。
A .公开招标采购方式B .邀请招标方式C .竞争性谈判方式D .询价方式(C )不是累进税率的基本形式。
A .全额累进税率B .超额累进税率C .超率累进税率D .定额累进税率(C )不是税率的基本形式。
工程经济第二次作业
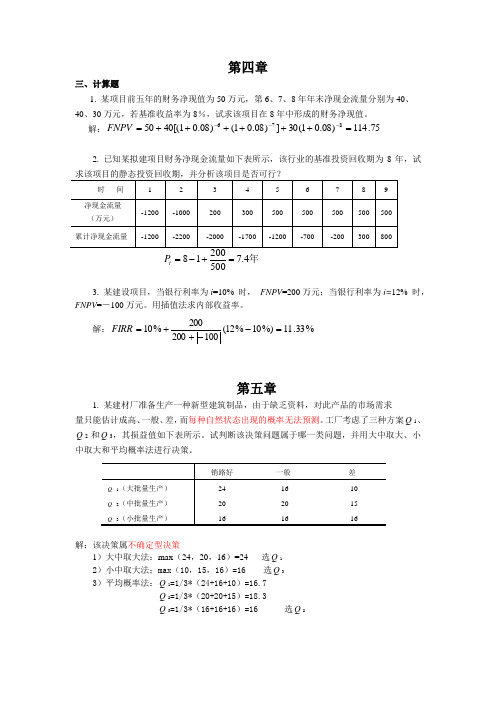
第四章三、计算题1. 某项目前五年的财务净现值为50万元,第6、7、8年年末净现金流量分别为40、 40、30万元,若基准收益率为8%,试求该项目在8年中形成的财务净现值。
解:75.114)08.01(30])08.01()08.01[(4050876=++++++=---FNPV2. 已知某拟建项目财务净现金流量如下表所示,该行业的基准投资回收期为8年,试年4.750018=+-=t P3. 某建设项目,当银行利率为i =10% 时, FNPV =200万元;当银行利率为i=12% 时,FNPV =-100万元。
用插值法求内部收益率。
解:%33.11%)10%12(100200200%10=--++=FIRR第五章1. 某建材厂准备生产一种新型建筑制品,由于缺乏资料,对此产品的市场需求 量只能估计成高、一般、差,而每种自然状态出现的概率无法预测。
工厂考虑了三种方案Q 1、Q 2和Q 3,其损益值如下表所示。
试判断该决策问题属于哪一类问题,并用大中取大、小中取大和平均概率法进行决策。
解:该决策属不确定型决策1)大中取大法:max (24,20,16)=24 选Q 12)小中取大法;max (10,15,16)=16 选Q 3 3)平均概率法:Q 1=1/3*(24+16+10)=16.7 Q 2=1/3*(20+20+15)=18.3Q 3=1/3*(16+16+16)=16 选Q 24..某企业引入一种新产品,寿命期均为5年,预测了销路有三种可能的自然状态及相应的概率。
每种状态又可能处于有竞争(概率为0.9)或无竞争(概率为0.1)的市场状态。
各资料如下表。
现面临设备选择,可选用Ⅰ设备或Ⅱ设备,投资额分别为200万元和10万元。
试用决策树法对设备选用进行决策。
当寿命期为多少年时,选Ⅰ设备有利?⑤=0.9×12+0.1×20=12.8⑥=0.9×(-20)+0.1×(-20)=-20②=0.6×73+0.2×12.8+0.2×(-20)=42.36净利润=5×42.36-200=11.8万元Ⅱ设备:⑦=11×0.9+30×0.1=12.9⑧=2×0.9+5×0.1=2.3⑨=-10③=0.6×12.9+0.2×2.3+0.2×(-10)=6.2净利润=6.2×5-10=21万元故应选Ⅱ设备为好。
第二次计分作业参考答案

江苏开放大学形成性考核作业学号姓名课程代码课程名称评阅教师第2次任务共4次任务江苏开放大学任务内容:(请将各题答案填在作答结果相应位置)专题讨论:规模经济:中国彩电行业的洗牌案例内容改革开放之后,国人的收入明显增加,冰箱、彩电、洗衣机替代自行车,缝纫机和收音机成为人们家庭建设上追求的新“三大件”。
当时的电视机是主要黑白的,后来彩电才进入了为数不多的家庭。
可无论是黑白电视还是彩色电视,由于日本的品牌质量出色,在市场上几乎占据了绝对的优势,人们茶余饭后津津乐道的是日立、东芝、索尼、JVC、三洋、松下等品牌。
当时中国的经济还处于极度的短缺当中,电视机在“票证时代”还是一种奢侈品,人们需要凭关系、走后门才能买到,如果哪个家庭拥有一台日本原装进口的14寸电视机是件令人羡慕的事。
1978年国家开始批准引进彩电生产线后,中国电视机行业开始迅猛发展。
据统计,到1985年,全国共引进了113条彩电装配生产线,几乎遍布于全国各省;彩电企业也遍地开花,到九十年代中期,全国的彩电企业超过了200家。
在这股迅猛发展的浪潮中,涌现出了长虹、TCL、康佳、创维、海尔等为国人所熟知的品牌。
1996年3月26日,长虹挑起行业内的第一次大规模价格战,电视机行业从此全面洗牌,据国家信息中心的统计,20世纪90年代中后期,有竞争力的彩电品牌尚有5、60个,价格战的冲击使得很多企业退出市场,高路华、乐华、嘉华、熊猫等品牌陆续消失;2006年,TCL、长虹、康佳、创维、海信、海尔和厦华等七大品牌占据了国内市场约75%的市场份额。
彩电业寡头垄断的市场结构特征越来越明显。
案例分析任何产业都有其适度的发展规模,而彩电业是一个规模经济性较为显著的产业。
二十世纪八十年代的迅猛发展使得中国电视机的产量大增,到1985年我国电视机年产量就超过美国,达到1663万台,成为仅次于日本的世界第二大电视机生产国。
1987年,我国电视机产量达到1934万台,一举超过日本,成为世界上最大的电视机生产国。
图论习题答案2
第四次作业
四(13).设M是二分图G的最大匹配,则 | M || X | max| S | | N ( S )| ,
SX
证明: | X | max| S | | N ( S )| min(| X | | S |) | N ( S )| ,而(X - S ) N ( S )是G的一个覆盖,则 min(| X | | S |) | N ( S )|是G的最小覆盖,
第七次作业
• 五(28).设sn是满足下列条件的最小整数,把 {1,2,...,sn}任划分成n个子集后,总有一个子集 中含有x+y=z的根,求s1,s2,s3是多少? • 解:n=1,枚举得s1=2; • s2=5 • s3=14
第七次作业
五(34).求证r(k, l) = r(l, k) 证明:若G含有K k 子图,则G c 含有k个顶点的独立集;若G含有 l个顶点的独立集,则G c 含有K l 子图。则命题成立。
五 (13).若 是单图 G 顶的最小次数,证明; 若 1则存在 1边着色, 使与每顶关联的边种有 1种颜色。 反证法:假设在 v1处无 i 0色 设 C (E 1 , E 2 ,..., E 1 )为 G 的( 1) 最佳边着色 第一步:构造点列: v1 , v 2 ,..., v h , v h 1 ,....., vl ,.... v1处无 i 0色, v j v j 1着 i j色,且在 v j点处 i j 色重复出现,可知在 v j1处仅一 个 i j色;证明如下: 用反证法证明,假设在 v j1处 i j色重复出现,将 v j v j 1改成 v j 所关联的边 没有的颜色 im,则可以对图 G 的找色进行改善。与 C 是最佳边着色矛盾, 假设不成立。 又 是单图 G 顶的最小次数,则必存 在最小整数 h使得 i h i l 第二步:着色调整: v j v j 1着 i j-1色 ( j 1,2,..., h ),所得新着色为 C ' 在 C '中, v1处多了个 i 0色, v h 1处少了个 i h 色,其他点的边着色数 不变, 所以 C ' 还是 1最佳边着色
中国石油大学(北京)操作系统 第二次在线作业满分答案
第二次在线作业单选题 (共30道题)展开收起1.(2.5分)在可变分区存储管理中,最优适应分配算法要求对空闲区表项按( )进行排列。
A、A.地址从大到小B、B.地址从小到大C、C.尺寸从大到小D、D.尺寸从小到大我的答案:D 此题得分:2.5分2.(2.5分)避免死锁的一个著名的算法是()。
A、A.先入先出法;B、B.银行家算法;C、C.优先级算法;D、D.资源按序分配法。
我的答案:B 此题得分:2.5分3.(2.5分)可重定位内存的分区分配目的为()。
A、A、解决碎片问题B、B、便于多作业共享内存C、C、回收空白区方便D、D、便于用户干预我的答案:A 此题得分:2.5分4.(2.5分)逻辑地址就是()。
A、A.用户地址B、B.相对地址C、C.物理地址D、D.绝对地址我的答案:B 此题得分:2.5分5.(2.5分)进程和程序的一个本质区别是()。
A、A.前者为动态的,后者为静态的;B、B.前者存储在内存,后者存储在外存;C、C.前者在一个文件中,后者在多个文件中;D、D.前者分时使用CPU,后者独占CPU。
我的答案:A 此题得分:2.5分6.(2.5分)某进程在运行过程中需要等待从磁盘上读入数据,此时该进程的状态将。
A、A.从就绪变为运行;B、B.从运行变为就绪;C、C.从运行变为阻塞;D、D.从阻塞变为就绪我的答案:C 此题得分:2.5分7.(2.5分)常不采用( )方法来解除死锁。
A、A.终止一个死锁进程B、B.终止所有死锁进程C、C.从死锁进程处抢夺资源D、D.从非死锁进程处抢夺资源我的答案:B 此题得分:2.5分8.(2.5分)设两个进程共用一个临界资源的互斥信号量为mutex,当mutex=-1时表示()A、A.一个进程进入了临界区,另一个进程等待B、B.没有一个进程进入了临界区C、C.两个进程都进入了临界区D、D.两个进程都在等待我的答案:A 此题得分:2.5分9.(2.5分)两个进程合作完成一个任务,在并发执行中,一个进程要等待其合作伙伴发来信息,或者建立某个条件后再向前执行,这种关系是进程间的()关系。
大学英语-第二次在线作业
大学英语(一)第二次在线作业单选题 (共40道题)展开收起1.(2.5分)–Take care! --__________.∙ A、I take.∙ B、Bye!∙ C、Thank you all the same.∙ D、I’m sorry.我的答案:B 此题得分:2.5分2.(2.5分)–Can I go out and have a walk? -- __________.∙ A、Go ahead.∙ B、Excuse me.∙ C、See you around.∙ D、Not at all.我的答案:A 此题得分:2.5分3.(2.5分)–Are you free tomorrow morning? -- ______________.∙ A、I’m afraid not.∙ B、I’m sorry.∙ C、I’m OK.∙ D、I’m fine.我的答案:A 此题得分:2.5分4.(2.5分)The trousers are ______, but Tom does not care a bit.∙ A、too a little small∙ B、a little too small∙ C、a too little small∙ D、a small too little我的答案:B 此题得分:2.5分5.(2.5分)She wore a dress to the party that was far more attr active than ______.∙ A、other girls∙ B、that of other girls∙ C、the other girls∙ D、those of other girls我的答案:D 此题得分:2.5分6.(2.5分)Although he is dead, his soul is still__________.∙ A、living∙ B、alive∙ C、lively∙ D、live我的答案:B 此题得分:2.5分7.(2.5分)The twin brothers are ______ in many ways.∙ A、like∙ B、alike∙ C、likely∙ D、likewise我的答案:B 此题得分:2.5分8.(2.5分)Peter arrived at 9 o’clock and Sam arrived 5 minute s .∙ A、later∙ B、latter∙ C、lately∙ D、last我的答案:A 此题得分:2.5分9.(2.5分)The harder the shrub is to grow, ______.∙ A、the more higher price it∙ B、the higher price it is∙ C、the higher the price is∙ D、the higher is the price我的答案:C 此题得分:2.5分10.(2.5分)The photographs of Mars taken by satellite are _____ _ taken from the earth.∙ A、clearest than those∙ B、clearer than that∙ C、much clear than those∙ D、much clearer than those我的答案:D 此题得分:2.5分11.(2.5分)______ anywhere in the United States costs less thana dollar when you dial it yourself.∙ A、Three-minute call∙ B、A three-minutes call∙ C、A three-minute call∙ D、A three-minutes-call我的答案:C 此题得分:2.5分12.(2.5分)We arrived ______ Professor Baker had already called the roll.∙ A、so lately that∙ B、as late that∙ C、so later that∙ D、so late that我的答案:D 此题得分:2.5分13.(2.5分)It is ______ that I would like to go to the beach.∙ A、so nice weather∙ B、such nice weather∙ C、so nice a weather∙ D、such a nice weather我的答案:B 此题得分:2.5分14.(2.5分)___Flight 302 to London _______until 7:30 tomorr ow morning.—No wonder I hear so many complaints from the passengers.∙ A、delay∙ B、delayed∙ C、has been delayed∙ D、is to be delayed我的答案:C 此题得分:2.5分15.(2.5分)—What is the man over there? —I don' t know for sure.But I think he can be ____but a teacher.∙ A、anybody∙ B、anything∙ C、nobody∙ D、nothing我的答案:A 此题得分:2.5分16.(2.5分)Where did you get to know your wife? —It was in t he university _____we studied together.∙ A、that∙ B、where∙ C、when∙ D、which我的答案:A 此题得分:2.5分17.(2.5分)—Emma 1ooks very happy.She _____have passed the exam.—I guess so.It’s not difficult after all.∙ A、should∙ B、could∙ C、must∙ D、might我的答案:C 此题得分:2.5分18.(2.5分)Among the most important questions the journalists wanted _____was how to keep the present economic growth with out causing damage to the environment?∙ A、to answe∙ B、being answered∙ C、answering∙ D、answered我的答案:D 此题得分:2.5分19.(2.5分)—Have you seen _________ watch? I left it here this morning. —I think I saw one somewhere. Is it _________ new on e?∙ A、a;/∙ B、a;the∙ C、the;a∙ D、a;a我的答案:D 此题得分:2.5分20.(2.5分)The Browns held _____ they called " family day" once each year.∙ A、that∙ B、what∙ D、when我的答案:B 此题得分:2.5分21.(2.5分)In some parts of London, missing a bus means _____ _____ for another hour.∙ A、waiting∙ B、to wait∙ C、wait∙ D、to be waiting我的答案:A 此题得分:2.5分22.(2.5分)The Foreign Minister said, “___________ our hope that the two sides will work towards peace.”∙ A、This is∙ B、There is∙ C、That is∙ D、It is我的答案:D 此题得分:2.5分23.(2.5分)The book _____ he bought yesterday is very interesti ng.∙ A、\∙ C、when∙ D、where我的答案:A 此题得分:2.5分24.(2.5分)He has not got a fever. That is to say, his temperat ure is ______.∙ A、common∙ B、normal∙ C、ordinary∙ D、low我的答案:B 此题得分:2.5分25.(2.5分)We have learned ____ the rocks on the moon are 35 00 million years ago.∙ A、how∙ B、which∙ C、that∙ D、what我的答案:C 此题得分:2.5分26.(2.5分)As soon as he entered the room , he ______ his cap and sat down.∙ A、took out∙ B、took away∙ C、took down∙ D、took off我的答案:D 此题得分:2.5分27.(2.5分)I’ve been here for three weeks now, and _____ I’ve enjoyed myself.∙ A、so far∙ B、as far∙ C、by far∙ D、to now我的答案:A 此题得分:2.5分28.(2.5分)It is a common observation ______ there are no two objects in nature that are exactly alike.∙ A、that∙ B、in that∙ C、which∙ D、in which我的答案:A 此题得分:2.5分29.(2.5分)I’ll do whatever I can _________ my English.∙ A、improve∙ B、to improve∙ C、improving∙ D、to improving我的答案:B 此题得分:2.5分30.(2.5分)——Tom, you are caught late again. ——Oh, _________ _.∙ A、not at all∙ B、just my luck∙ C、never mind∙ D、that’s all right我的答案:B 此题得分:2.5分31.(2.5分)—Oh, life is so boring! —Please don’t think so . I suppose you’ve come to the point _______ a change is needed.∙ A、where∙ B、when∙ C、which∙ D、as我的答案:A 此题得分:2.5分32.(2.5分)The engineers made two big plans for the dam, ____ ______ was never put in force.∙ A、one of them∙ B、which∙ C、one of which∙ D、every one of which我的答案:B 此题得分:2.5分33.(2.5分)I have no one __________ me, for I am a new comer here.∙ A、help∙ B、helping∙ C、to help∙ D、to have helped我的答案:C 此题得分:2.5分34.(2.5分)No one ____ that to his face. A.B. C.D.∙ A、dares say∙ B、dares saying∙ C、dare say∙ D、dare to say我的答案:C 此题得分:2.5分35.(2.5分)_______, you can gently improve your spoken English in a short time.∙ A、On the way∙ B、In this way∙ C、By the way∙ D、In the way我的答案:B 此题得分:2.5分36.(2.5分)—Oh, my God! So many students are coming out. How can you ____ your daughter? —That’s easy. My daughter i s wearing a red skirt today.∙ A、get out∙ B、find out∙ C、take out∙ D、pick out我的答案:D 此题得分:2.5分37.(2.5分)—May I go and play with Dick this afternoon, Mum?—No, you can’t go out _______ your work is being done.∙ A、before∙ B、until∙ C、as∙ D、the moment我的答案:C 此题得分:2.5分38.(2.5分)His sudden look of fear made _____ clear that he had something to do with the matter.∙ A、him∙ B、this∙ C、it∙ D、that我的答案:C 此题得分:2.5分39.(2.5分)Many people have been ill with a strange disease th ese days, _______ we’d never heard of before.∙ A、one∙ B、that∙ C、it∙ D、this我的答案:A 此题得分:2.5分40.(2.5分)—Are you satisfied with her work, sir? —Not at all. It couldn’t be any _______.∙ A、better∙ B、best∙ C、worse∙ D、worst我的答案:C 此题得分:2.5分。
14秋《听说(Ⅰ)》作业2-答案
A)Once a week.B)Twice a week.C)Three times a week.D)Four times a week.M: Your son seems to have made much progress in playing the piano. Does he attend any piano classes?W: Yes, he takes lessons twice a week, but from next week on, he will go to the class on Saturday evenings, too.Q: How often will the woman’s son have piano lessons from next week on?答案:C 分析:看选项就知道这题考的一个频度,那么到底是几次呢?我看对话怎么说的,男人的话不是很重要,只是引出问题。
女人的回答是本题的关键,女人先说是twice a week ,但千万不要忙着选 B(事情不会那么简单,听到的一般不是正确答案),女人接着来了也“but”转折,说从下周开始,他儿子星期六也将去上课。
Ok 那么本来是两次,下周起再加上周六的课,答案就是C 三次。
2.第二次作业问题2A) He left his notes at home.B) He doesn’t know where his notes are.C) He doesn’t want to land his notes to the woman.D) He agrees to lend her his notes.W: Do you mind if I borrow your notes.M: No, of course not. They are on my desk.Q: What does the man mean?答案:D 分析:四个选项中有一组对立项 C D 一个是同意借笔记,一个是不愿意借,答案很有可能是其中之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 Divide and ConquerA group of n Ghostbusters is battling n ghosts. Each Ghostbuster is armed with a proton pack, which shoots a stream at a ghost, eradicating it. A stream goes in a straight line and terminates when it hits the ghost. The Ghostbusters decide upon the following strategy. They will pair off with the ghosts, forming n Ghostbuster-ghost pairs, and then simultaneously each Ghostbuster will shoot a stream at his chosen ghost. As we all know, it is very dangerous to let streams cross, and so the Ghostbusters must choose pairings for which no streams will cross. Assume that the position of each Ghostbuster and each ghost is a fixed point in the plane and that no three positions are collinear.i Argue that there exists a line passing through one Ghostbuster and one ghost such the number of Ghostbusters on one side of the line equals the number of ghosts on the same side. Describe how to find such a line in O(n log n) time.ii Give an O(n2 log n)-time algorithm to pair Ghostbusters with ghosts in such a way that no streams cross.Answer:i -ii: We assume that all the points in the plane are not in same X or Y axis using mark to stand for ghostbuster or ghosts(mark 0 stand for ghostbuster and mark 1 stand for ghosts).(This can not affect the problem because when we get the same X or Y , we can add or minus a very little value to let all points’ X or Y are not same). First we get the deepest point (in other word, the minimum Y value). Also we compute the other points with this point ‘s angle in X axis and sort these other points with this angle. Then we iterate in this order, and get another mark which is different from the deepest point's mark also we line this twopoint ,and compute the bottom mark 0 's number and mark 1's number, they are the same , then we find the pair which is the deepest point and the iterate point. So we use this line to divide all points into two parts and recursive do the same above operation until the points' number is only 2 then we only get the line to connect this two points.Algorithm:Get_Pair(points[1-2N])if N>1initial a array points[1-2N] stand for the points of ghostbusters and ghostsfind the deepest point min_Point in the array pointsinitial the pair_Point and the index with 0get the other 2N-1 points with this min_Point 's angle in X axis and sort these anglesinitial num1 with 0 stand for the number of the other 2N-1 points which's mark is same with min_Pointinitial num2 with 0 stand for the number of the other 2N-1 points which's mark is not same with min_Pointfor i=1 to 2N-1if min_Point's mark is same with points[i]'s marknum1++elsenum2++endifif num1+1==num2get this point pair_Pointindex=ibreak;endifendforprint this pair (min_Point,pair_Point)using pair_Point to divide points into two parts point_one[1-index-1] andpoint_two[index+1-2*N]Get_Pair(point_one[1-index-1])Get_Pair(point_two[index+1-2*N])elseget the line to connect this two pointsendifWe will prove this algorithm is O(n log n) time, first we get the deepest point in O(n) time, next we compute the other points with this deepest point 's angle in X axis in O(n) time, we use quick_sort to sort these n angles in O(n log n). Last we iterator these angles in O(n) to find the pair. So all time we consume is only O(n log n) time.Next we will prove this algorithm always can find the pair. Now we assume the deepest point stand for the Ghostbusters using mark=0, so above this point, we have n-1Ghostbusters(mark=0) and n Ghosts(mark=1). So we can sort n-1 0 and n 1 in whole arrangement, no matter how we sort, we can get a index in 1 , which before this 1 we have the same number of 0 and 1. We can replace this problem with a new problem, we have a road for (0,0) point to (n-1,n) point , we only can move the one step in the X or Y direction. No matter which road we have, we must cross the line Y=X it means we must get the Ghost. Before this ghost, we have the same number of ghosts and ghostbusters.Last, we will prove that solving this problem is O(n2 log n).Easily, we get the T(n)=2*T(n/2)+O(n log n).We use mathematical induction for assuming that T(n)<= O(n2 log n)n=1, T(1)=O(n log n)<=O(n2 log n)assume n<k T(n)<=O(n2 log n)then n=k, T(k)=2*T(k/2)+O(k log k)<=2*O(k2 log (k/2)/ 4)+O(k log k)=O(k2 log(k/2) /2)+O(k log k)<=O(k2 log k)2 Divide and ConquerYou are interested in analyzing some hard-to-obtain data from two separate databases. Each database contains n numerical values-so there are 2n values total-and you may assume that no two values are the same. You’d like to determine the median of this set of 2n values, which we will define here to be the n th smallest value.However, the only way you can access these values is through queries to the databases. In a single query, you can specify a value k to one of the two databases, and the chosen database will return the k th smallest value that it contains. Since queries are expensive, you would liketo compute the median using as few queries as possible.Give an algorithm that finds the median value using at most O(log n) queries.Answer:First we can assume the two arrays are in ascending order because in this question we can specify a value k to one of the two arrays, and this system will return the k’t h smallest value that it contains. So in the following two arrays: An and Bn. (each array contains n different value and is in ascending order)So we get the median of two arrays: A[n/2] and B[n/2]. Before the A[n/2] value, there are only n/2-1 values, the same , before the B[n/2] value, there are only n/2-1values.(A[n/2]!=B[n/2] because all 2n values are not same). So we only have two conditions: i: A[n/2]<B[n/2] , before the B[n/2] value, there must be at least n/2-1+n/2-1+1=n-1values(n/2-1 before A[n/2] and n/2-1 before B[n/2] and 1 stand for A[n/2] itself). The same , before the A[n/2] value, there must be at most n/2-1+n/2-1=n-2. So the two arrays’ median value must be in the interval A[n/2+1] to A[n] and in the interval B[1] to B[n/2]. We can divide this problem into one small problem . At last , A and B only have one value , we get the small one which is the result.ii: A[n/2]>B[n/2] , the same, the two arrays’ median value must be in the interval A[1] toA[n/2] and in the interval B[n/2+1] to B[n].Algorithm:Get_Median(A[1-n],B[1-n])If the A and B only have one element thenReturn the small oneElseGet the median a and b stand for A and BIf a<bReturn Get_Median(A[n/2+1-n],B[1-n/2])ElseReturn Get_Median(A[1-n/2],B[n/2+1-n])EndifEndifNow , we will prove this algorithm is O(log n) time.In algorithm: we can have T(n)=T(n/2)+c when n>1 and T(1)=c (c is the constant value) , So we get T(n)=clog n. Then this algorithm is O(log n) time.3 Divide and ConquerGiven a convex polygon with n vertices, we can divide it into several separated pieces, such that every piece is a triangle. When n = 4, there are two different ways to divide the polygon; When n = 5, there are five different ways.Give an algorithm that decides how many ways we can divide a convex polygon with n vertices into triangles.Answer:We get the f(n) to stand for : the number of different ways to divide the n-polygon.f(1)=1;f(n)=f(1)*f(n-1)+f(2)*f(n-2)+....+f(n-1)*f(1) n>1;So the algorithm is:int f(int n)If n==1return 1;Elseint result=0;for i=1 to n-1result+=f(i)*f(n-i);Endforreturn result;Endif4 Counting InversionsRecall the problem of finding the number of inversions. As in the course, we are given a sequence of n numbers a1, ..., a n, which we assume are all distinct, and we define an inversion to be a pair i < j such that a i > a j .We motivated the problem of counting inversions as a good measure of how different two orderings are. However, one might feel that this measure i s too sensitive. Let’s call a pair a significant inversion if i < j and a i > 3a j .Given an O(n log n) algorithm to count the number of significant inversions between two orderings.Answer:Given a sequence of n numbers , we use a array D[1-n] which contains this n numbers. We can use Sort_Count function in the normal CountingInversions. Assume we divide D[1-n] into two half array D1[1-n/2] for D[1-n/2] and D2[1-n/2] for D[n/2+1-n], and we have already sort the two arrays D1 and D2 and computed the inversions’ numbers. Now what we only should do is to get the D1[i] and D2[j] (i and j is 1-n/2) and look whether this two number is inversed and at the same time we should merge this two sorted array.Now let us describe this problem: we already get two sorted arrays D1[1-n/2] and D2[1-n/2], we set three indexes i and j1 and j2, i and j2 is to iterate D1 and D2, j1 is to .D2[j1-j2-1]<D1[i] in other word, it means the current i’th value is bigger th an j1 to j2-1’s all values. When we iterate i’th number in D1 and j’th number in D2, we have two conditions : (because all numbers are distinct , so D1[i]!=D2[j2])i: D1[i]<D2[j2]. We look whether D1[i] is treble than D2[j1] , if D1[i]>3*D2[j1] then we add InverseCount with the number of D1 remaining arrays . (InverseCount stand for the current number of inversions) and at the same time, we add j1 to look the next element in D2. Else, we insent D1[i] value into new sorted array and add i to look the next element in D1.ii: D1[i]>D2[j2]. We insert D2[j2] value into new new sorted array and add j2 to look the next element in D2.Algorithm:Merge_and_Count(D1[1-n],D2[1-n])Initial InverseCount , i, j1, j2 with 0Initial new array NEW_D which contains all elements in ascending orderWhile D1 and D2 all is not emptyIf D1[i]<D2[j2]If D1[i]>3*D2[j1]Add InverseCount with the number of D1’s remaining’s elementsIncrement j1ElseInsert D1[i] into NEW_DIncrement iEndifElseInsert D2[j2] into NEW_DIncrement j2EndifEndWhileWhile D2 is not emptyInsert D2[j2] into NEW_DIncrement j2EndWhileWhile D1 is not emptyIf j1 is not iterate to the end of D2If D1[i]>3*D2[j1]Add InverseCount with the number of D1’s remaining’s elementsIncrement j1ElseInsert D1[i] into NEW_DIncrement iEndifElseInsert D1[i] into NEW_DIncrement iEndifEndWhileReturn InverseCountSort_and_Count(l,r)If l<rGet middle m between l and rGet RCL is Sort_and_Count(l,m) which stand for the left half array ‘s inversion’s numberGet RCR is Sort_and_Count(m+1,r) which stand for the right half array’s inversion’s numberGet RLR is Merge_and_Count(D1[l-m],D2[m+1-r]) which stand for the left and right ‘s inversion’s numberReturn RCL+RCR+RLREndif5 Counting InversionsThe attached file Q5.txt contains 100,000 integers between 1 and 100,000 (each row has a single integer), the order of these integers is random and no integer is repeated.1. Write a program to implement the SORT-AND-COUNT algorithms in your favorite lan-guage, find the number of inversions in the given file.2. In the lecture, we count the number of inversions in O(n log n) time, using the MERGE-SORT idea. Is it possible to use the QUICK-SORT idea instead ?If possible, implement the algorithm in your favorite language, run it over the given file, and compare its running time with the one above. If not, give a explanation.Answer:1: C++ Code:#include<iostream>#include<fstream>#include<memory.h>#include<stdlib.h>using namespace std;int N=100000;int data[100000];ofstream out("res.txt");long long merge_count(int l,int m,int r){int count=0;int* L=(int*)malloc((m-l+1)*sizeof(int));int* R=(int*)malloc((r-m)*sizeof(int));//memcpy(L,data+l*sizeof(int),(m-l+1)*sizeof(int));//memcpy(R,data+(m+1)*sizeof(int),(r-m)*sizeof(int));for(int i=l;i<=m;i++)L[i-l]=data[i];for(int i=m+1;i<=r;i++)R[i-m-1]=data[i];int i=0,j=0,k=l;for(;i<m-l+1&&j<r-m;){if(L[i]>R[j]){data[k++]=R[j++];count+=m-l-i+1;}else{data[k++]=R[i++];}}for(;i<m-l+1;){data[k++]=L[i++];}for(;j<r-m;){data[k++]=R[j++];}return count;}long long inversion_Counting(int l,int r){if(l<r){int m=(l+r)>>1;long long L=inversion_Counting(l,m);long long R=inversion_Counting(m+1,r);long long LR=merge_count(l,m,r);out<<L+R+LR<<endl;return L+R+LR;}elsereturn 0;}int main(){ifstream in("Q5.txt");for(int i=0;i<N;i++)in>>data[i];cout<<inversion_Counting(0,N-1);return 0;}The result is 1693706111.2. We cannot use QUICK_SORT idea to implement the InverseCounting. Because we cannot have the two sorted half array. When we use Merge_Sort, we first get two sorted half array and can compute one number in left array and another number in right array. In fact, we do the Merge_Sort function is the same with visiting tree in postorder. But we do the Quick_Sort function is the same with visiting tree in preorder. Only in postorder, we first get the two half arrays(the node's two children) in order, so we can visit thenode itself.6 SortingThe M ERGE-S ORT, Q UICK-S ORT and M ODIFIED-Q UICK-S ORT algorithms in the lecture slides are all recursive. However, by using a stack, all of them can be implemented in a iterative way. 1. Implement both the recursive version and iterative version of the three algorithms inyour favorite language.2.Run your implementation over three integer arrays whose sizes are 100, 000, 1, 000, 000,10, 000, 000 respectively. Record their running times and make a comparison.Answer:with C++ code in Linux System using Eclipse:M ERGE-S ORT Q UICK-S ORT100, 00040ms 50ms1, 000, 000980ms 422ms10, 000, 00011486ms 4980msM ERGE-S ORT-Itr Q UICK-S ORT-Itr100, 000114ms 46ms1, 000, 0001306ms 547ms 10, 000, 00014765ms 6429ms。
