(完整word)高中物理——受力分析专题习题及答案详细解答
高中物理受力分析专题习题及答案详细解答
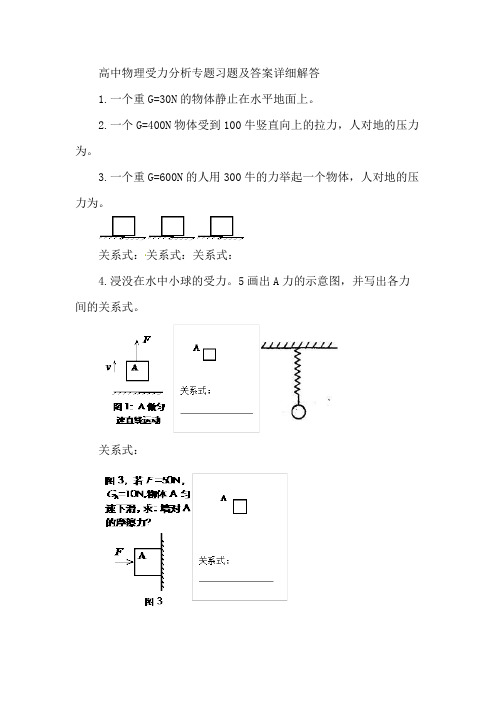
高中物理受力分析专题习题及答案详细解答1.一个重G=30N的物体静止在水平地面上。
2.一个G=400N物体受到100牛竖直向上的拉力,人对地的压力为。
3.一个重G=600N的人用300牛的力举起一个物体,人对地的压力为。
关系式:关系式:关系式:4.浸没在水中小球的受力。
5画出A力的示意图,并写出各力间的关系式。
关系式:6.关于杠杆的受力分析(1)13.如图11,若人用力F 匀速拉动吊箱,GA=1000N ,G 人=600N ,吊箱和动滑轮总重200N ,求:拉力F练习:试题详情1.将一金属块挂在竖直的弹簧测力计挂钩上,使其处于静止状态,下列说法正确的是A.弹簧测力计所受重力与金属块对弹簧测力计拉力是一相互作用力B.弹簧测力计对金属块的拉力与金属块所受重力的是一对平衡力C.金属块所受的重力与弹簧测力计所受的重力是一对平衡力D.弹簧测力计对金属块的拉力与金属块对弹簧测力计的拉力是一对平衡力2.如图7所示,用手向上拉物块A,当手对物块A的拉力为F1(F1≠0)时,物块A对手的拉力为F2,物块A对水平地面的压力为N1(N1≠0),水平地面对物块A的支持力为N2。
已知物块A受到的重力为G,则下列分析中正确的是A.拉力F1与F2是一对平衡力B.压力N1与重力G的大小相等C.压力N1与支持力N2是一对相互作用力D.拉力F1和支持力N2合力的大小与重力G的大小相等3.如图5所示,重为100N的物体B,在足够深的水中匀速下沉,通过滑轮组拉着重600N的物体A沿水平方向匀速运动,在4s内物体A移动了0.8米,已知B的密度是水的密度的5倍,动滑轮重12N,不计绳重及滑轮与绳之间的摩擦,g取10N/kgA.B对绳的拉力是20NB.图5B对绳的拉力的功率是16WC.A物体受摩擦力为148ND.滑轮组的机械效率为90%试题详情4.隔离物体进行受力分析试题详情5、如图12所示,物体M的重力为80N。
OBA是一个可以绕着O 点在竖直平面内转动的轻质杠杆,B0=3AO。
(完整word版)高中物理受力分析精选习题+答案
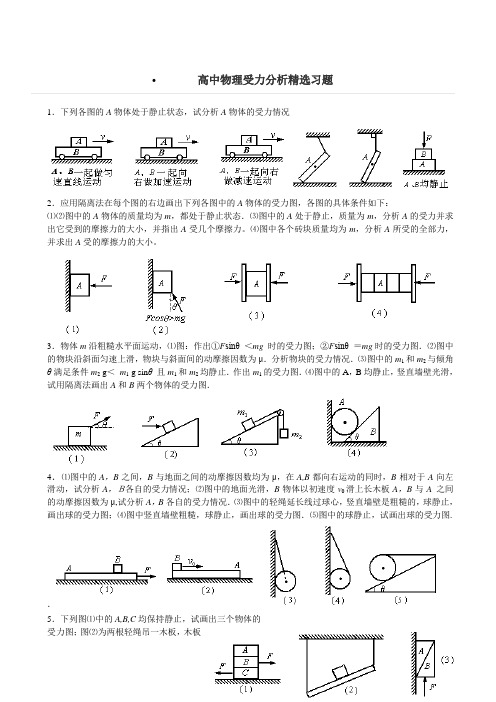
•高中物理受力分析精选习题1.下列各图的A物体处于静止状态,试分析A物体的受力情况2.应用隔离法在每个图的右边画出下列各图中的A物体的受力图,各图的具体条件如下:⑴⑵图中的A物体的质量均为m,都处于静止状态.⑶图中的A处于静止,质量为m,分析A的受力并求出它受到的摩擦力的大小,并指出A受几个摩擦力。
⑷图中各个砖块质量均为m,分析A所受的全部力,并求出A受的摩擦力的大小。
3.物体m沿粗糙水平面运动,⑴图:作出①F sinθ <mg时的受力图;②F sinθ =mg时的受力图.⑵图中的物块沿斜面匀速上滑,物块与斜面间的动摩擦因数为μ.分析物块的受力情况.⑶图中的m1和m2与倾角θ满足条件m2 g<m1 g sinθ且m1和m2均静止.作出m1的受力图.⑷图中的A,B均静止,竖直墙壁光滑,试用隔离法画出A和B两个物体的受力图.4.⑴图中的A,B之间,B与地面之间的动摩擦因数均为μ,在A,B都向右运动的同时,B相对于A向左滑动,试分析A,B各自的受力情况;⑵图中的地面光滑,B物体以初速度v0滑上长木板A,B与A之间的动摩擦因数为μ,试分析A,B各自的受力情况.⑶图中的轻绳延长线过球心,竖直墙壁是粗糙的,球静止,画出球的受力图;⑷图中竖直墙壁粗糙,球静止,画出球的受力图.⑸图中的球静止,试画出球的受力图..5.下列图⑴中的A,B,C均保持静止,试画出三个物体的受力图;图⑵为两根轻绳吊一木板,木板处于倾斜状态,另一个物块放在木板上,系统处于平衡状态,试分析木板的受力情况.图⑶中的A,B保持静止,试分析A帮B的受力情况.6.以下三个图中的物体全部处于静止状态,⑴图和⑵图画出C点的受力图,⑶图画出均匀棒的受力图.球面光滑.7.分析图⑴中定滑轮的受力情况,已知悬挂重物质量为m,并求出杆对滑轮的作用力.图⑵中的绳长L=2.5m,重物质量为m=4kg,不计绳子和滑轮质量,不计滑轮的摩擦.OA =1.5m.,取g =10m/s2.分析滑轮的受力情部并求出绳子对滑轮的拉力大小.图⑶:光滑球在水平推力F作用下处于静止状态,分析小球受力并求出斜面对小球的弹力大小.如图⑷,水平压力F =100N,A, B之间,A与墙壁之间的动摩擦因数均为μ=0.3,A、B受的重力均为10N.分析A物体的受力情况并求了它所受摩擦力的合力.如图⑸⑹,光滑球A、B放在水平面上,画出A,B的受力图8.画出下列各图中的光滑球的受力图,各图中的球均处于静止状态.9.如图所示,A,B两滑块叠放在水平面上,已知A与滑块B所受重力分别为G A= 10N,G B=20N,A与B间动摩擦因数μA=0.2,,B与水平面间的动摩擦因数μB=0.3.水平力F刚好能拉动滑块B,试分析两图中B滑块所受的力.并求出拉动滑块B所需的最小水平拉力分别是多大?10.如图⑴所示,三角形支架ABC的边长AB=20cm,BC= 15cm,在A点通过细绳悬挂一个重20N的物体,求AB杆受拉力的大小及AC杆受压力的大小?11.如图⑵所示,已知悬挂光滑球的绳子长度与球的半径相等,球的质量为m,求绳子的拉力和墙对球的弹力大小.图⑶中V型槽的夹角为60°,光滑球重100N,利用力的分解求出球对两接触面的压力大小.图⑷求三个力的合力分析弹力的实例与练习1.下列各图的接触面均为光滑接触面,A均保持静止状态.画出各图中A球所受的弹力.2.如下图,斜面和球均光滑,画出球受的弹力3.画出下列各图中A和B球所受的弹力4.画出下列各图中A球所受的弹力.各球面均看成光滑面.摩擦力的分析思路及其应用摩擦力分为滑动摩擦力与静摩擦力,它们均需要满足四个条件:两物体相互接触;接触面粗糙;存在相互作用的弹力;有相对滑动或相对滑动趋势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中专题习题——受力分析
例1如图6-1所示,A、B两物体的质量分别是m1和m2,其接触面光滑,与水平面的夹角为θ,若A、B与水平地面的动摩擦系数都是μ,用水平力F推A,使A、B一起加速运动,求:(1)A、B间的相互作用力(2)为维持A、B间不发生相对滑动,力F的取值范围。
分析与解:A在F的作用下,有沿A、B间斜面向上运动的趋势,据题意,为维持A、B 间不发生相对滑动时,A处刚脱离水平面,即A不受到水平面的支持力,此时A与水平面间的摩擦力为零。
本题在求A、B间相互作用力N和B受到的摩擦力f2时,运用隔离法;而求A、B组成的系统的加速度时,运用整体法。
(1)对A受力分析如图6-2(a)所示,据题意有:N1=0,f1=0
因此有:Ncosθ=m1g [1] , F-Nsinθ=m1a [2]
由[1]式得A、B间相互作用力为:N=m1g/cosθ
(2)对B受力分析如图6-2(b)所示,则:N2=m2g+Ncosθ[3] , f2=μN2 [4]
将[1]、[3]代入[4]式得: f2=μ(m1+ m2)g
取A、B组成的系统,有:F-f2=(m1+ m2)a [5]
由[1]、[2]、[5]式解得:F=m1g(m1+ m2)(tgθ-μ)/m2
故A、B不发生相对滑动时F的取值范围为:0<F≤m1g(m1+ m2)(tgθ-μ)/m2
例2如图1-1所示,长为5米的细绳的两端分别系于竖立在地面上相距为4米的两杆顶端A、B。
绳上挂一个光滑的轻质挂钩。
它钩着一个重为12牛的物体。
平衡时,绳中张力
T=____
分析与解:本题为三力平衡问题。
其基本思路为:选对象、分析力、画力图、列方程。
对平衡问题,根据题目所给条件,往往可采用不同的方法,如正交分解法、相似三角形等。
所以,本题有多种解法。
解法一:选挂钩为研究对象,其受力如图1-2所示
设细绳与水平夹角为α,由平衡条件可知:2TSinα=F,其中F=12牛
将绳延长,由图中几何条件得:Sinα=3/5,则代入上式可得T=10牛。
解法二:挂钩受三个力,由平衡条件可知:两个拉力(大小相等均为T)的合力F’与F大小相等方向相反。
以两个拉力为邻边所作的平行四边形为菱形。
如图1-2所示,其中力
的三角形△OEG与△ADC相似,则:得:牛。
心得:挂钩在细绳上移到一个新位置,挂钩两边细绳与水平方向夹角仍相等,细绳的张力仍不变。
例3如图2-12,m和M保持相对静止,一起沿倾角为θ的光滑斜面下滑,则M和m间的摩擦力大小是多少?
错解:以m为研究对象,如图2-13物体受重力mg、支持力N、摩擦力f,如图建立坐标有
再以m+N为研究对象分析受力,如图2-14,(m+M)g·sinθ=(M+m)a③
据式①,②,③解得f=0
所以m与M间无摩擦力。
分析与解:造成错解主要是没有好的解题习惯,只是盲目的模仿,似乎解题步骤不少,但思维没有跟上。
要分析摩擦力就要找接触面,摩擦力方向一定与接触面相切,这一步是堵
住错误的起点。
犯以上错误的客观原因是思维定势,一见斜面摩擦力就沿斜面方向。
归结还是对物理过程分析不清。
解答:因为m和M保持相对静止,所以可以将(m+M)整体视为研究对象。
受力,如图2-14,受重力(M十m)g、支持力N′如图建立坐标,根据牛顿第二定律列方程
x:(M+n)gsinθ=(M+m)a①
解得a=gsinθ
沿斜面向下。
因为要求m和M间的相互作用力,再以m为研究对象,受力如图2-15。
根据牛顿第二定律列方程
因为m,M的加速度是沿斜面方向。
需将其分解为水平方向和竖直方向如图2-16。
由式②,③,④,⑤解得f=mgsinθ·cosθ
方向沿水平方向m受向左的摩擦力,M受向右的摩擦力。
例4 如图2-25天花板上用细绳吊起两个用轻弹簧相连的两个质量相同的小球。
两小球均保持静止。
当突然剪断细绳时,上面小球A与下面小球B的加速度
为 [ ]
A.a1=g a2=g
B.a1=g a2=g
C.a1=2g a2=0
D.a1=0 a2=g
错解:剪断细绳时,以(A+B)为研究对象,系统只受重力,所以加速度为g,所以A,B 球的加速度为g。
故选A。
分析与解:出现上述错解的原因是研究对象的选择不正确。
由于剪断绳时,A,B球具有不同的加速度,不能做为整体研究。
解答:分别以A,B为研究对象,做剪断前和剪断时的受力分析。
剪断前A,B静止。
如图2-26,A球受三个力,拉力T、重力mg和弹力F。
B球受三个力,重力mg和弹簧拉力F′
A球:T-mg-F=0 ①
B球:F′-mg=0 ②
由式①,②解得T=2mg,F=mg
剪断时,A球受两个力,因为绳无弹性剪断瞬间拉力不存在,而弹簧有形米,瞬间形状不可改变,弹力还存在。
如图2-27,A球受重力mg、弹簧给的弹力F。
同理B球受重力mg 和弹力F′。
A球:-mg-F=ma A③
B球:F′-mg=ma B④
由式③解得a A=-2g(方向向下)
由式④解得a B=0
故C选项正确。
心得:(1)牛顿第二定律反映的是力与加速度的瞬时对应关系。
合外力不变,加速度不变。
合外力瞬间改变,加速度瞬间改变。
本题中A球剪断瞬间合外力变化,加速度就由0变为2g,而B球剪断瞬间合外力没变,加速度不变。
例5如图3-1所示的传送皮带,其水平部分 ab=2米,bc=4米,bc与水平面的夹角α=37°,一小物体A与传送皮带的滑动摩擦系数μ=0.25,皮带沿图示方向运动,速率为2米/秒。
若把物体A轻轻放到a点处,它将被皮带送到c点,且物体A一直没有脱离皮带。
求物体A从a点被传送到c点所用的时间。
分析与解:物体A轻放到a点处,它对传送带的相对运动向后,传送带对A的滑动摩擦力向前,则 A 作初速为零的匀加速运动直到与传送带速度相同。
设此段时间为t1,则:
a1=μg=0.25x10=2.5米/秒2 t=v/a1=2/2.5=0.8秒
设A匀加速运动时间内位移为S1,则:
设物体A在水平传送带上作匀速运动时间为t2,则
设物体A在bc段运动时间为t3,加速度为a2,则:
a2=g*Sin37°-μgCos37°=10x0.6-0.25x10x0.8=4米/秒2
解得:t3=1秒(t3=-2秒舍去)
所以物体A从a点被传送到c点所用的时间t=t1+t2+t3=0.8+0.6+1=2.4秒。
例6 如图2-1所示,轻质长绳水平地跨在相距为2L的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等。
在轻绳两端C、D分别施加竖直向下的恒力F=mg。
先托住物块,使绳处于水平拉直状态,由静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变。
(1)当物块下落距离h为多大时,物块的加速度为零?
(2)在物块下落上述距离的过程中,克服C端恒力F做功W为多少?
(3)求物块下落过程中的最大速度Vm和最大距离H?
分析与解:物块向下先作加速运动,随着物块的下落,两绳间的夹角逐渐减小。
因为绳子对物块的拉力大小不变,恒等于F,所以随着两绳间的夹角减小,两绳对物块拉力的合力将逐渐增大,物块所受合力逐渐减小,向下加速度逐渐减小。
当物块的合外力为零时,速度达到最大值。
之后,因为两绳间夹角继续减小,物块所受合外力竖直向上,且逐渐增大,物块将作加速度逐渐增大的减速运动。
当物块下降速度减为零时,物块竖直下落的距离达到最大值H。
当物块的加速度为零时,由共点力平衡条件可求出相应的θ角,再由θ角求出相应的距离h,进而求出克服C端恒力F所做的功。
对物块运用动能定理可求出物块下落过程中的最大速度Vm和最大距离H。
(1)当物块所受的合外力为零时,加速度为零,此时物块下降距离为h。
因为F恒等于mg,所以绳对物块拉力大小恒为mg,由平衡条件知:2θ=120°,所以θ=60°,由图2-2知:h=L*tg30°
=L [1]
(2)当物块下落h时,绳的C、D端均上升h’,由几何关系可得:h’=-L [2]
克服C端恒力F做的功为:W=F*h [3]
由[1]、[2]、[3]式联立解得:W=(-1)mgL
(3)出物块下落过程中,共有三个力对物块做功。
重力做正功,两端绳子对物块的拉力做负功。
两端绳子拉力做的功就等于作用在C、D端的恒力F所做的功。
因为物块下降距离h时动能最大。
由动能定理得:mgh-2W= [4]
将[1]、[2]、[3]式代入[4]式解得:Vm=
当物块速度减小为零时,物块下落距离达到最大值H,绳C、D上升的距离为H’。
由动能定理得:mgH-2mgH’=0,又H’=-L,联立解得:H=。
