勾股定理常见题型
3.1勾股定理(七大题型)(解析版)
（苏科版）八年级上册数学《第3章 勾股定理》3.1 勾股定理●勾股定理： 直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两条直角边长分别为a ，b ，斜边长为c ，那么a 2+b 2=c 2.◆1、勾股定理的应用条件：勾股定理只适用于直角三角形；◆2、勾股定理揭示的是直角三角形三边的关系，已知直角三角形中的任意两边可以求出第三边.◆3、勾股定理的几种变形式：勾股定理将“数”与“形”联系起来，体现了直角三角形三边之间的等量关系.如果直角三角形的两条直角边长分别为a ，b ，斜边长为c ，则a 2 + b 2 = c 2、 a 2 = c 2 - b 2、b 2 = c 2 - a 2；22b a c +=、22b c a -=、22a c b -=.【拓展】◎1、锐角三角形的三边关系是：在锐角三角形中，若三边长分别为a ，b ，c ，其中c 为最大边，则a 2+b 2＞c 2.◎2、钝角三角形的三边关系是：在钝角三角形中，若三边长分别为a ，b ，c ，其中c 为最大边，则a 2+b 2＜c 2.●通过拼图证明勾股定理的思路：（1）图形经过割补拼接后，只要没有重叠、没有空隙，面积就不会改变.（2）根据同一种图形的面积的不同表示方法列出等式.（3）利用等式性质变化验证结论成立，即拼出图形→写出图形面积的表达式→找出等量关系→恒等变形→推导命题结论.●下面列举几种证明方法：◆1、“赵爽弦图”证明：在图1中，大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和．即c2=12ab×4+（b﹣a）2，化简得：a2+b2＝c2．◆2、我国数学家邹元治的证明方法证明：在图2中，大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和．即（a+b）2＝c2+12ab×4，化简得：a2+b2＝c2．◆3、美国第二十任总统伽菲尔德的“总统证法”证明：在图3中，梯形的面积等于三个直角三角形的面积的和．即12（a+b）（a+b）=12ab×2+12c2，化简得：a2+b2＝c2．【例题1】在直角三角形中，两条直角边的长分别为9和12，则斜边的长为 ．【分析】根据勾股定理直接求出斜边的长即可．【解答】解：∵在直角三角形中，两条直角边的长分别为9和12，=15．故答案为：15．【点评】本题主要考查了勾股定理，解题的关键是熟练掌握勾股定理，如果直角三角形的两条直角边长为a、b，斜边长为c，那么a2+b2＝c2．【变式1-1】已知△ABC中，∠C＝90°，AB＝c，BC＝a，AC＝b．（1）如果a＝7，b＝24，求c；（2）如果a＝12，c＝13，求b．【分析】（1）利用勾股定理计算c=（2）利用勾股定理计算b=【解答】解：（1）在Rt△ABC中，∠C＝90°，由勾股定理得：c==＝25；（2）在Rt△ABC中，由勾股定理得：b==＝5．【点评】本题考查了勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．即：如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2+b 2＝c 2．注意勾股定理应用的前提条件是在直角三角形中．【变式1-2】（2022秋•东方期末）如图，在△ABC 中，AB ＝AC ＝10，BC ＝12，AD 平分∠BAC ，则AD 等于（ ）A ．6B ．7C ．8D ．9【分析】根据等腰三角形的三线合一得到AD ⊥BC ，BD ＝DC =12BC ＝6，根据勾股定理计算，得到答案．【解答】解：∵AB ＝AC ，AD 平分∠BAC ，∴AD ⊥BC ，BD ＝DC =12BC ＝6，在Rt △ABD 中，AD 8，故选：C ．【点评】本题考查的是勾股定理、等腰三角形的性质，如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2+b 2＝c 2．【变式1-3】（2022秋•新泰市期末）如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，则点C 到直线AB 的距离是（ ）A ．185B ．3C ．125D ．2【分析】作CD⊥AB于点D，根据勾股定理可以求得AB的长，然后根据面积法，可以求得CD的长．【解答】解：作CD⊥AB于点D，如右图所示，∵∠C＝90°，AC＝3，BC＝4，∴AB=5，∵AC⋅BC2=AB⋅CD2，∴3×42=5CD2，解得CD＝2.4，故选：C．【点评】本题考查勾股定理、三角形的面积，解答本题的关键是明确题意，画出相应的图形，利用勾股定理和面积法解答．【变式1-4】（2021春•连州市期中）如图所示，AB⊥BC，DC⊥BC，E是BC上一点，∠BAE＝∠DEC＝60°，AB＝3，CE＝4，则AD等于（ ）A．10B．12C．24D．48【分析】本题主要考查勾股定理运用，解答时要灵活运用直角三角形的性质．【解答】解：∵AB⊥BC，DC⊥BC，∠BAE＝∠DEC＝60°∴∠AEB＝∠CDE＝30°∵30°所对的直角边是斜边的一半∴AE＝6，DE＝8又∵∠AED ＝90°根据勾股定理∴AD ＝10．故选：A ．【点评】解决此类题目的关键是熟练掌握运用直角三角形两个锐角互余，30°所对的直角边是斜边的一半，勾股定理的性质．【变式1-5】如图，在△ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，分别以点A 和点B 为圆心，以相同的长（大于12AB ）为半径作弧，两弧相交于点M 和点N ，作直线MN 交AB 于点D ，连接CD ，则CD 的长为 ．【分析】根据勾股定理可以求得AB 的长，然后根据线段垂直平分线的判定方法可以得到MN 为线段AB 的垂直平分线，再根据直角三角形斜边上的中线等于斜边的一半，即可得到CD 的长．【解答】解：∵∠ACB ＝90°，AC ＝3，BC ＝4，∴AB ==5，连接NA ，NB ，MA ，MB ，如图所示，∵分别以点A 和点B 为圆心，以相同的长（大于12AB ）为半径作弧，两弧相交于点M 和点N ，∴NA ＝NB ，MA ＝MB ，∴直线MN 垂直平分AB ，∵直线MN 交AB 于点D ，∴点D 为AB 的中点，∴CD 为Rt △ACB 斜边上的中线，∴CD =12AB =52，故答案为：52．【点评】本题考查勾股定理、线段垂直平分线的性质，解答本题的关键是明确题意，利用数形结合的思想解答．【变式1-6】（2022春•河北区期末）如图，在△ABC中，CD⊥AB于点D，AC＝20，CD＝12，BD＝9．求AB与BC的长．【分析】根据勾股定理求出BC即可；根据勾股定理求出AD，求出AB即可．【解答】解：∵CD⊥AB，AC＝20，CD＝12，BD＝9，∴∠ADC＝∠BDC＝90°，在Rt△CDB中，由勾股定理得：BC=15，在Rt△ADC中，由勾股定理得：AD=16，∴AB＝AD+DB＝16+9＝25．答：AB的长为25，BC的长为15．【点评】本题考查了勾股定理的应用，关键是对定理的掌握和运用．【变式1-7】如图，在△ABC中，AC＝8，BC＝6，CE是AB边上的中线，CD是AB边上的高，且AE＝5．（1）求CD的长；（2）求DE的长．【分析】（1）先证明三角形ABC是直角三角形，再根据等面积法即可求解；（2）根据勾股定理求出BD的长即可求解．【解答】解：（1）∵CE是AB边上的中线，∴AE＝BE＝5，∴AB＝10，又∵AC＝8，BC＝6，∴AC2+BC2＝82+62＝100＝AB2，∴△ABC是直角三角形，又∵CD是△ABC的高，∴S△ABC=12AC⋅BC=12AB⋅CD，∴CD=AC⋅BCAB=4.8；（2）在Rt△BDC中，由勾股定理得，BD=3.6，∴DE＝BE﹣BD＝5﹣3.6＝1.4．【点评】本题考查了勾股定理，熟练掌握勾股定理是解题的关键．【例题2】勾股定理的验证方法很多，用面积（拼图）证明是最常见的一种方法．如图所示，一个直立的长方体在桌面上慢慢地倒下，启发人们想到勾股定理的证明方法，设AB＝c，BC＝a，AC＝b，证明中用到的面积相等关系是（ ）A．S△ABC+S△ABD＝S△AFG+S△AEFB．S梯形BCEF＝S△ABC+S△ABF+S△AEFC．S△BDH＝S△FGHD．S梯形BCEF＝S△ABC+S△ABF+S△AEF+S△FGH【分析】通过用两种方法计算梯形BCEF的面积即可证明勾股定理．【解答】解：∵矩形ACBD旋转得出矩形AGFE，∴△ABC≌△FAE，∴AB＝AF，∠BAC＝∠AFE，∵∠AFE+∠EAF＝90°，∴∠BAC+∠EAF＝90°，∴△ABF是等腰直角三角形，由题意知：S梯形BCEF =12（a+b）•（a+b）=12(a+b)2=12a2+ab+12b2，S△ABC+S△ABF+S△AEF=12ab+12ab+12c2=ab+12c2，∴12a2+ab+12b2=ab+12c2，∴a2+b2＝c2，故选：B．【点评】本题主要考查了勾股定理的证明，等腰直角三角形的判定，表示出图形面积的不同表达形式，建立等量关系是解题的关键．【变式2-1】（2022春•三门峡期末）我国是最早了解勾股定理的国家之一．据《周髀算经》记载，勾股定理的证明是在商代由商高发现的，故又称之为“商高定理”；三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释，又给出了另外一个证明．古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用．下面四幅图中，不能证明勾股定理的是（ ）A ．B ．C ．D ．【分析】由正方形面积公式、三角形面积公式以及梯形面积公式分别对各个选项进行判断即可．【解答】解：A 、大正方形的面积为：c 2，也可看作是4个直角三角形和一个小正方形组成，则其面积为：12ab ×4+（b ﹣a ）2＝a 2+b 2，∴a 2+b 2＝c 2，故A 选项能证明勾股定理；B 、大正方形的面积为：（a +b ）2，也可看作是2个矩形和2个小正方形组成，则其面积为：a 2+b 2+2ab ，∴（a +b ）2＝a 2+b 2+2ab ，∴B 选项不能证明勾股定理．C 、大正方形的面积为：（a +b ）2；也可看作是4个直角三角形和一个小正方形组成，则其面积为：12ab ×4+c 2＝2ab +c 2，∴（a +b ）2＝2ab +c 2，∴a 2+b 2＝c 2，故C 选项能证明勾股定理；D、梯形的面积为：12（a+b）（a+b）=12（a2+b2）+ab，也可看作是2个直角三角形和一个等腰直角三角形组成，则其面积为：12ab×2+12c2＝ab+12c2，∴12（a2+b2）+ab＝ab+12c2，∴a2+b2＝c2，故D选项能证明勾股定理；故选：B．【点评】本题考查了勾股定理的证明、正方形面积公式、三角形面积公式以及梯形面积公式，熟练掌握内弦图、外弦图是解题的关键．【变式2-2】“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b，若ab＝8，大正方形的面积为25，则小正方形的边长为（ ）A．9B．6C．4D．3【分析】分析题意，首先根据已知条件易得，中间小正方形的边长为：a﹣b；接下来根据勾股定理以及题目给出的已知数据即可求出小正方形的边长．【解答】解：由题意可知：中间小正方形的边长为：a﹣b，∵每一个直角三角形的面积为：12ab=12×8＝4，从图形中可得，大正方形的面积是4个直角三角形的面积与中间小正方形的面积之和，∴4×12ab+（a﹣b）2＝25，∴（a﹣b）2＝25﹣16＝9，∴a﹣b＝3．故选：D．【点评】本题考查勾股定理，解题的关键是熟练运用勾股定理以及完全平方公式．【变式2-3】（2022春•高安市期中）勾股定理被誉为“几何明珠”，如图是我国古代著名的“赵爽弦图”，它由4个全等的直角三角形拼成，已知大正方形面积为25，小正方形面积为1，若用a、b表示直角三角形的两直角边（a＞b），则下列说法：①a2+b2＝25，②a﹣b＝1，③ab＝12，④a+b＝7．正确的是（ ）A．①②B．①②③C．①②④D．①②③④【分析】根据勾股定理和大正方形面积为25，可以判断①；根据小正方形面积为1，可以判断②；根据大正方形面积为25，小正方形面积为1，可以得到四个直角三角形的面积，从而可以得到ab的值，即可判断③；根据完全平方公式可以判断④．【解答】解：由图可得，a2+b2＝c2＝25，故①正确；∵小正方形面积为1，∴小正方形的边长为1，∴a﹣b＝1，故②正确；∵大正方形面积为25，小正方形面积为1，∴12ab＝（25﹣1）÷4，解得ab＝12，故③正确；∵a2+b2＝25，ab＝12，∴（a+b）2＝a2+2ab+b2＝49，∴a+b＝7，故④正确；故选：D．【点评】本题考查勾股定理的证明、正方形的性质、直角三角形的面积，利用数形结合的思想解答是解答本题的关键．【变式2-4】如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC ＝6，BC＝5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到如图2所示的“数学风车”，则这个风车的外围周长是（ ）A ．36B ．76C ．66D ．12【分析】由题意∠ACB 为直角，利用勾股定理求得外围中一条边，又由AC 延伸一倍，从而求得风车的一个轮子，进一步求得四个．【解答】解：依题意，设“数学风车”中的四个直角三角形的斜边长为x ，则x 2＝122+52＝169，所以x ＝13，所以这个风车的外围周长是：（13+6）×4＝76．故选：B ．【点评】此题考查了勾股定理的证明，本题是勾股定理在实际情况中的应用，并注意隐含的已知条件来解答此类题．【变式2-5】用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题，这种方法称为等面积法，这是一种重要的数学方法，请你用等面积法来探究下列三个问题：（1）如图1是著名的“赵爽弦图”，由四个全等的直角三角形拼成，请用它验证勾股定理c 2＝a 2+b 2．（2）如图2，在Rt △ABC 中，∠ACB ＝90°，CD 是AB 边上的高，AC ＝4，BC ＝3，求CD 的长度；（3）如图1，若大正方形的面积是13，小正方形的面积是1，求（a +b ）2的值（a ＜b ）．【分析】（1）根据大正方形的面积的两种表示方法求解即可；（2）根据直角三角形的面积公式求解即可；（3）根据小正方形的为1得出2ab ＝12，再结合c 2＝13即可求解．【解答】解：（1）如图1，大正方形的面积＝c 2＝4×12ab +(b ―a )2，整理得，c2＝a2+b2；（2）在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，∴AB=5，∵S△ABC=12AC⋅BC=12AB⋅CD，∴CD=AC⋅BCAB=125；（3）∵大正方形的面积是13，小正方形的面积是1，∴c2＝13，（b﹣a）2＝1，∴a2+b2﹣2ab＝1，∴2ab＝12，∴（a+b）2＝a2+b2+2ab＝13+12＝25，即（a+b）2的值为25．【点评】本题考查了勾股定理的证明，正确表示出大正方形的面积的两种表示方法是解题的关键．【变式2-6】（2022春•巢湖市校级期中）学习勾股定理之后，同学们发现证明勾股定理有很多方法．某同学提出了一种证明勾股定理的方法：如图1点B是正方形ACDE边CD上一点，连接AB，得到直角三角形ACB，三边分别为a，b，c，将△ACB裁剪拼接至△AEF位置，如图2所示，该同学用图1、图2的面积不变证明了勾股定理．请你写出该方法证明勾股定理的过程．【分析】连接BF，由图1可得正方形ACDE的面积为b2，由图2可得四边形ABDF的面积为三角形ABF 与三角形BDF面积之和，再利用正方形ACDE的面积与四边形ABDF的面积相等即可证明．【解答】证明：如图，连接BF，∵AC ＝b ，∴正方形ACDE 的面积为b 2，∵CD ＝DE ＝AC ＝b ，BC ＝a ，EF ＝BC ＝a ，∴BD ＝CD ﹣BC ＝b ﹣a ，DF ＝DE +EF ＝a +b ，∵∠CAE ＝90°，∴∠BAC +∠BAE ＝90°，∵∠BAC ＝∠EAF ，∴∠EAF +∠BAE ＝90°，∴△BAE 为等腰直角三角形，∴四边形ABDF 的面积为：12c 2+12（b ﹣a ）（a +b ）=12c 2+12（b 2﹣a 2），∵正方形ACDE 的面积与四边形ABDF 的面积相等，∴b 2=12c 2+12（b 2﹣a 2），∴b 2=12c 2+12b 2―12a 2，∴12a 2+12b 2=12c 2，∴a 2+b 2＝c 2．【点评】本题考查勾股定理的证明，解题的关键是熟练掌握勾股定理的证明方法，一般利用拼图的方法，再利用面积相等证明．【例题3】如图，当正方形B的面积为64，正方形C的面积为100时，正方形A的面积为（ ）A．36B．25C．16D．6【分析】直接根据勾股定理进行解答即可．【解答】解：由图可知，△DEF是直角三角形，∴DE2+DF2＝EF2，∵正方形B的面积＝DF2，正方形C的面积＝EF2，正方形A的面积＝DF2，正方形B的面积为64，正方形C的面积为100，∴正方形A的面积＝100﹣64＝36．故选：A．【点评】本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解题的关键．【变式3-1】（2022秋•渠县期末）如图，所有阴影部分四边形都是正方形，所有三角形都是直角三角形，若正方形A、C、D的面积依次为4、6、18，则正方形B的面积为（ ）A．8B．9C．10D．12【分析】根据勾股定理、正方形的面积公式计算即可．【解答】解：由勾股定理，得正方形E的面积＝正方形C的面积+正方形D的面积，正方形E的面积＝正方形A的面积+正方形B的面积，则正方形B的面积＝18﹣6﹣4＝8，故选：A．【点评】本题考查了勾股定理，要熟悉勾股定理的几何意义，知道直角三角形两直角边的平方和等于斜边的平方．【变式3-2】（2022秋•南京期末）如图，在等腰Rt△ACB中，∠ACB＝90°，AC＝BC，且AB＝AB、AC、BC为直径画半圆，其中所得两个月形图案AFCD和BGCE（图中阴影部分）的面积之和等于（ ）A．8B．4C．2D．【分析】由等腰三角形的性质及勾股定理可求解AC＝CB＝2，进而可求得S△ACB＝2，再利用阴影部分的面积＝以AC为直径的圆的面积+△ACB的面积﹣以AB为直径的半圆的面积计算可求解．【解答】解：在等腰Rt △ACB 中，∠ACB ＝90°，AC ＝BC ，AB ＝∴AC 2+BC 2＝AB 2＝8，∴AC ＝CB ＝2，∴S △ACB =12AC •BC ＝2，∴S 阴影＝π（AC 2）2+S △ACB ―12π（AB 2）2＝π+2﹣π＝2，故选：C ．【点评】本题主要考查等腰直角三角形，勾股定理，理清阴影部分的面积＝以AC 为直径的圆的面积+△ACB 的面积﹣以AB 为直径的半圆的面积是解题的关键．【变式3-3】如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中S A ＝4，S B ＝2，S c ＝2，S D ＝1，则S ＝（ ）A ．25B ．20C ．9D ．5【分析】根据正方形的性质和勾股定理的几何意义解答即可．【解答】解：如图，根据勾股定理的几何意义，可知：S＝S F+S G＝S A+S B+S C+S D＝4+2+2+1＝9；即S＝9；故选：C．【点评】本题考查了正方形的性质、勾股定理的几何意义，关键是掌握两直角边的平方和等于斜边的平方．【变式3-4】如图，Rt△ABC中，分别以这个三角形的三边为边长作正方形，面积分别记为S1、S2、S2．如果S2+S1﹣S3＝18，则阴影部分的面积为 ．【分析】由勾股定理得出S2﹣S3＝S1，再根据S2+S1﹣S3＝18即可得出S1的值，即为图中阴影部分的面积．【解答】解：由勾股定理得，BC2﹣AC2＝AB2，即S2﹣S3＝S1，∵S2+S1﹣S3＝18，∴S 1＝9，由图形可知，阴影部分的面积=12S 1，∴阴影部分的面积=92，故答案为：92．【点评】本题考查了勾股定理，由勾股定理得出S 2﹣S 3＝S 1，是解题的关键．【变式3-5】（2022秋•绿园区校级期末）如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为16cm ，则正方形A ，B ，C ，D 的面积之和为 cm 2．【分析】如图根据勾股定理有S 正方形2+S 正方形3＝S 正方形1，S 正方形C +S 正方形D ＝S 正方形3，S 正方形A +S 正方形B ＝S 正方形2，等量代换即可求四个小正方形的面积之和．【解答】解：如右图所示，根据勾股定理可知，S 正方形2+S 正方形3＝S 正方形1，S 正方形C +S 正方形D ＝S 正方形3，S 正方形A +S 正方形B ＝S 正方形2，∴S 正方形C +S 正方形D +S 正方形A +S 正方形B ＝S 正方形2+S 正方形3＝S 正方形1＝162＝256（cm 2）．故答案为：256．【点评】本题考查了勾股定理的几何意义，关键是掌握两直角边的平方和等于斜边的平方．【变式3-6】如图，直角三角形ACB，直角顶点C在直线l上，分别过点A、B作直线l的垂线，垂足分别为点D和点E．（1）求证：∠DAC＝∠BCE；（2）如果AC＝BC．①求证：CD＝BE；②若设△ADC的三边分别为a、b、c，试用此图证明勾股定理．【分析】（1）根据直角三角形的定义和垂直的定义，可以证明结论成立；（2）①根据AAS可以证明结论成立；②根据S梯形ADEB＝S△ADC+S△ACB+S△CEB，代入字母计算即可证明结论成立．【解答】证明：（1）∵∠ACB＝90°，AD⊥DE于点D，∴∠DAC+∠ACD＝90°，∠ADC+∠BCE＝90°，∴∠DAC＝∠BCE；（2）①∵AD⊥DE于点D，BE⊥DE于点E，∴∠ADC＝∠CEB＝90°，由（1）知：∠DAC＝∠BCE，在△ADC和△CEB中，∠ADC=∠CEB∠DAC=∠ECB，AC=CB∴△ADC≌△CEB（AAS），∴CD＝BE；②由图可知：S 梯形ADEB ＝S △ADC +S △ACB +S △CEB ，∴(a b )(a b )2=ab 2+c 22+ab 2，化简，得：a 2+b 2＝c 2．【点评】本题考查勾股定理的证明，解答本题的关键是明确题意，利用数形结合的思想解答．【例题4】（2022秋•门头沟区期末）已知：如图，在△ABC 中，AB ＝AC ＝5，BC ＝8．求BC 边上的高的长．【分析】过点A 作AD ⊥BC 于点D ，根据等腰三角形的性质求出BD =12BC ＝4，根据勾股定理求出AD 的长即可．【解答】解：如图，过点A 作AD ⊥BC 于点D ，∵AB ＝AC ＝5，BC ＝8，AD ⊥BC ，∴BD ＝CD =12BC ＝4，∴AD==3，即BC 边上的高的长为3．【点评】此题考查了等腰三角形的性质、勾股定理等知识，熟练掌握等腰三角形的性质、勾股定理是解题的关键．【变式4-1】如图，在△ABC中，∠C＝90°，DE垂直平分AB，分别交AB，BC于D，E两点，若BE＝5，CE＝3，则AC的长为 ．【分析】先根据线段垂直平分线的性质可得BE＝AE＝5，然后在Rt△ACE中，利用勾股定理进行计算，即可解答．【解答】解：连接AE，∵DE垂直平分AB，∴BE＝AE＝5，∵∠C＝90°，CE＝3，∴AC==4，故答案为：4．【点评】本题考查了勾股定理，线段垂直平分线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．【变式4-2】（2021春•齐齐哈尔月考）已知：△ABC中，AC＝2，∠C＝30°，∠B＝45°，求AB和BC的长．【分析】作AD⊥BC，得∠ADC＝∠ADB＝90°，根据勾股定理和直角三角形30°所对的直角边是斜边的一半计算即可．【解答】解：作AD⊥BC，∴∠ADC＝∠ADB＝90°，∵∠C＝30°，∴AD=12AC＝1，在Rt△ACD，根据勾股定理得，CD=∵∠B＝45°，∴∠DAB＝∠B＝45°，∴BD＝AD＝1，则BC＝1∴AB=【点评】本题考查了解直角三角形，熟练掌握勾股定理和直角三角形中30°所对的直角边是斜边的一半，这两个定理的应用是解题关键．【变式4-3】（2022春•阳新县期末）△ABC中，AB＝13，AC＝15，高AD＝12，则BC的长为（ ）A．14B．4C．14或4D．以上都不对【分析】分两种情况讨论：锐角三角形和钝角三角形，根据勾股定理求得BD，CD，再由图形求出BC，在锐角三角形中，BC＝BD+CD，在钝角三角形中，BC＝CD﹣BD．【解答】解：（1）如图，锐角△ABC中，AB＝13，AC＝15，BC边上高AD＝12，在Rt△ABD中AB＝13，AD＝12，由勾股定理得BD2＝AB2﹣AD2＝132﹣122＝25，则BD＝5，在Rt△ABD中AC＝15，AD＝12，由勾股定理得CD2＝AC2﹣AD2＝152﹣122＝81，则CD＝9，故BC＝BD+DC＝9+5＝14；（2）钝角△ABC中，AB＝13，AC＝15，BC边上高AD＝12，在Rt△ABD中AB＝13，AD＝12，由勾股定理得BD2＝AB2﹣AD2＝132﹣122＝25，则BD＝5，在Rt△ACD中AC＝15，AD＝12，由勾股定理得CD2＝AC2﹣AD2＝152﹣122＝81，则CD＝9，故BC的长为DC﹣BD＝9﹣5＝4．故选：C．【点评】本题考查了勾股定理，把三角形边的问题转化到直角三角形中用勾股定理解答．【变式4-4】如图，Rt△ABC中，AC⊥CB，AC＝15，AB＝25，点D为斜边上动点．连接CD，在点D的运动过程中，当△ACD 为等腰三角形时，AD 的长为 ．【分析】分三种情况讨论，利用等腰三角形的性质，分别求解即可解决问题．【解答】解：①当AD ＝AC 时，△ACD 为等腰三角形，∵AC ＝15，∴AD ＝AC ＝15．②当CD ＝AD 时，△ACD 为等腰三角形，∵CD ＝AD ，∴∠DCA ＝∠CAD ，∵∠CAB +∠B ＝90°，∠DCA +∠BCD ＝90°，∴∠B ＝∠BCD ，∴BD ＝CD ，∴CD ＝BD ＝DA ＝12.5；③当CD ＝AC 时，△ACD 为等腰三角形，如图，作CH ⊥BA 于点H ，则12×AB ×CH =12×AC ×BC ，∵AC ＝15，BC ＝20，AB ＝25，∴CH ＝12，在Rt △ACH 中，AH =9，∵CD ＝AC ，CH ⊥BA ，∴DH ＝HA ＝9，∴AD ＝18，综上所述：AD 的值为15或12.5或18．故答案为：15或12.5或18．【点评】本题考查解直角三角形的应用，等腰三角形的判定和性质，勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．【例题5】如图，阴影部分表示以Rt △ABC 的各边为直径的三个半圆所组成的两个新月形，面积分别记作S 1和S 2．若S 1+S 2＝7，AB ＝6，则△ABC 的周长是（ ）A ．12.5B ．13C ．14D ．15【分析】根据勾股定理得到AC 2+BC 2＝AB 2，根据扇形面积公式、完全平方公式计算即可．【解答】解：由勾股定理得，AC 2+BC 2＝AB 2，∵S 1+S 2＝7，∴12×π×（AC 2）2+12×π×（BC 2）2+12×AC ×BC ―12×π×（AB 2）2＝7，∴AC ×BC ＝14，∴（AC +BC ）2＝AC 2+BC 2+2AC •BC ＝62+2×14＝64，∴AC +BC ＝8（负值舍去），∴△ABC 的周长＝AB +AC +BC ＝8+6＝14，故选：C ．【点评】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2+b 2＝c 2．【变式5-1】如图，三角形ABC中，∠C=90°，∠BAC的平分线交BC于D，DE⊥AB于E，已知CD=3，BD=5，求三角形ABC的周长．【分析】根据角平分线的性质得到DE=CD=3，根据勾股定理求出BE的长，再根据勾股定理列出方程，解方程得到答案．【解答】解：∵AD是∠BAC的平分线，∠C=90°，DE⊥AB，∴DE=CD=3，AC=AE，∵DE⊥AB，DE=3，BD=5，根据勾股定理得，BE=4，∴AC2+82=（AE+4）2，解得AE=6，则AC=6，∴三角形ABC的周长=AC+AB+BC=24．【点评】本题考查的是角平分线的性质和勾股定理的应用，掌握角的平分线上的点到角的两边的距离相等是解题的关键．【变式5-2】如图，△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，DE⊥AB于E，若AB＝10cm，AC＝6cm，则△BED周长为（ ）A．10cm B．12cm C．14cm D．16cm【分析】根据角平分线上的点到角的两边距离相等可得CD＝DE，再利用“HL”证明Rt△ACD和Rt△AED全等，根据全等三角形对应边相等可得AC＝AE，可求出BE，再利用勾股定理列式求出BC，最后根据三角形的周长列式计算即可得解．【解答】解：∵AD是∠CAB的平分线，∠C＝90°，DE⊥AB于E，∴CD＝DE，在Rt△ACD和Rt△AED中，AD=ADDC=DE，∴Rt△ACD≌Rt△AED（HL），∴AC＝AE＝6，∴BE＝AB﹣AE＝10﹣6＝4，由勾股定理得，BC==8，∴△BDE的周长＝BE+BD+CD＝BE+BD+CD＝BE+BC＝4+8＝12（cm）．故选：B．【点评】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，勾股定理，熟记性质并求出三角形全等是解题的关键．【变式5-3】在四边形ABCD中，∠ABC＝∠ADC＝90°，连接AC，点E为AC的中点，连接BE，DE．若DE=132，BC＝12，则△ABE的周长为 ．【分析】根据直角三角形斜边上的中线等于斜边的一边得到AC＝2BE＝2DE＝2AE＝13，再利用勾股定理求出AB＝5即可得到答案．【解答】解：∵∠ABC＝∠ADC＝90°，点E为AC的中点，∴AC＝2BE＝2DE＝2AE＝13，∵BC＝12，∴AB=5，∴△ABE的周长为AE+BE+AB=5+2×132=18，故答案为：18．【点评】本题主要考查了直角三角形斜边上的中线的性质，勾股定理，熟知直角三角形斜边上的中线等于斜边的一半是解题的关键．【例题6】（2022春•范县期中）如图，正方形ABCD中，AE⊥BE，且AE＝3，AB＝5，则阴影部分的面积是（ ）A．13B．15C．18D．19【分析】利用正方形的面积减去三角形的面积即可求出阴影部分的面积．【解答】解：∵AE⊥BE，且AE＝3，AB＝5，∴BE=4，∴S△ABE=12AE⋅BE=12×3×4=6，∵四边形ABCD是正方形，AB＝5，∴S正＝5×5＝25，∴S阴影＝S正﹣S△ABE＝25﹣6＝19．故选：D．【点评】本题主要考查正方形的性质与勾股定理，解题的关键是用割补法求阴影部分的面积．【变式6-1】如图，在△ABC中，AC＝BC＝17，AB＝16，求△ABC的面积．【分析】过C作CD⊥AB于D，根据等腰三角形的性质和勾股定理，以及三角形的面积公式即可得到结论．【解答】解：过C作CD⊥AB于D，∵AC＝BC＝17，AB＝16，∴AD＝BD=12AB＝8，∵AD2+CD2＝AC2，∴CD=15，∴S△ABC =12AB•CD=12×16×15=120．【点评】本题考查了勾股定理，三角形的面积的计算，等腰三角形的性质，熟练掌握勾股定理是解题的关键．【变式6-2】（2022春•桐城市期末）如图2，在△ABC 中，AC ＝8，AB ＝4，∠BAC ＝120°，求△ABC 的面积．【分析】过点C 作CD ⊥AB ，交BA 的延长线于点D ，由勾股定理求出CD 的长，利用三角形面积公式可求出答案．【解答】解：过点C 作CD ⊥AB ，交BA 的延长线于点D ，∵∠BAC ＝120°，∴∠DAC ＝60°，∴∠ACD ＝30°，∵AC ＝8，∴AD =12AC ＝4，∴CD =∴S △ABC =12AB •CD =12×=【点评】此题主要考查了勾股定理，三角形面积公式，求得出AB ，CD 的长是解题的关键．【变式6-3】如图在四边形ABCD 中，∠ABC ＝120°，AB ⊥AD ，BC ⊥CD ，AB ＝4，CD ＝5，求该四边形的面积．【分析】延长DA 和CB 交于O ，求出∠O ＝30°，根据含30度角的直角三角形性质求出OB 和OD ，根据勾股定理求出OA 和OC ，根据三角形面积公式求出即可．【解答】解：延长DA 和CB 交于O ，∵AB ⊥AD ，BC ⊥CD ，∴∠DAB ＝∠C ＝∠OAB ＝90°，∵∠D ＝60°，∴∠O ＝30°，∵AB ＝4，DC ＝5，∴OB ＝2AB ＝8，OD ＝2DC ＝10，由勾股定理得：OA ==OC =∴四边形ABCD 的面积是:S △OCD ﹣S △OAB =12×OC ×CD ―12×OA ×AB =12×5―12×【点评】本题考查了含30度角的直角三角形性质，勾股定理，三角形的面积的应用，注意：在直角三角形中，两直角边的平方和等于斜边的平方．【变式6-4】如图，已知在四边形ABCD 中，∠BCD ＝90°，BD 平分∠ABC ，AB ＝4，BD ＝10，BC ＝8，求四边形ABCD 的面积．【分析】过点D 作DE ⊥BA 的延长线于点E ，利用勾股定理和角平分线的性质可得出DE ＝DC ＝6，再利用三角形的面积公式结合S 四边形ABCD ＝S △ABD +S △BCD 可求出四边形ABCD 的面积．【解答】解：过点D 作DE ⊥BA 的延长线于点E ，如图所示．∵∠BCD＝90°，BD＝10，BC＝8，∴BD=6，∵BD平分∠ABC，∴DE＝DC＝6，∴S四边形ABCD ＝S△ABD+S△BCD，=12AB•DE+12BC•CD，=12×4×6+12×8×6，＝36．【点评】本题考查了角平分线的性质以及三角形的面积，利用角平分线的性质，找出DE＝8是解题的关键．【例题7】如图，在四边形ABCD中，∠ABC＝90°，CD⊥AD，AD2+CD2＝2AB2．（1）求证：AB＝BC；（2）当BE⊥AD于E时，试证明：BE＝AE+CD．【分析】（1）根据勾股定理AB2+BC2＝AC2，得出AB2+BC2＝2AB2，进而得出AB＝BC；（2）首先证明CDEF是矩形，再根据△BAE≌△CBF，得出AE＝BF，进而证明结论．【解答】证明：（1）连接AC．∵∠ABC＝90°，∴AB2+BC2＝AC2．∵CD⊥AD，∴AD2+CD2＝AC2．∵AD2+CD2＝2AB2，∴AB2+BC2＝2AB2，∴BC2＝AB2，∵AB＞0，BC＞0，∴AB＝BC．（2）过C作CF⊥BE于F．∵BE⊥AD，CF⊥BE，CD⊥AD，∴∠FED＝∠CFE＝∠D＝90°，∴四边形CDEF是矩形．∴CD＝EF．∵∠ABE+∠BAE＝90°，∠ABE+∠CBF＝90°，∴∠BAE＝∠CBF，∴在△BAE与△CBF中∴∠AEB=∠BFC ∠BAE=∠CBF AB=BC，∴△BAE≌△CBF．（AAS）∴AE＝BF．∴BE＝BF+EF＝AE+CD．【点评】此题主要考查了勾股定理的应用以及三角形的全等证明，根据已知得出四边形CDEF是矩形以及△BAE≌△CBF是解决问题的关键．【变式7-1】已知AD是△ABC的中线，∠C＝90°，DE⊥AB于点E，试说明AC2＝AE2﹣BE2．【分析】根据直角三角形的性质和勾股定理可得AE2﹣BE2＝（AD2﹣DE2）﹣（BD2﹣DE2）＝AD2﹣BD2＝AD2﹣CD2＝AC2，从而证明结论．【解答】证明：∵AD是△ABC的中线，∴BD＝CD．∵∠C＝90°，DE⊥AB于E，∴AE2﹣BE2＝（AD2﹣DE2）﹣（BD2﹣DE2）＝AD2﹣BD2＝AD2﹣CD2＝AC2．故AC2＝AE2﹣BE2．【点评】考查了直角三角形的性质和勾股定理，注意线段相互间的转化．【变式7-2】已知，如图，△ABC中，AB＞AC，AD为BC边上的高，M是AD边上任意一点．求证：AB2﹣AC2＝MB2﹣MC2．。
勾股定理经典题型
勾股定理已知两边求第三边例1．在直角三角形中,若两直角边的长分别为1cm，2cm ，则斜边长为_____________．例2．已知直角三角形的两边长为3、2，则另一条边长是________________．例3．在一个直角三角形中，若斜边长为5cm，直角边的长为3cm，则另一条直角边的长为 .例4． 一种盛饮料的圆柱形杯，测得内部底面半径为2.5㎝，高为12㎝，吸管放进杯里，杯口外面至少要露出4.6㎝，问吸管要做多长？利用列方程求线段的长例5． 把一根长为10㎝的铁丝弯成一个直角三角形的两条直角边，如果要使三角形的面积是9㎝2，那么还要准备一根长为____的铁丝才能把三角形做好．例6． 如图，将一个边长分别为4、8的长方形纸片ABCD折叠，使C 点与A 点重合，则EB 的长是 ．例7． 如图，铁路上A ，B 两点相距25km ，C ，D 为两村庄，DA ⊥AB 于A ，CB ⊥AB 于B ，已知DA=15km ，CB=10km ，现在要在铁路AB 上建一个土特产品收 购站E ，使得C ，D 两村到E 站的距离相等，则E 站应建在离A 站多少km 处？例8． 如图，某学校（A 点）与公路（直线L ）的距离为300米，又与公路车站（D 点）的距离为500米，现要在公路上 建一个小商店（C 点），使之与该校A 及车站D 的距离 相等，求商店与车站之间的距离．综合其它考点的应用 例9． 如图一个圆柱，底圆周长6cm ，高4cm ，一只蚂蚁沿外壁爬行，要从A 点爬到B 点，则最少要爬行 cm例10． 在直角ΔABC 中，斜边长为2，周长为2+6，求ΔABC 的面积．FED C B AA D EB CA B例11． 已知：如图，△ABC 中，AB ＞AC ，AD 是BC 边上的高．求证：AB 2-AC 2=BC(BD-DC)．例12． 如图∠B=90º，AB ＝16cm ，BC ＝12cm ，AD ＝21cm,CD=29cm求四边形ABCD 的面积．例13． 小明想测量学校旗杆的高度，他采用如下的方法：先将旗杆上的绳子接长一些，让它垂到地面还多1下端拉直，使它刚好接触地面，测得绳下端离旗杆底部5你能帮它计算一下旗杆的高度．判别一个三角形是否是直角三角形例14． 在△ABC 中，2:1:1::=c b a ，那么△ABC 是 。
勾股定理题型(很全面)
典型例题:一、利用勾股定理解决实际问题例题:水中芦苇梯子滑动1、有一个传感器控制的灯,安装在门上方,离地高4.5米的墙上,任何东西只要移至5米以内,灯就自动打开,一个身高1.5米的学生,要走到离门多远的地方灯刚好打开?2、如图,公路MN和公路PQ在P点处交汇,点A处有一所中学,AP=160米,点A 到公路MN 的距离为80米,假使拖拉机行驶时,周围100米以内会受到噪音影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响,请说明理由;如果受到影响,已知拖拉机的速度是18千米/小时,那么学校受到影响的时间为多少?3、如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我反走私A艇发现正东方向有一走私艇C以每小时6.4海里的速度偷偷向我领海开来,便立即通知正在MN在线巡逻的我国反走私艇B密切注意,反走私A艇通知反走私艇B时,A和C两艇的距离是20海里,A、B两艇的距离是12海里,反走私艇B测得距离C是16海里,若走私艇C的速度不变,最早会在什么时间进入我国领海?二、与勾股定理有关的图形问题1.已知△ABC是边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,第n个等腰直角三角形的斜边长是.2.如图,直线l经过正方形ABCD的顶点B,点A、C到直线l的距离分别是1、2,则正方形的边长是____ _____.3.在直线上依次摆着七个正方形(如图),已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积是S1,S2,S3,S4,则S1+S2+S3+S4=______ ___.4.如图,△ABC中,∠C=90°,(1)以直角三角形的三边为边向形外作等边三角形(如图①),探究S1+S2与S3的关系;(2)以直角三角形的三边为斜边向形外作等腰直角三角形(如图②),探究S1+S2与S3的关系;(3)以直角三角形的三边为直径向形外作半圆(如图③),探究S1+S2与S3的关系.图①图②图③5.如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a1,a2,a3,…,an,根据上述规律,则第n个正方形的边长an=___ _____记正方形AB-CD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,……,S n(n为正整数),那么S n=____ ____.6、如图,Rt△ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为.ABCDEFG1FE DAB CA B C D EG F F 三、关于翻折问题1、如图,折叠矩形纸片ABCD ,先折出折痕(对角线)BD ,再折叠,使AD 落在对角线BD 上,得折痕DG ,若AB = 2,BC = 1,求AG.2、如图,把矩形纸片ABCD 沿对角线AC 折叠,点B 落在点E 处,EC 与AD 相交于点F. (1)求证:△FAC 是等腰三角形;(2)若AB=4,BC=6,求△FAC 的周长和面积.3、如图,将矩形ABCD 沿直线AE 折叠,顶点D 恰好落在BC 边上F 点处,已知cm CE 6=,cm AB 16=,求BF 的长.4、如图,一张矩形纸片ABCD 的长AD=9㎝,宽AB=3㎝。
勾股定理知识点+类型+题型有答案版
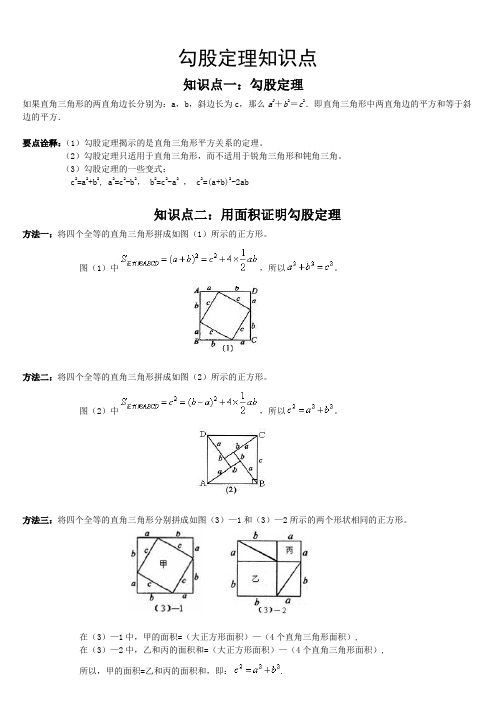
勾股定理知识点知识点一：勾股定理如果直角三角形的两直角边长分别为：a，b，斜边长为c，那么a2＋b2＝c2．即直角三角形中两直角边的平方和等于斜边的平方．要点诠释：（1）勾股定理揭示的是直角三角形平方关系的定理。
（2）勾股定理只适用于直角三角形，而不适用于锐角三角形和钝角三角。
（3）勾股定理的一些变式：c2=a2+b2, a2=c2-b2， b2=c2-a2， c2=(a+b)2-2ab知识点二：用面积证明勾股定理方法一：将四个全等的直角三角形拼成如图（1）所示的正方形。
图（1）中，所以。
方法二：将四个全等的直角三角形拼成如图（2）所示的正方形。
图（2）中，所以。
方法三：将四个全等的直角三角形分别拼成如图（3）—1和（3）—2所示的两个形状相同的正方形。
在（3）—1中，甲的面积=（大正方形面积）—（4个直角三角形面积）,在（3）—2中，乙和丙的面积和=（大正方形面积）—（4个直角三角形面积）,所以，甲的面积=乙和丙的面积和，即：.方法四：如图（4）所示，将两个直角三角形拼成直角梯形。
，所以。
知识点三：勾股定理的作用1．已知直角三角形的两条边长求第三边；2．已知直角三角形的一条边，求另两边的关系；3．用于证明平方关系的问题；4．利用勾股定理，作出长为的线段。
知识点四：勾股数满足不定方程x2+y2=z2的三个正整数，称为勾股数（又称为高数或毕达哥拉斯数），显然，以x,y,z为三边长的三角形一定是直角三角形。
熟悉下列勾股数，对解题有很大帮助：①3、4、5②5、12、13；③8、15、17；④7、24、25；⑤10、24、26；⑥9、40、41．②如果(a,b,c)是勾股数，当t>0时，以at,bt,ct为三角形的三边长，此三角形必为直角三角形。
勾股定理考查类型类型一：勾股定理的直接用法在Rt△ABC中，∠C=90°(1)已知a=6， c=10，求b，(2)已知a=40，b=9，求c；(3)已知c=25，b=15，求a.思路点拨:写解的过程中，一定要先写上在哪个直角三角形中，注意勾股定理的变形使用。
完整版)勾股定理知识点与常见题型总结
完整版)勾股定理知识点与常见题型总结勾股定理复勾股定理是指直角三角形两直角边的平方和等于斜边的平方，表示为a^2 + b^2 = c^2，其中a、b为直角三角形的两直角边，c为斜边。
勾股定理的证明常用拼图的方法。
通过割补拼接图形后，根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理。
常见的证明方法有以下三种：1.通过正方形的面积证明，即4ab + (b-a)^2 = c^2，化简可证。
2.四个直角三角形的面积与小正方形面积的和等于大正方形的面积，即4ab + c^2 = 2ab + c^2，化简得证。
3.通过梯形的面积证明，即(a+b)×(a+b)/2 = 2ab + c^2，化简得证。
勾股定理适用于直角三角形，因此在应用勾股定理时，必须明确所考察的对象是直角三角形。
勾股定理可用于解决直角三角形中的边长计算或直角三角形中线段之间的关系的证明问题。
在使用勾股定理时，必须把握直角三角形的前提条件，了解直角三角形中，斜边和直角边各是什么，以便运用勾股定理进行计算。
同时，应设法添加辅助线（通常作垂线），构造直角三角形，以便正确使用勾股定理进行求解。
勾股定理的逆定理是：如果三角形三边长a、b、c满足a^2 + b^2 = c^2，那么这个三角形是直角三角形，其中c为斜边。
a^2+b^2=c^2$是勾股定理的基本公式。
如果三角形ABC 不是直角三角形，我们可以类比勾股定理，猜想$a+b$与$c$的关系，并对其进行证明。
勾股定理的实际应用有很多。
例如，在图中，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2m，梯子的顶端B 到地面的距离为7m。
现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于3m。
同时梯子的顶端B下降至B′。
那么BB′的长度是小于1m的（选项A）。
又如，在图中，一根24cm的筷子置于底面直径为15cm，高8cm的圆柱形水杯中。
设筷子露在杯子外面的长度为h cm，则h的取值范围是7cm ≤ h ≤ 16cm（选项D）。
勾股定理常见题型总结
典型题型题型一：直接考查勾股定理例１.在ABC ∆中,90C ∠=︒．⑴已知6AC =,8BC =．求AB 的长⑵已知17AB =,15AC =,求BC 的长分析：直接应用勾股定理222a b c +=解：⑴10AB =⑵8BC =题型二：应用勾股定理建立方程例２.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD ＝⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为 ⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为分析：在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积．有时可根据勾股定理列方程求解解：⑴4AC , 2.4AC BC CD AB⋅== DB A C⑵设两直角边的长分别为3k ,4k ∴222(3)(4)15k k +=,3k ∴=,54S =⑶设两直角边分别为a ,b ,则17a b +=,22289a b +=,可得60ab =1302S ab ∴==2cm 例３.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长21E DCBA分析：此题将勾股定理与全等三角形的知识结合起来解：作DE AB ⊥于E,12∠=∠,90C ∠=︒∴ 1.5DE CD ==在BDE ∆中90,2BED BE ∠=︒=Rt ACD Rt AED ∆≅∆AC AE ∴=在Rt ABC ∆中,90C ∠=︒222AB AC BC ∴=+,222()4AE EB AC +=+3AC ∴=例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积答案：6题型三：实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 mAB C D E分析：根据题意建立数学模型,如图8AB =m ,2CD =m ,8BC =m ,过点D 作DE AB ⊥,垂足为E ,则6AE =m ,8DE =m在Rt ADE ∆中,由勾股定理得10AD答案：10m题型四：应用勾股定理逆定理,判定一个三角形是否是直角三角形例6.已知三角形的三边长为a ,b ,c ,判定ABC ∆是否为Rt ∆ ① 1.5a =,2b =, 2.5c = ②54a =,1b =,23c =解：①22221.52 6.25a b +=+=,222.5 6.25c ==∴ABC ∆是直角三角形且90C ∠=︒ ②22139b c +=,22516a =,222b c a +≠ABC ∴∆不是直角三角形 例7.三边长为a ,b ,c 满足10a b +=,18ab =,8c =的三角形是什么形状解：此三角形是直角三角形理由：222()264a b a b ab +=+-=,且264c = 222a b c ∴+= 所以此三角形是直角三角形题型五：勾股定理与勾股定理的逆定理综合应用 例8.已知ABC ∆中,13AB =cm ,10BC =cm ,BC 边上的中线12AD =cm ,求证：AB AC =证明：D CB AAD 为中线,5BD DC ∴==cm在ABD ∆中,22169AD BD +=,2169AB =222AD BD AB ∴+=, 90ADB ∴∠=︒,222169AC AD DC ∴=+=,13AC =cm ,AB AC ∴=。
勾股定理题型大全
1.已知等腰三角形的周长为24，腰长为x ，则x 的取值范围是 ································ （ ）． A ）x ＞12 （B ）x ＜6 （C ）6＜x ＜12 （D ）0＜x ＜122.如图，等边三角形ABC 中，AD 是BC 上的高，取AC 的中点E ， 连结DE ，则图中与DE 相等的线段有 ····························· （ ）． （A ）1条 （B ）2条 （C ）3条 （D ）4条3.如图：∠EAF=15°，AB=BC=CD=DE=EF ，则∠DEF 等于（ ）。
A 、90° B 、 75° C 、70° D 、60°4.．如图所示，要在河边修建一个水泵站，分别向张村、李庄送水，那么水泵站应修在河边什么地方，可使所用水管最短？画图并说明理由。
5、（10分）①如图：A 、B 是两个蓄水池，都在河流a 的 同侧，为了方便灌溉作物，要在河边建一个抽水站， 将河水送到A 、B 两地，问该站建在河边什么地方，•②如图：某地有两所大学和两条相交叉的公路，（点M ，N 表示大学，AO ，BO 表示公路）.现计划修建 一座物资仓库，希望仓库到两所大学的距离相等，到 两条公路的距离也相等。
勾股定理解题的十种常见类型习题
05 利用勾股定理求折叠中线段长
利用勾股定理求折叠中线段长·木子老师
06 利用勾股定理求动点中线段长
利用勾股定理求动点中线段长·木子老师
07 利用勾股定理求实际中的距离
利用勾股定理求实际中的距离·木子老师
08 利用勾股定理解传统数学文化
问题
利用勾股定理解传统数学文化问题·木子老师
09 利用勾股定理求最短距离
利用勾股定理求最短距离·木子老师
10 利用勾股定理求解分类中的最
短距离
利用勾股定理求解分类中的最短距离 ·木子老师
谢谢欣赏Leabharlann 勾股定理解题的十种常见题型
授课老师：木子老师
01 利用勾股定理求线段长
利用勾股定理求线段长·木子老师
02 利用勾股定理说明线段相等
利用勾股定理说明线段相等·木子老师
03 利用勾股定理说明线段之间的
平方关系
利用勾股定理说明线段之间的平方关系·木子老师
04 利用勾股定理求四边形中线段
长
利用勾股定理求四边形中线段长·木子老师
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
专题一：勾股定理与面积
知识点精讲：
类型一“勾股树”及其拓展类型求面积
典型例题：
1．如图（16），大正方形的面积可以表示为，又可以表示为，由此可得等量关系______________________,整理后可得：___________．
2．图中字母所代表的正方形的面积为144的选项为( )
3．“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形．如图，每一个直角三角形的两条直角边的长分别是3和6，则大正方形与小正方形的面积差是()
A．9 B．36 C．27 D．34
4．如图所示的大正方形是由八个全等的直角三角形和一个小正方形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若正方形EFGH的边长为2，则S1＋S2＋S3＝________．
5．如图，所有三角形都是直角三角形，所有四边形都是正方形，已知S1＝4，S2＝9，S3＝8，S4＝10，则S＝() A．25 B．31 C．32 D．40
6．如图，已知在Rt ABC
△中，︒
=
∠90
ACB，4
AB=，分别以AC，BC为直径作半圆，面积分别记为1S，2S，
则
12
S S
+的值等于________
7．如图，已知直角△ABC的两直角边分别为6，8，分别以其三边为直径作半圆，则图中阴影部分的面积是________．8．如图所示为一种“羊头”形图案，其作法是：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形②和②，…，依此类推，若正方形①的面积为64，则正方形⑤的面积为( )
A．2 B．4 C．8 D．16
a
a
a
a
b
b
b
b
c
c
c
c
图(16)
8
6
C
B
A
A
D
C
B
规律与小结：
做“勾股树”及其拓展类型的题，把握住以两条直角边为边长或直径延展出来的正方形或圆的面积和，等于以斜边为边长或直径延展出来的正方形或圆的面积。
类型二 构造直角三角形求面积或长度
9．如图，在△ABC 中，AB ＝AC ＝13，BC ＝10，点D 为BC 的中点， DE ⊥AB ，垂足为点E ，则DE 的长为( ) A.1013 B.1513 C.6013 D.7513
10．等腰三角形的腰长为10，底边长为12，则这个等腰三角形的面积为 。
规律与小结：
1.学会借助现有的直角，构造直角三角形；
2.等腰三角形“三线合一”，一定要牢牢把握。
3.求斜边上的高，要学会先求出直角三角形的面积，再求斜边上的高。
类型三 结合乘法公式巧求面积或长度
11．已知Rt △ABC 中，∠C ＝90°，若a ＋b ＝7cm ，c ＝5cm ，则Rt △ABC 的面积是( ) A ．6cm 2 B ．9cm 2 C ．12cm 2 D ．15cm 2
12、如图，在直角三角形中，∠ACB=90°,BC=15,AC=20,CD 是斜边AB 上的高，则AD —BD ＝ 。
13、已知正方形ABCD 的边长为3，正方形EFGH 内接于ABCD ，AE ＝a ，AF ＝b ，(a<b) 且S EFGH ＝5 则b-a ＝ 。
规律与小结：
牢记常见的勾股数——“3,4,5”、“5,12,13”、“8,15,17”、“7,24,25”，当三条边同时扩大相同的倍数时，仍然满足勾股定理。
类型四 巧妙割补求面积
14．如图，点E 在正方形ABCD 内，满足∠AEB ＝90°，AE ＝6，BE ＝8，则阴影部分的面积是( ) A ．48 B ．60 C ．76 D ．80
A
B
C
D F G
H
E
15．如图，若∠BAD ＝∠DBC ＝90°，AB ＝3，AD ＝4，BC ＝12，则CD ＝( ) A ．5
B ．13
C ．17
D ．18
16．如图所示是一块地，已知AD ＝8米，CD ＝6米，∠D ＝90°，AB ＝26米，BC ＝24米，则这块地的面积是________． 规律与小结：
将不规则图形利用转化思想转化成规则图形来求面积，此过程中通常需要构造直角三角形，也就是利用勾股定理的逆定理，判断三边能否满足2
2
2
c b a =+，从而确定是否为直角三角形。
专题二：知识点2 勾股定理与折叠,轴对称，动点
典型例题：
17．如图，在Rt △ABC 中，∠B ＝90°，AB ＝3，BC ＝4，将△ABC 折叠，使点B 恰好落在边AC 上与点B ′重合，AE 为折痕，则EB ＝________．
18、矩形ABCD 中，AD=4cm ，AB=10cm ，按如图方式折叠，使点B 与点D 重合，折痕为EF ， 则DE ＝________．
19．如图，长方形纸片ABCD 沿对角线AC 折叠，设点D 落在D ′处，BC 交AD ′于点E ，AB ＝6cm ，BC ＝8cm ，则阴影部分的面积＝________．
20．如图所示，正方形ABCD 的边长为6，△ABE 是等边三角形， 点E 在正方形ABCD 内，在对角线AC 上有一点P ， 使PD+PE 的和最小，则这个最小值为多少？
21.如图，∠AOB ＝90°，OA ＝9cm ，OB ＝3cm ，一机器人在点B 处看见一个小球从点A 出发沿着AO 方向匀速滚向点O ，机器人立即从点B 出发，沿BC 方向匀速前进拦截小球，恰好在点C 处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC 是多少？
规律与小结：
1.折叠与对称题型一定要注意折叠之后的边是对应相等的。
2.该种题型通常需要设未知数x ，将含有未知数x 的量放在一个直角三角形中，应用勾股定理。
A
B
C
D
E
F
C 1。