固体物理试题库
固体物理学-试题及答案

得
分
二、简答与作图题(每题10分,共20分)
1、在考虑晶格振动对晶体热容的贡献时,爱因斯坦模型和德拜模型分别是怎样的?并定性说明二者的结果.
2、画体心立方晶格结构的金属在(100),(110),(111)面上原子排列。
2、体心立方晶体结构中原子球的排列方式为(ABAB,ABCABC),六角密排晶体结构中原子球的排列方式为(ABAB,ABCABC)。
3、在简立方晶体结构中,与(100)、(110)、(111)晶面等效的晶面数分别为,,。
4、固体结合的类型一般有:离子键结合、、、范德瓦尔斯键结合等.
5、固体的热容量在常温附近遵守杜珑-帕蒂定律,即等于;在低温下,固体的热容量随温度降低而(升高,降低)。
3、解:,,5分;,5分。
4、解:一维晶格的能带E(k) = ε0−β − 2γcos(ka),10分;电子速度,5分;在边界,,,5分.
4、(无机非金属专业选作)解:第一能带,5分;第二能带,5分;第三能带,5分;第四能带,5分。
课程考试试题纸
课程名称:
固体物理学
考试方式:
闭卷
印刷份数:
学院:
任课教师:
专业年级:
题பைடு நூலகம்
号
一
二
三
四
五
六
七
八
总分
阅卷
教师
得
分
……………………………………………………………………………………………………
得
分
一、填空题(每小题2分,共30分)
1、对简立方晶体结构,立方体边长为a,其最近邻的原子数为,最近邻原子的间距为。次近邻的原子数为,次近邻原子的间距为。
初中固体物理试题及答案

初中固体物理试题及答案一、选择题(每题2分,共20分)1. 固体物质的分子排列特点是:A. 无规则排列B. 规则排列C. 部分规则排列D. 完全无序排列答案:B2. 固体物质的分子间作用力是:A. 引力B. 斥力C. 引力和斥力D. 无作用力答案:C3. 下列物质中,属于晶体的是:A. 玻璃B. 橡胶C. 食盐D. 沥青答案:C4. 晶体与非晶体的主要区别在于:A. 颜色B. 形状C. 熔点D. 分子排列答案:D5. 固体物质的熔化过程需要:A. 吸收热量B. 放出热量C. 保持热量不变D. 无法判断答案:A6. 固体物质的硬度与下列哪项因素有关:A. 分子间作用力B. 分子质量C. 分子体积D. 分子形状答案:A7. 固体物质的导电性与下列哪项因素有关:A. 分子间作用力B. 分子运动速度C. 电子的自由移动D. 分子的排列方式答案:C8. 晶体的熔点与下列哪项因素有关:A. 晶体的纯度B. 晶体的颜色C. 晶体的形状D. 晶体的密度答案:A9. 固体物质的热膨胀现象说明:A. 分子间距离不变B. 分子间距离减小C. 分子间距离增大D. 分子间距离先增大后减小答案:C10. 固体物质的热传导性与下列哪项因素有关:A. 分子间作用力B. 分子运动速度C. 电子的自由移动D. 分子的排列方式答案:A二、填空题(每空1分,共20分)1. 固体物质的分子排列特点是________,而非晶体物质的分子排列特点是________。
答案:规则排列;无规则排列2. 固体物质的熔化过程中,分子间________,分子间距离________。
答案:作用力减弱;增大3. 晶体的熔点与________有关,而非晶体没有固定的熔点。
答案:晶体的纯度4. 固体物质的硬度与分子间________有关,分子间作用力越强,硬度越大。
答案:作用力5. 固体物质的热膨胀现象是由于温度升高,分子间距离________。
答案:增大三、简答题(每题10分,共30分)1. 简述晶体与非晶体的区别。
高校物理专业固体物理学期末考试试卷及答案

高校物理专业固体物理学期末考试试卷及答案一、选择题(每题2分,共40分)1. 下列哪种材料是典型的固体?A. 水B. 空气C. 玻璃D. 油2. 表征物质导电性质的关键因素是:A. 导热系数B. 形变C. 导电子数D. 电阻率3. 相互作用力程远大于它的大小尺度的物质状态是:A. 液体B. 气体C. 等离子体D. 固体4. 根据原子内部粒子组织排列方式的不同,将固体分为晶体和非晶态,以下哪种属于非晶态?A. 钻石B. 石英C. 玻璃D. 铜5. 材料的抗拉强度指的是:A. 材料在拉伸过程中发生断裂的能力B. 材料的硬度C. 材料的耐磨性D. 材料的延展性(以下为第6题至第40题的选项省略)二、填空题(每题3分,共30分)1. 固体的最基本由原子、分子或离子组成的单位结构叫作_____________。
2. 点阵是固体晶体结构中原子、离子或分子的_____________组成的排列方式。
3. 若一堆物体在某种温度下开始熔化,则该温度即为该物质的_____________点。
4. 固体由于结构的紧密性,其密度通常较_____________。
5. 金属中导电电子为材料的_____________。
6. 非晶态材料的特点是_____________无规律的原子组织结构。
(以下为第7题至第30题的空格省略)三、问答题(共30分)1. 简述固体物理学研究的基本内容和意义。
解答:固体物理学研究的基本内容主要包括固体材料的结构、性质和应用等方面。
它通过研究固体的微观结构和宏观性质,探索物质内部的相互作用和运动规律,从而深入了解固体物质的特性和行为。
固体物理学的研究对于提高材料的功能和性能具有重要意义。
通过深入研究固体的结构和性质,我们可以开发出更好的材料,改善材料的导电、导热、机械强度等性能,为社会发展和工业生产提供重要支持。
同时,固体物理学的研究还能够为其他领域的科学研究提供基础和支撑,如电子学、光学、磁学等。
固体物理题库-zzk-第一至第五章
第一章 晶体结构和X 射线1、试证体心立方和面心立方各自互为正、倒格子2、如果基矢a,b,c 构成正交关系,证明晶面族(h k l )的面间距满足:222)()()(1c l b k a hd hkl ++=3、证明以下结构晶面族的面间距:(1) 立方晶系:d hkl =a [h 2+k 2+l 2]-1/2(2) 六角晶系:2/12222])()(34[-+++=c l ahk k h d hkl 4、等体积的硬球堆积成体心立方结构和面心立方结构,试求他们在这两种结构中的致密度分别为0.68和0.74。
5、试证密积六方结构中,c/a=1.633。
6、在立方晶胞中,画出(1 0 1),(0 2 1),(221)和(012)晶面。
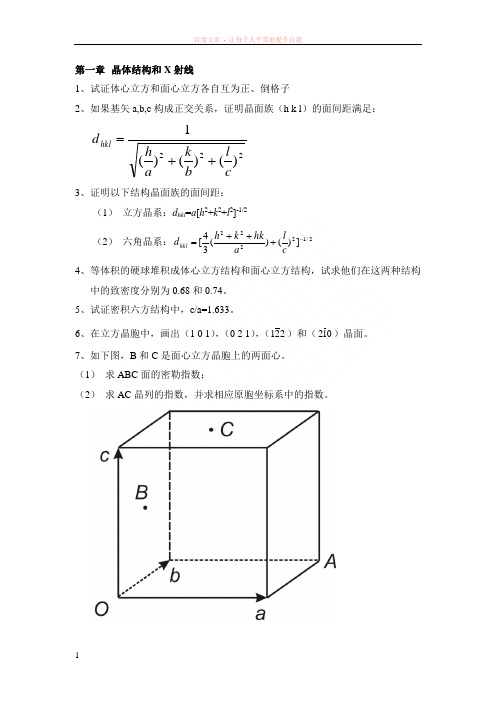
7、如下图,B 和C 是面心立方晶胞上的两面心。
(1) 求ABC 面的密勒指数;(2) 求AC 晶列的指数,并求相应原胞坐标系中的指数。
8、六角晶胞的基矢为.,223,223k c c j a i a b j a i a a =+-=+=求其倒格子基矢。
9、求晶格常数为a 的面心立方和体心立方晶体晶面族(h 1 h 2 h 3)之间的面间距(指导p30,10)。
10、讨论六角密积结构,X 光衍射的消光条件。
11、求出体心立方、面心立方的几何因子和消光条件。
12、原胞和晶胞的区别?13、倒空间的物理意义?14、布拉格衍射方程,原子和几何结构因子在确定晶格结构上分别起何作用?15、什么是布拉格简单格子,什么是复式格子?第二章 自由电子气1、设有一个长度为L 的一维金属线,它有N 个导电电子,若把这些导电电子看成自由电子气,试求:(1) 电子的状态密度(2) 绝对零度下的电子费米能级,以及费米能级随温度的变化关系。
(3) 电子的平均能量。
(4) 电子的比热。
2、二维电子气的能态密度2)( πm E N =,证明费米能 ]1ln[/2-=T mk n B F b eT k E π 3、求出一维金属中自由电子的能态密度、费米能级、电子的平均动能以及一个电子对于比热的贡献。
固体物理期末考试题及答案

固体物理期末考试题及答案一、选择题(每题2分,共20分)1. 晶体中原子排列的周期性结构被称为:A. 晶格B. 晶胞C. 晶面D. 晶向答案:A2. 描述固体中电子行为的基本理论是:A. 经典力学B. 量子力学C. 相对论D. 电磁学答案:B3. 以下哪项不是固体物理中的晶体缺陷:A. 点缺陷B. 线缺陷C. 面缺陷D. 体缺陷答案:D4. 固体物理中,晶格振动的量子称为:A. 声子B. 光子C. 电子D. 空穴答案:A5. 以下哪个不是固体的电子能带结构:A. 价带B. 导带C. 禁带D. 散射带答案:D二、简答题(每题10分,共30分)6. 解释什么是晶格常数,并举例说明。
晶格常数是晶体中最小重复单元的尺寸,通常用来描述晶体的周期性结构。
例如,立方晶系的晶格常数a是指立方体的边长。
7. 简述能带理论的基本概念。
能带理论是量子力学在固体物理中的应用,它描述了固体中电子的能量分布。
在固体中,电子的能量不是连续的,而是分成一系列的能带。
价带是电子能量较低的区域,导带是电子能量较高的区域,而禁带是两带之间的能量区域,电子不能存在。
8. 什么是费米能级,它在固体物理中有什么意义?费米能级是固体中电子的最高占据能级,它与温度有关,但与电子的化学势相等。
在绝对零度时,费米能级位于导带的底部,它决定了固体的导电性质。
三、计算题(每题15分,共30分)9. 假设一个一维单原子链的原子质量为m,相邻原子之间的弹簧常数为k。
求该链的声子频率。
解:一维单原子链的声子频率可以通过下面的公式计算:\[ \omega = 2 \sqrt{\frac{k}{m}} \]10. 给定一个半导体的电子亲和能为Ea,工作温度为T,求该半导体在该温度下的费米-狄拉克分布函数。
解:费米-狄拉克分布函数定义为:\[ f(E) = \frac{1}{e^{\frac{E-E_F}{kT}} + 1} \] 其中,E是电子的能量,E_F是费米能级,k是玻尔兹曼常数,T 是温度。
固体物理40题

1. 设晶体中的每个振子的零点振动能.试用德拜模型求晶体的零点振动能.证明:根据量子力学零点能是谐振子所固有的,与温度无关,故T=0K 时振动能0E 就是各振动模零点能之和。
()()()000012mE E g d E ωωωωωω==⎰将和()22332s V g v ωωπ=代入积分有402339168m m s V E N v ωωπ==,由于098m B D B D k E Nk ωθθ==得 一股晶体德拜温度为~210K ,可见零点振动能是相当大的,其量值可与温升数百度所需热能相比拟.2. 试画出二维长方格子的第一、第二布里渊区.3. 证明:在磁场中运动的布洛赫电子,在K 空间中,轨迹面积A n 和在r 空间的轨迹面积S n之间的关系A n= (qB hc)2S n()d k d rc qv B q B dt dt⋅=-⨯=--⋅解: dk qB dr dt c dt∴=⋅ t k qBr c两边对积分,即 =22()()n n A r c S k qB∴== 4. 证明:面心立方晶格的倒格子为体心立方. 解:面心立方晶格的基矢为()()()a a aa j ,b ,c 222k i k i j =+=+=+ 则面心立方原胞体积3V []4a abc ⋅⨯==a 2bc V π*⨯=面心立方倒格矢 ()()2384a i k i j a π=⋅+⨯+()ai j k π-++2=()b a i j k π*=-+2同理: ,()ac i j k π*=+-2 a b c ***显然,,为体心立方原胞基矢,因此面心立方晶格倒格子为体心立方 5. 证明:根据倒格子的定义证明简单立方格子体积与其倒格子体积成反比解:设简单立方晶格常数为a ,则基矢为a ,b ,c ,V a ai a j ak ===3体积=其倒格矢2312b 2a a i V aππ⨯==,3122b 2a a j V a ππ⨯==,1232b 2a a k V a ππ⨯== 则倒格子体积()31232[]V b b b Vπ*=⋅⨯=6. 是否存在与库伦力无关的晶型,为什么?答:不存在与库仑力无关的晶型,因为①共价结合中电子虽不能脱离电负性 的原子,但靠近的两个原子各给出一个电子,形成电子共有的形状,位于两原子之间通过库仑力把两个原子结合起来。
固体物理考试试题

1、解理面:矿物晶体在外力作用下严格沿着一定结晶方向破裂,并且能裂出光滑平面的性质称为解理,这些平面称为解理面。
性质:解理面一般光滑平整,一般平行于面间距最大,面网密度最大的晶面,因为面间距大,面间的引力小,这样就造成解理面一般的晶面指数较低,如Si的解理面为(111)。
晶体中原子的排列是长程有序的,这种现象称为晶体内部结构的周期性。
晶体内部结构的周期性可以用晶格来形象地描绘。
晶格是由无数个相同单元周期性地重复排列组成的。
2、晶格场中电子运动状态:在周期性势场中,属于某个原子的电子既可以在该原子附近运动,也可以在其它的原子附近运动,即可以在整个晶体中运动。
即局域化运动、共有化运动。
晶体中(也就是周期性势场中)的电子的运动是既有局域化的特征又有共有化特征。
3、固体热容组成:固体的热容是原子振动在宏观性质上的一个最直接的表现。
杜隆·伯替定律------在室温和更高的温度,几乎全部单原子固体的热容接近3NkB。
在低温热容与T3成正比。
(晶格热振动)晶格热容固体的热容(电子的热运动)电子热容每一个简谐振动的平均能量是kBT ,若固体中有N个原子,则有3N个简谐振动模,总的平均能量: E=3NkBT热容: Cv = 3NkB热容的本质:反映晶体受热后激发出的晶格波与温度的关系;对于N个原子构成的晶体,在热振动时形成3N个振子,各个振子的频率不同,激发出的声子能量也不同;温度升高,原子振动的振幅增大,该频率的声子数目也随着增大;温度升高,在宏观上表现为吸热或放热,实质上是各个频率声子数发生变化。
影响热容的因素:1. 温度对热容的影响高于德拜温度时,热容趋于常数,低于德拜温度时,与(T / D)3成正比。
2. 键强、弹性模量、熔点的影响德拜温度约为熔点的0.2—0.5倍。
3. 无机材料的热容对材料的结构不敏感混合物与同组成单一化合物的热容基本相同。
4. 相变时,由于热量不连续变化,热容出现突变。
5. 高温下,化合物的摩尔热容等于构成该化合物的各元素原子热容的总和(c=niCi)ni :化合物中i元素原子数;Ci:i元素的摩尔热容。
固体物理题目总汇

固体物理题目总汇填空题1、根据固体材料中原子排列的方式可以将固体材料分为晶体、非晶体和准晶体。
2、晶体结构=点阵+基元3、晶体的比热包括晶格比热和电子比热。
4、结晶学中,属于立方晶系的布拉维晶胞有简单立方、体心立方和面心立方三种。
5、密堆结构有两种:六方密堆积和立方密堆积。
6、原子电负性在一个周期内由左到右不断升高,周期表由上到下,负电性逐渐降低。
7、限定波矢q的取值范围在第一布里渊区8、金属的未满能带叫价带或导带。
1、人们利用某射线衍射测定晶体结构。
3、晶体的热学性质,如比热、热膨胀和热传导等就与晶格振动密切有关。
4、声子是一种准粒子,不具有通常意义下的动量,常把q称为声子的准动量。
5、根据晶体缺陷在空间延伸的线度晶体缺陷可分为点缺陷~线缺陷、面缺陷和体缺陷。
6、V心是F心的反型体。
1、晶体的基本结构单元称为基元2、面心立方晶胞的晶格常数为a,其倒格子原胞的体积等于323/a33、布拉维空间点阵共有14种,归为7种晶系。
5、一维双原子链的色散关系中频率较低的一支叫声学支(声频支),它很像单原子链中的声学支,;频率较高的一支则叫光学支(光频支)。
6、面缺陷有堆垛层错、小角晶界和晶粒间界三种主要形式。
8、一般情况下晶体电子的近似质量是张量,自由电子的惯性质量是标量。
9、对复式晶格,格波可分为声学波和光学波。
1、体心立方结构的第一布里渊区是菱形十二面体。
2、已知某晶体的基矢取为a1、a2、a3,某一晶面在三个基矢上的截距分别为3,2,-1,则该晶面的晶面指数为2363、倒格矢体现了晶面的面间距和法向。
8、晶体中的载流子是电子和空穴2、正格子原胞体积与倒格子原胞体积之积为233、金刚石晶体的基元含有2个原子,其晶胞含有8个碳原子。
6、准晶是介于周期性晶体和非晶玻璃之间的一种新的固体物质形态。
8、晶格振动的简化模型主要有爱因斯坦模型和德拜模型。
1、面心立方结构的第一布里渊区是十四面体。
2、代表基元中的几何点称为格点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、名词解释1、晶态--晶态固体材料中的原子有规律的周期性排列,或称为长程有序。
2、非晶态--非晶态固体材料中的原子不就是长程有序地排列,但在几个原子的范围内保持着有序性,或称为短程有序。
3、准晶--准晶态就是介于晶态与非晶态之间的固体材料,其特点就是原子有序排列,但不具有平移周期性。
4、单晶--整块晶体内原子排列的规律完全一致的晶体称为单晶体。
5、多晶--由许多取向不同的单晶体颗粒无规则堆积而成的固体材料。
6、理想晶体(完整晶体)--内在结构完全规则的固体,由全同的结构单元在空间无限重复排列而构成。
7、空间点阵(布喇菲点阵)--晶体的内部结构可以概括为就是由一些相同的点子在空间有规则地做周期性无限重复排列,这些点子的总体称为空间点阵。
8、节点(阵点)--空间点阵的点子代表着晶体结构中的相同位置,称为节点(阵点)。
9、点阵常数(晶格常数)--惯用元胞棱边的长度。
10、晶面指数—描写布喇菲点阵中晶面方位的一组互质整数。
11、配位数—晶体中与某一原子相邻的原子数。
12、致密度—晶胞内原子所占的体积与晶胞体积之比。
13、原子的电负性—原子得失价电子能力的度量;电负性=常数(电离能+亲与能)14、肖特基缺陷—晶体内格点原子扩散到表面,体内留下空位。
15、费仑克尔缺陷--晶体内格点原子扩散到间隙位置,形成空位-填隙原子对。
16、色心--晶体内能够吸收可见光的点缺陷。
17、F心--离子晶体中一个负离子空位,束缚一个电子形成的点缺陷。
18、V心--离子晶体中一个正离子空位,束缚一个空穴形成的点缺陷。
19、近邻近似--在晶格振动中,只考虑最近邻的原子间的相互作用。
20、Einsten模型--在晶格振动中,假设所有原子独立地以相同频率ωE振动。
21、Debye模型--在晶格振动中,假设晶体为各向同性连续弹性媒质,晶体中只有3支声学波,且ω=vq 。
22、德拜频率ωD──Debye模型中g(ω)的最高频率。
23、爱因斯坦频率ωE──Einsten模型中g(ω)的最可几频率。
24、电子密度分布--温度T时,能量E附近单位能量间隔的电子数。
25、接触电势差--任意两种不同的物质A、B接触时产生电荷转移,并分别在A与B上产生电势V A、V B,这种电势称为接触电势,其差称为接触电势差。
25、BLoch电子费米气--把质量视为有效质量→m,除碰撞外相互间无互作用,遵守费米分布的Bloch电子的集合称为BLoch电子费米气。
26、惯用元胞(单胞):既能反映晶格周期性,又能反映其对称性的结构单元。
27、简谐近似:晶体中粒子相互作用势能泰勒展开式中只取到二阶项的近似。
28、杜隆-伯替定律:高温下固体比热为常数。
29、晶体的对称性:经过某种对称操作后晶体能自身重合的性质。
30、格波的态密度函数(振动模式密度):在ω附近单位频率间隔内的格波总数。
31、晶体结合能:原子在结合成晶体过程中所释放出来的能量。
32、倒格矢:其中为正格子元胞体积。
我们称b 1、b 2、b 3为倒格子基矢。
33、带隙(禁带):晶体中电子运动状态不允许占据的能量范围。
34、摩尔热容:每摩尔物质升高或降低单位温度吸收或释放出的热量。
35、空间群:晶格全部对称操作的集合。
36、色散关系:晶格振动中ω与q 之间的关系。
37、第一布里渊区:离到格子原点最近的倒格矢中垂面围成的区域。
38、晶面:由布拉菲格子中不共线的三个格点所决定的平面。
39、格波:晶体中粒子的振动模式。
40、德拜定律:低温下固体比热与T 3成正比。
41、布洛赫定律:晶体中的电子波函数就是由晶格周期性调制的调幅平面波,即:ψ(K →、r →)=u(→K 、r →)e i k r →→⋅ u(K →、r →)=u(k r →→,+R n →)另一种表示:ψ(k r →→,+R n →)=→→⋅R k i e ψ(k r →→,)。
42、基元:构成晶体的全同的基本结构单元43、倒格子:以正格子基矢决定的倒格矢平移所得到的一个周期性的空间格子。
44、能态密度:给定体积的晶体,单位能量间隔内所包含的电子状态数。
45、声子:对于晶格振动,ω为格波谐振子的能量量子,称其为声子。
46、布里渊区:在倒格子中,以某一点为坐标原点,作所有倒格矢的垂直平分面,倒格子空间被这些平面分成许多区域,这些区域称为布里渊区。
47、费米面:K 空间中,能量E 为费米能E F 的等能面称为费米面。
48、功函数:晶体中电子所处势阱深度E 0与费米能E F 之差,称为功函数49、离子晶体:质点间通过离子键相互作用结合而成的晶体。
二、单项选择题1、 晶体结构的基本特性就是( B )A 、各向异性B 、周期性C 、自范性D 、同一性2、 晶体的性能特点不具有( C )A 、各向异性B 、均一性C 、各向同性D 、对称性3、单质半导体的晶体结构类型就是( A )。
A 、金刚石型结构B 、闪锌矿型结构C 、钙钛矿结构D 、密堆积结构4、共价键的基本特点不具有( D )。
A 、饱与性B 、方向性C 、键强大D 、各向同性5、晶体中的点缺陷不包括( D )。
A、肖特基缺陷B、佛伦克尔缺陷C、自填隙原子D、堆垛层错6、离子晶体的基本特点有( C )A、低熔点B、高塑性C、高强度D、半导性7、氯化钠晶体结构就是由( B )A、由二套面心格子沿体对角线方向滑1/4长度套构而成B、由二套面心立方格子沿晶轴方向滑1/2长度套构而成C、由二套体心立方格子沿体对角线方向滑1/4长度套构而成D、由一套体心格子与一套面心格子沿体对角线方向滑1/4长度套构而成8、布里渊区的特点包括( B )A、各个布里渊区的形状都不相同B、各布里渊区经过适当的平移,都可移到第一布里渊区且与之重合C、每个布里渊区的体积都不相等D、晶体结构的布喇菲格子虽然相同,但其布里渊区形状却不会相同9、金属晶体的热传导主要就是通过( A )传输实现的A、电子B、声子C、光子D、质子10、在一维单原子链的晶格振动中,有( A )支声学波、( A )支光学波。
A、1,0B、1,1C、3,3D、3,611、依照量子自由电子论,K空间中电子的等能面就是( A )。
A、球面B、椭球面C、抛物面D、不规则曲面12、根据能带理论,电子的能态密度随能量变化的趋势就是随能量增高而( D )。
A、单调增大B、不变C、单调减小D、复杂变化13、周期性边界条件决定了电子的波矢K在第一布里渊区内可取值数量与晶体的初基元胞数N( A )。
A、相等B、大于C、小于D、不一定14、按照费米分布,费米能级所对应的能态电子占据的几率为( B )。
A、1B、0、5C、015、根据能带的能量就是波矢的周期函数的特点,能带的表示图式可以有三种。
以下不正确的就是( D )。
A、简约区图式B、扩展区图式C、反复图式D、单一图式16、量子自由电子论就是建立在( B )的基本假设之上的。
A、周期性势场B、恒定势场C、无势场17、晶体的宏观特性包括( A )A、各向异性B、周期性C、重复性D、单一性18、不属于半导体主要晶体结构类型的就是( D )。
A、金刚石型结构B、闪锌矿型结构C、钙钛矿结构D、密堆积结构19、晶体中的线缺陷包括( C )。
A、小角晶界B、空位C、螺位错D、堆垛层错20、根据能带的能量就是波矢的周期函数的特点,能带的表示图式可以有三种。
图示属于( A )。
A、简约区图式B、扩展区图式C、重复图式D、周期图式21、金刚石结构就是由( A )A、由二套面心格子沿体对角线方向滑1/4长度套构而成B、由二套简单立方格子沿体对角线方向滑1/4长度套构而成C、由二套体心立方格子沿体对角线方向滑1/4长度套构而成D、由一套体心格子与一套面心格子沿体对角线方向滑1/4长度套构而成22、布里渊区的特点不包括( A )A、各个布里渊区的形状都就是相同的(不同的)B、各布里渊区经过适当的平移,都可移到第一布里渊区且与之重合C、每个布里渊区的体积都就是相同的D、无论晶体就是由哪种原子组成,只要布喇菲格子相同,其布里渊区形状也就相同23、绝缘晶体的热传导就是通过( B )传输实现的A、电子B、声子C、光子D、质子24、在一维双原子链的晶格振动中,有(A)支声学波、(A)支光学波。
A、1,1B、2,2C、3,3D、4,425、按照费米分布,绝对0度时费米能以下的能态电子占据的几率为( A )。
A、1B、0、5C、026、能带理论就是建立在( A )的基本假设之上的。
A、周期性势场B、恒定势场C、无势场三、填空1、晶体结构的基本特点就是具有( 周期)性与( 重复)性、2、离子晶体的( 光学波)波会引起对远红外线的吸收、3、描述晶体对称性可以概括为( 32 )个点群,( 230 )个空间群、4、金属主要就是依靠( 电子)导热,而绝缘体主要依靠( 声子)导热、5、对一维晶体,其晶格振动仅存在( 声学)波,而二、三维晶体振动既有( 声学)波,又有( 光学)波、6、对于量子化的自由电子,其K空间中的等能面为( 球面)、7、费米能就是指电子占据几率为( 1/2 )的电子态本征能量大小、8、能带理论中,电子的E~K关系具有( 倒格子)周期性、9、对晶格常数为a的简单立方晶体,与正格矢R=ai+2aj+2ak正交的倒格子晶面族的面指数为( 122 )、10、离子晶体的(光学波)会引起离子晶体的极化、11、金刚石晶体的结合类型就是典型的(共价结合)晶体, 它有( 6 )支格波、12、两种不同金属接触后,费米能级高的带(正)电、四、判断对错1、各向异性就是晶体的基本特性之一。
( √)2、单质半导体与二元化合物半导体的主要晶体结构类型为金刚石型结构与闪锌矿型结构。
( √)3、各布里渊区经过适当的平移,仍无法移到第一布里渊区且与之重合。
(×)4、在一维单原子链的晶格振动中,有1支光学波、无声学波。
( ×)5、依照能带理论,电子的能态密度随能量变化的趋势总就是随能量增高而增大。
(×)6、周期性边界条件决定了电子的波矢K在第一布里渊区内可取值数量与晶体的初基元胞数N相等。
( √)7、同一晶体在绝对0度时的费米能大于绝对0度时以上时的费米能。
( √)8、能带理论就是建立在恒定势场的基本假设之上的。
( ×)9、晶体的宏观特性包括各向异性、解理性、周期性、重复性。
( ×)10、空位、小角晶界、螺位错、堆垛层错都就是晶体中的线缺陷。
(×)11、共价晶体的基本特点有高强度、高硬度、高熔点。
(√)12、布里渊区的特点包括A、B、C:A、各个布里渊区的形状都就是相同的B、各布里渊区经过适当的平移,都可移到第一布里渊区且与之重合C、每个布里渊区的体积都就是相同的D、无论晶体就是由哪种原子组成,只要布喇菲格子相同,其布里渊区形状也就相同(×)13、绝缘晶体的热传导就是通过声子传输实现的。
