美国大学生数学建模竞赛数据及评阅分析_吴孟达
大学生数学建模竞赛简介及试题分析

程以及技术含量 5)关于模型的有说服力的检验及精道的优缺点分析 6)由模型得到的关于问题有实际意义的结论 7)某个方面突出的亮点
美国(国际)大学生数学建模竞赛特点
7 是否给出了清晰的摘要。
美国大学生数学建模竞赛论文等级
不合格论文(Unsuccessful Participants)
合格论文(Successful Participants)
乙级论文(Honorablus)
(一等奖)
特级提名论文(Finalist)
赛题内容涉及经济、管理、环境、资源、生态、医学、 安全、未来科技等众多领域。
MCM/ICM 着重强调:
研究问题、解决方案的原创性,团队合作、交流以及结果的合理性。
美国大学生数学建模竞赛题目
每个团队在下列问题中选择且只能选择一个问题, 并提交解决方案。
MCM 问题A(连续) MCM 问题B(离散) MCM 问题C (对于数据的见解) ICM 问题D(运筹学或网络科学) ICM 问题E(环境科学) ICM 问题F (政策)
特级论文(优胜论文)(Outstanding Winner)
评委眼中数学建模竞赛论文 论文的评审流程
提交的论文 不合格论文 合格论文 下一轮论文
淘汰轮
乙级论文
下一轮
摘要与框架
最 评奖轮 终
评
分析与理解
奖 轮
甲级论文 下一轮
结构严谨 条理清晰 简单易读 结果以最简单最明了的方式表达
模型 方法 结果
Are Fingerprints Unique?
我校在美国大学生数学建模竞赛中喜获佳绩

我校在美国大学生数学建模竞赛中喜获佳绩近日,2011年美国大学生数学建模竞赛成绩在竞赛官方网站公布(/undergraduate/contests/mcm/contests/2011/results/),我校的六支参赛队喜获三个一等奖(Meritorious)和一个二等奖(Honorable Mention)。
获得一等奖的代表队分别是由张战国老师指导的宋海滨、王锐、孙玉婷(C 题);由李放歌老师指导的燕姗姗、李军、孙国朋(C题);由杨月莹老师指导的崔迪、朱元杰、房强(B题)。
另外由杨月莹老师指导的李旭、商婷婷、呼建欣(C题)荣获了二等奖。
据悉,美国大学生数学建模竞赛包括数学建模竞赛(MCM:A题和B题)和交叉学科建模竞赛(ICM:C题)。
竞赛以通信形式进行,由3名学生组成一队,在4天时间内自由地收集材料、调查研究,利用计算机、专业软件和互联网等工具,完成一篇包含模型的假设、建立和求解等方面的全英文论文。
论文按时提交美国主办机构,由美国组织专家对全球各地提交的论文进行统一评审。
2011年美国大学生数学建模竞赛吸引了来自包括加拿大、中国、德国、英国在内的17个国家和地区10491名在校大学生参加。
MCM一等奖的获奖率仅为13%,ICM一等奖的获奖率为20%,我校今年的一等奖获奖率与我省其他参赛高校相比名列前茅。
附黑龙江省各高校获奖信息:参赛学校参赛队数优于一等奖一等奖二等奖成功参赛奖哈尔滨工业大学259 2 27 110 120哈尔滨工程大学72 6 29 37东北农业大学 6 3 1 2哈尔滨理工大学11 1 4 6东北林业大学 5 3 2黑龙江大学 4 2 2黑龙江八一农垦大学 5 5理学院。
美国大学生数学建模竞赛对我国高校数学教学的启示

研 究 问题 、 解决 方 案 的 原创 性 、 团队合作、 交 流 以 及
结 果 的合理 性 。MC M 的 宗 旨 是 鼓 励 大 学 师 生 对 范
V o 1 . 1 l N o . 3
Fe b .2 0 1 3
I ) Ol : 1 0 . 3 9 6 9 / j . i s s n . 2 0 9 5 — 3 3 3 X. 2 0 1 3 . 0 3 . 0 2 7
美 国 大 学 生 数 学 建 模 竞 赛 对 我 国 高 校 数 学 教 学 的 启 示
吕小光 , 姜 乐 , 成 青松
( L淮海工学院 理学 院 , 江苏 连云港 2 2 2 0 0 5 ;2 . 电子科技大学 数学科学学 院, 四川 成都 6 3 1 7 l 1 )
摘 要 : 作为数 学建模 领域 内的 国际性权 威 赛事 , 美 国 大 学 生数 学 建 模 竞 赛 受 到 了全 世 界 各 大 高校
当今 社 会 发 展 越 来 越 快 , 各 种 竞 争 压 力 越 来 越 大 , 对人 才 的要求 也 越来越 高 。人 才 的竞争 , 实 际 上 就 是 教 育 的竞 争 、 能 力 发 展 的 竞 争 。 在 传 统 的 教 育
人 ( 本 科 生) 一 组在 四天 时 间 内 , 就 指 定 的 问 题 完 成 从 建 立模 型 、 求解 、 验 证 到 论 文 撰 写 的 全 部 工 作 。 竞
大 洲 的 数 千 名 大 学 生 参 加 。 M CM / I CM 着 重 强 调
建 模 竞 赛 对 高 校 教 师 队 伍 的 能 力 是 一 个 很 大 的 挑 战, 需 要他 们 进一步 提高 能力 和素 质 , 同 时 也 需 要 各
美国大学生数学建模竞赛题解析与研究

推荐
《美国大学生数学建模竞赛题解析与研究(第5辑)》内容新颖、实用性强,可作为指导学生参加美国大学生 数学建模竞赛的主讲教材,也可作为本科生、研究生学习和准备全国大学生、研究生数学建模竞赛的参考书,同 时也可供研究相关问题的科研人员orward by Sol Garfunkel ICM竞赛主席序 Forward by Chris Arney 丛书简介 前言 I Mathematical Modeling for MCM/ICM 2013 Chapter 1 Introduction Chapter 2 General Methodology 2.1 Before the Contest 2.2 Reading the Problem
谢谢观看
图书目录
第1章棒球“最佳击球点”问题 1.1问题分析 1.1.1棒球?球棒 1.1.2分析问题与提出假设 1.2定位球棒的最佳击球点 1.2.1一个初步的想法:定位最佳击球点 1.2.2布罗迪功效模型 1.2.3考虑击球手的舒适度 1.3不同材质球棒的特性分析 1.3.1“软木化”的球棒与普通木质球棒的对比 1.3.2铝制球棒与普通木质球棒的对比
美国大学生数学建模竞赛题解析与研 究
2014年高等教育出版社出版的图书
01 内容简介
03 推荐
目录
02 图书目录 04 目录
《美国大学生数学建模竞赛题解析与研究》是2014年高等教育出版社出版的图书,作者是赵仲孟、王嘉寅。
内容简介
《美国大学生数学建模竞赛题解析与研究(第3辑)》内容简介:本系列丛书是以美国大学生数学建模竞赛 (MCM/ICM)题为主要研究对象,结合竞赛特等奖的论文,对相关的问题进行深入细致的解析与研究。《美国大 学生数学建模竞赛题解析与研究(第3辑)》的主要内容包括:棒球“最佳击球点”问题、重新平衡受人类影响的 生态系统问题、泛太平洋垃圾带问题、犯罪情报分析的建模问题、交通环岛的优化设计问题和能源与移动问题。 《美国大学生数学建模竞赛题解析与研究(第3辑)》可作为指导大学生学习和准备美国大学生数学建模竞赛的主 讲教材,也可作为大学生、研究生学习和准备全国大学生、研究生数学建模竞赛的参考书,同时可供研究相关问 题的人员参考使用。
美国大学生数学建模竞赛的命题与评阅指导课件

2. MCM/ICM 题目的不同之处
• ICM问题通常是全球关注的问题,不依赖于文化背景 • 这就更有利于中国学生。因为某些MCM问题有时
偏重文化与传统的背景,如MCM 2006B,机场轮椅 问题,MCM2021A,交通灯设计,Stop sign(路口暂时 停的标记牌),yield sign〔并道时必需看来车方向〕 在中国没有此类警示牌,MCM2021A, Ultimate Brownie Pan 等,很多中国学生无此概念。 • 参赛的学生根据自己的特长,选择不同类型的题目。
SOL GARFUNKEL, EXECUTIVE DIRECTOR, COMAP
“I hope that you will to work on the exciting and important problems you see here, and that you will join the MCM/ICM contest and rewarding work of increasing the awareness of the importance of Mathematical Modeling.〞
初评过程---论文分类
初评〔第一阶段triage judging〕,也称为鉴别评审阶段。 每篇论文在此阶段中按质量分为以下三类: 第一类是可以进入下一阶段评审的论文; 第二类是满足竞赛要求,但却缺乏以进入下一阶段评
审的论文,这类论文为合格论文; 第三类是不符合竞赛要求的论文,这类论文为不合格
论文。
31
Tianjin University
• Mathematical Modeling for the MCM/ICM Contest , Volume 2
• MCM/ICM评委 • 内容简介 • 1-4章:2021年4个竞赛题的分析、点评与解答 • 第5章:对数学建模研究当前热点问题的拓展 • 实用性强,可供参加美赛的读者参考使用
2022年美国大学生数学建模竞赛(MCMICM)获奖情况数据统计

2022年美国大学生数学建模竞赛(MCMICM)获奖情况数据统计美赛介绍美国大学生数学建模竞赛【MCM】是数学建模领域内的国际性权威赛事,由美国自然基金协会和美国数学应用协会共同主办,美国数学学会、运筹学学会、工业与应用数学学会等多家机构协办。
自 1985 年以来,美国大学生数学建模竞赛已经成功举办38 届,2022 年吸引了来自全球各高校的27205支队伍参加,通过获奖数据分析,可以快速掌握美赛的获奖概率,充分进行备赛拿奖。
奖项说明Outstanding Winners 俗称O奖也叫作特等奖Finalist 俗称F奖也叫作特等奖提名奖Meritorious Winners 俗称M奖也叫作一等奖Honorable Mentions 俗称H奖也叫作二等奖Successful Participants 俗称S奖也叫作成功参赛奖Unsuccessful Participants 俗称U奖也叫作不成功参赛奖Disqualified Teams 俗称D奖被取消评奖资格参赛情况2022年美赛共有参赛队伍27205个参赛学生80693名,2021年参赛队伍26112个,比较起来增加了1093个队伍。
2022MCM与ICM的参加情况:15105个队伍参加MCM(55%)12100个队伍参加ICM(45%)vs2021MCM与ICM的参加情况:10053个队伍参加MCM(38.5%)16059个队伍参加ICM(61.5%)可以发现同比去年MCM参与比上升,ICM参与比则有所下降。
ps:在成绩表里面共有7列,分别是:队号、学校、国家、指导教师、题目、奖项以及附加奖项,其中附加奖项指的是获得列特等奖后,额外获得的奖项。
特大喜讯在这里数模君要公布一个喜讯:2022年数模乐园惊现四支美赛O 奖(outstanding winners)队伍!其中一位更是获得了o奖冠名奖!工业与应用数学学会(SIAM)将指定一个来自 MCM 问题 A 和 B 的优秀团队作为 SIAM 获奖者。
2013美赛结果分析

2013年美国大学生数学建模竞赛结果发布COMAP非常高兴地宣布第29届大学生数学建模竞赛(MCM)结果。
今年共有5636支队伍参加了比赛,分别代表14个国家和地区。
以下11支队伍提交的论文被评定为优胜论文(OUTSTANDING WINNERS):Beijing Univ. of Posts and Telecomm, China(北京邮电大学:郭众鑫、吴帆、王蓓丹;指导教师:贺祖国)Bethel University, Arden Hills, MNColorado College, Colorado Springs, COFudan University, China(复旦大学:王坤睿、许晶、曾溦;指导教师:杨翎)Nanjing University, China(南京大学:陈炜、刘威志、杨岑莹;指导教师:瞿慧)Peking University, China(北京大学:金冲、刘博闻、吴蒙; 指导教师:刘旭峰)Shandong University, China(山东大学:宋炎侃、徐珂、伊凡;指导教师:Hengxu Zhang)Shanghai Jiaotong University, China(上海交通大学:文理斌、吴婧元、王聪; 指导教师:Yuehui Zhang)Tsinghua University, China(清华大学: 高鹏飞、何博硕、邹天忻;指导教师:吴昊)University of Colorado Boulder, Boulder, CO (2)今年的竞赛时间是从2013年1月31日(星期四)到2013年2月4日(星期一)。
在这段时间里,由三名学生组成的本科生或高中生队伍从两个竞赛问题中选择一个,认真研究并建模,最终提交一份解决方案。
今年MCM的主要形式通过网络展开。
参赛队伍需要在规定的时间内通过COMAP的MCM网站注册、获得竞赛材料并下载题目和数据。
今年MCM的两个问题被公认为具有很大的挑战性。
美赛数据及评阅分析
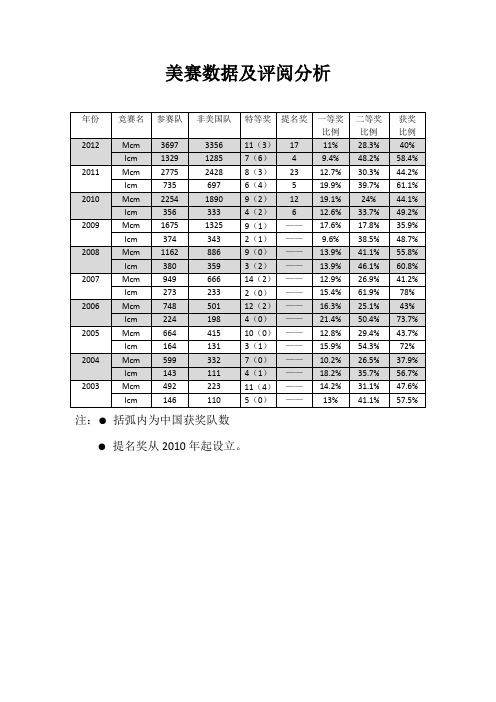
美赛数据及评阅分析注:●括弧内为中国获奖队数●提名奖从2010年起设立。
分析:● 10年间年均增长25%,近5年年均增长33.8%。
●美国参赛队增长不明显,增长队数主要来自于非美国队,这其中主要来自于中国参赛队的增长。
●2012年非美国参赛队占比已经达到了90.8%。
分析:● 10年间年均增长31.6%,近三年年均增长90%。
●10年间美国参赛队几乎未增加,增长队数主要来自于中国参赛队。
●2012年非美国参赛队占比已经达到了96.7%。
分析:●特等奖获奖比例平均为:1.03%●一等奖获奖比例平均为:14.7%●二等奖获奖比例平均为:28%●总获奖比例平均为:43.73%分析:●特等奖获奖比例平均为:1.4%●一等奖获奖比例平均为:15%●二等奖获奖比例平均为:45%●总获奖比例平均为:61.4%据美赛“评委评论”介绍,美赛评阅过程大致分为三轮。
第一轮可以称为“淘汰轮(the triage round)”。
此轮评阅主要以摘要信息以及论文整体结构为评判依据,时间大约是5~10分钟。
每个评委以“通过”“不通过”计分,事先应当设置有大致的“通过”比例(此轮与国内研赛的网评阶段相类似)。
当两位评委意见不一致时可以协商达成一致意见,如果仍不能达成一致意见,则请第三位评委评阅。
有“评论”介绍说:这一轮的淘汰率大约为45%,通过这一轮评审的参赛队大约有80%的获奖概率。
关于如何通过这一轮评审,评委给出的建议是:1、摘要至关重要,必须清晰且信息量充分,评委关心的是你对问题的理解是否准确,你建立的模型及使用的方法是否恰当,以及根据你所建模型得到的主要结果和主要结论是否合理。
过于冗长的技术性描述将阻碍评委对你的结果的关注。
2、你的论文应当有良好的组织架构,以使得评委能够在5~8分钟内理解你的论文的关键信息。
第二轮可以称为“评奖轮(the Preliminary Rounds )”。
每篇论文由若干(应当不超过三名)评委评阅,以5分或10分制计分,每位评委评阅每篇论文的时间大约在15~30分钟之间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
给出了 MCM 和ICM 中国队和美国队参赛队数的变化。
图1分析:
● MCM 参赛队数10年间年均增长25%,近5年年均增长33.8%,增速明显加快。
● 美国参赛队增长不明显,增长队数主要来自于中国参赛队的增长。
收 稿 日 期 :2012-11-09 通 讯 作 者 :吴 孟 达 ,E-mail:mdwu@nudtwmd.com
摘 要:统计了美国大学生数学建模竞赛近十年的参赛数据,对其评阅过程进行 了 分 析,得 出 了 一 些 有 参 考 价 值 的 结论。 关 键 词 :美 国 大 学 生 数 学 建 模 竞 赛 ;中 国 大 学 生 数 学 建 模 竞 赛 ;获 奖 比 例 ;评 阅 过 程
中 图 分 类 号 :O29 文 献 标 志 码 :A 文 章 编 号 :2095-3070(2012)04-0075-04
3 26 1 273 2 373 687 1 854 332 1 282 342 849 357 627 235 466 194 389 125 295 103 195 105
11(3) 7(6) 8(3) 6(4) 9(2) 4(2) 9(1) 2(1) 9(0) 3(2)
图2 ICM 参赛队数变化图 图3 MCM 获奖比例 图4 ICM 获奖比例
2 评 阅 过 程 分 析
据 美 赛 “评 委 评 论 ”介 绍 ,美 赛 评 阅 过 程 大 致 分 为 三 轮 。 第一轮可以称为“淘汰轮(the Triage Round)”。此轮评阅主要以摘要信息以及论文整体结构为 评 判 依 据 ,时 间 大 约 是 5~10 分 钟 。 每 个 评 委 以 “通 过 ”、“不 通 过 ”计 分 ,事 先 应 当 设 置 有 大 致 的 “通 过 ”比 例 (此 轮 与 国内研赛的网评阶段相类似)。当两位 评 委 意 见 不 一 致 时 可 以 协 商 达 成 一 致 意 见,如 果 仍 不 能 达 成 一 致 意 见 ,则 请 第 三 位 评 委 评 阅 。 有 “评 论 ”介 绍 说 ,这 一 轮 的 淘 汰 率 大 约 为 45% ,通 过 这 一 轮 评 审 的 参 赛 队 大 约 有 80% 的 获 奖 概 率 。 关 于 如 何 通 过 这 一 轮 评 审 ,评 委 给 出 的 建 议 是 : 1)摘 要 至 关 重 要 ,必 须 清 晰 且 信 息 量 充 分 。 评 委 关 心 的 是 你 对 问 题 的 理 解 是 否 准 确 ,你 建 立 的 模 型 及 使 用的方法是否恰当,以及根据你所建模型得到的主要结果和主要结论是否合理 。 过 于 冗 长 的 技 术 性 描 述 将 · 76 ·
14(2) 2(0)
12(2) 4(0)
10(0) 3(1) 7(0) 4(1)
11(4) 5(0)
17 4
23 5
12 6
-- -- -- -- -- -- -- -- -- -- -- -- -- --
11% 9.4% 12.7% 19.9% 19.1% 12.6% 17.6% 9.6% 13.9% 13.9% 12.9% 15.4% 16.3% 21.4% 12.8% 15.9% 10.2% 18.2% 14.2% 13%
78% 43% 73.7% 43.7% 72% 37.9% 56.7% 47.6% 57.5%
注:● 特等奖一栏括弧内为中国获奖队数。 ● 提名奖从2010年起设立。
从 表 1 可 以 看 出 ,近 十 年 参 赛 队 主 要 来 自 中 国 和 美 国 ,只 有 很 少 一 部 分 来 自 其 他 国 家 。 图 1 和 图 2 分 别
图1 MCM 参赛队数变化图
图3分析: ● 特等奖获奖比例平均为 1.08%,近五年获奖比例平均 为0.46%。由于参赛规模扩大,此 奖 项 获 奖 比 例 下 降 趋 势 比 较明显。 ● 一等奖获奖比例平均为14.7%。 ● 二等奖获奖比例平均为28%。 ● 总获奖比例平均为43.73%。 ● 获奖比例起伏较大。 图4分析: ● 特等奖获奖比例平 均 为 1.4%,近 五 年 获 奖 比 例 平 均 为 0.76% ,获 奖 比 例 下 降 趋 势 比 较 明 显 。 ● 一等奖获奖比例平均为15% ● 二等奖获奖比例平均为45% ● 总获奖比例平均为61.4% ● 获奖比例起伏较大。 作为比较,全国大学生 数 学 建 模 竞 赛 (以 下 简 称 “国 赛”) 获奖 情 况 统 计 如 下:一 等 奖 获 奖 比 例 平 均 约 为 1.5%,一、二 等 奖 总 获 奖 比 例 平 均 约 为 8% 。
28.3% 48.2% 30.3% 39.7% 24% 33.7% 17.8% 38.5% 41.1% 46.1% 26.9% 61.9% 25.1% 50.4% 29.4% 54.3% 26.5% 35.7% 31.1% 41.1%
40% 58.4% 44.2% 61.1% 44.1% 49.2% 35.9% 48.7% 55.8% 60.8% 41.2%
1 数 据 分 析
美国大学生数学建模竞赛(以下简称“美赛”)创办于 1985 年,已经有 27 年的历史,本文拟对美赛近 10 年 来 的 参 赛 情 况 及 评 阅 过 程 做 一 个 大 致 的 分 析 。 表 1 是 美 赛 近 10 年 参 赛 队 数 及 获 奖 比 例 统 计 。
表 1 美 赛 近 十 年 参 赛 队 数 及 获 奖 比 例 统 计
5分或10分制计分,每位评委评阅每篇论 文 的 时 间 大 约 在 15~30 分 钟 之 间。 然 后 将 所 有 论 文 按 总 分 由 高 到 低 排 序 ,按 既 定 比 例 依 顺 序 确 定 一 、二 等 奖 。
在 此 轮 评 阅 中 ,评 委 最 关 心 的 问 题 是 : 1)参 赛 者 对 问 题 意 义 及 重 心 的 理 解 是 否 准 确 到 位 ; 2)是 否 题 目 中 所 有 问 题 都 得 到 了 回 答 ; 3)模 型 与 建 模 过 程 的 一 致 性 如 何 ,表 述 是 否 清 晰 ; 4)模 型 的 技 术 含 量 如 何 ; 5)由 模 型 得 到 的 结 果 是 否 合 理 ,有 无 合 理 性 及 可 靠 性 检 验 。 第 三 轮 可 以 称 为 “最 终 评 审 轮 (the Final Judging Round)”。 每 道 题 目 在 第 二 轮 中 排 名 最 高 的 二 、三 十 篇 论 文 将 进 入 此 轮 评 审 。 此 轮 评 审 大 约 有 6~8 位 评 委 ,最 终 获 得 特 等 奖 的 论 文 必 须 经 过 所 有 评 委 的 评 审 。 在 此 轮 中 ,评 委 会 仔 细 考 量 论 文 的 模 型 、方 法 与 结 果 ,对 一 篇 特 等 奖 论 文 的 期 望 是 : 1)一 篇 信 息 量 充 分 的 摘 要 ; 2)对 问 题 本 质 的 洞 察 能 力 (very good insight into the problem); 3)文 章 思 路 清 晰 且 有 很 好 的 一 致 性 ; 4)一 个 完 整 而 且 高 质 量 的 模 型 ,包 括 假 设 、建 模 过 程 以 及 技 术 含 量 (it presented a high-quality applica- tion of the complete modeling process); 5)关 于 模 型 的 有 说 服 力 的 检 验 以 及 精 到 的 优 缺 点 分 析 ; Why do you think your model is good?Against what baseline can you compare/validate it? How sensitive is your model to slight changes in the parameters you have chosen?(sensitivity analy- sis) Complete the analysis circle:Are your recommendations practical in the problem context? 6)由 模 型 得 到 的 关 于 问 题 的 有 实 际 意 义 的 结 论 ; 7)某 个 方 面 的 突 出 亮 点 (it demonstrated noteworthy originality and creativity in their modeling effor)。 与 国 赛 相 比 较 ,美 赛 评 阅 过 程 有 以 下 特 点 : 1)遵 循 一 个 原 则 :获 奖 等 级 越 高 的 论 文 被 评 阅 次 数 越 多 。 国 赛 也 有 类 似 的 做 法 ,但 评 阅 次 数 差 异 要 小 一 些。 2)对结果的宽容度较大。例如1999年“大碰撞”,关于小行星碰撞地球 后 可 能 对 人 类 带 来 的 危 害,发 表 的优秀论文中,有的论文说没有影响,有的论文说有毁灭性影响。在历年“评委评 论”中,评 委 多 次 强 调 论 文 的“一致性”,也就是国赛中经常有人提到的要“自圆其说”。评阅中结果重要性的淡化 对 评 委 的 评 阅 水 平 提 出了更高的要求。 3)在 “评 委 评 论 ”中 ,常 常 有 评 委 强 调 考 察 参 赛 论 文 的 “两 个 理 解 ”,即 对 问 题 的 理 解 与 对 所 用 方 法 的 理 解 (Modelers can frequently gain creditability by demonstrating that they understand the problem in its con- text),一 个 理 想 的 模 型 无 非 是 “两 个 理 解 ”的 完 美 结 合 (One key to successful model building is to adapt ex- isting theory or models properly to the problem at hand,whether derived or researched,it is imperative to demonstrate an understanding of the model you are)。 因 此 ,“两 个 理 解 ”在 很 大 程 度 上 体 现 了 参 赛 者 的 建 模 能 力 。 当 然 ,这 样 评 价 学 生 的 建 模 能 力 对 评 委 的 评 阅 能 力 要 求 会 更 高 。 4)与 国 赛 不 同 的 是 ,美 赛 论 文 常 常 需 要 提 交 一 份 2 页 以 内 的 执 行 摘 要 ,其 阅 读 对 象 假 定 为 论 文 成 果 的 应 用 方 ,以 成 果 特 点 介 绍 及 可 操 作 内 容 为 主 ,不 需 要 技 术 细 节 。 这 些 内 容 在 实 际 应 用 课 题 研 究 中 往 往 也 是 课 题 成果应用方所关心的。此环节的设立体现了美赛对可执行结论的重视。美赛优秀论文通常也有单独一节 “The Conclusions”。
