数学必修二第一章空间几何体测试题
必修2第一章《空间几何体》单元测试题
广东省佛山市南海区九江中学数学选修1-1 圆锥曲线测试卷高二（）班学号姓名分数一选择题(每题 4分,8 小题共 32 分,答案填在后边的表内 )1)如图 ,椭圆c1, c2和双曲线 c3 ,c4的离心率分别是 e1 , e2 , e3 ,e4,则有y C4( )C 3(A)e2< e1< e4< e3(B) e1 < e2 < e4 < e3o x C 1(C)e2< e1< e3< e4(D) e1 < e2 < e3 < e4C 22)若椭圆的方程为4x 9 y 360，则其长轴长为( )(A) 3(B)4(C) 6(D) 93)P4,2 2是抛物线上一点，焦点在x 轴，则此抛物线是()(A)x 2 4 2y(B)y2 4 2y (C) x 22y(D) y22x4)若 a c8, a2c234 ，则知足上述条件的双曲线离心率为（）5(B)5(C)67(A)4(D)6355)若点 M ( x, y) 知足( x2) 2y 2( x 2) 2y 2 2 ，则点 M 的轨迹表示的曲线是( )(A)双曲线(B) 双曲线的左支(C)双曲线的右支(D) 双曲线两支在x轴上方部分6)椭圆 x2y2 1 上一点p到一个焦点的距离为1，则p到另一焦点的距离为( )925(A) 2(B) 4(C) 8(D) 247)mn< 0是方程x2y 21表示双曲线实轴在y 轴的() m n(A)充足条件(B)必需条件(C) 充要条件(D)不用要亦不充足条件8)方程x 2y 21(10k20) 所表示的曲线是（）25k9 k(A)焦点在 x 轴的椭圆(B) 焦点在y轴的椭圆(C)焦点在 x 轴的双曲线(D) 焦点在y轴的双曲线二填空题 (每题4分,6小题共24 分 ,答案填在后边的表上)9)焦距为 2 5 ，一条准线为x 5.的双曲线方程是510)椭圆 y2x21与双曲线x2y2 1 有同样的焦点,则 a.4a22a11)直线 2x ay 3 0过椭圆x2y21的焦点 ,则 a. 81212)椭圆 x 2y 21的离心率e10,则 m.m5513)若抛物线 y2x 与直线y mx1没有交点 , 则m的取值范围是14)某圆锥曲线的一个焦点为（0，3），且过（ 3， 1），则其标准方程是______________九江中学数学选修2-1圆锥曲线测试卷05. 12. 12.高二（一、选择题答案填下表题号1答案2）班3学号456姓名78分数二、填空题答案填下表题号91011121314答案三、解答题 (共 44 分)15)（ 16 分）求知足以下条件的圆锥曲线标准方程：(1)两极点为（ 3， 0）、（3， 0），两焦点为（ 1， 0）、（1， 0）；(2) e 2 ，焦点在y轴，且a+c=6解：16)（10分）双曲线的离心率为5，且与椭圆x 2y 21有共同焦点，求此双曲线的标准方程294及渐近线方程。
高中数学必修二测试题及答案人教版
第一章 空间几何体一、选择题1．有一个几何体的三视图如下图所示，这个几何体可能是一个( )．主视图 左视图 俯视图 (第1题) A ．棱台 B ．棱锥 C ．棱柱 D ．正八面体2．如果一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是( )．A ．2＋2B ．221＋C ．22＋2 D ．2＋13．棱长都是1的三棱锥的表面积为( )．A ．3B ．23C ．33D ．434．长方体的一个顶点上三条棱长分别是3，4，5，且它的8个顶点都在同一球面上，则这个球的表面积是( )．A ．25πB ．50πC ．125πD ．都不对 5．正方体的棱长和外接球的半径之比为( )． A ．3∶1 B ．3∶2 C ．2∶3 D ．3∶36．在△ABC 中，AB ＝2，BC ＝1.5，∠ABC ＝120°，若使△ABC 绕直线BC 旋转一周，则所形成的几何体的体积是( )．A ．29πB ．27πC ．25πD ．23π7．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是( )．A ．130B ．140C ．150D ．1608．如图，在多面体ABCDEF 中，已知平面ABCD 是边长为3的正方形，EF ∥AB ，EF ＝23，且EF 与平面ABCD 的距离为2，则该多面体的体积为( )．A ．29 B ．5 C ．6 D ．2159．下列关于用斜二测画法画直观图的说法中，错误．．的是( )． A ．用斜二测画法画出的直观图是在平行投影下画出的空间图形B ．几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同C ．水平放置的矩形的直观图是平行四边形D ．水平放置的圆的直观图是椭圆10．如图是一个物体的三视图，则此物体的直观图是( )．(第8题)(第10题)二、填空题11．一个棱柱至少有______个面，面数最少的一个棱锥有________个顶点，顶点最少的一个棱台有________条侧棱．12．若三个球的表面积之比是1∶2∶3，则它们的体积之比是_____________．13．正方体ABCD－A1B1C1D1 中，O是上底面ABCD的中心，若正方体的棱长为a，则三棱锥O－AB1D1的体积为_____________．14．如图，E，F分别为正方体的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面上的射影可能是___________．(第14题)15．已知一个长方体共一顶点的三个面的面积分别是2、3、6，则这个长方体的对角线长是___________，它的体积为___________．16．一个直径为32厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高9厘米则此球的半径为_________厘米．三、解答题17．有一个正四棱台形状的油槽，可以装油190 L，假如它的两底面边长分别等于60 cm 和40 cm，求它的深度．18 *．已知半球内有一个内接正方体，求这个半球的体积与正方体的体积之比．[提示：过正方体的对角面作截面]19．如图，在四边形ABCD中，∠DAB＝90°，∠ADC＝135°，AB＝5，CD＝22，AD＝2，求四边形ABCD绕AD旋转一周所成几何体的表面积及体积．(第19题)20．养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用)，已建的仓库的底面直径为12 m，高4 m，养路处拟建一个更大的圆锥形仓库，以存放更多食盐，现有两种方案：一是新建的仓库的底面直径比原来大4 m(高不变)；二是高度增加4 m(底面直径不变)．(1)分别计算按这两种方案所建的仓库的体积；(2)分别计算按这两种方案所建的仓库的表面积；(3)哪个方案更经济些？第一章 空间几何体参考答案A 组一、选择题 1．A解析：从俯视图来看，上、下底面都是正方形，但是大小不一样，可以判断可能是棱台．2．A解析：原图形为一直角梯形，其面积S ＝21(1＋2＋1)×2＝2＋2．3．A解析：因为四个面是全等的正三角形，则S 表面＝4×43＝3． 4．B解析：长方体的对角线是球的直径， l ＝2225＋4＋3＝52，2R ＝52，R ＝225，S ＝4πR 2＝50π． 5．C解析：正方体的对角线是外接球的直径． 6．D解析：V ＝V 大－V 小＝31πr 2(1＋1.5－1)＝23π．7．D解析：设底面边长是a ，底面的两条对角线分别为l 1，l 2，而21l ＝152－52，22l ＝92－52，而21l ＋22l ＝4a 2，即152－52＋92－52＝4a 2，a ＝8，S 侧面＝4×8×5＝160． 8．D解析：过点E ，F 作底面的垂面，得两个体积相等的四棱锥和一个三棱柱，V ＝2×31×43×3×2＋21×3×2×23＝215．9．B解析：斜二测画法的规则中，已知图形中平行于 x 轴的线段，在直观图中保持原长度不变；平行于 y 轴的线段，长度为原来的一半．平行于 z 轴的线段的平行性和长度都不变．10．D解析：从三视图看底面为圆，且为组合体，所以选D. 二、填空题11．参考答案：5，4，3．解析：符合条件的几何体分别是：三棱柱，三棱锥，三棱台．12．参考答案：1∶22∶33．r 1∶r 2∶r 3＝1∶2∶3，31r ∶32r ∶33r ＝13∶(2)3∶(3)3＝1∶22∶33．13．参考答案：361a ．解析：画出正方体，平面AB 1D 1与对角线A 1C 的交点是对角线的三等分点， 三棱锥O －AB 1D 1的高h ＝33a ，V ＝31Sh ＝31×43×2a 2×33a ＝61a 3． 另法：三棱锥O －AB 1D 1也可以看成三棱锥A －OB 1D 1，它的高为AO ，等腰三角形OB 1D 1为底面．14．参考答案：平行四边形或线段．15．参考答案：6，6．解析：设ab ＝2，bc ＝3，ac ＝6，则V = abc ＝6，c ＝3，a ＝2，b ＝1， l ＝1＋2＋3＝6． 16．参考答案：12．解析：V ＝Sh ＝πr 2h ＝34πR 3，R ＝32764×＝12． 三、解答题 17．参考答案：V ＝31(S ＋S S ′＋S )h ，h ＝S S S S V ′＋′＋3＝6001＋4002＋60030001903×＝75．18．参考答案：如图是过正方体对角面作的截面．设半球的半径为R ，正方体的棱长为a ，则CC'＝a ，OC ＝22a ，OC'＝R ．(第18题)在Rt △C'CO 中，由勾股定理，得CC' 2＋OC 2＝OC' 2，即 a 2＋(22a )2＝R 2． ∴R ＝26a ，∴V 半球＝26πa 3，V 正方体＝a 3． ∴V 半球 ∶V 正方体＝6π∶2． 19．参考答案：S 表面＝S 下底面＋S 台侧面＋S 锥侧面＝π×52＋π×(2＋5)×5＋π×2×22 ＝(60＋42)π． V ＝V 台－V 锥 ＝31π(21r ＋r 1r 2＋22r )h －31πr 2h 1 ＝3148π．20．解：(1) 参考答案：如果按方案一，仓库的底面直径变成16 m ，则仓库的体积V 1＝31Sh ＝31×π×(216)2×4＝3256π(m 3)．如果按方案二，仓库的高变成8 m ，则仓库的体积COAV 2＝31Sh ＝31×π×(212)2×8＝3288π(m 3)．(2) 参考答案：如果按方案一，仓库的底面直径变成16 m ，半径为8 m ． 棱锥的母线长为l ＝224＋8＝45， 仓库的表面积S 1＝π×8×45＝325π(m 2)． 如果按方案二，仓库的高变成8 m ．棱锥的母线长为l ＝226＋8＝10，仓库的表面积S 2＝π×6×10＝60π(m 2)．(3) 参考答案：∵V 2＞V 1，S 2＜S 1，∴方案二比方案一更加经济些．。
高中数学必修2第1章《空间几何体》高考真题及答案
高中数学必修2第1章《空间几何体》高考真题及答案一、选择题1．【05广东】 已知高为3的直棱柱ABC —A ′B ′C ′的底面是边长为1的正三角形（如图1所示），则三棱锥B ′—ABC 的体积为 A ．41B ．21C ．63D ．43图22．【05福建·理】如图2，长方体ABCD —A 1B 1C 1D 1中，AA 1=AB=2，AD=1，点E 、F 、G分别是DD 1、AB 、CC 1的中点，则异面直线A 1E 与GF 所成的角是A ．515arccosB ．4π C ．510arccos D ．2π3．【05湖北·理】如图3，在三棱柱C B A ABC '''-中，点E 、F 、H 、K 分别为C A '、B C '、B A '、C B '' 的中点，G 为ΔABC 的重心从K 、H 、G 、B '中取一点作为P ，使得该棱柱恰有2条棱与平面PEF 平行，则P 为A ．KB ．HC ．GD ．B '图3 图44．【05湖南·理】如图4，正方体ABCD －A 1B 1C 1D 1的棱长为1，O 是底面A 1B 1C 1D 1的中心，如图1 A C 1A C则O 到平面AB C 1D 1的距离为 A ．21B ．42C ．22 D ．235．【05湖北·文】木星的体积约是地球体积的30240倍，则它的表面积约是地球表面积的A ．60倍B ．6030倍C ．120倍D ．12030倍6．【05江苏】正三棱柱111C B A ABC -中，若AB=2，11AA =则点A 到平面BC A 1的距离为A ．43 B ．23 C ．433 D ．3 7．【05江西·理】矩形ABCD 中，AB=4，BC=3，沿AC 将矩形ABCD 折成一个直二面角B－AC －D ，则四面体ABCD 的外接球的体积为A ．π12125 B ．π9125 C ．π6125 D ．π3125 9．【05全国Ⅰ·理】一个与球心距离为1的平面截球所得的圆面面积为π，则球的表面积为A ．π28B ．π8C ．π24D ．π410．【05全国Ⅰ·理】如图5，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且BCF ADE ∆∆、均为正三角形，EF ∥AB ，EF=2，则该多面体的体积为 A ．32 B ．33C ．34D ．23 图511．【05全国Ⅱ·理】将半径都为１的４个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最小值为 AB ．C ．D12．【05全国Ⅱ·文】ABC ∆的顶点在平面α内，A 、C 在α的同一侧，AB 、BC 与α所成的角分别是30o 和45o ．若AB ＝３，BC＝AC ＝５，则AC 与α所成的角为 A ．60o B ．45o C ．30o D ．15o13．【05全国Ⅲ·理】设三棱柱ABC-A 1B 1C 1的体积为V ，P 、Q 分别是侧棱AA 1、CC 1上的点，且PA=QC 1，则四棱锥B-APQC 的体积为A ．16V B ．14V C ．13V D ．12V14．【05山东·理】设地球半径为R ，若甲地位于北纬045东经0120，乙地位于南纬度075 东经0120，则甲、乙两地球面距离为 AB ．6R π C ．56R πD ．23R π 15．【05重庆·理】如图6，在体积为1的三棱锥A —BCD 侧棱AB 、AC 、AD 上分别取点E 、F 、G ， 使AE : EB=AF : FC=AG : GD=2 : 1，记O 为三平面BCG 、CDE 、DBF 的交点，则三棱锥O —BCD 的体积等于 A ．91 B ．81 C ． 71 D ．41图6 图716．【05重庆·文】有一塔形几何体由若干个正方体构成，构成方式如图7所示，上层正方体下底面的四个顶点是下层正方体上底面各连接中点，已知最底层正方体的棱长为2，且该塔形的表面积（含最底层正方体的底面面积）超过39，则该塔形中正方体的个数至少是 A ．4 B ．5 C ．6 D ．7二、填空题1．【05辽宁】如图8，正方体的棱长为1，C 、D 分别是两条棱的中点，A 、B 、M 是顶点，那么点M 到截面ABCD 的距离是 .图8 图9M1A2．【05江西·理】如图9，在直三棱柱ABC —A 1B 1C 1中，AB=BC=2，BB 1=2，ο90=∠ABC ，E 、F 分别为AA 1、C 1B 1的中点，沿棱柱的表面从E 到F 两点的最短路径的长度为 .3．【05北京春考·理】如图10，正方体1111D C B A ABCD -的棱长为a ，将该正方体沿对角面D D BB 11切成两块，再将这两块拼接成一个不是正方体的四棱柱，那么所得四棱柱的全面积为_________．4．【05江西·理】如图11，在三棱锥P —ABC 中，PA=PB=PC=BC ，且2π=∠BAC ，则PA与底面ABC 所成角为 .5． 【05上海·理】 如图12，有两个相同的直三棱柱，高为2a，底面三角形的三边长分别为3a 、4a 、5a (0)a >。
数学必修二经典试题
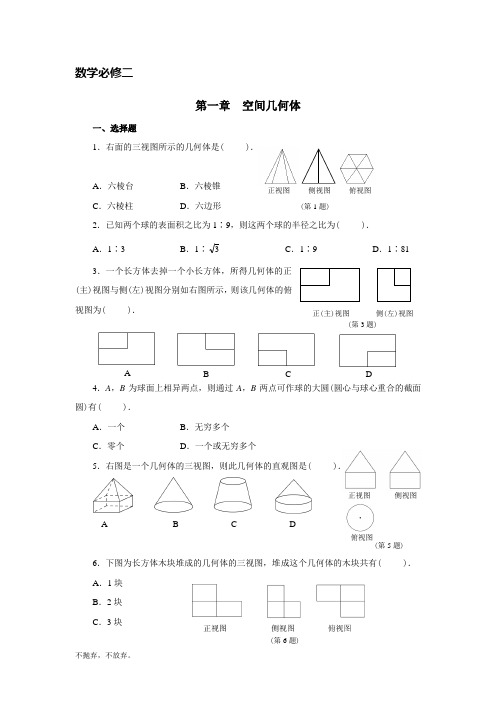
数学必修二第一章 空间几何体一、选择题1．右面的三视图所示的几何体是( )．A ．六棱台B ．六棱锥C ．六棱柱D ．六边形 (第1题)2．已知两个球的表面积之比为1∶9，则这两个球的半径之比为( )． A ．1∶3B ．1∶3C ．1∶9D ．1∶813．一个长方体去掉一个小长方体，所得几何体的正(主)视图与侧(左)视图分别如右图所示，则该几何体的俯视图为( )．4．A ，B 为球面上相异两点，则通过A ，B 两点可作球的大圆(圆心与球心重合的截面圆)有( )．A ．一个B ．无穷多个C ．零个D ．一个或无穷多个5．右图是一个几何体的三视图，则此几何体的直观图是( )． )．A B C D6．下图为长方体木块堆成的几何体的三视图，堆成这个几何体的木块共有( )． A ．1块 B ．2块 C ．3块正(主)视图侧(左)视图ABCD(第3题)正视图侧视图俯视图(第5题)正视图俯视图侧视图(第6题)D．4块7．关于斜二测画法画直观图说法不正确的是()．A．在实物图中取坐标系不同，所得的直观图有可能不同B．平行于坐标轴的线段在直观图中仍然平行于坐标轴C．平行于坐标轴的线段长度在直观图中仍然保持不变D．斜二测坐标系取的角可能是135°8．如图，下列几何体各自的三视图中，有且仅有两个视图相同的是()．①正方体②圆锥③三棱台④正四棱锥(第8题)A．①②B．①③C．①④D．②④9．一正方体的各顶点都在同一球面上，用过球心的平面去截这个组合体，截面图不能是()．A B C D10．如果一个三角形的平行投影仍然是一个三角形，则下列结论正确的是()．A．原三角形的内心的平行投影还是投影三角形的内心B．原三角形的重心的平行投影还是投影三角形的重心C．原三角形的垂心的平行投影还是投影三角形的垂心D．原三角形的外心的平行投影还是投影三角形的外心二、填空题11．一圆球形气球，体积是8 cm3，再打入一些空气后，气球仍然保持为球形，体积是27 cm3．则气球半径增加的百分率为．12．底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的体对角线的长分别是9和15，则这个棱柱的侧面积是．13．右图是一多面体的展开图，每个面内都给了字母，请根据要求回答问题：①如果A 是多面体的下底面，那么上面的面是 ； ②如果面F 在前面，从左边看是面B ，那么上面的面是 ．14．一个几何体的三视图如下图所示，则此几何体的体积是 ．三、解答题15．圆柱内有一个四棱柱，四棱柱的底面是圆柱底面的内接正方形．已知圆柱表面积为6 ，且底面圆直径与母线长相等，求四棱柱的体积．16．下图是一个几何体的三视图(单位：cm ) (1)画出这个几何体的直观图(不要求写画法)； (2)求这个几何体的表面积及体积.(第14题)4俯视图正视图侧视图4 43俯视图A BC B ＇A ＇ C ＇1 1 正视图B ＇B A ＇A 3 侧视图ABC1 (第16题)(第13题)17．如图，在四边形ABCD 中，∠DAB ＝90°，∠ADC ＝135°，AB ＝5，CD ＝22，AD ＝2，求四边形ABCD 绕直线AD 旋转一周所成几何体的表面积及体积．18．已知正方体、球、底面直径与母线相等的圆柱，它们的表面积相等，试比较它们的体积V 正方体，V 球，V 圆柱的大小．19．如图，一个圆锥形容器的高为a ，内装有一定量的水．如果将容器倒置，这时水所形成的圆锥的高恰为2a，求原来水面的高度．20．如图，四棱柱的底面是菱形，各侧面都是长方形．两个对角面也是长方形，面积分别为Q 1，Q 2．求四棱柱的侧面积．第二章 点、直线、平面之间的位置关系一、选择题1．垂直于同一条直线的两条直线一定( )． A ．平行B ．相交C ．异面D ．以上都有可能2．正四棱柱1111D C B A ABCD 中，AB AA 2＝1，则异面直线11AD B A 与所成角的余弦值为( )．(第20题)(第19题)(第17题)A ．51 B ．52 C ．53 D ．54 3．经过平面外两点与这个平面平行的平面( )． A ．可能没有B ．至少有一个C ．只有一个D ．有无数个4．点E ，F ，G ，H 分别为空间四边形ABCD 中AB ，BC ，CD ，AD 的中点，若AC ＝BD ，且AC 与BD 所成角的大小为90°，则四边形EFGH 是（ ）．A ．菱形B ．梯形C ．正方形D ．空间四边形5．已知 m ，n 为异面直线，m ⊂平面 ，n ⊂平面 β，∩ ＝l ，则( )． A ．l 与m ，n 都相交 B ．l 与m ，n 中至少一条相交C ．l 与m ，n 都不相交D ．l 只与m ，n 中一条相交6．在长方体ABCD -A 1B 1C 1D 1中，AB ＝AD ＝23，CC 1＝2，则二面角C 1-BD -C 的大小为( )．A ．30°B ．45°C ．60°D ．90°7．如果平面外有两点A ，B ，它们到平面 的距离都是a ，则直线AB 和平面的位置关系一定是( )．A ．平行B ．相交C ．平行或相交D ．AB ⊂8．设m ，n 是两条不同的直线，，是两个不同的平面．下列命题中正确的是( )．A ．⊥，m ⊥，n ∥⇒m ⊥nB ．∥，m ⊥，n ∥⇒m ⊥nC ．m ⊥，n ⊂，m ⊥n ⇒⊥D ．⊥，∩＝m ，n ⊥m ⇒n⊥9．平面∥平面，AB ，CD 是夹在 和 之间的两条线段，E ，F 分别为AB ，CD 的中点，则EF 与 的关系是( )．A ．平行B ．相交C ．垂直D ．不能确定10．平面 ⊥平面 ，A ∈α，B ∈β，AB 与两平面 ，β所成的角分别为4π和6π，过A ，B 分别作两平面交线的垂线，垂足为A ′，B′，则AB ∶A ′B ′ 等于( )．A ．2∶1B ．3∶1C ．3∶2D ．4∶3二、填空题11．下图是无盖正方体纸盒的展开图，在原正方体中直线AB ，CD 所成角的大小为 ．12．正三棱柱ABC -A 1B 1C 1的各棱长均为2，E ，F 分别是AB ，A 1C 1的中点，则EF 的长是 ．13．如图，AC 是平面 的斜线，且AO ＝a ，AO 与 成60º角，OC ，AA ′⊥于A ′，∠A ′OC ＝45º，则点A 到直线OC 的距离是 ．(第13题)14．已知正四棱锥的底面边长为2，侧棱长为5，则侧面与底面所成二面角的大小为 ．15．已知a ，b 为直线，为平面，a ∥，b ∥，对于a ，b 的位置关系有下面五个(第12题)AB CA 1B 1C 1EFDCAB(第11题)结论：①平行；②垂直不相交；③垂直相交；④相交；⑤不垂直且不相交． 其中可能成立的有 个．三、解答题16．正方体AC 1的棱长为a ． (1)求证：BD ⊥平面ACC 1A 1；(2)设P 为D 1D 中点，求点P 到平面ACC 1A 1的距离．17．如图，ABCD 是正方形，O 是该正方形的中心，P 是平面ABCD 外一点，PO 底面ABCD ，E 是PC 的中点．求证：(1)P A ∥平面BDE ； (2)BD ⊥平面P AC ．18．如图，在四棱锥P -ABCD 中，PD ⊥平面ABCD ，PD ＝DC ＝BC ＝1，AB ＝2，AB ∥DC ，∠BCD ＝90°．(1)求证：PC ⊥BC ；(2)求点A 到平面PBC 的距离．19．如图，棱长为1的正方体ABCD -A 1B 1C 1D 1中， (1)求证：AC ⊥平面B 1D 1DB ； (2)求证：BD 1⊥平面ACB 1； (3)求三棱锥B -ACB 1体积．20. 已知△BCD 中，∠BCD ＝90°，BC ＝CD ＝1，AB ⊥平面BCD ，∠ADB ＝60°，E ，F 分别是AC ，AD 上的动点，且AC AE ＝ADAF＝(0＜＜1)． (1)求证：不论 为何值，总有平面BEF ⊥平面ABC ；(2)当为何值时，平面BEF ⊥平面ACD ？POEC DBA(第17题)D 1C 1B 1A 1CD BA(第19题)(第18题)第三章 直线与方程一、选择题1．下列直线中与直线x －2y ＋1＝0平行的一条是( )． A ．2x －y ＋1＝0 B ．2x －4y ＋2＝0 C ．2x ＋4y ＋1＝0D ．2x －4y ＋1＝02．已知两点A (2，m )与点B (m ，1)之间的距离等于13，则实数m ＝( )． A ．－1B ．4C ．－1或4D ．－4或13．过点M (－2，a )和N (a ，4)的直线的斜率为1，则实数a 的值为( )． A ．1B ．2C ．1或4D ．1或24．如果AB ＞0，BC ＞0，那么直线Ax ―By ―C ＝0不经过的象限是( )． A ．第一象限B ．第二象限C ．第三象限D ．第四象限5．已知等边△ABC 的两个顶点A (0，0)，B (4，0)，且第三个顶点在第四象限，则BC 边所在的直线方程是( )．A ．y ＝－3xB ．y ＝－3(x －4)C ．y ＝3(x －4)D ．y ＝3(x ＋4)6．直线l ：mx －m 2y －1＝0经过点P (2，1)，则倾斜角与直线l 的倾斜角互为补角的一条直线方程是( )．A ．x ―y ―1＝0B ．2x ―y ―3＝0C ．x ＋y －3＝0D ．x ＋2y －4＝07．点P (1，2)关于x 轴和y 轴的对称的点依次是( )． A ．(2，1)，(－1，－2) B ．(－1，2)，(1，－2) C ．(1，－2)，(－1，2)D ．(－1，－2)，(2，1)8．已知两条平行直线l 1 : 3x ＋4y ＋5＝0，l 2 : 6x ＋by ＋c ＝0间的距离为3，则b ＋c ＝( )．A ．－12B ．48C ．36D ．－12或489．过点P (1，2)，且与原点距离最大的直线方程是( )． A ．x ＋2y －5＝0 B ．2x ＋y －4＝0 C ．x ＋3y －7＝0D ．3x ＋y －5＝010．a ，b 满足a ＋2b ＝1，则直线ax ＋3y ＋b ＝0必过定点( )． A ．⎪⎭⎫⎝⎛21 ，61 －B ．⎪⎭⎫ ⎝⎛61 － ，21C ．⎪⎭⎫⎝⎛61 ，21D ．⎪⎭⎫ ⎝⎛21 － ，61二、填空题11．已知直线AB 与直线AC 有相同的斜率，且A (1，0)，B (2，a )，C (a ，1)，则实数a 的值是____________．12．已知直线x －2y ＋2k ＝0与两坐标轴所围成的三角形的面积不大于1，则实数k 的取值范围是____________．13．已知点(a ，2)(a ＞0)到直线x －y ＋3＝0的距离为1，则a 的值为________． 14．已知直线ax ＋y ＋a ＋2＝0恒经过一个定点，则过这一定点和原点的直线方程是 ____________________．15．已知实数x ，y 满足5x ＋12y ＝60，则22 ＋ y x 的最小值等于____________． 三、解答题 16．求斜率为43，且与坐标轴所围成的三角形的周长是12的直线方程． 17．过点P (1，2)的直线l 被两平行线l 1 : 4x ＋3y ＋1＝0与l 2 : 4x ＋3y ＋6＝0截得的线段长|AB |＝2，求直线l 的方程．18．已知方程(m 2―2m ―3)x ＋(2m 2＋m －1)y ＋6－2m ＝0(m ∈R )． (1)求该方程表示一条直线的条件；(2)当m 为何实数时，方程表示的直线斜率不存在？求出这时的直线方程； (3)已知方程表示的直线l 在x 轴上的截距为－3，求实数m 的值； (4)若方程表示的直线l 的倾斜角是45°，求实数m 的值．19．△ABC 中，已知C (2，5)，角A 的平分线所在的直线方程是y ＝x ，BC 边上高线所在的直线方程是y ＝2x －1，试求顶点B 的坐标．第四章 圆与方程一、选择题1．圆C 1 : x 2＋y 2＋2x ＋8y －8＝0与圆C 2 : x 2＋y 2－4x ＋4y －2＝0的位置关系是( )． A ．相交B ．外切C ．内切D ．相离2．两圆x 2＋y 2－4x ＋2y ＋1＝0与x 2＋y 2＋4x －4y －1＝0的公共切线有( )． A ．1条B ．2条C ．3条D ．4条3．若圆C 与圆(x ＋2)2＋(y －1)2＝1关于原点对称，则圆C 的方程是( )． A ．(x －2)2＋(y ＋1)2＝1 B ．(x －2)2＋(y －1)2＝1 C ．(x －1)2＋(y ＋2)2＝1D ．(x ＋1)2＋(y －2)2＝14．与直线l : y ＝2x ＋3平行，且与圆x 2＋y 2－2x －4y ＋4＝0相切的直线方程是( )． A ．x －y ±5＝0 B ．2x －y ＋5＝0 C ．2x －y －5＝0D ．2x －y ±5＝05．直线x －y ＋4＝0被圆x 2＋y 2＋4x －4y ＋6＝0截得的弦长等于( )． A ．2B ．2C ．22D ．426．一圆过圆x 2＋y 2－2x ＝0与直线x ＋2y －3＝0的交点，且圆心在y 轴上，则这个圆的方程是( )．A ．x 2＋y 2＋4y －6＝0B ．x 2＋y 2＋4x －6＝0C ．x 2＋y 2－2y ＝0D ．x 2＋y 2＋4y ＋6＝07．圆x 2＋y 2－4x －4y －10＝0上的点到直线x ＋y －14＝0的最大距离与最小距离的差是( )．A ．30B ．18C ．62D ．528．两圆(x －a )2＋(y －b )2＝r 2和(x －b )2＋(y －a )2＝r 2相切，则( )． A ．(a －b )2＝r 2 B ．(a －b )2＝2r 2 C ．(a ＋b )2＝r 2D ．(a ＋b )2＝2r 29．若直线3x －y ＋c ＝0，向右平移1个单位长度再向下平移1个单位，平移后与圆x 2＋y 2＝10相切，则c 的值为( )．A ．14或－6B ．12或－8C ．8或－12D ．6或－1410．设A (3，3，1)，B (1，0，5)，C (0，1，0)，则AB 的中点M 到点C 的距离|CM | ＝( )．A ．453B ．253 C ．253 D ．213二、填空题11．若直线3x －4y ＋12＝0与两坐标轴的交点为A ，B ，则以线段AB 为直径的圆的一般方程为____________________．12．已知直线x ＝a 与圆(x －1)2＋y 2＝1相切，则a 的值是_________． 13．直线x ＝0被圆x 2＋y 2―6x ―2y ―15＝0所截得的弦长为_________． 14．若A (4，－7，1)，B (6，2，z )，|AB |＝11，则z ＝_______________．15．已知P 是直线3x ＋4y ＋8＝0上的动点，P A ，PB 是圆(x －1)2＋(y －1)2＝1的两条切线，A ，B 是切点，C 是圆心，则四边形P ACB 面积的最小值为 ．三、解答题16．求下列各圆的标准方程：(1)圆心在直线y ＝0上，且圆过两点A (1，4)，B (3，2)；(2)圆心在直线2x ＋y ＝0上，且圆与直线x ＋y －1＝0切于点M (2，－1)．17．棱长为1的正方体ABCD －A 1B 1C 1D 1中，E 是AB 的中点，F 是BB 1的中点，G 是不抛弃，不放弃。
(完整版)高一数学必修2第一章空间几何体测试题(答案)
则四边形 EFGH 是
；
②若 AC BD ， 则四边形 EFGH 是
．
三、解答题： 解答应写出文字说明、证明过程或演算步骤 (共 76 分 )．
15．（ 12 分）将下列几何体按结构分类填空
①集装箱；②油罐；③排球；④羽毛球；⑤橄榄球；⑥氢原子；⑦魔方；
⑧金字塔；⑨三棱镜；⑩滤纸卷成的漏斗；○ 11 量筒；○12 量杯；○13 十字架．
（ 1）具有棱柱结构特征的有
；（ 2）具有棱锥结构特征的有
；
（ 3）具有圆柱结构特征的有
；（ 4）具有圆锥结构特征的有
；
（ 5）具有棱台结构特征的有
；（ 6）具有圆台结构特征的有
；
（ 7）具有球结构特征的有
；（ 8）是简单集合体的有
；
（ 9）其它的有
．
16．（ 12 分）已知： a ,b ,a b A, P b, PQ // a.求证： PQ .．
C．③④
3．棱台上下底面面积分别为 16 和 81,有一平行于底面的截面面积为
（） D ． ①②③④
36,则截面戴的两棱台高
的比为
（）
A ．1∶ 1
B． 1∶ 1
C． 2∶ 3
D ．3∶4
4．若一个平行六面体的四个侧面都是正方形 ,则这个平行六面体是
（）
A ．正方体
B．正四棱锥
C．长方体
D ．直平行六面体
2la
Q1 2 Q2 2
S侧 4al 2 Q12 Q2 2
19．解：设 A1B1C1D1 是棱台 ABCD －A2B2C2D 2 的中截面，延长各侧棱交于
P 点.
a
∵ BC=a ，B2C2=b ∴ B1C1=
人教版高一数学必修二第一章空间几何体章末检测题 附答案解析
必修二 第一章 空间几何体章末检测题一、选择题1．右面的三视图所示的几何体是( )．A ．六棱台B ．六棱锥C ．六棱柱D ．六边形 (第1题)2．已知两个球的表面积之比为1∶9，则这两个球的半径之比为( )． A ．1∶3B ．1∶3C ．1∶9D ．1∶813．一个长方体去掉一个小长方体，所得几何体的正(主)视图与侧(左)视图分别如右图所示，则该几何体的俯视图为( )．4．A ，B 为球面上相异两点，则通过A ，B 两点可作球的大圆(圆心与球心重合的截面圆)有( )．A ．一个B ．无穷多个C ．零个D ．一个或无穷多个5．右图是一个几何体的三视图，则此几何体的直观图是( )． )．A B C D6．下图为长方体木块堆成的几何体的三视图，堆成这个几何体的木块共有( )． A ．1块 B ．2块 C ．3块 D ．4块正(主)视图侧(左)视图ABCD(第3题)正视图侧视图俯视图(第5题)正视图俯视图侧视图(第6题)7．关于斜二测画法画直观图说法不正确的是()．A．在实物图中取坐标系不同，所得的直观图有可能不同B．平行于坐标轴的线段在直观图中仍然平行于坐标轴C．平行于坐标轴的线段长度在直观图中仍然保持不变D．斜二测坐标系取的角可能是135°8．如图，下列几何体各自的三视图中，有且仅有两个视图相同的是()．①正方体②圆锥③三棱台④正四棱锥(第8题)A．①②B．①③C．①④D．②④9．一正方体的各顶点都在同一球面上，用过球心的平面去截这个组合体，截面图不能是()．A B C D10．如果一个三角形的平行投影仍然是一个三角形，则下列结论正确的是()．A．原三角形的内心的平行投影还是投影三角形的内心B．原三角形的重心的平行投影还是投影三角形的重心C．原三角形的垂心的平行投影还是投影三角形的垂心D．原三角形的外心的平行投影还是投影三角形的外心二、填空题11．一圆球形气球，体积是8 cm3，再打入一些空气后，气球仍然保持为球形，体积是27 cm3．则气球半径增加的百分率为．12．底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的体对角线的长分别是9和15，则这个棱柱的侧面积是．13．右图是一多面体的展开图，每个面内都给了字母，请根据要求回答问题：①如果A 是多面体的下底面，那么上面的面是 ；②如果面F 在前面，从左边看是面B ，那么上面的面是 ． 14．一个几何体的三视图如下图所示，则此几何体的体积是 ．三、解答题15．圆柱内有一个四棱柱，四棱柱的底面是圆柱底面的内接正方形．已知圆柱表面积为6 ，且底面圆直径与母线长相等，求四棱柱的体积．16．下图是一个几何体的三视图(单位：cm ) (1)画出这个几何体的直观图(不要求写画 法)；(2)求这个几何体的表面积及体积.题)侧视图俯视BBA C 正视BA侧视(第16题)17．如图，在四边形ABCD 中，∠DAB ＝90°，∠ADC ＝135°，AB ＝5，CD ＝22，AD ＝2，求四边形ABCD 绕直线AD 旋转一周所成几何体的表面积及体积．18．已知正方体、球、底面直径与母线相等的圆柱，它们的表面积相等，试比较它们的体积V 正方体，V 球，V 圆柱的大小．19．如图，一个圆锥形容器的高为a ，内装有一定量的水．如果将容器倒置，这时水所形成的圆锥的高恰为2a，求原来水面的高度．20．如图，四棱柱的底面是菱形，各侧面都是长方形．两个对角面也是长方形，面积分别为Q 1，Q 2．求四棱柱的侧面积．(第20题)(第19题)(第17题)参考答案一、选择题 1．B解析：由正视图和侧视图可知几何体为锥体，由俯视图可知几何体为六棱锥． 2．A解析：由设两个球的半径分别为r ，R ，则 4 r 2∶4πR 2＝1∶9. ∴ r 2∶R 2＝1∶9， 即r ∶R ＝1∶3．3．C解析：在根据得到三视图的投影关系，∵正视图中小长方形位于左侧，∴小长方形也位于俯视图的左侧；∵小长方形位于侧视图的右侧，∴小长方形一定位于俯视图的下侧， ∴ 图C 正确．4．D解析：A ，B 不在同一直径的两端点时，过A ，B 两点的大圆只有一个；A ，B 在同一直径的端点时大圆有无数个．5．D解析：由几何体的正视图和侧视图可知，几何体上部分为圆锥体，由三个视图可知几何体下部分为圆柱体，∴ 几何体是由圆锥和圆柱组成的组合体．6．D解析：由三视图可知几何体为右图所示，显然组成几何体的长方体木块有4块．7．C解析：由平行于x 轴和z 轴的线段长度在直观图中仍然保持不变，平行于y 轴的线段长度在直观图中是原来的一半，∴ C 不对．8．D解析：①的三个视图均相同；②的正视图和侧视图相同；③的三个视图均不相同；④的正视图和侧视图相同．∴有且仅有两个视图相同的是②④．9．A(第6题)解析：B 是经过正方体对角面的截面；C 是经过球心且平行于正方体侧面的截面；D 是经过一对平行的侧面的中心，但不是对角面的截面．10．B解析：在平行投影中线段中点在投影后仍为中点，故选B ． 二、填空题 11．50%．解析：设最初球的半径为r ，则8＝34πr 3；打入空气后的半径为R ，则27＝34πR 3． ∴ R 3∶r 3＝27∶8．∴ R ∶r ＝3∶2．∴气球半径增加的百分率为50%． 12．160．解析：依条件得菱形底面对角线的长分别是22515-＝200和2259-＝56． ∴菱形的边长为4256256220022=⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛＝ 8． ∴棱柱的侧面积是5×4×8＝160． 13．F ，C ．解析：将多面体看成长方体， A ，F 为相对侧面．如果A 是多面体的下底面，那么上面的面是F ；如果面F 在前面，从左边看是面B ，则右面看必是D ，于是根据展开图，上面的面应该是C ．14．80．解析：由三视图可知，几何体是由棱长为4的正方体和底面边长为4，高为3的四棱锥组成，因此它的体积是V ＝43＋31×42×3＝64＋16＝80．三、解答题15．参考答案：设圆柱底面圆半径为r ，则母线长为2r ． ∵圆柱表面积为6π，∴ 6π＝2πr 2＋4πr 2． ∴ r ＝1．∵ 四棱柱的底面是圆柱底面的内接正方形， ∴ 正方形边长为2． ∴ 四棱柱的体积V ＝(2)2×2＝2×2＝4． 16．(1)略．(2)解：这个几何体是三棱柱．由于底面△ABC 的BC 边上的高为1，BC ＝2，∴ AB ＝2． 故所求全面积S ＝2S △ABC ＋S BB ′C ′C ＋2S ABB ′A ′＝8＋62(cm 2)． 几何体的体积V ＝S △ABC ·BB ′＝21×2×1×3＝3(cm 3)． 17．解：S 表面＝S 下底面＋S 台侧面＋S 锥侧面＝π×52＋π×(2＋5)×5＋π×2×22＝(60＋42)π．V ＝V 台－V 锥＝31π(21r ＋r 1r 2＋22r )h －31πr 2h 1＝3148π．18．解：设正方体的边长为a ，球的半径为r ，圆柱的底面直径为2R ， 则6a 2＝4πr 2＝6πR 2＝S ．∴ a 2＝6S ，r 2＝π4S，R 2＝π6S ． ∴(V 正方体)2＝(a 3)2＝(a 2)3＝36⎪⎭⎫⎝⎛S ＝2163S ，(V 球)2＝23π34⎪⎭⎫⎝⎛r ＝916π2(r 2)3＝916π23π4⎪⎭⎫ ⎝⎛S ≈1083S ，(V 圆柱)2＝(πR 2×2R )2＝4π2(R 2)3＝4π23π6⎪⎭⎫⎝⎛S ≈1623S ．∴V 正方体＜V 圆柱＜V 球．19．解：设水形成的“圆台”的上下底面半径分别为r ，R ，高为h ，则R r ＝aha -． 则依条件得3π·h ·(r 2＋rR ＋R 2)＝3π·2a ·22⎪⎭⎫⎝⎛R ，化简得(h －a )3＝－87a 3．解得h ＝a －873a ．即h ＝⎪⎪⎭⎫ ⎝⎛-271a ． 20．解：设底面边长为a ，侧棱长为l ，底面的两对角线长分别为c ，d ．则⎪⎪⎩⎪⎪⎨⎧③ ＝ 21 ＋ 21② ＝ ① ＝ 22221a d c Q dl Q cl ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛33(第20题)由 ① 得c ＝l Q 1，由 ② 得d ＝l Q 2，代入 ③ 得212⎪⎭⎫ ⎝⎛l Q ＋222⎪⎭⎫⎝⎛l Q ＝a 2．∴21Q ＋22Q ＝4l 2a 2， ∴2la ＝2221＋Q Q ． 故S 侧＝4al ＝22221＋Q Q ．。
高中数学必修2 第一章 空间几何体(A卷)
高中数学必修2 第一章空间几何体（A卷）试卷一、选择题（共19题；共71分）1.下列说法正确的是()A.用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台B.棱柱的底面一定是平行四边形C.棱锥的底面一定是三角形D.用任意一个平面去截球体得到的截面一定是一个圆面【答案】D【考点】柱体结构特征,台体结构特征【解析】A不正确，因为根据棱台的定义，要求棱锥底面和截面平行；B不正确，棱柱的底面不一定是平行四边形，可以是任意多边形；C不正确，棱锥的底面不一定是三角形，三棱锥的底面是三角形，其他不是；D正确，故选D.2.一个圆锥的母线长为20 cm，母线与轴的夹角为30°，则圆锥的高为()A.B.C.20cmD.10 cm【答案】A【考点】锥体结构特征【解析】如图所示，在Rt△ABO中，AB＝20 cm，∠A＝30°，所以.3.一个正方体内有一个内切球，作正方体的对角面，所得截面图形是下图中的()A.B.C.D.【答案】B【考点】柱体结构特征,球体结构特征,组合体结构特征【解析】由组合体的结构特征知，球与正方体各面相切，与各棱相离，故选B.4.下面图形中是正方体展开图的是()A.B.C.D.【答案】A【考点】柱体结构特征【解析】由正方体表面展开图性质知A是正方体的展开图；B折叠后第一行两个面无法折起来，而且下边没有面，故不能折成正方体；C缺少一个正方形；D折叠后有一个面重合，另外还少一个面，故不能折成正方体．故选A.5.如图，在正方体ABCD－A1B1C1D1中，M，N分别是BB1，BC的中点，则图中阴影部分在平面ADD1A1上的投影为()A.B.C.D.【答案】A【考点】柱体结构特征,投影【解析】点D在平面ADD1A1上的投影为点D，点M在平面ADD1A1上的投影为AA1的中点，点N在平面ADD1A1上的投影为DA的中点，连接三点可知A正确.6.下面的三视图对应的物体是()A.B.C.D.【答案】D【考点】组合体结构特征,三视图【解析】从俯视图可以看出直观图的下面部分为三个长方体，且三个长方体的宽度相同．只有D满足这两点，故选D.7.如图，的斜二测直观图为等腰Rt△A′B′C′，其中A′B′＝2，则的面积为()A.2B.4C.D.【答案】D【考点】空间几何体的三视图与直观图【解析】∵Rt是一平面图形的直观图，直角边长为A′B′＝2，∴直角三角形的面积是，∵平面图形与直观图的面积的比为，∴原平面图形的面积是.故选D.8.如图，B′C′∥x′轴，A′C′∥y′轴，则下面直观图所表示的平面图形是()A.正三角形B.锐角三角形C.钝角三角形D.直角三角形【答案】D【考点】空间几何体的三视图与直观图【解析】因为B′C′∥x′轴，A′C′∥y′轴，所以直观图中BC∥x轴，AC∥y轴，所以三角形是直角三角形．故选D.9.《算数书》竹简于上世纪八十年代在湖北省张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“禾盖”的术：置如其周，令相乘也，又以高乘之，三十六成一.该术相当于给出了由圆锥的底面周长L与高h，计算其体积V的近似公式.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么，近似公式相当于将圆锥体积公式中的圆周率π近似取为()A.B.C.D.【答案】D【考点】空间几何体的表面积与体积【解析】设圆锥的底面半径为r，则圆锥的底面周长L＝2πr，∴，∴.令，提，故选D.10.正三棱锥的一个侧面面积与底面面积之比为2：3，则此三棱锥的高与斜高之比为()A.B.C.1∶2D.【答案】A【考点】几何体的表面积【解析】如图：SO⊥平面ABC，SE⊥AB，∵△ABC为正三角形，∴CE＝3OE，侧面面积S△SAB＝×AB×SE，底面面积S△ABC＝×AB×CE＝×AB×3OE，∵一个侧面面积与底面面积之比为2：3，∴∴SE＝2OE，∴在直角三角形SOE中，∠ESO＝30°，∴，故选A.11.一个正四棱柱的各个顶点都在一个半径为2 cm的球面上，如果正四棱柱的底面边长为2 cm，那么该棱柱的表面积为()A.(2＋4) cm2B.(4＋8) cm2C.(8＋16) cm2D.(16＋32) cm2【答案】C【考点】几何体的表面积,组合体的表面积和体积【解析】∵一个正四棱柱的各个顶点都在一个半径为2 cm的球面上，正四棱柱的底面边长为2cm，球的直径为正四棱柱的体对角线，∴正四棱柱的体对角线为4，正四棱柱的底面对角线长为，∴正四棱柱的高为，∴该棱柱的表面积为，故选C.12.已知在半径为2的球面上有A、B、C、D四点，若AB＝CD＝2，则四面体ABCD的体积的最大值为() A.B.C.2D.【答案】B【考点】几何体的体积,组合体的表面积和体积【解析】如图所示，OA、OB、OC、OD四条线段把四面体ABCD分成四个三棱锥，且三棱锥B－ODC与A－ODC同底，三棱锥D －AOB与C－AOB同底．在三棱锥B－ODC和A－ODC中，底面积为，高分别为B到平面ODC的距离与A到平面ODC的距离，只有AB⊥平面ODC时，两距离之和才能取得最大值2，所以其体积和最大值为.同理可得三棱锥D－AOB与C－AOB的体积和的最大值为.所以四面体ABCD的体积的最大值为.13.如果轴截面为正方形的圆柱的侧面积是4π，那么圆柱的体积等于()A.πB.2πC.4πD.8π【答案】B【考点】几何体的表面积,几何体的体积【解析】设圆柱母线长为l，底面半径为r，由题意得解得∴V＝πr2l＝2π.圆柱14.如图是一个三棱锥的三视图，那么这个三棱锥的四个面中直角三角形的个数有()A.1个B.2个C.3个D.4个【答案】D【考点】柱体结构特征,三视图【解析】由题意可知，几何体是三棱锥，其放置在长方体中形状如图所示，利用长方体模型可知，此三棱锥的四个面中，全部是直角三角形．故选D.15.用一个平行于圆锥底面的平面截这个圆锥，截得的圆台上、下底面的面积之比为1∶16，截去的圆锥的母线长是3 cm，则圆台的母线长是()A.9 cmB.10 cmC.12 cmD.15 cm【答案】A【考点】锥体结构特征,台体结构特征【解析】∵截得的圆台上、下底面的面积之比为1∶16，∴圆台的上、下底面半径之比是1∶4，如图，设圆台的母线长为y，小圆锥底面与被截的圆锥底面半径分别是x，4x，根据相似三角形的性质得，解此方程得y＝9，所以圆台的母线长为9 cm.故选A.16.球与圆台的上、下底面及侧面都相切，且球面面积与圆台的侧面积之比为3∶4，则球的体积与圆台的体积之比为()A.6∶13B.5∶14C.3∶4D.7∶15【答案】A【考点】空间几何体的表面积与体积,几何体的表面积,几何体的体积,组合体的表面积和体积【解析】如图所示，作圆台的轴截面等腰梯形ABCD，球的轴截面圆O内切于梯形ABCD.设球的半径为R，圆台的上、下底面半径分别为r1、r2，由平面几何知识知，圆台的高为2R，母线长为r1＋r2.∵∠AOB＝90°，OE⊥AB(E为切点)，∴R2＝OE2＝AE·BE＝r1·r2.由已知S球∶S圆台侧＝4πR2∶π(r1＋r2)2＝3∶4.(r1＋r2)2＝R2.. 17.如图是一梯形OABC的直观图，其直观图面积为S，求梯形OABC的面积( )A.B.C.D.【考点】空间几何体的三视图与直观图【解析】设O′C′＝h，则原梯形是一个直角梯形且高为2h.过C′作C′D′⊥O′A′于D′，则.由题意知即.又原直角梯形面积为所以梯形OABC的面积为.18.如图是在底面半径为2，母线长为4的圆锥中内接一个高为的圆柱，求圆柱的表面积（）A.B.C.D.【考点】柱体结构特征,锥体结构特征,几何体的表面积【解析】如图所示，设圆锥的底面半径为R，圆柱的底面半径为r，表面积为S，则R＝OC＝2，AC＝4，.易知△AEB∽△AOC，∴，即，∴r＝1，S底＝2πr2＝2π，S侧＝2πr·h＝π.∴S＝S＋S侧＝2π＋π＝(2＋)π.底19.如图在三棱柱ABC－A1B1C1中，各侧棱都垂直于底面且底面为等腰直角三角形，∠ACB＝90°，AC＝BC＝4，AA1＝4，E，F分别在AC，BC上，且CE＝3，CF＝2，几何体EFC－A1B1C1的体积是（）A.B.C.20D.【答案】C【考点】几何体的体积,组合体的表面积和体积【解析】所求几何体EFC－A1B1C1的体积，转化为两个棱锥A1－CEF和的体积之和，∵三棱柱ABC－A1B1C1中，各侧棱都垂直于底面且底面为等腰直角三角形，∠ACB＝90°，AC＝BC＝4，AA1＝4，E，F分别在AC，BC上，且CE＝3，CF＝2，∴.∴几何体EFC－A1B1C1的体积为4+16=20.二、解答题（共3题；共29分）20.如图，正方体ABCD－A′B′C′D′的棱长为a，连接A′C′，A′D，A′B，BD，BC′，C′D，得到一个三棱锥A′－BC′D，求：(1).三棱锥A′－BC′D的表面积与正方体表面积的比值（）A.B.C.D.【答案】A【考点】几何体的表面积【解析】∵ABCD－A′B′C′D′是正方体，∴A′B＝A′C′＝A′D＝BC′＝BD＝C′D＝∴三棱锥A′－BC′D的表面积为，而正方体的表面积为6a2，故三棱锥A′－BC′D的表面积与正方体表面积的比值为. (2).三棱锥A′－BC′D的体积( )A.B.C.D.【答案】A【考点】几何体的体积【解析】三棱锥A′－ABD，C′－BCD，D－A′D′C′，B－A′B′C′是完全一样的.故.21.已知直角三角形ABC，其中∠ABC＝60°，∠C＝90°，AB＝2.(1).△ABC绕斜边AB旋转一周所形成的几何体的表面积( )A.B.C.D.【答案】B【考点】锥体结构特征,几何体的表面积【解析】如图以斜边AB为轴旋转一周，得旋转体是以AB边的高CO为底面半径的两个圆锥组成的组合体．∵AB＝2，CB＝1，∠B＝60°，∴CB＝sin 30°·AB＝1，CA＝cos 30°·AB＝，，故此旋转体的表面积S＝π×OC×AC＋π×OC×BC.(2).△ABC绕斜边AB旋转一周所形成的几何体的体积( )A.B.C.D.【答案】C【考点】几何体的体积【解析】故此旋转体的体积.22.如图，一个圆锥的底面半径为1，高为3，在圆锥中有一个半径为x的内接圆柱.(1).试用x表示圆柱的高( )A.h＝3－xB.h＝2－3xC.h＝3－2xD.h＝3－3x【答案】D【考点】柱体结构特征,锥体结构特征【解析】设所求的圆柱的底面半径为x，它的轴截面如图，BO＝1，PO＝3，圆柱的高为h，由图，得，即h＝3－3x.(2).圆柱的最大侧面积是（）A.B.C.D.2【答案】C【考点】柱体结构特征【解析】∵S圆柱侧＝2πhx＝2π(3－3x)x＝6π(x－x2)，当时，圆柱的侧面积取得最大值为.。
高中数学必修二第一章测试题及答案
第一章 空间几何体一、选择题1．有一个几何体的三视图如下图所示，这个几何体可能是一个( )．主视图 左视图 俯视图 (第1题)A ．棱台B ．棱锥C ．棱柱D ．正八面体2．如果一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是( )．A ．2＋2B ．221＋ C ．22＋2 D ．2＋13．棱长都是1的三棱锥的表面积为( )． A ．3B ．23C ．33D ．434．长方体的一个顶点上三条棱长分别是3，4，5，且它的8个顶点都在同一球面上，则这个球的表面积是( )． A ．25πB ．50πC ．125πD ．都不对5．正方体的棱长和外接球的半径之比为( )． A ．3∶1B ．3∶2C ．2∶3D ．3∶36．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是( )． A ．130B ．140C ．150D ．1607．如图是一个物体的三视图，则此物体的直观图是( )．(第7题)8．已知a 、b 、c 是直线，β是平面，给出下列命题： ①若c a c b b a //,,则⊥⊥；②若c a c b b a ⊥⊥则,,//；③若b a b a //,,//则ββ⊂；④若a 与b 异面，且ββ与则b a ,//相交；⑤若a 与b 异面，则至多有一条直线与a ，b 都垂直. 其中真命题的个数是 A ．1 B ．2 C ．3 D ．4二、填空题9．若三个球的表面积之比是1∶2∶3，则它们的体积之比是_____________．10．正方体ABCD －A 1B 1C 1D 1 中，O 是上底面ABCD 的中心，若正方体的棱长为a ，则三棱锥O －AB 1D 1的体积为_____________． 11．已知一个长方体共一顶点的三个面的面积分别是2、3、6，则这个长方体的对角线长是___________，它的体积为___________．三、解答题12 ．已知半球内有一个内接正方体，求这个半球的体积与正方体的体积之比．13．如图，在四边形ABCD 中，∠DAB ＝90°，∠ADC ＝135°，AB ＝5，CD ＝22，AD ＝2，求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积．(第13题)15.S 是正三角形ABC 所在平面外的一点，如图SA ＝SB ＝SC ， 且2ASB BSC CSA π∠=∠=∠=，M 、N 分别是AB 和SC 的中点．求异面直线SM 与BN 所成的角的余弦值．B M ANCS第一章 空间几何体参考答案一、选择题 1．A解析：从俯视图来看，上、下底面都是正方形，但是大小不一样，可以判断可能是棱台． 2．A解析：原图形为一直角梯形，其面积S ＝21(1＋2＋1)×2＝2＋2． 3．A解析：因为四个面是全等的正三角形，则S 表面＝4×43＝3． 4．B解析：长方体的对角线是球的直径，l ＝2225＋4＋3＝52，2R ＝52，R ＝225，S ＝4πR 2＝50π． 5．C解析：正方体的对角线是外接球的直径． 6．D解析：设底面边长是a ，底面的两条对角线分别为l 1，l 2，而21l ＝152－52，22l ＝92－52，而21l ＋22l ＝4a 2，即152－52＋92－52＝4a 2，a ＝8，S 侧面＝4×8×5＝160．7．D解析：过点E ，F 作底面的垂面，得两个体积相等的四棱锥和一个三棱柱，V ＝2×31×43×3×2＋21×3×2×23＝215．8．D解析：从三视图看底面为圆，且为组合体，所以选D. 9.A 二、填空题10．参考答案：1∶22∶33．r 1∶r 2∶r 3＝1∶2∶3，31r ∶32r ∶33r ＝13∶(2)3∶(3)3＝1∶22∶33．11．参考答案：361a ．解析：画出正方体，平面AB 1D 1与对角线A 1C 的交点是对角线的三等分点， 三棱锥O －AB 1D 1的高h ＝33a ，V ＝31Sh ＝31×43×2a 2×33a ＝61a 3．另法：三棱锥O －AB 1D 1也可以看成三棱锥A －OB 1D 1，它的高为AO ，等腰三角形OB 1D 1为底面． 12．参考答案：6，6．解析：设ab ＝2，bc ＝3，ac ＝6，则V = abc ＝6，c ＝3，a ＝2，b ＝1，l ＝1＋2＋3＝6．三、解答题 13．参考答案：如图是过正方体对角面作的截面．设半球的半径为R ，正方体的棱长为a ，则CC'＝a ，OC ＝22a ，OC'＝R ．(第14题)在Rt △C'CO 中，由勾股定理，得CC' 2＋OC 2＝OC' 2， 即 a 2＋(22a )2＝R 2． ∴R ＝26a ，∴V 半球＝26πa 3，V 正方体＝a 3． ∴V 半球 ∶V 正方体＝6π∶2． 14．参考答案：S 表面＝S 下底面＋S 台侧面＋S 锥侧面＝π×52＋π×(2＋5)×5＋π×2×22 ＝(60＋42)π．V ＝V 台－V 锥＝31π(21r ＋r 1r 2＋22r )h －31πr 2h 1 ＝3148π． 15.证明：连结CM ，设Q 为CM 的中点，连结QN 则QN∥SM∴∠QNB 是SM 与BN 所成的角或其补角 连结BQ ，设SC ＝a ，在△BQN 中 BN ＝a 25 NQ ＝21SM ＝42a BQ ＝a 414∴COS∠QNB＝5102222=⋅-+NQ BN BQ NQ BNCO A。
必修二同步练习(第一章空间几何体测试卷)
第一章 空间几何体测试卷( 时间 60分钟 总分 100分)班级_______________ 姓名______________ 分数_____________一、选择题（每小题5分，共50分）1．正方体的内切球和外接球的半径之比为A B 2 C ． D2．一个棱柱是正四棱柱的条件是A ．底面是正方形，有两个侧面是矩形B ．底面是正方形，有两个侧面垂直于底面C ．底面是菱形，且有一个顶点处的三条棱两两垂直D ．每个侧面都是全等矩形的四棱柱3．过圆锥的高的三等分点作平行于底面的截面，它们把圆锥侧面分成的三部分的面积之比为A ．1：2：3B ．1：3：5C ．1：2：4D ．1：3：94．已知正方形的直观图是有一条边长为4的平行四边形，则此正方形的面积是A ．16B ．16或64C ．64D ．都不对5．下列说法正确的是A ．圆锥的侧面展开图是一个等腰三角形B ．棱柱即是两个底面全等且其余各面都是矩形的多面体C ．任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥D ．通过圆台侧面上一点，有无数条母线6．圆锥的轴截面是等腰直角三角形，侧面积是，则圆锥的体积是A ．643π B ．1283π C ．64π D ． 7．若一棱锥的底面积是8，则这个棱锥的中截面（过棱锥高的中点且平行于底面的截面）的面积是A ．4B ．．2D 8．若一圆柱的侧面展开图是一个正方形，则这个圆柱的全面积和侧面积之比是A ．122ππ+ B ．144ππ+ C ．12ππ+ D ．142ππ+ 9．有一个几何体的三视图如右图所示，这个几何体应是一个A ．棱台B ．棱锥C ．棱柱D ．都不对10．如图，一个封闭的立方体，它的六个表面各标有A,B,C,D,E,F 这六个字母之一，现放置成如图的三种不同的位置，则字母A,B,C 对面的字母分别为A ．D ,E ,FB ．F ,D ,EC ．E, F ,D D ．E, D,F二、填空题（每小题5分，共20分）11．一个半球的全面积为Q ，一个圆柱与此半球等底等体积，则这个圆柱的全面积是 .12．半径为R 的半圆卷成一个圆锥，则它的体积为________________.13．在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体，则截去8个三棱锥后 ，剩下的几何体的体积是___________.14．如图，E 、F 分别为正方体的面11A ADD 、面11B B CC 的中心，则四边形E BFD 1在该正方体的面上的射影可能是__________.三、解答题（共44分）15．（本题15分）在底半径为2母线长为4的圆锥中内接一个高为3的圆柱，求圆柱的表面积16．（本题15分）一个几何体的三视图如右图所示：求这个几何体的表面积和体积.参考答案1-10题 DDBBC ACAAD ； 11、Q 910；12、3243R π；13、56；14、②③； 15、R=1,h=3,S=2π+2π3； 16、 表面积S=27+239;体积V=439.。
[人教版]高中数学必修2第一章_空间几何体练习试题和答案(全)
![[人教版]高中数学必修2第一章_空间几何体练习试题和答案(全)](https://img.taocdn.com/s3/m/99bdf95e6137ee06eef9184f.png)
第一章空间几何体空间几何体的结构一、选择题1、下列各组几何体中是多面体的一组是（）A 三棱柱四棱台球圆锥B 三棱柱四棱台正方体圆台C 三棱柱四棱台正方体六棱锥D 圆锥圆台球半球2、下列说法正确的是（）A 有一个面是多边形，其余各面是三角形的多面体是棱锥B 有两个面互相平行，其余各面均为梯形的多面体是棱台C 有两个面互相平行，其余各面均为平行四边形的多面体是棱柱D 棱柱的两个底面互相平行，侧面均为平行四边形3、下面多面体是五面体的是（）A 三棱锥B 三棱柱C 四棱柱D 五棱锥4、下列说法错误的是（）A 一个三棱锥可以由一个三棱锥和一个四棱锥拼合而成B 一个圆台可以由两个圆台拼合而成C 一个圆锥可以由两个圆锥拼合而成D 一个四棱台可以由两个四棱台拼合而成5、下面多面体中有12条棱的是（）A 四棱柱B 四棱锥C 五棱锥D 五棱柱6、在三棱锥的四个面中，直角三角形最多可有几个（）A 1 个B 2 个C 3个D 4个二、填空题7、一个棱柱至少有————————个面，面数最少的棱柱有————————个顶点，有—————————个棱。
8、一个棱柱有10个顶点，所有侧棱长的和为60，则每条侧棱长为————————————9、把等腰三角形绕底边上的高旋转1800，所得的几何体是——————10、水平放置的正方体分别用“前面、后面、上面、下面、左面、右面”表示。
图中是一个正方体的平面展开图，若图中的“似”表示正方体的前面，“锦”表示右面，“程”表示下面。
则“祝”“你”“前”分别表示正方体的—————祝你前程似锦三、解答题：11、长方体ABCD —A 1B 1C 1D 1中，AB ＝3，BC ＝2，BB 1＝1，由A 到C 1在长方体表面上的最短距离为多少AA 1B 1BCC 1D 1D12、说出下列几何体的主要结构特征（1）（2）（3）空间几何体的三视图和直观图一、选择题1、两条相交直线的平行投影是（ ） A 两条相交直线 B 一条直线C 一条折线D 两条相交直线或一条直线 2、如图中甲、乙、丙所示，下面是三个几何体的三视图，相应的标号是（ ）① 长方体 ② 圆锥 ③ 三棱锥 ④ 圆柱 A ②①③ B ①②③ C ③②④ D ④③②正视图侧视图俯视图 正视图 侧视图 俯视图 正视图 侧视图 俯视图甲 乙 丙3、如果一个几何体的正视图和侧视图都是长方形，则这个几何体可能是（ ）A 长方体或圆柱B 正方体或圆柱C 长方体或圆台D 正方体或四棱锥 4、下列说法正确的是（ ）A 水平放置的正方形的直观图可能是梯形B 两条相交直线的直观图可能是平行直线C 平行四边形的直观图仍然是平行四边形D 互相垂直的两条直线的直观图仍然互相垂直5、若一个三角形，采用斜二测画法作出其直观图，其直观图面积是原三角形面积的（ ） A 21倍 B42倍 C 2倍 D 2倍 6、如图（１）所示的一个几何体，，在图中是该几何体的俯视图的是（ ）（１） 二、选择题7、当圆锥的三视图中的正视图是一个圆时，侧视图与俯视图是两个全等的———————三角形。
高中数学必修二第一章《空间几何体》单元测试卷及答案
的表面积为（）
7.—个正方体的体积是8,则这个正方体的内切球的表面积是（）
A.8nB.6nC.4nD. n
&如图是一个空间几何体的三视图，如果直角三角形的直角边长均为1,那么这个几何体
的体积为（）
1
c1
1
A.1
B .-
C .-
1
V-3 4 6 168 36 128
2
三、解答题（本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤）
40
17•【答案】-°cm.
3
【解析】如图，设圆锥母线长为I，则』-，所以I理cm.
I43
其中AB=AC,AD丄BC,且BC的长是俯视图正六边形对边的距离，即BC .3a,AD是
正六棱锥的高，即AD 3a，所以该平面图形的面积为-.3a 3a -a2.
2
1
1
1一，故选C.
3
3
9.【答案】
B
【解析】
设圆锥底面半径为
r，则-23r
8，
16
•r上，所以米堆的体积为
2
4
3
1 1
3
16
320
5
故堆放的米约为
320
1.6222，故选B.
4 3
3
9
9
10.【答案】B
【解析】由题意知棱柱的高为2.3cm，底面正三角形的内切圆的半径为.3 cm,
•••底面正三角形的边长为6cm，正三棱柱的底面面积为9 3cm2,•••此三棱柱的体积
2 2
(3)设这个正六棱锥的底面积是S,体积为V,则S6出a2兰a2,
数学测试题(必修2)第一章 空间几何体
第一章 空间几何体一、选择题1．有一个几何体的三视图如下图所示，这个几何体应是一个( )A .棱台B .棱锥C .棱柱D .都不对2．棱长都是1的三棱锥的表面积为（ ）A. B. C. D. 3．长方体的一个顶点上三条棱长分别是3,4,5，且它的8个顶点都在同一球面上，则这个球的表面积是（ ）A ．25πB ．50πC ．125πD ．都不对4．正方体的内切球和外接球的半径之比为（ ）A． B2 C．D5．在△ABC 中，02, 1.5,120AB BC ABC ==∠=,若使绕直线BC 旋转一周，则所形成的几何体的体积是（ ） A. 92π B. 72π C. 52π D. 32π 6．底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是（ ）A ．130B ．140C ．150D ．1607．如果一个水平放置的图形的斜二测直观图是一个底面为045，腰和上底均为1的等腰梯形，那么原平面图形的面积是（ ）A ． 22+B ． 221+ C ． 222+ D ． 21+ 8．半径为R 的半圆卷成一个圆锥，则它的体积为（ ）A．3R B3R C3R D3R 9．一个正方体的顶点都在球面上，它的棱长为2cm ，则球的表面积是（ ）主视图 左视图 俯视图C Ａ．28cm π Ｂ．212cm πＣ．216cm π Ｄ．220cm π10．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为（ ）A ．7 Ｂ．6 Ｃ．5 Ｄ．311．棱台上、下底面面积之比为1:9,则棱台的中截面分棱台成两部分的体积之比是( )A ．1:7 Ｂ．2:7 Ｃ．7:19 Ｄ．5:1612．如图，在多面体ABCDEF 中，已知平面ABCD 是边长为3的正方形，//EF AB ,32EF =,且EF 与平面ABCD 的距离为2，则该多面体的体积为（ ）A ．92Ｂ．5 Ｃ．6 Ｄ．15213．下图是由哪个平面图形旋转得到的（ ）A B C D14．过圆锥的高的三等分点作平行于底面的截面，它们把圆锥侧面分成的三部分的面积之比为（ ）A . 1:2:3B . 1:3:5C . 1:2:4D . 1:3:915．在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方形，则截去8个三棱锥后 ，剩下的几何体的体积是（ ）A. 23B. 76C. 45D. 5616．已知圆柱与圆锥的底面积相等，高也相等，它们的体积 分别为1V 和2V ，则12:V V =（ ）A . 1:3B . 1:1C . 2:1 D. 3:117．如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A . 8:27B . 2:3C . 4:9D . 2:918．有一个几何体的三视图及其尺寸如下（单位cm ），则该几何体的表面积及体积为：A . 224cm π，212cm πB . 215cm π，212cm πC . 224cm π，236cm πD . 以上都不正确二、填空题1．一个棱柱至少有 _____个面，面数最少的一个棱锥有 ________个顶点，顶点最少的一个棱台有 ________条侧棱。
必修2第一章空间几何体测试题
空间几何体测试题姓名______班级________分数______________一.选择题1.向高为H的水瓶中匀速注水，注满为止，如果注水量V与水深h的函数关系如下面左图所示，那么水瓶的形状是（）2. 棱长都是1的三棱锥的表面积为（）A A. 3B 23C 33D 433.一个正三棱柱（底面是正三角形，侧棱与底面垂直的三棱柱）的侧棱长和底面边长相等，体积为32，它的三视图中的俯视图如右图所示，左视图是一个矩形，则这个矩形的面积是（）A．4 B．22 C．32D．34. 如右图，某几何体的正视图与侧视图都是边长为1的正方形，且体积为12。
则该几何体的俯视图可以是( )5.正方体的内切球外接球的体积之比为( )A. 1∶3B. 1∶3C. 1∶33D. 1∶96．有一个几何体的三视图及其尺寸如下（单位cm），则该几何体的表面积及体积为：A. 224cmπ，212cmπ B. 215cmπ，212cmπC. 224cmπ，236cmπ D.以上都不正确7.一个几何体的三视图如图所示，则这个几何体的体积等于( )(A) 4 (B) 6 (C) 8 (D)128.已知一个几何体的三视图如图所示, 则这个几何体的体积为( )A.8/3B.4C.8D.169．一个三角形在其直观图中对应一个边长为1正三角形，原三角形的面积为（）A．46B．43C．23D．2610.如图，已知三棱锥的底面是直角三角形，直角边长分别为3和4，过直角顶点的侧棱长为4，且垂直于底面，该三棱锥的主视图是（）65题号 1 2 3 4 5 6 7 8 9 10 答案二.填空题11. 一球与棱长为2cm 的正方体的各棱相切，则球的体积是______12.若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是_______3cm .（第13题）13.一个的空间几何体的三视图如图所示,则该几何体的体积为_______14.一个与球心距离为1的平面截球所得的圆面面积为π，则球的表面积为 _________ 15．正四棱台的两底边长分别为1cm,2cm,高是1cm,它的侧面积为______cm 2.16.圆柱形容器内盛有高度为3cm 的水，若放入三个相同的珠（球的半径与圆柱的底面半径相同）后，水恰好淹没最上面的球（如右下图所示），则球的半径是____cm. 17.一个几何体的三视图及其尺寸如图所示，则该几何体的侧面积为_______cm 2.（第17题） （第16题）三.解答题18．画出下列空间几何体的三视图．19.一个圆台的母线长为12cm ，两底面面积分别是24cm π和225cm π，求： （1）圆台的高1OO 的长度；（2）截得此圆台的圆锥的母线长SA 的长度．20.一个正三棱柱的三视图如图所示,（1）做出该三棱柱的斜二测直观图（不要求叙述过程） （2）求这个三棱柱的表面积和体积.21.某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P －EFGH,下半部分是长方体ABCD －EFGH. 图5、图6分别是该标识墩的正(主)视图和俯视图.（1）请画出该安全标识墩的侧(左)视图;（2）求该安全标识墩的体积俯视图正(主)视图88侧(左)视8222正(主)视 2 2侧(左)视图 俯视图。
【人教A版】高中数学必修2第一章《空间几何体》单元测试题
高中数学必修2第一章《空间几何体》单元测试题(时间：120分钟满分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求的)1．下列说法正确的是()A．棱柱的侧面可以是三角形B．正方体和长方体都是特殊的四棱柱C．所有的几何体的表面都能展成平面图形D．棱柱的各条棱都相等2．小红拿着一物体的三视图(如图所示)给小明看，并让小明猜想这个物件的形状是()A．长方形B．圆柱C．立方体D．圆锥3．如图所示的直观图表示的四边形的平面图形A′B′C′D′是()A．任意梯形B．直角梯形C．任意四边形D．平行四边形4．半径为R的半圆卷成一个圆锥，则它的体积为()A.324πR3 B.38πR3C.524πR3 D.58πR35．如图所示为一个简单几何体的三视图，则其对应的实物是()6．若长方体相邻三个面的面积分别为2，3，6，则长方体的体积等于()A． 6 B．6C．6 6 D．367．一个几何体的三视图如下图所示，已知这个几何体的体积为103，则h 为()A．32B． 3C．3 3 D．5 38．过球的一条半径的中点作垂直于该半径的平面，则所得截面圆的面积与球的表面积的比值为()A.316 B.916C.38 D.9329．一个正方体内接于一个球，过球心作一截面，如图所示，则截面所有可能的图形是()A．①③B．②④C．①②③D．②③④10．若某几何体的三视图(单位：cm)如图所示，则此几何体的体积是()A．24 cm3B．40 cm3C．36 cm3D．48 cm311．如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是28π3，则它的表面积是()A．17πB．18πC．20πD．28π12．如图，在棱长为1的正方体ABCD-A1B1C1D1中，E是棱BC上的一点，则三棱锥D1B1C1E的体积等于()A.13 B.512C.36 D.16二、填空题(本大题共4个小题，每小题5分，共20分．把答案填在题中的横线上)13．圆台的底面半径为1和2，母线长为3，则此圆台的体积为________．14．圆柱形容器内部盛有高度为8 cm的水，若放入三个相同的球(球的半径为圆柱的底面半径相同)后，水恰好淹没最上面的球(如图所示)，则球的半径是________cm.15．已知一个正三棱柱的侧棱长和底面边长相等，体积为23，它的三视图中的俯视图如下图所示，侧视图是一个矩形，则这个矩形的面积是________．16．如图是一个棱长为1的无盖正方体盒子的平面展开图，A，B，C，D为其上四个点，则以A，B，C，D为顶点的三棱锥的体积为________．三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)如图所示是一个长方体截去一个角得到的几何体的直观图及正视图和侧视图(单位：cm)．(1)画出该多面体的俯视图，并标上相应的数据；(2)按照给出的数据，求该几何体的体积．18.(本小题满分12分)一个圆锥形容器和一个圆柱形容器的轴截面如图所示，两容器内所盛液体的体积正好相等，且液面高度h也相等，用a将h表示出来．19．(本小题满分12分)把一块边长为10的正方形铁片按如图所示的阴影部分裁下，用余下的四个全等的等腰三角形加工成一个正四棱锥形容器，试建立容器的容积V与等腰三角形的底边边长x的函数关系式，并求出函数的定义域．20．(本小题满分12分)在底面半径为2，母线长为4的圆锥中内接一个高为3的圆柱，求圆柱的表面积．21．(本小题满分12分)如图所示是已知几何体的三视图(单位：cm)．(1)画出这个几何体的直观图(不要求写画法)；(2)求这个几何体的表面积及体积．22．(本小题满分12分)已知一圆锥的母线长为10 cm，底面半径为5 cm.(1)求它的高；(2)若该圆锥内有一球，球与圆锥的底面及圆锥的所有母线都相切，求球的体积．高中数学必修2第一章《空间几何体》单元测试题(时间：120分钟满分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求的)1．下列说法正确的是()A．棱柱的侧面可以是三角形B．正方体和长方体都是特殊的四棱柱C．所有的几何体的表面都能展成平面图形D．棱柱的各条棱都相等答案：B2．小红拿着一物体的三视图(如图所示)给小明看，并让小明猜想这个物件的形状是()A．长方形B．圆柱C．立方体D．圆锥解析：由正视图和侧视图可知该几何体是棱柱或圆柱，则D不可能．再由俯视图是圆可知该几何体是圆柱．答案：B3．如图所示的直观图表示的四边形的平面图形A′B′C′D′是()A．任意梯形B．直角梯形C．任意四边形D．平行四边形解析：AB∥Oy，AD∥Ox，故A′B′⊥A′D′.又BC∥AD且BC≠AD，所以为直答案：B4．半径为R的半圆卷成一个圆锥，则它的体积为()A.324πR3 B.38πR3C.524πR3 D.58πR3解析：设圆锥的底面半径为r，高为h.依题意πR＝2πr，所以r＝R 2，则h＝R2－T2＝3 2R.所以圆锥的体积V＝13πr2n＝13π⎝⎛⎭⎪⎫R22·32R＝324πR3.答案：A5．如图所示为一个简单几何体的三视图，则其对应的实物是()解析：根据三种视图的对角线的位置关系，容易判断A正确．答案：A6．若长方体相邻三个面的面积分别为2，3，6，则长方体的体积等于()A． 6 B．6C．6 6 D．36解析：设长方体的长、宽、高分别为a，b，c，则不妨设ab＝6，ac＝3，所以a 2b 2c 2＝2×3×6＝6. 故长方体的体积V ＝abc ＝ 6. 答案：A7．一个几何体的三视图如下图所示，已知这个几何体的体积为103，则h 为( )A ．32B ． 3C ．3 3D ．5 3解析：由三视图可知，该几何体是四棱锥，其底面是长为6，宽为5的矩形，高为h ，所以V ＝13×6×5×h ＝103，解得h ＝ 3.答案：B8．过球的一条半径的中点作垂直于该半径的平面，则所得截面圆的面积与球的表面积的比值为( )A.316B.916C.38D.932解析：设球的半径为R ，截面圆的半径为r ， 则⎝ ⎛⎭⎪⎫R 22＋r 2＝R 2，所以r 2＝34R 2. 故S 截面S 球＝πr 24πR 2＝14×34＝316. 答案：A9．一个正方体内接于一个球，过球心作一截面，如图所示，则截面所有可能的图形是()A．①③B．②④C．①②③D．②③④解析：当截面平行于正方体的一个侧面时得③，当截面过正方体的体对角线时得②，当截面不平行于任何侧面也不过体对角线时得①，但无论如何都不能截出④.答案：C10．若某几何体的三视图(单位：cm)如图所示，则此几何体的体积是()A．24 cm3B．40 cm3C．36 cm3D．48 cm3解析：由三视图可知，该几何体是由一个三棱柱截去两个全等的与三棱柱等底面且高为2的三棱锥形成的，故该几何体的体积V＝12×4×3×8－2×13×12×4×3×2＝40(cm3)，故选B.答案：B11．如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是28π3，则它的表面积是()A．17πB．18πC ．20πD ．28π解析：根据三视图还原出几何体，再根据表面积公式求解． 由三视图可知其对应几何体应为一个切去了18部分的球，由43πr 3×78＝28π3，得r ＝2，所以此几何体的表面积为4πr 2×78＋3×14πr 2＝17π，故选A. 答案：A 12．如图，在棱长为1的正方体ABCD -A 1B 1C 1D 1中，E 是棱BC 上的一点，则三棱锥D 1B 1C 1E 的体积等于( )A.13B.512C.36D.16解析：VD 1B 1C 1E ＝VE B 1C 1D 1＝13S △B 1C 1D 1·CC 1＝13×12×12×1＝16，故选D.答案：D二、填空题(本大题共4个小题，每小题5分，共20分．把答案填在题中的横线上)13．圆台的底面半径为1和2，母线长为3，则此圆台的体积为________． 解析：作圆台的轴截面如图所示，则r 1＝O 1D ＝1，r 2＝O 2A ＝2，AD ＝3.所以圆台的高h ＝AD 2－AH 2＝32－（2－1）2＝2 2.因此圆台的体积V ＝π3(r 21＋r 22＋r 1r 2)h ＝14 2 π3.答案：1423π14．圆柱形容器内部盛有高度为8 cm 的水，若放入三个相同的球(球的半径为圆柱的底面半径相同)后，水恰好淹没最上面的球(如图所示)，则球的半径是________cm.解析：设球的半径为r ，放入3个球后，圆柱液面高度变为6r ，则有πr 2·6r ＝8πr 2＋3×43πr 3，即2r ＝8，所以r ＝4.答案：415．已知一个正三棱柱的侧棱长和底面边长相等，体积为23，它的三视图中的俯视图如下图所示，侧视图是一个矩形，则这个矩形的面积是________．解析：设正三棱柱的侧棱与底面边长为a ，则V三棱柱＝34a 2·a ＝23，所以a ＝2，因此底面正三角形的高2×sin 60°＝ 3.故侧视图(矩形)的面积S ＝3×2＝2 3.答案：2 316．如图是一个棱长为1的无盖正方体盒子的平面展开图，A ，B ，C ，D 为其上四个点，则以A ，B ，C ，D 为顶点的三棱锥的体积为________．解析：将展开图还原为正方体，如图所示．故以A ，B ，C ，D 为顶点的三棱锥的体积V ＝V C ABD ＝13×⎝ ⎛⎭⎪⎫12×12×1＝16. 答案：16三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)如图所示是一个长方体截去一个角得到的几何体的直观图及正视图和侧视图(单位：cm)．(1)画出该多面体的俯视图，并标上相应的数据；(2)按照给出的数据，求该几何体的体积．解：(1)该几何体的俯视图如图所示．(2)该几何体的体积V ＝V 长方体－V 三棱柱＝4×4×6－13×(12×2×2)×2＝2843(cm 3)．18.(本小题满分12分)一个圆锥形容器和一个圆柱形容器的轴截面如图所示，两容器内所盛液体的体积正好相等，且液面高度h 也相等，用a 将h 表示出来．解：V 圆锥液＝πh 2·h 3， V 圆柱液＝π·(a 2)2·h ，由已知得πh 33＝π·(a 2)2h ，所以h ＝32a .19．(本小题满分12分)把一块边长为10的正方形铁片按如图所示的阴影部分裁下，用余下的四个全等的等腰三角形加工成一个正四棱锥形容器，试建立容器的容积V 与等腰三角形的底边边长x 的函数关系式，并求出函数的定义域．解：在Rt △EOF 中，EF ＝5，OF ＝12x ，则EO ＝25－14x 2，于是V ＝13x 225－14x 2. 依题意，函数的定义域为{x |0＜x ＜10}．20．(本小题满分12分)在底面半径为2，母线长为4的圆锥中内接一个高为3的圆柱，求圆柱的表面积．解：设圆锥的底面半径为R ，圆柱的底面半径为r ，表面积为S ，则R ＝OC ＝2，AC ＝4，AO ＝42－22＝2 3.如图所示易知△AEB ∽△AOC ， 所以AE AO ＝EB OC ，即323＝r 2，所以r ＝1， S 底＝2πr 2＝2π，S 侧＝2πr ·h ＝23π.所以S ＝S 底＋S 侧＝2π＋23π＝(2＋23)π.21．(本小题满分12分)如图所示是已知几何体的三视图(单位：cm)．(1)画出这个几何体的直观图(不要求写画法)；(2)求这个几何体的表面积及体积．解：(1)这个几何体的直观图如图所示．(2)这个几何体可看成是由正方体AC 1及直三棱柱B 1C 1Q A 1D 1P 的组合体． 由P A 1＝PD 1＝2，A 1D 1＝AD ＝2，可得P A 1⊥PD 1.故所求几何体的表面积S ＝5×22＋2×2×2＋2×12×(2)2＝22＋42(cm 2)，所求几何体的体积V ＝23＋12×(2)2×2＝10(cm 3)．22．(本小题满分12分)已知一圆锥的母线长为10 cm ，底面半径为5 cm.(1)求它的高；(2)若该圆锥内有一球，球与圆锥的底面及圆锥的所有母线都相切，求球的体积．解：(1)它的高为102－52＝53(cm)．(2)其轴截面如图所示．设球的半径为r cm.由题意知△SCE与△SBD相似，则r5＝53－r10.解得r＝533.于是，所求球的体积V球＝4π3r3＝4π3⎝⎛⎭⎪⎫5333＝5003π27(cm3)．。
人教A版高中数学必修二 第一章 空间几何体复习 检测试题 有答案
第一章 空间几何体 测试题一、选择题1、已知△ABC 的平面直观图△A ′B ′C ′是边长为a 的正三角形，那么原△ABC 的面积为（ ）A.32a 2B.34a 2C.62a 2 D.6a 2 2．一个直角三角形绕斜边所在直线旋转360°形成的空间几何体为（ ）A ．一个圆锥B ．一个圆锥和一个圆柱C ．两个圆锥D ．一个圆锥和一个圆台 3、一个四面体的三视图如图所示，则该四面体的表面积是（ ）A.13+B.23+C.122+D.224． 某几何体的三视图如图所示（单位：cm ）,则该几何体的体积是（ ）A.38cmB.312cmC.332cm 3 D.340cm 35．半径为R 的半圆卷成一个圆锥，则它的体积为( )A.324πR 3B.38πR 3C.524πR 3D.58πR 3 6、如图,△O'A'B'是水平放置的△OAB 的直观图,A'O'=6,B'O'=2,则△OAB 的面积是()A.6B.3错误！未找到引用源。
C.6错误！未找到引用源。
D.127、圆锥的高扩大到原来的2倍,底面半径缩短到原来的21错误！未找到引用源。
,则圆锥的体积( )A .缩小到原来的一半B .扩大到原来的2倍C .不变D .缩小到原来的61错误！未找到引用源。
8、 若三棱锥的三条侧棱两两垂直，且其长度分别为1，2，3，则此三棱锥的外接球的表面积为 ( )A ．6πB ．12πC ．18πD ．24π9．若底面是正三角形的三棱柱的正视图如图D12所示，则其侧面积等于( )A. 3 B ．2 C ． 2 3 D ．6俯视图侧（左）视图正（主）视图22211121正视图侧视图俯视图2222图D12图D1310．如图D13所示，网格纸上正方形小格的边长为1(表示1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm ，高为6 cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.1311．某几何体三视图如下，其中三角形的三边长与圆的直径均为2，则该几何体体积为A.3283π3+ B.323π3+ C.433π3+ D.43π3+12．如图所示，则这个几何体的体积等于（ ） A.4 B.6 C.8 D.1213.已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.错误！未找到引用源。
高中数学必修二第一章《空间几何体》单元测试卷及答案
高中数学必修二第一章《空间几何体》单元测试卷及答案（2套）测试卷一一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的）1．已知某空间几何体的三视图如图所示，则此几何体为（ ）A ．圆台B ．四棱锥C ．四棱柱D ．四棱台2．如图，△O ′A ′B ′是水平放置的△OAB 的直观图，则△OAB 的面积为（ ）A ．6B ．32C ．62D ．123．已知一个底面是菱形的直棱柱的侧棱长为5，菱形的对角线的长分别是9和15，则这个棱柱的侧面积是（ ） A ．3034B ．6034C ．3034135+D ．1354．半径为R 的半圆卷成一个圆锥，则它的体积为（ ） A ．3324R π B ．338R π C ．3525R π D ．358R π 5．已知圆柱与圆锥的底面积相等，高也相等，它们的体积分别为V 1和V 2，则V 1：V 2＝（ ） A ．1：3B ．1：1C ．2：1D ．3：16．若一个底面是正三角形的三棱柱的正视图如下图所示，其顶点都在一个球面上，则该球的表面积为（ ）A ．163π B ．193π C ．1912π D ．43π7．一个正方体的体积是8，则这个正方体的内切球的表面积是（ ） A ．8πB ．6πC ．4πD ．π8．如图是一个空间几何体的三视图，如果直角三角形的直角边长均为1，那么这个几何体的体积为（ ）A ．1B ．12 C ．13D ．169．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有（ ）A ．14斛B ．22斛C ．36斛D ．66斛103cm 的内切球，则此棱柱的体积是（ ） A ．393B ．354cmC ．327cmD ．318311．如图，网格纸上正方形小格的边长为1(表示1cm )，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ）A ．1727 B ．59C ．1027 D ．1312．如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为（ ）A ．3500cm 3πB ．3cm 3866πC ．3cm 31372πD ．3cm 32048π 二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上） 13．一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号)．①三棱锥；②四棱锥；③三棱柱；④四棱柱；⑤圆锥；⑥圆柱．14．用斜二测画法画边长为2的正三角形的直观图时，如果在已知图形中取的x 轴和正三角形的一边平行，则这个正三角形的直观图的面积是__________________．15．棱锥的高为16，底面积为512，平行于底面的截面面积为50，则截得的棱台的高为__________________．16．如图是一个组合几何体的三视图，则该几何体的体积是__________________．三、解答题（本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤）17．(10分)把一个圆锥截成圆台，已知圆台的上、下底面半径的比是1:4，母线长为10cm．求圆锥的母线长．18．(12分)如图是一个几何体的正视图和俯视图．（1）试判断该几何体是什么几何体？（2）画出其侧视图，并求该平面图形的面积；（3）求出该几何体的体积．19．(12分)如下图，一个圆锥形的空杯子上面放着一个半球形的冰淇淋，如果冰淇淋融化了，会溢出杯子吗？请用你的计算数据说明理由．20．(12分)已知某几何体的侧视图与其正视图相同，相关的尺寸如图所示，求这个几何体的体积．21．(12分)如图所示，设计一个四棱锥形冷水塔塔顶，四棱锥的底面是正方形，侧面是全等的等腰三角形，已知底面边长为2m，高为7m，制造这个塔顶需要多少铁板？22．(12分)如图，正方体ABCD－A′B′C′D′的棱长为a，连接A′C′，A′D，A′B，BD，BC′，C′D，得到一个三棱锥．求：（1）三棱锥A′－BC′D的表面积与正方体表面积的比值；（2）三棱锥A′－BC′D的体积．）答案一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的）1．【答案】D【解析】由几何体的三视图可得，该几何体为四棱台．故选D．【解析】△OAB 是直角三角形，OA ＝6，OB ＝4，∠AOB ＝90°，∴164122OAB S =⨯⨯=△．故选D ．3．【答案】A【解析】由菱形的对角线长分别是9和15，得菱形的边长为22915334222⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭，则这个菱柱的侧面积为3434530342⨯⨯=．故选A ． 4．【答案】A【解析】依题意，得圆锥的底面周长为πR ，母线长为R ，则底面半径为2R，高为32R ，所以圆锥的体积2313332224R R R ⎛⎫⨯π⨯⨯=π ⎪⎝⎭．故选A ． 5．【答案】D【解析】()121::3:13V V Sh Sh ⎛⎫== ⎪⎝⎭．故选D ．6．【答案】B【解析】设球半径是R ，依题意知，该三棱柱是一个底面边长为2，侧棱长为1的正三棱柱，记上，下底面的中心分别是O 1，O ，易知球心是线段O 1O 的中点，于是222123192312R ⎛⎫⎛⎫=+= ⎪ ⎪ ⎪⎝⎭⎝⎭，因此所求球的表面积是2191944123R ππ=π⨯=， 故选B ． 7．【答案】C【解析】设正方体的棱长为a ，则a 3＝8，所以a ＝2，而此正方体内的球直径为2，所以S 表＝4πr 2＝4π．故选C ． 8．【答案】C【解析】该几何体的直观图为如图所示的四棱锥P －ABCD ，且P A ＝AB ＝AD ＝1，P A ⊥AB ，P A ⊥AD ，四边形ABCD 为正方形，则2111133V =⨯⨯=，故选C ．【解析】设圆锥底面半径为r ，则12384r ⨯⨯=，∴163r =，所以米堆的体积为21116320354339⎛⎫⨯⨯⨯⨯= ⎪⎝⎭，故堆放的米约为320 1.62229÷≈，故选B ． 10．【答案】B【解析】由题意知棱柱的高为23cm ，底面正三角形的内切圆的半径为3cm ， ∴底面正三角形的边长为6cm ，正三棱柱的底面面积为293cm ，∴此三棱柱的体积()3932354cm V =⨯=．故选B ．11．【答案】C【解析】由零件的三视图可知，该几何体为两个圆柱组合而成，如图所示．切削掉部分的体积V 1＝π×32×6-π×22×4-π×32×2＝20π(cm 3)， 原来毛坯体积V 2＝π×32×6＝54π(cm 3)．故所求比值为1220105427V V π==π．故选C ． 12．【答案】A【解析】设球的半径为R ，则由题知球被正方体上面截得圆的半径为4， 球心到截面圆的距离为R －2，则R 2＝(R －2)2＋42，解得R ＝5．∴球的体积为3345500cm 33π⨯π=．故选A ．二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上） 13．【答案】①②③⑤【解析】三棱锥的三视图中含有三角形，∴正视图有可能是三角形，满足条件． 四棱锥的三视图中含有三角形，满足条件． 三棱柱的三视图中含有三角形，满足条件． 四棱柱的三视图中都为四边形，不满足条件． 圆锥的三视图中含有三角形，满足条件． 圆柱的三视图中不含有三角形，不满足条件． 故答案为①②③⑤．14．【答案】6415．【答案】11【解析】设棱台的高为x ，则有2165016512x -⎛⎫= ⎪⎝⎭，解之，得x ＝11． 16．【答案】36＋128π【解析】由三视图可知该组合几何体下面是一个圆柱，上面是一个三棱柱，故所求体积为1346168361282V =⨯⨯⨯+π⨯=+π．三、解答题（本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．【答案】403cm ． 【解析】如图，设圆锥母线长为l ，则1014l l -=，所以cm 403l =．18．【答案】（1）正六棱锥；（2）见解析，232a ；（3）332a ．【解析】（1）由该几何体的正视图和俯视图可知该几何体是一个正六棱锥． （2）该几何体的侧视图如图．其中AB ＝AC ，AD ⊥BC ，且BC 的长是俯视图正六边形对边的距离，即3BC a =，AD 是正六棱锥的高，即3AD a =，所以该平面图形的面积为2133322a a a =．（3）设这个正六棱锥的底面积是S ，体积为V ，则223336S =，所以2313333322V a a a =⨯⨯=．19．【答案】不会，见解析．【解析】因为()33314144134cm 2323V R =⨯π=⨯⨯π⨯≈半球，()22311412201cm 33V r h =π=π⨯⨯≈圆锥，134<201，所以V 半球<V 圆锥，所以，冰淇淋融化了，不会溢出杯子． 20．【答案】74V π=． 【解析】由三视图可知，该几何体是大圆柱内挖掉了小圆柱，两个圆柱高均为1，底面是半径为2和32的同心圆，故该几何体的体积为23741124V π⎛⎫=π⨯-π⨯= ⎪⎝⎭．21．【答案】282m ．【解析】如图所示，连接AC 和BD 交于O ，连接SO ．作SP ⊥AB ，连接OP ．在Rt △SOP 中，)7m SO =，()11m 2OP BC ==，所以)22m SP =， 则△SAB 的面积是)2122222m 2⨯⨯=．所以四棱锥的侧面积是)242282m ⨯，即制造这个塔顶需要282m 铁板．22．【答案】（13；（2）33a ．【解析】（1）∵ABCD －A ′B ′C ′D ′是正方体， ∴2A B A C A D BC BD C D a ''''''======，∴三棱锥A ′－BC ′D 的表面积为213422232a a a ⨯=．而正方体的表面积为6a 2，故三棱锥A ′－BC ′D 的表面积与正方体表面积的比值为2233a ． （2）三棱锥A ′－ABD ，C ′－BCD ，D －A ′D ′C ′，B －A ′B ′C ′是完全一样的．故V三棱锥A′－BC′D＝V正方体－4V三棱锥A′－ABD＝3 32114323a a a a-⨯⨯⨯=测试卷二一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的）1．下图中的图形经过折叠不能围成棱柱的是（）2．一个几何体的三视图如图所示，则这个几何体的体积等于（）A．4 B．6 C．8 D．123．下列命题中，正确的命题是（）A．存在两条异面直线同时平行于同一个平面B．若一个平面内两条直线与另一个平面平行，则这两个平面平行C．底面是矩形的四棱柱是长方体D．棱台的侧面都是等腰梯形4．水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如图所示，是一个正方体的表面展开图，若图中“2”在正方体的上面，则这个正方体的下面是（）A．0 B．9 C．快D．乐5．如图，O A B'''△是水平放置的OAB△的直观图，则AOB△的面积是（）。
高中数学必修二必修2习题：第1章空间几何体1.1.1Word版含解析
第一章 1.1 1.1.1一、选择题1．下面多面体中，是棱柱的有()A．1个B．2个C．3个D．4个[答案] D[解析]根据棱柱的定义进行判定知，这4个图都满足．2．下列说法正确的是()A．有2个面平行，其余各面都是梯形的几何体是棱台B．多面体至少有3个面C．各侧面都是正方形的四棱柱一定是正方体D．九棱柱有9条侧棱，9个侧面，侧面为平行四边形[答案] D[解析]选项A错误，反例如图1；一个多面体至少有4个面，如三棱锥有4个面，不存在有3个面的多面体，所以选项B错误；选项C错误，反例如图2，上、下底面是全等的菱形，各侧面是全等的正方形，它不是正方体；根据棱柱的定义，知选项D正确．3．下列说法中正确的是()A．所有的棱柱都有一个底面B．棱柱的顶点至少有6个C．棱柱的侧棱至少有4条D．棱柱的棱至少有4条[答案] B[解析]棱柱有两个底面，所以A项不正确；棱柱底面的边数至少是3，则在棱柱中，三棱柱的顶点数至少是6，三棱柱的侧棱数至少是3，三棱柱的棱数至少是9，所以C、D 项不正确，B项正确．4．下列图形经过折叠可以围成一个棱柱的是()[答案] D[解析]A、B、C中底面图形的边数与侧面的个数不一致，故不能围成棱柱．故选 D.5．观察如图所示的四个几何体，其中判断不正确的是()A．①是棱柱B．②不是棱锥C．③不是棱锥D．④是棱台[答案] B[解析]①是棱柱，②是棱锥，③不是棱锥，④是棱台，故选 B.6．用一个平面去截一个三棱锥，截面形状是()A．四边形B．三角形C．三角形或四边形D．不可能为四边形[答案] C[解析]按如图①所示用一个平面去截三棱锥，截面是三角形；按如图②所示用一个平面去截三棱锥，截面是四边形．二、填空题7．八棱锥的侧面个数是________.[答案]8[解析]八棱锥有8个侧面．8．下列说法正确的是________.①一个棱锥至少有四个面；②如果四棱锥的底面是正方形，那么这个四棱锥的四条侧棱都相等；③五棱锥只有五条棱；④用与底面平行的平面去截三棱锥，得到的截面三角形和底面三角形相似．[答案]①④[解析]①正确．②不正确．四棱锥的底面是正方形，它的侧棱可以相等．也可以不等．③不正确．五棱锥除了五条侧棱外，还有五条底边，故共10条棱．④正确．三、解答题9．判断如图所示的几何体是不是棱台？为什么？[解析]①②③都不是棱台，因为①和③都不是由棱锥所截得的，故①③都不是棱台，虽然②是由棱锥所截得的，但截面不和底面平行，故不是棱台，只有用平行于棱锥底面的平面去截棱锥，底面与截面之间的部分才是棱台．10．如图所示的几何体中，所有棱长都相等，分析此几何体的构成？有几个面、几个顶点、几条棱？[解析]这个几何体是由两个同底面的四棱锥组合而成的八面体，有8个面，都是全等的正三角形；有6个顶点；有12条棱.一、选择题1．(2016嘉峪关一中高一检测)下面说法正确的是()A．棱锥的侧面不一定是三角形B．棱柱的各侧棱长不一定相等C．棱台的各侧棱延长必交于一点D．用一个平面截棱锥，得到两个几何体，一个是棱锥，另一个是棱台[答案] C[解析]棱台的各侧棱延长后必交于一点，故选 C.2．以三棱台的顶点为三棱锥的顶点，这样可以把一个三棱台分成三棱锥的个数为() A．1 B．2C．3 D．4[答案] C[解析]如图所示，在三棱台ABC－A1B1C1中，分别连接A1B，A1C，BC1，则将三棱台分成3个三棱锥，即三棱锥A－A1BC，B1－A1BC1，C－A1BC1.3．(2016·日照高一检测)如图，将装有水的长方体水槽固定底面一边后倾斜一个小角度，则倾斜后水槽中的水形成的几何体是()A．棱柱B．棱台C．棱柱与棱锥的组合体D．不能确定[答案] A[解析]倾斜后水槽中的水形成的几何体是棱柱．4．某同学制作了一个对面图案相同的正方体礼品盒(如图)，则这个正方体礼品盒的表面展开图应该为()[答案] A[解析]两个☆不能并列相邻，B、D错误；两个不能并列相邻，C错误，故选 A.也可通过实物制作检验来判断．二、填空题5．五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个五棱柱的对角线共有________条.[答案]10[解析]在上底面选一个顶点，同时在下底选一个顶点，且这两个顶点不在同一侧面上，这样上底面每个顶点对应两条对角线，所以共有10条．6．在正方体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是________(写出所有正确结论的编号).①矩形；②不是矩形的平行四边形；③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；④每个面都是等边三角形的四面体；⑤每个面都是直角三角形的四面体．[答案]①③④⑤[解析]在如图正方体ABCD－A1B1C1D1中，若所取四点共面，则只能是正方体的表面或对角面．即正方形或长方形，∴①正确，②错误．棱锥A－BDA1符合③，∴③正确；棱锥A1－BDC1符合④，∴④正确；棱锥A－A1B1C1符合⑤，∴⑤正确．三、解答题7．一个几何体的表面展开平面图如图.(1)该几何体是哪种几何体；(2)该几何体中与“祝”字面相对的是哪个面？与“你”字面相对的是哪个面？[解析](1)该几何体是四棱台；(2)与“祝”相对的面是“前”，与“你”相对的面是“程”．8．根据如图所示的几何体的表面展开图，画出立体图形.[解析]图1是以ABCD为底面，P为顶点的四棱锥．图2是以ABCD和A1B1C1D1为底面的棱柱．其图形如图所示．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章空间几何体检测试题
(时间：120分钟满分：150分)
一、选择题(每小题5分，共50分)
1．下列命题正确的是( )
A．棱柱的底面一定是平行四边形
B．棱锥的底面一定是三角形
C．棱锥被平面分成的两部分不可能都是棱锥
D．棱柱被平面分成的两部分可以都是棱柱
2．若正棱锥底面边长与侧棱长相等，则该棱锥一定不是( )
A．三棱锥 B．四棱锥 C．五棱锥 D．六棱锥
3．给出四个命题：
①各侧面都是正方形的棱柱一定是正棱柱；②底面是矩形的平行六面体是长方体；
③有两个侧面垂直于底面的棱柱一定是直棱柱；④长方体一定是正四棱柱．
其中正确命题的个数是( )
A．0个 B．1个 C．2个 D．3个
4．如图11是一幅电热水壶的主视图，它的俯视图是( )
图11
5．已知各顶点都在一个球面上的正四棱柱的高为4，体积为16，则这个球的表面积是( ) A．16π B．20π C．24π D．32π
6．两个球的体积之和为12π，且这两个球的大圆周长之和为6π，那么这两球半径之差是( )
A.1
2
B．1 C．2 D．3
7．已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同一侧且相距是1，那么这个球的半径是( )
A．4 B．3 C．2 D．5
8．纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北．现又沿该正方体的一些棱将正方体剪开、外面朝上展平，得到如图12所示的平面图形，则标“△”的面的方位是( )
A．南 B．北 C．西 D．下
9．图13是一个几何体的三视图，根据图中数据，可得该几何体的表面积是( )
图13图12
A．32π B．16π C．12π D．8π图14
10．在△ABC中，AB＝2，BC＝1.5，∠ABC＝120°，如图14.若将△ABC绕BC旋转一周，则所形成的旋转体的体积是( )
A.9
2
π B.
7
2
π C.
5
2
π D.
3
2
π
二、填空题(每小题5分，共20分)
11．正三棱柱的底面边长为2，高为2，则它的体积为__________．
12．圆台的高是12 cm，上、下两个底面半径分别为4 cm和9 cm，则圆台的侧面积是__________．13．已知四棱锥PABCD的底面是边长为6的正方形，侧棱PA⊥底面ABCD，且PA＝8，则该四棱锥的体积是________．
14．在平面上，若两个正三角形的边长比为1∶2，则它们的面积比为1∶4，类似地，在空间内，若两个正四面体的棱长比为1∶2，则它们的体积比为__________．
三、解答题(共80分)
15．(12分)圆柱的轴截面是边长为5 cm的正方形ABCD，求圆柱的侧面上从A到C的最短距离．
16．(12分)如图15，设计一个正四棱锥形冷水塔塔顶，高是0.85 m，底面的边长是
1.5 m，制造这种塔顶需要多少平方米铁板(精确到0.1 m2)?
图15
17．(14分)如图16是一个奖杯的三视图．求这个奖杯的体积(精确到0.01 cm3)．
图16
18．(14分)如图17，一个直三棱柱形容器中盛有水，且侧棱AA1＝8.若侧面AA1B1B水平放置时，液面恰好过AC，BC，A1C1的中点，则当底面ABC水平放置时，液面的高为多少？
图17 19．(14分)如图18，已知一个圆锥的底面半径为R，高为H，在其中有一个高为x的内接圆柱．
(1)求圆柱的侧面积；
(2)当x为何值时，圆柱的侧面积最大．
图18
20．(14分)如图19，在正四棱台内，以小底为底面，大底面中心为顶点作一内接棱锥．已知棱台小底面边长为b，大底面边长为a，并且棱台的侧面积与内接棱锥的侧面面积相等，求这个棱锥的高，并指出有解的条件．
图19
第一章自主检测
1．D 2.D 3.A 4.D 5.C 6.B
7．B 解析：如图D60，设球的半径是r ，则π·BD 2＝5π，π·AC 2＝8π，∴BD 2
＝5， AC 2＝8.又AB ＝1，设OA ＝x .∴x 2＋8＝r 2，(x ＋1)2＋5＝r 2.解得r ＝3. 8．B 9.C
10．D 解析：旋转体的体积就是一个大圆锥体积减去一个小圆锥的体积，13·π·(3)2
×52
－
13·π·(3)2×1＝32π. 11．2 3 12.169π cm 2 13.96 14.1∶8 15．解：如图D61，由圆柱的轴截面是边长为5 cm 的正方形，知：圆柱高CD 为5 cm ，底面半径为2.5 cm ，底面周长为5π cm，则AD 为2.5π cm，圆柱侧面上从A 到C 的最短距离即是矩形ABCD 的对角线长为
52＋ 2.5π2＝5
2
π2＋4 (cm)．
16．解：SE ＝0.852＋0.752.所需铁板面积为S ＝4×⎝ ⎛⎭
⎪⎫
12×1.5×0.852＋0.752≈3.4(m 2)．
17．解：由三视图可以得到奖杯的结构，底座是一个正四棱台，杯身是一个长方体，顶部是球体．
V 正四棱台＝1
3×5×(152＋15×11＋112)≈851.667(cm 3)，V 长方体＝18×8×8＝1152(cm 3)，
V 球＝4
3
π×33≈113.097(cm 3)，所以，这个奖杯的体积为V ＝V 正四棱台＋V 长方体＋V 球≈2116.76(cm 3)．
18．解：当侧面AA 1B 1B 水平放置时，纵截面中水液面积占1－14＝34，所以水液体积与三棱柱体积比为3
4
.
当底面ABC 水平放置时，液面高度为8×3
4
＝6.
19．解：(1)设内接圆柱底面半径为r .其轴截面如图D62.
S 圆柱侧＝2πr ·x . ①∵r R
＝H －x H ，∴r ＝R
H
(H －x )． ②
②代入①，得S 圆柱侧＝2πx ·R H (H －x )＝2πR
H
(－x 2＋Hx )(0<x <H )．
(2)S 圆柱侧＝2πR H (－x 2
＋Hx )＝2πR H ⎣⎢⎡⎦⎥⎤－⎝ ⎛⎭⎪⎫x －H 22＋H 24，
∴x ＝H 2
时，S 圆柱侧最大＝πRH 2
.
20．解：如图D63，过高OO 1和AD 的中点E 作棱锥和棱台的截面，得棱台的斜高EE 1和棱锥的斜高EO 1. 设OO 1＝h ，所以
S 锥侧＝1
2·4b ·EO 1＝2bEO 1，
S 台侧＝1
2(4a ＋4b )·EE 1＝2(a ＋b )·EE 1.所以2bEO 1＝2(a ＋b )EE 1. ①
由于OO 1E 1E 是直角梯形，其中OE ＝b 2，O 1E 1＝a
2
.
由勾股定理，有EE 21＝h 2＋⎝ ⎛⎭⎪⎫a 2－b 22，EO 21＝h 2＋⎝ ⎛⎭⎪⎫
b 22
. ②
①式两边平方，把②代入，得b 2
⎝ ⎛⎭⎪⎫h 2＋b 2
4＝(a ＋b )2⎣⎢⎡⎦
⎥⎤h 2
＋⎝ ⎛⎭⎪⎫a 2－b 22.
解得h 2
＝a 2b 2－a 24a ＋2b ，所以h ＝12 a 2b 2－a 2a ＋2b
.
显然，由于a >0，b >0，所以此题当且仅当a <2b 时才有解．。