2013年九年级数学中考模拟题 (39)
2013年中考数学模拟题(含答案)

2013年中考数学模拟题一、选择题(每小题3分,共15分)1.下列运算正确的是 ( )A. x 2·x 3=x 6B. –2x -2=- 14x 2 C.(-x 2)3=x 5 D.-x 2-2x 2=-3x 2 2.在平面直角坐标系中,点P (-1,-1)关于x 轴的对称点在( ) A.第一象限 B. 第二象限C.第三象限D. 第四象限3.某班5位同学的身高(单位:厘米)分别155,160,160,161,169,这组数据中,下列说法错误的是 ( )A.众数是160B.中位数是160C.平均数是161D.方差是24.如图,PA 切⊙O 于A ,∠P=30°,OP =2,则⊙O 的半径的是 ( )A.21B.1C. 2D.45.已知圆锥的母线长为5cm ,底面半径为3cm ,则此圆锥的侧面积为 ( )A. 12πcm 2B. 15πcm 2C. 20πcm 2D. 30πcm 2二、填空题(每小题4分,共20分)6.已知代数式2x 2-x+1的值等于2,则代数式 4x 2-2x+5的值为___________.7.若反比例函数y=- x8的图象经过点(m ,-2m ),则m 的值为___________.8、十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是黄灯的概率是________.9.如图,CD⊥AB,BE⊥AC,请你再添加一个条件:________使ΔABE≌ΔACD。
10.如图,在 RtΔABC中,∠C=90°,AB=4cm,AC=23cm,以B为圆心,以BC为半径作弧交AB于D,则阴影部分的面积是 _____cm2。
三、解答题(每小题6分,共30分)11.有这样一道题:“计算x2-2x+1x2-1÷x-1x2+x-x 的值,其中x=2007”。
甲同学把“x=2007”错抄成“x=2070”,但他的计算结果也是正确的,你说这是怎么回事?12. ,并把解集在数轴上表示出来。
七一中学九年级数学中考模拟试题

2012—2013学年度下学期九年级数学五月检测试题命题人:肖显斌一、选择题 (共10小题, 每小题3分, 共30分) 1. 下列四个数: -3, -2, 0, 1, 最大的数是( )A . -3B . -2C . 0D . 1 2. 函数y =1-x 中自变量x 的取值范围是( )A . x ≥1B . x ≥-1C . x ≤1D . x ≤-1 . 3. 不等式组⎩⎨⎧≤-≥+32152x x 的解集表示在数轴上正确的是( )A B C D 4. 下列事件中必然事件有( )①掷一枚质地均匀的硬币正面朝上;②从一副普通扑克牌中任意抽取一张, 点数是6; ③三角形任意两边之和大于第三边. A .1个 B . 2个 C . 3个 D . 0个 5. 若x 1, x 2是方程x 2+4x -2=0的两根, 则x 1+x 2的值是( )A . 4B . -4C . 2D . -26. 由若干个大小相同的小正方体组成的几何体的 三视图如图所示, 则这个几何体只能是( )A B C D 7. 如图, 点E 在BC 的延长线上, 下列条件中不能..判定AB ∥CD 的是( ) A .∠1=∠2; B .∠B =∠DCE ;C .∠3=∠4;D .∠D +∠DAB =180°8. 如图是经典手机游戏“俄罗斯方块”中的图案, 图1 中有8个矩形, 图2中有11个矩形, 图3 中有15个矩形, 根据此规律, 图5中共有( )个矩形A . 19B . 25C . 26D . 319. 九年级某班在一次数学考试中某道单选题的答题情况进行了统计, 制成如下统计图, 下列判断中正确的有( )个①该班共有50人参加考试 ②选A 有8人 ③若每道选择题的分值为3分, 该题正确答案是C , 则这个班此题的均分为1.68. A . 0 B . 1 C . 2 D . 3 10. 已知: AB 是⊙O 的直径, AD 、BC 是⊙O 的切线, P 是⊙O 上一动点,若AD =3, AB =4, BC =6, 则△PCD 的面积的最小值是( ) A . 2 B . 4 C . 8 D . 9 二、填空题(每小题3分, 共18分) 11. 计算:sin 30︒= .12. 据从民政部获悉, 4月20日四川芦山发生里氏7.0级大地震以来, 全国各地积极支持芦山地震灾区抗震救灾, 在短时间内各地共向芦山地震灾区捐款18950万元, 将18950万元用科学记数法表示为 元. 13. 某班六名女生的体重(单位:kg )分别是:35, 36, 37, 39, 39, 40. 这组数据的中位数是 . 14. 小华和爷爷在一环形跑道上匀速跑步, 两人在同一起点顺时针出发, 两人离起点较近的环形距离y 与时间t 之间关系如图所示, 出发后小华第一次与爷爷相遇的时间为 分. 15、如图, 双曲线x k y =与x y 6-=上分别有两点A 、B , AB ∥x 轴, 直线y =x +b 过点A , 另交xky =于C , 交x 轴、y 轴于M 、N , 若MC =CA =AN , 且△ABC 面积为1, 则k = .第14题 第15题 第16题16. 已知: E 、F 分别是矩形ABCD 的边AD 、CD 上一点, 且DF =CF , ∠DEF =2∠CBF ,若AB =4, BC =6, 则AE = . 三、解答题 17. (6分)解方程:1321x x =+. 18. (6分)已知一次函数b kx y +=的图象经过A (0, 2), B (-3, 1), 求不等式2kx +1≥0的解集. 19. (6分)在 △ABC 中, D 为BC边的中点, DE ⊥ AB ,DF ⊥ AC ,垂足分别为E 、F , 且DE =DF . 求证:AB =AC .图1图2图320. (7分)小明和小华做游戏, 将如图所示两个转盘各转动一次, 再将所转到的两个数字相加. (1) 用树状图或列表法写出所有可能得到的结果;(2) 若两数之和为奇数, 小明胜; 否则小华胜.21. (7分) 在直角坐标系中, △ABC 的顶点坐标是A (-1, 2), B (-3, 1), C (0, -1).(1) 若将ABC △向右平移2个单位得到A B C '''△, 画出A B C '''△, A 点的对应点A '的坐标是______;(2) 若将A B C '''△绕点C ′按顺时针方向旋转90后得到∆A 1B 1C ′, 则A ′点对应点A 1的坐标 是 .(3) 直接写出两次变换过程中线段BC 扫过的面积 之和为 .22. (8分) 已知:AB 、AC 是⊙O 的切线, B 、C 是切点, BD 是⊙O 的直径, 连接AO 、CD .(1) 求证:OA ∥CD ;(2) 过D 点作AC 的平行线, 分别交AB 、AO 于E 、F , 若AB =BD , 求tan ∠BDE 的值.23. (10分)一座拱桥的轮廓是抛物线型(如图1所示), 拱高6m , 跨度20m , 相邻两支柱间的距离均为5m .(1) 将抛物线放在所给的平面直角坐标系中(如图2所示), 求抛物线的解析式; (2) 求支柱EF 的长度;(3) 拱桥下地平面是双向行车道(正中间是一条宽2m 的隔离带), 若并排行驶宽2m 、高3m 的汽车,要求车与车之间, 车与隔离带之间的间隔均为0.5米, 车与桥的竖直距离至少为0.1米, 问其中一条行车道最多能同时并排行驶几辆车?图1 图224. (10分) 如图1, 在RT △ABC 中, ∠ACB =90°(1) 以AB 为直角边向形外作Rt △ABD , 并且与Rt △ABC 相似. 若AC =4, BC =3, 求△ABD 的周长.(2) 如图2, 设正方形MDHN 、DEFG 、EPQR 的周长分别为C 1、C 2、C 3, 求证: C 1+C 3=C 2. (3) 如图3, 作CD ⊥AB , DE ⊥ AC , 垂足分别为D 、E , 设△ADE , △BCD , △ABC 的周长分别为C 1、C 2、C 3. 直接写出321C C C +的最大值为________.图1 图2 图325. (12分) 已知: 直线y =21x -3分别交x 轴于A , 交y 轴于B , 抛物线C 1: y =x 2+4x +b 的顶点D 在直线AB 上.(1) 求抛物线C 1的解析式;(2) 将抛物线C 1的顶点沿射线DA 的方向平移得抛物线C 2, 抛物线C 2交y 轴于C , 顶点为E , 若CE ⊥AB , 求抛物线C 2的解析式;(3) 将直线AB 沿y 轴正方向平移t (t >0)个单位得直线l , 抛物线C 1的顶点在直线AB 上平移得抛物线C 3, 直线l 和抛物线C 3相交于P 、Q , 求当t 为何值时, P 、Q 之间的距离为45?。
2013年中考数学模拟试题及答案
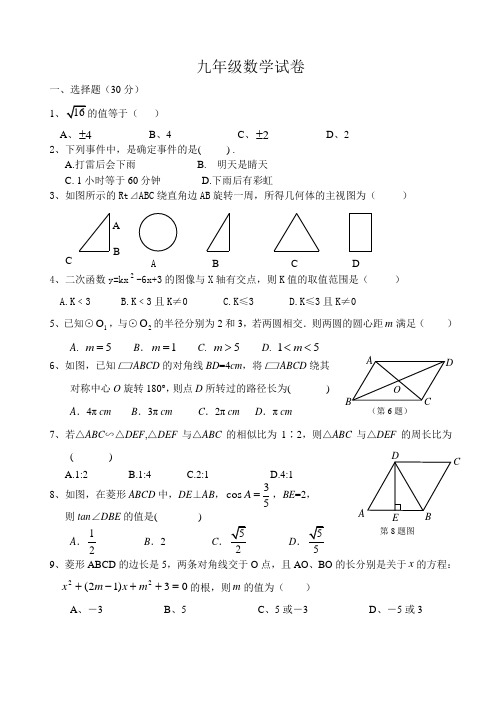
九年级数学试卷一、选择题(30分) 1)A 、4±B 、4C 、2±D 、2 2、下列事件中,是确定事件的是( ) .A.打雷后会下雨B. 明天是睛天C. 1小时等于60分钟D.下雨后有彩虹3、如图所示的Rt ⊿ABC 绕直角边AB 旋转一周,所得几何体的主视图为( )4、二次函数y=kx 2) A.K ﹤3 B.K ﹤3且K ≠0 C.K ≤3 D.K ≤3且K ≠05、已知⊙1O ,与⊙2O 的半径分别为2和3,若两圆相交.则两圆的圆心距m 满足( ) A . 5m = B .1m = C . 5m > D . 15m <<6、如图,已知□ABCD 的对角线BD =4cm ,将□ABCD 绕其对称中心O 旋转180°,则点D 所转过的路径长为( ) A .4π cmB .3π cmC .2π cmD .π cm7、若△ABC ∽△DEF ,△DEF 与△ABC 的相似比为1∶2,则△ABC 与△DEF 的周长比为( )A.1:2B.1:4C.2:1D.4:1 8、如图,在菱形ABCD 中,DE ⊥AB ,3cos 5A =,BE =2, 则tan ∠DBE 的值是( )A .12 B .2 C .2 D .59、菱形ABCD 的边长是5,两条对角线交于O 点,且AO 、BO 的长分别是关于x 的方程:03)12(22=++-+m x m x 的根,则m 的值为( )A 、-3B 、5C 、5或-3D 、-5或3CC第8题图(第6题)ABCDO10、已知二次函数2(0)y ax bx c a =++≠的图象如右图所示, 下列结论: ①0abc > ②b a c <+③20a b += ④()(1a b m am b m +>+≠的实数), 其中正确的结论有( )A 1个B .2个C . 3个D .4个二、填空题(18分) 11、在函数y =x 的取值范围是 . 12、已知三角形两边长是方程2560x x -+=的两个根,则三角形的第三边c 的取值范围是13、从1,2,3,…,19,20这二十个整数中任意取一个数,这个数是3的倍数的概率是 . 14、在半径为1的⊙O 中,弦AB 、AC 的长分别为2和3,则∠BAC 的度数为 。
2013年九年级第一次模拟考试数学试卷及答案201339

………………………………………………装…………订…………线………………………………………………2013年九年级第一次模拟考试数学试卷本试卷满分为120分,考试时间为120分钟.一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.9-的相反数是 ( )A .19-B .19C .9-D .92.首届中国(北京)国际服务贸易交易会(京交会)于2012年6月1日闭幕,本届京交会期间签订的项目成交总金额达60 110 000 000美元,将60 110 000 000用科学记数法表示应为( ) A .96.01110⨯ B .960.1110⨯ C .106.01110⨯D .110.601110⨯3.已知:直线l 1∥l 2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于( )A .30°B .35°C .40°D .45°4.文文设计了一个关于实数运算的程序,按此程序,输入一个数后,输出的数比输入的数的平方小1( )A .5B .6C .7D .85.如图,在平行四边形ABCD 中,AD =5,AB =3,AE 平分∠BAD 交BC 边于点E ,则线段12 l 1l 2BE ,EC 的长度分别为 ( )A .2和3B .3和2C .4和1D .1和46.我市某一周每天的最高气温统计如下:27,28,29,29,30,29,28(单位:℃),则这组数据的极差与众数分别为( ) A .2,28B .3,29C .2,27D .3,28 7.化简xxx x -+-112的结果是( )A .x +1B .x -1 C .—x D . x8.如图是一个用相同的小立方块搭成的几何体的三视图,则 组成这个几何体的小立方块的个数是 ( )A .2B .3C .4D .59.如图,已知正方形ABCD 的对角线长为2,将正方形ABCD 沿直线EF 折叠,则图中阴影部分的周长 为( )A . 8B . 4C . 8D . 610.已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列结论:①240b ac ->;②0abc >;③80a c +>; ④930a b c ++<.其中,正确结论的个数是 ()A .1B .2C .3D .4二、填空题(本大题共6个小题;每小题3分,共18分.把答案写在题中横线上)11.已知(m ⎛=⨯- ⎝⎭,则m 的范围是 . 12.如图,在第1个△ABA 1中,∠B =20°,AB=A 1B ,在A 1B上取一点C ,延长AA 1到A 2,使得A 1A 2=A 1C ;在A 2C 上取一点D ,延长A 1A 2到A 3,使得A 2A 3=A 2D ;……,按此做法进行下去,第n 个三角形的以A n 为顶点的内角的度数为 .13.如图,圆柱形玻璃杯高为12cm 、底面周长为18cm ,在杯内离杯底4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为 cm .14.已知点A (m ,0)是抛物线221y x x =--与x 轴的一个交点,则代数式2242013m m -+的值是 .15.如图,已知∠ABC =90°,AB =πr ,BC =πr2,半径为r 的⊙O 从点A 出发,沿A →B →C方向滚动到点C 时停止,则圆心O 运动的路程是.16.如图,在等腰梯形ABCD 中,AD ∥BC ,BC =4AD =AB CD EA 1A 2A 3A 4A n∠B =45°,直角三角板含45°角的顶点E 在边 BC 上移动,一直角边始终经过点A ,斜边与CD 交于 点F ,若△ABE 为等腰三角形,则CF 的长等于 .三、解答题(本大题共10个小题;共82分.解答应写出文字说明、证明过程或演算步骤)17.(本题满分4分)计算:02112sin30( 3.14)()2π---︒+-+.18.(本小题满分4分)如图,在边长为1的小正方形组成的网格中,△AOB 的三个顶点均在格点上,点A 、B 的坐标分别为(3,2)、(1,3).△AOB 绕点O 逆时针旋转90º后得到△A 1OB 1. (1)点A 关于O 点中心对称的点的坐标为 ; (2)点A 1的坐标为 ;(3)在旋转过程中,点B 经过的路径为 1BB ,那么 1BB 的长为 .19.(本小题满分8分)某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.(1)该顾客至少可得到元购物券,至多可得到元购物券;(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.20.(本小题满分8分)6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:(1)直接写出a的值,并补全频数分布直方图;(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?21.(本小题满分8分)为配合“书香进校园”活动的开展,学校决定为各班级添置图书柜.原计划用4000元购买若干个书柜,由于市场价格变化,每个单价上涨20元,实际购买时多花了400元.求书柜原来的单价是多少元?22.(本小题满分9分)如图,△ABC 是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB 、BC 、CA 跑步(小路的宽度不计).观测得到点B 在点A 的南偏东30°方向上,点C 在点A 的南偏东60°的方向上,点B 在点C 的北偏西75°方向上,AC 间距离为400米.1.414 1.732≈≈)23.(本小题满分9分)如图,矩形OABC 的顶点A 、C 分别在x 、y 轴的正半轴上,点D 为对角线OB 的中点,点E (4,n )在边AB 上,反比例函数ky =x(k ≠0)在第一象限内的图象经过点D 、E ,且tan ∠BOA =12. (1)求边AB 的长;(2)求反比例函数的解析式和n 的值;(3)若反比例函数的图象与矩形的边BC 交于点F ,将矩形折叠,使点O 与点F 重合,折痕分别与x 、y 轴正半轴交于点H 、G ,求线段OG 的长.北24.(本小题满分10分)(1)如图1,在矩形ABCD 中,AB=2BC ,M 是AB 的中点.直接写出∠BMD 与∠ADM 的倍数关系;(2)如图2,若四边形ABCD 是平行四边形, AB=2BC ,M 是AB 的中点,过C 作CE ⊥AD 与AD 所在直线交于点E .若∠A 为锐角,则∠BME 与∠AEM 有怎样的倍数关系,并证明你的结论.M D BA CE ADC25.(本小题满分10分)某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为等腰直角三角形,直角边长(单位:cm)在10~60之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的直角边长成正比例,在营销过程中得到了下面表格中的数据.(1)求一张薄板的出厂价与直角边长之间满足的函数关系式;(2)已知出厂一张直角边长为20cm的薄板,获得的利润是80元(利润=出厂价-成本价).①求一张薄板的利润与直角边长之间满足的函数关系式;②当直角边长为多少时,出厂一张薄板获得的利润最大?最大利润是多少?参考公式:抛物线2(0)y ax bx c a=++≠的顶点坐标是24() 24b ac ba a--,薄板的直角边长(cm)20 50 出厂价(元/张)100 22026.(本小题满分12分)如图,已知A (5,0),B (3,0),点C 在y 轴的正半轴上,45CBO ︒∠=,CD AB ∥,90CDA = ∠.点P 从点Q (8,0)出发,沿x 轴向左以每秒1个单位长的速度运动,运动时间为秒.(1)求点D 的坐标;(2)当∠CPB =120°时,求的值;(3)以点P 为圆心,PC 为半径的⊙P 随点P 的运动而变化,当⊙P 与四边形ABCD 的边(或边所在的直线)相切时,求的值.数学模拟参考答案一一、选择题1D 2C 3B 4B 5B 6B 7D 8C 9C10D二、填空题 11.5<m <6;12.0180()2n -;13.15;14.2015;15.2πr ;16.25,2或432- 三、解答题 17、解:原式=11214=52-⨯++.………………………4分 18、解:(1)(﹣3,﹣2). ………………………1分(2) (﹣2,3). ………………………2分(3. ………………………4分19、解:(1)10,50. ………………………4分 (2)画树状图:………6分从上图可以看出,共有12种等可能结果,其中大于或等于30元共有8种可能结果,因此, P (不低于30元)=82123=. ………………………8分 20、2.解:(1)a =0.28. ………………………1分补全频数分布直方图如下: ………………………3分 (2)成绩优秀的学生约为:1000×3228100+=600(人).……5分 (3)被抽查的学生中得分为80分的至少有11人. …………8分 21、解:设书柜原来的单价是x 元, …………1分 由题意得:40004400x x 20=+,解得:x =200. ………6分 经检验:x =200是原分式方程的解.答:书柜原来的单价是200元. …………8分22、解:延长AB 至D 点,作CD ⊥AD 于D .根据题意得∠BAC =30°,∠BCA =15°, ∴∠DBC =∠DCB =45°. …………2分 在Rt △ADC 中,∵AC =400米,∠BAC =30°,∴CD =BD =200米. …………4分 ∴BCAD∴AB =AD -BD =(200)米. …………7分∴三角形ABC 的周长为400+200≈829(米).∴小金沿三角形绿化区的周边小路跑一圈共跑了829米.………9分 23、解:(1)∵点E (4,n )在边AB 上,∴OA =4,在Rt △AOB 中,∵tan ∠BOA =12,∴AB =OA ×tan ∠BOA =4×12=2. …………2分 (2)由(1),可得点B 的坐标为(4,2),∵点D 为OB 的中点,∴点D (2,1). ∵点D 在反比例函数ky=x(k ≠0)的图象上, ∴21k =,解得k =2.∴反比例函数解析式为2y=x.……4分 又∵点E (4,n )在反比例函数图象上,∴21n==42.……6分(3)如图,设点F (a ,2),∵反比例函数的图象与矩形的边BC 交于点F ,∴22=a,解得a =1.∴CF =1.连接FG ,设OG =t ,则OG =FG =t ,CG =2﹣t ,在Rt △CGF 中,GF 2=CF 2+CG 2,即t 2=(2﹣t )2+12,解得t =54,∴OG =t =54.…………9分24、 (1)∠BMD= 3 ∠ADM ………………3分 (2)联结CM ,取CE 的中点F ,联结MF ,交DC 于N ,四边形ABCD 是平行四边形,∴A E ∥BC,∴四边形ABCE 是梯形.………………7分∵M 是AB 的中点,∴MF ∥AE ∥BC ,∴∠AEM=∠1,∠2=∠4,∵AB=2BC ,∴BM=BC ,∴∠3=∠4.∵CE ⊥AE ,∴MF ⊥EC ,又∵F 是EC 的中点,∴ME=MC ,∴∠1=∠2.∴∠1=∠2=∠3.∴∠BME =3∠AEM . ………………10分25、解:依题意,设等腰直角三角形薄板的直角边长为x , 则221mx y =成本价,n kx y +=出厂价(10<x <60 ) ,则y y y =-利润出厂价成本价 ………………3分 (1)在n kx y +=出厂价(10<x <60 )中,20=x 时,100=y ;50=x 时,220=yFAMBCED4321∴⎩⎨⎧=+=+2205010020n k n k ,∴⎩⎨⎧==204n k ,∴204+=x y 出厂价(10<x <60 );………………5分(2)221204mx x y y y -+=-=成本出厂价利润,且20=x 时,80=y , ∴802021202042=⋅-+⨯m 解得:101=m ,∴2042012++-=x x y 利润; ………………7分(3)在2042012++-=x x y 利润中,由参考公式,40)201(24=-⨯-=x ,且(10<40<60 ),所以,出厂一张直角边长为40cm 的薄板获得的利润最大,最大利润是10020404402012=+⨯+⨯-=最大利润y (元). ………………10分 26、解:(1)如图,CBO ︒ ∠=45,∴△CBO 是等腰直角三角形,故3COBO ==,∴(0,3)C ,又∵A(5,0),CD AB ∥,90CDA =∠,∴D(5,3); ………………3分 (2)∵∠CPB=120°,∴∠PCO=30°,在RtPCO ∆中,t an OP OC =⋅∠,∴38-=-=OP OQ t ; ………………5分(3) 以点P 为圆心,PC 为半径的P ⊙随点P 的运动而变化,P ⊙与四边形ABCD 的边相切,有三种情况:①P ⊙与BC 边相切时,C 是切点,如图1, 此时,PCBC ⊥,CBO ︒ ∠=45,∴△PBC 为等腰直角三角形, ∴3===OC OB PO , ∴11=+=OQ PO PQ ,∴111==PQt; ………………7分 ②P ⊙与DC 边相切时,C 是切点,如图2,此时,PC OC 与重合, ∴8=PQ ,∴81==PQt ;…………9分 ③P ⊙与AD 边相切时,A 是切点,如图3,此时,PA PC =,设x OP =,则在Rt POC ∆中,由勾股定理得:222OC OP PC=-,9)5(22=--x x ,∴6.1=x ,∴4.66.18=-=-=OP OQ PQ ,4.61==PQt . 综上所述,满足条件的值共有三个,即,11,或8,或6.4.………………12分。
2013-2014学年九年级数学中考考前复习试卷及答案

2013-2014学年下学期4月模拟考试数学试卷(总分:150分,时间:120分钟)一、选择题(每小题3分,10个小题,共30分)1 ).3A - .3B .3C ± .D 92、13-的相反数的倒数是( ) .3A 1.3B .3C - 1.3D -3、下列各数:22060,,,172π∙中无理数个数是( ).2A 个 .3B 个 .4C 个 .5D 个4、下列运算中,计算结果正确的是( ).321A x x -= 2.222B x x x += 325.()C a a -=- 2.D x xx ⋅= 5、下列函数中,y 随x 的增大而减小的是( ).A y x =- 1.B y x =- 3.(0)C y x x=-> .(0)D y x x => 6、正在修建的巴陕高速公路建成后,巴中到西安只要3小时左右。
其设计时速:80公里/时,路线全长113公里,总投资137.1亿元。
把数值137.1亿用科学计数法表示为( )9.1.37110A ⨯ 10.1.37110B ⨯ 11.1.37110C ⨯ 12.1.37110D ⨯7、下列调查,适合用普查方式的是( ).A 了解一批水稻种子的合格率 .B 了解恩阳河中鱼的种类.C 了解九年级一班学生对“社会主义核心价值观”的知晓率 .D 了解巴中电视台《新闻365》栏目的收视率8、图1是二次函数222y ax bx a =++- (,a b 为常数)的图像,则a 的值是( ).1B .2C -.D9、成巴高速公路全长308km ,一辆货车和一辆轿车同时从巴中、成都两地相向开出,经1小时45分钟到达同一地点,相遇时,轿车比货车多行30km ,设轿车、货车的速度分别是x /km h ,y /km h 则下列方程组正确的是( )7()308.430x y A x y ⎧+=⎪⎨⎪-=⎩ 105()308.105()30x y B x y +=⎧⎨-=⎩7()3084.7()304x y C x y ⎧+=⎪⎪⎨⎪-=⎪⎩ 45()308.45()30x y D x y +=⎧⎨-=⎩10、如图2,在平面直角坐标系中, 点P 在第一象限,P 与x 轴相切于点Q ,与y 轴交于(0,2)M 、(0,8)N 两点,则点P 的坐标是( ).(5,3)A .(5,4)B .(4,5)C .(3,5)D二、填空题(每小题3分,10个小题,共30分) 11、把多项式:25510x x +-分解因式______________. 12、函数y =x 的取值范围是___________. 13、1O 与2O 的半径分别是方程27110x x -+=的两根,如果两圆相切,那么圆心距是______________________.14、分式方程:2231x x x x=+-的解是___________________.15、某药品原价每盒25元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在每盒售价16元,则该药品平均每次降价的百分率是_____________.16、已知关于x 的一元二次方程x 2-4x+k-5=0有两个相等的实数根,则k 的值为______________.17、如图3,一束光线从y 轴上点(0,1)A 发出,经过x 轴上点C 反射后,经过点(6,2)B , 则点C 的坐标是___________.18、如图4,已知矩形OABC 的面积为1003,它的对角线OB 与 双曲线ky x=相交于点D ,且:5:3OB OD =,则k =_______.19、已知点1(,3)P a 和2(4,)P b 关于y 轴对称,则2014()a b +的值为_____.20、二次函数223y x =的图像如图5所示, 点1A ,2A ,3A ,,2014A 在y 轴正半轴 上,1B ,2B ,3B ,,2014B 在二次函数第一象限的图像上,若11OB A ,122A B A ,233A B A ,,201320142014A B A 都为等边三角形,求:11OB A 的边长_______,122A B A 的边长20132014A B 初三4月月考数学试题答卷一、选择题:10小题,共tan 2+23、(8分)先化简,再求值22122()121x x x x x x x x ----÷+++,其中x 满足210x x --=.24、(8分)解不等的式组:212(1)1x xx-≤⎧⎨+≥-⎩,并将解集在数轴上表示出来.25、(8分)若方程组:ax y bx by a+=⎧⎨-=⎩的解是11xy=⎧⎨=⎩,求2()()()a b a b a b+--+的值.26、(10分)某学校团委选派“志愿者”到各个街道进行党的群众路线知识宣传,若每个街道安排4人,还剩78人,若每个街道安排8人,最后一个街道不足8人,但不少于4人。
2013年徐州市中考模拟考试数学试题

2013年徐州市中考模拟考试数学试题一、选择题:(本大题共8个小题.每小题3分;共24分) 1.3-的倒数是( )A .13-B .13C .3-D .32.下列运算正确的是( ) A.632a a a =⋅ B.()236aa =C.55a a a ÷= D.224x x x +=3.估算219+的值是在( )A. 5和6之间B. 6和7之间C. 7和8之间D. 8和9之间4.如图,AD BC ∥,点E 在BD 的延长线上,若155ADE ∠=,则DBC ∠的度数为( ) A.35B.50C.45D.255.在()()222y xy x 的括号( )中,分别填上“+”或“-”,在所得的代数式中,能构成完全平方式的概率是( )A.41B. 21C. 43D. 16.与如图所示的三视图对应的几何体是( )7.小明在九年级进行的六次数学测验成绩如下(单位:分):76、82、91、85、84、85,则这次数学测验成绩的众数和中位数分别为( )A .91,88B .85,88C .85,85D .85,84.58.如图,AB 是半圆ACB 的直径,半径OC ⊥AB 于点O ,AD 平分∠CAB 交弧BC 于点D ,连接CD 、OD ,给出以下四个结论:(1)AC ∥OD (2)CE=OE (3)△ODE ∽△ADO (4)2CD 2=CE ×AB 其中正确的个数是( )A. 1B. 2C. 3D. 4ADECA B C D二、填空题:(本大题共10个小题.每小题3分,共30分)9.函数11+=xy自变量x的取值范围是______________.10.分解因式:29xy x-=____________11.2012年江苏省财政收入为5860亿元,用科学记数法表示“5860亿”的结果是:12.若关于x的方程220xx m--=有两个不相等的实数根,则m的取值范围是.13.代数式238a b-++的值为18,那么代数式962b a-+14.如图,已知△ABC中,∠A=50°,剪去∠A15.如图,平行四边形ABCD中,AB3=,5BC=,AC的垂直平分线交AD于E,则CDE△的周长是__________.16.点P在双曲线(0)ky kx=≠上,点(12)P',与点P关于y轴对称,则此双曲线的解析式为.17.如图,如果将半径为9cm的圆形纸片剪去一个13圆周的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为18.一次函数1y kx b=+与2y x a=+的图像如图,则下列结论①0k<;②0a>;③当3x<时,12y y<中,正确的序号是三、解答题:(本大题共10个小题,计86分.解答应写出文字说明、演算步骤.)19. (本小题满分10分)(1021)(1);+-(2)化简:23111a a aa a a-⎛⎫-⎪-+⎝⎭·第18題C20. (本小题满分10分)(1)解方程1x -3+1=2-x x -3. (2) 解不等式组205121123x x x ->⎧⎪+-⎨+⎪⎩,≥,21.(本小题满分8分)某小区从不同住宅楼中随机选取了200名居民,调查小区居民双休日的学习状况,并将得到的资料制成扇形统计图和频数分布直方图.(1)在这个调查中,200名居民双休日在家学习的有____________人;(2)在这个调查中,在图书馆等场所学习的居民学习时间的平均数和众数分别是多少? (3)估计该小区2 000名居民双休日学习时间不少于4小时的人数.22.(本题7分)北京时间2013年4月20日8:02,在四川雅安发生7.0级强震,政府迅速派出救援队前往救援。
2013年湖北省黄冈中学中考第二次模拟考试数学试题

黄冈中学2013届初三年级第二次模拟考试数学试题一、选择题(本大题共8小题,每小题3分,共24分、在每小题给出的四个选顶中,只有一项是符合题目要求的)1、-32的绝对值是()A.32B.-32C.D.2、据法新社3月20日报道,全球管理咨询公司麦肯锡预计中国网络销售额将达到4200亿美元(约合2.6万亿人民币),中国将因此成为世界最大的网络零售市场,其中数据4200亿用科学记数法表示错误的是()A.4.2×103亿B.4.2×1011C.0.42×104亿D.4.2×107万3、如图,直线AB、CD相交于点O,OE平分∠BOD,若∠COE=160°,则∠AOC等于()A.20°B.40°C.60°D.80°4、下列计算正确的是()A.(-p2q)3=-p5q3B.(12a2b3c)÷(6ab2)=2abC.(a5)2=a7D.a3a4=a75、某几何体的三视图如图,则该几何体是()A.球B.圆柱C.圆锥D.长方体6、一元二次方程x2+x=1的两根为x1,x2,则()A.x1+x2=1B.x1x2=1C.x1+x2=-1D.7、如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,,则⊙O的半径为()A.B.C.8D.128、甲、乙两人准备在一段长为1200m的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100m处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两人之间的距离y(m)与时间t(s)的函数图象是()二、填空题(每小题3分,共21分)9、化简的结果是__________.10、分解因式4x2-8x+4=__________.11、如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连结CD,若AB=4cm,则△BCD的面积为__________cm2.12、“五一”期间,我市某街道办事处举行了“迎全运,促和谐”中青年篮球友谊赛.获得13、如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则k的值为__________.14、一个圆锥的母线长为4,侧面积为8π,则这个圆锥的底面圆的半径是__________.15、在平面直角坐标系中、若四条直线:l1:直线x=1;l2:过点(0,-1)且与x轴平行的直线;l3:过点(1,3)且与x轴平行的直线;l4:直线y=kx-3所围成的凸四边形的面积等于12,则k的值为__________.三、解答下列各题(本大题共75分)16、(本小题6分)解不等式组:17、(本小题6分)如图,△ABC与△BEF都是等边三角形,D是BC上一点,且CD=BE,求证:∠EDB=∠CHD.18、(本小题7分)2013年某市初中毕业生升学体育集中测试项目包括体能(耐力)类项目和速度(跳跃、力量、技能)类项目.体能类项目从游泳和中长跑中任选一项,速度类项目从立定跳远、50米跑等6项中任选一项.某校九年级共有200名女生在速度类项目中选择了立定跳远,现从这200名女生中随机抽取10名女生进行测试,下面是她们测试结果的条形图.(另附:九年级女生立定跳远的计分标准)九年级女生立定跳远计分标准(1)求这10名女生在本次测试中,立定跳远距离的极差,立定跳远得分的众数和平均数.(2)请你估计该校选择立定跳远的200名女生得满分的人数.19、(本小题6分)某班用抽签的方式,在甲、乙、丙、丁四位同学中挑选2位同学,代表该班参加学校卫生大检查,请用列表法或树状图法,求乙被选中的概率.20、(本小题7分)某学校后勤人员到一家文具店给九年级的同学购买考试用文具包,文具店规定一次购买400个以上,可享受8折优惠,若给九年级学生每人购买一个,不能享受8折优惠,需付款1936元;若多买88个,同样只需付款1936元,请问该学校九年级学生有多少人?21、(本小题8分)如图,已知等边△ABC,以边BC为直径的圆与AB、AC分别交于点D、点E.过点D作DF⊥AC,垂足为F.(1)判断DF与⊙O的位置关系,并证明你的结论;(2)过点F作FH⊥BC,垂足为H,若FH的长为4,求BC的长.22、(本小题8分)为了开发利用海洋资源,某勘测飞机欲测量一岛屿的两端A、B的距离,飞机在距海平面垂直高度为300米的C处测得端点A的俯角为60°,然后飞机沿着俯角30°的方向俯冲到D点,发现端点B的俯角为45°,而此时飞机距离海平面的垂直高度为100米,求岛屿两端A、B的距离.(结果精确到0.1米,)23、(本小题12分)某大学生创业团队新研发了一日常科技产品,决定在市场上进行试推销,已知团队试推销期间每天需固定支出各种费用(差旅费、人工费、托运费等)800元,该产品成本价为每个5元,经测算若按成本价5元/个进行推销时,每天可销售1440个,若每个每提高1元,每天就少销售120个,为便于测算,每个产品的售价x(元)只取整数,设该团队的日净收入为y元.(1)写出y与x的函数关系式,并指出x的取值范围;(2)团队若要使得日净收入最大,同时尽可能多的推销产品以扩大人气,则每个产品的售价应定为多少元?此时日净收入是多少?(3)若要求日净收入不低于3000元,则每个产品的售价应定在什么范围?24、(本小题15分)如图,点A在y轴上,点B在x轴上,以AB为边作正方形ABCD,P为正方形ABCD的对称中心,正方形ABCD的边长为,tan∠ABO=3.直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从原点O出发沿OM方向以个单位每秒速度运动,设运动时间为t秒.(1)分别写出A,C,P三点的坐标;(2)经过坐标原点O且顶点为P的抛物线是否经过C点,请说明理由?(3)当t为何值时,△ANO与△DMR相似?(4)设△HCR面积为S,求S与t的函数关系式;并求以A、B、C、R为顶点的四边形是梯形时t的值.。
2013年中考数学模拟试卷(一、二)(A3版)-----

2013年中考数学模拟试卷(一)(满分120分,考试时间100分钟)一、选择题(每小题3分,共24分)1.9的平方根是【】A.3 B.-3 C.±3 D.62.某种微粒子,测得它的质量为0.000 067 46克,这个质量用科学记数法表示(保留三个有效数字)应为【】A.6.75×10-5克B.6.74×10-5克C.6.74×10-6克D.6.75×10-6克3.下列图形中,既是轴对称图形又是中心对称图形的共有【】A.1个B.2个C.3个D.4个4.某市5月上旬前五天的最高气温如下(单位:°C):28,29,31,29,33,对这组数据,下列说法错误的是【】A.平均数是30 B.众数是29 C.中位数是31 D.极差是55.如图,二次函数2y ax bx c=++的图象经过(-1,1),(2,-1)两点,下列关于这个二次函数的叙述正确的是【】A.当x=0时,y的值大于1 B.当x=3时,y的值小于0C.当x=1时,y的值大于1 D.y的最大值小于水平面主视方向第5题图第6题图第7题图6.两个大小不同的球在水平面上靠在一起,组成如图所示的几何体,则该几何体的左视图是【】A.两个外离的圆B.两个相交的圆C.两个外切的圆D.两个内切的圆A.30°B.45°C.60°D.90°FEDA第8题图第10题图第13题图二、填空题(每小题3分,共21分)∠AEC=_________.11.圆锥的底面圆直径和母线长均为80cm,则它的侧面展开图的圆心角是_________.12.某市初中毕业男生体育测试项目有四项,其中“立定跳远”、“1 000米跑”、“掷实心球”为必测项目,另一项从“篮球运动”或“一分钟跳绳”中选一项测试.小亮、小明和大刚从“篮球运动”或“一分钟跳绳”中选择同一个测试项目的概率是__________.16.(8分)先化简2111122xx x x⎛⎫-÷⎪-+-⎝⎭,然后从-2≤x≤2的范围内选择一个合适的整数作为x的值代入求值.17.(9分)为了更好地宣传吸烟的危害,某中学九年级一班数学兴趣小组设计了如下调查问卷,调查了部分吸烟人群,并将调查结果绘制成统计图.42%调查结果的扇形统计图调查结果的条形统计图ACBDE根据以上信息,解答下列问题:(1)本次接受调查的总人数是_________人,并把条形统计图补充完整.(2)在扇形统计图中,C选项的人数百分比是________,E选项所在扇形的圆心角的度数是________.(3)若某地区约有烟民14万人,试估计对吸烟有害持“无所谓”态度的约有多少人?M A E F D B C 18.(9分)已知:如图,四边形ABCD 是正方形,BD 是对角线,BE 平分∠DBC 交DC 于E 点,交DF 于M 点,F 是BC 延长线上一点,且CE =CF . (1)求证:BM ⊥DF ;(2)若正方形ABCD 的边长为2,求ME ·MB 的值.19.(9分)甲、乙两地相距300km ,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA 表示货车离甲地的距离y (km )与时间x (h )之间的函数关系,折线BC -CD -DE 表示轿车离甲地的距离y (km )与时间x (h )之间的函数关系.请根据图象,解答下列问题:(1)线段CD 表示轿车在途中停留了________h ;(2)求线段DE 对应的函数解析式;(3)求轿车从甲地出发后经过多长时间追上货车.20.(9分)如图所示,当小华站立在镜子EF 前的A 处时,他看自己的脚在镜中的像的俯角为45°;如果小华向后退0.5米到B 处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据1.73)21.(10分)某商店为了抓住文化艺术节的商机,决定购进A ,B 两种艺术节纪念品.若购进A 种纪念品8件,B 种纪念品3件,需要950元;若购进 A 种纪念品5件,B 种纪念品6件,需要800元. (1)求购进A ,B 两种纪念品每件各需多少元.(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这 100件纪念品的资金不少于7 500元,但不超过7 650元,那么该商店共有几种进货方案?(3)若销售每件A 种纪念品可获利润20元,每件B 种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?22.(10分)在正方形ABCD 中,对角线AC ,BD 交于点O ,点P 在线段BC 上(不与点B 重合),∠BPE =12∠ACB ,PE 交BO 于点E ,过点B 作BF ⊥PE ,垂足为F ,交AC 于点G . (1)当点P 与点C 重合时(如图1),求证:△BOG ≌△POE ; (2)通过观察、测量,猜想:BF PE=________,并结合图2证明你的猜想;(3)把正方形ABCD 改为菱形,其他条件不变(如图3),若∠ACB =α,求BF PE的值.(用含α的式子表示)(1)求过点A ,O ,B 的抛物线解析式.(2)在(1)中抛物线的对称轴上是否存在点M ,使△AOM 的周长最小?若存在,求出点M 的坐标;若不存在,请说明 理由.(3)在x 轴下方的抛物线上是否存在一点P ,过点P 作x 轴 的垂线,交直线AB 于点E ,线段OE 把△AOB 分成两个三角 形,使其中一个三角形的面积与四边形BPOE 的面积之比为 2:3?若存在,求出点P 的坐标;若不存在,请说明理由.y11ACD E FG OAD E F G OOGF ED BCA2013年中考数学模拟试卷(二)(满分120分,考试时间100分钟)一、选择题(每小题3分,共24分)1. 某市1月份某天的最高气温是5℃,最低气温是-3℃,那么这天的温差(最高气温减最低气温)是【 】A .-2℃B .8℃C .-8℃D .2℃2. 下列四个图形中,既是轴对称图形又是中心对称图形的有【 】A .4个B .3个C .2个D .1个3. 某市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x 棵, 则根据题意列出方程正确的是【 】 A .5(211)6(1)x x +-=- B .5(21)6(1)x x +=- C .5(211)6x x +-=D .5(21)6x x +=4. 一次函数|1|y mx m =+-的图象过点(0,2),且y 随x 的增大而增大,则m =【 】A .-1B .3C .1D .-1或35. 如图所示,把一张矩形纸片对折,折痕为AB ,再把以AB 的中点O 为顶点的平角∠AOB 三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O 为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是【 】BOA BAAA .正三角形B .正方形C .正五边形D .正六边形6. 在平面直角坐标系中,对于平面内任意一点(x ,y ),若规定以下两种变换:①f (x ,y ) = (y ,x ),如f (2,3) = (3,2);②g (x ,y ) = (-x ,-y ),如g (2,3) =(-2,-3).按照以上变换有f (g (2,3)) =f (-2,-3) =(-3,-2),那么 g (f (-6,7)) =【 】A .(7,6)B .(7,-6)C .(-7,6)D .(-7,-6)7. 如图,等边△ABC 的周长为6π,半径为1的⊙O 从与AB 相切于点D 的位置出发,在△ABC 外部按顺时针方向沿三角形滚动,又回到与AB 相切于点D 的位置,则⊙O 自转了【 】 A .2周 B .3周 C .4周 D .5周第7题图 第8题图8. 如图,直角梯形AOCD 的边OC 在x 轴上,O 为坐标原点,CD 垂直于x 轴,点D 的坐标为(5,4),AD =2.若动点E ,F 同时从点O 出发,点E 沿折线OA -AD -DC 运动,到达C 点时停止;点F 沿OC 运动,到达C 点时停止,它们运动的速度都是每秒1个单位长度.设点E 运动x 秒时,△EOF 的面积为y (平方单位),则y 关于x 的函数图象大致为【 】二、填空题(每小题3分,共21分)9. x 的取值范围是_________.10. 如图,E ,F 分别是正方形ABCD 的边BC ,CD 上的点,BE =CF ,连接AE ,BF .将△ABE 绕正方形的对角线交点O按顺时针方向旋转到△BCF ,则旋转角的度数为_________.F BN CO 第10题图 第12题图11. 一个盒子里有完全相同的三个小球,球上分别标有数字-1,1,2.随机摸出一个小球(不放回),其数字记为p ,再随机摸出另一个小球,其数字记为q ,则满足关于x 的方程20x px q ++=有实数根的概率是_________.12. 如图,矩形OABC 内接于扇形MON ,当CN =CO 时,∠NMB 的度数是 .13. 如图1,用8个同样大小的小立方体粘成一个大立方体,得到的几何体的三视图如图2所示,若小明从这8个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图2,则他取走的小立方体最多可以是_____个.14. 如图,□ABCD 的顶点A ,C 在双曲线11y x =-上,B ,D 在双曲线22y x=上,122k k =(k 1>0),AB ∥y 轴,S □ABCD =24,则k 1=_________.15. 已知:在△ABC 中,AC =a ,AB 与BC 所在直线成45°角,AC 与BC cosC=),则A C 边上的中线长是____________.三、解答题(本大题共8小题,满分75分)16. (8分)已知x 是一元二次方程x 2-2x +1=0的根,求代数式2352362x x x x x -⎛⎫÷+- ⎪--⎝⎭的值.17.(9分)九(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:请解答以下问题:(1)把上面频数分布直方图补充完整,并计算:a=_______,b=________;(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;(3)若该小区有1 000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?18.(9分)如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与B C相交于点N,连接BM,DN.(1)求证:四边形BMDN是菱形;(2)若AB=4,AD=8,求MD的长.A B MODC19.(9分)如图,四边形ABCD是正方形,其中A(1,1),B(3,1),D(1,3).反比例函数myx=(x>0)的图象经过对角线BD的中点M,与BC,CD的边分别交于点P,Q.(1)直接写出点M,C的坐标;(2)求直线BD的解析式;(3)线段PQ与BD是否平行?并说明理由.(10分)已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.根据以上信息,解答下列问题:(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?(2)请你帮该物流公司设计租车方案;(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.22.(10分)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm.现有两个动点P,Q分别从点A和点B同时出发,其中点P以1厘米/秒的速度沿AC向终点C运动;点Q以1.25厘米/秒的速度沿BC向终点C运动.过点P作PE∥BC交AD于点E,连接EQ.设动点运动时间为t秒(t>0).(1)连接PQ,在运动过程中,不论t取何值时,总有线段PQ与线段AB平行,为什么?(2)连接DP,当t为何值时,四边形EQDP能成为平行四边形?(3)当t为何值时,△EDQ为直角三角形?23.(11分)已知抛物线y=ax2+bx+c(a>0)的图象经过点B(12,0)和C(0,-6),对称轴为直线x=2.(1)求该抛物线的解析式.(2)点D在线段AB上,且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点Q 以某一速度从C出发沿线段CB匀速运动,是否存在某一时刻,使线段PQ被直线CD垂直平分?若存在,请求出此时两点的运动时间t(秒)和点Q的运动速度;若不存在,请说明理由.(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐标;若不存在,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年中考数学模拟试卷一、选择题(下列各题所附的四个选项中,有且只有一个是正确的)1.2-的倒数是()A12- B 2 C 2± D 2-【考查有理数的倒数、相反数有关概念.】【参考答案】A【题目来源】自编2.连云港市花果山是全国著名的风景点之一.每年约接待海内外游客15000万人次,这个数可用科学记数法表示为()人A 81015.0⨯ B 91015.0⨯ C 8105.1⨯ D 91015⨯【考查科学记数法,培养学生了解家乡,热爱家乡的情感.注意单位统一.】【参考答案】C【题目来源】自编3.函数y=x+1 中自变量x的取值范围是()A x≤-1B x≥-1C x>-1D x<-1【考查函数的有关概念,函数自变量的取值范围,解不等式.评讲要点:二次根式aa(≥0)】【参考答案】B【题目来源】自编4.等腰三角形的顶角为120,腰长为4cm,则它的底边长为()A 23cm B334cm C 4cm D 34cm【考查等腰三角形的有关概念,直角三角形中的勾股定理,300角所对的直角边等于斜边的一半等,是一个小综合题.】【参考答案】D【题目来源】自编5.下列命题是假.命题的是()A 若x y<,则x+2010<y+2010B 单项式2347x y-的系数是-4C 反比例函数2yx=,当0x>时,y随x的增大而减小;D 平移不改变图形的形状和大小【考查不等式的性质、单项式的系数、反比例函数的图像和性质、真假命题等知识点.评讲要点:单项式的系数是整个单项式的数字因数,即74-;对于C 答案,要提醒学生注意,若没有条件0x >,它也是假命题】 【参考答案】B 【题目来源】自编二、填空题(每小题3分,共30分)6.若b a =54,则b a b a +-= .【考查比例的性质.】【参考答案】91-【题目来源】自编7.在实数范围内因式分解:4y 2-8= .【考查在实数范围内因式分解,提取公因式法和平方差公式的应用.很多学生只把它提取公因式得到错误答案:4(y 2-2)】 【参考答案】4(y+2)(y-2) 【题目来源】自编8、如图:过点A 作x 轴的垂线分别交反比例函数xy x y 31==与 与点B 、D ,分别过B 、D 作y 轴的垂线,垂足为C 、E ,则四边形ECBD 的面积是【重点考查学生灵活运用反比例函数的能力.】 【参考答案】4 【题目来源】自编9、如果关于x 的分式方程131=---xx a x 无解,则a 的值为 【考查学生对分式方程为什么会产生增根的理解和掌握,分式方程有增根和无解的区别和联系.】 【参考答案】-2或1 【题目来源】自编 三、解答题11.计算:20100+|-1|-3sin60°+ 2-3.【考查学生对0指数幂的理解,有理数的绝对值,特殊值的余弦值,考查的知识点较多,需要学生有扎实的基本功】【参考答案】解:原式=1+1-23+81=81812816--=85oxAB EDCy【题目来源】自编12.化简求值:22221211a a a a a a a-+-÷+-+,其中a =【参考答案】解:原式=2(1)12(1)(1)(1)a a a a a a a -+++--=12a a +=3a∴当a=原式【题目来源】自创 13.解不等式组:⎩⎨⎧≥+<-15202x x ,并把其解集在数轴上表示出来.【考查解不等式(组)】【参考答案】原不等式组的解为:-2≤x <2【题目来源】自创14.某企业2007年盈利1500万元,2009年克服全球金融危机的不利影响,仍实现盈利2160万元.从2007年到2009年,如果该企业每年盈利的年增长率相同,求:(1)该企业2008年盈利多少万元?(2)若该企业盈利的年增长率继续保持不变,预计2010年盈利多少万元? 【该问题考查学生的利用数学知识解决实际问题的能力.培养学生的数学建模思想.既有助于学生在解决问题的过程中感受数学的魅力和价值,】 【参考答案】解:(1)设每年盈利的年增长率为x , 根据题意,得21500(1)2160x +=.解得120.2 2.2x x ==-,(不合题意,舍去).1500(1)1500(10.2)1800x ∴+=+=.答:2008年该企业盈利1800万元. (2)2160(10.2)2592+=.答:预计2010年该企业盈利2592万元. 【题目来源】自创③④①②④ ③②①m mmmnnnn5.如图,将正方形沿图中虚线(其中m <n )剪成①②③④四块图形,用这四块 图形恰能拼成一个......矩形(非正方形). (1) 画出拼成的矩形的简图;(2)求nm的值. (3)图中的点A,B,C 分别在正方形边长的的什么位置?所拼成的矩形是什么矩形?【注重实践操作能力的考查,培养学生“做数学”的能力.动手实践、自主探索与合作交流是学生学习数学的重要方式,数学学习活动应当是一个生动活泼、主动的和富有个性的过程.此题直观、形象,通过剪切、实验、观察、猜想等手段和合情推理,达到问题解决,适合学生现有认知水平和实践能力.学生动手操作实践是数形结合思想的探究和深化,是更高层次的数形结合,通过学生手脑结合,培养了学生的创新能力.】【参考答案】解:(1)说明:其它正确拼法可相应赋分.(2)解法一:由拼图前后的面积相等得:2)(])[(n m n n n m +=++因为y ≠0,整理得:01(2=-+nmn m解得:215-=n m (负值不合题意,舍去) (3)点A,B,C 分别是正方形各边的黄金分割点,所拼成的矩形是黄金矩形.【试题来源】参照安徽09中考试卷改编.16.为扩大内需,国务院决定在全国实施“家电下乡”政策。
第一批列入家电下乡的产品为彩电、冰箱、洗衣机和手机四种产品,某县一家家电商场,今年一季度对以上四种产品的销售情况进行了统计,绘制了如下的统计图,请你根据统计图中的信息解答下列问题:(1)该商场一季度彩电销售的数量是 台.BAC数量(台E这四种产品的总销售量是 台. (2)求洗衣机占总销售量的百分比. (3)请补全条形统计图和扇形统计图.【本题突出了对学生的图表信息的收集与处理能力的考查.通过本题,可以引导学生关注社会,关注数学与生活的联系,增强用数学的意识,学会用数学头脑去思考问题,体现了“生活数学化,数学生活化”.】 【参考答案】 解(1)150 ;500(2)1-40%-20%-50÷500=10% (3)【试题来源】参照中考试卷17.如图,AB 是⊙O 的直径,AE 平分BAF ∠,交⊙O 于点E ,过点E 作⊙O 的切线CD ,交AF 的延长线于点D ,交AB 的延长线于点C . (1)求证:ED AF ⊥;(2)若2CB =,4CE =,求AE 的长.【本题考查切线的性质及圆的有关计算。
念及切线与过切点的半径之间的关系;线平行的判定和性质等有关知识。
.】 【参考答案】 解:(1)连接OE, ∵CD 是⊙O 过E 点的切线 ,∴OE ⊥CD ∵OE=OA; ∴∠OEA=OAE ∵AE 平分BAF ∠; ∴OAE=EAD ∴∠OEA=EAD;∴OE ∥AD;∴ED AF ⊥(2) 在 Rt △OEC 中 ,设⊙O 半径为r,222(2)4r r ∴+=+ ,3r ∴=Rt △ADC ∽Rt △OECAE ∴====【题目来源】课本中的典型例题改编.18.如图,大楼AB 的高为16米,远处有一塔CD ,小李在楼底A 处测得塔顶D 处的仰角为60°,在楼顶B 处测得塔顶D 处的仰角为45°.其中A C 、两点分别位于B D 、两点正下方,且A C 、两点在同一水平线上,求塔CD 的高度. 【本题旨在考查三角函数中特殊角的三角函数值,利用直角三角形有关知识解决实际问题】 【参考答案】解:作BE CD ⊥于E ,可得Rt BED △和矩形ACEB , 则有16CE AB AC BE ===,, 在Rt BED △中,45DBE DE BE AC ∠===°,在Rt DAC △中,60t a n 6D A D C A ∠==︒=°,,1616DE DC AC +=∴+=,,解得:8AC =,所以塔CD 的高度为24)米.【试题来源】参照中考试卷19.如图,已知抛物线的顶点坐标为M(1,4),与x 轴交于A 、B 两点(点A 在点B 左侧),与y 轴交于点C (0,3)。
(1)求抛物线的解析式;(2)求BCO ACO ∠∠sin tan 与的乘积;(3)在线段BC 边上是否存在点P ,使得以B 、O 、P 为顶点的三角形与△BAC 相似?若存在,求出点P 的坐标;若不存在,请说明理由。
(4)在对称轴上是否存在一点P ,使|PC-PB|的值最大,请求出点P 的坐标。
【该题以二次函数为背景,但却打破了以往程式化的设问方式,而是带有浓郁的探究成分,勾勒出了“在两个点确定的情况下,用待定系数法确定函数解析式.第(3)小题是一个连续的动态过程,将代数演绎与几何直观有机地结合了起来. 本题考查的主旨并非是对解题方法和技巧的机械运算,而是巧妙地考查了学生直观思维的过程与方法,正所谓“四两拨千斤”就是这个道理.该题从命题技术上采用“宽入窄出、缓步提升”的分层次考查策略,既关注了不同数学水平学生的解题需要,又突出了题目应有的选拔作用.即便是综合题和压轴题,其解题思路和方法也可以在课本上找到原型.】 【参考答案】解:(1)324)1(22++-=+--=x x x y (2)A(-1,0) B(3,0) C(0,3),OA=1,OC=3,OB=3,BC=23622231sin tan =⨯=∠⋅∠ACB CAG (3) 当BAC BPO ∆∆∽时,P()2,1(1分)当BCA BPO ∆∆∽时,P()49,43 (2分)(4)存在,理由是:利用对称性原理:求出C 点的对称点N(2,3),过B 、N 作直线,交对称轴于点P 。
通过相似或求出直线BN 的方程,即可求出P 的值(6,1)【试题来源】参照中考试卷。
