求阴影面积(1)
小升初数学几何求阴影部分面积题带解析
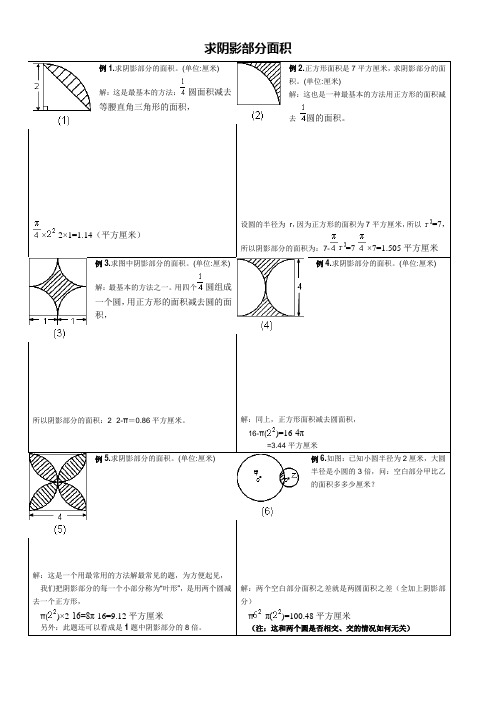
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
北师大六年级阴影部分面积1

求阴影部分的面积
• 正方形面积减去圆 把阴影部分的每一 个小部分称为“叶形”, 是用两个圆减去一个正 方形就是阴影部分的面 积。
• 另外:此题还可以看成 是1题中阴影部分的8倍。
求阴影部分的面积
求阴影部分的面积
• 正方形面积可用 (对角线长×对 角线长÷2)求
求阴影部分的面积。
• 圆面积的 减去 等腰直角三角形 的面积 就是阴 影部分的面积。
例2.正方形面积是7平方厘米,求阴 影部分的面积。(单位:厘米)
例2.正方形面积是7平方厘米,求阴 影部分的面积。(单位:厘米)
• 正方形的面积减 去 圆的面积就 是阴影部分的面 积。
求阴影部分的面积
• 四个 圆组成 一个圆,用正方 形的面积减去圆 的面积就是阴影 部分的面积。
• 用圆面积的 减去正方形的面 积就是阴影部分 的面积。
求阴影部分的面积
• 右面正方形上部 阴影部分的面积, 等于左面正方形 下部空白部分面 积,割补以后阴 影部分的面积就 是 圆的面积。
求阴影部分的面积
• 把右面的正 方形平移至 左边的正方 形部分,则 阴影部分合 成一个长方 形,
求阴影部分的面积
• 连对角线后 将“叶形” 剪开移到右 上面的空白 部分,阴影部 分就可以凑 成正方形面 积的一半。
求阴影部分的面积
外圆半径4厘米,内圆半径3厘米,求阴影部分面积。
.图中四个圆的半径都是1厘米,求阴影
部分的面积。
史上最全几何阴影面积的解法(1)

【史上最全】初中数学几何阴影面积的3种解法|知识点
初中备考指南1周前
为所有考生和家长,加油!
栏目导语:这是小许老师精心设计的初中知识点学习板块,以语数外基础和提高性考点为主,也会有物化,史政生地等科目知识点合集。
在这里你会对未学提前了解,对已学知识有更好的理解,欢迎转发,收藏!
“几何”问题不仅是初中数学的重点,到了高中数学学习中也占很大比重,内容是循序渐进的,所以基础一定要打好。
这里,就来具体说说如何把这类题的分数拿到手,更准确地说就是初中生要掌握3个方法,才能够解决大部分求解几何图形阴影面积的题目。
公式法
这属于最简单的方法,阴影面积是一个常规的几何图形,例如三角形、正方形等等。
简单举出2个例子:
和差法
攻略一直接和差法
这类题目也比较简单,属于一目了然的题目。
只需学生用两个或多个常见的几何图形面积进行加减。
攻略二构造和差法
从这里开始,学生就要构建自己的数学图形转化思维了,学会通过添加辅助线进行求解。
割补法
割补法,是学生拥有比较强的转化能力后才能轻松运用的,否则学生看到这样的题目还是会无从下手。
尤其适用于直接求面积较复杂或无法计算时,通过对图形的平移、旋转、割补等,为利用公式法或和差法求解创造条件。
攻略一全等法
攻略二对称法
攻略三平移法
攻略四旋转法
距离中考越来越近,希望家长不要再给孩子压力,同时还要开导孩子,中考只是一场普通的考试。
希望同学们也能平时练习要严谨,中考考场放轻松,祝所有同学考个好成绩。
阴影面积知识点

阴影面积知识点阴影面积是指物体在光线照射下,光线无法到达的部分所形成的阴影所占据的面积。
计算阴影面积可以帮助我们了解光的传播规律以及物体之间的相互遮挡关系。
下面我们来逐步思考一下如何计算阴影面积。
步骤一:了解光的传播规律在计算阴影面积之前,我们首先需要了解光线是如何传播的。
光线遵循直线传播原理,也就是说光线会沿着直线路径传播。
当光线遇到物体时,会发生折射、反射和吸收等现象。
步骤二:确定光源位置和物体形状在计算阴影面积时,我们需要知道光源的位置以及物体的形状。
光源的位置决定了光线的传播方向,而物体的形状决定了光线与物体的交互方式。
步骤三:确定光线的路径根据光源位置和物体形状,我们可以确定光线的路径。
光线可以直接到达的区域不会形成阴影,而无法到达的区域则会形成阴影。
步骤四:计算阴影面积一种简单的计算阴影面积的方法是通过将物体投影到一个平面上,然后计算投影面积。
投影面积就是阴影面积的一部分。
我们可以使用几何图形的投影公式来计算阴影面积。
步骤五:考虑物体间的相互遮挡关系在实际情况中,多个物体之间可能存在相互遮挡的关系。
在计算阴影面积时,我们需要考虑这些遮挡关系。
当一个物体遮挡住另一个物体时,被遮挡的部分不会形成阴影。
步骤六:应用实例为了更好地理解阴影面积的计算方法,我们可以通过一个简单的实例来进行演示。
假设我们有一个光源位于物体的正上方,物体是一个矩形,边长分别为a和b。
我们可以通过将物体投影到一个平面上,然后计算投影面积来计算阴影面积。
步骤七:总结通过以上步骤,我们可以初步了解如何计算阴影面积。
在实际应用中,我们可以根据具体情况进行调整和改进。
阴影面积的计算方法对于建筑设计、光线传播模拟等领域具有重要的应用价值。
希望本文能够对读者有所启发,增加对阴影面积知识点的理解与应用能力。
求阴影部分的面积(一)ppt课件

A
D
精选
探讨二:太极图中,黑色部分的面积是多少呢?(π≈3)
精选
割补法:割、补的面积相等
探讨二:太极图中,黑色部分的面积怎么求呢?(π≈3)
S= S圆÷2 =3×10²÷2 =150(cm²)
精选
10cm 10cm
求阴影部分的面积是多少?
6cm
S阴影=4×6=24(cm²)
4cm
精选
等分法、 拼组法
精选
探讨五: 巧解法
已知大正方形的面积是80cm²,你会求圆的面积吗?
小正方形的边长=圆的半径
a
a=r
r
a²=r²
精选
小结
今天你有什么收获?
精选
2cm
精选
方法1:
2cm 2cm
5/29/2020
精选
方法1:
2cm 2cm
S空白=(S正方形-S圆)×2 S阴影=S正方形-S空白
5/29/2020
精选
方法2:
20
精选
方法2:
S阴影=2× S圆- S正方形
5/29/2020
精选
求阴影部分的面积是多少?
5/29/2020
精选
5/29/2020
求阴影部分的面积(一)
数学 人教版六年级上册
郑州市二七区大学路小学 赵精选延芳
S=S大-S小
S=a²
1 2
S圆
S=πr²
1 4
S圆
S=ah
S=1 ah
2 S=1 (a+b)h
2
S=ab
精选
和差法
探讨一:涂油漆部分的面积是多少呢?
3dm
精选
E
6dm
苏教版五年级下册数学重点求阴影部分面积专项和答案 (1)

解:将两个同样的图形拼在一起成为 圆减等腰直角三角形
[π ÷4- ×5×5]÷2
=( π- )÷2=3.5625平方厘米
解:面积为4个圆减去8个叶形,叶形面积为: π -1×1= π-1
所以阴影部分的面积为:4π -8( π-1)=8平方厘米
例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。如果圆周π率取3.1416,那么花瓣图形的的面积是多少平方厘米?
分析:连接角上四个小圆的圆心构成一个正方形,各个小圆被切去 个圆,
(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)
例8.求阴影部分的面积。(单位:厘米)
解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为 圆,
所以阴影部分面积为: π( )=3.14平方厘米
例9.求阴影部分的面积。(单位:厘米)
解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,
所以面积为:1×2=2平方厘米
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
解:设小圆半径为r,4 =36, r=3,大圆半径为R, =2 =18,
将阴影部分通过转动移在一起构成半个圆环,
所以面积为:π( - )÷2=4.5π=14.13平方厘米
例21.图中四个圆的半径都是1厘米,求阴影部分的 面积。
例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积。
解:连PD、PC转换为两个三角形和两个弓形,
两三角形面积为:△APD面积+△QPC面积= (5×10+5×5)=37.5
六年级数学求阴影部分的面积含答案

包含与排除和旋转对称课前预习铅球比赛场地有人参加过铅球比赛么?有谁知道铅球的比赛场地是什么样子的?如何才能画一个标准的铅球比赛场地呢?铅球的比赛场地是一个扇形的比赛场地,上面有环形的尺度,下面介绍一种铅球比赛场地的画法。
在学校运动会、小型比赛及体育教学中,铅球场地往往都被安排在远离径赛场地的“偏僻角落里”。
其一,是为了安全;其二,是为了保护塑胶场地;其三,是铅球比赛需要土质场地或草皮。
铅球场地的传统画法是:先用测绳测量,再用标枪沿测绳划出痕迹,后用白灰浇出白线。
而往往“偏僻角落里”的场地质地较差,高洼不平,杂草丛生,即使勉强画上白线,也模糊不清、参差不齐、宽窄不一。
况且在比赛过程中,人为踩踏,器械砸击、风吹雨淋,使角度线、远度线和延长线变得更加模糊,裁判员需经常描画,给裁判工作带来诸多不便。
本人在实际教学、裁判工作中摸索出一种用白布条(或白塑料编织材料)代替白灰绘制比赛场地的方法。
第一:材料与制作用白布裁剪、缝制成宽5厘米、厚3—4层的白布条,长度可根据比赛的组别,及实际情况而定,可剪短,可接长。
第二:具体画法把白布条沿用测绳已测量好的角度线、远度线和延长线拉直且相吻合,用长铁钉钉地固定两端,再沿白布条的两边缘每隔1—2米用铁钉交错钉牢,用醒目的颜色在白布条上注明远度数字。
第三:延用此法可延用于其他田赛项目的比赛场地、以及径赛项目的起点、终点和弯直道交接线的绘制。
第四:备用比赛完毕后,将铁钉拔出,白布条捆扎、收藏好以备下次再用。
瞧,用这法绘制比赛场地,既经济实用,避免重复测画场地,又能及时、公正、准确地测定学生和运动员的练习和比赛成绩。
您不妨一试。
知识框架圆的知识:1. 当一条线段绕着它的一个端点O 在平面上旋转一周时,它的另一端点所画成的封闭曲线叫做圆,点O 叫做这个圆的圆心.2. 连结一个圆的圆心和圆周上任一点的线段叫做圆的半径.3. 连结圆上任意两点的线段叫做圆的弦.过圆心的弦叫做圆的直径.4. 圆的周长与直径的比叫做圆周率.圆周上任意两点间的部分叫做弧.5. 圆周长=直径×π.=半径×2π 圆面积=π×半径2.扇形的知识:1. 扇形是圆的一部分,它是由圆心角的两条半径和圆心角所对的弧组成的图形.顶点在圆心的角叫做圆心角. 2. 我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几.那么一般的求法是什么呢?关键是360n. 3. 扇形中的弧长= 180r n π.扇形的周长= 180r n π+2r.扇形的面积=3602r n π =.弓形的知识:弦与它所对的弧所组成的图形叫做弓形。
求阴影部分面积

答:阴影部分的面积是20.75平方厘米
19.2π-4.
【解析】
试题分析:由图可知,阴影部分的面积是两个圆心角为90°,且半径为2的扇形的面积与正方形的面积的差.可据此求出阴影部分的面积.
试题解析:S阴影=2S扇形-S正方形
=2× =2π-4.
答:两弧所夹叶形部分的面积为2π-4.
(2)大正方形的面积减去矩形的面积即可得出阴影部分的面积,也可得出三个代数式 、 、 之间的等量关系;
(3)由(2)所得出的关系式,可求出 的值;
(4)画出长3m+n,宽m+n的长方形即可求解.
试题解析:(1)图②中的阴影部分的面积为 ;
(2) ;
(3) =25,∴ =±5;
(4)如图所示:
考点:完全平方公式的几何背景.
(1)求图乙中阴影部分的面积.
(2)观察图乙,请你写出三个代数式 、 、 之间的等量关系式.
(3)根据(2)中的结论,若 , ,求 的值.
(4)有许多代数恒等式可以用图形的面积来表示.如图丙,它表示了 .
试画一个几何图形,使它的面积能表示: .
15.如图,在甲、乙两个4×4的方格图中,每个小正方形的边长都为1.
【解析】
试题分析:根据轴对称的性质可得阴影部分的面积等于△ABC的面积.
∵AE⊥BD,EB=ED,
∴B,D关于AC轴对称,
∴阴影部分的面积等于△ABC的面积
考点:本题考查的是轴对称的性质
点评:解答本题的关键是根据轴对称的性质得到阴影部分的面积等于△ABC的面积.
18.20.75平方厘米
【解析】
分析:阴影部分的面积=梯形的面积﹣半圆的面积,所以这里只要求得半圆的半径,即可解决问题.
