备战2019年高考物理 大题精做 专题02 匀变速直线运动的计算——追及相遇
高中物理专题:匀变速直线运动的研究-追及相遇问题

高中物理专题:匀变速直线运动的研究-追及相遇问题追及相遇问题分析方法1、 相遇问题相遇问题分为追及相遇和相向运动相遇两种情形,其主要条件是两物体在相遇处的位置坐标相同。
具体分析方法如下:(1) 列出两物体运动的位移方程,注意两个物体运动时间之间的关系。
(2) 利用两物体相遇时必处在同一位置,寻找两物体位移间的关系。
(3) 寻找问题中隐含的临界条件。
(4) 与追及中的解题方法相同。
例题1:甲乙两物体相距S ,同时同向沿同一直线运动,甲在前面做初速度为零,加速度为a 1的匀加速直线运动,乙在后面做初速度为V 0,加速度为a 2的匀加速直线运动,则( )A.若a 1=a 2,则两物体可能相遇一次B.若a 1>a 2,则两物体可能相遇两次C.若a 1<a 2,则两物体可能相遇两次D.若a 1>a 2,则两物体也可能相遇一次或不相遇例题2:甲、乙辆汽车沿同一平直公路同向匀速行驶,甲车在前,乙车在后,它们行驶的速度均为16m/s.已知甲在紧急刹车时加速度a 1=3m/s 2,乙车紧急刹车时加速度a 2=4 m/s 2,乙车司机的反应时间为0.5s ,求为保证两车在紧急刹车过程中不相撞,甲、乙行驶过程中至少应保持多大距离.2、追及问题的图像关系①匀加速追匀速能追上且只能相遇一次;交点意义:速度相等,两物体相距最远)②匀减速追匀速当V 减=V 匀时,如果ΔS=S 0,则恰能追上,这也是避免相撞的临界条件,只能相遇一次。
若ΔS <S 0,则不能追上(其中S 0为开始时两物体的距离)交点意义:速度相等时若未追上,则距离最近.若ΔS >S 0能相遇两次③匀速追匀加速规律同上②④匀速追匀减速规律同上①⑤匀加速追匀减速规律同上①⑥匀减速追匀加速规律同上②例题3:汽车正以10m/s的速度在平直的公路上前进,突然发现正前方有一辆自行车以4m/s的速度做同方向的匀速直线运动,汽车立即关闭油门做加速度大小为6m/s2的匀减速运动,汽车恰好不碰上自行车,求关闭油门时汽车离自行车多远?课堂练习:1.汽车由静止开始在平直的公路上行驶,0~60s内汽车的加速度随时间变化的图线如右图所示。
匀变速直线运动之相遇、追与问题详解与习题

匀变速直线运动之相遇、追及问题详解及习题一、追及问题 1. 速度小者追速度大者类型图象说明匀加速追匀速①t=t 0 以前,后面物体与前面物体间距离增大②t=t 0 时,两物体相距最远为x0+Δx③t=t 0 以后,后面物体与前面物匀速追匀减速体间距离减小④能追及且只能相遇一次匀加速追匀减速2. 速度大者追速度小者匀减速追匀速开始追及时,后面物体与前面物体间的距离在减小,当两物体速度相等时,即t=t0 时刻:①若Δx=x0, 则恰能追及,两物体只匀速追匀加速能相遇一次,这也是避免相撞的临界条件②若Δx<x0, 则不能追及,此时两物体最小距离为x0- Δ x③若Δx>x0, 则相遇两次,设t1 时刻Δx1=x0, 两物体第一次相遇,则t2 时刻两物体第二次相遇匀减速追匀加速小汽车从静止开始以3m/s 2 的加速度行驶,恰有一自行车以6m/s 的速度从车边匀速驶过。
求:(1)汽车从开动后到追上自行车前两者的最大距离(2)汽车从开动后经多长时间能追上自行车?二、匀速追匀减速2 某人骑自行车以8m/s 的速度前进,某时刻在他前面3m处以10m/s 的速度同向行驶的汽车开始关闭发动机,并以2m/s 的加速度匀减速前进,此人追上汽车之前何时距离最远?需要多少秒才能追上汽车?三、匀加速追匀减速2某量超速货车以40m/s 的速度从警车面前驶过, 2 秒后警车以3m/s 开始追击并鸣笛示警,货车 2 秒后听到警笛声开始作2m/s2 的匀减速直线运动,问警车开始追击多久后能追上货车?行驶的距离是多少?四、匀减速追匀速汽车正以10m/s 的速度在平直公路上前进,突然发现正前方有一辆自行车以4m/s 的速度做同方向的匀速直线运动,汽车立即关闭油门做加速度大小为6m/s2 的匀减速运动,要使汽车恰不碰上自行车,求关闭油门时汽车离自行车多远?(1)汽车和自行车各自做什么运动?(2)两者速度相等之前距离如何变化,速度相等之后距离如何变化?(3)如果在两者速度相等时汽车还没碰上自行车,以后还会有相碰的危险吗?2 一个步行者以6m/s 的最大速率跑步去追赶被红灯阻停的公共汽车,当他距离公共汽车25m 时,绿灯亮了,车子以1m/s 的加速度匀加速启动前进,问该人能否赶上该公共汽车?(1)两者速度相等之前距离如何变化,速度相等之后距离如何变化?(2)在两者速度相等时人还没追上汽车,以后还有可能追上吗?(3)通过计算讨论该人能否追上公共汽车?六、匀减速追匀加速2某货车以30m/s 的速度行驶在公路上,突然司机发现前方150m处有辆小轿车正从静止开始做加速度为2m/s 匀加速直2线运动,0.5 秒以后货车司机开始以3m/s 加速度作匀减速直线运动,问两车是否会相撞,如果会,从开始发现到相撞需要多少时间?如果不会,则最近距离是多少?练习1、平直公路上有甲、乙两辆汽车,甲以0.5m/s2 的加速度由静止开始行驶,乙在甲的前方200m处以5m/s 的速度做同方向的匀速运动,问:(1) 甲何时追上乙?甲追上乙时的速度为多大?此时甲离出发点多远?(2) 在追赶过程中,甲、乙之间何时有最大距离?这个距离为多少?2、汽车正以10m/s 的速度在平直的公路上前进,突然发现正前方有一辆自行车以4m/s 的速度做同方向的匀速直线运动,汽车立即关闭油门做加速度大小为6m/s2 的匀减速运动,汽车恰好不碰上自行车,求关闭油门时汽车离自行车多远?3、货车正在以v1=10m/s 的速度在平直的公路上前进,货车司机突然发现在其正后方S0=25 米处有一辆小车以v2 =20m/s 的速度做同方向的匀速直线运动,货车司机为了不让小车追上,立即加大油门做匀加速运动。
高中物理《直线运动》核心考点精讲2:追击相遇问题解题技巧与例题精讲

高中物理《直线运动》核心考点精讲2 《追击相遇问题解题技巧与例题精讲》(附例题解析)一、追及和相遇问题的概述1.当两个物体在同一直线上运动时,由于两物体的运动情况不同,所以两物体之间的距离会不断发生变化,这时就会涉及追及、相遇或避免相碰等问题。
2.追及与相遇问题的实质是研究两个物体的时空关系,只要满足两个物体在同一时间到达同一地点,即说明两个物体相遇。
二、追及、相遇问题两种典型情况1. 速度小者追速度大者2. 速度大者追速度小者则恰能追上,两三、追及与相遇问题的求解方法1. 分析法应用运动学公式,抓住一个条件、两个关系,列出两物体运动的时间、位移、速度及其关系方程,再求解。
(1) 一个条件:二者速度相等。
它往往是能否追上或距离最大、最小的临界条件,也是分析判断的切入点。
(2)两个关系:即时间关系和位移关系。
可通过画草图找出两物体的位移关系,也是解题的突破口。
2. 极值法设相遇时间为t,根据条件列出方程,得到关于t的一元二次方程,再利用数学求极值的方法求解。
在这里,常用到配方法、判别式法、重要不等式法等。
3. 图象法在同一坐标系中画出两物体的运动图线。
位移图线的交点表示相遇,速度图线抓住速度相等时的“面积”关系找位移关系。
4. 能否追上的判断方法常见情形:物体A追物体B,开始二者相距x0,则(1) A 追上B 时,必有x A-x B=x0,且v A≥v B。
(2) 要使两物体恰不相撞,必有x A-x B=x0,且v A≤v B。
5. 若被追赶的物体做匀减速直线运动,一定要注意判断追上前该物体是否已经停止运动。
四、求解追及和相遇问题的思路和技巧1. 解题思路分析两物体运动过程→画运动示意图→找两物体位移关系→列位移方程212. 两点解题技巧【典例1】(2018年全国卷II 、19) (多选)甲、乙两汽车在同一条平直公路上同向运动,其速度-时间图像分别如图中甲、乙两条曲线所示。
已知两车在t 2时刻并排行驶。
匀变速直线运动应用--追及和相遇问题完美版

匀变速直线运动应用--追及和相遇问题【学习目标】1、掌握追及及相遇问题的特点2、能熟练解决追及及相遇问题【自主学习】两物体在同一直线上追及、相遇或避免碰撞问题中的条件是:两物体能否同时到达空间某位置。
因此应分别对两物体研究,列出位移方程,然后利用时间关系、速度关系、位移关系而解出。
一、 追及问题1、追及问题中两者速度大小与两者距离变化的关系。
甲物体追赶前方的乙物体,若甲的速度大于乙的速度,则两者之间的距离 。
若甲的速度小于乙的速度,则两者之间的距离 。
若一段时间内两者速度相等,则两者之间的距离 。
2、追及问题的特征及处理方法:“追及”主要条件是:两个物体在追赶过程中处在同一位置,常见的情形有三种:⑴ 初速度为零的匀加速运动的物体甲追赶同方向的匀速运动的物体乙,一定能追上,追上前有最大距离的条件:两物体速度 ,即v v =乙甲。
⑵ 匀速运动的物体甲追赶同向匀加速运动的物体乙,存在一个能否追上的问题。
判断方法是:假定速度相等,从位置关系判断。
①若甲乙速度相等时,甲的位置在乙的后方,则追不上,此时两者之间的距离最小。
②若甲乙速度相等时,甲的位置在乙的前方,则追上。
③若甲乙速度相等时,甲乙处于同一位置,则恰好追上,为临界状态。
解决问题时要注意二者是否同时出发,是否从同一地点出发。
⑶ 匀减速运动的物体追赶同向的匀速运动的物体时,情形跟⑵类似。
3、分析追及问题的注意点:⑴ 要抓住一个条件,两个关系:一个条件是两物体的速度满足的临界条件,如两物体距离最大、最小,恰好追上或恰好追不上等。
两个关系是时间关系和位移关系,通过画草图找两物体的位移关系是解题的突破口。
⑵若被追赶的物体做匀减速运动,一定要注意追上前该物体是否已经停止运动。
⑶仔细审题,充分挖掘题目中的隐含条件,同时注意v t -图象的应用。
二、相遇⑴ 同向运动的两物体的相遇问题即追及问题,分析同上。
⑵ 相向运动的物体,当各自发生的位移绝对值的和等于开始时两物体间的距离时即相遇。
(完整版)匀变速直线运动追及问题
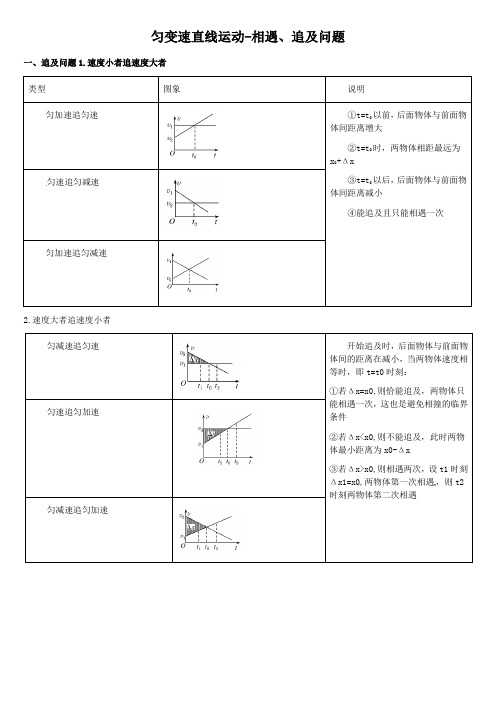
匀变速直线运动-相遇、追及问题一、追及问题1.速度小者追速度大者类型图象说明匀加速追匀速①t=t0以前,后面物体与前面物体间距离增大②t=t0时,两物体相距最远为x0+Δx③t=t0以后,后面物体与前面物匀速追匀减速体间距离减小④能追及且只能相遇一次匀加速追匀减速2.速度大者追速度小者匀减速追匀速开始追及时,后面物体与前面物体间的距离在减小,当两物体速度相等时,即t=t0时刻:①若Δx=x0,则恰能追及,两物体只能相遇一次,这也是避免相撞的临界匀速追匀加速条件②若Δx<x0,则不能追及,此时两物体最小距离为x0-Δx③若Δx>x0,则相遇两次,设t1时刻Δx1=x0,两物体第一次相遇,则t2时刻两物体第二次相遇匀减速追匀加速小汽车从静止开始以 3m/s2的加速度行驶,恰有一自行车以6m/s的速度从车边匀速驶过。
求:(1)汽车从开动后到追上自行车前两者的最大距离(2)汽车从开动后经多长时间能追上自行车?二、匀速追匀减速某人骑自行车以8m/s的速度前进,某时刻在他前面3m处以10m/s的速度同向行驶的汽车开始关闭发动机,并以2m/s2的加速度匀减速前进,此人追上汽车之前何时距离最远?需要多少秒才能追上汽车?三、匀加速追匀减速某量超速货车以40m/s的速度从警车面前驶过,2秒后警车以3m/s2开始追击并鸣笛示警,货车2秒后听到警笛声开始作2m/s2的匀减速直线运动,问警车开始追击多久后能追上货车?行驶的距离是多少?四、匀减速追匀速汽车正以 10m/s的速度在平直公路上前进,突然发现正前方有一辆自行车以4m/s的速度做同方向的匀速直线运动,汽车立即关闭油门做加速度大小为 6m/s2的匀减速运动,要使汽车恰不碰上自行车,求关闭油门时汽车离自行车多远?(1)汽车和自行车各自做什么运动?(2)两者速度相等之前距离如何变化,速度相等之后距离如何变化?(3)如果在两者速度相等时汽车还没碰上自行车,以后还会有相碰的危险吗?一个步行者以6m/s的最大速率跑步去追赶被红灯阻停的公共汽车,当他距离公共汽车 25m时,绿灯亮了,车子以 1m/s2的加速度匀加速启动前进,问该人能否赶上该公共汽车?(1)两者速度相等之前距离如何变化,速度相等之后距离如何变化?(2)在两者速度相等时人还没追上汽车,以后还有可能追上吗?(3)通过计算讨论该人能否追上公共汽车?六、匀减速追匀加速某货车以30m/s的速度行驶在公路上,突然司机发现前方150m处有辆小轿车正从静止开始做加速度为2m/s2匀加速直线运动,0.5秒以后货车司机开始以3m/s2加速度作匀减速直线运动,问两车是否会相撞,如果会,从开始发现到相撞需要多少时间?如果不会,则最近距离是多少?课堂练习1、平直公路上有甲、乙两辆汽车,甲以0.5m/s2的加速度由静止开始行驶,乙在甲的前方200m处以5m/s的速度做同方向的匀速运动,问:(1)甲何时追上乙?甲追上乙时的速度为多大?此时甲离出发点多远?(2)在追赶过程中,甲、乙之间何时有最大距离?这个距离为多少?2、汽车正以10m/s的速度在平直的公路上前进,突然发现正前方有一辆自行车以4m/s的速度做同方向的匀速直线运动,汽车立即关闭油门做加速度大小为6m/s2的匀减速运动,汽车恰好不碰上自行车,求关闭油门时汽车离自行车多远?3、货车正在以v1=10m/s的速度在平直的公路上前进,货车司机突然发现在其正后方S0=25米处有一辆小车以v2=20m/s的速度做同方向的匀速直线运动,货车司机为了不让小车追上,立即加大油门做匀加速运动。
匀变速直线运动中的追及相遇问题.

解1:(公式法)
当两车的速度速度相等时,
x汽
两车之间的距离最大。
△x
x自
v汽 at v自
t v自 6 s 2s
a3
xm
x自
x汽
v自t
1 2
at 2
6
2m
1 2
3 22 m
6m
解2:(图像法)
v-t图像的斜率表示物体的加速度 v/ms-1
6 tan 3
t0
t0 2s
6
α
o
t0
汽车 自行车
பைடு நூலகம்
s vt2 v02 0 (6)2 m 6m
2a
23
表示汽车相对于自行车是向后运动的,其相对于自行车
的位移为向后6m.
(2)同地出发,速度小者A(初速度为零的匀加速) 追速度大者B(匀速)
①当A匀加速至与B速度相等前,A、B距离越来越大; 当A超过B速度后, A、B距离越来越小。
② 当 v1=2v2 A追上B。A追上B所用的时间等于 它们之间达到最大距离时间的两倍。
v
A
v1
v2
B
o
t0
2t0 t
❖例1.汽车正以10m/s的速度在平直 公路上前进,突然发现正前方有一 辆自行车以4m/s的速度做同方向 的匀速直线运动,汽车立即关闭油 门做加速度大小为6m/s2的匀减速 运动,汽车恰好不碰上自行车,求 关闭油门时汽车离自行车多远?
1 2
(20 10)t0
100
t0 20 s
a tan 20 10 0.5
20
a 0.5m / s2
v/ms-1
20
A
10
o
t0
B t/s
高考物理匀变速直线速运动规律应用追及和相遇问题(附答案)

20XX 年高考物理一轮复习第5讲 匀变速直线速运动规律应用2——追及和相遇问题知识点拨:1.匀减速物体追赶同向匀速运动物体时,恰能追上或恰追不上的临界条件是:即将靠近时,追赶者的速度等于或小于被追赶者的速度。
当追赶者的速度大于被追赶者的速度时,能追上;当追赶者的速度小于被追赶者的速度时,不能追上。
2.初速度为零的匀加速运动的物体追赶同向匀速运动物体时,追上前者前两者具有最大的间距的条件是追赶者的速度等于被追赶者的速度。
3.解答问题时常常利用函数判别式和V-t 图像等方法,求极值问题。
备考训练:1.汽车甲沿着平直的公路以速度v 做匀速直线运动.当它路过某处的同时,该处有一辆汽车乙开始做初速度为零的匀加速运动去追赶甲车.根据上述的已知条件 ( )A .可求出乙车追上甲车时乙车的速度B .可求出乙车追上甲车时乙车所走的路程C .可求出乙车从开始起动到追上甲车时所用的时间D .不能求出上述三者中任何一个2.一个步行者以6.0 m/s 的最大速率跑步去追赶被红灯阻停的公共汽车,当它距离公共汽车25m 时,绿灯亮了,汽车以1m/s 2的加速度匀加速起动前进, 则 ( )A .人能追上汽车,追车过程人共跑了36mB .人不能追上汽车,人和车最近距离为7mC .人能追上汽车,追上车前人共跑了43mD .人不能追上汽车,自车子开动后,人和车相距越来越远3.甲、乙两物体从同一地点沿同一方向做直线运动的速度图像如图5-1所示,则 ( ) A .两个物体两次相遇的时间是2s 和6s B .4s 末甲在乙的后面 C .2s 末两物体相距最远D .甲物体一直向前运动而乙物体向前运动2s ,随后向后运动 图5-14.从某一高度相隔1s 释放两个相同的小球甲和乙,不计空气阻力,它在空中任一时刻 ( ) A .甲、乙两球距离越来越大,甲、乙两球速度之差越来越大 B .甲、乙两球距离始终保持不变,甲、乙两球速度之差保持不变 C .甲、乙两球距离越来越大,但甲、乙两球速度之差保持不变 D .甲、乙两球距离越来越小,甲、乙两球速度之差越来越小 5.A 、B 两质点的v -t 图像如图5-2所示,设它们在同一条直线上运动,在t =3s 时它们在中途相遇,由图可知( )A .A 比B 先启程 B .A 比B 后启程C .两质点启程前A 在B 前面4mD .两质点启程前A 在B 后面2m6.甲物体以1 m/s 的速度做匀速直线运动,出发5s 后,另一物体乙从同一地点由静止开始以0.4 m/s 2的加速度向同一方向做匀加速直线运动,求:(1)乙物体出发后经几秒钟才能追上甲物体?(2)甲、乙两物体相遇前它们之间的最大距离是多少?s )7.甲车以10米/秒,乙车以4米/秒的速率在同一直车道中同向前进,若甲车驾驶员在乙车后方距离d处发现乙车,立即踩刹车使其车获得-2米/秒2的加速度,为使两车不致相撞,d的值至少应为多少?8.在一条平直的公路上,乙车以10m/s的速度匀速行驶,甲车在乙车的后面做初速度为15m/s,加速度大小为0.5m/s2的匀减速运动,则两车初始距离L满足什么条件时可以使:(1)两车不相遇;(2)两车只相遇一次;(3)两车能相遇两次。
高考物理精做02匀变速直线运动的计算__追及相遇大题精做新人教版

精做02 匀变速直线运动的计算——追及相遇1.(2015·福建卷)一摩托车由静止开始在平直的公路上行驶,其运动过程的v–t图象如图所示,求:(1)摩托车在0~20 s这段时间的加速度大小a;(2)摩托车在0~75 s这段时间的平均速度大小v。
【答案】(1)1.5 m/s2 (2)20 m/s【名师点睛】本题主要识图能力,理解v–t图象的含义,利用图象求解加速度与位移、平均速度等。
2.(2017·驻马店一中月考)2016年世界中学生五人制足球锦标赛落下帷幕,代表中国参赛的河南男队和河北女队取得了优异成绩。
五人制足球的赛场长40 m,宽20 m,如图所示。
在比赛中,攻方队员在中线附近突破防守队员,将足球沿边路向前踢出,足球的运动可视为在地面上做初速度为v1=6 m/s的匀减速直线运动,加速度大小为a1=1 m/s2。
该队员将足球踢出后立即由静止启动追赶足球,他的运动可看作是匀加速直线运动,最大加速度为a2=1 m/s2,能达到的最大速度为v2=4 m/s。
该队员至少经过多长时间能追上足球?【答案】由于x2+x3<x1,故足球停止运动时,前锋队员没有追上足球,然后前锋队员继续以最大速度匀速运动追赶足球,由匀速运动公式得代入数据解得前锋队员追上足球的时间【名师点睛】能否追上的关键看速度相等时追上没有,当后者速度最大时追上没有,当前者停止运动时,追上没有,分步骤,按位移、时间、速度前后衔接,所以问题都可以一步一步解决,需要认真分析,踏实解题,一步一个脚印。
3.一辆超速车以90 km/h的速度在学校区域内行驶,当这辆违章行驶的汽车刚刚超过一辆警车时,警车立即从静止开始以2.5 m/s2匀加速追去。
求:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精做02 匀变速直线运动的计算——追及相遇1.(2015·福建卷)一摩托车由静止开始在平直的公路上行驶,其运动过程的v–t图象如图所示,求:(1)摩托车在0~20 s这段时间的加速度大小a;(2)摩托车在0~75 s这段时间的平均速度大小v。
【答案】(1)1.5 m/s2 (2)20 m/s【名师点睛】本题主要识图能力,理解v–t图象的含义,利用图象求解加速度与位移、平均速度等。
2.(2018·湖北省长阳县第一高级中学)甲、乙两辆车在同一直道路上向右匀速行驶,甲车的速度为v1=16 m/s,乙车的速度为v2=12 m/s,乙车在甲车的前面。
当两车相距L=6 m时,两车同时开始刹车,从此时开始计时,甲车以大小为a1=2 m/s2的加速度刹车,6 s后立即改做匀速运动,乙车刹车的加速度大小为a2=1 m/s2,求(1)从两车刹车开始计时,两车速度相等的时刻;(2)两车相遇的次数及各次相遇的时刻。
【答案】(1)4 s和8 s (2)3次,2 s、6 s、10 s【解析】(1)设刹车后经过t时间两车速度相等,则有:v1–a1t=v2–a2t解得:t=4 s6 s后甲车匀速,则速度:v=v1–a1t1=4 m/s两车速度再次相等时,则有:v=v2–a2t′解得:t′=8 s(2)在甲减速时,设经时间t相遇,甲和乙的位移分别为x1、x2,则有:x1=v1t–12a1t2x2=v2t–12a2t2又有:x1–x2=L解得:t1=2 s或t2=6 s甲车减速时间恰好为6 s,即在甲车减速阶段,相遇两次,第1次t1=2 s,第2次t2=6 s 第2次相遇时甲车的速度为:v′1=v1–a1t2=4 m/s乙车的速度为:v′2=v2–a2t2=6 m/s设再经Δt甲追上乙,则有:v′1Δt=v′2Δt–12a2(Δt)2代入数据解得:Δt=4 s此时乙仍在做减速运动,此解成立,所以甲、乙两车第3次相遇,相遇时刻为:t3=t2+Δt=10 s 3.(2018·福建省闽侯二中五校教学联合体)某汽车以10 m/s的速度行驶,驾驶员发现正前方20 m处有一辆与汽车同方向行驶的自行车,正以4 m/s的速度匀速行驶,驾驶员以–1 m/s2的加速度开始刹车,停下前是否发生车祸?判断并写出运算过程.【答案】不会发生车祸4.(2018·衡水金卷)长传突破是足球运动中运用远距离空中过顶传球突破对方防线的战术方法。
防守队员甲在本方球门前某位置M抢截得球,将球停在地面上,利用对方压上进攻后不及回防的时机,瞬间给予球一个速度v,使球斜飞入空中,最后落在对方禁区附近地面上P点处。
在队员甲踢球的同时,突前的同伴队员乙由球场中的N点向P点做直线运动,队员乙在N点的初速度度12m/sv 队员乙在NP间先匀加速运动,加速度24m/s a =,速度达到28m/s v =后匀速运动。
经过一段时间后,队员乙恰好在球落在P 点时与球相遇,已知MP 的长度60m s =,NP 的长度11.5m L =,将球员和球视为质点,忽略球在空中运动时的空气阻力,重力加速度取取210m/s g =。
(1)求足球在空中的运动时间;(2)求队员甲在M 点给予足球的速度v 的大小。
【答案】(1)2 s (2)【解析】(1)足球在空中的运动时间与球员乙的直线运动时间相同211v v at =+得到:1 1.5s t =222112v v aL -=,122L L v t -=得到:20.5s t =得到:m/s v =5.(2018·内蒙古自治区杭锦后旗奋斗中学)如图所示是某一次接力训练。
已知甲、乙两运动员经短距离加速后都能达到并保持10 m/s 的速度跑完全程。
设乙从起跑后到接棒前的运动是匀加速的,加速度大小为3 m/s 2。
乙在接力区前端听到口令时起跑,在甲、乙相遇时完成交接棒。
在某次练习中,甲以v =10 m/s 的速度跑到接力区前端s 0=14.0 m 处向乙发出起跑口令。
已知接力区的长度为L =20 m 。
求: (1)此次练习中甲、乙两运动员交接棒处离接力区前端(即乙出发的位置)的距离。
(2)为了达到理想成绩,需要乙恰好在速度达到与甲相同时被甲追上,则甲应在接力区前端多远时对乙发出起跑口令?【答案】(1)6 m (2)16.7 m 【解析】(1)乙加速最长时间m 10s 3v t a ==2m m 12s at vt +=代入数据解得:16.7m s ≈6.(2018·吉林省实验中学)甲、乙两车同时同地同向出发,在同一水平公路上做直线运动,甲的初速度v甲=16 m/s ,加速度大小a 甲=2 m/s 2,做匀减速直线运动,乙以初速度v 乙=4 m/s ,加速度大小a 乙=1 m/s 2,做匀加速直线运动,求:(1)两车再次相遇前二者间的最大距离; (2)到两车再次相遇所需的时间。
【答案】(1)24 m (2)8 s【解析】(1)二者相距最远时的特征条件是:速度相等,即v 甲t =v 乙tv甲t=v甲–a甲t1;v乙t=v乙+a乙t1,得:t1=–v va a甲乙甲乙=4 s相距最远Δx=x甲–x乙=(v甲t1–12a甲t12)–(v乙t1+12a乙t12)=24 m。
(2)再次相遇的特征是:二者的位移相等,即v甲t2–12a甲t22=v乙t2+12a乙t22,代入数值化简得12t2–32t22=0解得:t2=8 s,t2′=0(即出发时刻,舍去)7.(2018·重庆市闽侯二中五校教学联合体)某电视剧制作中心要拍摄一特技动作,要求特技演员从80 m 的大楼楼顶自由下落到行驶的汽车上。
若演员开始下落的同时,水平路面上的汽车从90 m远处由静止向楼底直线行驶,先匀加速到最大速度30 m/s,再匀速行驶到楼底,为保证演员能安全落到汽车上(不计空气阻力,人和汽车看成质点,g=10 m/s2),求:(1)汽车经多长时间开到楼底;(2)汽车匀加速运动的时间和加速度的大小。
【答案】(1)4 s (2)15 m/s2联立上述式子解得t1=2 s所求加速度a=Δv/t=30/2=15 m/s28.(2018·衡水金卷)一辆货车正以12 m/s的速度在平直公路上前进,发现有货物掉下后,立即松开油门以大小为22m/s的加速度做匀减速直线运动,货车开始做匀减速直线运动的同时,在其后面16 m处一辆自行车上的人立即拾到货物从静止出发,以22m/s的加速度同方向追赶货车,已知自行车能达到的最大速度为8 m/s,求:(1)货车做匀减速运动的位移大小;(2)自行车至少经过多次时间能追上货车; 【答案】(1)136m x = (2)8.5s t =【解析】(1)已知货车的初速度为112m/s v =,加速度大小为212m/s a = 货车做匀减速运动的时间为111126s 2v t a === 货车做匀减速运动的位移为11112636m 22v t x ⨯=== (2)已知该自行车的加速度为222m/s a =,最大速度为28m/s v = 自行车做匀加速运动达到最大速度的时间和位移分别为22284s 2v t a ===,2228416m 22v t x ⨯===自行车追上货车的时间138.5s t t t =+=9.长200 m 的列车匀加速通过长1 000 m 的隧道,列车刚进隧道时的速度是20 m/s ,完全出隧道时速度是24 m/s ,求:(1)列车过隧道时的加速度是多大? (2)通过隧道所用的时间是多少? 【答案】(1)0.07 m/s 2 (2)57.1 s【解析】(1)已知列车的初速度v 0=20 m/s 、末速度v =24 m/s 、运动的位移x =1 200 m 可以用匀变速直线运动的位移速度关系式:v 2−v 02=2ax 解得:a =0.07 m/s 2(2)当已知初速度v 0=20 m/s 、末速度v =24 m/s 、加速度a =0.07 m/s 2 用速度时间关系式:v =v 0+at 得:t =57.1 s【名师点睛】本题是匀变速直线运动的基本公式的直接应用,属于比较简单的题目,解题时要学会选择合适公式,这样很多问题就会迎刃而解了。
10.物体以一定的初速度v 0冲上固定的光滑斜面,到达斜面最高点C 时速度恰为零,如图所示。
已知物体第一次运动到斜面长度3/4处的B 点时,所用时间为t ,求物体从B 滑到C 所用的时间。
【答案】t【解析】解法一 比例法对于初速度为0的匀加速直线运动,在连续相等的时间里通过的位移之比为x 1:x 2:x 3:···:x n =1:3:5:···(2n –1)现有x BC :x AB =4AC x :43ACx =1:3 通过x AB 的时间为t ,故通过x BC 的时间t BC =t 解法二 中间时刻速度法可以看出v B正好等于AC段的平均速度,因此B点是中间时刻的位置因此有t BC=t解法三利用有关推论对于初速度为0的匀加速直线运动,通过连续相等的各段位移所用的时间之比为t1:t2:t3:···:t n=1:(2–1):(3–2):···现将整个斜面分成相等的四段,如图所示。
设通过BC段的时间为t x,那么通过BD、DE、EA的时间分别为:t BD=(2–1)t x,t DE=(3–2)t x,t EA=(2–3)t x又t BD+t DE+t EA=t,得t x=t11.兰渝铁路的开通,为广大广安市民的生活、工作带来极大的方便。
某次动车起于广安市,经南充市、遂宁市、止于成都东站。
由于一些车次的动车需经停某些车站,因此不同车次的动车运行时间略有不同,这引起了物理爱好者的兴趣。
现简化动车运行物理模型,假设在南充站停靠的动车在停靠南充站前以速度v0=234 km /h做匀速直线运动,经停该站的动车先做匀减速直线运动,在该站短暂停留后,做匀加速直线运动出站,当速度达到v0=234 km /h时又开始做匀速直线运动,全过程的v—t图象如图所示。
求:(1)动车离开南充站时的加速度大小;(2)动车停靠南充站比不停靠该站运行多经历的时间。
【答案】(1)5 m/s2(2)136.5 s【解析】(1)由图知加速时间t2=13 s则所求时间 1234()136.5s t t t t t ∆=++-=12.羚羊从静止开始奔跑,经过50 m 的距离能加速到最大速度25 m/s ,并能维持一段较长时间,猎豹从静止开始奔跑,经过60 m 的距离能加速到最大速度30 m/s ,以后只能维持这个速度4.0 s ,设猎豹距离羚羊x 米时开始攻击,羚羊则从猎豹1.0 s 后开始奔跑,假设羚羊和猎豹在加速阶段分别做匀加速运动,且沿同一直线,求:(1)猎豹要在最大速度减速前追上羚羊,x 应在什么范围内取值? (2)猎豹要在加速阶段追上羚羊,x 应在什么范围内取值? 【答案】(1)55m x ≤ (2)31.875m x ≤ 【解析】羚羊在加速时平均速度为m11012.5m/s 2v v +== 则加速所需时间为1114s x t v == 其加速度为2m1116.25m/s v a t == 猎豹加速的平均速度为m22015m/s 2v v +==则加速时间为2224s x t v ==其加速度为2m2227.5m/s v a t ==依题意有:21''x x x ≥+∆故有2131.875m x x x ''∆≤-=13.4×100 m 接力赛是最为激烈的比赛项目之一,有甲乙两运动员在训练交接棒的过程中发现,甲短距离加速后能保持9 m/s 的速度跑完全程。
