《弧长与扇形面积》课件1-优质公开课-沪科9下精品
合集下载
沪科版九年级数学下册第二十四章《弧长与扇形面积》公开课课件

如图:在△AOC中,∠AOC=900,∠C=150,以O为 圆心,AO为半径的圆交AC于B点,若OA=6, 求弧AB的长。
C
B
O
A
由组成圆心角的 两条半径和圆心角所对的 弧所围成的图形叫扇形.
A
B
O
n°
o
(1)半径为R的圆,面积是多少? S=πR2 (2)圆面可以看作是多少度的圆心角所对的扇形?
O
180
9
例1、制造弯形管道时,要先按中心线计算“展直 长度”,再下料,试计算图所示管道的展直长度 L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
l 10090050015(7m0m)
180
因此所要求的展直长度 L 270 1057 20 9 (m7m)0 答:管道的展直长度为2970mm.
A
B
O
O
l nR
180
S扇形
nR2
360
比较扇形面积与弧长公式, 用弧长表示扇形面积:
S扇形
1 2
lR
1、已知扇形的圆心角为120°,半径为2,
则这个扇形的面积S扇形=_ 4 .
3
2、已知扇形面积为 1 ,圆心角为60°,
则这个扇形的半径R=3___2 _.
3、已知半径为2cm的扇形,其弧长为
则阴影部分面积等于 。
C
B
O
A
(3)1°圆心角所对扇形面积是多少?
S扇形
nR2
360
若设⊙O半径为R, n°的
圆心角所对的扇形面积为S,
则
nR2
S扇形 360
A
O
B
1、人才教育不是灌输知识,而是将开发文化宝库的钥匙,尽我们知道的交给学生。 2、一个人的知识如果只限于学校学习到的那一些,这个人的知识必然是十分贫乏的2021/10/152021/10/152021/10/1510/15/2021 2:25:32 PM 3、意志教育不是发扬个人盲目的意志,而是培养合于社会历史发展的意志。 4、智力教育就是要扩大人的求知范围 5、最有价值的知识是关于方法的知识。 6、我们要提出两条教育的诫律,一、“不要教过多的学科”;二、“凡是你所教的东西,要教得透彻”2021年10月2021/10/152021/10/152021/10/1510/15/2021 7、能培养独创性和唤起对知识愉悦的,是教师的最高本领2021/10/152021/10/15October 15, 2021 8、先生不应该专教书,他的责任是教人做人;学生不应该专读书,他的责任是学习人生之道。2021/10/152021/10/152021/10/152021/10/15
沪科版九年级数学下册第二十四章《弧长与扇形的面积(第1课时)》优课件

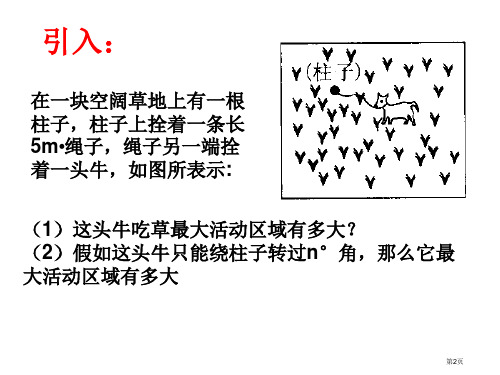
根 3m 长的绳子,
一端栓在柱子
上,另一端栓着
一只羊, 羊的
5
活动最大区域
面积是 5m .
5m 4m o A
5m
4m
o B
C
•不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年4月3日星期日2022/4/32022/4/32022/4/3 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/32022/4/32022/4/34/3/2022 •正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/4/32022/4/3April 3, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
谢谢观赏
You made my day!
我们,还在路上……
例2制造弯形管道时,要先按中心线计算“展直长
度”,再下料,试计算图所示管道的展直长度L(单
位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
L 10090050015(7m0m)
180
因此所要求的展直长度 L 270 1057 20 9 (m7m0 ) 答:管道的展直长度为2970mm.
1.已知弧所对的圆心角为900,半径是4,则弧 长为______
0.1m).
如下图,由组成圆心角的两条半径和圆心角
所对的弧所围成的图形叫做扇形。
B
B
弧 圆圆心心角角
A
扇形
O A
探索研究 2
如果圆的半径为R,则圆的面积为 R 2,
l°的圆心角对应的扇形面积为
R 2 360
沪科版九年级数学下册:弧长与扇形面积ppt课件

例2 如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面 高0.3 m.求截面上有水部分的面积(结果保留小数点后两位). 由弦及其所对的弧组成的图形叫做弓形.
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
解:如图,连接OA,OB,过点O作弦AB的垂线,
垂足为D,交AB于点C,连接AC.
有水部分的面积:
S =S扇形OAB - SΔOAB
120π 0.62 1 AB • OD
360
2
0.12π 1 0.6 3 0.3 2
0.22(m2 )
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
A
D
B
C
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
随堂演练
1. 120°的圆心角对的弧长是6π,则此弧所在圆
北方,两地的经度大致相同,两地的实际距离为5 000
希腊里(1 希腊里≈158.5 m). 当太阳光线在塞伊尼直
射时,同一时刻在亚历山大测量太阳光线偏离
α
直射方向的角为α.实际测得α是7.2°,
A
由此估算出了地球的周长,你能 进行计算吗?
S O
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
解:∵太阳光线可看作平行的,∴圆心角∠AOS=α=7.2°. 设地球的周长为C,则
的半径是( C )
A.3
B.4
C.9
D.18
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
2. AB为⊙O的直径,点C在⊙O上,若∠OCA=50°, AB=4,则B⌒C的长为( B )
A. 10 π
3
B. 10 π
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
解:如图,连接OA,OB,过点O作弦AB的垂线,
垂足为D,交AB于点C,连接AC.
有水部分的面积:
S =S扇形OAB - SΔOAB
120π 0.62 1 AB • OD
360
2
0.12π 1 0.6 3 0.3 2
0.22(m2 )
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
A
D
B
C
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
随堂演练
1. 120°的圆心角对的弧长是6π,则此弧所在圆
北方,两地的经度大致相同,两地的实际距离为5 000
希腊里(1 希腊里≈158.5 m). 当太阳光线在塞伊尼直
射时,同一时刻在亚历山大测量太阳光线偏离
α
直射方向的角为α.实际测得α是7.2°,
A
由此估算出了地球的周长,你能 进行计算吗?
S O
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
解:∵太阳光线可看作平行的,∴圆心角∠AOS=α=7.2°. 设地球的周长为C,则
的半径是( C )
A.3
B.4
C.9
D.18
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
沪科版九年级数学下册:弧长与扇形 面积ppt 课件
2. AB为⊙O的直径,点C在⊙O上,若∠OCA=50°, AB=4,则B⌒C的长为( B )
A. 10 π
3
B. 10 π
初中数学《弧长及扇形的面积》公开课课件

(1)要求扇子外围的弧长,需要知道哪些量?
(2)怎样求这把扇子一面用纸的面积?
圆心角度数,半径长度
大扇形面积—小扇形面积
弧长和扇形的面积公式
如果扇形的半径为r,圆心角为n°,那么
=
扇形 =
1
扇形 =
2
探求新知3——求弓形的面积
A
S阴影= S扇形-S△
B
S阴影=
2.观察该公式,它与我们学过的哪一个公式很类似?
弧长和扇形的面积公式
如果扇形的半径为r,圆心角为n°,那么
=
扇形 =
1
扇形 =
2
练习2
1. 已知扇形的圆心角为120°,半径为20,则该扇形的面积____.
2.已知扇形面积为
3
,圆心角为60°,则这个扇形的半径R=___.
探索新知1——弧长公式
例1:制造弯形管道时,要先按中心线计算“展直长度”,再下料,
试计算图中所示管道的展直长度 l (结果保留,单位:mm)
思考:
展直长度指的是谁的长?
探求新知1——弧长公式
练习1
1.一个扇形半径是3,圆心角是240°,这个扇形的弧长是( C )
A. 2π
B. π
C. 4π
D. 12π
:
(2)说一说你是如何计算每一个弧长的。
圆心角的度数n°
360°
180°90°ຫໍສະໝຸດ 60°1°n°
计算过程
扇形的弧长 l
探索新知1——弧长公式
活 动(1)已知扇形半径为r,请计算不同圆心角度数所对的弧长,并填表。
:
(2)说一说你是如何计算每一个弧长的。
(2)怎样求这把扇子一面用纸的面积?
圆心角度数,半径长度
大扇形面积—小扇形面积
弧长和扇形的面积公式
如果扇形的半径为r,圆心角为n°,那么
=
扇形 =
1
扇形 =
2
探求新知3——求弓形的面积
A
S阴影= S扇形-S△
B
S阴影=
2.观察该公式,它与我们学过的哪一个公式很类似?
弧长和扇形的面积公式
如果扇形的半径为r,圆心角为n°,那么
=
扇形 =
1
扇形 =
2
练习2
1. 已知扇形的圆心角为120°,半径为20,则该扇形的面积____.
2.已知扇形面积为
3
,圆心角为60°,则这个扇形的半径R=___.
探索新知1——弧长公式
例1:制造弯形管道时,要先按中心线计算“展直长度”,再下料,
试计算图中所示管道的展直长度 l (结果保留,单位:mm)
思考:
展直长度指的是谁的长?
探求新知1——弧长公式
练习1
1.一个扇形半径是3,圆心角是240°,这个扇形的弧长是( C )
A. 2π
B. π
C. 4π
D. 12π
:
(2)说一说你是如何计算每一个弧长的。
圆心角的度数n°
360°
180°90°ຫໍສະໝຸດ 60°1°n°
计算过程
扇形的弧长 l
探索新知1——弧长公式
活 动(1)已知扇形半径为r,请计算不同圆心角度数所对的弧长,并填表。
:
(2)说一说你是如何计算每一个弧长的。
沪科版九年级数学下册弧长与扇形面积ppt市公开课一等奖省优质课获奖课件
O
第13页
巩固练习:
1.钟表轴心到分针针端长为5cm,那么经过40分钟,分 针针端转过弧长是( )
A. 10 cm
3
B. 20 cm
3
C. 25 cm
3
D. 50 cm
3
• 2.已知半径2cm扇形,其弧长为 4 ,则这个
扇形面积是_______.
3
第14页
课堂小结: 经过本节课学习你有何收获?
1、熟练记住弧长公式; 2、熟练记住扇形面积公式; 3、熟练利用公式计算。
第15页
布置作业:
课堂作业: 必做题:书本56页 课后练习1、2. 选做题:书本56页习题25.9第4题, 课外作业: 书本57页习题25.9第5,6,8
第16页
第17页
在赛伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射
方向角为a,他实际测得a是7.2度,由此估算出了地球周长,你
能计算吗?
解:因为太阳光线可看作平行,所以圆心角∠AOS=a=7.2度
设地球周长(即⊙O周长)为C,则
C
 ̄⌒
=
AS
360
 ̄
7.2
⌒
∴C=50 AS =50×5000
a
A S
=250000≈39625(km) 答:过南北极地球周长约为39625km。
(3)1°圆心角所对弧长是多少?C 2 R R
360 180
若设⊙O半径为R, n°圆心角所正确弧长
为 C ,则 C n R
180 A
B
(4)140°圆心角所对
弧长是多少?
n°
C 140 R 7 R
180
9
O
第7页
思索2:
27.3 第1课时 弧长和扇形面积(课件)九年级数学下册(华东师大版)

D.
C. -
例3 如图27.3-3,AC 是汽车挡风玻璃前的雨刷器,如果AO
=45 cm,CO =5 cm,当AC 绕点O 顺时针旋转90°时,求雨
刷器AC 扫过的面积.
解:∵△ A′C′O 是△ ACO 绕点O 旋转90°得到的,
∴△ AOC ≌△ A′OC′.
∴雨刷器AC 扫过的面积= 扇形OAA′的面积-扇形
旋转的度数为 n°,则
nπ 10
15.7, 解得 n ≈ 90°.
180
因此,滑轮旋转的角度约为 90°.
A
O·
1-1 制造弯形管道时,要先按中心线计算“展直长度”,
再下料,试计算如图所示管道的展直长度 L (单位:mm,
精确到 1 mm).
解:弧 AB 的长为
A
B
100 900
l
180
=
360 2
1 2
πr
2
90
360
45
360
1
90
=
360
4
45
1
360 8
1 2
πr
4
1 2
πr
8
n
360
n
360
n
πr 2
360
扇形面积公式
半径为 r 的圆中,圆心角为 n° 的扇形的面积
nπr
S扇形 =
.
360
2
注意 ①公式中 n 的意义:n 表示 1° 圆心角的倍数,
它是不带单位的;②公式要理解记忆(即按照上面推
O
S扇形
nπr
l
180
n πr 2
《弧长与扇形面积》课件1-优质公开课-沪科9下精品

问题情境
制造弯形管道时,要先按中心线计算“展直长 度”,再下料,试计算图所示管道的展直长度 L(单位:mm,精确到1mm)
A 700mm
C
B R=900mm 100 O
700mm D
探求新知
思考:(1)半径为R的圆,周长是多少? (2)1°的圆心角所对弧长是多少? (3)n°的圆心角所对弧长是多少?
l= n R
180
n° 1° O
例1 一滑轮装置如图24-63,滑轮的半径R=10cm,当 重物上升15.7cm时,问滑轮的一条半径OA绕轴心O 按逆时针方向旋转的角度?(假设绳索与滑轮之间没
有滑动,π取3.14)
解 设半径OA绕轴心O按逆时针方向旋转n°,则
解方程,得
n R =15.7
180
内切⊙O 切 边BC于D点,则图中阴影部分的
面积为( C)
A
A.cm2 B. 3 cm2
3
C.2cm2 D. 3cm 2
O
B
D
C
当堂训练 2.(08·潍坊)如图,正六边形内接于圆O, 圆O 的半径为10,则圆中阴影部分的面积为______.
100 150 3
O
随堂训练
6、(2009年长春)如图,方格纸中4个 小正方形的边长均为1,则图中阴影部分三个
知道扇形圆心角α.由刚学过的弧长计算方法,可
得
2 r
360o
g2 l
∴
=360o r =360o 4
360o
g
l
2
=
288o 360o
502
=2000
(cm2
)
点击中考
2. (2006,武汉)如图,⊙A、⊙B、⊙C、⊙D相 互外离,它们的半径都是1,顺次连接四个圆心得到 四边形ABCD,则图形中四个扇形(空白部分)的面 积之和是___________.
制造弯形管道时,要先按中心线计算“展直长 度”,再下料,试计算图所示管道的展直长度 L(单位:mm,精确到1mm)
A 700mm
C
B R=900mm 100 O
700mm D
探求新知
思考:(1)半径为R的圆,周长是多少? (2)1°的圆心角所对弧长是多少? (3)n°的圆心角所对弧长是多少?
l= n R
180
n° 1° O
例1 一滑轮装置如图24-63,滑轮的半径R=10cm,当 重物上升15.7cm时,问滑轮的一条半径OA绕轴心O 按逆时针方向旋转的角度?(假设绳索与滑轮之间没
有滑动,π取3.14)
解 设半径OA绕轴心O按逆时针方向旋转n°,则
解方程,得
n R =15.7
180
内切⊙O 切 边BC于D点,则图中阴影部分的
面积为( C)
A
A.cm2 B. 3 cm2
3
C.2cm2 D. 3cm 2
O
B
D
C
当堂训练 2.(08·潍坊)如图,正六边形内接于圆O, 圆O 的半径为10,则圆中阴影部分的面积为______.
100 150 3
O
随堂训练
6、(2009年长春)如图,方格纸中4个 小正方形的边长均为1,则图中阴影部分三个
知道扇形圆心角α.由刚学过的弧长计算方法,可
得
2 r
360o
g2 l
∴
=360o r =360o 4
360o
g
l
2
=
288o 360o
502
=2000
(cm2
)
点击中考
2. (2006,武汉)如图,⊙A、⊙B、⊙C、⊙D相 互外离,它们的半径都是1,顺次连接四个圆心得到 四边形ABCD,则图形中四个扇形(空白部分)的面 积之和是___________.
弧长和扇形面积(公开课)课件

电磁学
在电磁学中,弧长和扇形面积可以用 于计算带电粒子在磁场中运动的轨迹 长度和角度,进而研究电磁场的变化 。
在日常生活中的应用
建筑学
在建筑学中,弧长和扇形面积可以用 于计算各种形状的建筑物的表面积、 体积等参数,进而进行建筑设计、施 工和预算等工作。
艺术
在艺术领域中,弧长和扇形面积可以 用于设计各种形状的艺术作品,例如 雕塑、绘画等,使作品更加美观、协 调。
圆心角与弧长的关系
通过弧长公式可以看出,圆心角越大 ,弧长越长。
弧长计算的实例
实例1
一个圆的半径为5cm,圆 心角为60°,求弧长。
实例2
一个圆的半径为8cm,圆 心角为90°,求弧长。
实例3
一个圆的半径为10cm,圆 心角为120°,求弧长。
03
扇形面积的计算方法
扇形面积公式
总结词
扇形面积公式是计算扇形面积的关键公式,它基于圆的面积 和圆心角。
02
弧长的计算公式:对于半径为r的 圆,其对应的圆心角为θ(以弧度 为单位),弧长l可以通过公式 l=rθ计算得出。
扇形面积的定义
扇形面积是指由圆心角和半径确定的 扇形区域的面积,通常用字母"A"表 示。
扇形面积的计算公式:对于半径为r的 圆,其对应的圆心角为θ(以弧度为单 位),扇形面积A可以通过公式 A=(θ/2π)×πr²计算得出。
详细描述
扇形面积公式为 (S = frac{1}{2} r^2 (θ)),其中 (S) 是扇形面 积,(r) 是半径,(θ) 是圆心角(以弧度为单位)。这个公式 是计算扇形面积的基础,通过它可以将扇形的面积与半径和 圆心角联系起来。
扇形面积公式的应用
总结词
在电磁学中,弧长和扇形面积可以用 于计算带电粒子在磁场中运动的轨迹 长度和角度,进而研究电磁场的变化 。
在日常生活中的应用
建筑学
在建筑学中,弧长和扇形面积可以用 于计算各种形状的建筑物的表面积、 体积等参数,进而进行建筑设计、施 工和预算等工作。
艺术
在艺术领域中,弧长和扇形面积可以 用于设计各种形状的艺术作品,例如 雕塑、绘画等,使作品更加美观、协 调。
圆心角与弧长的关系
通过弧长公式可以看出,圆心角越大 ,弧长越长。
弧长计算的实例
实例1
一个圆的半径为5cm,圆 心角为60°,求弧长。
实例2
一个圆的半径为8cm,圆 心角为90°,求弧长。
实例3
一个圆的半径为10cm,圆 心角为120°,求弧长。
03
扇形面积的计算方法
扇形面积公式
总结词
扇形面积公式是计算扇形面积的关键公式,它基于圆的面积 和圆心角。
02
弧长的计算公式:对于半径为r的 圆,其对应的圆心角为θ(以弧度 为单位),弧长l可以通过公式 l=rθ计算得出。
扇形面积的定义
扇形面积是指由圆心角和半径确定的 扇形区域的面积,通常用字母"A"表 示。
扇形面积的计算公式:对于半径为r的 圆,其对应的圆心角为θ(以弧度为单 位),扇形面积A可以通过公式 A=(θ/2π)×πr²计算得出。
详细描述
扇形面积公式为 (S = frac{1}{2} r^2 (θ)),其中 (S) 是扇形面 积,(r) 是半径,(θ) 是圆心角(以弧度为单位)。这个公式 是计算扇形面积的基础,通过它可以将扇形的面积与半径和 圆心角联系起来。
扇形面积公式的应用
总结词
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S弓形= S扇形+S△
D
感悟: ①当弓形面积小于半圆时 S弓形= S扇形-S△
②当弓形面积大于半圆时 S弓形= S扇形+S△
A
E 0
B
C
效果检测 3. 已知等边三角形ABC的边长为a,分别以A、
a B、C为圆心,以 为半径的圆相切于点D、 E、 2
F,求图中阴影部分的面积S.
A
F
B D
E C
当堂训练 1.(08· 眉山)如图,等边△ABC 的边长为12cm,
探求新知
由组成圆心角的两条半径和圆心角所对的弧所 围成的图形叫做扇形 扇形
O
扇形面积越大,圆心角就越大
小试牛刀
下列图形是扇形吗?
探求新知
思考:(1)半径为R的圆,面积是多少?
(2)1°的圆心角所对的扇形面积是多少?
(3)n°的圆心角所对扇形面积是多少?
nR S= 360
2
1 = lR 2
n° 1° O
180 =15.7
小试牛刀 1.已知弧所对的圆心角为90°,半径是4,则弧长 为____ 2 。
2. 已知一条弧的半径为9,弧长为8π ,那么这条弧 160 所对的圆心角为____ 3. 钟表的轴心到分针针端的长为5cm,那么经过40 分钟,分针针端转过的弧长是( B ) 50 20 10 25 cm cm A. C. cm B. cm D. 3 3 3 3
出了地球的周长,你能进行计算吗?
解 因为太阳光线可看作平行的,所以圆心角
∠AOS=α=7.2°.
设地球的周长(即⊙O的周长)为C,则 C 360 = =50, AS 7.2 ∴
C 50 AS 50 5000 250000 (希腊里)
≈39625(km)
答:地球的周长约为39625km. 我们知道,地球周长约为40000m.可见,2000前, 埃拉托塞尼的估算结果已经相当精确了.
例2 古希腊埃拉托塞尼曾给出一个估算地球周长
(或子午圈长)的简单方法.如图24-64,点S和点A
分别表示埃及的赛伊尼和亚历ll!大两地,亚历山大
在赛伊尼的北方,两地的经度大致相同,两地的实际
距离为5000希腊里(1希腊里≈158.5m).当太阳光线
在赛伊尼直射时,同一时刻在亚历山大测量太阳光线
偏离直射方向的角为α,实际测得α是7.2°,由此估算
得
2 r
360
2 l
r 40 ∴ = 360 = 360 = 288 l 50 288 2 2 2 S= l = 50 = 2000 (cm ) 360 360
点击中考
2. (2006,武汉)如图,⊙A、⊙B、⊙C、⊙D相 互外离,它们的半径都是1,顺次连接四个圆心得到 四边形ABCD,则图形中四个扇形(空白部分)的面 积之和是___________.
例3如图24-66,圆锥形的烟囱帽,它的底面直径为 80cm,母线为50cm.在一块大铁皮上剪裁时,如 何画出这个烟囱帽的侧面展开图?求出该侧面展 开图的面积.
解 烟囱帽的侧面展开图是扇形,如图24-67,设该
扇形的面积为S.
在铁皮上画一个扇形,除需知道扇形半径l外,还需
知道扇形圆心角α.由刚学过的弧长计算方法,可
B A
D
C
点击中考
3.(2007,山东)如图所示,分别以n边形的 顶点为圆心,以单位1为半径画圆,则图中阴影 部分的面积之和为 个平方单位.
当堂训练 6. (08· 鄂州)如图,Rt△ABC中,∠C=90°,
∠A=30°,BC=2,O、H分别为AB、AC的中点,
将△ABC顺时针旋转120°到△A1BC1的位置,
随堂训练 1、已知扇形的圆心角为120°,半径为2,则这个
4 扇形的面积S扇形=____. 3
1 2、已知扇形面积为 ,圆心角为60°,则这个 3
扇形的半径R=____ 2 .
4 3、已知半径为2cm的扇形,其弧长为 , 3 4 2 cm 则这个扇形的面积是_________ . 3
变式训练 练习:如图、水平放置的圆柱形排水管道的截 面半径是0.6cm,其中水面高0.9cm,求截面上 有水部分的面积。
Q P
颗粒归仓
nR 1.弧长公式: l 180 2 nR 1 2.扇形面积公式: S lR 360 2
注意: (1)两个公式的联系和区别;
n R l= 180
n° 1° O
例1 一滑轮装置如图24-63,滑轮的半径R=10cm,当
重物上升15.7cm时,问滑轮的一条半径OA绕轴心O
按逆时针方向旋转的角度?(假设绳索与滑轮之间没
有滑动,π取3.14)
解 设半径OA绕轴心O按逆时针方向旋转n°,则 n R 解方程,得 n≈90. 答:滑轮按逆时针方向旋转的角度约为90°.
内切⊙O 切 边BC于D点,则图中阴影部分的 A 面积为( C)cm B. 3
D.
3cm
2
B
O D C
当堂训练
2.(08· 潍坊)如图,正六边形内接于圆O, 圆O
的半径为10,则圆中阴影部分的面积为______.
100 150 3
O
随堂训练 6、(2009年长春)如图,方格纸中4个 小正方形的边长均为1,则图中阴影部分三个 3 小扇形的面积和为 (结果保留 π 8
则整个旋转过程中线段OH所扫过的面积为( C )
7 7 4 7 3 B. 3 A. 3 8 3 8 4 C. D. 3 3
A1 H1 C1
H O
C B
O1
A
4.如图:AB是半圆的直径,AB=2r, C、D是半圆 的三等分点,则阴影部分的面积等于
A C
O
D
B
5.巧解难题:如图,扇形OAB的圆心角为90°,半 径为R,分别以OA、OB为直径在扇形内作半圆,P、 Q分别表示两个阴影部分的面积,那么P和Q大小关 系是( A ) A.P=Q B.P>Q C.P<Q D.无法确定
问题情境
制造弯形管道时,要先按中心线计算“展直长 度”,再下料,试计算图所示管道的展直长度 L(单位:mm,精确到1mm)
A 700mm 100 C O
B R=900mm 700mm
D
探求新知 思考:(1)半径为R的圆,周长是多少? (2)1°的圆心角所对弧长是多少? (3)n°的圆心角所对弧长是多少?
D
感悟: ①当弓形面积小于半圆时 S弓形= S扇形-S△
②当弓形面积大于半圆时 S弓形= S扇形+S△
A
E 0
B
C
效果检测 3. 已知等边三角形ABC的边长为a,分别以A、
a B、C为圆心,以 为半径的圆相切于点D、 E、 2
F,求图中阴影部分的面积S.
A
F
B D
E C
当堂训练 1.(08· 眉山)如图,等边△ABC 的边长为12cm,
探求新知
由组成圆心角的两条半径和圆心角所对的弧所 围成的图形叫做扇形 扇形
O
扇形面积越大,圆心角就越大
小试牛刀
下列图形是扇形吗?
探求新知
思考:(1)半径为R的圆,面积是多少?
(2)1°的圆心角所对的扇形面积是多少?
(3)n°的圆心角所对扇形面积是多少?
nR S= 360
2
1 = lR 2
n° 1° O
180 =15.7
小试牛刀 1.已知弧所对的圆心角为90°,半径是4,则弧长 为____ 2 。
2. 已知一条弧的半径为9,弧长为8π ,那么这条弧 160 所对的圆心角为____ 3. 钟表的轴心到分针针端的长为5cm,那么经过40 分钟,分针针端转过的弧长是( B ) 50 20 10 25 cm cm A. C. cm B. cm D. 3 3 3 3
出了地球的周长,你能进行计算吗?
解 因为太阳光线可看作平行的,所以圆心角
∠AOS=α=7.2°.
设地球的周长(即⊙O的周长)为C,则 C 360 = =50, AS 7.2 ∴
C 50 AS 50 5000 250000 (希腊里)
≈39625(km)
答:地球的周长约为39625km. 我们知道,地球周长约为40000m.可见,2000前, 埃拉托塞尼的估算结果已经相当精确了.
例2 古希腊埃拉托塞尼曾给出一个估算地球周长
(或子午圈长)的简单方法.如图24-64,点S和点A
分别表示埃及的赛伊尼和亚历ll!大两地,亚历山大
在赛伊尼的北方,两地的经度大致相同,两地的实际
距离为5000希腊里(1希腊里≈158.5m).当太阳光线
在赛伊尼直射时,同一时刻在亚历山大测量太阳光线
偏离直射方向的角为α,实际测得α是7.2°,由此估算
得
2 r
360
2 l
r 40 ∴ = 360 = 360 = 288 l 50 288 2 2 2 S= l = 50 = 2000 (cm ) 360 360
点击中考
2. (2006,武汉)如图,⊙A、⊙B、⊙C、⊙D相 互外离,它们的半径都是1,顺次连接四个圆心得到 四边形ABCD,则图形中四个扇形(空白部分)的面 积之和是___________.
例3如图24-66,圆锥形的烟囱帽,它的底面直径为 80cm,母线为50cm.在一块大铁皮上剪裁时,如 何画出这个烟囱帽的侧面展开图?求出该侧面展 开图的面积.
解 烟囱帽的侧面展开图是扇形,如图24-67,设该
扇形的面积为S.
在铁皮上画一个扇形,除需知道扇形半径l外,还需
知道扇形圆心角α.由刚学过的弧长计算方法,可
B A
D
C
点击中考
3.(2007,山东)如图所示,分别以n边形的 顶点为圆心,以单位1为半径画圆,则图中阴影 部分的面积之和为 个平方单位.
当堂训练 6. (08· 鄂州)如图,Rt△ABC中,∠C=90°,
∠A=30°,BC=2,O、H分别为AB、AC的中点,
将△ABC顺时针旋转120°到△A1BC1的位置,
随堂训练 1、已知扇形的圆心角为120°,半径为2,则这个
4 扇形的面积S扇形=____. 3
1 2、已知扇形面积为 ,圆心角为60°,则这个 3
扇形的半径R=____ 2 .
4 3、已知半径为2cm的扇形,其弧长为 , 3 4 2 cm 则这个扇形的面积是_________ . 3
变式训练 练习:如图、水平放置的圆柱形排水管道的截 面半径是0.6cm,其中水面高0.9cm,求截面上 有水部分的面积。
Q P
颗粒归仓
nR 1.弧长公式: l 180 2 nR 1 2.扇形面积公式: S lR 360 2
注意: (1)两个公式的联系和区别;
n R l= 180
n° 1° O
例1 一滑轮装置如图24-63,滑轮的半径R=10cm,当
重物上升15.7cm时,问滑轮的一条半径OA绕轴心O
按逆时针方向旋转的角度?(假设绳索与滑轮之间没
有滑动,π取3.14)
解 设半径OA绕轴心O按逆时针方向旋转n°,则 n R 解方程,得 n≈90. 答:滑轮按逆时针方向旋转的角度约为90°.
内切⊙O 切 边BC于D点,则图中阴影部分的 A 面积为( C)cm B. 3
D.
3cm
2
B
O D C
当堂训练
2.(08· 潍坊)如图,正六边形内接于圆O, 圆O
的半径为10,则圆中阴影部分的面积为______.
100 150 3
O
随堂训练 6、(2009年长春)如图,方格纸中4个 小正方形的边长均为1,则图中阴影部分三个 3 小扇形的面积和为 (结果保留 π 8
则整个旋转过程中线段OH所扫过的面积为( C )
7 7 4 7 3 B. 3 A. 3 8 3 8 4 C. D. 3 3
A1 H1 C1
H O
C B
O1
A
4.如图:AB是半圆的直径,AB=2r, C、D是半圆 的三等分点,则阴影部分的面积等于
A C
O
D
B
5.巧解难题:如图,扇形OAB的圆心角为90°,半 径为R,分别以OA、OB为直径在扇形内作半圆,P、 Q分别表示两个阴影部分的面积,那么P和Q大小关 系是( A ) A.P=Q B.P>Q C.P<Q D.无法确定
问题情境
制造弯形管道时,要先按中心线计算“展直长 度”,再下料,试计算图所示管道的展直长度 L(单位:mm,精确到1mm)
A 700mm 100 C O
B R=900mm 700mm
D
探求新知 思考:(1)半径为R的圆,周长是多少? (2)1°的圆心角所对弧长是多少? (3)n°的圆心角所对弧长是多少?
