2016年高考文科数学全国卷2
2016年高考文科数学全国卷2(含详细答案)
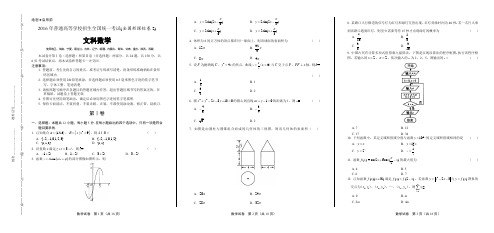
数学试卷 第1页(共18页) 数学试卷 第2页(共18页) 数学试卷 第3页(共18页)绝密★启用前2016年普通高等学校招生全国统一考试(全国新课标卷2)文科数学使用地区:海南、宁夏、黑龙江、吉林、辽宁、新疆、内蒙古、青海、甘肃、重庆、陕西、西藏本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共24题,共150分,共6页.考试结束后,将本试卷和答题卡一并交回. 注意事项:1. 答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内.2. 选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.3. 请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.4. 作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑.5. 保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀.第Ⅰ卷一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知集合{}123A =,,,{}2|9B x x =<,则A B =( ) A. {2,1,0,1,2,3}--B. {2,1,0,1,2}--C. {1,2,3}D. {1,2}2. 设复数z 满足3z i i +=-,则=z ( )A. 12i -+B. 12i -C. 32i +D. 32i -3. 函数()sin y A x ωϕ=+的部分图像如图所示,则A. 2sin(2)6y x π=-B. 2sin(2)3y x π=-C. 2sin()6y x π=+D. 2sin()3y x π=+4. 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为( )A. 12πB. 323πC. 8πD. 4π5. 设F 为抛物线C :24y x =的焦点,曲线0ky k x =>()与C 交于点P ,PF x ⊥轴,则=k( )A.12 B. 1 C. 32D. 26. 圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则=a( )A. 43-B. 34-C.D. 27. 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积( )A. 20πB. 24πC. 28πD. 32π8. 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为 ( )A. 710B. 58C. 38D. 3109. 中国古代有计算多项式值得秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的2x =,2n =,依次输入的a 为2,2,5,则输出的s = ( )A. 7B. 12C. 17D. 3410. 下列函数中,其定义域和值域分别与函数lg 10x y =的定义域和值域相同的是 ( )A. y x =B. lg y x =C. 2x y =D. 1y x=11. 函数() = cos26cos()2f x x x π+-的最大值为( )A. 4B. 5C. 6D. 712. 已知函数()()f x x ∈R 满足()(2)f x f x =-,若函数223y x x =--与()y f x =图象的交点为11x y (,),22x y (,),…,m m x y (,),则1mi i x =∑=A. 0B. mC. 2mD. 4m姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第4页(共6页) 数学试卷 第5页(共6页) 数学试卷 第6页(共6页)第Ⅱ卷本卷包括必考题和选考题两部分.第13~12题为必考题,每个试题考生都必须作答.第22~24为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分. 13. 已知向量a ()4m =,,b ()32=-,,且a ∥b ,则m =________.14. 若x ,y 满足约束条件10,30,30,x y x y x -++--⎧⎪⎨⎪⎩≥≥≤则2z x y =-的最小值为________.15. ABC ∆的内角A B C ,,的对边分别为a b c ,,,若4cos 5A =,5cos 13C =,1a =,则b =________.16. 有三张卡片,分别写有1和2,1和3,2和3.甲、乙、丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.三、解答题:解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分)等差数列{}n a 中,344a a +=,576a a +=.(Ⅰ)求{}n a 的通项公式;(Ⅱ)设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]0=,[2.6]2=.18. (本小题满分12分)某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:(Ⅰ)记A 为事件:“一续保人本年度的保费不高于基本保费”。
2016年高考新课标2文科数学及答案
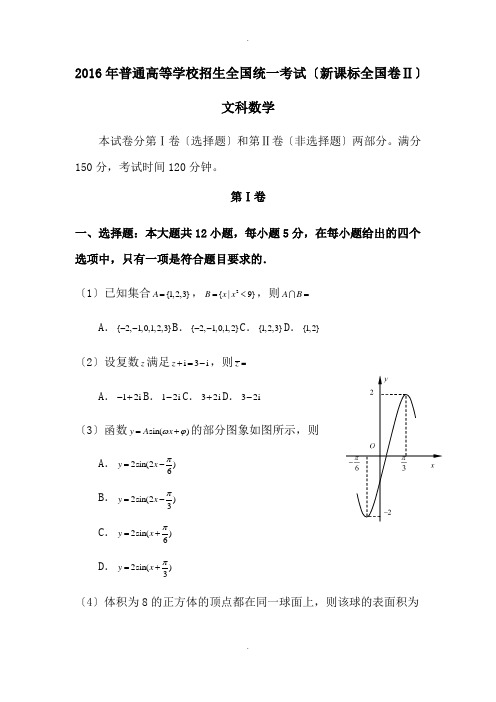
2016年普通高等学校招生全国统一考试〔新课标全国卷Ⅱ〕文科数学本试卷分第Ⅰ卷〔选择题〕和第Ⅱ卷〔非选择题〕两部分。
满分150分,考试时间120分钟。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 〔1〕已知集合{1,2,3}A =,2{|9}B x x =<,则AB =A .{2,1,0,1,2,3}--B .{2,1,0,1,2}--C .{1,2,3}D .{1,2} 〔2〕设复数z 满足i 3i z +=-,则z =A .12i -+B .12i -C .32i +D .32i -〔3〕函数sin()y A x ωϕ=+的部分图象如图所示,则A .2sin(2)6y x π=-B .2sin(2)3y x π=-C .2sin()6y x π=+D .2sin()3y x π=+〔4〕体积为8的正方体的顶点都在同一球面上,则该球的表面积为A .12πB .323πC .8πD .4π〔5〕设F 为抛物线2:4C y x =的焦点,曲线(0)k y k x=>与C 交于点P ,PF x⊥轴,则k =A .12B .1C .32D .2〔6〕圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a =A .43-B .34-C .3D .2〔7〕右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为A .20πB .24πC .28πD .32π〔8〕某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为A .710B .58C .38D .310 (9)中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的2x =,2n =,依次输入的a 为2,2,5,则输出的s =44 4A .7B .12C .17D .34〔10〕下列函数中,其定义域和值域分别与函数lg 10x y =的定义域和值域相同的是A .y x =B .lg y x =C .2x y =D.y〔11〕函数()cos26cos()2f x x x π=+-的最大值为A .4B .5C .6D .7 〔12〕已知函数()()f x x ∈R 满足()(2)f x f x =-,若函数2|23|y x x =--与()y f x =图象的交点为11(,)x y ,22(,)x y ,…,(,)m m x y ,则1mi i x ==∑A .0B .mC .2mD .4m第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分. 〔13〕已知向量(,4)m =a ,(3,2)=-b ,且a ∥b ,则m =.〔14〕若x ,y 满足约束条件10,30,30,x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩则2z x y =-的最小值为.〔15〕ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,若4cos 5A =,5cos 13C =,1a =,则b =.〔16〕有三X 卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一X 卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2〞,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1〞,丙说:“我的卡片上的数字之和不是5〞,则甲的卡片上的数字是.三、解答题:解答应写出文字说明,证明过程或演算步骤. 〔17〕〔本小题满分12分〕 等差数列{}n a 中,344a a +=,576a a +=. 〔Ⅰ〕求{}n a 的通项公式;〔Ⅱ〕设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]0=,[2.6]2=..(18)〔本小题满分12分〕某险种的基本保费为a〔单位:元〕,继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:〔Ⅰ〕记A为事件:“一续保人本年度的保费不高于基本保费〞.求()P A的估计值;〔Ⅱ〕记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%〞.求()P B的估计值;〔Ⅲ〕求续保人本年度的平均保费的估计值.〔19〕〔本小题满分12分〕如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE CF =,EF 交BD 于点H ,将DEF △沿EF 折到D EF '△的位置. 〔Ⅰ〕证明:AC HD '⊥;〔Ⅱ〕若5AB =,6AC =,54AE =,22OD '=,求五棱锥D ABCFE '-的体积.(20)〔本小题满分12分〕已知函数()(1)ln(1)=+--.f x x x a x〔Ⅰ〕当4a=时,求曲线()y f xf处的切线方程;=在(1,(1))〔Ⅱ〕若当(1,)f x>,求a的取值X围.x∈+∞时,()0(21)〔本小题满分12分〕已知A 是椭圆22:143x y E +=的左顶点,斜率为(0)k k >的直线交E 于A ,M 两点,点N 在E 上,MA NA ⊥.〔Ⅰ〕当||||AM AN =时,求AMN △的面积; 〔Ⅱ〕当2||||AM AN =时,证明:2k <.请考生在第〔22〕、〔23〕、〔24〕题中任选一题做答,如果多做,按所做的第一题记分.〔22〕〔本小题满分10分〕选修4–1:几何证明选讲如图,在正方形ABCD 中,E ,G 分别在边DA ,DC 上〔不与端点重合〕,且DE DG =,过D 点作DF CE ⊥,垂足为F . 〔Ⅰ〕证明:B ,C ,G ,F 四点共圆;〔Ⅱ〕若1AB =,E 为DA 的中点,求四边形BCGF 的面积.〔23〕〔本小题满分10分〕选修4–4:坐标系与参数方程 在直角坐标系xOy 中,圆C 的方程为22(6)25x y ++=.〔Ⅰ〕以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程;〔Ⅱ〕直线l 的参数方程是cos ,sin ,x t y t αα=⎧⎨=⎩〔t 为参数〕,l 与C 交于A ,B 两点,||10AB =,求l 的斜率.〔24〕〔本小题满分10分〕选修4–5:不等式选讲 已知函数11()||||22f x x x =-++,M 为不等式()2f x <的解集.〔Ⅰ〕求M ;〔Ⅱ〕证明:当a ,b M ∈时,|||1|a b ab +<+.参考答案第Ⅰ卷一. 选择题:本大题共12小题。
2016年高考新课标2文科数学真题及答案

2016年普通高等学校招生全国统一考试(新课标全国卷Ⅱ)文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分,考试时间120分钟。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)已知集合{1,2,3}A =,2{|9}B x x =<,则A B =A .{2,1,0,1,2,3}--B .{2,1,0,1,2}--C .{1,2,3}D .{1,2} (2)设复数z 满足i 3i z +=-,则z =A .12i -+B .12i -C .32i +D .32i -(3)函数sin()y A x ωϕ=+的部分图象如图所示,则A .2sin(2)6y x π=-B .2sin(2)3y x π=-C .2sin()6y x π=+D .2sin()3y x π=+(4)体积为8的正方体的顶点都在同一球面上,则该球的表面积为A .12πB .323πC .8πD .4π(5)设F 为抛物线2:4C y x =的焦点,曲线(0)k y k x=>与C 交于点P ,PF x ⊥轴,则k =A .12B .1C .32D .2(6)圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a =A .43-B .34-C.2(7)右图是由圆柱与圆锥组合而成的几何体 的三视图,则该几何体的表面积为A .20πB .24πC .28πD .32π(8间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为A .710B .58C .38D .310 (9)中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的2x =,2n =,依次输入的a 为2,2,5,则输出的s =A .7B .12C .17D .34(10)下列函数中,其定义域和值域分别与函数lg 10x y =的定义域和值域相同的是A .y x =B .lg y x =C .2x y =D.y =(11)函数()cos26cos()2f x x x π=+-的最大值为A .4B .5C .6D .7 (12)已知函数()()f x x ∈R 满足()(2)f x f x =-,若函数2|23|y x x =--与()y f x =图象的交点为11(,)x y ,22(,)x y ,…,(,)m m x y ,则1mi i x ==∑A .0B .mC .2mD .4m第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分. (13)已知向量(,4)m =a ,(3,2)=-b ,且a ∥b ,则m =.(14)若x ,y 满足约束条件10,30,30,x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩则2z x y =-的最小值为.(15)ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,若4c o s 5A =,5cos 13C =,1a =,则b =.(16)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是.三、解答题:解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分) 等差数列{}n a 中,344a a +=,576a a +=. (Ⅰ)求{}n a 的通项公式;(Ⅱ)设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]0=,[2.6]2=.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求()P A的估计值;(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求()P B的估计值;(Ⅲ)求续保人本年度的平均保费的估计值.如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD上,AE CF =,EF 交BD 于点H ,将DEF △沿EF 折到DEF'△的位置. (Ⅰ)证明:AC HD '⊥;(Ⅱ)若5AB =,6AC =,54AE =,OD '=求五棱锥D ABCFE '-的体积.(20)(本小题满分12分)D 'OECHFDBA已知函数()(1)ln(1)=+--.f x x x a x(Ⅰ)当4a=时,求曲线()f处的切线方程;y f x=在(1,(1))(Ⅱ)若当(1,)f x>,求a的取值范围.x∈+∞时,()0(21)(本小题满分12分)已知A 是椭圆22:143x y E +=的左顶点,斜率为(0)k k >的直线交E 于A ,M 两点,点N 在E 上,MA NA ⊥.(Ⅰ)当||||AM AN =时,求AMN △的面积; (Ⅱ)当2||||AM AN =2k <.请考生在第(22)、(23)、(24)题中任选一题做答,如果多做,按所做的第一题记分.(22)(本小题满分10分)选修4–1:几何证明选讲如图,在正方形ABCD 中,E ,G 分别在边DA ,DC 上(不与端点重合),且DE DG =,过D 点作DF CE ⊥,垂足为F . (Ⅰ)证明:B ,C ,G ,F 四点共圆;(Ⅱ)若1AB =,E 为DA 的中点,求四边形BCGF 的面积.(23)(本小题满分10分)选修4–4:坐标系与参数方程 在直角坐标系xOy 中,圆C 的方程为22(6)25x y ++=.(Ⅰ)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程;(Ⅱ)直线l 的参数方程是cos ,sin ,x t y t αα=⎧⎨=⎩(t 为参数),l 与C交于A ,B 两点,||AB =l 的斜率.(24)(本小题满分10分)选修4–5:不等式选讲 已知函数11()||||22f x x x =-++,M 为不等式()2f x <的解集.(Ⅰ)求M ;(Ⅱ)证明:当a ,b M ∈时,|||1|a b ab +<+.E GD CBA参考答案第Ⅰ卷一. 选择题:本大题共12小题。
2016年高考文科数学全国2卷试题与答案(Word版)

2016 年普通高等学校招生全国统一考试文科数学注意事项:一、选择题:本大题共12 小题。
每小题 5 分,在每个小题给出的四个选项中,只有一项是符合要求的。
2(1)已知集合 A {1,2,3},B { x | x 9} ,则 A B(A ){ 2,1,0,1,2,3} (B){ 2,1,0,1,2} (C){1 ,2,3} (D){1 ,2}(2)设复数z 满足z i 3 i ,则z =(A ) 1 2i (B)1 2i (C)3 2i (D)3 2i(3) 函数y =Asin( x ) 的部分图像如图所示,则(A )y 2sin(2 x ) (B)y 2sin(2 x)6 3(C)y 2sin(2 x+ ) (D)y 2sin(2 x+ )6 3(4) 体积为8 的正方体的顶点都在同一球面上,则该球面的表面积为(A )12 (B)323(C)(D)(5) 设F 为抛物线C:y2=4x 的焦点,曲线y=2=4x 的焦点,曲线y= kx(k>0)与C 交于点P,PF ⊥x 轴,则k=(A )12 (B)1 (C)32 (D)222- 2x- 8y+13=0 的圆心到直线ax+ y- 1=0 的距离为1,则a= (6) 圆x +y(A )-43 (B)-34(C) 3 (D)2(7) 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π(B)24π(C)28π(D)32π(8) 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40 秒.若一名行人来到该路口遇到红灯,则至少需要等待15 秒才出现绿灯的概率为(A )710 (B)58(C)38(D)310(9) 中国古代有计算多项式值得秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的 a 为2,2,5,则输出的s=(A )7 (B)12 (C)17 (D)34lgx 的定义域和值域相同的是(10) 下列函数中,其定义域和值域分别与函数y=10(A )y= x(B)y=lg x(C)y=2x(D)y 1x(11) 函数πf (x) cos2 x 6cos( x) 的最大值为2(A )4(B)5 (C)6 (D)7(12) 已知函数f(x )(x∈R)满足f(x)=f(2-x),若函数y=|x2-2x-3| 与y= f( x) 图像的交点为(x1,y1),(x2,y2),⋯,m(x m,y m),则xi=i 1(A)0 (B) m (C) 2m (D) 4m二.填空题:共4小题,每小题5分.(13) 已知向量a=(m,4),b=(3,-2) ,且a∥b,则m=___________.x y 1 0x y 3 0,则z= x-2y 的最小值为__________ (14) 若x,y 满足约束条件x 3 0(15)△ABC 的内角A,B,C 的对边分别为a,b,c,若cos4 5A ,cos C,a=1,则b=____________.5 13(16)有三张卡片,分别写有 1 和2,1 和3,2 和3. 甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________________.三、解答题:解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分12 分)等差数列{ a n } 中,a3 a 4 4, a5 a 7 6(I )求{ a n }的通项公式;(II)设b n =[ an ],求数列{bn} 的前10 项和,其中[x] 表示不超过x 的最大整数,如[0.9]=0,[2.6]=2(18)(本小题满分12 分)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:计表:随机调查了该险种的200 名续保人在一年内的出险情况,得到如下统(I )记 A 为事件:“一续保人本年度的保费不高于基本保费”。
2016年高考全国2卷文数试题与答案

2016年普通高等学校招生全国统一考试文科数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的、号填写在本试卷和答题卡相应位置上。
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号框涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号框。
写在本试卷上无效。
3.答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷一、 选择题:本大题共12小题。
每小题5分,在每个小题给出的四个选项中,只有一项是符合要求的。
(1)已知集合{123}A =,,,2{|9}B x x =<,则A B =I (A ){210123}--,,,,, (B ){21012}--,,,, (C ){123},, (D ){12},(2)设复数z 满足i 3i z +=-,则z =(A )12i -+(B )12i -(C )32i +(D )32i - (3) 函数=sin()y A x ωϕ+的部分图像如图所示,则(A )2sin(2)6y x π=-(B )2sin(2)3y x π=-(C )2sin(2+)6y x π=(D )2sin(2+)3y x π=(4) 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为 (A )12π(B )323π(C )8π(D )4π (5) 设F 为抛物线C :y 2=4x 的焦点,曲线y =kx(k >0)与C 交于点P ,PF ⊥x 轴,则k = (A )12(B )1 (C )32(D )2 (6) 圆x 2+y 2−2x −8y +13=0的圆心到直线ax +y −1=0的距离为1,则a = (A )−43(B )−34(C )3(D )2(7) 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π(B )24π(C )28π(D )32π(8) 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为 (A )710(B )58(C )38(D )310(9)中国古代有计算多项式值得九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的a 为2,2,5,则输出的s = (A )7 (B )12 (C )17 (D )34(10) 下列函数中,其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是 (A )y =x (B )y =lg x (C )y =2x (D )y x=(11) 函数π()cos 26cos()2f x x x =+-的最大值为 (A )4(B )5(C )6 (D )7(12) 已知函数f (x )(x ∈R )满足f (x )=f (2-x ),若函数y =|x 2-2x -3| 与y =f (x ) 图像的交点为(x 1,y 1),(x 2,y 2),…,(x m ,y m ),则1=mi i x =∑(A)0 (B)m (C) 2m (D) 4m 二.填空题:共4小题,每小题5分.(13) 已知向量a =(m ,4),b =(3,-2),且a ∥b ,则m =___________.(14) 若x ,y 满足约束条件103030x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩,则z =x -2y 的最小值为__________(15)△ABC 的角A ,B ,C 的对边分别为a ,b ,c ,若4cos 5A =,5cos 13C =,a =1,则b =____________.(16)有三卡片,分别写有1和2,1和3,2和3. 甲,乙,丙三人各取走一卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________________.三、解答题:解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分)等差数列{n a }中,34574,6a a a a +=+=(I )求{n a }的通项公式; (II)设nb =[na ],求数列{nb }的前10项和,其中[x]表示不超过x 的最大整数,如[0.9]=0,[2.6]=2(18)(本小题满分12分)某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年的出险情况,得到如下统计表:(I )记A 为事件:“一续保人本年度的保费不高于基本保费”。
2016全国2卷高考文科数学试卷及答案(同名9984)

2016年普通高等学校招生全统一考试文科数学本试卷分第Ⅰ卷〔选择题〕和第Ⅱ卷〔非选择题〕两部分,共24题,共150分第Ⅰ卷一、选择题:此题共12小题,每题5分,在每题给出的四个选项中,只有一项是符合题目要求的。
(1) 已知集合{}3,2,1=A ,{}92<=x x B ,则=B A 〔A 〕{}3,2,1,0,1,2-- 〔B 〕{}2,1,0,1- 〔C 〕{}3,2,1 〔D 〕{}2,1(2) 设复数z 满足i i z -=+3,则=z〔A 〕i 21+- 〔B 〕i 21- 〔C 〕i 23+ 〔D 〕i 23- (3) 函数)sin(ϕω+=x A y 的部分图像如下图,则〔A 〕)62sin(2π-=x y 〔B 〕)32sin(2π-=x y 〔C 〕)62sin(2π+=x y 〔D 〕)32sin(2π+=x y (4) 体积为8的正方体的顶点都在同一球面上,则该球面的外表积为〔A 〕π12 〔B 〕π332〔C 〕π8 〔D 〕π4 (5) 设F 为抛物线C :x y 42=的焦点,曲线)0(>=k xky 与C 交于点P ,x PF ⊥轴,则=k 〔A 〕21 〔B 〕1 〔C 〕23〔D 〕2 (6) 圆0138222=+--+y x y x 的圆心到直线01=-+y ax 的距离为1,则=a〔A 〕3 〔B 〕43〔C 〕3 〔D 〕2 (7) 右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的外表积为〔A 〕20π〔B 〕24π 〔C 〕28π 〔D 〕32π精品否是 0n k >输出s结束a1+=+⋅=k k a x s s遇到红灯,则至少需要等待15秒才出现绿灯的概率为〔A 〕107 〔B 〕85 〔C 〕83 〔D 〕103 (9) 中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,假设输入的2=x ,2=n ,依次输入的a 为2,2,5,则输出的=s 〔A 〕7 〔B 〕12 〔C 〕17 〔D 〕34 (10)以下函数中,其定义域和值域分别与函数xy lg 10=的定义域和值域相同的是〔A 〕x y = 〔B 〕x y lg = 〔C 〕xy 2= 〔D 〕xy 1=(11)函数)(x x x f -+=2cos6 2 cos )(π的最大值为 〔A 〕4 〔B 〕5 〔C 〕6 〔D 〕7(12)已知函数)( )(R x x f ∈满足)2()(x f x f -=,假设函数322--=x x y 与)(x f y =图像的交点为),(,),,(),,(2211m m y x y x y x ⋯,则∑=mi ix1〔A 〕0 〔B 〕m 〔C 〕m 2 〔D 〕m 4第Ⅱ卷本卷包括必考题和选考题两部分。
2016全国新课标2卷高考文科数学及答案解析

2015年普通高等学校招生全国统一考试(新课标Ⅱ卷)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知集合{}{}30|,21|<<=<<-=x x B x x A ,则=⋃B A ( )A .(-1,3)B .(-1,0)C .(0,2)D .(2,3) 2.若a 为实数,且i iai+=++312,则=a ( ) A .-4 B .-3 C .3 D .43.根据下面给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )A .逐年比较,2008年减少二氧化硫排放量的效果最显着B .2007年我国治理二氧化硫排放显现成效C .2006年以来我国二氧化硫年排放量呈减少趋势D .2006年以来我国二氧化硫年排放量与年份正相关 4.向量()1,1-=a ,()2,1-=b ,则()=⋅+a b a 2 ( )A .-1B .0C .1D .25.设n S 是等差数列{}n a 的前n 项和,若3531=++a a a ,则=5S ( )A .5B .7C .9D .116.一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.157.已知三点()01,A ()30,B ,()32,C ,则ABC ∆外接圆的圆心到原点的距离为( )A.53B.213C.253D.438.右边程序框图的算法思路源于我国古代数学名着《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的=a ( )第8题图A .0B .2C .4D .14 9.已知等比数列{}n a 满足411=a ,()14453-=a a a ,则=2a ( ) A .2 B .1 C.12 D.1810.已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点.若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π11.如图,长方形ABCD 的边AB =2,BC =1,O 是AB 的中点.点P 沿着边BC ,CD 与DA 运动,记∠BOP =x ,将动点P 到A ,B 两点距离之和表示为x 的函数f (x ),则y =f (x )的图象大致为( ) 12.设函数()()2111ln x x x f +-+=,则使得()()12->x f x f 成立的x 的取值范围是( )A.⎝⎛⎭⎪⎫13,1 B.()∞+⋃⎪⎭⎫ ⎝⎛∞,,131- C.⎝ ⎛⎭⎪⎫-13,13 D.⎪⎭⎫ ⎝⎛∞+⋃⎪⎭⎫ ⎝⎛∞,,3131-- 第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.已知函数()x ax x f 23-=的图象过点()4,1-,则=a ________.14.若x ,y满足约束条件⎩⎨⎧x +y -5≤0,2x -y -1≥0,x -2y +1≤0,则y x z +=2的最大值为________.15.已知双曲线过点()34,,且渐近线方程为x y 21±=,则该双曲线的标准方程为________.16.已知曲线x x y ln +=在点()1,1处的切线与曲线()122+++=x a ax y 相切,则=a ________.三、解答题(解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分) ABC ∆中,D 是BC 上的点,AD 平分BAC ∠,DC BD 2= (1)求CBsin sin (2)若︒=∠60BAC ,求B ∠18.(本小题满分12分)某公司为了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频数分布表.图①B 地区用户满意度评分的频数分布表(1)在图②中作出B 地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).图②(2)根据用户满意度评分,将用户的满意度分为三个等级:估计哪个地区用户的满意度等级为不满意的概率大?说明理由.19.(本小题满分12分)如图,长方体1111D C B A ABCD -中,16=AB ,10=BC ,81=AA ,点E ,F 分别在11B A ,11C D 上,411==F D E A .过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形. (1)在图中画出这个正方形(不必说明画法和理由); (2)求平面α把该长方体分成的两部分体积的比值.20.(本小题满分12分)已知椭圆C :12222=+by a x ()0.>>b a 的离心率为22,点()22,在C 上.(1)求C 的方程;(2)直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M .证明:直线OM 的斜率与直线l 的斜率的乘积为定值. 21.(本小题满分12分)已知函数()()x a x x f -+=1ln . (1)讨论()x f 的单调性;(2)当()x f 有最大值,且最大值大于22-a 时,求a 的取值范围.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.22. (本小题满分10分)选修4-1:几何证明选讲如图O 是等腰三角形AB C 内一点, ⊙O 与△ABC 的底边BC 交于M ,N 两点,与底边上的高交于点G ,且与AB ,AC 分别相切于E ,F 两点. (I )证明EF ∥BC .(II )若AG 等于⊙O 的半径,且AE MN ==,求四边形EBCF 的面积23.(本小题满分10分)选修4-4:坐标系与参数方程 在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩(t 为参数,且0t ≠ ),其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:.C C ρθρθ==(I )求2C 与3C 交点的直角坐标;(II )若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB最大值24.(本小题满分10分)选修4-5:不等式选讲 设a ,b ,c ,d 均为正数,且a +b =c +d .证明: (1)若ab >cd ,则a +b >c +d ;(2)a +b >c +d 是|a -b |<|c -d |的充要条件.2015·新课标Ⅱ卷 第8页1、选A2、故选D3、选D4、选C5、解:在等差数列中,因为6、解:如图所示,选D.7、选B.8、故选B.9、解:因为{}),1(4,414531-==a a a a a n 满足所以,.21241,2,2),1(4123144424=⨯=====-=q a a q q a a a a a 所以,所以又解得故选C. 10、解:因为A,B 都在球面上,又为该球面上动点,C AOB ,90︒=∠所以 三棱锥的体积的最大值为3661213132==⨯⨯R R R ,所以R=6,所以球的表面积为 S=14442=R ππ,故选C.11、解:如图,当点P 在BC 上时, 当4π=x时取得最大值51+,以A,B 为焦点C,D 为椭圆上两定点作椭圆,显然,当点P 在C,D 之间移动时PA+PB<51+.又函数)(x f 不是一次函数,故选B.12、解:因为函数时函数是增函数是偶函数,),0[,11)1ln()(2+∞∈+-+=x xx x f .131,)12(,12)12()(22<<->∴->∴->x x x x x x f x f 解得 故选A.第二卷一、 填空题:本大题共4个小题,每小题5分 13、答:a=-214、解:当x=3,y=2时,z=2x+y 取得最大值8. 15、解:设双曲线的方程为.43,4),0(422=≠=-k k k y x )代入方程,解得,点(16、解:.122,11'-=∴+=x y xy ,切线方程为切线的斜率为 二、 解答题:解答应写出文字说明,证明过程或演算步骤。
2016年高考文科数学全国卷2(含详细答案)
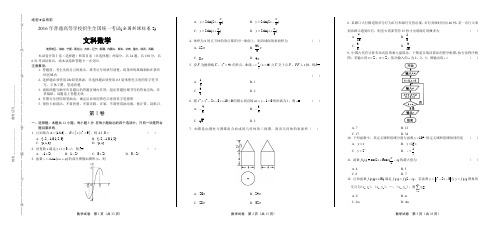
数学试卷 第1页(共33页) 数学试卷 第2页(共33页) 数学试卷 第3页(共33页)绝密★启用前2016年普通高等学校招生全国统一考试(全国新课标卷2)文科数学使用地区:海南、宁夏、黑龙江、吉林、辽宁、新疆、内蒙古、青海、甘肃、重庆、陕西、西藏本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共24题,共150分,共6页.考试结束后,将本试卷和答题卡一并交回. 注意事项:1. 答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内.2. 选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.3. 请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.4. 作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑.5. 保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀.第Ⅰ卷一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知集合{}123A =,,,{}2|9B x x =<,则A B =( ) A. {2,1,0,1,2,3}--B. {2,1,0,1,2}--C. {1,2,3}D. {1,2}2. 设复数z 满足3z i i +=-,则=z ( )A. 12i -+B. 12i -C. 32i +D. 32i -3. 函数()sin y A x ωϕ=+的部分图像如图所示,则A. 2sin(2)6y x π=-B. 2sin(2)3y x π=-C. 2sin()6y x π=+D. 2sin()3y x π=+4. 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为( )A. 12πB. 323πC. 8πD. 4π5. 设F 为抛物线C :24y x =的焦点,曲线0ky k x =>()与C 交于点P ,PF x ⊥轴,则=k( )A.12 B. 1 C. 32D. 26. 圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则=a( )A. 43-B. 34-C.D. 27. 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积( )A. 20πB. 24πC. 28πD. 32π8. 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为 ( )A. 710B. 58C. 38D. 3109. 中国古代有计算多项式值得秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的2x =,2n =,依次输入的a 为2,2,5,则输出的s = ( )A. 7B. 12C. 17D. 3410. 下列函数中,其定义域和值域分别与函数lg 10x y =的定义域和值域相同的是 ( )A. y x =B. lg y x =C. 2x y =D. 1y x=11. 函数() = cos26cos()2f x x x π+-的最大值为( )A. 4B. 5C. 6D. 712. 已知函数()()f x x ∈R 满足()(2)f x f x =-,若函数223y x x =--与()y f x =图象的交点为11x y (,),22x y (,),…,m m x y (,),则1mi i x =∑=A. 0B. mC. 2mD. 4m姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第4页(共6页) 数学试卷 第5页(共6页) 数学试卷 第6页(共6页)第Ⅱ卷本卷包括必考题和选考题两部分.第13~12题为必考题,每个试题考生都必须作答.第22~24为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分. 13. 已知向量a ()4m =,,b ()32=-,,且a ∥b ,则m =________.14. 若x ,y 满足约束条件10,30,30,x y x y x -++--⎧⎪⎨⎪⎩≥≥≤则2z x y =-的最小值为________.15. ABC ∆的内角A B C ,,的对边分别为a b c ,,,若4cos 5A =,5cos 13C =,1a =,则b =________.16. 有三张卡片,分别写有1和2,1和3,2和3.甲、乙、丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.三、解答题:解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分)等差数列{}n a 中,344a a +=,576a a +=.(Ⅰ)求{}n a 的通项公式;(Ⅱ)设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]0=,[2.6]2=.18. (本小题满分12分)某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:(Ⅰ)记A 为事件:“一续保人本年度的保费不高于基本保费”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学试卷 第1页(共18页) 数学试卷 第2页(共18页) 数学试卷 第3页(共18页)绝密★启用前2016年普通高等学校招生全国统一考试(全国新课标卷2)文科数学使用地区:海南、宁夏、黑龙江、吉林、辽宁、新疆、内蒙古、青海、甘肃、重庆、陕西、西藏本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共24题,共150分,共6页.考试结束后,将本试卷和答题卡一并交回. 注意事项:1. 答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内.2. 选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.3. 请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.4. 作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑.5. 保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀.第Ⅰ卷一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知集合{}123A =,,,{}2|9B x x =<,则A B = ( )A. {2,1,0,1,2,3}--B. {2,1,0,1,2}--C. {1,2,3}D. {1,2}2. 设复数z 满足3z i i +=-,则=z ( )A. 12i -+B. 12i -C. 32i +D. 32i -3. 函数()sin y A x ωϕ=+的部分图像如图所示,则A. 2sin(2)6y x π=-B. 2sin(2)3y x π=-C. 2sin()6y x π=+D. 2sin()3y x π=+4. 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为( )A. 12πB.323πC. 8πD. 4π5. 设F 为抛物线C :24y x =的焦点,曲线0k y k x=>()与C 交于点P ,PF x ⊥轴,则=k( )A.12 B. 1 C. 32D. 26. 圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则=a ( )A. 43- B. 34-C.D. 27. 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积( )A. 20πB. 24πC. 28πD. 32π8. 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为( )A.710 B. 58C. 38D. 3109. 中国古代有计算多项式值得秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的2x =,2n =,依次输入的a 为2,2,5,则输出的s = ( )A. 7B. 12C. 17D. 3410. 下列函数中,其定义域和值域分别与函数lg 10x y =的定义域和值域相同的是 ( )A. y x =B. lg y x =C. 2x y =D. 1y x=11. 函数() = cos26cos()2f x x x π+-的最大值为( )A. 4B. 5C. 6D. 712. 已知函数()()f x x ∈R 满足()(2)f x f x =-,若函数223y x x =--与()y f x =图象的交点为11x y (,),22x y (,),…,m m x y (,),则1mi i x =∑=A. 0B. mC. 2mD. 4m姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第4页(共6页) 数学试卷 第5页(共6页) 数学试卷 第6页(共6页)第Ⅱ卷本卷包括必考题和选考题两部分.第13~12题为必考题,每个试题考生都必须作答.第22~24为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分. 13. 已知向量a ()4m =,,b ()32=-,,且a ∥b ,则m =________.14. 若x ,y 满足约束条件10,30,30,x y x y x -++--⎧⎪⎨⎪⎩≥≥≤则2z x y =-的最小值为________.15. ABC ∆的内角A B C ,,的对边分别为a b c ,,,若4cos 5A =,5cos 13C =,1a =,则b =________.16. 有三张卡片,分别写有1和2,1和3,2和3.甲、乙、丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.三、解答题:解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分)等差数列{}n a 中,344a a +=,576a a +=.(Ⅰ)求{}n a 的通项公式;(Ⅱ)设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]0=,[2.6]2=.18. (本小题满分12分)某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:(Ⅰ)记A 为事件:“一续保人本年度的保费不高于基本保费”。
求P A ()的估计值;(Ⅱ)记B 为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”. 求()P B 的估计值;(Ⅲ)求续保人本年度的平均保费估计值.19. (本小题满分12分)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE=CF ,EF 交BD 于点H .将DEF ∆沿EF 折到'D EF △的位置.(Ⅰ)证明:'AC HD ⊥; (Ⅱ)若5AB =,6AC =,54AE =,'OD =求五棱锥'D ABCEF -体积.20. (本小题满分12分)已知函数()()l (n 11)x x x a x f -=+-.(Ⅰ)当=4a 时,求曲线=()y f x 在(1(1))f ,处的切线方程;(Ⅱ)若当(1)x∈+∞,时,()f x >0,求a 的取值范围.21. (本小题满分12分)已知A 是椭圆E :22143x y +=的左顶点,斜率为0k k >()的直线交E 于A ,M 两点,点N 在E 上,MA NA ⊥.(Ⅰ)当AM AN =时,求AMN △的面积; (Ⅱ)当2AM AN =2k <.请考生在第22~24题中任选一题作答,如果多做,则按所做的第一题计分. 22. (本小题满分10分)选修41-:几何证明选讲如图,在正方形ABCD 中,E ,G 分别在边DA ,DC 上(不与端点重合),且D E D G =,过D 点作DF CE ⊥,垂足为F .(Ⅰ)证明:B,C ,G ,F 四点共圆;(Ⅱ)若1AB =,E 为DA 的中点,求四边形BCGF 的面积.23. (本小题满分10分)选修44-:坐标系与参数方程在直角坐标系xOy 中,圆C 的方程为()226=25x y ++.(Ⅰ)以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,求C 的极坐标方程;(Ⅱ)直线l 的参数方程是=cos sin x t a y t a ⎧⎨=⎩,,(t 为参数),l 与C 交于A ,B 两点,AB 求l 的斜率.24. (本小题满分10分)选修45-:不等式选讲已知函数1122f x x x =-++(),M 为不等式f x <2()的解集. (Ⅰ)求M ;(Ⅱ)证明:当a b M ∈,时,1a b ab +<+.{1,2}A B=【提示】先求出集合A B的值. 【考点】一元二次不等式的解法,集合的运算2π(3)12=【提示】先通过正方体的体积,求出正方体的棱长,然后求出球的半径,即可求出球的表π2416π=12π248π2=,2π24π=,故该2328πS S++=【提示】空间几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是0222+=,2226+=,62517k+=,17,选C.根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量数学试卷第8页(共18页)数学试卷第9页(共18页)-【解析】因为a b∥,所以-【考点】平面向量的坐标运算'=BD HD H⊥平面AC OH O=,所以ABC9EF=;2数学试卷第11页(共6页)数学试卷第12页(共6页)116 (2)3kx-=+由题设,直线222数学试卷第13页(共18页)数学试卷第14页(共18页)数学试卷第15页(共18页)数学试卷第16页(共6页)数学试卷第17页(共6页)数学试卷第18页(共6页)。
