几何五大模型蝴蝶模型
小学数学几何五大模型讲解——蝴蝶模型

小学数学几何五大模型讲解——蝴蝶模型
上次课为大家讲解了小学几何五大模型中的等积模型,今天为大家讲解一下五大模型中的蝴蝶模型。
蝴蝶模型是小学几何中的重点和难点,希望对大家的学习有所帮助。
蝴蝶模型又称梯形蝴蝶定理,是指在一个梯形中连接对角线后形成四个三角形。
如图
下面给学生们留一道练习题,你们可以做一下。
有关蝴蝶模型的知识今天就为学生们讲到这里,下次为大家讲解第三大模型——燕尾模型。
大家今后在数学方面有什么问题难题,可以私信向吴老师提问。
小学奥数-几何五大模型(蝴蝶模型)..

模型三 蝴蝶模型(任意四边形模型)任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?ODCBA【分析】 根据蝴蝶定理求得312 1.5AOD S =⨯÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平方千米,所以人工湖的面积是7.5 6.920.58-=平方千米【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?任意四边形、梯形与相似模型B【解析】 ⑴根据蝴蝶定理,123BGC S ⨯=⨯V ,那么6BGC S =V ;⑵根据蝴蝶定理,()():12:361:3AG GC =++=. (???)【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。
如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
AB C DOH GA BC D O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。
小学奥数-几何五大模型(蝴蝶模型)知识讲解

小学奥数-几何五大模型(蝴蝶模型)模型三 蝴蝶模型(任意四边形模型)任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?ODCBA【分析】 根据蝴蝶定理求得312 1.5AOD S =⨯÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平方千米,所以人工湖的面积是7.5 6.920.58-=平方千米【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?任意四边形、梯形与相似模型B【解析】 ⑴根据蝴蝶定理,123BGC S ⨯=⨯V ,那么6BGC S =V ;⑵根据蝴蝶定理,()():12:361:3AG GC =++=. (???)【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。
如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
ABCDOH GA BCD O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。
几何五大模型-蝴蝶模型

4、如图,梯形ABCD中, 、 的面积分别为1.2和2.7,求梯形ABCD的面积.
5、如下图,一个长方形被一些直线分成了若干个小块,已知三角形 的面积是 ,三角形 的面积是 ,求四边形 的面积.
6、长方形中,若三角形1的面积与三角形3的面积比为4比5,四边形2的面积为36,则三角形1的面积为________.
2、图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷。那么最大的一个三角形的面积是多少公顷?
板块二梯形模型的应用
【知识梳理】
梯形中比例关应份数为 .
梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)
板块一任意四边形模型
【例题精讲】
例1如图,某公园的外轮廓是四边形ABCD,被对角线AC、BD分成四个部分,△AOB面积为1平方千米,△BOC面积为2平方千米,△COD的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?
【举一反三】
1、如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知。
例3如图, , ,求梯形的面积。
【举一反三】
1、如下图,梯形ABCD的AB平行于CD,对角线AC,BD交于O,已知 与 的面积分别为25平方厘米与35平方厘米,那么梯形ABCD的面积是________平方厘米.
例4如图,梯形ABCD的对角线AC与BD交于点O,已知梯形上底为2,且三角形ABO的面积等于三角形BOC面积的 ,求三角形AOD与三角形BOC的面积之比.
小学的奥数-几何五大模型(蝴蝶模型)

模型三 蝴蝶模型(任意四边形模型)任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?ODCBA【分析】 根据蝴蝶定理求得312 1.5AOD S =⨯÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平方千米,所以人工湖的面积是7.5 6.920.58-=平方千米【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?任意四边形、梯形与相似模型B【解析】 ⑴根据蝴蝶定理,123BGC S ⨯=⨯V ,那么6BGC S =V ;⑵根据蝴蝶定理,()():12:361:3AG GC =++=. (???)【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。
如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
AB C DOH GA BC D O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。
小学六年级奥数 五大模型——蝴蝶模型、燕尾模型
1
【例2】(★★★)
如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别 为2、5、8平方厘米,那么余下的四边形OFBC的面积为 ___________平方厘米。
【例3】 (★★★)
如图,ABCD长方形中,阴影部分是直角三角形且面积为54,OD 的长是16,OB的长是9。那么四边形OECD的面积是多少?
五大模型——蝴蝶模型、燕尾模型
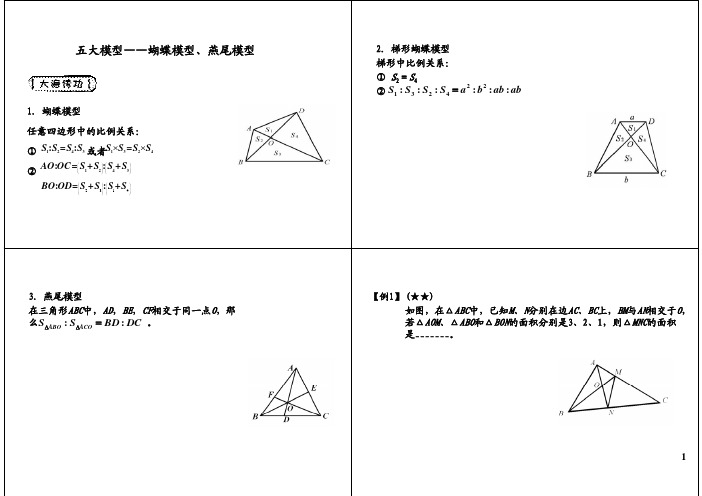
1.蝴蝶模型
任意四边形中的比例关系:
①
S :S =S :S
12
43
或者S1
S 3
=
S 2
S 4
② AO:OC = S +S : S +S
1
2
4
3
BO:OD= S +S : S +S
ቤተ መጻሕፍቲ ባይዱ
2
3
Aa D S1
S2 O S4
S3
B
C
b
二、本讲经典例题 例1,例4,例6,例7,例8
3.燕尾模型 在三角形ABC中,AD,BE,CF相交于同一点O,那么 SABO : SACO BD : DC 。
4
1
4
3.燕尾模型
在三角形ABC中,AD,BE,CF相交于同一点O,那 么SABO : SACO BD : DC 。
2.梯形蝴蝶模型 梯形中比例关系: ① S2=S4 ② S1 : S3 : S2 : S4 a2 : b2 : ab : ab
五大模型——蝴蝶模型、燕尾模型
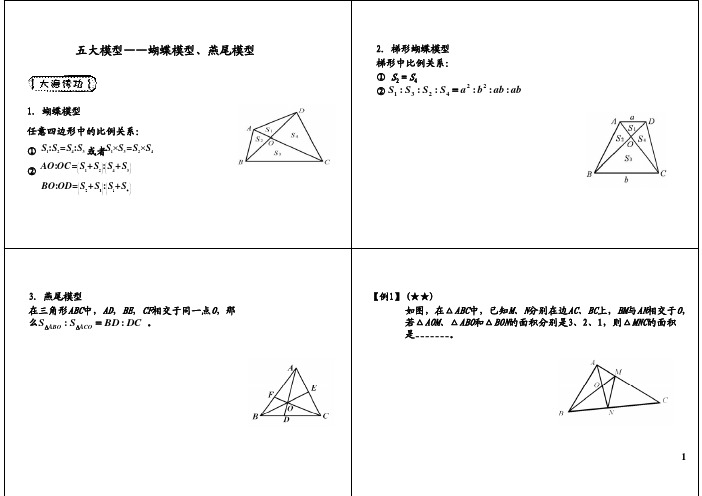
1.蝴蝶模型
任意四边形中的比例关系:
①
S :S =S :S
12
43
或者S1
S 3
=
S 2
S 4
② AO:OC = S +S : S +S
1
2
4
3
BO:OD= S +S : S +S
2
3
1
4
3.燕尾模型
在三角形ABC中,AD,BE,CF相交于同一点O,那 么SABO : SACO BD : DC 。
①
S :S =S :S
12
43
或者S1
S 3
=
S 2
S 4
② AO:OC = S +O:OD= S +S : S +S
2
3
1
4
3
2.梯形蝴蝶模型 梯形中比例关系: ① S2=S4 ② S1 : S3 : S2 : S4 a2 : b2 : ab : ab
2.梯形蝴蝶模型 梯形中比例关系: ① S2=S4 ② S1 : S3 : S2 : S4 a2 : b2 : ab : ab
【例1】 (★★) 如图,在△ABC中,已知M、N分别在边AC、BC上,BM与AN相交于O, 若△AOM、△ABO和△BON的面积分别是3、2、1,则△MNC的面积 是_______。
Aa D S1
S2 O S4
S3
B
C
b
二、本讲经典例题 例1,例4,例6,例7,例8
3.燕尾模型 在三角形ABC中,AD,BE,CF相交于同一点O,那么 SABO : SACO BD : DC 。
4
【例4】(★★★★) 如图,在一个边长为6的正方形中,放入一个边长为2的正方形, 保持与原正方形的边平行,现在分别连接大正方形的一个顶点与 小正方形的两个顶点,形成了图中的阴影图形,那么阴影部分的 面积为_________。
小学奥数几何篇五大模型蝴蝶定理(附答案)

小学奥数几何篇五大模型蝴蝶定理一、蝴蝶定理的定义与公式蝴蝶定理是小学奥数几何篇中的一个重要模型,它描述了在等腰三角形中,一条平行于底边的线段将底边平分,并且这条线段与等腰三角形的两腰相交于同一点时,该线段的中点与等腰三角形的顶点、底边的中点以及两腰上的交点形成一个等腰三角形。
蝴蝶定理的公式如下:设等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,则AG=BG=CG。
二、蝴蝶定理的应用1. 在等腰三角形中求边长:通过蝴蝶定理,可以快速求出等腰三角形中未知边的长度。
例如,已知等腰三角形ABC中,AB=AC,底边BC 的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求AG的长度。
解答:根据蝴蝶定理,AG=BG=CG,又因为AB=AC,所以AG=AB/2=a。
2. 在等腰三角形中求角度:通过蝴蝶定理,可以求出等腰三角形中未知角的度数。
例如,已知等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求∠AGB的度数。
解答:由于AG=BG=CG,所以△AGB是等边三角形,∠AGB=60°。
3. 在等腰三角形中求面积:通过蝴蝶定理,可以求出等腰三角形中未知部分的面积。
例如,已知等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求△AGB的面积。
解答:由于△AGB是等边三角形,所以△AGB的面积=(a^2 √3)/ 4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4、如图,梯形ABCD中, 、 的面积分别为1.2和2.7,求梯形ABCD的面积.
5、如下图,一个长方形被一些直线分成了若干个小块,已知三角形 的面积是 ,三角形 的面积是 ,求四边形 的面积.
6、长方形中,若三角形1的面积与三角形3的面积比为4比5,四边形2的面积为36,则三角形1的面积为________.
【举一反三】
1、在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是多少平方厘米?
【课堂总结】
我的收获
我的疑惑
【课后作业】
1、如图相邻两个格点间的距离是1,则图中阴影三角形的面积为_________。
2、如图,每个小方格的边长都是1,求三角形ABC的面积。
求:⑴三角形BGC的面积;⑵AG:GC=?
例2 如图,四边形ABCD的对角线AC与BD交于点O(如图所示)。如果三角形ABD的面积等于三角形BCD的面积的 ,且AO=2,DO=3,那么CO的长度是DO的长度的_________的对角线交于O点, 、 、 、 的面积依次是2、4、4和6。求:⑴求 的面积;⑵求 的面积。
_________________个性化辅导讲义
年 级:
时间
年月日
课 题
蝴蝶模型
教学目标
1.熟记蝴蝶模型,
2.学会使用蝴蝶模型解决问题。
3.学着对平面图形进行对比,培养发现特征的能力。
教 学 内 容
【温故知新】
默写公式:
【知识梳理】
模型三 蝴蝶模型
任意四边形中的比例关系(“蝴蝶定理”):
① 或者
②
蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
2、图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷。那么最大的一个三角形的面积是多少公顷?
板块二 梯形模型的应用
【知识梳理】
梯形中比例关系(“梯形蝴蝶定理”):
①
② ;
③ 的对应份数为 .
梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)
7、如图,正方形 面积为 平方厘米, 是 边上的中点.求图中阴影部分的面积.
8、如图面积为 平方厘米的正方形 中, 是 边上的三等分点,求阴影部分的面积.
9、如图,正六边形面积为 ,那么阴影部分面积为多少?
例3如图, , ,求梯形的面积。
【举一反三】
1、如下图,梯形ABCD的AB平行于CD,对角线AC,BD交于O,已知 与 的面积分别为25平方厘米与35平方厘米,那么梯形ABCD的面积是________平方厘米.
例4 如图,梯形ABCD的对角线AC与BD交于点O,已知梯形上底为2,且三角形ABO的面积等于三角形BOC面积的 ,求三角形AOD与三角形BOC的面积之比.
板块一任意四边形模型
【例题精讲】
例1如图,某公园的外轮廓是四边形ABCD,被对角线AC、BD分成四个部分,△AOB面积为1平方千米,△BOC面积为2平方千米,△COD的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?
【举一反三】
1、如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知。
