采用SPSS多元Logistic回归分析方法对船舶碰撞风险量化
基于机器学习的船舶碰撞风险评估与预测

基于机器学习的船舶碰撞风险评估与预测船舶碰撞是海上运输中一个重要而严峻的问题。
为了确保航行安全和减少事故风险,船舶碰撞风险评估和预测变得至关重要。
近年来,机器学习在航海安全领域得到了广泛应用,它可以通过分析大量的航行数据来识别和预测潜在的碰撞风险。
本文将介绍基于机器学习的船舶碰撞风险评估与预测的方法和应用。
首先,我们需要了解船舶碰撞风险评估和预测的基本原理。
基于机器学习的方法主要通过分析船舶的动态性能和环境因素来评估碰撞风险。
这些因素包括船舶的速度、航向、目标船舶的动态特征、水深、天气、交通情况等。
通过收集和分析大量的航行数据,并将其与历史碰撞事故数据进行比较,机器学习模型可以学习到不同因素之间的关系和规律,并进行风险评估和预测。
其次,我们介绍一些常用的机器学习算法和模型在船舶碰撞风险评估与预测中的应用。
首先是决策树算法,它可以根据不同特征的重要性对数据进行分类和预测。
决策树算法可以根据船舶的动态特征和环境因素,对碰撞风险进行快速准确的评估。
其次是支持向量机(SVM)算法,它可以通过构建高维空间中的划分超平面,对不同类别的数据进行分类和预测。
SVM算法在船舶碰撞风险评估中可以通过学习不同航线上的船舶运行模式,识别出可能发生碰撞的区域。
此外,还有神经网络、随机森林等算法也可以在船舶碰撞风险评估与预测中发挥重要作用。
除了算法和模型的选择,数据的质量和数量也对船舶碰撞风险评估与预测的准确性起到关键作用。
船舶碰撞风险评估需要大量的航行数据作为输入,包括船舶的位置、速度、航向、姿态等信息。
为了提高数据质量,我们需要确保数据的采集、传输和存储过程的稳定和可靠性。
同时,为了提高数据数量和多样性,我们可以采用自动化系统或传感器来收集更多的航行数据,并利用数据挖掘和预处理技术对数据进行清洗和筛选。
此外,为了提高船舶碰撞风险评估与预测的准确性,我们还可以结合其他相关领域的知识和技术。
例如,通过融合航海学、物理学、气象学等领域的知识,可以建立更全面和准确的模型,提高预测的准确性。
采用SPSS多元Logistic回归分析方法对船舶碰撞风险量化 李舒泓

采用SPSS多元Logistic回归分析方法对船舶碰撞风险量化李舒泓摘要:本文将采用SPSS多元Logistic回归分析方法,以1993-2013年英国港口海域船舶碰撞事故调查资料进行统计后,论证人为因素对于后果严重度的影响。
关键词:SPSS多元Logistic回归分析方法;船舶风险;量化一、船舶碰撞事故后果等级划分(一)国内水上交通事故分级船舶交通事故损失程度常常作为评估碰撞事故等级的标准,我国交通运输部《水上交通事故统计办法》中规定的水上交通事故分级标准表,根据伤亡人数、造成的直接经济损失和水域环境污染情况等要素,将事故分为特别重大事故、重大事故、较大事故、一般事故和小事故五个等级。
(二)国际水上交通事故分类国际海事组织(IMO)按照事故后果的严重程度将事故分成三个级别,重大事故、大事故和一般事故。
(三)本文碰撞后果等级划分从上述表格可以看出,国内外常常把事故分为四个等级,而单纯针对碰撞事故来说,事故中往往船舶受损较多,而人员伤亡较少。
因此,本文将碰撞后果分为四个等级,分级标准主要为船舶受损的严重程度。
二、评测指标确定由上可见,国内外,关于事故等级的划分标准不尽相同,而单纯针对碰撞事故来说,事故中常是船舶受损较多,而人员伤亡较少。
如果出现人员死亡的情况,船体一般是受到很大的撞击,损坏比较严重,如果漏油造成严重的环境污染,那么通常也是船体受损严重所引起的,所以本文主要将从船体受损程度的角度来选定事故后果的评测指标。
本文将基于前人的研究成果,选取人的因素、船舶的设备因素和环境因素共3个主要指标对英国船舶碰撞后果进行评估。
(一)人的因素据保守统计,由人的因素直接或间接导致的船舶碰撞事故频发不断。
本文通过对众多船舶碰撞事故调查报告的分析与统计,将事故中人的因素分为6个等级,并按权重进行划分。
对应的模型中参数值如表1所示。
表1 人的因素参数表(四)事故后果等级将四种事故后果等级分为:事故后果={轻微、中等、较严重、严重}={1、2、3、4、5、6}。
利用SPSS进行logistic回归分析(二元、多项)之欧阳法创编

线性回归是很重要的一种回归方法,但是线性回归只适用于因变量为连续型变量的情况,那如果因变量为分类变量呢?比方说我们想预测某个病人会不会痊愈,顾客会不会购买产品,等等,这时候我们就要用到logistic回归分析了。
Logistic回归主要分为三类,一种是因变量为二分类得logistic回归,这种回归叫做二项logistic回归,一种是因变量为无序多分类得logistic回归,比如倾向于选择哪种产品,这种回归叫做多项logistic 回归。
还有一种是因变量为有序多分类的logistic回归,比如病重的程度是高,中,低呀等等,这种回归也叫累积logistic回归,或者序次logistic 回归。
二值logistic回归:选择分析——回归——二元logistic,打开主面板,因变量勾选你的二分类变量,这个没有什么疑问,然后看下边写着一个协变量。
有没有很奇怪什么叫做协变量?在二元logistic回归里边可以认为协变量类似于自变量,或者就是自变量。
把你的自变量选到协变量的框框里边。
细心的朋友会发现,在指向协变量的那个箭头下边,还有一个小小的按钮,标着a*b,这个按钮的作用是用来选择交互项的。
我们知道,有时候两个变量合在一起会产生新的效应,比如年龄和结婚次数综合在一起,会对健康程度有一个新的影响,这时候,我们就认为两者有交互效应。
那么我们为了模型的准确,就把这个交互效应也选到模型里去。
我们在右边的那个框框里选择变量a,按住ctrl,在选择变量b,那么我们就同时选住这两个变量了,然后点那个a*b的按钮,这样,一个新的名字很长的变量就出现在协变量的框框里了,就是我们的交互作用的变量。
然后在下边有一个方法的下拉菜单。
默认的是进入,就是强迫所有选择的变量都进入到模型里边。
除去进入法以外,还有三种向前法,三种向后法。
一般默认进入就可以了,如果做出来的模型有变量的p值不合格,就用其他方法在做。
再下边的选择变量则是用来选择你的个案的。
基于聚类分析的船舶碰撞结果分析的开题报告

基于聚类分析的船舶碰撞结果分析的开题报告一、研究背景及意义船舶交通事故是海上安全的重要问题之一,既关系到生命财产安全,也直接影响航运市场的稳定和发展,因此船舶碰撞事故的研究具有重要的现实意义。
聚类分析是一种有效的数据分析方法,可以将样本分成若干个群组,以发现数据中存在的同类事物或规律。
本研究基于聚类分析的方法,对船舶碰撞事故的结果进行分析,以期探究船舶碰撞事故发生的规律和原因,对海上安全管理和船舶碰撞事故预防提供参考。
二、研究内容及方法1. 研究内容(1)船舶碰撞事件的调查和分析;(2)基于聚类分析的数据处理和结果分析;(3)利用统计分析方法和数据可视化技术对研究结果进行展示和解读。
2. 研究方法(1)收集有关船舶碰撞事件的数据,包括碰撞海域、船舶类型、气象条件、事故原因等;(2)对数据进行预处理和归一化处理,以消除数据之间的量纲差异和确保数据可比性;(3)利用聚类分析方法对数据进行分组,并通过评价指标来评估聚类结果的合理性;(4)对聚类结果进行统计分析和数据可视化,分析船舶碰撞事件的分布特征、主要影响因素等。
三、预期成果及意义1. 预期成果通过本研究,将得到以下预期成果:(1)构建基于聚类分析的船舶碰撞事件数据分析模型;(2)分析船舶碰撞事件的影响因素和变化趋势;(3)为船舶碰撞事故的预防和海上安全管理提供科学依据。
2. 意义(1)深入探究船舶碰撞事故的发生规律和原因,有利于提高海上安全管理的水平;(2)为政府制定航运政策和规划提供参考;(3)有助于航运企业更好地制定防范船舶碰撞事故的措施。
四、研究进度安排本研究计划分为以下几个阶段:(1)阶段一(2021年9月至11月):对国内外相关研究文献进行调研和归纳,构建船舶碰撞事件数据分析模型;(2)阶段二(2021年12月至2022年1月):收集船舶碰撞事件的数据,并进行处理和预处理;(3)阶段三(2022年2月至6月):基于聚类分析方法对数据进行分组,评估聚类结果的合理性,进一步分析船舶碰撞事件的影响因素和分布规律等;(4)阶段四(2022年7月至9月):分析研究结果,并通过统计分析和数据可视化技术对结果进行展示和解读。
SPSS 危险度分析和Logistic回归

A
10
Logistic回归的应用4
4. 比较各因素对于发病的相对重要性 比较各标准化偏回归系数bi’ 绝对值的大小,绝对值大的对发病的作用也 大。
5. 考察因素之间的交互作用 如考察XL和XK之间的交互作用是否显著,再增加一各指标:XLK= XL*XK ,如其偏回归系数bLK显著,则XL和XK之间的交互作用显著。
A
4
危险度分析3
分层分析步骤: (1)计算各层的比数比,作显著性检验。 (2)检验各层的总体比数比是否相同。
如差异有统计学意义,结束。 (3)如差异无统计学意义,
计算公共比数比。 (4)检验公共比数比和1之间的差异是否有统计学意义。
A
5
SPSS中的实现
AnalyzeDescriptive Statistics Crosstabs Statistics对话框中选取Risk选项,分层分析另外选
(1) 当Xi为二值变量时,如吸烟(1=吸,0=不吸) exp(bi)为吸烟对于发病的比数比
A
9
Logistic回归的应用3
(2)当Xi为等级变量时,如吸烟(0=不吸,1=少量,2=中等,3=大 量)。 exp(bi)为每增加一个等级,发病的相对危险度
如大量对于不吸其发病的相对危险度为: exp(3bi) (3)当Xi为连续变量时,如年龄(岁)
2. 因素分析 分析哪些因素(协变量)对疾病的发生有显著作用。 对各偏回归系数作显著性检验,如显著,则说明在排除其它因素的 影响后,该因素与发病有显著关系。
A
8
Logistic回归的应用2
3. 求各因素在排除其它因素的影响后,对于发病的相对危险度 (或比数比) 如某因素Xi的偏回归系数为bi, 则该因素Xi对于发病的比数比为 exp(bi)
多元回归分析的精辟分析spss

1、利用OLS(ordinary least squares)来做多元回归可能是社会学研究中最常用的统计分析方法。
利用此法的基本条件是应变项为一个分数型的变项(等距尺度测量的变项),而自变项之测量尺度则无特别的限制。
当自变项为类别变项时,我们可依类别数(k)建构k-1个数值为0与1之虚拟变项(dummy variable)来代表不同之类别。
因此,如果能适当的使用的话,多元回归分析是一相当有力的工具。
2、多元回归分析主要有三个步骤:5 G7 M5 K" T5 d z. p" I8 N─ 第一、利用单变项和双变项分析来检视各个准备纳入复回归分析的变项是否符合OLS线性回归分析的基本假定。
─ 选定回归模式,并评估所得到的参数估计和适合度检定(goodness of fit)。
2 L! ]2 Z3 o, A$ J* g─ 在我们认真考虑所得到的回归分析结果前,应做残余值(residuals)之诊断分析(diagnosis)。
但通常我们是先确定回归模式之设定(specification)是否恰当后,才会做深入之残余值分析。
3、回归分析的第一步是一一检视每个即将纳入回归分析模式的变项。
首先,我们必须先确定应变项有足够的变异(variability),而且是接近常态分配(回归系数的估计并不要求应变项是常态分配,但对此估计做假设测定时,则是要求残余值应为常态分配。
而应变项离开常态分配的状态很远时,残余值不是常态分配的可能性增大)。
其次,各自变项也应该有适当的变异,并且要了解其分配之形状和异常的个案(outlying cases;outliers)。
7 t% `+ K3 y2 Y9 P% o7 n1 ^-Y我们可用直方图(histogram)和Normal P-P(probability plot)图等来测定应变项是否拒绝其为常态分配的假设,以及是否有异常之个案。
同样的,我们可用直方图和其它单变项之统计来检视各个自变项之分配形状、程度,以及异常个案等。
使用spss进行多元回归分析
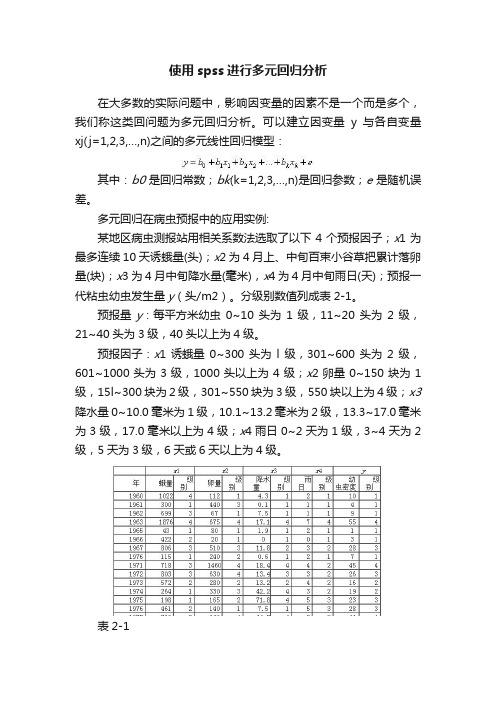
使用spss进行多元回归分析在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。
可以建立因变量y与各自变量xj(j=1,2,3,…,n)之间的多元线性回归模型:其中:b0是回归常数;bk(k=1,2,3,…,n)是回归参数;e是随机误差。
多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y(头/m2)。
分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1数据保存在“DATA6-5.SAV”文件中。
1)准备分析数据在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼虫密度”变量,并输入数据。
再创建蛾量、卵量、降水量、雨日和幼虫密度的分级变量“x1”、“x2”、“x3”、“x4”和“y”,它们对应的分级数值可以在SPSS数据编辑窗口中通过计算产生。
或者打开已存在的数据文件“DATA6-5.SAV”。
2)启动线性回归过程单击SPSS主菜单的“Analyze”下的“Regression”中“Linear”项,将打开如图2-2所示的线性回归过程窗口。
图2-2 线性回归对话窗口3) 设置分析变量设置因变量:用鼠标选中左边变量列表中的“幼虫密度[y]”变量,然后点击“Dependent”栏左边的向右拉按钮,该变量就移到“Dependent”因变量显示栏里。
运用SPSS建立多元线性回归模型并进行检验---副本[1]
![运用SPSS建立多元线性回归模型并进行检验---副本[1]](https://img.taocdn.com/s3/m/919a8eb504a1b0717fd5ddc7.png)
计量经济学实验报告一.实验目的:1、学习和掌握用SPSS做变量间的相关系数矩阵;2、掌握运用SPSS做多元线性回归的估计;3、用残差分析检验是否存在异常值和强影响值4、看懂SPSS估计的多元线性回归方程结果;5、掌握逐步回归操作;6、掌握如何估计标准化回归方程7、根据输出结果书写方程、进行模型检验、解释系数意义和预测;二.实验步骤:1、根据所研究的问题提出因变量和自变量,搜集数据。
2、绘制散点图和样本相关阵,观察自变量和因变量间的大致关系。
3、如果为线性关系,则建立多元线性回归方程并估计方程。
4、运用残差分析检验是否存在异常值点和强影响值点。
5、通过t检验进行逐步回归。
6、根据spss输出结果写出方程,对方程进行检验(拟合优度检验、F检验和t检验)。
7、输出标准化回归结果,写出标准化回归方程。
8、如果通过检验,解释方程并应用(预测)。
三.实验要求:研究货运总量y与工业总产值x1,农业总产值x2,居民非商品支出x3,之间的关系。
详细数据见表:(1)计算出y,x1,x2,x3的相关系数矩阵。
(2)求y关于x1,x2,x3的三元线性回归方程(3)做残差分析看是否存在异常值。
(4)对所求方程拟合优度检验。
(5)对回归方程进行显著性检验。
(6)对每一个回归系数做显著性检验。
(7)如果有的回归系数没有通过显著性检验,将其剔除,重新建立回归方程,在做方程的显著性检验和回归系数的显著性检验。
(8)求标准化回归方程。
(9)求当x1=75,x2=42,x3=3.1时y。
并给出置性水平为99%的近似预测区间。
(10)结合回归方程对问题进行一些基本分析。
四.绘制散点图或样本相关阵相关性货运总量工业总产值农业总产值 居民非商品支出货运总量Pearson 相关性1.556 .731*.724*显著性(双侧).095.016 .018 N10 10 10 10 工业总产值Pearson 相关性.556 1.155 .444 显著性(双侧) .095 .650.171 N10 11 11 11 农业总产值Pearson 相关性.731*.155 1.562 显著性(双侧) .016 .650 .072N10 11 11 11 居民非商品支出 Pearson 相关性.724* .444 .562 1显著性(双侧).018 .171 .072 N10111111*. 在 0.05 水平(双侧)上显著相关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
采用SPSS多元Logistic回归分析方法对船舶碰撞风险量化
摘要:本文将采用SPSS多元Logistic回归分析方法,以1993-2013年英国港口海
域船舶碰撞事故调查资料进行统计后,论证人为因素对于后果严重度的影响。
关键词:SPSS多元Logistic回归分析方法;船舶风险;量化
一、船舶碰撞事故后果等级划分
(一)国内水上交通事故分级
船舶交通事故损失程度常常作为评估碰撞事故等级的标准,我国交通运输部《水上交通事故统计办法》中规定的水上交通事故分级标准表,根据伤亡人数、
造成的直接经济损失和水域环境污染情况等要素,将事故分为特别重大事故、重
大事故、较大事故、一般事故和小事故五个等级。
(二)国际水上交通事故分类
国际海事组织(IMO)按照事故后果的严重程度将事故分成三个级别,重大
事故、大事故和一般事故。
(三)本文碰撞后果等级划分
从上述表格可以看出,国内外常常把事故分为四个等级,而单纯针对碰撞事
故来说,事故中往往船舶受损较多,而人员伤亡较少。
因此,本文将碰撞后果分
为四个等级,分级标准主要为船舶受损的严重程度。
二、评测指标确定
由上可见,国内外,关于事故等级的划分标准不尽相同,而单纯针对碰撞事
故来说,事故中常是船舶受损较多,而人员伤亡较少。
如果出现人员死亡的情况,船体一般是受到很大的撞击,损坏比较严重,如果漏油造成严重的环境污染,那
么通常也是船体受损严重所引起的,所以本文主要将从船体受损程度的角度来选
定事故后果的评测指标。
本文将基于前人的研究成果,选取人的因素、船舶的设备因素和环境因素共
3个主要指标对英国船舶碰撞后果进行评估。
(一)人的因素
据保守统计,由人的因素直接或间接导致的船舶碰撞事故频发不断。
本文通
过对众多船舶碰撞事故调查报告的分析与统计,将事故中人的因素分为6个等级,并按权重进行划分。
对应的模型中参数值如表1所示。
表1人的因素参数表
(二)船舶的设备因素
船舶的设备性能不同,船舶碰撞事故的后果也有差别。
本文通过对众多船舶
碰撞事故调查报告的分析与统计,将事故中船舶的设备因素分为5个等级,并按
权重进行划分。
对应的模型中参数值如表5所示。
表5 船舶的设备因素参数表
(三)环境因素
恶劣的自然环境不利于船舶航行,易导致不同程度的船舶碰撞后果。
本文通
过对众多船舶碰撞事故调查报告的分析与统计,将事故中环境因素分为5个等级,并按权重进行划分。
对应的模型中参数值如表6所示。
表6环境因素参数表
环境因素环境因素无明显影响两船交汇处海况不良
模型中取值 0 1
环境因素交通密度高
助航环境不良大风浪或大潮汐流
模型中取值 2 3
环境因素能见度不良
自然环境不良
模型中取值 4
(四)事故后果等级
将四种事故后果等级分为:事故后果={轻微、中等、较严重、严重}={1、2、
3、4、5、6}。
三、模型的数据来源
为了保证本文数据的准确性以及样本的广泛性,本文主要查找了英国安全委
员会、英国海事调查委员会,获得部分事故报告资料。
四、模型的建立
(一)输入数据
本文采用SPSS软件进行多元Logistic回归分析。
首先将收集到的数据按上文
的分类方法依次分组输入到SPSS中。
(二)多元Logistic回归分析
打开多元Logistic回归分析对话框。
在该对话框中,因变量栏中选择后果分类,因子栏中选入人因等级分类、船舶的设备因素等级分类、环境因素等级分类
这六项,选择确定即可输出数据。
(三)多元Logistic回归输出
对104组数据进行多元Logistic回归分析,得出观察值处理摘要、模式适合
度信息、假R平方及概似比测试。
卡方统计资料是-2对数概似值最终模型和降级模型之间的差异。
降级模型透
过省略最终模型中的效果而形成。
虚无假设是指该结果的所有参数都为0。
a.此降级模型相等于最终模型,因为省略效果不会增加自由度。
b.在赫氏(Hessian)矩阵中发现非预期的异常值。
这指示应排除某些预测值变
量或应合并某些种类。
五、多元Logistic回归分析结果及验证
根据多元回归分析规定,模型拟合中的显著水平越低说明模型拟合越好,似
然比检验中的显著水平小于0.05即为有影响的因素,该因素可参与到概率计算。
通过表8 概似比测试可得,模型拟合显著水平为0.000,因此本次研究显著水平
达到要求。
通过概似比测试比较,可以得到人的因素对于后果等级的影响最大,其次是
船舶设备的因素,最后是环境因素。
结果表明,在所研究的英国海峡的碰撞事故中,主要由人的综合因素(包括操作程序不当或违规操作、人员沟通不充分、工
作制度不合理等)所导致的碰撞事故后果最为严重,主要由船舶设备(包括导灯、号型或信号显示不当、航海资料不全、通讯系统故障或失灵等)所导致的碰撞事
故后果一般,主要由环境因素(包括大风浪或大潮汐流、能见度不良、自然环境
不良等)导致的碰撞事故后果最轻。
参考文献:
【1】中华人民共和国交通运输部.水上交通事故统计办法.中华人民共和
国交通运输部令2014年第15号,2014.
【2】IMO. Guidelines for formal safety assessment for use in the IMO rule-making process. International Maritime Organization(IMO), London, 2002.
【3】丛叶盛.长兴岛港水域船舶碰撞风险分析研究:(硕士学位论文).大连:大连海事大学,2015.。
