2010年中考数学模拟考试试卷 七
2010年中考模拟数学卷参考答案

2010年中考模拟试卷 数学参考答案及评分标准三、解答题(本题有8小题,第17~19题每题6分,第20~21题8分,第22~23题每题10分,第24题12分,共66分) 17、(本题满分6分) 解:∵方程2233x mx x -=--无解∴方程2233x mx x -=--有增根x=3------------2分∴方程两边同乘以(x-3),得:26x m -=------------2分∴当x=3时,m =分 18、(本题满分6分)解:过C 点作BA 的延长线交于点E ,------------1分∵AB =AC =10,∠B =022.5 ∴∠EAC =045∴△EAC 为等腰直角三角形------------1分设AE =EC =X,则AB =AC =10∴x =∴111022S A B E C ∆=⋅=⨯⨯=≈35.42m ------------2分又∵53.610⨯2cm =362m >35.42m ------------1分 ∴预订草皮够用------------1分19、(本题满分6分)解:答案不唯一,酌情给分。
20、(本题满分8分)解:(1)18 0.55------------各1分(2)图略--------------共4分(虚设组不设各扣1分)(3)0.55±0.1均为正确------------2分 21、(本题满分8分) 解:(1)正确的结论:①②③------------2分(2)错误理由:当a >0时,只有1x >2x >0或2x <1x <0时,1y <2y 而2x <0<1x 时,1y >2y ------------4分 改正:当a >0时,在同一象限内,函数a y x=,y 随x 增大而减小-----2分22、(本题满分10分)解:(1)如右图------------共6分(030,045角,线段a 各1分,余酌情给分)(2)设AB =x,则R t △ABC 中,OB =x ,由题意得:6+ x ------------1分得,1)x =≈8米------------2分 答:旗杆高度约为8米。
2010年河南中考数学模拟试卷及答案
2010年河南中考数学模拟试卷及答案一、选择题(每小题3分,共18分)1. 如图,两温度计读数分别为我国某地今年2月份某天的最低气温与最高气温,那么这天的最高气温比最低气温高 【 】 A .5°C B .7°C C .12°C D .-12°C2. 某市2010年第一季度财政收入为46.40亿元,用科学记数法(结果保留两个有效数字)表示为 【 】A.81040⨯元 B.9100.4⨯元 C.9104⨯元 D.8104⨯元3. 下列说法正确的是 【 】 A .一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖。
B .一组数据2,3,3,6,8,5的众数与中位数都是3。
C .“打开电视,正在播放关于世博会的新闻”是必然事件。
D .若甲组数据的方差31.02=甲S ,乙组数据的方差02.02=乙S ,则乙组数据比甲组数据稳定。
4.一个无盖的正方体盒子的平面展开图可以是下列图形中的 【 】.A.只有图① B.图③、图② C.图②、图③ D.图①、图③5. 如图,一次函数y1=x-1与反比例函数y2=x 2的图像交于点A (2,1),B (-1,-2),则使y1>y2的x的取 值范围是 【 】 A. x>2 B. x>2 或-1<x<0 C. -1<x<2 D. x>2 或x<-16如图为二次函数y=ax 2+bx +c 的图象,在下列说法中:①ac <0; ②方程ax 2+bx +c=0的根是x 1= -1, x 2= 3③a +b +c >0 ④当x >1时,y 随x 的增大而增大。
把正确的都选上应为 【 】 A①② B.①②③ C.①②④ D.①②③④二、填空题(每小题3分,共27分) 7. .25的算术平方根是 . .8. 将一副直角三角尺如图放置,已知AE BC ∥,则AFD ∠的度数是 . . 9. 某药品原价每盒25元,为了响应国家解决老百姓看病贵的号召,经过连续16元,则该药品平均每次降价的百分率是______两次降价,现在售价每盒10如图:平行四边形ABCD 的周长为16, AC 、BD相③② ①BA 23题图交于点O ,OE ⊥AC 交AD 于E ,则△DCE 的周长为 . 11. 如图,ABC △内接于⊙O ,30C ∠=,2AB =,则 ︵ AB 长(结果保留π)______.12.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其它完全相同.小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是 . .13、正方形ABCD 在坐标系中的位置如图所示,将正方形ABCD 绕D 点顺时针旋转90°后,B 点的坐标为 .14.如图,直角梯形纸片ABCD ,AD ⊥AB ,AB =8,AD =CD =4,点E 、F 分别在线段AB 、AD 上,将△AEF沿EF 翻折,点 A 的落点记为P .当P落在直角梯形ABCD 内部时,PD 的最小值等于 .15.在ABC △中,AB AC =,以AB 为直径的O ⊙交BC 于点MMN AC ⊥ 于点N .若1202BAC AB ∠==°,,则图中阴影部分的面积(结果保留π)是 .二、解答题(本大题8个小题,共75分)16.(8分)解方程:22111x x x -=--17.(9分)如图,正方形ABCD 中,E 是AD 边上一点,且BE=CE ,BE 与对角线AC 交于点F ,联结DF ,交EC 于点G .(1)求证:∠ABF =∠ADF ;(2)求证:DF ⊥EC .18.(9分)2008年北京奥运会后,同学们为了解某品牌A ,B 两种型号冰箱的销售状况,王明对其专卖店开业以来连续七个月的销售情况进行了统计,并将得到的数据制成如下的统计表:月份一月 二月 三月 四月 五月 六月 七月 A 型销售量(单位:台) 10 14 17 16 13 14 14 B 型销售量(单位:台)6101415161720(1)完成下表(结果精确到0.1):平均数 中位数 方差 A 型销售量 14 B 型销售量1418.6图1 30︒30︒B D A C 图3C AD B 图2 D 1C 1B 1C A D B 图4CA DB (2)请你根据七个月的销售情况在图中绘制成折 线统计图,并依据折线图的变化趋势,对专卖店今 后的进货情况提出建议(字数控制在20~50字).l9.(9分) 某校部分住校生,放学后到学校锅炉房打水,每人接水2升,他们先同时打开两个放水笼头,后来因故障关闭一个放水笼头。
2010年中考模拟试卷 数学

2010年中考模拟试卷 数学考生须知:1.本试卷分试题卷和答题卷两部分。
满分120分,考试时间100分钟。
2.答题前,必须在答题卷的左上角填写校名、姓名和班级、学号、试场号、座位号。
3.所有答案都必须做在答题卷标定的位置上,务必注意试题序号和答题序号相对应。
4.考试结束后,上交试题卷和答题卷。
试 题 卷 一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内,注意可以用多种不同的方法来选取正确答案。
1、(原创)已知△ABC 中,∠C =90︒,SinA=21,则tanB 的值是(▲)A. 33 B. 2 C. 1 D. 32、萧山历史上规模最大、投资最多、涉及面最广的交通基础设施工程 “12881”工程就是争取用三年时间,在全区范围内推进“一桥两隧八纵八横一绕”工程建设,完成交通道路投资428.6亿元,新建、改建道路273公里,到2011年基本形成“城乡贯通、区间快速、主次分明、东网加密”的全区交通道路网络体系。
将428.6亿元用科学记数法表示为(▲)A .910286.4⨯元 B 、11104286.0⨯元 C 、1010286.4⨯元 D 、10104286.0⨯元3、图中BOD ∠的度数是(▲) A 、550 B 、1100 C 、1250 D 、15004、(原创)将211292.0128,,,,化简成最简二次根式后,随机抽取其中一个根式,与 2 被开方数相同的概率是(▲)A.15B.25C.35D.455、(改编)若干杯奶茶摆放在桌子上,实物图片左边所给的是它的三视图,则这一堆奶茶共有(▲)A.5杯B. 6杯C.9杯D.12杯D(第8题)(第5题)6、(原创)已知),),(,2211(yxyx是反比例函数xy1-=图象上两点,且210xx,则21yy-的值是(▲)A.正数B.负数C.非正数D.非负数7、小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能...是(▲)A B C D8、如图,已知矩形ABCD中,AB=8,BC=π5.分别以B、D为圆心,AB为半径画弧,两弧分别交对角线BD于点E、F,则图中阴影部分的面积为(▲)A.π4 B.π5 C.π8 D.π109、(原创)如图是一次函数y=kx+b和y=mx+n的图像,则不等式组的解是(▲)A.x≤1B.x≤1或 x≥4C.1≤x≤4D.0≤x≤4y10、(改编)如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,2)且平行于x轴的直线l2的一个交点;……按照这样的规律进行下去,点A n的坐(▲)A.(1,12++nn) B.(nn,12+) C.(nn,2) D.(nn,12-)二、认真填一填(本题有6个小题,每小题4分,共24分)要注意认真看清题目的条件和要填写的内容,尽量完整地填写答案。
2010年中考模拟数学试卷和答案

2010年中考模拟试卷数 学考生须知:1.本试卷分试题卷和答题卷两部分,满分120分,考试时间100分钟 .2.答题时,应该在答题卷指定位置内写明校名,姓名和准考证号 .3.所有答案都必须做在答题卷标定的位置上,请务必注意试题序号和答题序号相对应 .4.考试结束后,上交试题卷和答题卷试题卷一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的 .注意可以用多种不同的方法来选取正确答案 .1. 如果0=+b a ,那么a ,b 两个实数一定是( )A.都等于0B.一正一负C.互为相反数D.互为倒数2. 要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是( )A.调查全体女生B.调查全体男生C.调查九年级全体学生D.调查七、八、九年级各100名学生 3. 直四棱柱,长方体和正方体之间的包含关系是( )4. 有以下三个说法:①坐标的思想是法国数学家笛卡儿首先建立的;②除了平面直角坐标系,我们也可以用方向和距离来确定物体的位置;③平面直角坐标系内的所有点都属于四个象限 .其中错误的是( )A.只有①B.只有②C.只有③D.①②③ 5. 已知点P (x ,y )在函数x xy -+=21的图象上,那么点P 应在平面直角坐标系中的( )A.第一象限B. 第二象限C. 第三象限D. 第四象限6. 在一张边长为4cm 的正方形纸上做扎针随机试验,纸上有一个半径为1cm 的圆形阴影区域,则针头扎在阴影区域内的概率为( )A.161 B.41 C.16π D.4π 7. 如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x ,那么x 的值( ) A.只有1个 B.可以有2个 C.有2个以上,但有限 D.有无数个8. 如图,在菱形ABCD 中,∠A=110°,E ,F 分别是边AB 和BC的中点,EP ⊥CD 于点P ,则∠FPC=( ) A.35° B.45° C.50° D.55°9. 两个不相等的正数满足2=+b a ,1-=t ab ,设2)(b a S -=,则S 关于t 的函数图象是( )A.射线(不含端点)B.线段(不含端点)C.直线D.抛物线的一部分10. 某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第k 棵树种植在点)(k k k y x P ,处,其中11=x ,11=y ,当k≥2时,⎪⎪⎩⎪⎪⎨⎧---+=----+=--]52[]51[])52[]51([5111k k y y k k x x k k k k ,[a ]表示非负实数a 的整数部分,例如[2.6]=2,[0.2]=0 .按此方案,第2009棵树种植点的坐标为( )A.(5,2009)B.(6,2010)C.(3,401) D (4,402)二. 认真填一填(本题有6个小题,每小题4分,共24分)要注意认真看清楚题目的条件和要填写的内容,尽量完整地填写答案 11. 如图,镜子中号码的实际号码是___________ .12. 在实数范围内因式分解44-x = _____________________ . 13. 给出一组数据:23,22,25,23,27,25,23,则这组数据的中位数是___________;方差(精确到0.1)是_______________ .14. 如果用4个相同的长为3宽为1的长方形,拼成一个大的长方形,那么这个大的长方形的周长可以是______________ .15. 已知关于x 的方程322=-+x mx 的解是正数,则m 的取值范围为______________ . 16. 如图,AB 为半圆的直径,C 是半圆弧上一点,正方形DEFG 的一边DG 在直径AB 上,另一边DE 过ΔABC 的内切圆圆心O ,且点E 在半圆弧上 .①若正方形的顶点F 也在半圆弧上,则半圆的半径与正方形边长的比是______________;②若正方形DEFG 的面积为100,且ΔABC 的内切圆半径r =4,则半圆的直径AB = __________ .三. 全面答一答(本题有8个小题,共66分)解答应写出文字说明、证明过程或推演步骤 .如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以 . 17. (本小题满分6分)如果a ,b ,c 是三个任意的整数,那么在2b a +,2c b +,2ac +这三个数中至少会有几个整数?请利用整数的奇偶性简单说明理由 .18. (本小题满分6分)如图,,有一个圆O 和两个正六边形1T ,2T .1T 的6个顶点都在圆周上,2T 的6条边都和圆O 相切(我们称1T ,2T 分别为圆O 的内接正六边形和外切正六边形) . (1)设1T ,2T 的边长分别为a ,b ,圆O 的半径为r ,求a r :及b r :的值; (2)求正六边形1T ,2T 的面积比21:S S 的值 .如图是一个几何体的三视图 . (1)写出这个几何体的名称;(2)根据所示数据计算这个几何体的表面积;(3)如果一只蚂蚁要从这个几何体中的点B 出发,沿表面爬到AC 的中点D ,请你求出这个线路的最短路程 .20. (本小题满分8分)如图,已知线段a .(1)只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC ,以AB 和BC 分别为两条直角边,使AB=a ,BC=a 21(要求保留作图痕迹,不必写出作法); (2)若在(1)作出的RtΔABC 中,AB=4cm ,求AC 边上的高 .学校医务室对九年级的用眼习惯所作的调查结果如表1所示,表中空缺的部分反映在表2的扇形图和表3的条形图中.(1)请把三个表中的空缺部分补充完整;(2)请提出一个保护视力的口号(15个字以内).22. (本小题满分10分)如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P .(1)求证:AF=BE;(2)请你猜测∠BPF的度数,并证明你的结论.在杭州市中学生篮球赛中,小方共打了10场球 .他在第6,7,8,9场比赛中分别得了22,15,12和19分,他的前9场比赛的平均得分y 比前5场比赛的平均得分x 要高 .如果他所参加的10场比赛的平均得分超过18分 (1)用含x 的代数式表示y ;(2)小方在前5场比赛中,总分可达到的最大值是多少? (3)小方在第10场比赛中,得分可达到的最小值是多少?24. (本小题满分12分)已知平行于x 轴的直线)0(≠=a a y 与函数x y =和函数xy 1=的图象分别交于点A 和点B ,又有定点P (2,0) . (1)若0>a ,且tan ∠POB=91,求线段AB 的长; (2)在过A ,B 两点且顶点在直线x y =上的抛物线中,已知线段AB=38,且在它的对称轴左边时,y 随着x 的增大而增大,试求出满足条件的抛物线的解析式; (3)已知经过A ,B ,P 三点的抛物线,平移后能得到259x y =的图象,求点P 到直线AB 的距离 .2010年中考模拟试卷数学参考答案一、仔细选一选(每小题3分,芬30分)二. 认真填一填(本题有6个小题,每小题4分,共24分) 11、326512.)2)(2)(2(2-++x x x 13、23;2.614、14或16或2615、46-≠->m m 或16、①5∶2 ;②21三. 全面答一答(本题有8个小题,共66分) 17、(本题6分)至少会有一个整数 .因为三个任意的整数a,b,c 中,至少会有2个数的奇偶性相同,不妨设其为a ,b , 那么2ba +就一定是整数 . 18、(本题4分)(1)连接圆心O 和T 1的6个顶点可得6个全等的正三角形 . 所以r ∶a=1∶1;连接圆心O 和T 2相邻的两个顶点,得以圆O 半径为高的正三角形, 所以r ∶b=3∶2;(2) T 1∶T 2的连长比是3∶2,所以S 1∶S 2=4:3):(2=b a .19、(本题6分)(1) 圆锥; (2) 表面积S=πππππ164122=+=+=+r rl S S 圆扇形(平方厘米)(3) 如图将圆锥侧面展开,线段BD 为所求的最短路程 . 由条件得,∠BAB ′=120°,C 为弧BB ′中点,所以BD =33 .20、(本题8分)(1)作图如右,ABC ∆即为所求的直角三角形;(2)由勾股定理得,AC =52cm , 设斜边AC 上的高为h, ABC ∆面积等于h ⨯⨯=⨯⨯52212421,所以554=h 21、(本题8分)(1)补全的三张表如下:(表一)(2)例如:“象爱护生命一样地爱护眼睛!”等 . 22、(本题10分)(1)∵BA=AD ,∠BAE=∠ADF ,AE=DF , ∴△BAE ≌△ADF ,∴BE=AF ; (2)猜想∠BPF=120° .∵由(1)知△BAE ≌△ADF ,∴∠ABE=∠DAF .∴∠BPF=∠ABE+∠BAP=∠BAE ,而AD ∥BC ,∠C=∠ABC=60°, ∴∠BPF=120° . 23、(本题10分)(1)9191215225++++=x y ;(2)由题意有x x >++++9191215225,解得x <17,所以小方在前5场比赛中总分的最大值应为17×5-1=84分;(3)又由题意,小方在这10场比赛中得分至少为18×10 + 1=181分, 设他在第10场比赛中的得分为S ,则有81+(22+15+12+19)+ S ≥181 .解得S≥29,所以小方在第10场比赛中得分的最小值应为29分 .24、(本题12分)(1)设第一象限内的点B (m,n ),则tan ∠POB 91==m n ,得m=9n ,又点B 在函数xy 1=的图象上,得m n 1=,所以m =3(-3舍去),点B 为)31,3(,而AB ∥x 轴,所以点A (31,31),所以38313=-=AB ;(2)由条件可知所求抛物线开口向下,设点A (a , a ),B (a 1,a ),则AB =a1- a =38, 所以03832=-+a a ,解得313=-=a a 或 .当a = -3时,点A (―3,―3),B (―31,―3),因为顶点在y = x 上,所以顶点为(-35,-35),所以可设二次函数为35)35(2-+=x k y ,点A 代入,解得k= -43,所以所求函数解析式为35)35(432-+-=x y .同理,当a = 31时,所求函数解析式为35)35(432+--=x y ;(3)设A (a , a ),B (a 1,a ),由条件可知抛物线的对称轴为aa x 212+= .设所求二次函数解析式为:)2)1()(2(59++--=aa x x y .点A (a , a )代入,解得31=a ,1362=a ,所以点P 到直线AB 的距离为3或136.。
2010年中考模拟卷数学参考答案

2010年中考模拟卷数学参考答案二.认真填一填(本题有6个小题,每小题4分,共24分) 11.4(x+3)(x-3) 12.10≠≥x x 且 13.15414.6)1(2+--=x y 15. ︒20 16.)12,1222(22++++n nn n n n P n 三.全面答一答(本题有8个小题,共66分) 17.(本小题满分6分) 解:11)1()1)(1(1----+⨯+=a a a a a a a 原式…………………………………………………2分 =12111--=--a a a …………………………………………………2分 当a=-2时,原式=34…………………………………………………2分18.(本题满分6分) 解:可以做2)1(-n n 条直线…………………………………………………3分 理由如下:平面上有n 个点,两点确定一条直线。
取第一个点A 有n 种取法,取第二个点B(n-1)种取法,所以一共可连成n(n-1)条直线,但AB 和BA 是同一条直线,所以应除以2,得2)1(-n n 条直线 …………………………………………………3分 19.(本题满分6分)解:过点A 作BC 的垂线段,垂足为D ,则由题可知,∠BAD=30°,∠DAC=60° ∵∠BAD=30°,△ABD 为直角三角形, ∴BD=3223663==AD …………………………………………………2分同理可得3663==AD CD …………………………………………………2分∴楼高AB=2.152388≈…………………………………………………2分 20.(本小题6分)(1)21人 …………………………………………………1分(2)众数 90 中位数80…………………………………………………2分(3)从平均数和中位数的角度来比较,一班的成绩比二班好;从平均数和众数的角度来比较,一班的成绩不如二班;从B 级以上(包括B 级)的人数的角度来比较,一班的成绩比二班好。
2010年初中数学中考模拟试题答案
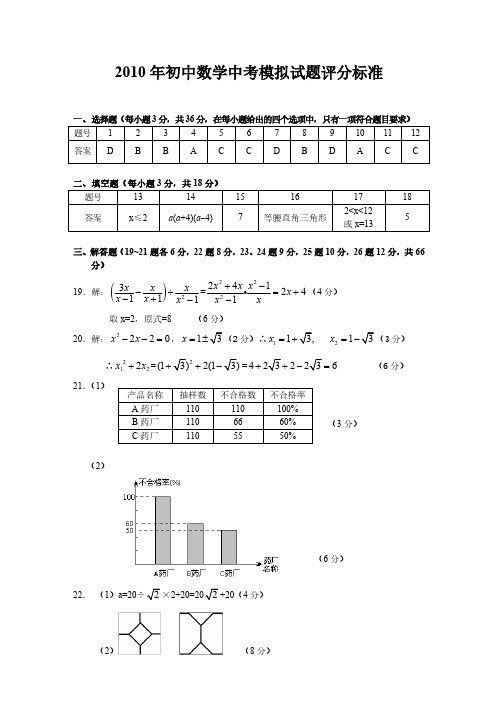
在 R t △ADE 中, EA =r, DE=6-r, AD=x,
∴ x 2 6 r 2 r 2 ,r= 1 x 2 +3,
∵ EF= EA, ∴AF=2DE,
即 y =2(6-r)=- 1 x 2 +6, (6 分) 6
D
E
C
∵AB∥CD,
∴∠AFE=∠CEF,
G
∴∠AEF=∠AFE, ∴AE=AF, ∵AE=EF,
A
B
F
( 图3 )
∴AE=AF=CE=CF, ∴△AEF 和△CEF 都是正三角形,
∴四边形 AECF 是菱形,且∠CEF=60°,
∴∠BCF=30°,
1
∴BF=
1
CF=
AF= 1 AB=2,
BC= 2 3 .(12 分)
223
②点 F 是 AB 的中点时, y =3,
图 D
E
C
H
G
A
( 图 1)
D
E
B F
C
G
A
B F
( 图2 )
1
即-
x 2 +6=3,∴ x = 3
2 .(8 分)
6
(3)(如图 3).
当x=2
3 时,
︵图 F 是AC的中点。此时,四边形 AECF 菱形.(9 分)
理由如下:
︵ ∵点 F 是AC的中点,∴∠AEF=∠CEF, AF=CF,
2.85×20+2.85×1.5×10+2.85×2×(x-30)=128.25,x=35(5 分)
∴调整后水费是:3.3×20+3.3×1.5×10+3.3×2×5=148.5(元)(6 分)
2010年中考数学模拟卷(7)

2010年中考数学模拟卷(7)一.选择题(本题有8小题,每题3分,计24分)1.6-的相反数是( )A .6-B .6C .61-D .61 2.下列运算正确的是( )A .624a a a =⋅B .23522=-b a b aC .()523a a =-D .()633293b a ab =3.如图所示,若数轴上的两点A 、B 表示的数分别为a 、b ,则下列结论正确的是( )A .021>-a b B .0>-b a C .02>+b a D .0>+b a4.为筹备班级的初中毕业联欢会,班长对全班学生爱吃哪几种水果作了民意调查.那么最终买什么水果,下面的调查数据中最值得关注的是( )A .中位数B .平均数C .众数D .加权平均数5.打开某洗衣机开关,在洗涤衣服时(洗衣机内无水),洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y (升)与时间x (分钟)之间满足某种函数关系,其函数图象大致为( )6.已知圆锥的底面半径为1cm ,母线长为3cm ,则其全面积为( )A .π2cmB .π32cmC .π42cmD .π72cm7.下列三视图所对应的直观图是( )8.用一把带有刻度的直尺,①可以画出两条平行的直线a 与b ,如图⑴;②可以画出∠AOB的平分线OP ,如图⑵所示;③可以检验工件的凹面是否为半圆,如图⑶所示;④可以量出一个圆的半径,如图⑷所示.这四种说法正确的个数有( )A .1个B .2个C .3个D .4个二.填空题(本题有9小题,每题3分,计27分)9.分解因式:()2212x x -+= . 10.不等式≤-125x ()342-x 的解集是 .11.在一个不透明的口袋中装有若干个只有颜色不同的球,如果口袋中装有4个红球,且摸出红球的概率为31,那么袋中共有 个球.12.梯形的中位线长为3,高为2,则该梯形的面积为 .13.如图,AC AB = ,要使ACD ABE ∆∆≌,应添加的条件是_________ (添加一个条件即可).14.如图,量角器外缘上有A 、B 两点,它们所表示的读数分别是80°、50°,则ACB ∠的度数为 .--1--15.直线42-=x y 与两坐标轴围成的三角形的面积为 平方单位长度.16.小龙加工240个零件与小明加工300个零件用的时间相同,已知小明每小时比小龙多加工10个,设小明每小时加工x 个零件,则可列方程为 .17.化简222211yxy x x y x y x ++÷⎪⎪⎭⎫ ⎝⎛++-的结果为 . 三.解答题(本题有3小题,每题12分,计36分)18.如图,在一个10×10的正方形DEFG 网格中有一个ABC ∆.⑴在网格中画出ABC ∆向下平移3个单位得到的111C B A ∆;⑵在网格中画出ABC ∆绕C 点逆时针方向旋转90°得到的222C B A ∆;⑶若以EF 所在的直线为x 轴,ED 所在的直线为y 轴建立直角坐标系,写出1A 、2A 两点的坐标.19.点D 是⊙O 的直径CA 延长线上一点,BD 是⊙O 的切线,切点为点B ,点E 是劣弧BC 上一点,︒=∠25BEA .求D ∠的度数.20.在一个不透明的盒子中放有四张分别写有数字1,2,3,4的红色卡片和三张分别写有数字1,2,3的蓝色卡片,卡片除颜色和数字外完全相同.⑴从中任意抽取一张卡片,求该卡片上写有数字1的概率;⑵将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率.四.解答题(本题有3小题,21题8分,22、23题各10分,计28分)21.如图为二次函数c bx ax y ++=2的图象,请你根据图中信息解答问题:⑴求抛物线的解析式及顶点坐标;⑵若点A (1,1y ),B (2-,2y ),C (2,3y )在其图象上,求出1y 、2y 、3y 的大小关系.--2--22. 姚明将带队来我市体育馆进行表演比赛,市体育局在策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x (张),总费用为y (元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)方案二:直接购买门票方式如图所示.解答下列问题:⑴方案一中,y 与x 的函数关系式为 ; 方案二中,当1000≤≤x 时,y 与x 的函数关系式为 ,当100>x 时,y 与x 的函数关系式为 ;⑵如果购买本场篮球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;⑶甲、乙两单位分别采用方案一、方案二购买本场篮球赛门票共700张,花去总费用计56000元,求甲、乙两单位各购买门票多少张.23.某园林为保护年久倾斜的古树,用一根木棍加以支撑,如图1所示,图2是其示意图,已知︒=∠60B ,︒=∠45ACB ,m BC 10=,求支撑点A 距地面的高度.四.解答题(本题有3小题,24题11分, 25,26题各12分,计35分)24.如图,梯形ABCD 中,BC AD //,cm CD AB 20==,cm AD 40=,︒=∠120D ,点P 、Q 同时从C 点出发,分别以s cm /2和s cm /1的速度沿着线段CB 和线段CD 运动,当Q 到达点D ,点P 也随之停止运动.设运动时间为t (s )⑴当t 为何值时,CPQ ∆与ABP ∆相似;⑵设APQ ∆与梯形ABCD 重合的面积为S (2cm ),求S 与t 的函数关系式,并写出自变量的取值范围.--3--25.已知点P 是矩形ABCD 边AB 上的任意一点(与点A 、B 不重合)⑴如图1,现将PBC ∆沿PC 翻折得到PEC ∆;再在AD 上取一点F ,将PAF ∆沿PF 翻折得到PGF ∆,并使得射线PE 、PG 重合,试问FG 与CE 的位置关系如何,请说明理由; ⑵在⑴中,如图2,连接FC ,取FC 的中点H ,连接GH 、EH ,请你探索线段GH 和线段EH 的数量关系,并说明你的理由;⑶如图3,分别在AD 、BC 上取点F 、C ',使得C BP APF '∠=∠,与⑴中的操作相类似,即将PAF ∆沿PF 翻折得到PGF ∆,并将C PB '∆沿C P '翻折得到C PE '∆,连接C F ',取C F '的中点H ,连接GH 、 EH ,试问⑵中的结论还成立吗?请说明理由.26.如图,在平面直角坐标系中,矩形OABC 的顶点A (0,3),C (1-,0).将矩形OABC 绕原点顺时针旋转90°,得到矩形C B A O '''.设直线B B '与x 轴交于点E ,与y 轴交于点F ,抛物线c x ax y ++=22的图象经过点C 、E 、F .解答下列问题:⑴分别求出直线B B '和抛物线所表示的函数解析式;⑵将EOF ∆沿直线EF 翻折,点O 落在点P 处,请你判断点P 是否在抛物线上,说明理由. ⑶将抛物线进行平移,使它经过点C ',求此时抛物线的解析式.--4--。
2010年中考模拟试卷 数学卷

2010年中考模拟试卷 数学卷(考试时间:100分钟,满分:120分)一、仔细选一选:(本大题有10小题,每小题3分,共30分.请选出每小题中一个符合题意的正确选项,不选、多选、错选,均不给分) 1. 观察下列银行标志,从图案看是轴对称图形的有……………………………………( )(A )1个 (B )2个 (C )3个 (D )4个 2、如图,BC∥DE,∠1=107°, ∠AED=67°, 则∠A 的大小是( ) A .25° B.35° C.40° D.60°3、左图是由八个相同小正方体组合而成的几何体,则其左视图是( ).4、有下列表述:①正数与负数的差不一定是正数;②a 一定不是负数; ③实数与数轴上的点一一对应;④平方根等于它本身的数是0或1;4;⑥若两数相乘,积为正,则这两个数一定具有相同的符号;其中正确的有( )个A. 1B. 2C. 3D. 45、如图,在菱形ABCD 中, ∠BAD =80°,AB 的垂直平分线交对角线AC 于点F ,E 为垂足,连接DF 。
则∠CDF 等于 ( ) A. 60° B. 65° C. 70 D. 80° 6、如图,平面直角坐标系中,在边长为1的正方形ABCD 的边上有一动点P 沿运动一周,则P 的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是( )A .B .C .D .(第03题图) A B C D7、下列说法正确的有 ( )(1)如图3(a ),可以利用刻度尺和三角板测量圆形工件的直径; (2)如图3(b ),可以利用直角曲尺检查工件是否为半圆形; (3)如图3(c ),两次使用丁字尺(CD 所在直线垂直平分线段AB )可以找到圆形工件的圆心;(4)如图3(d ),测倾器零刻度线和铅垂线的夹角,就是从P 点看A 点时仰角的度数.A .1个B .2个C .3个D .4个8、直角三角形纸片的两直角边长分别为6,8,现将ABC △如图那样折叠,使点A 与点B 重合,折痕为DE ,则tan CBE ∠的值是( ) A .247B.3 C .724D .139、如图,三个方格代表三位数的数字,且甲、乙两人分别将3、6的号码排列如下,然后等机会在两组1——9的9个号码中各选出一个数,将它们分别在两个空格中填上,则排出的数甲大于乙的概率是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(第12题图)图5B (第14题图) 2010年中考数学模拟考试试卷 七※ 考试时间120分钟 试卷满分150分一、选择题(下列各题的备选答案中,只有一个是正确的,请将正确答案的选项填在下表相应题号下的空格内.每小题3分,共24分)1.2 A.2±B. 2-C. 2D.42.3.若多项式mx x +2+4能用完全平方公式分解因式,则m的值可以是 A.4 B. -4 C. ±2 D ±44.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1 米处折断,树尖B 恰好碰到地面,经测量AB=2米,则树高为A.5米B.3米C. (5+1)米D. 3 米5.⊙O 1的半径是2 cm, ⊙O2的半径是5 cm ,圆心距是4 cm ,则两圆的位置关系是 A. 相交 B.外切 C.外离 D.内切6.已知一个多边形的内角和是外角和的4倍,则这个多边形是 A.八边形 B. 十二边形 C. 十边形 D. 九边形7.若(2,k )是双曲线xy 1=上的一点,则函数x k y )1(-=的图象经过 A.一、三象限 B.二、四象限 C.一、二象限 D.三、四象限8.已知二次函数(2≠++=a c bx ax y 4个结论,其中正确的结论是A. 0<abc C. 02=-b a D. 042<-ac b二、填空题(每小题3分,共24分)9.地球到太阳的距离为km,将km 用科学记数 表示为_________________ km.10.李红同学为了在中考体育加试中取得好成绩,每天自己在家里练习做一分钟仰卧起坐,妈妈统计了她一个星期做的次数:30、28、24、30、25、30、22.则李红同学一个星期做仰卧起坐的次数的中位数和众数分别是_________________.11.在平面直角坐标系中,点P(a-1,a)是第二象限内的点,则a 的取值范围是_________________12.如图所示,王老师想在一张等腰梯形的硬纸板ABCD 上剪下两个扇形,做成两个圆锥 形教具.已知AB=AD=30cm,BC=60cm,则她剪下后剩余纸板的周长是___________ cm (结果保留π).13.将红、黄、蓝三种除颜色不同外,其余都相同的球,放在不透明的 纸箱里,其中红球4个,蓝球3个,黄球若干个.若每次只摸一球(摸出后放回),摸出红球的概率是52,则黄球有_______________个.14.如图所示,平行四边形ABCD 的周长是18 cm ,对角线AC 、BD 相交于点O,若△AOD 与△AOB 的周长差是5 cm ,则边AB 的长是 15. 如图所示,直线a 经过正方形ABCD 的顶点A,分别过顶点B 、D 作 DE ⊥a 于点E 、BF ⊥a 于点F ,若DE=4,BF=3,则EF 的长为16.有一组数: 269,177,105,53,21,请观察它们的构成规律,用你发现 的规律写出第n (n 为正整数)个数为________________.三、解答题(本题16分,17题8分,18题8分) 17.(1)︳-33︱-︒30cos 2-12-22-+(3-π)C 第2题图 (第4题图)(第15题图)2A(2) 先化简,再求值.34)311(2+-÷+-x x x ,其中x=3.18.如图,已知△ABC 中,AB=AC,∠A=36°.(1)尺规作图:在AC 上求作一点P,使BP+PC=AB.(保留作图痕迹,不写作法)(2)在已作的图形中,连接PB,以点P 为圆心,PB 长为半径画弧交AC 的延长线于点E ,若BC=2cm ,求扇形PBE 的面积.四、解答题(本题20分,每小题 10分)19. 如图所示,甲乙两人准备了可以自由转动的转盘A 、B,每个转盘被分成几个面积相等的扇形,并在每个扇形内标上数字.(1)只转动A 转盘,指针所指的数字是2的概率是多少?(2)如果同时转动A 、B 两个转盘,将指针所指的数字相加,则和是非负数的概率是多少?并用树状图或表格说明理由。
(如果指针指在分割线上,那么重转一次,直到指针指向某一区域为止)20.红星中学开展了“绿化家乡,植树造林 ”活动,并对该校的甲、乙、丙、丁四个班 级种树情况进行了考察,并将收集的数据绘制了图①和图②两幅尚不完整的统计图. 请根据图中提供的信息,完成下列问题:(1)这四个班共种_______________棵树. (2)请你补全两幅统计图.(3)若四个班种树的平均成活率是90%,全校共种树2000棵,请你估计这些树中,成活的树约有多少棵?五、解答题(每题10分,共20分)21. 如图,张明站在河岸上的G 点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C 的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.8米,BG=1米,BG 平行于AC 所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求小船C 到岸边的距离CA 的长?(参考数据:73.13≈,结果保留两位有效数字).22.某旅游景点为了吸引游客,推出的团体票收费标准如下:如果团体人数不超过25人,每张票价150元,x C B GFD BA C30°第 3 页 共 7 页如果超过25人,每增加1人,每张票价降低2元,但每张票价不得低于100元,阳光旅行社共支付团体票价4800元,则阳光旅行社共购买多少张团体票?六、解答题(每题10分,共20分)23如图,已知矩形ABCD 内接于⊙O ,BD 为⊙O 直径,将△BCD 沿BD 所在的直线翻折后,得到点C 的对应点N 仍在⊙O 上,BN 交AD 与点M.若∠AMB=60°,⊙O 的半径是3cm. (1)求点O 到线段ND 的距离.(2)过点A 作BN 的平行线EF ,判断直线EF 与⊙O 的位置关系并说明理由.24.小张骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶.他距乙地的距离与时间的关系如图中折线所示,小李骑摩托车匀速从乙地到甲地,比小张晚出发一段时间,他距乙地的距离与时间的关系如图中线段AB所示.(1)小李到达甲地后,再经过___小时小张到达乙地;小张骑自行车的速度是___千米/小时. (2)小张出发几小时与小李相距15千米?(3)若小李想在小张休息期间与他相遇,则他出发的时间x 应在什么范围?(直接写出答案)25.如图,一个直角三角形纸片的顶点A 在∠MON 的边OM 上移动,移动过程中始终保持AB ⊥ON 于点B,AC ⊥OM于点A.∠MON 的角平分线OP 分别交AB 、AC 于D 、E 两点.(1)点A 在移动的过程中,线段AD 和AE 有怎样的数量关系,并说明理由.(2)点A 在移动的过程中,若射线ON 上始终存在一点F 与点A 关于OP 所在的直线对称,判断并说明以A 、D 、F 、E 为顶点的四边形是怎样特殊的四边形?(3)若∠MON=45°,猜想线段AC 、AD 、OC 之间有怎样的数量关系,并证明你的猜想.4-4-3-2-211-10-1-1-2-3-1-2-3B转盘A转盘开始-3八、解答题(本题14分)26.如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(-1,0),(5,0),(0,2).(1)求过A、B、C三点的抛物线解析式.(2)若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P运动的时间为t秒,(0≤t≤6)设△PBF的面积为S.能否成为直角三角形?若能,直接写出点F的坐标;若不能,请说明理由.2010年中考数学模拟考试试卷七参考答案一、选择题(每题3分,共24分)1.C2.B3. D4. C5.A6.C7.A8.B二、填空题(每题3分,共24分)9. 1.5×108 10.2830 11.0<a<1 12. 120013. 3 14. 17 15. 7 16.三、解答题(本题16分,17题10分,18题6分)17.(1)解:原式= 33-3-23-41+1 ……………3分=43……………5分(2)解:34)311(2+-÷+-xxx=34)3133(2+-÷+-++xxxxx………………1分=32+⨯+xx…………………3分………………4分………………………5分18. (1)…………3分如图射线BD即为所求………………………4分(2)如图:等腰△PAB, 等腰△BCP ………………………6分四、解答题(每题 10分,本题20分)19.解:(1)指针指向2的概率是……………2分(2)或表格法:1122+-nn21x第 5 页 共 7 页……………8分因为共有12种结果,每种结果出现的可能性相同,其中含有负数的结果有7种,所以和是负数的概率是 . ………10分 20.(12分(28分(3)90%×2000=1800(棵) 答:成活1800棵树. ………10分 五、解答题(每题10分,共20分)21. (1)解:(法一):过点O 作OG ⊥ND 于点G∴∠OGD=90°∵四边形ABCD 是矩形,∴∠C =90° 由翻折得∠N=∠C = 90°= ∠…………1分∴OG ∥BN ∵∠NBD=30°∴∠GOD=30° …………3分在Rt △OGD 中,cos30°= ,OD=3 ∴OG= …………5分 (法二):过点O 作OG ⊥ND 于点G则DG=NG …………1分 ∵OB=OD∴OG 是△BDN 的中位线∴OG= BN ∵四边形ABCD 是矩形, ∠C=90° ∴BD 是⊙O 直径 ∵OD=3∴BD=6 …………3分 在Rt △BND 中,cos30°= ∴BN= ∴OG= …………5分 (2)相切.证明:连接OA 交BN 与H.∵∠DBN=30°,由翻折得∠DBC=∠DBN=30°.∵∠ABC=90°∴∠ABO=60°. …………1分 ∵OA=OB,∴△ABO 是等边三角形 . …………3分 ∴∠AOB=60°.∴∠BHO=90°.又∵EF ∥BN , ∴∠FAH=90°.∴OA ⊥EF.∴EF 与⊙O 相切. …………5分22. 解:∵150×25=3750<4800∴购买的团体票超过25张. …………1分设共购买了x 张团体票 . …………2分 由题意列方程得 []4800)25(2150=--⨯x x ………5分x 2-100x+2400=0 …………6分解得 x 1=60 x 2=40 …………8分当x 1=60时,不符题意,舍去x 2=40符合题意 ∴x=40 …………9分答:共购买了40张团体票 . …………10分 六、解答题(每题10分,共20分)23. 解:过点B 作BE ⊥AC 于点E,延长DG 交CA 于点H,得Rt △ABE 和矩形BEHG ……………2 分在Rt △ABE 中, ∴BE=8,AE=6 . ……………4分∵DG=1.5,BG=1∴DH=DG+GH=1.5+8=9.5AH=AE+EH=6+1=7 ……………6分 在Rt △CDH 中, ∵∠C=∠FDC=30°, DH=9.5,tan30°= ∴ CH=9.53 ……………8分又∵CH=CA+7 即9.53=CA+7∴CA=9.15 ≈ 9.2米 ……………9分 答:CA 的长约是9.2米. ……………10分24.(1)1 15 ……………2分 (2)解:设EF 的解析式是111b x k y +=,AB 的解析式是222b x k y +=.根据题意得 ……………4分解得∴ ……………6分当21y y =时,即)36060(13515-=+-x x ,∴ . …………8分 11560b k +=1190b k +=228120b k +=2260b k +=151-=k 1351=b 602=k 3602-=b 127ODOG21BDBN 33236=⨯)(233cm 10,34===AB AE BE i )(233cm 135151+-=x y 5331=x CH DH360602-=x y6(3)3≤x ≤4 ……………10分 七、解答题(本题12分)25.(1) AE=AD ………2分 (2)菱形 ………3分 (法一):连接DF 、EF∵点F 与点A 关于直线OP 对称, E 、D 在OP 上,∴AE=FE,AD=FD . ………5分由(1)得AE=AD∴AE=FE=AD=FD∴四边形ADFE 是菱形 ………7分 (法二):连接AF 交DE 于点G,连接DF,EF.点F 与点A 关于直线OP 对称可知:AF ⊥DE, AE=FE, ………3分 ∴AG=FG, 又∵AE=AD ∴DG=EG∴四边形ADFE 是平行四边形 ………6分 ∵AF ⊥DE∴平行四边形ADFE 是菱形 ………7分 (3)OC= AC+AD ………8分 (法一):证明:连接EF.∵点F 与点A 关于直线OP 对称, ∴AO=OF∵AC ⊥OM, ∠MON=45°∴∠OAC=90° ∴∠ACO=∠MON=45°∴………10分 由(2)知四边形ADFE 是菱形 ∴EF ∥AB AD=EF ∵AB ⊥ON ∴∠ABC=90°∴∠EFC=∠ABC =90° ∵∠ACO=45° ∴∠ACO=∠CEF∴FC = EF =AD 又∵OC=OF+FC∴OC = AC+AD ………12分 (法2)证明:连接EF. ∵AC ⊥OM, ∠MON=45° ∴∠OAC=90° ∴∠ACO =∠MON =45°∴由(2)知四边形ADFE 是菱形 ∴EF ∥AB AD=EF ∵AB ⊥ON ∴∠ABC=90°∴∠EFC=∠ABC=90° ∵∠ACO=45°∴∠FEC = ∠ACO =45° ………9分 ∴FC=FE=AD ∵∠AOE=∠FOE∵OE=OE, ∠OAC=∠OFE=90°∵△OAE ≌△OFE ………11分 ∴OA=OF ∴OF=AC又∵OF+FC=OC∴AC+AD=OC ………12分 (法3)证明:延长EA 到G 点,使AG=AE ∵∠OAE=90°∴OA ⊥GE∴OG=OE ∴∠AOG=∠EOA∵∠AOC=45°,OP 平分∠AOC ∴∠AOE=22.5°∴∠AOG=22.5°∠G=67.5° ∴∠COG=∠G=67.5°∴CG=OC ………10分 由(1)得AD=AE∵AD=AE=AG∴AC+AD=OC ………12分 八、解答题(本题14分)26.解:(1)(法一)设抛物线的解析式为y=ax 2+bx+c(a ≠0),把A(-1,0),B(5,0)C(0,2)三点代入解析式得a-b+c=0 a= 25a+5b+c=0 解得 b= ∴ ……3分 c=2 c=2 (2当点P 在Rt △∵∠∴∠=∴y 52-58FG 258522++-=x x y第 7 页 共 7 页∵∠POC=∠FDP∴△CPO ∽△PFD ……………5分 ∴PF POFD =∵∴6分 ∴S △PBF 8分 当点P ∵△CPO 9分 ∴∴S △PBF 11分 (3)能12分t=1或14分说明:以上答案为参考答案,其他方法相应给分。
