简单几何模型
小学数学五大几何模型

小学数学五大几何模型知识框架一、等积模型DC BA①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、共角定理(鸟头定理)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.:():()ABC ADE S S AB AC AD AE =⨯⨯△△(1)(2)(3)(4)三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”): ①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.S 4S 3S 2S 1O DC BA梯形中比例关系(“梯形蝴蝶定理”):①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.A BC DO baS 3S 2S 1S 4四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCD ABCDEF G①AD AE DE AFAB AC BC AG ===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.五、共边定理(燕尾定理)有一条公共边的三角形叫做共边三角形。
小学数学几何必考五大模型

今天就为大家推荐一篇小学数学几何五大模型的内容。
一、等积 模①型等底等高的两个三角形面积相等;
AB
②两个三角形高相等,面积比等于它们的底之比;
两个三角形底相等,面积比等于它们的高之S比1 ;S2
典型例题
【例1】如图,正方形ABCD的边长为6,AE= 1.5,CF= 2.长
方形EFGH的面积为?
H
H
A
D
A
D
E
E
G
G
B FC
B
FC
【解析】连接DE,DF,则长方形EFGH的面积是三角形DEF面 积的二倍.
三角形DEF的面积等于正方,所形以的长面方积形减E去FG三H面个积三为角33. 形的面积,
【巩固】如图所示,正方形ABCD的边长为8厘米,长方形EBGF 的长BG为10厘米,那么长方形的宽为几厘米?
【解析】本题主要是让学生会运用等底等高的两个平行四边形面积 相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等 于与它等底等高的平行四边形面积的一半.
【巩固】如图所示,正方形ABCD的边长为8厘米,长方形EBGF 的长BG为10厘米,那么长方形的宽为几厘米?
证明:连接AG(我们通过△ABG把这两个长方形和正方形联系在一起)
∴ 正方形ABCD与长方形EFGB面积相等。长方形的宽=8 ×8÷10=6.4(厘
【例2】长方形ABCD的面积为36cm2,E 、F、G为各边 中点,H为AD边上任意一点,问阴影部分面积是多少 ?
【解析解,】H法C 一,:如寻下找图可:利用的条件,连接BH
如右图
66个常用几何模型分类汇编

66个常用几何模型分类汇编一、三角形模型1. 等边三角形:三条边长度相等的三角形。
2. 直角三角形:其中一个角为直角的三角形。
3. 等腰三角形:两条边长度相等的三角形。
4. 锐角三角形:三个内角都小于90度的三角形。
5. 钝角三角形:其中一个内角大于90度的三角形。
6. 等腰锐角三角形:两个角为锐角,且两条边长度相等的三角形。
7. 直角等腰三角形:一个角为直角,两条边长度相等的三角形。
8. 等腰钝角三角形:一个角为钝角,两条边长度相等的三角形。
9. 等边锐角三角形:三个内角都小于90度,三条边长度相等的三角形。
二、四边形模型10. 矩形:四个角都是直角的四边形。
11. 正方形:四条边长度相等,四个角都是直角的四边形。
12. 平行四边形:对角线相互平分,两对边平行的四边形。
13. 菱形:四个边长度相等,对角线相等的四边形。
14. 梯形:有且仅有一对对边平行的四边形。
15. 阳角梯形:其中一对边为直角的梯形。
16. 等腰梯形:有两边相等的梯形。
三、圆模型17. 圆:平面上所有到圆心距离相等的点的集合。
18. 圆环:由两个同心圆构成的几何图形。
四、多边形模型19. 六边形:有六条边的多边形。
20. 正六边形:六个角都是直角的六边形。
21. 正多边形:所有边和角都相等的多边形,如正三角形、正四边形等。
22. 不规则多边形:边长度或者角度不相等的多边形。
五、体积与表面积模型23. 正方体:六个面都是正方形的立体。
24. 长方体:六个面都是矩形的立体。
25. 正圆柱:底面为圆的圆柱。
26. 正圆锥:底面为圆的圆锥。
27. 正棱柱:底面为正多边形的棱柱。
28. 正棱锥:底面为正多边形的棱锥。
29. 正四面体:四个面都是三角形的立体。
30. 正六面体:六个面都是正方形的立体。
六、相似模型31. 相似三角形:对应角相等,对应边成比例的三角形。
32. 相似四边形:对应角相等,对应边成比例的四边形。
七、坐标几何模型33. 点:一个位置的坐标表示。
小升初平面几何常考五大模型

一、等积变换模型1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
三、蝴蝶定理模型(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的。
)四、相似三角形模型相似三角形:是形状相同,但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为由题知DC/GP=GC/PK,即DC/(DC-4)=(4+PK)/PK,令DC=a,PK=c,则a=4+c,则S△DEK=a^2+16+c*(4-c)/2+c^2-ac-a(4+a)/2=a^2/2+c^2/2-ac-2a+2c+16=(c+4)^2/2+c^2/2-c( c+4)-2(c+4)+2c+16=16。
1、图17是一个正方形地板砖示意图,在大正方形ABCD中AA1=AA2=BB1=BB2=CC1=CC2=DD1=D D2,中间小正方形 EFGH的面积是16平方厘米,四块蓝色的三角形的面积总和是72平方厘米,那么大正方形ABCD的面积是多少平方厘米?分析与解连AC和BD两条大正方形的对角线,它们相交于O,然后将三角形AOB放在D PC处(如图18和图19)。
已知小正方形EFGH的面积是16平方厘米,所以小正方形EFGH的边长是4厘米。
又知道四个蓝色的三角形的面积总和是72平方厘米,所以两个蓝色三角形的面积是72÷2=36平方厘米,即图19的正方形OCPD中的小正方形的面积是36平方厘米,那么这个正方形的边长就是6厘米。
八大类几何模型+60种解题技巧

一、常见的八大类几何模型在解决几何题目时,我们经常会遇到一些常见的几何模型。
这些模型包括但不限于:直角三角形、等腰三角形、等边三角形、直接相似三角形、等腰梯形、菱形、正方形和矩形。
1. 直角三角形直角三角形是一个内角为90度的三角形。
在求解直角三角形题目时,可以运用勾股定理、正弦定理、余弦定理等方法。
2. 等腰三角形等腰三角形是指两边相等的三角形。
在解决等腰三角形问题时,可以利用等角定理、等边角定理等。
3. 等边三角形等边三角形是指三边相等的三角形。
解决等边三角形问题时,可以利用等边三角形的性质,如高、中线等。
4. 直接相似三角形直接相似三角形是指对应角相等的两个三角形。
在对直接相似三角形进行解题时,可以利用相似三角形的性质,如边比例定理等。
5. 等腰梯形等腰梯形是指有两对对边相等的梯形。
解决等腰梯形问题时,可以运用梯形的性质以及各边的关系。
6. 菱形菱形是指四条边都相等的四边形。
在解决菱形问题时,可以利用菱形的性质,如对角线垂直平分、对角相等等。
7. 正方形正方形是指四条边相等且四个角均为直角的四边形。
解决正方形问题时,可以利用正方形的性质,如对角线相等、对角线垂直等。
8. 矩形矩形是指四边均为直角的四边形。
在解决矩形问题时,可以利用矩形的性质,如对角线相等、邻边互相垂直等。
二、60种解题技巧在解决几何题目时,我们还可以运用一些解题技巧来更快更准确地得出答案。
下面列举了60种解题技巧,以供参考。
1. 勾股定理2. 余弦定理3. 正弦定理4. 度角关系5. 弧度制下的两点间弧长相关关系6. 三角恒等变形7. 各角平分线8. 高度定理9. 中线定理10. 角平分线定理11. 等角定理12. 外角定理13. 内角定理14. 中位线定理15. 等腰三角形的性质16. 等边三角形的性质17. 相似三角形的三边对应比例关系18. 相似三角形的高度关系19. 相似三角形的边对应比例关系20. 相似三角形的面积关系21. 三角形高到底关系22. 三角形高乘底除以2的面积公式23. 三角形内切圆24. 三角形外接圆25. 正方形的性质26. 矩形的对角线关系27. 矩形的邻边互相垂直关系28. 长方形的面积公式29. 长方形的周长公式30. 菱形的性质31. 菱形对角线垂直平分32. 平行四边形的性质33. 平行四边形的对角线相等关系34. 平行四边形的对角互补35. 梯形的中位线关系36. 梯形的对角线垂直关系37. 梯形的高关系38. 圆的性质39. 圆周角的关系40. 圆心角的关系41. 切线关系42. 切线长定理43. 余弦定理的推广44. 余角关系45. 同位角关系46. 交叉线定理47. 锐角三角函数的关系48. 平行线夹角关系49. 余切函数的关系50. 同义形的面积公式51. 直角三角形斜边上的高52. 各角平分线角度关系53. 三角形中位线长度关系54. 三角形中位线平行长的关系55. 等角三角形三角函数的关系56. 三角形半周长乘外切圆内切圆面积关系57. 圆相关不等式58. 反证法59. 斜率性质60. 坐标系下平移关系解决几何问题时,首先要熟练掌握常见的八大类几何模型,然后灵活运用各种解题技巧,以便更加高效地解决问题。
完整版)初中数学经典几何模型

完整版)初中数学经典几何模型初中数学经典几何模型(模型即套路),是初中数学里的重要部分。
在解决几何证明问题时,我们可以运用这些模型,从而更加高效地解决问题。
人们常说几何很困难,其中一个难点就在于辅助线的运用。
为了更好地运用辅助线,我们需要把握定理和概念,并且刻苦加钻研,找出规律凭经验。
在绘制图形时,我们可以利用角平分线向两边作垂线,或者将图形对折来寻找对称关系。
利用角平分线的平行线,我们可以构造等腰三角形。
同时,我们也可以尝试将角平分线加上垂线,从而将三条线合为一条。
线段垂直平分线时,我们可以将线段向两端延长或缩短来验证线段的倍数与半数关系。
在三角形中,连接两中点可以构造出中位线,同时延长中线也可以等于中线。
对于平行四边形,我们可以找到对称中心等分点。
在梯形中,我们可以利用高线平移一腰来解决问题。
同时,平行移动对角线,补成三角形也是常见的方法。
当证明相似时,我们可以通过比线段,添加平行线来构造相似三角形。
在等积式子比例换时,寻找线段也是很关键的。
直接证明有困难时,我们可以通过等量代换来简化问题。
在计算圆的相关问题时,我们可以利用半径与弦长计算,或者利用勾股定理来计算切线长度。
同时,在判断是否为切线时,我们可以通过半径垂线来进行辨别。
在解决相交圆的问题时,我们需要注意作公共弦。
对于内外相切的两个圆,我们可以通过切点来构造公切线。
同时,我们也可以利用连心线来确定切点。
在绘制图形时,我们需要注意勿改变虚线的位置。
基本作图也是很关键的,我们需要熟练掌握。
在解题时,我们需要多动脑筋,经常总结方法。
同时,我们也需要注意方法的灵活性,不要盲目乱添线。
在选用分析综合方法时,我们需要根据具体情况进行选择。
最重要的是,我们需要虚心勤学,加以苦练,才能在数学上取得更好的成绩。
斜边上作高线,比例中项一大片。
--。
在斜边上作高线,可以得到比例中项一大片。
半径与弦长计算,弦心距来中间站。
--。
通过计算半径和弦长,可以得到弦心距。
小学奥数几何五大模型
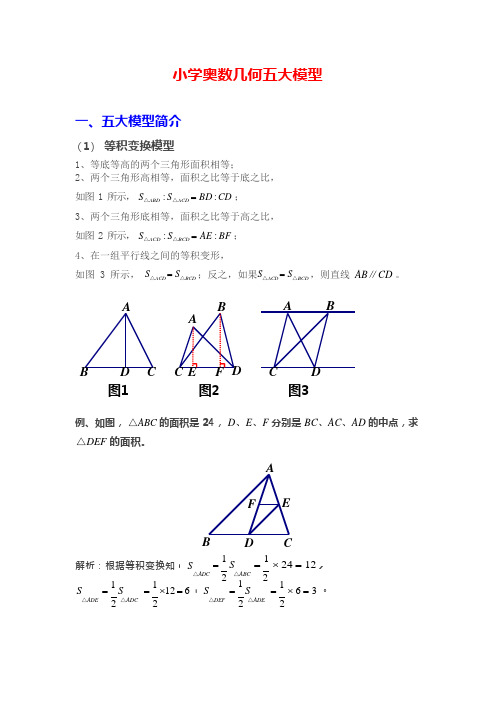
小学奥数几何五大模型一、五大模型简介(1) 等积变换模型1、等底等高的两个三角形面积相等;2、两个三角形高相等,面积之比等于底之比, 如图 1 所示, S △ABD : S △ACD = BD : CD ;3、两个三角形底相等,面积之比等于高之比, 如图 2 所示, S △ACD : S △BCD = AE : BF ;4、在一组平行线之间的等积变形,如图 3 所示, S △ACD = S △BCD ;反之,如果S △ACD = S △BCD ,则直线 AB ∥CD 。
图1图2图3例、如图, △ABC 的面积是 24, D 、E 、F 分别是 BC 、AC 、AD 的中点,求 △DEF 的面积。
解析:根据等积变换知, S = 1 S = 1 ⨯ 24 = 12 , S = 1S △ADC= 1 ⨯12 = 6 , S 2 △ABC = 1 S 2= 1 ⨯ 6 = 3 。
△ADE2 △ADC2 △DEF2 △ADE 2(2)鸟头模型(共角定理)1、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;2、共角三角形的面积之比等于对应角(相等或互补)两夹边的乘积之比。
如下图△ABC 中,D、E 分别是AB、AC 上或AB、AC 延长线上的点。
则有:S△ADES△ABC=AD ⨯AE。
AB ⨯AC我们现在以互补为例来简单证明一下共角定理!证明:如图,连接BE ,根据等积变换模型知,S△ADE: S△ABE=AD : AB 、S△ABE: S△CBE=AE : CE ,所以S△ABE:S△ABC=S△ABE:(S△ABE+S△CBE)=AE:AC。
因此S△ADE =S△ADE ⨯S△ABE =AD⨯AE=AD ⨯AE。
S△ABCS△ABES△ABCAB AC AB ⨯AC例、如图,在△ABC 中,点D 在BA 的延长线上,点E 在AC 上,且AB : AD = 5 : 2,AE : EC = 3: 2 ,△ADE 的面积为 12 平方厘米,求△ABC 的面积。
初中数学30种模型汇总(最全几何知识点)

10.等面积模型:D是BC的中点
20.平移构造全等
30.二次函数中平行四边形存在性模型
01.三线八角
同位角:找F型
内错角:找Z型
同旁内角:找U型
02.拐角模型
一.锯齿型
1
1
3
2
2
3
4
∠1+∠3=∠2
∠1+∠2=∠3 +∠4
左和=右和
二.鹰嘴型
1
1
2
3
3
2
∠1+∠3=∠2
∠1+∠3=∠2
鹰嘴+小=大
一.大小等边三角形
虚线相等,且夹角为60°
(全等,八字形)
四.大小等腰三角形(顶角为α)
结论:虚线相等,且夹角为α
(全等,八字形)
三. 大小等腰直角三角形
结论:虚线相等,且夹角为90°
(全等,八字形)
二.大小正方形
结论:虚线相等,且夹角为90°
(全等,八字形)
15.半角模型
条件:正方形ABCD
∠EDF=45°
证:EF=AE+CF
条件:CD=AD,∠ADC=90°
∠EDF=45°
∠A+∠C=180°
证明:EF=AE+CF
条件:AB=AD
∠B+∠D=180°
∠EAF=1 ∠BAD
2
证明:EF=BE+DF
条件:AB=AC,∠BAC=90°
∠DAE=45°
证明:DE2=BD2+CE2
△CEF为直角三角形
初中数学30种模型汇总
(最全几何知识点)
01.三线八角
02.拐角模型
03.等积变换模型
